Taylor展开(二)

3 复变函数的Taylor级数

3.1 收敛半径的问题

令\(F(x)=\dfrac{1}{1-x^2}\)，\(G(x)=\dfrac{1}{1+x^2}\)，我们考虑\(F(x),G(x)\)在点\(x_0\)处的幂级数展开.

预备：\(f(x)=\dfrac{1}{x+a}\)（\(a\in\R\)）在\(x_0\)（\(x_0\ne-a\)）处的幂级数展开：

因为\(f'(x)=(-1)\dfrac{1}{(x+a)^2}\)，\(f''(x)=(-1)(-2)\dfrac{1}{(x+a)^3}\)，可得\(f^{(n)}(x)=\dfrac{(-1)^nn!}{(x+a)^{n+1}}\)，所以 \[ \Align{ f(x) &=\sum_{k=0}^\infty \dfrac1{k!} \cdot \dfrac{(-1)^kk!}{(x_0+a)^{k+1}} \cdot (x-x_0)^k \\ &=\sum_{k=0}^\infty \dfrac{(-1)^k}{(x_0+a)^{k+1}}(x-x_0)^k &(x\in I) } \] 由比值法：\(\lim\limits_{k\to\infty}\abs{\dfrac{(-1)^{k+1}/(x_0+a)^{k+2}}{(-1)^k/(x_0+a)^{k+1}}}=\abs{\dfrac1{x_0+a}}\)，所以收敛半径\(|x_0+a|\). 注意到\(f(x)\)的奇点为\(x=-a\)，而\(|x_0+a|\)是展开点\(x_0\)到奇点\(a\)的距离，所以\(f(x)\)某一点展开的收敛半径是这点到奇点的距离.

因为\(F(x)=\dfrac{1}{1-x^2}=\dfrac12\pqty{\dfrac{1}{x+1}-\dfrac{1}{x-1}}\)，而\(\dfrac{1}{x+1}\)和\(\dfrac{1}{x-1}\)均可以在\(x_0\ne\pm1\)处幂级数展开，它们的收敛半径分别为\(|x_0+1|\)和\(|x_0-1|\)，所以\(F(x)\)在\(x_0\)的幂级数展开收敛半径为 \[ R=\min\set{|x_0+1|,|x_0-1|} \] 即\(x_0\)到最近的奇点的距离（\(F(x)\)有两个奇点\(-1,1\)）.

再看\(G(x)\)，它的分母在实数域上无法因式分解，但是在复数域上可以，所以裂项得到 \[ G(x)=\dfrac{1}{1+x^2}=\dfrac1{2\i}\pqty{\dfrac{1}{x-\i}-\dfrac{1}{x+\i}} \] 其中\(\dfrac{1}{x-\i}\)和\(\dfrac{1}{x+\i}\)在任意\(x_0\in\R\)处都可以幂级数展开，收敛半径为\(|x_0-\i|\)和\(|x_0+\i|\)，表示的就是实轴上一点\(x_0\)到虚数\(\pm\i\)的距离，根据勾股定理，这个距离为\(\sqrt{1+x_0^2}\)，所以\(G(x)\)的收敛半径 \[ R=\sqrt{1+x_0^2} \] 代入\(x_0=0\)，得到\(R=1\)，这也就解释了\(\S2.3\)最后留下来的问题. 而解决这个问题的过程中，我们把视野拓展到了复数域，这启示我们，如果要了解更多关于幂级数的知识，需要在一个更高的视角——复数域上讨论.

3.2 复变函数的Taylor级数

以复数为自变量和因变量的函数\(w=f(z)\)称为复变函数. 和实变函数\(y=f(x)\)一样，我们可以用Taylor级数逼近复变函数. 我们仍然采用任意阶导数相等的方法，可以得到和实变函数的Taylor级数形式相同的表达式： \[ f(z)=\sum_{k=0}^\infty\dfrac{f^{(k)}(z_0)}{k!}(z-z_0)^k \quad (z\in D) \] 其中\(z_0\)是复平面区域\(D\)中的某个点. 我们对函数\(w=f(z)\)的要求是它在\(D\)上任意阶可导. 如果一个函数\(w=f(z)\)在区域\(D\)内任意一点\(z_0\)的邻域\(|z-z_0|<r\)内都可以表示成Taylor级数形式，那么称\(w=f(z)\)在\(D\)上是解析的.

解析函数的定义是：\(f\)在区域\(D\)内任意一点的邻域上都可以表示成自身的Taylor级数. \(f\)可以是实变量的或者复变量的.

此外，我们可以仿照实变函数定义复变函数可导：存在极限\(\lim\limits_{z\to z_0}\dfrac{f(z)-f(z_0)}{z-z_0}\)（\(z,z_0\in D\)）. 复可导要求\(z_0\)以任意方式趋近\(z\)时极限都存在. 复可导是比实可导要强的条件.

• \(w=f(z)\)在区域\(D\)上每一点都可导（称之为全纯），那么它任意阶可导，而且解析.
• \(y=f(x)\)在开区间\(I\)上可导，甚至任意阶可导（光滑），但是仍然不能保证它解析.
  • 例如\(f(x)=\e^{-1/x^2}\)（另外规定\(f(0)=0\)）在\((-\infty,+\infty)\)上光滑，但在任何包含原点的区间上都不解析.

复变函数的Taylor级数形式上和实变函数的相同，计算起来也是相似的.

指数函数\(\displaystyle\e^z=\sum_{k=0}^\infty\frac{x^k}{k!}\)（\(z\in\C\)），下面展示了动画.

黄色的格线坐标系在\(w=\e^z\)变换后的结果，蓝色的是Taylor展开的结果. 随着项数的增加，蓝色的格线近乎和黄色格线重合.

对于一些解析的实变函数，我们可以利用它的Taylor展开直接将它们推广到复数域，上面的指数函数就是一个例子，其他的例如三角函数等基本初等函数也可以这样推广.

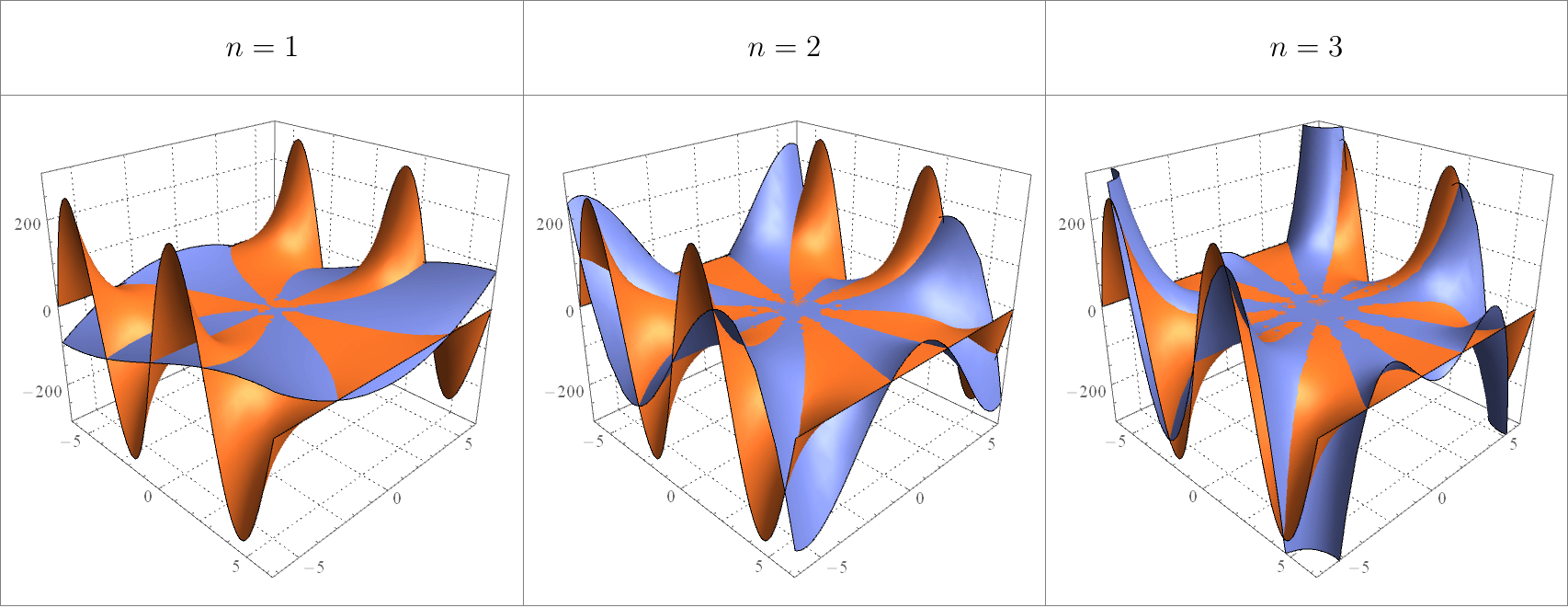
下图画出例了正弦函数\(w=\sin{z}\)的实部和它的Taylor多项式\(\displaystyle P_n(z)=\sum_{k=0}^{n}\frac{(-1)^{k}}{(2k+1)!}z^{2k+1}\)的实部，三幅图中，\(n\)分别等于\(1,2,3\).

3.3 收敛圆盘

复值的Taylor多项式\(S_n(z)=\sum_{k=0}^n a_kz^k\)自然也有收敛或发散一说. 实数级数的敛散性是由绝对值刻画的，复数级数的敛散性是由模刻画的：对于给定\(z=z_0\)，我们说\(S_n(z_0)\)收敛到\(A\)，如果\(S_n(z_0)\)在复平面上能够任意接近\(A\). 即不论正数\(\varepsilon\)有多小，总存在\(N\in\N_+\)，使得\(|S_n(z_0)-A|<\varepsilon\)对于\(n>N\)恒成立.

• 如果\(S_n(z_0)\)收敛到\(A\)，那么无穷级数\(S(z_0)=\sum_{k=0}^\infty a_kz_0^k=A\).
• 如果\(S_n(z_0)\)不收敛到任何复数，那么\(S(z_0)\)发散.

与实数幂级数的收敛区间是\(|x|<R\)一样，复数幂级数的收敛区域应当是\(|z|<R\). 由于复数乘方的性质， \[ |z^n|=|z|^n \] 所以幂级数在\(z_0\)收敛与否是由\(|z_0|\)决定的.

对于以原点为中心的幂级数\(\sum a_kz^k\)，存在圆\(|z|=R\)，使得幂级数在圆内处处收敛，在圆外处处发散. \(R\)称为收敛半径，\(|z|<R\)的所有点称为收敛圆盘(Disc of convergence)，\(|z|=R\)的所有点称为收敛圆.

• \(R\)可能为\(0\)，此时幂级数仅在\(z=0\)收敛；\(R\)也可能为\(+\infty\)，此时幂级数在整个复平面上收敛.

收敛半径的求法于实幂级数一样（参考Taylor展开(一)的F.2），但实际上在\(\S3.1\)的讨论中我们已经看到了另外一种方法：

定理：\(f(z)\)在\(z_0\)处幂级数展开的收敛半径是\(z_0\)到最近的一个奇点的距离.

• 奇点(Singularity)指的是函数没有良好定义的点，例如\(w=\dfrac1{z-1}\)的奇点是\(1\).

在之前的例子中，若将\(y=\dfrac{1}{1+x^2}\)拓展到复数域，则\(w=\dfrac{1}{1+z^2}\)在\(z=0\)处的收敛半径是它到最近的奇点（\(\pm\i\)）的距离\(1\).

下图为\(w=\dfrac{1}{1+z^2}\)的实部. 可以发现在\(z=\pm\i\)处图像不连续. 黄色平面\(\Re(z)=0\)和\(\Im(z)=0\)和图像曲面的交线分别为\(y=\dfrac1{1+x^2}\)和\(y=\dfrac{1}{1-x^2}\)的图像曲线，它们在\(x=0\)处Taylor展开（蓝色）收敛半径都是\(1\)，收敛圆如图白色圆圈.

4 应用

Taylor展开应用广泛，在物理中，常用来近似较为复杂的函数.

→ 小量近似

\((1+x)^{\alpha}\)（\(\alpha\in\R\)）在\(x=0\)处的Taylor展开： \[ \Align{ (1+x)^\alpha=1 +\dfrac{\alpha(1+0)^{\alpha-1}}{1!}x +\dfrac{\alpha(\alpha-1)(1+0)^{\alpha-2}}{2!}x^2 +\dots \quad (-1<x<1) } \] 取前两项，便得到了\((1+x)^\alpha\)在原点附近的二阶近似\(1+\alpha x\).

→ 单摆的运动

设单摆的摆角为\(\theta\)，摆长\(L\)（轻杆），重力加速度\(g\)，时间\(t\)，则仅在重力作用下，有 \[ g\sin{\theta}=-L\dv{^2\theta}{t^2} \] 注意到它是一个关于\(\theta\)的非线性微分方程（有一个\(\sin{\theta}\)），难解，如果取\(\sin{\theta}\)的Taylor展开前一项\(\theta\)近似，则有 \[ L\theta''+g\theta=0 \Rightarrow \theta=C_1\sin\pqty{\sqrt{\frac{g}{L}}t+C_2} \] 当初始角\(\theta_0\)足够小，单摆的运动可近似为周期\(T=2\pi\sqrt{\dfrac{L}{g}}\)的简谐运动. 分别取初始角\(\theta_0=\dfrac{\pi}{10},\dfrac{\pi}{3},\dfrac{8\pi}{9}\)，初始角速度为\(0\)，可以画出下面的\(\theta-t\)图像并和真实情况比对：

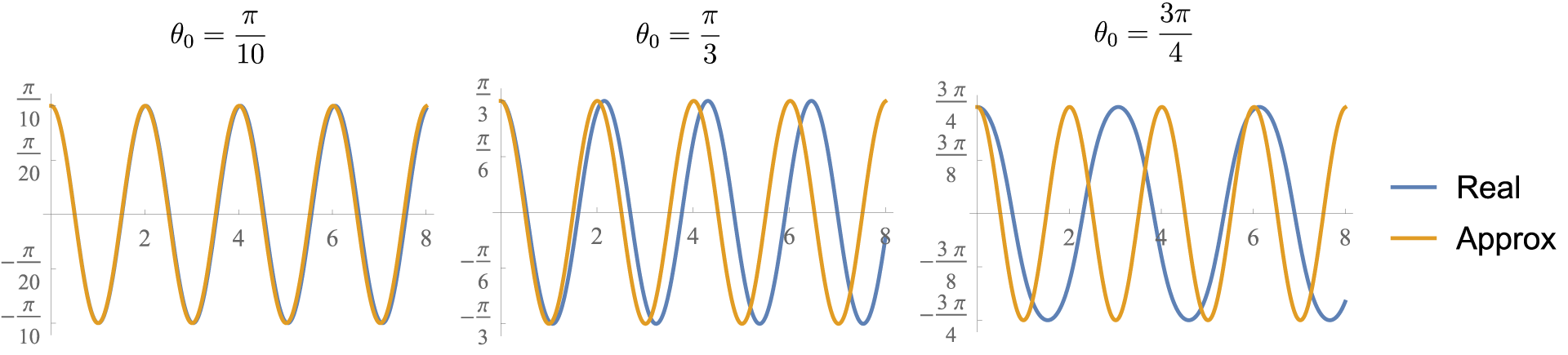
蓝色为精确解，黄色为近似解.

关于周期\(T\)，它实际上和初始角度\(\theta_0\)和初始角速度\(\omega_0\)都有关，取\(\omega_0=0\)，画出\(T-\theta_0\)图像.

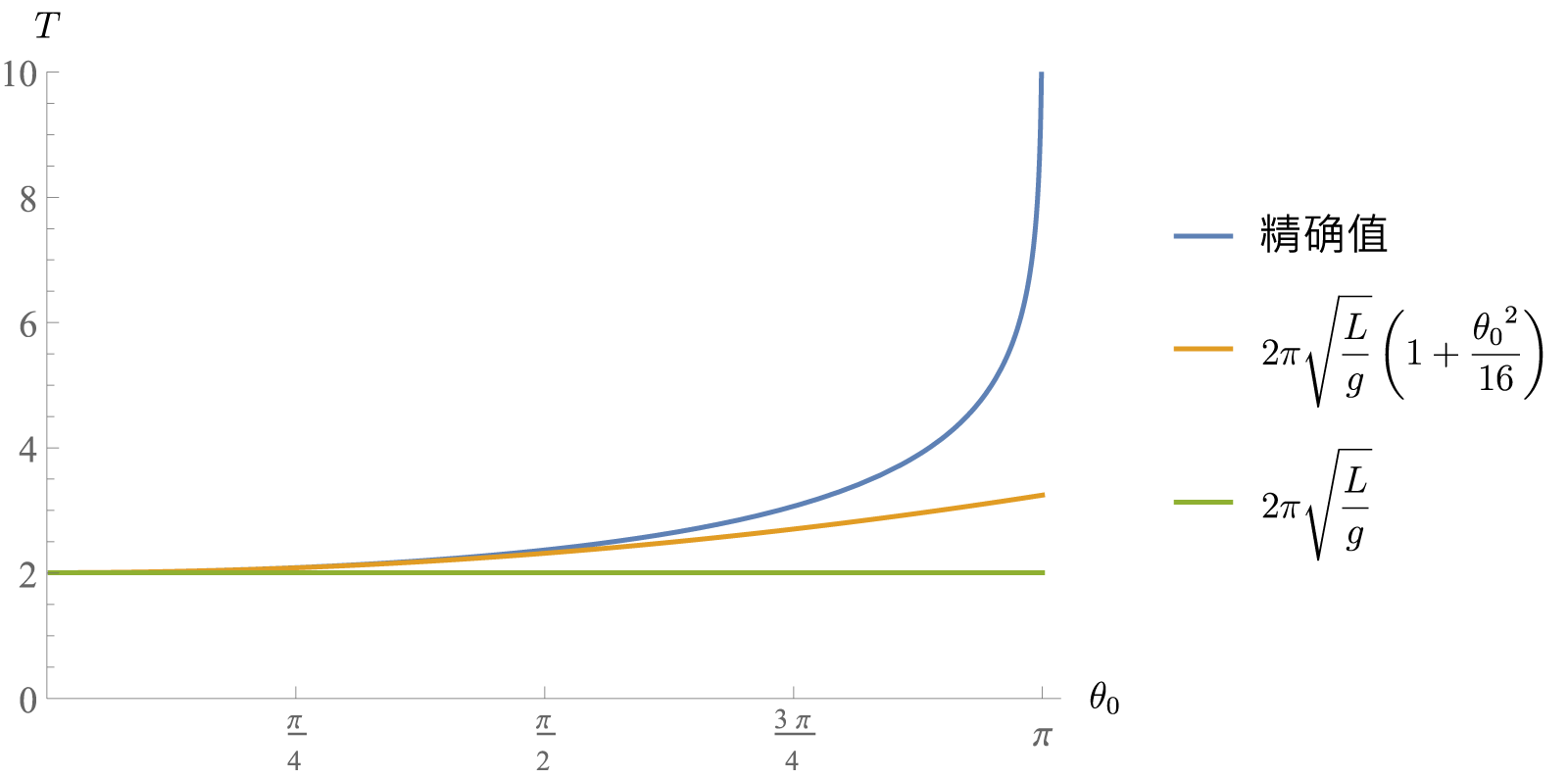
单摆周期的精确公式为\(\displaystyle\sqrt{\frac{2L}g}\int_{-\theta_0}^{\theta_0}\frac{\dd\theta}{\sqrt{\cos{\theta}-\cos{\theta_0}}}\)，不容易计算，如果利用\(\cos{x}\)的Taylor展开式，取前两项\(\cos{x}\approx1-\dfrac12x^2\)，代入分母中得到\(\cos{\theta-\cos{\theta_0}}\approx\dfrac12\pqty{\theta_0^2-\theta^2}\)，这样便容易求出结果为 \[ T\approx 2\pi\sqrt\frac{L}{g} \] 就是近似求解微分方程组得出的结果. 当然，Taylor展开也可以取更多的项，例如取三项后得到的结果是 \[ T\approx2\pi\sqrt\frac{L}{g}\pqty{1+\frac{\theta_0^2}{16}} \]

下图中，蓝色是周期的精确值，绿色和黄色的是取Taylor展开前几项后得到的近似结果，在\(\theta_0\)很小的时候，它们的差别不大. 也可以把绿色和黄色的函数看作蓝色函数的Taylor多项式逼近.

→ 胡克定律

胡克定律的微观解释：一个原子在稳定状态总会位于势能最低点，设原子间作用力的势能函数为\(U(x)\)，其中\(x\)是位置，它的势能最低点是\(x_0\)，最低势能为\(U_0\)，则对\(U(x)\)在\(x=x_0\)进行Taylor展开得到 \[ U(x)=U_0+k_1(x-x_0)+k_2(x-x_0)^2+\dots \] 只取前三项，\(U(x)\approx U_0+k_1(x-x_0)+k_2(x-x_0)^2\)，极小值处一阶导数为\(0\)，所以\(k_1=0\)；又因为势能对位置的导数的相反数是力，所以原子间作用力 \[ F=-\dv{U}{x}\approx-k_1-2k_2(x-x_0)=-2k_2(x-x_0)=-k\Delta x \] 其中\(\Delta x=x-x_0\)，有负号的原因是力和偏移量\(\Delta x\)的方向相反. 这样我们就得到了胡克定律，它实际上是一个近似的结果.

→ 72法则

设一项投资（考虑复利）单位时间的收益率为\(r\)（\(0<r\ll1\)），设本金为\(1\)，则时间\(t\)（\(t>0\)）后资金变为\((1+r)^t\)，如果我们想要投资翻倍，那么有 \[ \Align{ t=\log_{1+r}2=\frac{\ln2}{\ln(1+r)} } \] 因为正数\(r\)远小于\(1\)，所以利用\(\ln(1+r)\)在\(r=0\)处的Taylor展开\(\ln(1+r)\approx r-\dfrac{r^2}2+\dfrac{r^2}3-\dots\)，只取第一项，得到\(t\approx\dfrac{\ln2}{r}\)，又\(\ln{2}\approx0.693\approx0.72\)（近似成\(0.72\)是为了计算方便），这样可以用公式 \[ t\approx\frac{72\%}{r} \] 来大致计算资金翻倍的时间，这便是金融学中的"72法则". 例如，某项存款的年利率是\(4\%\)，则本金翻倍的时间约为\(18\)年.

→ 其他数学领域

Taylor展开在求极限中也有用： \[ \Align{ \lim_{x\to0}\frac{\sin{x}-x}{x^3} &=\lim_{x\to0}\frac{\pqty{ x-\dfrac{x^3}{3!}+\dfrac{x^5}{5!}-\dots }-x}{x^3} \\ &=\lim_{x\to0}\pqty{-\frac1{3!}+\frac{x^2}{5!}-\dots} =-\frac1{3!}=-\frac16 } \] 还有诸如：

• 求解微分方程.

• 求积分. \(\e^{x^2}\)的原函数没办法用初等函数表示，但是可以利用Taylor展开求得级数解： \[ \Align{ \e^x&=\sum_{n=0}^\infty \frac{x^n}{n!} & (-\infty<x<+\infty) \\ \xrightarrow{x替换成x^2} \e^{x^2}&=\sum_{n=0}^\infty \frac{x^{2n}}{n!} & (-\infty<x<+\infty) } \] 逐项积分得到\(\displaystyle\int\e^{x^2}\dd{x}=\sum_{n=0}^\infty\frac{x^{2n+1}}{(2n+1)n!}\).

  下图展示了原函数的精确解（上面的无穷级数）与上面求和式当\(n=1,2,3\)时的解.

  

• 求级数\(1-\dfrac12+\dfrac13-\dfrac14+\dots\)，直接利用\(f(x)=\ln(1+x)=x-\dfrac12x^2+\dfrac13x^2-\dots(-1<x\le1)\)，代入\(x=1\)得到\(f(1)=\ln2=1-1/2+1/3-\dots\)就是原级数的值.

• 不等式证明与放缩.

例如，证明当\(0<x<1\)，\(\dfrac{x}{1+x}<\ln(1+x)<x\).

Taylor展开得到 \[ \Align{ \e^x &= 1+x+\frac{x^2}{2!}+\frac{x^3}{3!}+\dots \\ \Rightarrow 1+x &< \e^x < 1+x+x^2+\dots=\dfrac{1}{1-x} \quad (0<x<1) } \] 两边取对数， \[ \ln(1+x)<x<\ln{\frac1{1-x}} \] 右侧用\(\dfrac{x}{1+x}\)替换\(x\)，得到 \[ \dfrac{x}{1+x}<-\ln\pqty{1-\dfrac{x}{1+x}}=\ln(1+x) \] 综合上面两式，有 \[ \dfrac{x}{1+x}<\ln(1+x)<x \]

---