Taylor展开(一)
1 用多项式拟合函数
多项式函数是一个比较简单的函数,它只涉及加、减、乘三种运算,容易求值,对于高阶导数和积分也有一套固定的方法,如果能用它们来近似一些较为复杂的函数,岂不美哉?
自然,我们选择的多项式应和原来的函数应该近似得较好,最常见的要求是使得多项式和原来的函数在某些点的函数值甚至若干阶导数值相同. 这种多项式被称为插值多项式(Interpolating polynomial).
下图展示了一个插值多项式,橙色为余弦函数,蓝色的多项式函数在点\(-\pi,-\dfrac\pi2,0,\dfrac\pi2,\pi\)与余弦函数相等.
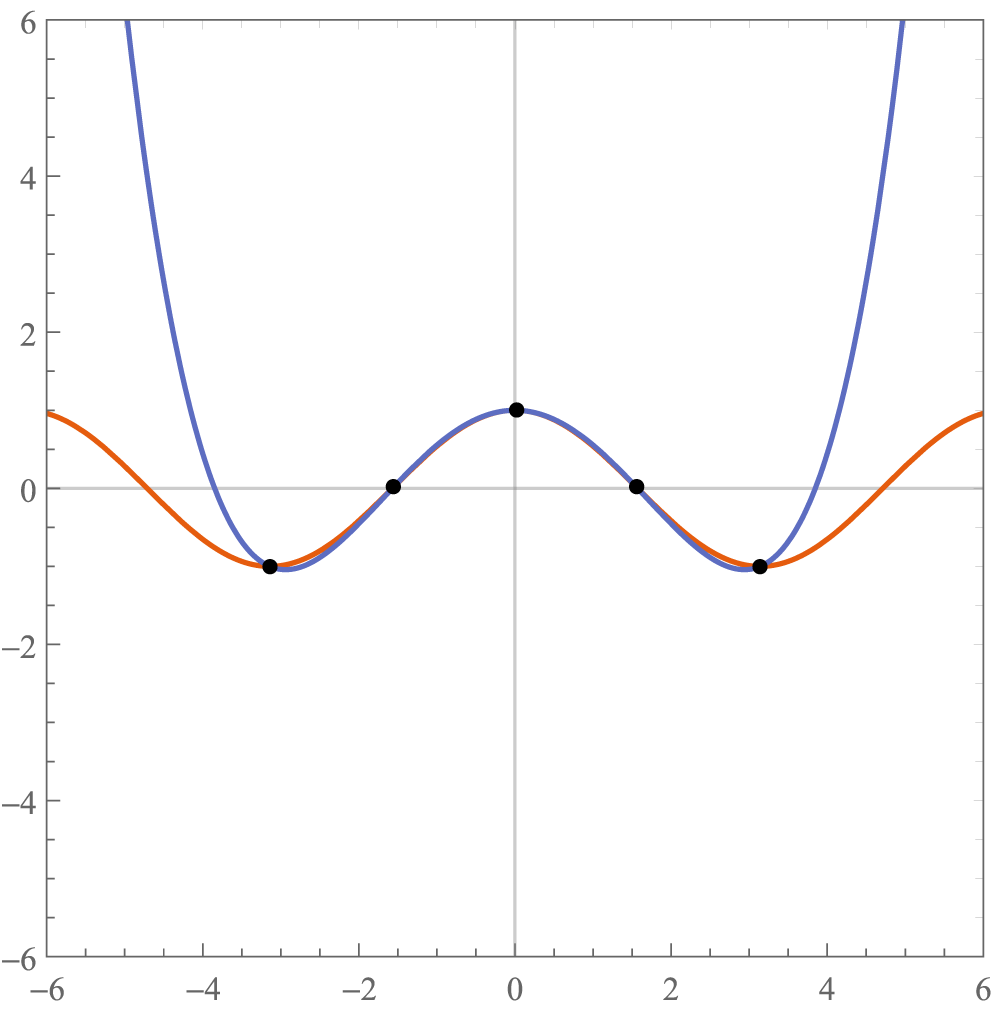
1.1 导数相等
我们看其中一种方法:令某点处多项式和原函数各阶导数相等. 从导数的几何意义开始:
函数在某一点的一阶导数表示切线斜率;二阶导数反映凹凸性;三阶导数表示凹凸性的变化……可见,使用一阶到高阶的导数能够表达函数在某一点周围的信息.
对于\(n\)次多项式 \[ P_n(x)=a_0+a_1x^1+a_2x^2+\dots+a_nx^n \] 我们可以令当\(x=0\)时,它的函数值和\(1\)至\(n\)阶导数分别和原来的函数\(f(x)\)相等,从而求出系数\(a_0,\dots a_n\). 现在对\(P_n(x)\)求导:
\(P_n(x)=a_0+a_1x^1+a_2x^2+a_3x^3+a_4x^4+\dots+a_nx^n\).
每求一次导数,\(x\)的次数向前提出来,并且次数减去\(1\). 因为我们之后要将\(x=0\)代入求得导数值,所以只需要关注导数的常数项即可,因为含\(x\)的项都是\(0\).
求\(k\)阶导数后,\(P^{(k)}_n(x)\)的常数项是由原来的\(k\)次项变来的.(求一次导数,次数减去\(1\),所以更低次的项都会变成\(0\),更高次的项仍然含\(x\).)
\(P'_n(0)=(a_1x^1)'=1\times a_1\).
\(P''_n(0)=(a_2x^2)''=(2\times a_2x)'=2\times1\times a_2\).
\(P_n'''(0)=(a_3x^3)'''=(3\times a_3x^2)''=(3\times2\times a_3x^1)'=3\times2\times1\times a_3\).
\(P''''_n(0)=(a_4x^4)''''=(4\times a_4x^3)'''=(4\times3\times a_4x^2)''=(4\times3\times2\times a_4x^1)'=4\times3\times2\times1\times a_4\).
\(\dots\)
\(P_n^{(n)}(0)=n!a_n\).
可以发现一些规律:每求一次导数,\(x\)的次数就会向前提出来,所以,求\(k\)阶导数之后,\(a_k\)的系数是\(k!\). 如果令各阶导数\(P^{(k)}_n(0)=f^{(k)}(0)\),则有 \[ \Align{ P_n^{(k)}(0) = k!a_k = f^{(k)}(0) \Rightarrow a_k=\frac{f^{(k)}(0)}{k!} } \] 这样便得到了系数的表达式,将其带回原来的多项式,得到 \[ \Align{ P_n(x) &=\frac{f(0)}{0!}x^0+\frac{f'(0)}{1!}x^1+\frac{f''(0)}{2!}x^2+\frac{f'''(0)}{3!}x^3 +\dots+\frac{f^{(n)}(0)}{n!}x^n \\ &=\sum_{k=0}^n\pqty{\frac{f^{(k)}(0)}{k!} \cdot x^k} } \] (其中:认为"零阶导数"\(f^{(0)}(x)\)就是\(f(x)\)本身;\(x^0=1\);\(0!=1\).)
这个多项式能够在\(x=0\)附近较好地近似\(f(x)\). 当\(n\)越来越大时,"误差"也会越来越小,如下面的动画所示,其中\(f(x)=\sin(x)\).
取\(n=3\),\(f(0)=0\),\(f'(0)=\cos(0)=1\),\(f''(0)=-\sin(0)=0\),\(f'''(0)=-\cos(0)=-1\). 所以 \[ \sin{x} \approx P_3(x) = \frac{0}{0!}+\frac{1}{1!}x+\frac{0}{2!}x^2+\frac{-1}{3!}x^3 = x-\frac{x^3}6 \] 代入一个值,如\(x=0.5\),计算机算得\(P_3(0.5)\approx0.479167\),\(\sin(0.5)\approx0.479426\),两者是非常接近的,相对误差约为\(0.5\textperthousand\).
1.2 另外的方法
上面的方法利用了一个点的各阶导数相等来构造出拟合多项式,我们也可以在区间\(I\)内取很多个点,令各个点处的多项式值和函数值相等,来构造拟合多项式. 设互异的点\(x_i\in I\)(\(i=1,2,\dots,n\)),且\(f(x)\)在\(x_i\)上的函数值是已知的,分别为\(y_i\)(\(i=1,2,\dots,n\)),设多项式\(P(x)\)满足 \[ P(x_i)=y_i \quad (i=1,2,\dots,n) \] 此时\(P(x)\)是最简单的一种插值多项式. 构造方法也很简单,我们考虑一个简单的例子,令\(n=3\),不妨设 \[ P(x) = A(x)y_1 + B(x)y_2 + C(x)y_3 \] 其中多项式\(A(x),B(x),C(x)\)满足:
- \(B(x_1)=C(x_1)=0\),\(A(x_2)=C(x_2)=0\),\(A(x_3)=B(x_3)=0\).
- \(A(x_1)=1\),\(B(x_2)=1\),\(C(x_3)=1\).
这样能保证函数值相等. 现在我们只需求出\(A(x),B(x),C(x)\).
因为\(A(x_2)=A(x_3)=0\),所以\((x-x_2)\)和\((x-x_3)\)一定是\(A(x)\)的因式,即\(A(x)=\alpha(x-x_2)(x-x_3)\),同理可以得到\(B(x)=\beta(x-x_1)(x-x_3)\),\(C(x)=\gamma(x-x_1)(x-x_2)\).
又因为\(A(x_1)=B(x_2)=C(x_3)=1\),所以\(\alpha=\dfrac{1}{(x_1-x_2)(x_1-x_3)}\),同理可以求出\(\beta,\gamma\). 代入\(P(x)\)得到 \[ P(x)= \frac{(x-x_2)(x-x_3)}{(x_1-x_2)(x_1-x_3)}y_1 + \frac{(x-x_1)(x-x_3)}{(x_2-x_1)(x_2-x_3)}y_2 + \frac{(x-x_1)(x-x_2)}{(x_3-x_1)(x_3-x_2)}y_3 \] 就是所求的多项式,容易验证,将\(x_i\)代入后,函数值为\(y_i\).
上面的求解过程可以推广到更多个点的情形;同时可以看出一个\(n\)个点的插值多项式最多是\((n-1)\)次的.
下图展示了两个插值多项式的图像.
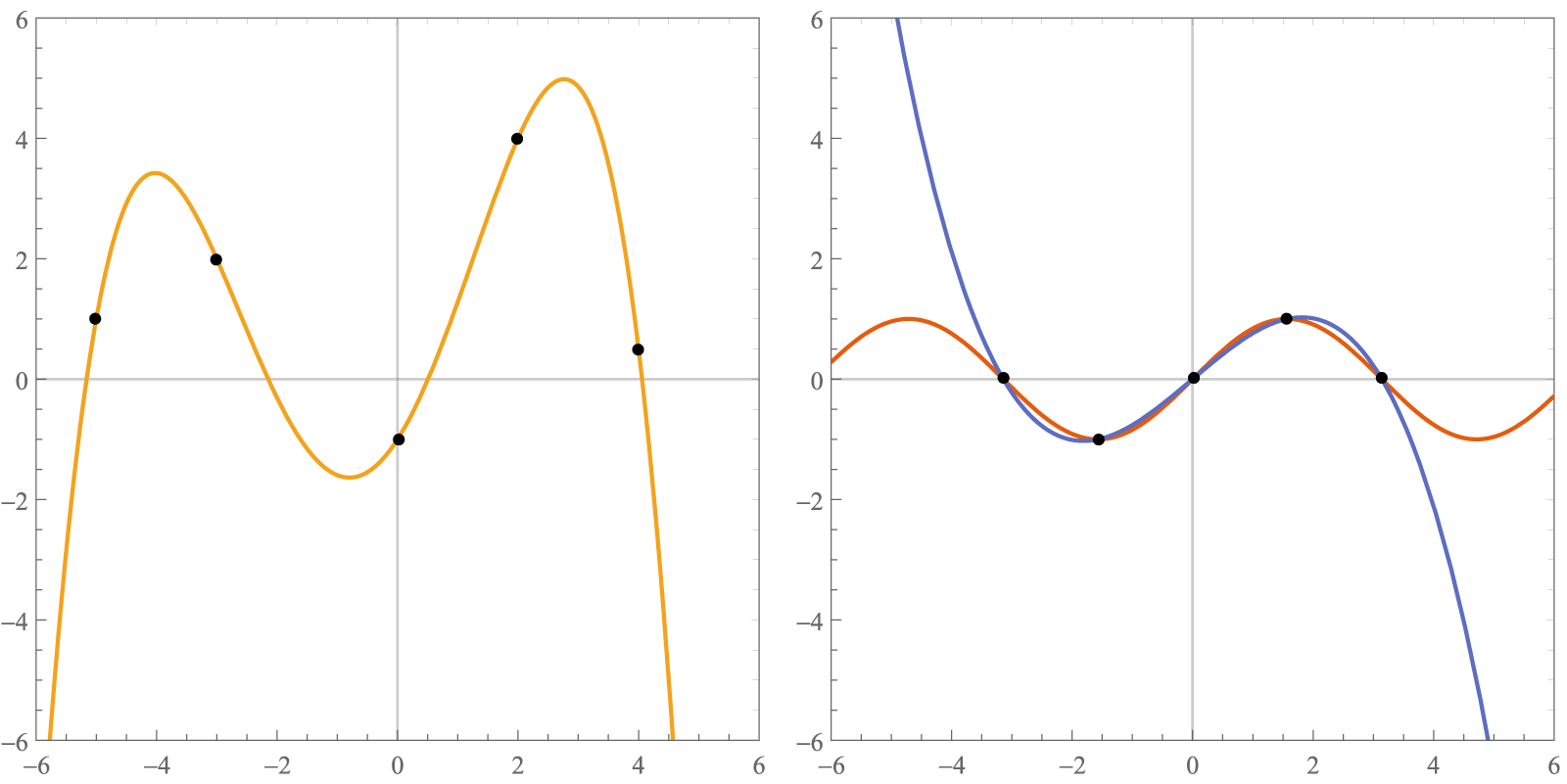
- 左图表示经过5个定点的插值多项式.
- 右图是插值多项式对\(f(x)=\sin{x}\)的拟合,插值点为\(-\pi,-\dfrac\pi2,0,\dfrac\pi2,\pi\).
2 Taylor级数
2.1 Taylor多项式与余项
把我们之前在\(\S1.1\)得到多项式拿过来, \[ P_n(x)=\sum_{k=1}^n\pqty{\frac{f^{(k)}(0)}{k!} \cdot x^k} \] 它是在\(x=0\)处对函数的近似(也称为Maclaurin公式),如果我们选取任意一点\(x=a\)呢?只需要把\(f^{(k)}(0)\)改成\(f^{(k)}(a)\),再把幂函数\(x^k\)平移,变成\((x-a)^k\),得到 \[ P_n(x)=\sum_{k=1}^n\pqty{\frac{f^{(k)}(a)}{k!} \cdot (x-a)^k} \] 它能够在\(x=a\)处近似\(f(x)\). 但是近似总会有误差,设\(R_n(x)=f(x)-P_n(x)\),\(R_n(x)\)称为余项,用来刻画误差. 引入余项后,原来的函数可以表示为 \[ \Align{ f(x) &=P_n(x)+R_n(x) \\ &=\sum_{k=0}^n\pqty{\frac{f^{(k)}(a)}{k!} \cdot (x-a)^k}+R_n(x) } \] 这就是\(f(x)\)在\(x=a\)处的Taylor公式,\(P_n(x)\)称为\(f(x)\)的\(n\)次Taylor多项式. 需要\(f(x)\)在包含\(a\)的开区间内有\(n\)阶导数.
Taylor公式的余项有多种形式:
- Peano余项:\(R_n(x)=o((x-a)^n)\),是一个\((x-a)^n\)的高阶无穷小量.
- Lagrange余项:\(R_n(x)=\dfrac{f^{(n+1)}(\xi)}{(n+1)!}\cdot(x-a)^{n+1}\)(\(\xi\)在\(x\)和\(a\)之间). 这里需要\(f(x)\)有\((n+1)\)阶导数.
当\(x\to a\)的时候可以发现,Lagrange余项的结论要强于Peano余项. Peano余项定性地给出了"误差",而Lagrange余项定量地给出了"误差".
2.2 几何意义
对于Taylor公式有一个几何理解. 由Newton-Lebniz公式, \[ \int_a^x f'(s)\dd{s}=f(x)-f(a) \Rightarrow f(x)=f(a)+\int_a^xf'(s)\dd{s} \] 如下图,\(f(x)\)就等于\(f(a)\)加上\(f'(x)\)的图像在以\(a\)和\(x\)为端点的区间上和\(x\)轴围成的(带符号)面积.
实际上,\(f(a)\)也可以理解为\(f'(x)\)在\(a\)点左侧与\(x\)轴围成的面积.
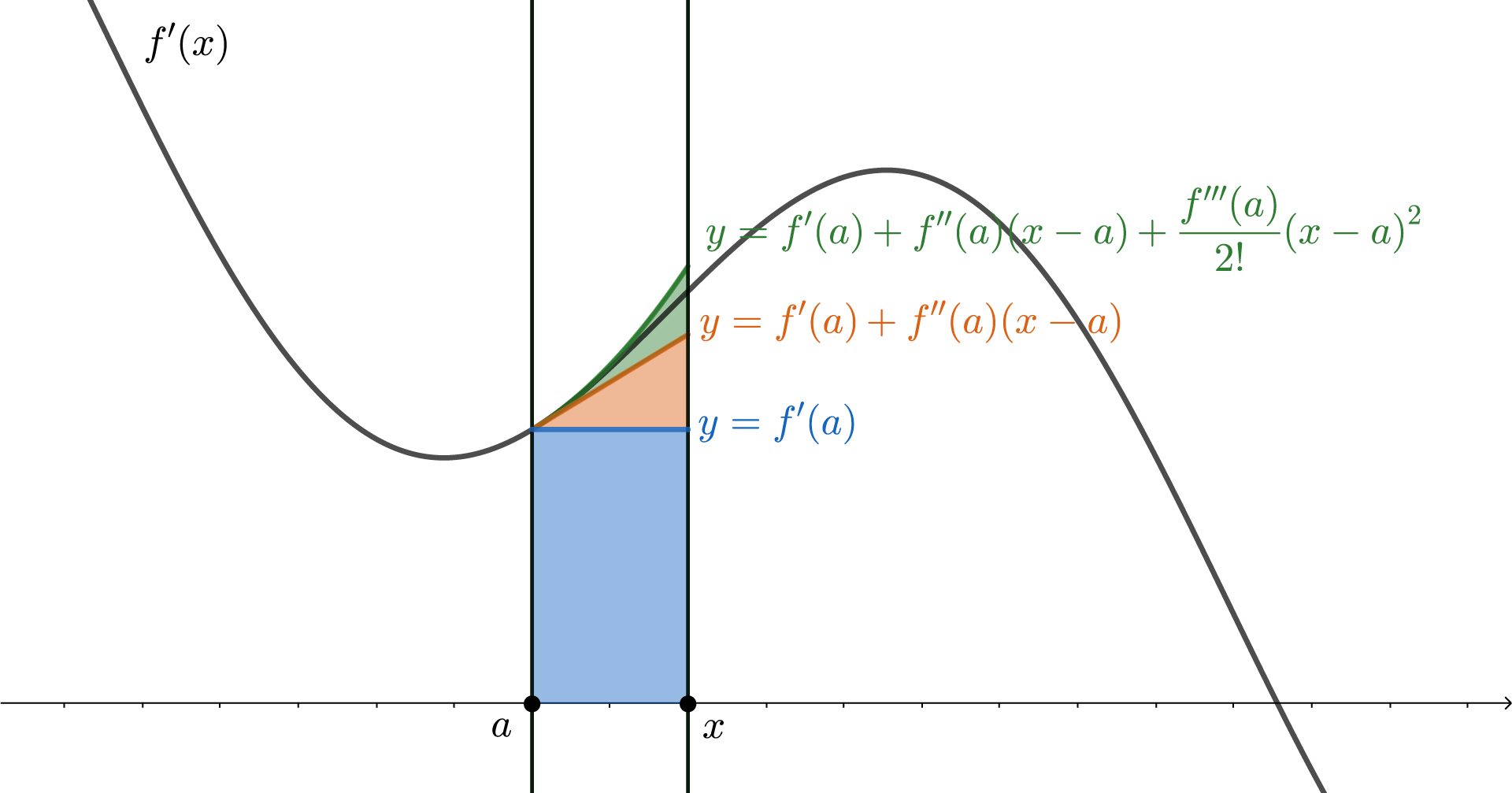
我们现在用不同的精确度来近似\(f'(x)\)和\(x\)轴之间的面积,即 \[ f(x)\approx f(x)+S_{\text{approx}} \] 如果我们用蓝色线段和\(x\)轴之间的面积来近似\(f'(x)\)和\(x\)轴围成的面积,\(\displaystyle S_{\text{approx}}=\int_a^x{\color[rgb]{0.08,0.40,0.75}f'(a)}\dd{x}\),所以 \[ f(x) \approx f(a) + {f'(a)(x-a)} \] 更精确一些,我们用橙色线段和\(x\)轴之间的面积. 橙色线段是\(f'(x)\)在\(a\)处的切线段,斜率为\(f''(a)\),所以切线方程为\({\color[rgb]{0.86,0.38,0.08}y=f'(a)+f''(a)(x-a)}\),面积的估计值 \[ \Align{ S_{\text{approx}} &=\int_x^a \pqty{{\color[rgb]{0.86,0.38,0.08}f'(a)+f''(a)(x-a)}}\dd{x} ={f'(a)(x-a)} + {\frac{f''(a)}{2!}(x-a)^2} } \] 将结果代入\(f(x)\approx f(x)+S_{\text{approx}}\), \[ f(x) \approx f(a)+ {f'(a)(x-a)} + {\frac{f''(a)}{2!}(x-a)^2} \] 可以发现,这三项恰好是\(f(x)\)的Taylor多项式的前三项. 如果再精确一些,用绿色曲线和\(x\)轴之间的面积来近似,其中绿色曲线为\({\color[rgb]{0.18,0.49,0.20}y=f'(a)+f''(a)(x-a)+\dfrac{f'''(a)}{2!}(x-a)^2}\).
蓝色、橙色、绿色曲线方程右端分别是\(f'(x)\)在\(a\)点处的零次、一次、二次Taylor多项式.
对其求定积分,再把近似值代入,得到 \[ f(x)\approx f(a)+f'(a)(x-a)+\frac{f''(a)}{2!}(x-a)^2 +\frac{f'''(a)}{3!}(x-a)^3 \] 得到了Taylor多项式的前四项. 可见,如果我们用更精确的曲线近似地求出\(f'(x)\)和坐标轴之间面积,那么就会得到Taylor多项式的更多项. 这可以作为Taylor多项式的一个几何意义.
2.3 Taylor级数与收敛性
上面提到的Taylor多项式近似函数的方法中,我们取了一个定值\(n\),求出了\(n\)次Taylor多项式,之后再加上一个误差项. 试想:如果我们令\(n\)趋于无穷大,得到无穷多次的Taylor"多项式",那么这个"多项式"是不是能够任意的接近原来的函数,这样就没有误差了?
先给出定义:
如果\(f(x)\)在\(a\)的某个邻域上任意阶可导,那么 \[ \sum_{k=0}^\infty \frac{f^{(k)}(a)}{k!}(x-a)^k \] 为\(f(x)\)在\(a\)处的Taylor级数(Taylor series). Taylor级数是否收敛到原来的函数?因为余项\(R_n(x)=f(x)-P_n(x)\),所以如果在\(a\)的某个邻域上,当\(n\to\infty\)时,\(R_n(x)\)能够趋于\(0\),那么\(P_n(x)\)就收敛到\(f(x)\),此时我们称\(f(x)\)在能够在\(a\)的这个邻域上可以展开成幂级数(反之亦然),这个幂级数称为\(f(x)\)在\(a\)的Taylor展开.
上面的名词"级数"指的是无穷多项的求和(详见[F.1]).
举个例子,
\(f(x)=\e^x\)在\(x=0\)处的Lagrange余项是\(R_n(x)=\dfrac{\e^{\xi}}{(n+1)!}x^{n+1}\)(\(|\xi|<|x|\)),因为 \[ |R_n(x)|\le\frac{\e^{|x|}}{(n+1)!}|x|^{n+1}\to0\quad(n\to\infty) \] 对\(x\in(-\infty,+\infty)\)恒成立,所以\(\e^x\)的Taylor展开对\(x\in\R\)成立,展开式为 \[ \e^x =\sum_{k=0}^\infty\frac{x^k}{k!} =1+x+\frac{x^2}{2!}+\frac{x^3}{3!}+\frac{x^4}{4!}+\dots+\frac{x^n}{n!}+\dots \]
有时,Taylor展开只有在某一个区域内成立,例如\(\dfrac{1}{1+x^2}=1-x^2+x^4-x^6+\dots\)只有在\(|x|<1\)时成立,因为当\(x>1\)时幂级数显然不收敛.
实际上,我们有很多方法判断Taylor级数是否收敛,在何时收敛,见[F.2].
一些初等函数的Taylor展开:
\(\displaystyle\sin{x}=\sum_{k=0}^\infty\frac{(-1)^k}{(2k+1)!}x^{2k+1}=x-\frac{x^3}{3!}+\frac{x^5}{5!}-\frac{x^7}{7!}+\dots\)(\(-\infty<x<+\infty\)),只有奇数次幂.
\(\displaystyle\cos{x}=\sum_{k=0}^\infty\frac{(-1)^k}{(2k)!}x^{2k}=1-\frac{x^2}{2!}+\frac{x^4}{4!}-\frac{x^6}{6!}+\dots\)(\(-\infty<x<+\infty\)),只有偶数次幂.
从这里可以看出三角函数和指数函数的关系. 我们直接利用Taylor展开式,将指数函数推广到复数域.
将\(\i x\)代入\(\e^x\)的展开式,得到 \[ \Align{ \e^{\i x} =\sum_{k=0}^\infty\frac{\i^kx^k}{k!} &=1+\i^1x+\i^2\frac{x^2}{2!}+\i^3\frac{x^3}{3!}+\i^4\frac{x^4}{4!} +\i^5\frac{x^5}{5!} +\dots+\i^n\frac{x^n}{n!}+\dots \\ &=1+\i x-\frac{x^2}{2!}-\i\frac{x^3}{3!}+\frac{x^4}{4!} +\i\frac{x^5}{5!} +\dots+\i^n\frac{x^n}{n!}+\dots \\ &=\pqty{1-\frac{x^2}{2!}+\frac{x^4}{4!}-\dots} +\i\pqty{x-\frac{x^3}{3!}+\frac{x^5}{5!}-\dots} \\ &=\cos{x}+\i\sin{x} } \] 即\(\e^{\i x}=\cos{x}+\i\sin{x}\)(\(x\in\R\)),是非常著名的Euler公式.
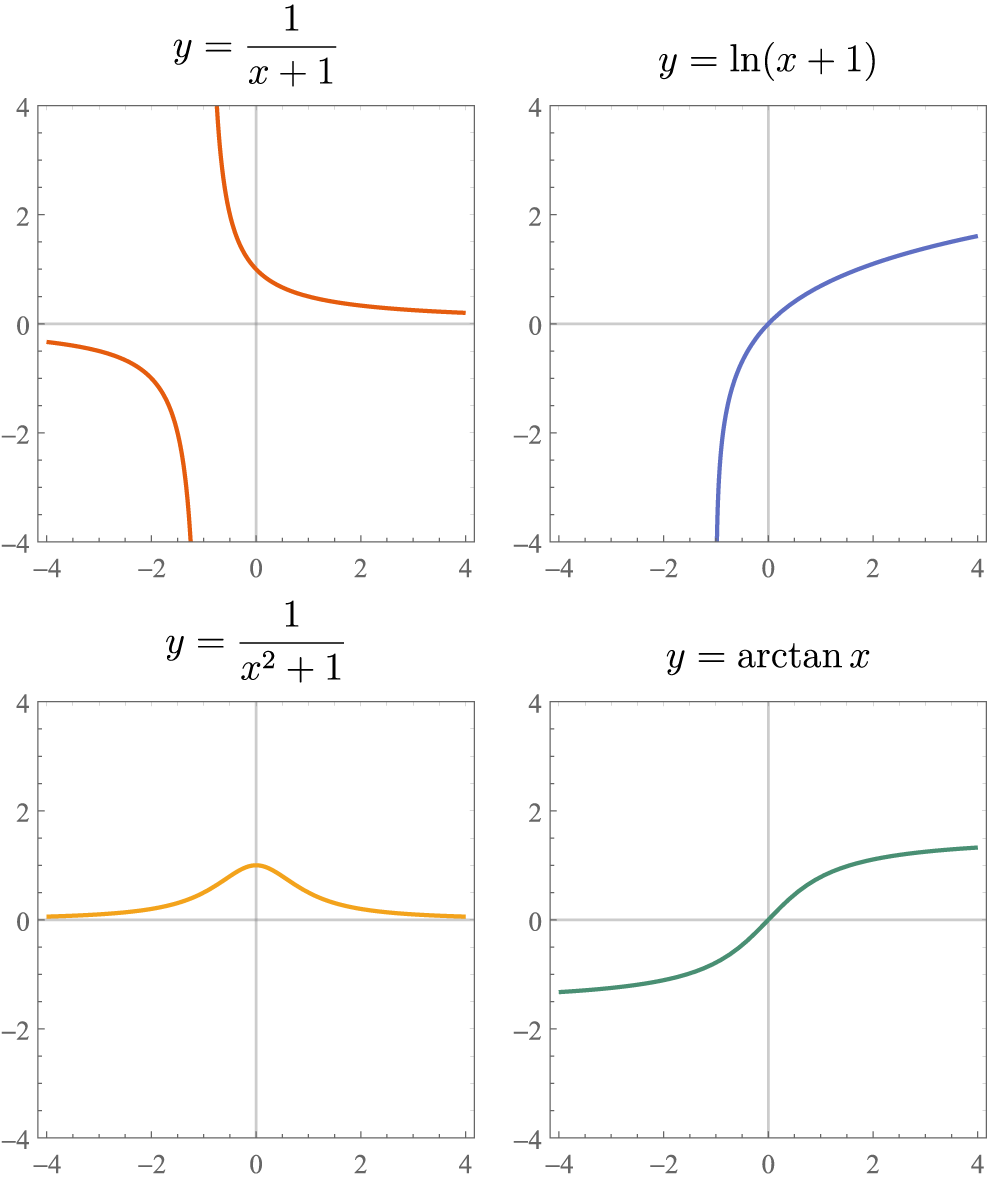
\(\displaystyle\frac{1}{x+1}=\sum_{k=0}^\infty(-1)^kx^k=1-x+x^2-x^3+x^4-x^5+\dots\)(\(-1<x<1\)).
逐项求z导数(限制\(x>-1\)),得到
\(\displaystyle\ln(x+1)=\sum_{k=1}^\infty\frac{(-1)^k}{k}x^k=x-\frac{x^2}2+\frac{x^3}3-\frac{x^4}4+\dots\)(\(-1<x\le1\)).
将\(x'=x^2\)代入最初的式子,得到
\(\displaystyle\dfrac{1}{1+x^2}=\sum_{k=0}^\infty(-1)^kx^{2k}=1-x^2+x^4-x^6+\dots\)(\(-1<x<1\)).
逐项求积分,得到
\(\displaystyle\arctan{x}=\sum_{k=0}^\infty\frac{(-1)^k}{2k+1}x^{2k+1}=x-\frac{x^3}3+\frac{x^5}5-\frac{x^7}7+\dots\)(\(-1<x<1\)).
对于函数\(y=\dfrac1{x+1}\)和\(y=\ln(x+1)\),它们在\(x=-1\)处不连续,所以\(x=0\)的展开式的收敛半径理应是到\(1\)为止了;而\(y=\dfrac1{1+x^2}\)和\(y=\arctan{x}\)在定义域内都是连续且光滑的,但是由推导过程可以发现,它们在\(x=0\)处的Taylor展开式收敛半径仍然为\(1\),虽然理论上足够严谨,但是还是难免令人心生疑问:好好的一个函数为什么展开式只在\((-1,1)\)收敛?
Footnotes
F.1 级数
级数(Series)是无穷多个数(或式子)的求和,例如 \[ 1+\frac12+\frac13+\frac14+\dots+\frac1n+\dots \] 上面这个级数的每一项都是常数,也称为常数项级数,对应地,级数的每一项还可能是函数,例如 \[ u_1(x)+u_2(x)+u_3(x)+\dots+u_n(x)+\dots \] 是一个函数级数,具体的例如 \[ 1+x+x^2+x^3+\dots+x^n+\dots \] 它的一般项是幂函数\(x^n\),称它为幂级数(Power series). 幂级数是一类函数级数,它的每一项都是形如\(a_n(x-x_0)^n\)的幂函数.
之后的附注中我们会仅讨论\(x_0=0\)时的情况,因为更一般的情况可以由平移\(x'=x-x_0\)得到.
F.2 幂级数的收敛特性
对于\(x\in\R\),有些\(x\)的值能够使幂级数收敛到定值,有些会使幂级数发散到无穷大\(\infty\). 设 \[ S_n(x)=\sum_{k=0}^n a_kx^k \] 是幂级数前\(n\)项之和,而级数本身是无穷项的,即\(\lim_{n\to\infty} S_n(x)\). 如果这个极限存在,有\(\lim_{n\to\infty} S_n(x)=S(x)\),称\(S(x)\)为和函数.
等比级数,也称几何级数,是一类重要的级数,形如 \[ a+aq+aq^2+aq^3+\dots=\sum_{k=0}^\infty aq^n \] 利用等比数列求和公式,\(S_n=\dfrac{1-q^n}{1-q}a\),可以发现:当\(|q|<1\),级数收敛;当\(|q|>1\),级数发散.
等比级数很重要,之后许多判断收敛的方法都要拿等比级数作为"基准".
假设级数收敛,因为部分和与一般项满足\(u_n(x)=S_n(x)-S_{n-1}(x)\),所以此时 \[ \lim_{n\to\infty} u_n(x)=\lim_{n\to\infty}(S_{n}(x)-S_{n-1}(x)) =\lim_{n\to\infty} S_n(x)-\lim_{n\to\infty} S_{n-1}(x)=S(x)-S(x)=0 \] 所以幂级数在某一区域收敛的必要条件是一般项\(u(x)\)趋于\(0\). (这个结论对一般的级数也是成立的.)
对于幂级数,需要对每个\(x\)的取值都判断它是否使得级数收敛. 使得幂级数收敛的所有点的集合称为幂级数的收敛域. 幂级数的收敛域有一个特殊的结构:
对于幂级数\(\sum_{k=0}^\infty a_kx^k\),存在定值\(R\ge0\),幂级数在以\(x_0\)为中心,\(R\)为半径的区间内收敛,区间外发散,端点处需要另行判断,称\(R\)是幂级数的收敛半径(Radius of convergence).
- 如果\(R=0\),幂级数仅在\(0\)处收敛,代入得到和函数为\(0\).
- 如果\(R\in(0,+\infty)\),幂级数在\(x_0\)的邻域\((-R,+R)\)内收敛,端点需要另行判断.
- 如果\(R=+\infty\),幂级数在实数域上收敛.
当\(R>0\)时,\((-R,R)\)称为幂级数的收敛区间(收敛区间一定是开区间,收敛域可能含有端点).
收敛区间\((-R,R)\)也即\(|x|<R\). 当\(n\)很大的时候,决定\(S_n(x)\)的是\(x\)的绝对值,和符号等其他因素没关系了,只有绝对值小于某个值的时候,级数才会收敛.
怎样判断幂级数的收敛性,或求出收敛半径?
比值判别法(d'Alembert判别法)是一种判断级数是否收敛的方法:对于任意级数\(\sum_{k=1}^n a_k\),如果 \[ \lim_{n\to\infty}\abs{\frac{a_{n+1}}{a_n}}=\rho \] 那么:当\(\rho<1\)时级数收敛;\(\rho=1\)时可能收敛或发散,请利用其他方法判断;\(\rho>1\)时发散. 这里面的级数可以是常数项级数,也可以是函数项级数.
理解起来,就是如果\(\rho<1\),即当后一项和前一项的比值是小于\(1\)的,那么级数是收敛的,大致可以认为当\(n\)很大,一般项要大致呈现一个公比\(|q|<1\)的等比数列的趋势.
可以使用比值判别法求出幂级数的收敛半径:我们把幂数级数\(\sum_{n=0}^\infty b_nx^n\)代入比值法的式子, \[ \rho=\lim_{n\to\infty}\abs{\frac{b_{n+1}x^{n+1}}{b_nx^n}}=|x|\lim_{n\to\infty}\abs{\frac{b_{n+1}}{b_n}} \] 为了方便,记\(B=\lim_{n\to\infty}\abs{\dfrac{b_{n+1}}{b_n}}\),
- 当\(\rho<1\)即\(|x|B<1\)也就是\(|x|<\dfrac1{B}\),级数收敛.
- 当\(\rho=1\)即\(|x|=\dfrac1{B}\),不确定.
- 当\(\rho>1\)即\(|x|>\dfrac1{B}\),发散.
所以,收敛区间是\(\pqty{-\dfrac1{B},\dfrac1{B}}\),收敛半径就是\(\dfrac1B\).(当\(B=0\),认为收敛半径是\(+\infty\),收敛区间是\(\R\);当\(B=+\infty\),收敛半径为零,级数只在\(x=0\)收敛.) 所以说,对于次数连续的(即\(a_0+a_1x^1+a_2x^2+\dots\),\(x\)的次数从\(1\)到无穷大连续不间断)幂级数,只需要求出系数之比的极限,就得到了收敛半径.
例子:
\(\sum_{k=0}^\infty\dfrac{x^k}{k!}\),系数比值\(\lim_{n\to\infty}\abs{\dfrac{1/(n+1)!}{1/n!}}=\lim_{n\to\infty}\abs{\dfrac1{n+1}}=0\),所以收敛半径是\(+\infty\),在实数域上收敛.
\(\sum_{k=0}^\infty k!{x^k}\),系数比值\(\lim_{n\to\infty}\abs{\dfrac{1/(n+1)!}{1/n!}}=\lim_{n\to\infty}\abs{n+1}=+\infty\),收敛半径是\(0\),仅在\(x=0\)处收敛.
\(\sum_{k=1}^\infty\dfrac{x^{2k}}{(2k)!}\),注意这里只有偶数次幂项,缺少了奇数次幂项,不能直接用系数比值法求收敛半径,但是仍然可以用d'Alembert判别法, \[ \lim_{n\to\infty}\abs{\frac{x^{2n+2}/(2n+2)!}{x^{2n}/(2n)!}} =\lim_{n\to\infty}\abs{\frac{x^2}{(2n+1)(2n+2)}}=0<1 \] 这个极限和\(x\)无关,所以不论\(x\)取何值,级数均会收敛.
根值判别法(Cauchy根值判别法),对于级数\(\sum_{k=1}^n a_k\),如果 \[ \rho=\limsup_{n\to\infty} \sqrt[n]{|a_n|} \] 那么:当\(\rho<1\),收敛;\(\rho>1\),发散;\(\rho=1\)且\(\sqrt[n]{|a_n|}\ge1\),发散'';其他情况不确定.
其中\(\limsup\)指数列上极限,如果数列收敛,那么它就等于数列极限\(\lim\);如果数列不收敛,那么它等于所有收敛子列的极限值的上确界.
例如\(\set{a_n}=1,2,3,1,2,3,\dots\)的极限不存在,但是上极限存在:\(\displaystyle\limsup_{n\to\infty}a_n=3\).
同样拿等比级数解释,设\(\set{a_n}=1,q,q^2,q^3,\dots,q^{n-1},\dots\),则级数\(\sum a_n\)用根值判别法判断收敛性有 \[ \rho=\limsup_{n\to\infty}\sqrt[n]{|q^{n-1}|}=q \] 当\(q<1\)时收敛;\(q>1\)时发散. 推广一下,就是如果级数大致呈公比\(q<1\)的等比级数的趋势的话就会收敛,呈现出\(q>1\)的等比级数的趋势就会发散.