旋转的参考系
1 牛顿定律与惯性力
1687年7月5日,牛顿发表巨著《自然哲学的数学原理》,其中包括了力学三定律:
- 第一定律:若施加于某物体的外力为零,则该物体的运动速度不变.(惯性定律)
- 第二定律:施加于物体的外力等于物体的加速度乘以质量.(加速度定律)
- 第三定律:相互作用的两个物体之间的作用力和反作用力总是大小相等,方向相反,作用在同一条直线上.(作用力与反作用力定律)
这三条定律是经典力学的基础. 但是,第一和第二定律不是在每个参考系下都成立的. 例如在汽车刹车时,虽然以汽车为参考系时,人一直静止,但是人会感到一股向前的力,此时牛一和牛二不适用了. 我们称适用牛顿第一定律的参考系为惯性参考系(Inertial reference frame),不适用的称为非惯性参考系.
在非惯性系中,如果我们要描述力\(\vb{F}\)与加速度\(\vb{a}\)的关系,要怎么办呢?从参考系变换来看:设一个运动的质点为\(1\),非惯性系为\(2\),惯性系为\(3\),则质点\(1\)相对\(3\)的加速度\(=1\)相对\(2\)的加速度\(+2\)相对\(3\)的加速度,即 \[ \vb{a}_{13}=\vb{a}_{12}+\vb{a}_{23} \] 或\(\vb{a}_{13}-\vb{a}_{23}=\vb{a}_{12}\),两边同时乘以质点的质量\(m\)得到 \[ \Align{ m\vb{a}_{13}-m\vb{a}_{23} &= m\vb{a}_{12} \\ \vb{F} - m\vb{a}_{23} &= m\vb{a}_{12} } \] 其中\(\vb{F}=m\vb{a}_{13}\)是质点受的力(在\(3\)中用牛顿第二定律可得). 在非惯性系\(2\)中,质点受力\(\vb{F}\)和加速度\(\vb{a}_{12}\)满足如上关系式. 我们令\(\vb{F}_{\rm I}=-m\vb{a}_{23}\),称之为惯性力(Inertial force),它和质点质量与非惯性系的加速度有关. 现在,牛顿第二定律可以修正为 \[ \vb{F}+\vb{F}_{\rm I}=m\vb{a} \] 这是在任意参考系中都成立的. 可以发现,惯性参考系就是本身的加速度为零的参考系.
对于某些状况,牛顿运动定律并不适用,这时候需要更进阶的物理理论:超高速或非常强烈重力场的状况下,我们需要相对论解释一些天体运动和现象,例如黑洞;在微观尺度,我们需要量子力学解释原子发射光谱等物理现象. 但是现代工程学里,对于一般应用案例,像车辆或飞机的运动,牛顿运动定律已能准确地解释和计算工程师遇到的问题.(引自Wikipedia)
2 旋转参考系中的惯性力
求解惯性力,关键在于求出非惯性系的加速度. 对于平动的非惯性系,加速度就是平动加速度\(\vb{a}\),很简单;但是对于旋转的参考系,加速度可能与物体的位置和参考系的旋转状态(角速度)都有关,推导起来没那么直接了.
2.1 推导与结论
设一个惯性系为\(i\),旋转系为\(r\),旋转的角速度矢量为\(\vb*{\omega}\)(方向不变,即定轴转动),质点\(m\)的位矢为\(\vb{r}\)(在不同的参考系下有\(\vb{r}_i\),\(\vb{r}_r\)).
质点在\(i\)下的速度为位矢对时间的导数,利用[F.2]的结论,有 \[ \Align{ \vb{v}_i =\pqty{\dv{\vb{r}}{t}}_i =\bqty{\pqty{\dv{}{t}}_r+\vb*\omega\times}\vb{r}_r } \] 加速度为速度的导数,再次利用[F.2]的结论,有 \[ \Align{ \vb{a}_i = \pqty{\dv{\vb{v}}{t}}_i &= \bqty{\pqty{\dv{}{t}}_r+\vb*\omega\times} \bqty{\pqty{\dv{\vb{r}}{t}}_r+\vb*\omega\times\vb{r}_r} \\ &= \pqty{\dv{^2\vb{r}}{t^2}}_r +2\vb*\omega\times\pqty{\dv{\vb{r}}{t}}_r +\dv{\vb*\omega}{t}\times\vb{r}_r +\vb*\omega\times(\vb*\omega\times\vb{r}_r) \\ &= \vb{a}_r + 2\vb*\omega\times\vb{v}_r + \vb*\beta\times\vb{r}_r - \omega^2\vb{r}_r } \]
其中\(\vb*\beta\)为旋转的角加速度;\(\vb*\omega\times(\vb*\omega\times\vb{r}_r)=-\omega^2\vb{r}_r\)可以由叉积的几何意义推出. 移项、两边同时乘以\(m\)有 \[ m\vb{a_r} = \vb{F} +\pqty{\orange{-2m\vb*\omega\times\vb{v}_r}} +\pqty{\blue{-m\vb*\beta\times\vb{r}_r}} +\green{m\omega^2\vb{r}_r} \]
\(\vb{F}=m\vb{a}_i\)是质点所受外力;而惯性力一共有三项,对应了三种惯性力:
- 科里奥利力(Coriolis force):\(\vb{F}_{\rm Coriolis}=-2m\vb*\omega\times\vb{v}_r\).
- 欧拉力(Euler force):\(\vb{F}_{\rm Euler}=-m\vb*\beta\times\vb{r}_r\).
- 离心力(Centrifugal force):\(\vb{F}_{\rm centrifugal}=m\omega^2\vb{r}_r\).
此时\(\vb{F}_{\rm I}=\vb{F}_{\rm Coriolis}+\vb{F}_{\rm Euler}+\vb{F}_{\rm centrifugal}\),修正的牛顿第二定律\(m\vb{a}_r = \vb{F}+\vb{F}_{\rm I}\)成立.
2.2 离心力
惯性离心力\(\vb{F}_{\rm centrifugal}=m\omega^2\vb{r}_r\)的方向是从旋转中心指向质点的,也就是能把物体"甩出去"的一种力. 只要物体的旋转半径不为零,就会收到惯性离心力的影响. 在坐车的时候,转弯时你会感一股向外的力,便是惯性离心力.
2.3 科里奥利力
科里奥利力,是法国气象学家、工程师科里奥利(Gustave Gaspard de Coriolis)在1835年提出的.
由\(\vb{F}_{\rm Coriolis}=-2m\vb*\omega\times\vb{v}_r=2m\vb{v}_r\times\vb*\omega\)可知,仅对旋转系中运动的物体(\(\vb{v}_r\ne\vb0\))收到科里奥利力的作用,科氏力的方向与速度方向垂直,所以不改变速度大小,仅改变方向.
下面的动画形象展示了科里奥利力. 一个黄色质点在光滑的、旋转的圆盘上匀速运动,在外部惯性参考系看来,质点不受任何力(左);但在圆盘系看来,质点收到一个惯性力,即科里奥利力(右),力(蓝色矢量)始终与速度(红色矢量)方向垂直,只改变速度方向,所以质点相对于圆盘作匀速圆周运动.
由于地球本身就是一个巨大的旋转参考系,所以在上面运动的物体都会收到科里奥利力作用,所以科里奥利力的理论应用很广泛.
2.4 欧拉力
欧拉力是以欧拉(Leonhard Euler)命名的,\(\vb{F}_{\rm Euler}=-m\vb*\beta\times\vb{r}_r\),欧拉力只有在非匀速旋转的非惯性系中存在,它的方向和"旋转加速"的方向相反. 在骑旋转木马时,当木马开始加速旋转,你会感到一股向后的力;当木马减速至停止旋转,你会感到一股向前的力,这就是欧拉力.
3 地球上的科里奥利力
我们认为地球绕着地轴以约\(\omega=\dfrac{360^\circ}{24\,{\rm h}}\approx0.0042^\circ/{\rm s}\)的角速度自西向东自转. 因为匀速自转、角速度不变,所以欧拉力为零;因为角速度很小,所以\(\omega^2\)可以忽略不计,所以不考虑离心力,所以只剩下科里奥利力.
3.1 大小和方向
对于在地面运动的质点\(m\)(速度平行于地面),我们以正东、正北方为\(x,y\)轴方向,正上方为\(z\)方向,建立右手系. 地球的角速度矢量为\(\vb*\omega\),指向北极星.
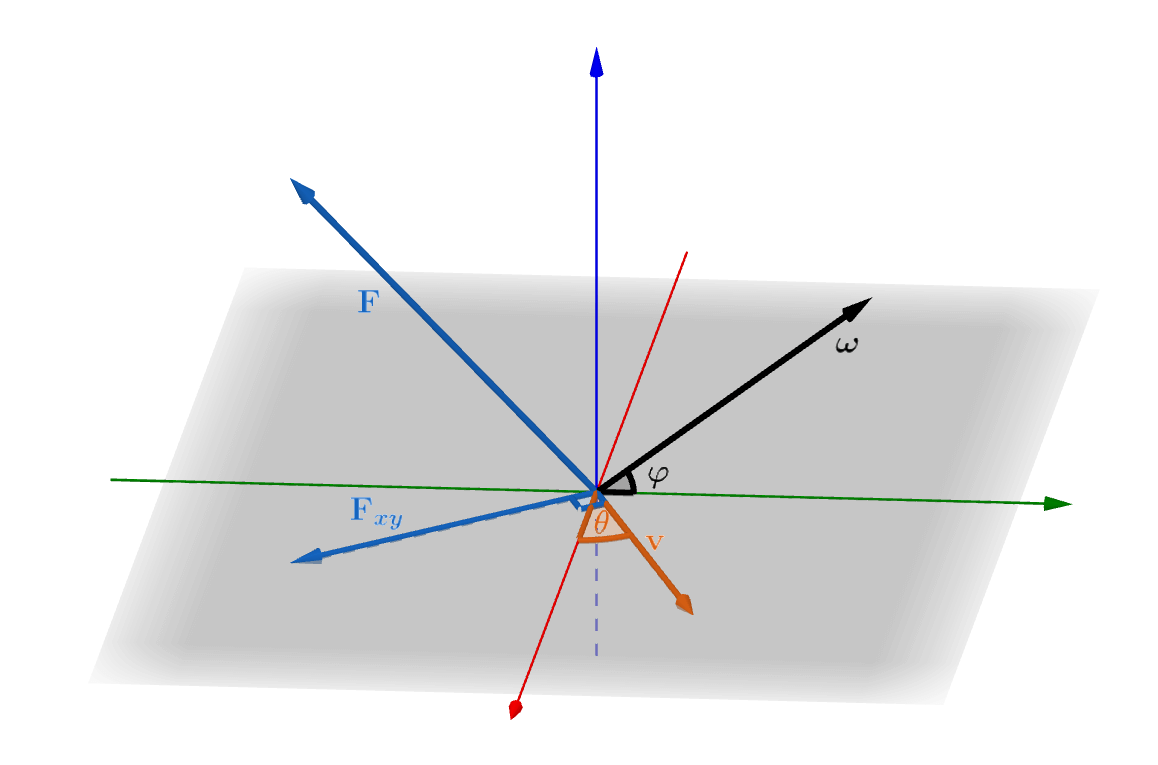
设\(m\)的速度大小为\(v\),方向(它只在\(x-y\)平面内运动)为\((\cos{\theta},\sin{\theta})\)(\(\theta\in\itvLr{0,2\pi}\),是与\(x\)轴夹角)方向,则速度矢量 \[ \vb{v}=(v\cos{\theta},v\sin{\theta},0) \] 而地球自转的角速度矢量朝向北极星方向,与地面夹角为当地纬度\(\varphi\)(\(\varphi\in\bqty{-\dfrac\pi2,\dfrac{\pi}{2}}\),北半球取正,南半球取负,赤道为\(0\)),所以角速度矢量 \[ \vb*\omega=(0,\omega\cos\varphi,\omega\sin\varphi) \] 由\(\vb{F}=2m\vb{v}\times\vb*\omega\)得到科里奥利力为\(2mv\omega(\sin\varphi\sin\theta,-\sin\varphi\cos\theta,\cos\varphi\cos\theta)\). 我们只关心科里奥利力的水平方向分量,因为在竖直方向上,科里奥利力相对于重力可以忽略不计(因为\(\omega\)很小). 科氏力的水平分量为 \[ \vb{F}_{xy}=2mv\omega\sin\varphi(\sin\theta,-\cos\theta) \] 它的大小为\(F=2mv\omega\abs{\sin\varphi}\),方向为\(\sin\varphi(\sin\theta,-\cos\theta)\)的方向. 据此有如下结论.
结论:科里奥利力的水平分量:
- 大小只与纬度和速度大小有关,当速度大小一定时,纬度越高,力越大,赤道为\(0\).
- 方向和速度方向垂直,
- 北半球(\(\sin\varphi>0\)),朝向速度右边.
- 南半球(\(\sin\varphi<0\)),朝向速度左边.
我们代入一系列具体值,求出不同纬度和速度对应的科里奥利加速度(水平分量)的大小\(({\rm m/s^2})\),来感受一下科里奥利力的影响:
| 纬度 | \(1{\rm m/s}\) | \(250{\rm m/s}\) | \(7000{\rm m/s}\) |
|---|---|---|---|
| \(0^\circ\) | \(0\) | \(0\) | \(0\) |
| \(40^\circ\) | \(0.000093\) | \(0.023\) | \(0.65\) |
| \(90^\circ\) | \(0.00015\) | \(0.036\) | \(1.02\) |
人步行的速度约为\(1{\rm m/s}\),科里奥利力对人走路的影响极小.
民航客机的巡航速度约为\(250{\rm m/s}\). 相对于重力、推力、或者扰动气流的作用等,科里奥利力对客机的作用很小,可以忽略不计.
洲际导弹的飞行速度约为\(7000{\rm m/s}\),这时科里奥利加速度最大可达到\(1.02{\rm m/s^2}\),约为重力加速度的\(1/10\). 而且洲际导弹大部分时间是在无动力、低阻力(约\(2000{\rm km}\)高空)情况下飞行的,且飞行距离长(大于\(8000{\rm km}\)),此时科里奥利力不可忽视,必须纳入弹道计算.
3.2 傅科摆
早在古希腊时期,一些毕达哥拉斯学派的人们就认为地球在自己转动,而非"天空"在转动产生了昼夜交替. 亚里士多德则认为地球是静止不动的,周围的恒星在围绕地球转动,托勒密的日心说也是基于此.
这种思想一直延续到16世纪,直到哥白尼提出日心说的时候. 地球自转会使得赤道略鼓,两极略平. 牛顿在《原理》书中预测了这种变化会以\(1:230\)的比例发生. 直到18世纪,人们才通过测量证实了哥白尼和牛顿观点.
由于地球自转,地球参考系中的物体会受科里奥利力的作用,这会导致北半球竖直下落的物体向右偏转. 18世纪末19世纪初,三位欧洲物理学家令一个球从\(158.5\)米高处落下,这个球向右偏转了\(27.4\)毫米,与计算值基本吻合.
最著名的证明地球自转的实验是由物理学家傅科(Léon Foucault)于 1851年进行的傅科摆实验.

傅科制作了一个\(67\)米长的、挂有\(28\)千克铅球的摆,即傅科摆(Foucault pendulum),挂在法国巴黎先贤祠(上图). 在摆受重力而摆动的同时,它受到科里奥利力而向右偏. 傅科摆的进动简单、直接地证明了地球的自转.
进动就是物体旋转轴方向的改变.
摆只受重力和拉力正常摆动时,转轴是过摆的中心,且垂直于摆动平面的直线. 当摆向右偏转时,转轴也会偏转,即进动;进动的周期为转轴旋转\(360^\circ\)的时间.
下面是一个傅科摆(近似)轨迹示意图(偏转程度被极度夸大了).
设摆长为\(L\),纬度\(\varphi\)(南负北正),地球自转角速度\(\omega\),则当摆的摆角非常小的时候:
摆动的周期(摆动一个来回时间)约为\(T_0=2\pi\sqrt{\dfrac{L}{g}}\).
进动的周期(摆的转轴旋转\(360^\circ\)的时间)约为\(T_p=\dfrac{2\pi}{\omega\abs{\sin\varphi}}\gg1{\rm s}\).
代入\(\omega=\dfrac{2\pi}{1\,{\rm day}}\),得\(T_p=\dfrac{1\,{\rm day}}{\abs{\sin\varphi}}\).
在赤道,傅科摆不会出现进动现象(或进动周期无穷大);在\(49^\circ{\rm N}\)的巴黎,周期为\(1.33\)天,即每小时\(11.28^\circ\);在南北极,进动的周期最小,为\(1\)天.
此外,傅科摆的轨迹在水平面上的投影是一条内摆线,即一个小圆在大圆内滚动时,小圆上某一点的轨迹.(其中小圆与大圆半径之比\(\dfrac{r}{R}=\dfrac12\pqty{1-\dfrac{T_0}{T_p}}\))
3.3 大气运动
当空气或者水质点\(m\)以速度\(v\)水平运动时,会受到大小为\(2mv\omega\abs{\sin\varphi}\)的科里奥利力,因为位移与地球半径相比较小,我们假定纬度\(\varphi\)不变.
如果\(m\)在水平方向不受其他力(质点靠惯性运动),那么它的轨迹将会是一个圆:
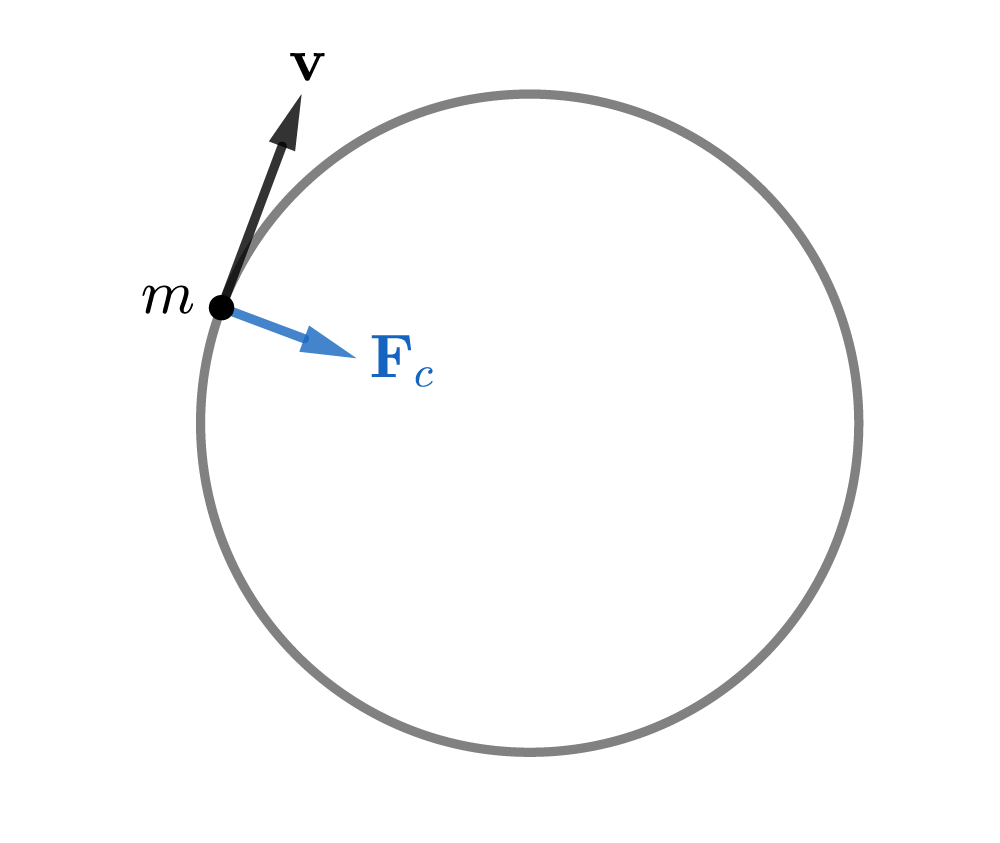
这个圆称为惯性圆(Inertial circle),设其半径为\(R\),则有 \[ m\frac{v^2}{R}=2mv\omega\abs{\sin\varphi} \] 解得\(R=\dfrac{v}{2\omega\abs{\sin\varphi}}\). 在中纬度地区,\(2\omega\abs{\sin\varphi}\)约为\(10^{-4}{\rm s^{-1}}\),所以对于\(10{\rm m/s}\)的典型大气速度,惯性圆半径是\(100{\rm km}\),运动周期为\(17{\rm h}\);对于\(0.1{\rm m/s}\)的典型洋流速度,半径是\(1{\rm km}\).
地球上各地惯性圆如下图,北半球质点顺时针转,南半球逆时针转.

上面的讨论是基于空气在惯性下运动这一情况的,实际上,在水平方向上,空气还会受:
阻力\(\vb{F}_r\):近地面空气与地面(下垫面)摩擦产生的阻力,与空气速度方向相反,大小与速度成正比: \[ \vb{F}_r=-k\vb{v} \] 空气内部不同部分相对运动产生的阻力很小,可以忽略不计.
水平气压梯度力\(\vb{F}_{g}\):造成空气(在水平方向上)由高气压处流向低气压处的力,它总是垂直于等压面、指向气压下降最快的方向,且它的大小正比于气压下降的速度. \(\vb{F}_g\)产生的加速度为: \[ \vb{a}_g=-\frac1\rho\nabla{P} \] 其中\(\rho\)为空气密度,约在\(1{\rm kg/m^3}\)量级;\(\nabla{P}\)是向量,称为"压力梯度",它的大小为气压上升的速度,方向为气压上升最快的方向. \(\nabla{P}\)的大小很小,约在\(10^{-4}{\rm N/m}\)量级. 梯度力的数量级和科氏力是接近的.
我们假设水平方向上,等压线是直线,且等距、平行(类似于匀强电场的特点).
在对流层高空,没有阻力\(\vb{F}_r\),所以气体只受到梯度力\(\vb{F}_g\)和科氏力.
红色矢量为速度;黑色、蓝色向量分别为梯度力、科氏力.
最开始只有梯度力,空气开始运动后便有了科氏力,运动方向开始向右偏转,速度逐渐增大. 偏转到与等压线平行时,我们理想地认为此时梯度力与科氏力平衡:\(\vb{F}_c+\vb{F}_g=\vb0\),所以空气开始沿着平行于等压线方向匀速运动. 此时的运动平衡状态称为"地转平衡".
但是实际上,并不会出现这种巧合的平衡:在速度与等压线平行时,科氏力大于梯度力,导致速度继续向右偏,一直回到初始的那条等压线,再重复以上运动,形成周期性震荡. 其实空气的轨迹和带电粒子在匀强电场与磁场的复合场中的运动轨迹相似,它们的运动方程的形式是相似的: \[ \Align{ m\vb{a} &= 2m\vb{v}\times\vb*\omega+\vb{F}_g \\ m\vb{a} &= q\vb{v}\times\vb{B}+q\vb{E} \\ } \]
在近地面,需要考虑阻力.
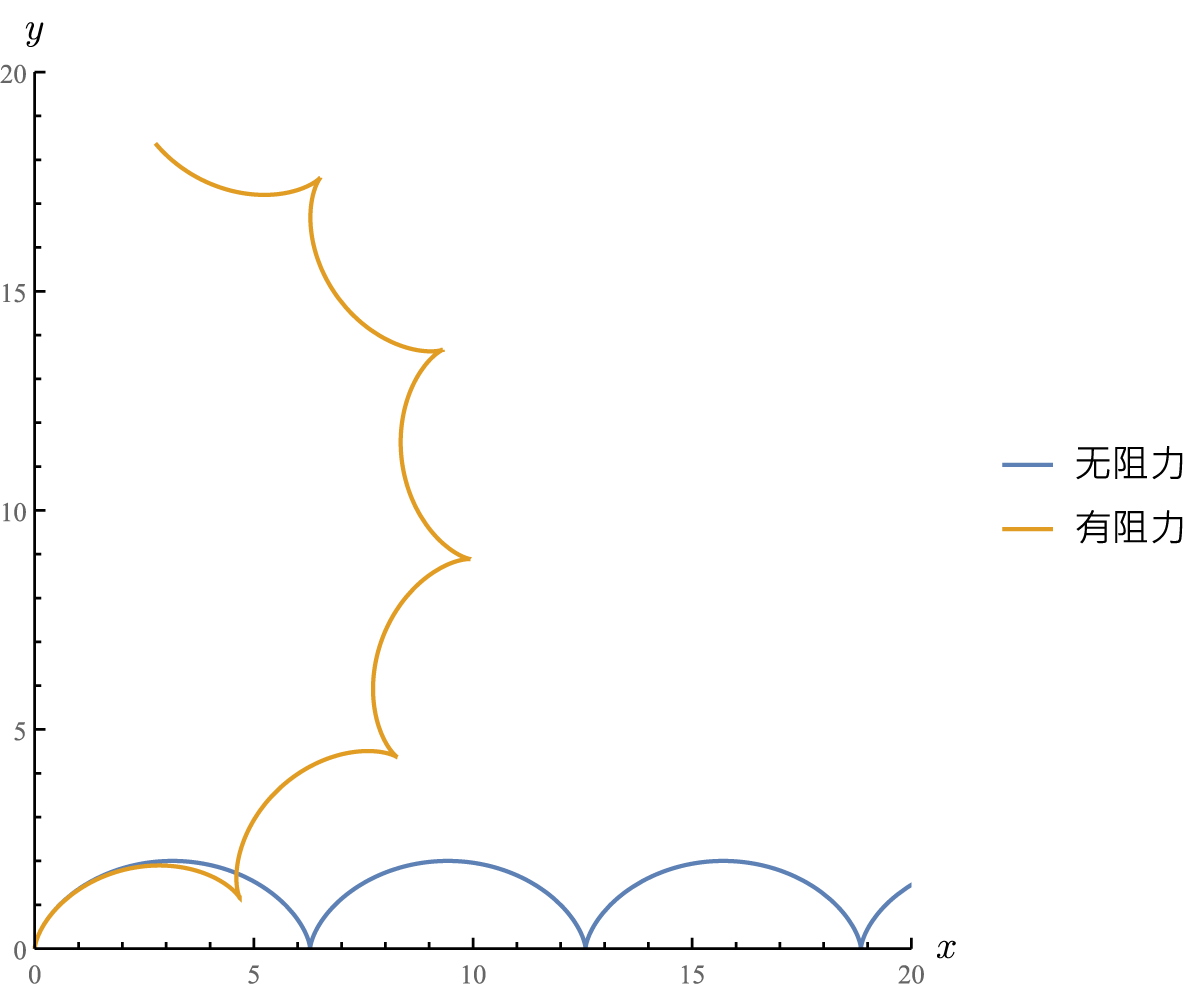
阻力减小了速度,削弱了科氏力的影响,所以运动偏转得没那么厉害. 近似地,速度近似斜交于等压线.
在真实情况下,需要考虑更多的影响因素,空气会形成不一样的轨迹. 下图展示了无阻力/有阻力情况下空气的轨迹示意图.
除了地转平衡之外,还有平衡模型如:
旋转平衡:梯度力和惯性离心力的平衡.
如龙卷风,水槽排水形成的漩涡,或者秋风刮起时,地上的叶子转起来的现象.
梯度平衡:梯度力、科氏力与惯性离心力平衡
如下面提到的气旋.
参考:Balanced Flow.
由于科里奥利力的存在,在大气环流和气旋现象中,可以明显地发现气流的偏转. 下图为地球上的风带以及气旋(北半球、南半球).
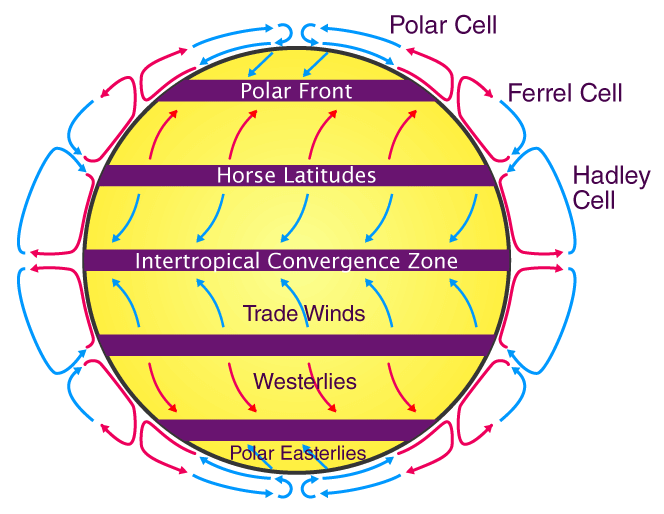 |
 |
|---|
Footnotes
F.1 关于叉乘
除了点积,向量还有一种叉积(Cross product)运算. 两个三维向量的叉积是另一个三维向量: \[ \vb{a}\times\vb{b}=\vb{c} \] 其中,\(\vb{c}\)同时垂直与\(\vb{a},\vb{b}\)两个向量,它的大小是\(\vb{a},\vb{b}\)确定的平行四边形的面积,方向由右手定则确定. 当\(\vb{a}\)与\(\vb{b}\)平行时,它们的叉积为零向量. 本文对叉积知识的要求不高,了解大小、方向的判定方法即可即可.
\(\vb{c}\)的模长:\(\abs{\vb{c}}=\abs{\vb{a}}\abs{\vb{b}}\sin\lr{\vb{a},\vb{b}}\).
右手定则:
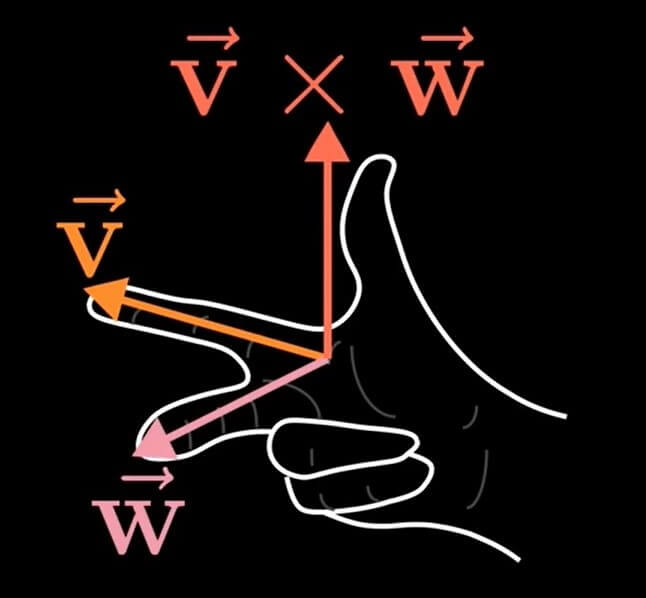
根据右手定则可以注意到,叉乘不满足交换律. 但是它具有:
- 反交换律:\(\vb{a}\times\vb{b}=-\vb{b}\times\vb{a}\).
- 线性性:\(\vb{a}\times(\lambda\vb{b}+\vb{c})=\lambda\vb{a}\times\vb{b}+\vb{a}\times\vb{c}\).
根据叉乘的定义就可以发现,三维空间的单位正交基\(\vu{i},\vu{j},\vu{k}\)满足\(\vu{i}\times\vu{j}=\vu{k}\),\(\vu{j}\times\vu{k}=\vu{i}\),\(\vu{k}\times\vu{i}=\vu{j}\)(三者轮换). 可以利用这个关系来导出叉积的坐标公式.
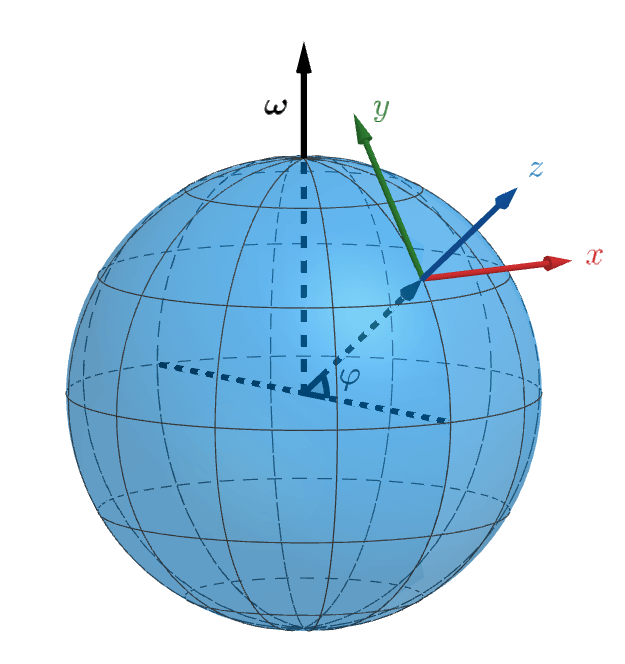
F.2 系间坐标的关系
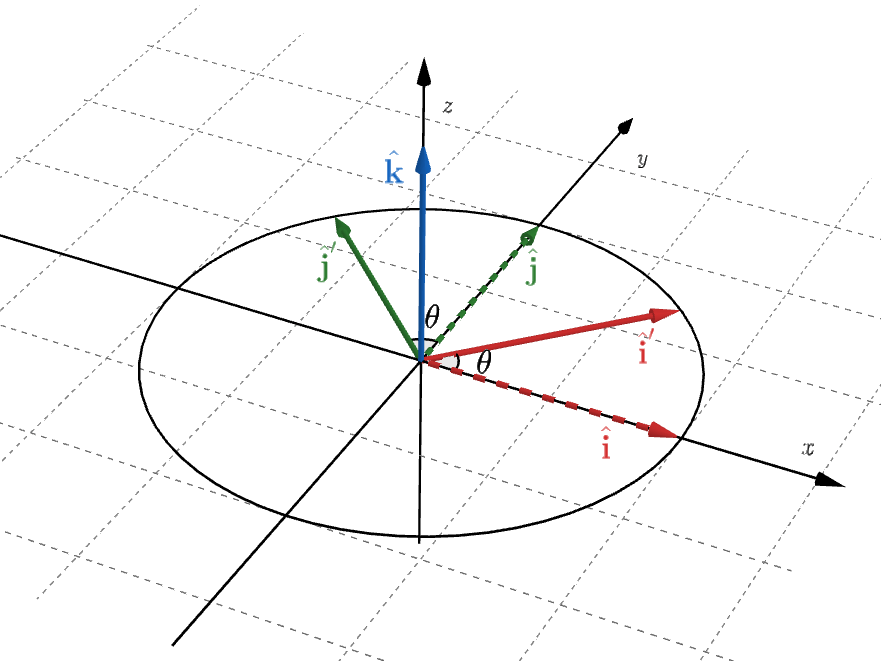
不妨以旋转系\(r\)的角速度\(\vb*\omega\)方向为\(z\)轴建立右手系,设惯性系\(i\)的单位正交基底(上图虚线)为\(\vu{i},\vu{j},\vu{k}\),旋转系\(r\)的基底(上图实线)为 \[ \Align{ \vu{i}'&=\pmqty{\cos\theta&\sin\theta&0}\T \\ \vu{j}'&=\pmqty{-\sin\theta&\cos\theta&0}\T \\ \vu{k}'&=\pmqty{0&0&1}\T } \] 其中\(\theta\)是旋转的角度,角速度大小\(\omega=\dv{\theta}{t}\);\(\theta,\omega\)和基向量\(\vu{i}',\vu{j}',\vu{k}'\)都是关于\(t\)的函数. 现在我们求出基向量的导数:利用复合函数求导法则有 \[ \Align{ \dv{\vu{i}'}{t}&=\pmqty{-\omega\sin\theta&\omega\cos\theta&0}\T=\omega\vu{j}' \\ \dv{\vu{i}'}{t}&=\pmqty{-\omega\cos\theta&-\omega\sin\theta&0}\T=-\omega\vu{i}' \\ \dv{\vu{k}'}{t}&=\vb0 \\ } \] 考虑叉积的几何意义(可参考[F.1]),有 \[ \dv{\vu{i}'}{t}=\vb*\omega\times\vu{i}', \quad \dv{\vu{j}'}{t}=\vb*\omega\times\vu{j}', \quad \dv{\vu{k}'}{t}=\vb*\omega\times\vu{k}' \] 所以如果\(r\)中的向量值函数\(\vb*{f}(t)=P(t)\vu{i}'+Q(t)\vu{j}'+R(t)\vu{k}'\),那么利用乘积求导法则,我们可以求出它在\(i\)参考系下的导数: \[ \Align{ \pqty{\dv{\vb*{f}}{t}}_i &= \pqty{\dv{P}{t}\vu{i}'+P\dv{\vu{i}'}{t}} +\pqty{\dv{Q}{t}\vu{j}'+Q\dv{\vu{j}'}{t}} +\pqty{\dv{R}{t}\vu{k}'+R\dv{\vu{k}'}{t}} \\ &= \pqty{\dv{P}{t}\vu{i}'+\dv{Q}{t}\vu{j}'+\dv{R}{t}\vu{k}'} +\bqty{\vb*\omega\times\pqty{P(x)\vu{i}+Q(x)\vu{j}+R(x)\vu{j}}} \\ &= \pqty{\dv{\vb*{f}}{t}}_r + \vb*\omega\times\vb*{f} } \] 其中\(\pqty{\dv{\vb*{f}}{t}}_r\)是\(\vb*{f}\)在\(r\)参考系下的导数. 上式揭露了两个参考系下向量函数导数的关系,如果提出公因子\(\vb*{f}\),则上式可以化简为: \[ \pqty{\dv{\vb*{f}}{t}}_i=\bqty{\pqty{\dv{}{t}}_r+\vb*\omega\times}\vb*{f} \] 将\(\bqty{\pqty{\dv{}{t}}_r+\vb*\omega\times}\)整体地看作一个算子. 这个式子在推导旋转参考系的惯性力中会用到.