ODE4 线性微分方程

1 向量

现在我们来关注线性（齐次）微分方程的求解. 从二阶的起步， \[ y''=py'+qy \] 我们把它扩写成方程组： \[ \Cases{ y'=y' \\ y''=py'+qy } \] 再改写成向量形式：令\(\vb{Y}=\pmqty{y\\y'}\)，\(\vb{A}=\pmqty{0&1\\q&p}\)，则有 \[ \vb{Y}'=\vb{AY} \tag{1.1} \] 这是一个关于向量\(\vb{Y}\)的一阶线性微分方程. 至此，我们完成了高阶方程\(\longrightarrow\)多个一阶组的转化.

方程\(\text{1.1}\)表示的含义是：有一个随时间变化的向量（函数）\(\vb{Y}(t)\)，它的变化率\(\vb{Y}'(t)\)等于一个矩阵作用于自身\(\vb{AY}(t)\)，如下面的动画所示：

薛定谔方程(Schrödinger equation)是一个线性微分方程： \[ \dv{}{t}\blue{\ket{\psi}} = \frac{1}{\i\hbar} \hat{H} \blue{\ket{\psi}} \] 其中\(\blue{\ket{\psi(t)}}\)是描述量子系统状态的向量；\(\hat{H}\)是一个线性算子；\(\i\)是虚数单位，\(\hbar\)是约化普朗克常数. 薛定谔方程的结构和\(\displaystyle\dv{}{t}\blue{ \vb{Y}}=\vb{A}\blue{\vb{Y}}\)十分相似.

2 叠加原理

我们先不着急求解，而是研究一下这个方程的性质： \[ \vb{Y}'(t)=\vb{AY}(t) \] 线性齐次微分方程的一个重要特性是叠加原理(superposition principle)：如果\({\color{royalblue}\vb{Y}_1}(t)\)与\({\color{forestgreen}\vb{Y}_2}(t)\)都是方程的解，那么它们的线性组合\(\alpha{\color{royalblue}\vb{Y}_1}(t)+\beta{\color{forestgreen}\vb{Y}_2}(t)\)也是方程的解.

原因：线性齐次微分方程\(\displaystyle\dv{}{t}\vb{Y}=\vb{AY}\)的左右两边都是线性的： \[ \Align{ \dv{}{t}( \alpha{\color{royalblue}\vb{Y}}_1+ \beta{\color{forestgreen}\vb{Y}_2}) &= \alpha\dv{}{t}{\color{royalblue}\vb{Y}}_1 + \beta\dv{}{t}{\color{forestgreen}\vb{Y}_2} \\ \vb{A}( \alpha{\color{royalblue}\vb{Y}}_1+ \beta{\color{forestgreen}\vb{Y}_2}) &= \alpha\vb{A}{\color{royalblue}\vb{Y}}_1 + \beta\vb{A}{\color{forestgreen}\vb{Y}_2} } \] 线性(linear)的含义就是保持线性运算（加法和数量乘法）：如果 \[ \Cases{ F({\color{royalblue}\vb{v}}+{\color{forestgreen}\vb{w}}) = F({\color{royalblue}\vb{v}})+F({\color{forestgreen}\vb{w}}) \\ F(\alpha{\color{royalblue}\vb{v}}) = \alpha F({\color{royalblue}\vb{v}}) } % \textsf{, 合起来就是} % F(\alpha{\color{royalblue}\vb{v}}+\beta{\color{forestgreen}\vb{w}}) % =\alpha F({\color{royalblue}\vb{v}}) % +\beta F({\color{forestgreen}\vb{w}}) \] （其中\(\alpha,\beta\)是实数，\(\vb{v},\vb{w}\)是向量）那么称映射\(F\)是线性的. 导数算子\(\displaystyle\dv{}{t}\)，矩阵\(\vb{A}\)都是线性的.

例如，

• 对于人口模型\(N'=rN\)，当初始人口是\(n\)，有\(N=N_1(t)\)，那么初始人口为\({\color{coral}2}n\)时，\(N={\color{coral}2}N_1(t)\).

• 一个简谐振子在\(P\)处自由释放，得到\(x={\color{royalblue}x_1}(t)\)，在原点处以初速度\(v\)释放，得到\(x={\color{forestgreen}x_2}(t)\)，则在\(P\)处以初速度\(v\)释放，有\(x={\color{royalblue}x_1}(t)+{\color{forestgreen}x_2}(t)\).

  

  在相空间中的表现就是向量的线性运算.

• 薛定谔方程是线性的，量子系统的状态\(|\Psi(t)\rangle\)也满足叠加原理.

3 指数函数

现在来求解方程.

注意到向量微分方程\(\vb{Y}'(t)=\vb{AY}(t)\)和一阶微分方程\(y'(t)=ay(t)\)的形式是相同的，其实它们解的形式也相同： \[ y(t)=\e^{at}\cdot y_0 \quad\textsf{和}\quad \vb{Y}(t)=\e^{\vb{A}t}\cdot \vb{Y}_0 \] 其中\(y_0=y(0)\)是一个初值条件；\(\vb{Y}_0=\vb{Y}(0)=\pmqty{y{(0)}\\y'{(0)}}\)，包含了\(2\)个初值条件.

\(\e^{\vb{A}}\)称为矩阵\(\vb{A}\)的指数函数. 回想指数函数\(f(x)=\e^x\)的Taylor级数： \[ \small{ \e^x =1+\frac{x^1}{1!}+\frac{x^2}{2!}+\dots =\sum_{k=0}^\infty \frac{x^k}{k!} \quad (x\in\R) } \] 照葫芦画瓢，矩阵指数就是 \[ \small{ \e^{\vb{A}} =\vb{I}+\frac{\vb{A}^1}{1!}+\frac{\vb{A}^2}{2!}+\dots =\sum_{k=0}^\infty \frac{\vb{A}^k}{k!} \quad (\vb{A}\textsf{是$2\times2$方阵}) } \] （认为\(\vb{A}^0=\vb{I}\)为单位阵）一般把\(\e\)指数函数\(\e^{\vb{A}}\)记作\(\exp(\vb{A})\)；函数输出的结果还是一个\(2\times2\)的矩阵.

当然，也可以用第二篇「一阶微分方程」\(\S4\)中的思路（从差分到微分）来推导矩阵指数.

现在我们来直观地感受一下矩阵指数. 矩阵表示了一个线性变换，\(\purple{\exp(\vb{A}t)}\cdot\vb{Y}_0\)表示的就是一个线性变换\(\purple{\exp(\vb{A}t)}\)作用在了向量\(\vb{Y}_0\)身上.

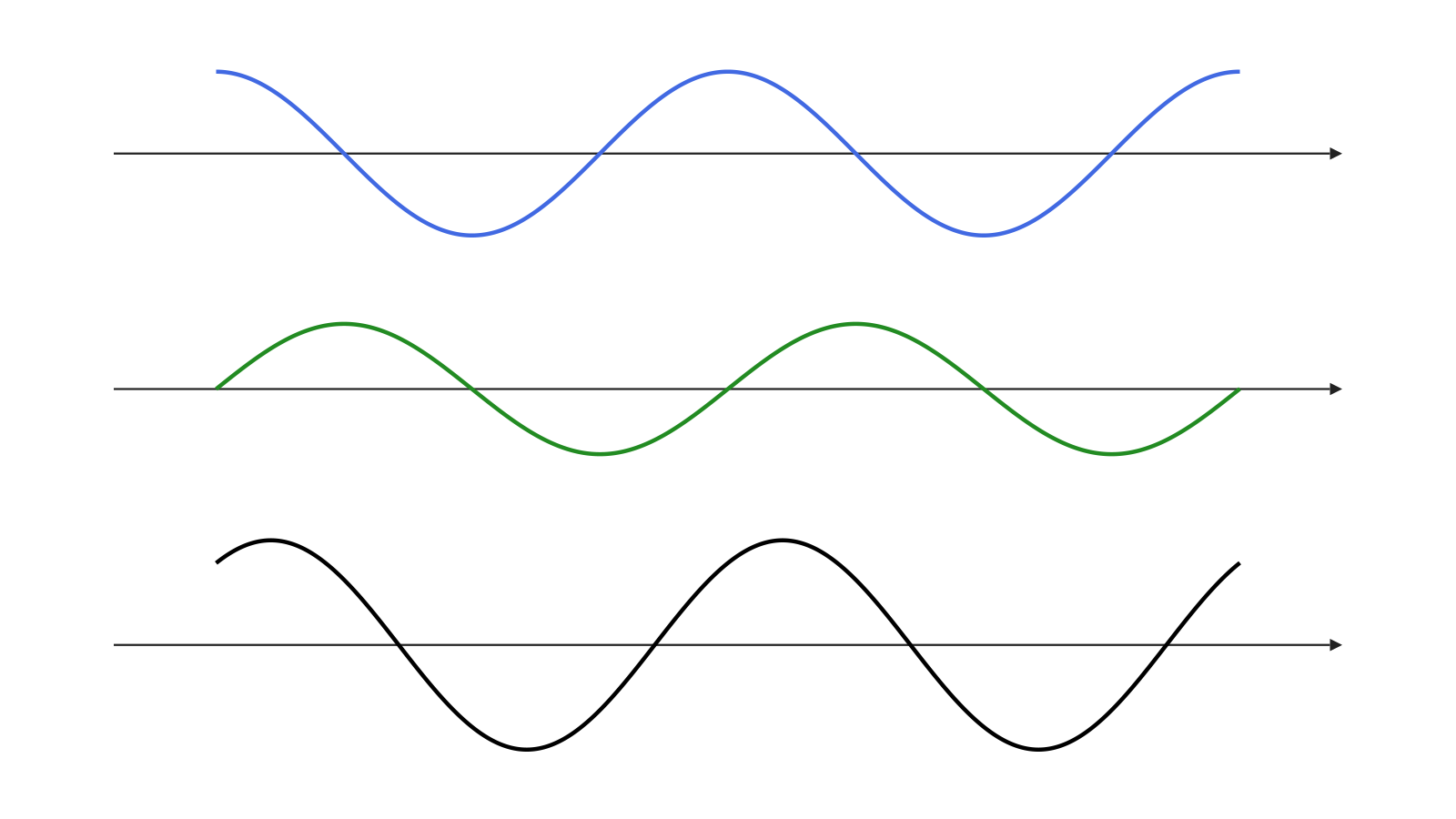
举一个具体的例子，简谐振子的运动方程是\(\Cases{x'=v\\v'=-\dfrac{k}{m}x}\). 不妨让\(\dfrac km=1\)，那么 \[ \pmqty{x\\v}'=\pmqty{0&1\\-1&0}\pmqty{x\\v} \] 发现\(\vb{A}=\pmqty{0&1\\-1&0}\)是一个顺时针\(90^\circ\)的旋转矩阵，也就是说\(\vb{Y}'\)的变化率与\(\vb{Y}'\)垂直，也就是说，\(\vb{Y}\)在\(x-v\)相平面中做匀速圆周运动（如下），\(x,v\)与\(t\)的关系都是正弦式的.

我们再来计算\(\exp(\vb{A}t)\)，注意到\(\vb{A}\)的幂是以\(4\)为周期的（因为顺时针旋转\(4\)个\(90^\circ\)后又回到了初始状态）： \[ \begin{array}{} \vb{A}^0=\pmqty{1&0\\0&1} & \vb{A}^1=\pmqty{0&1\\-1&0} & \vb{A}^2=\pmqty{-1&0\\0&-1} & \vb{A}^3=\pmqty{0&-1\\1&0} \\ \vb{A}^4=\pmqty{1&0\\0&1} & \dots\dots \end{array} \] 所以 \[ \Align{ \exp(\vb{A}t) &=\vb{A}^0 +\frac{\vb{A}^1t^1}{1!} +\frac{\vb{A}^2t^2}{2!} +\frac{\vb{A}^3t^3}{3!}+\dots \\ &=\pmqty{1&0\\0&1} +\pmqty{0&\frac{t^1}{1!}\\-\frac{t^1}{1!}&0} +\pmqty{-\frac{t^2}{2!}&0\\0&-\frac{t^2}{2!}} +\pmqty{0&-\frac{t^3}{3!}\\\frac{t^3}{3!}&0}+\dots \\ &=\pmqty{ {\color{orange}1-\frac{t^2}{2!}+\frac{t^4}{4!}-\dots} & {\color{orangered}\frac{t^1}{1!}-\frac{t^3}{3!}+\frac{t^5}{5!}-\dots} \\ -\pqty{{ \color{orangered}\frac{t^1}{1!}-\frac{t^3}{3!}+\frac{t^5}{5!}-\dots }} & {\color{orange}1-\frac{t^2}{2!}+\frac{t^4}{4!}-\dots} } \\ &=\pmqty{ {\color{orange}\cos{t}} & {\color{orangered}\sin{t}} \\ -{\color{orangered}\sin{t}} & {\color{orange}\cos{t}} } } \] （最后一步利用了\(\color{orange}\cos{t}\)和\(\color{orangered}\sin{t}\)的Taylor展开式）矩阵\(\pmqty{ {\color{orange}\cos{t}} & {\color{orangered}\sin{t}}\\-{\color{orangered}\sin{t}} & {\color{orange}\cos{t}} }\)恰好是顺时针旋转\(t\)（弧度）的矩阵，那么\(\vb{Y}=\pmqty{ {\color{orange}\cos{t}} & {\color{orangered}\sin{t}} \\-{\color{orangered}\sin{t}} & {\color{orange}\cos{t}} }\vb{Y}_0\)表示：\(\vb{Y}\)从\(\vb{Y}_0\)开始，顺时针匀速旋转.

那么，对于一个一般的\(\vb{A}\)，怎样求\(\purple{\exp(\vb{A}t)}\)？我们当然希望矩阵\(\vb{A}\)越简单越好，简化的方式就是把它写成更简单的矩阵的乘积（把线性变换分解为更简单的变换的复合）. 线性代数的一大主题就是把复杂的矩阵（线性算子）分解为简单的矩阵（线性算子）的乘积（复合）.

4 向量空间

我们再来研究一下二阶线性微分方程的解集\(V=\set{f\,|\,f''=pf'+qf}\). 我们知道，叠加原理描述了\(V\)对加法、数量乘法的封闭性： \[ \Align{ \textsf{如果}f,g\in V, \hspace{5pt}& \textsf{那么}f+g\in V \\ \textsf{如果}f\in V, \hspace{5pt}& \textsf{那么}\alpha f\in V \quad (\alpha\in\R) } \]

其中，函数的加法和数乘的概念是很自然的：

• 加法：\((f+g)(x)=f(x)+g(x)\).
• 数量乘法：\((\alpha f)(x)=\alpha f(x)\)（\(\alpha\in\R\)）.

这样的集合\(V\)十分特殊，以至于我们专门给它了一个定义.

我们把这种定义了加法与数量乘法（且对这两种运算封闭）的集合\(V\)称作向量空间(vector space)，\(V\)里面的元素\(f,g,\dots\)叫做向量(vector).

这里的定义是简化版本. 要成为一个向量空间，\(V\)上的加法、数量乘法还要满足一些性质，比如交换律、结合律、分配律.

我们在高中接触过平面向量，那时我们定义平面向量\(\vb{a}\)是一个有方向、有大小的量，可以形象地表示为二维空间中的有向线段\(\va{OA}\)，也可以表示成有序实数对\((x,y)\)；与之类似的，物理中的矢量是一个有大小、方向的量，而且满足平行四边形法则……

"向量空间"就是这些概念的推广：以上这些（平面向量的集合、有序实数对的集合、某一点上所有矢量的集合、函数的集合……）都是向量空间.

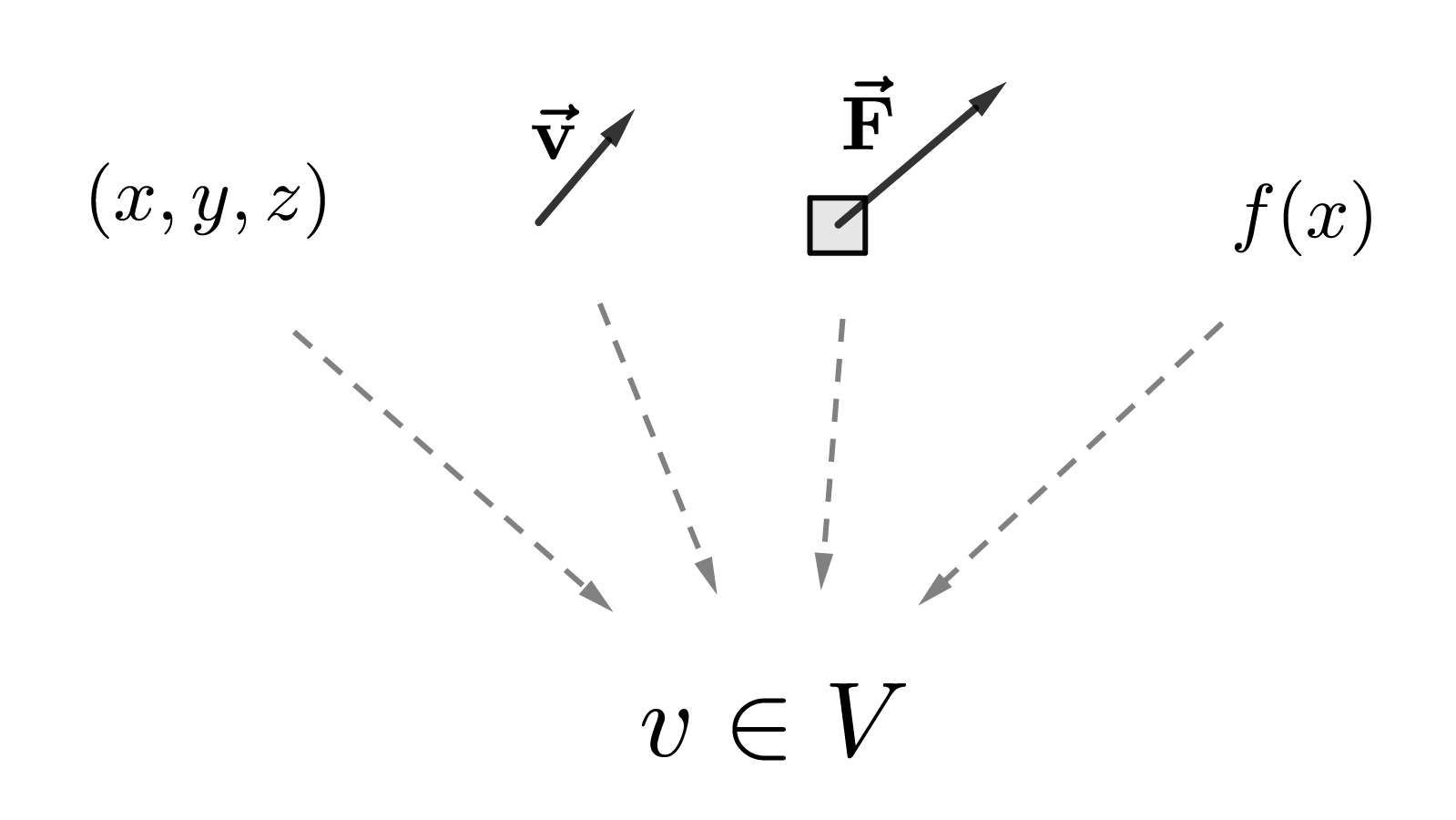
"向量"的本质既不是它的长度、方向，也不是怎样来表示向量（箭头、有序数组……），而是它的线性运算： \[ \large \alpha\blue{v}+\beta\blue{w} \] 而向量空间的本质，就是定义了线性运算（也叫线性结构）的集合\(V\)（所以也叫线性空间），向量就是线性空间里面的元素. 定义了线性结构之后，我们还可以往\(V\)上附加其他东西：

• 线性相关与线性无关的概念. 进而可以引出基底、维度、坐标……

• 内积. 作为点积的推广，内积本质上是一个函数，把两个向量\((v,w)\)映射到一个实数，一般记作\(\lr{v,w}\)（注意这不是中学课本里的"夹角"）.

  • 内积为我们带来的"长度"、"夹角"等概念：\(\abs{v}=\sqrt{\lr{v,v}}\)，\(\cos(v,w\textsf{的夹角})=\dfrac{\lr{v,w}}{\abs{v}\cdot\abs{w}}\).

    这时候我们就可以谈及一个向量的"大小"或者"方向"了.

    我们甚至可以说一个函数\(f\)的"长度"（范数），或者两个函数\(f,g\)"正交"（内积为\(0\)）.

• 线性映射，也就是两个线性空间\(V,W\)之间，保持线性运算的函数\(T\). 有了它，就可以构建起两个线性空间之间的关系……

  如果把线性空间比作舞台，那线性映射就是舞台上的表演. 线性映射的理论是线性代数中最精彩的部分.

• ……

当然，普适的代价是抽象（Abstractness is the price of generality），如果要得出脱离于具体实例的结论，当然要抛弃一部分具体与直观；但是在研究的过程中，借助直观的实例来探究、理解还是很有帮助的.

下面是一些个人想法\((^-\,_\Lambda\,^-\,)\)

在学习抽象概念的时候，极为重要的一点就是理解这个概念，构建起概念间的关系，形成框架. 在此之后，再往里面填充细节（比如定理的证明、习题等）.

比如一棵树，先长枝干，再长叶子，那么这棵树的长势、形态就非常清晰明了；如果先是一堆叶子的话，东一片西一片，就会显得凌乱复杂了. 像后者这样学习，越学越乱.

当然，概念的理解与框架的构建是艰难的过程. 看到一个定义的时候，你可能完全不知所云，想破脑袋也不知道这个鬼东西是怎么来的，为什么要定义成这个样子. 这时候可以借助"直观"来理解，或者干脆往后学或者去干别的事情. 在这之后总会有一天，你忽然就明白了（脑回路对上了），"原来xxx就是xxx！"，豁然开朗. 学习就是这样一个让自己的观点重构、理解深入的过程.

• 学习不图快，也不必急，只要理解层次到了，那顿悟就是一瞬间的事.
• 上面的"直观"包括但不限于通常说的"几何直观"，只要你构建了清晰的框架，代数什么的也可以很直观.