ODE3 二阶微分方程

1 简谐运动

一个无阻尼简谐振子的运动方程如下： \[ mx''(t)=-kx(t) \] 其中\(m,k>0\). 这是一个二阶线性微分方程. 我们知道，弹簧振子作简谐运动，方程的解是余弦函数： \[ x(t)=A\cos(\sqrt{\dfrac km} \cdot t+\varphi) \] 其中包含两个待定常数：振幅\(A\)、初相\(\varphi\)，它们和初始位置\(x(0)\)以及初始速度\(x'(0)\)有关.

\(x-t\)图线切线的斜率就是速度，在振子的示意图中用橙色的向量表示.

1.1 相空间

描述这个系统的状态需要位移\(x\)和速度\(v=x'\)两个量，我们不妨画出\(v-x\)图. 根据能量守恒： \[ \frac12kx^2+\frac12mv^2=E_0(系统机械能) \] 这是一个椭圆的方程.

椭圆上的每个点\((x,v)\)都是系统某一时刻的状态. 实际上，\(v-x\)平面中的每一个点\((v,x)\)都代表了系统的一个可能的状态：改变系统的初始值，就能够得到不同大小的椭圆.

我们把\(v-x\)平面叫做相空间(phase space)，把其中的那个椭圆叫做轨线(trajectory).

相空间包含了系统所有的状态. 一个\(n\)阶的微分方程的相空间是\(n\)维的.

一阶微分方程\(N'=rN\)的相空间是一条直线.
二阶微分方程\(x''=-\dfrac kmx\)的相空间是一个二维平面（也称为相平面）. 为什么是二维的？因为要确定一个简谐振子的振动状况需要两个量：初始位置\(x_0\)和初始速度\(v_0\).

轨线是相空间中的一条曲线，它描述了系统的一种演化方式.

1.2 向量场

在上一篇文章中，我们研究了一阶微分方程. 一阶方程的相空间是一条直线，如下图中的\(v\)轴. 同时，我们在相空间上建立了一个向量场：把每一点\(v\)都对应到了一个一维向量\(v'\)，来表示\(v\)的变化率.

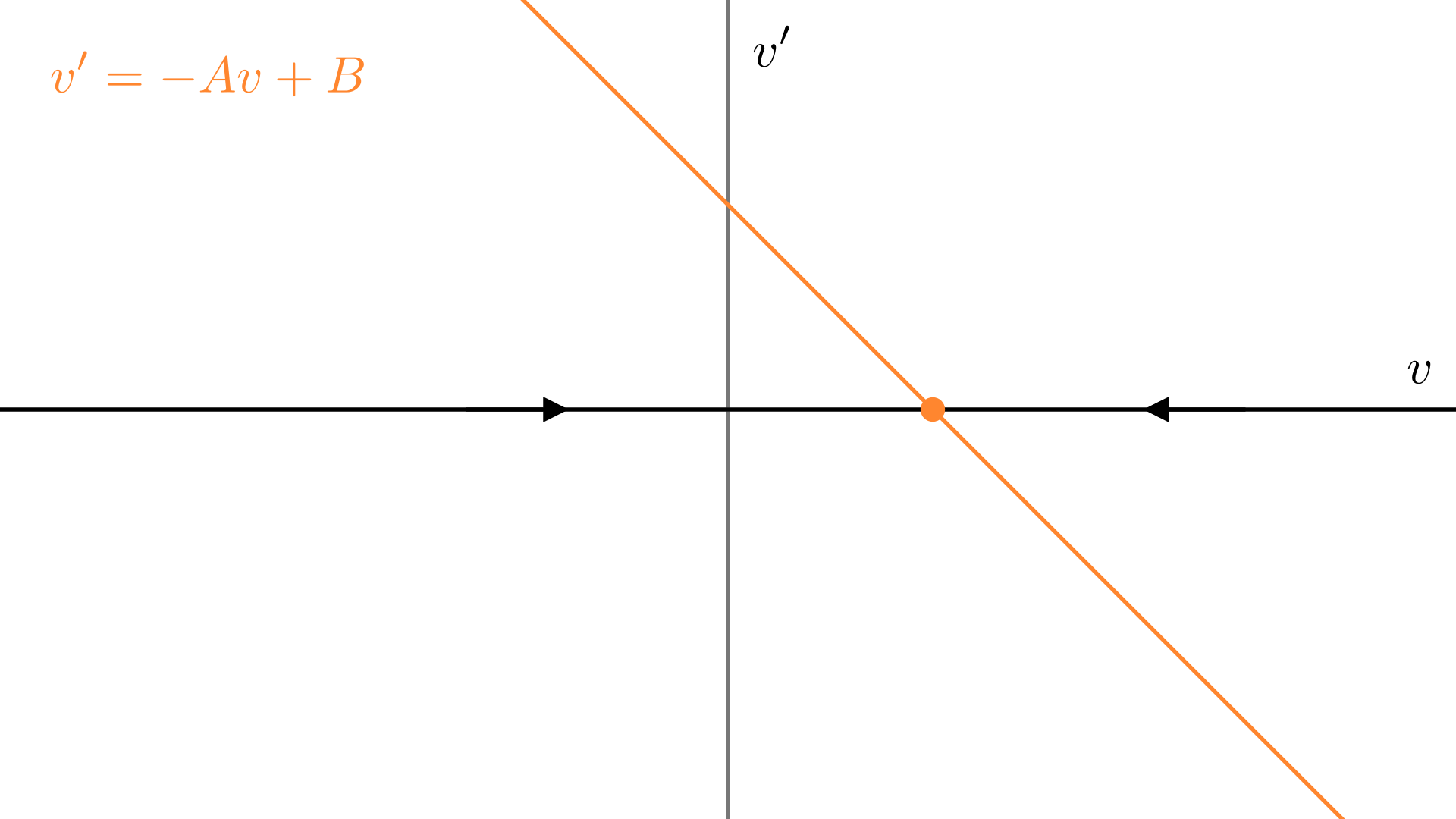
对于二阶方程，我们也可以画出它的"向量场". 令\(x'=v\)，点\((x,v)\)处的向量就是此处的变化率，即 \[ \dv{}{t}\pmqty{\orange{ x}\\\blue{ v}} = \pmqty{x'\\v'} = \pmqty{\blue{ v}\\-\frac km \orange{ x}} \]

*这里把向量的两个分量纵向排列\(\pmqty{\ast\\\ast}\)（"列向量"），理解起来和横着写的\((\ast,\ast)\)（"行向量"）一样.

这个向量形式的式子等价于方程组 \[ \Cases{x'=v\\v'=-\frac km x} \] 这个方程组与原方程是等价的，但是这里的最高阶数是\(1\). 一般我们采用变量替换的方式来把高阶微分方程转化为一阶微分方程组，使得问题易于考虑，同时便于可视化.

于是可以画出这个向量场（向量的长度由颜色体现）：

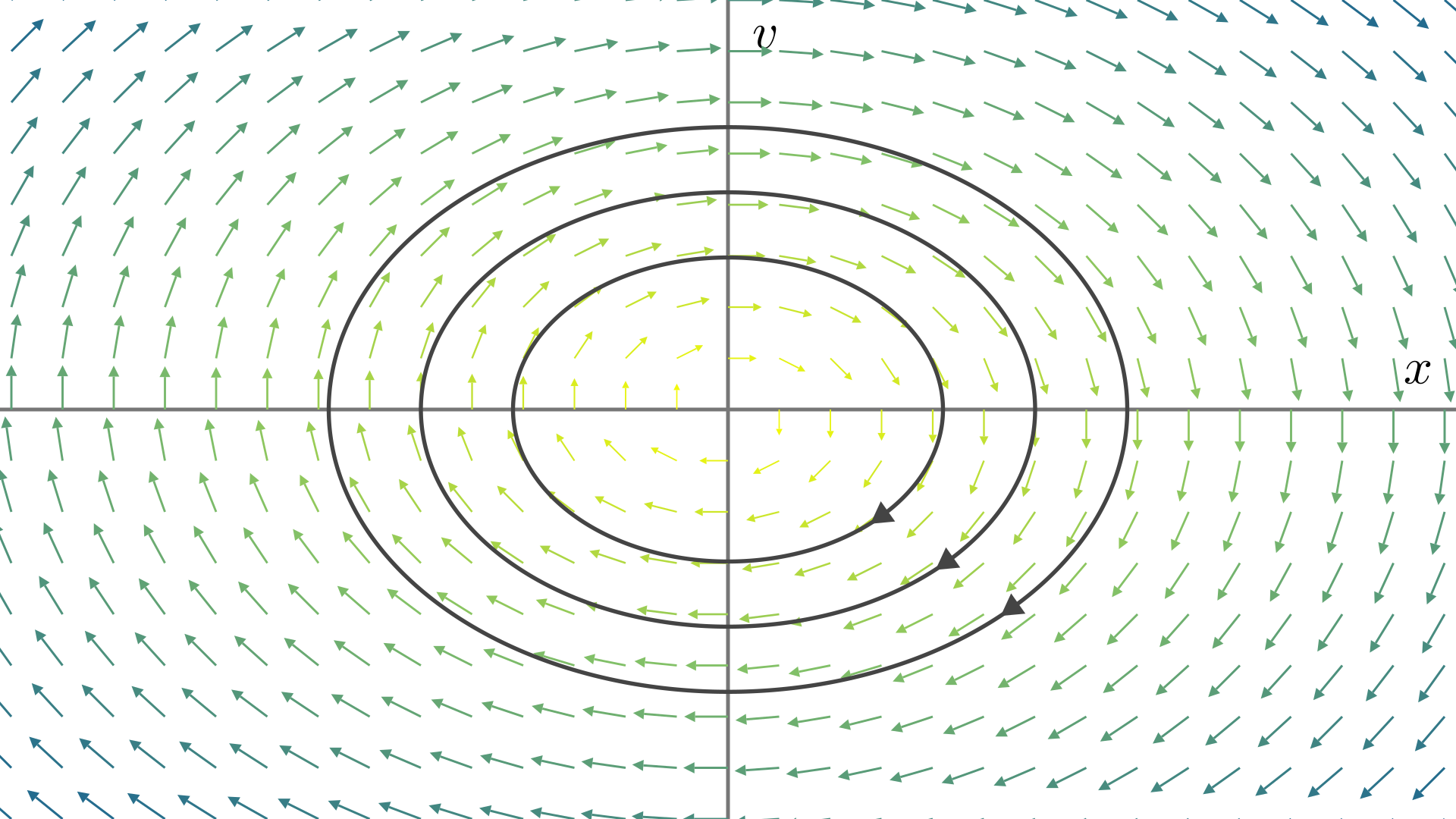
注意到，轨线上每一点处的向量总是与轨线相切的，而且指向轨线延伸的方向（即\(t\)增大的方向）.

现在我们在方程中加入一个阻尼项\(-\mu x'(t)\)（\(\mu>0\)），表示正比于速度的阻力. \[ mx''=-\mu x'-kx \] 写成向量形式 \[ \dv{}{t} \pmqty{x\\v} = \pmqty{v\\-\frac{k}{m} x-\frac\mu{m} v} \] 我们画出向量场和轨线. 由于能量损失，轨线不再是一条封闭的曲线，而是逐渐向原点靠近，振幅越来越小. 调整的\(\mu\)的值，可以发现\(\mu\)越大，\(v\)随衰减得越快，如下图. 光看方程是很难得到这一点的.

我们可以发现，当\(\mu>0\)时，原点\((0,0)\)是一个稳定的不动点，所有的解都会趋于原点.

1.3 不动点

回顾：我们知道，对于一阶线性微分方程 \[ y'=ay \] 不动点的性质是由\(a\)的正负决定的：

如果\(a>0\)，恰有一个不动点，且是不稳定的；
如果\(a<0\)，恰有一个不动点，且是稳定的；
如果\(a=0\)，所有的点都是不动点.

一个二阶（齐次）线性微分方程的一般形式是 \[ y''-py'-qy=0 \] 令\(\vb{y}=\pmqty{y\\y'}\)，于是有\(\dv{}{t}\pmqty{y\\y'}=\pmqty{y'\\y''}=\pmqty{y'\\py'+qy}\). 再进一步，我们可以地把方程写成\(\vb{y}'=\vb{A}\vb{y}\)的形式，与一阶方程相似. 不过这里的\(\vb{A}\)是一个\(2\times2\)的矩阵. \[ \dv{}{t} {\color{green} \pmqty{y\\y'}} = \pmqty{y'\\py'+qy} = {\color[rgb]{.12,.39,.6}\pmqty{0&1\\q&p}} {\color{green} \pmqty{y\\y'}} \] 所以\(\vb{A}={\color[rgb]{.12,.39,.6}\pmqty{0&1\\q&p}}\). 不动点满足\(\vb{y}'=\vb{Ay}=\vb0\)，原点\(\vb0\)一定是一个不动点. 那么，我们有没有一种方法，能够判断\(\vb{A}\)的"正负"，从而判断不动点的稳定性？

回顾一阶方程\(y'=ay\)，它的向量场分布在一条直线上. \(y\)始终沿着这条直线趋近/远离不动点（原点）.

现在，方程的向量场变成了二维的平面，于是我们可以考虑降维：是否存在某条过原点的直线，使得这条直线上面的\(\vb{y}\)是沿着这条直线趋近/远离不动点的？也就是考虑 \[ \lambda\vb{y} = \dv{}{t}\vb{y} = \vb{Ay} \] 其中\(\lambda\)是一个数，\(\vb{y}\)是某个特定方向上向量. \(\lambda\vb{y}\)表示\(\vb{y}\)始终沿着一条直线运动. 如果我们能够解出\(\lambda\)，那么就可以作出如下判断：

如果\(\lambda>0\)，那么这条直线上的\(\vb{y}\)会远离不动点.
如果\(\lambda<0\)，那么这条直线上的\(\vb{y}\)会靠近不动点.
如果\(\lambda=0\)，那么这条直线上的点都是不动点.

对于\(\vb{Ay}=\lambda\vb{y}\)（\(\vb{y}\ne\vb0\)），我们称\(\lambda\)是\(\vb{A}\)的一个特征值，\(\vb{y}\)是所\(\lambda\)对应的特征向量.

要了解特征值与特征向量，可观看视频：特征向量与特征值.

特征值\(\lambda\)满足特征方程： \[ \lambda^2-p\lambda-q=0 \] 有两个根\(\lambda_1,\lambda_2\)（称为特征根）.

首先考虑\(\lambda_1,\lambda_2\)都不为零的情况.

如果\(\lambda_1,\lambda_2\)是两个互不相同的实根，那么它们对应的特征向量也线性无关. 所以，在两个方向上，\(\vb{y}\)是被纯拉伸的.
- \(\lambda_1,\lambda_2\)同号，那么所有的\(\vb{y}\)都趋于不动点（两根小于零），或者所有的\(\vb{y}\)都远离不动点（两根大于零）. 分别对应了"山谷"（稳定结点）和"山顶"（不稳定结点）.
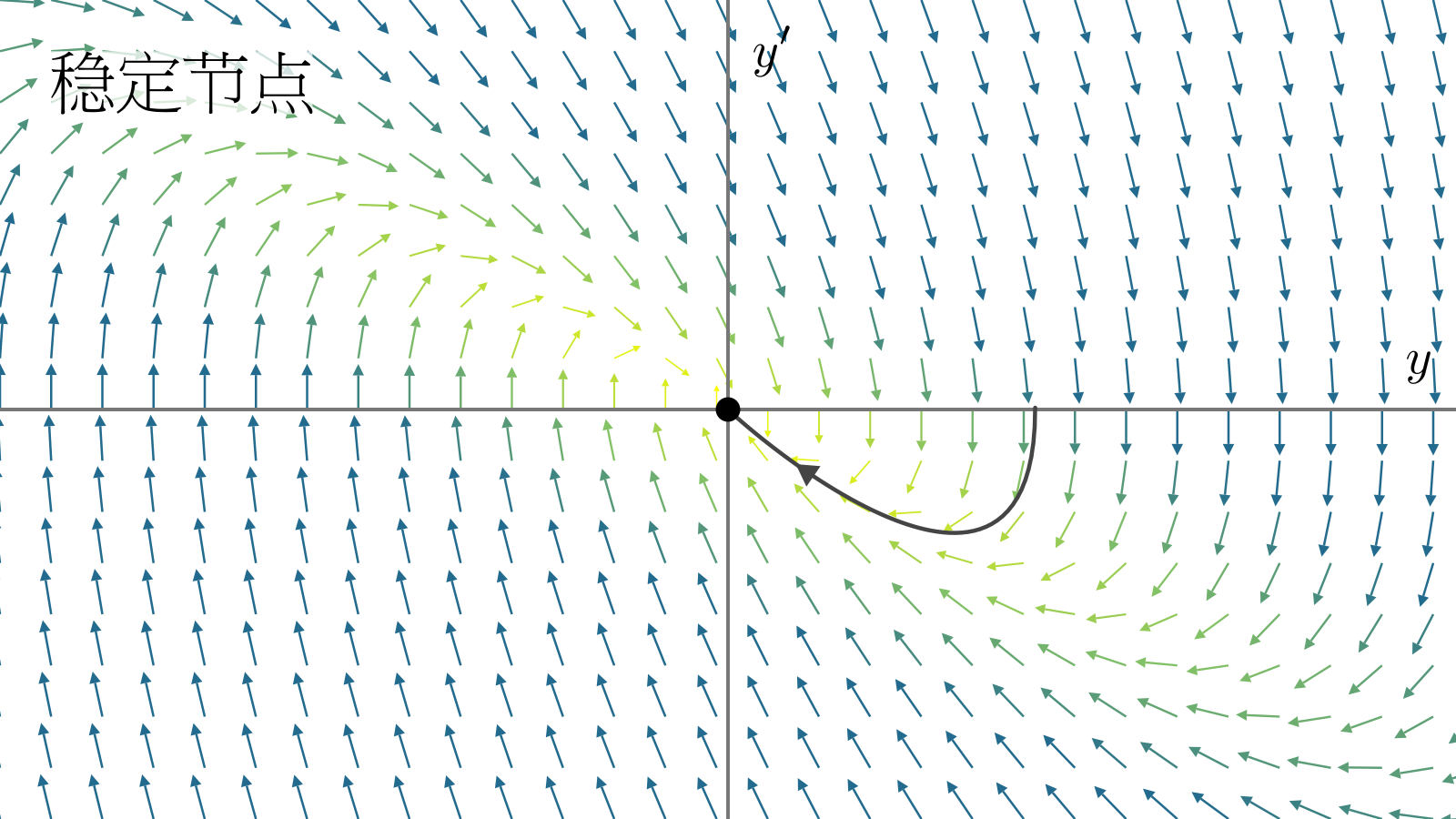
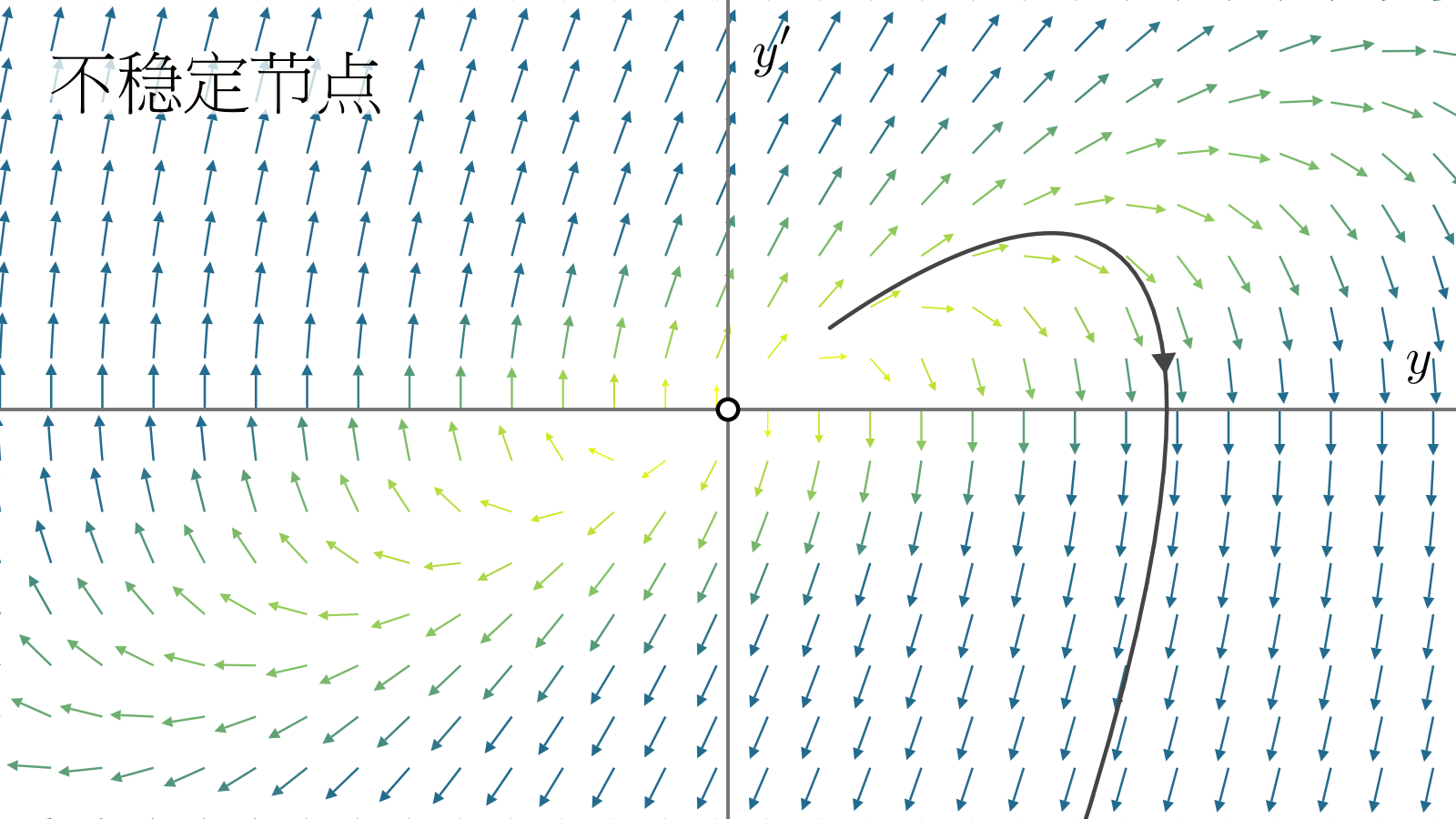
- \(\lambda_1,\lambda_2\)异号，那么不动点在一个方向上是吸引的，另一个方向上是排斥的，不动点称为鞍点.
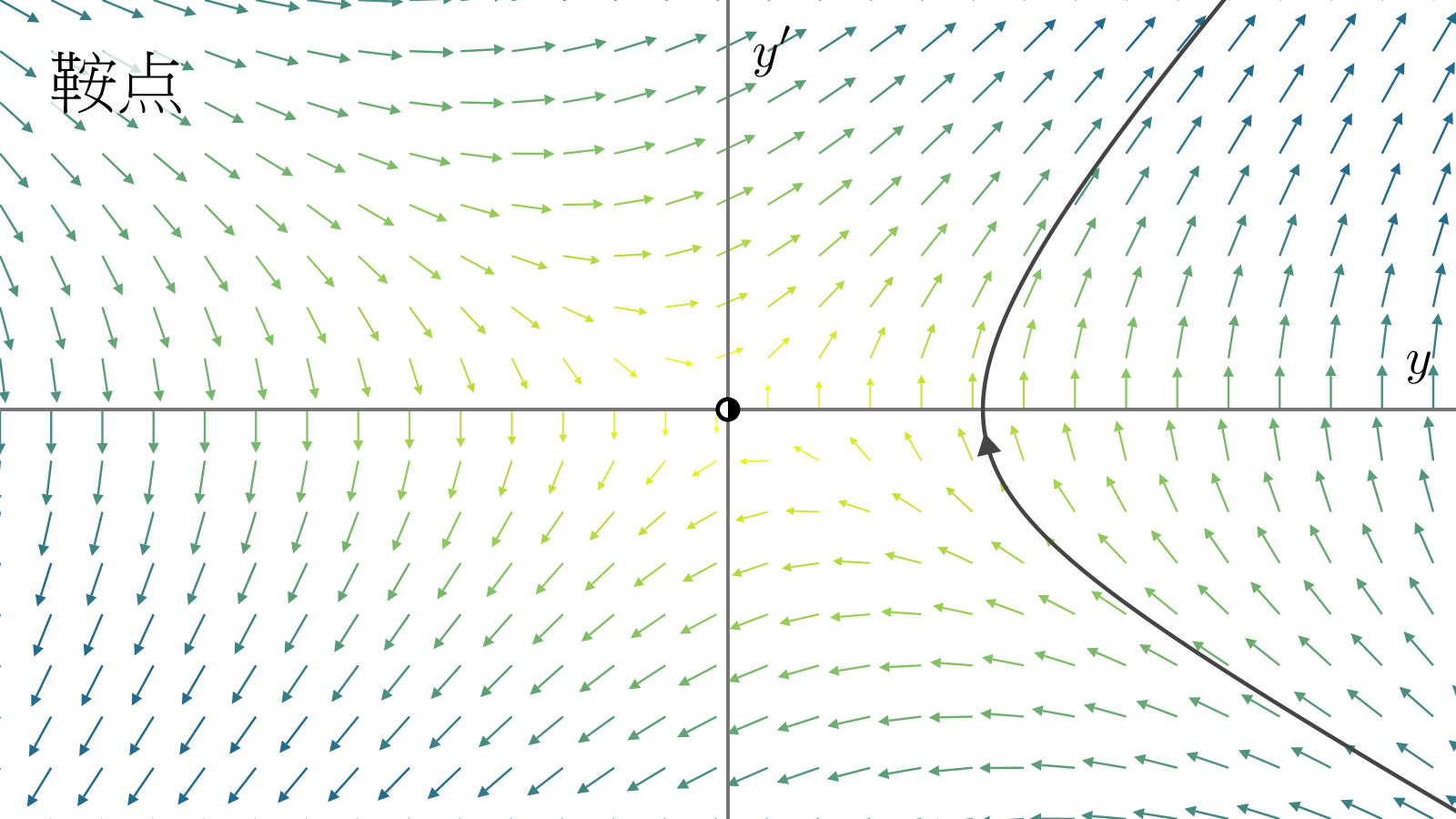
方程的通解为\(y=A\e^{\lambda_1t}+B\e^{\lambda_2t}\)，\(A,B\)是待定常数. 如果至少一个根大于\(0\)，那么\(y\)是以指数的速度无限制增大的.
如果\(\lambda_1,\lambda_2\)是两个相等的实根，与上面\(\lambda_1,\lambda_2\)同号的情况比较相似，可以按照根的正负判断不动点稳定性.
如果\(\lambda_1,\lambda_2\)是两个共轭虚根，情况变得有意思了. 此时通解为\(y=A\e^{\lambda_1t}+B\e^{\lambda_2t}\)，虚指数在几何上表现为旋转.
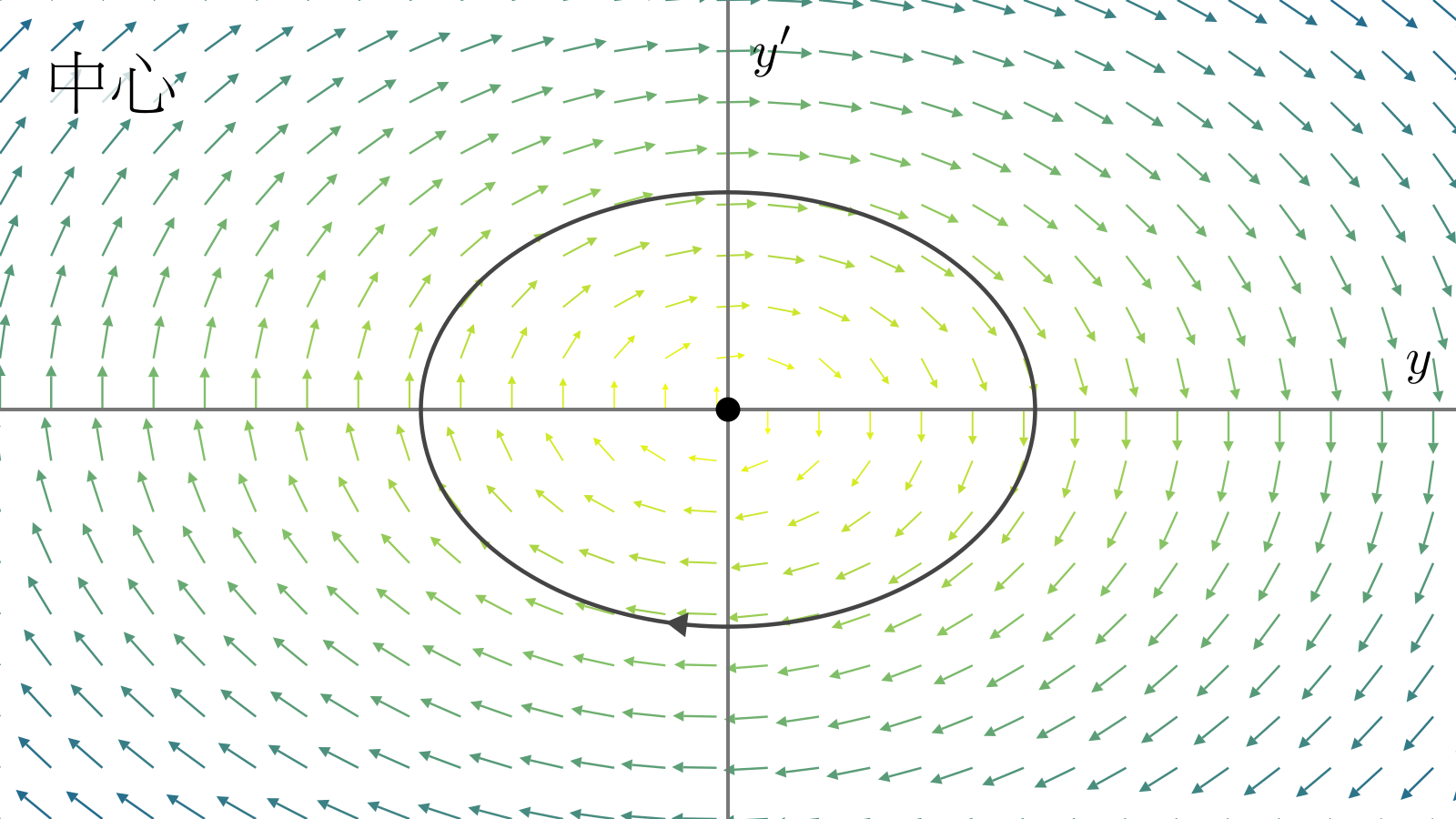
- 如果\(\lambda_1,\lambda_2\)是纯虚数，那么\(\vb{y}\)就会绕着不动点转圈（无阻尼简谐振子）.
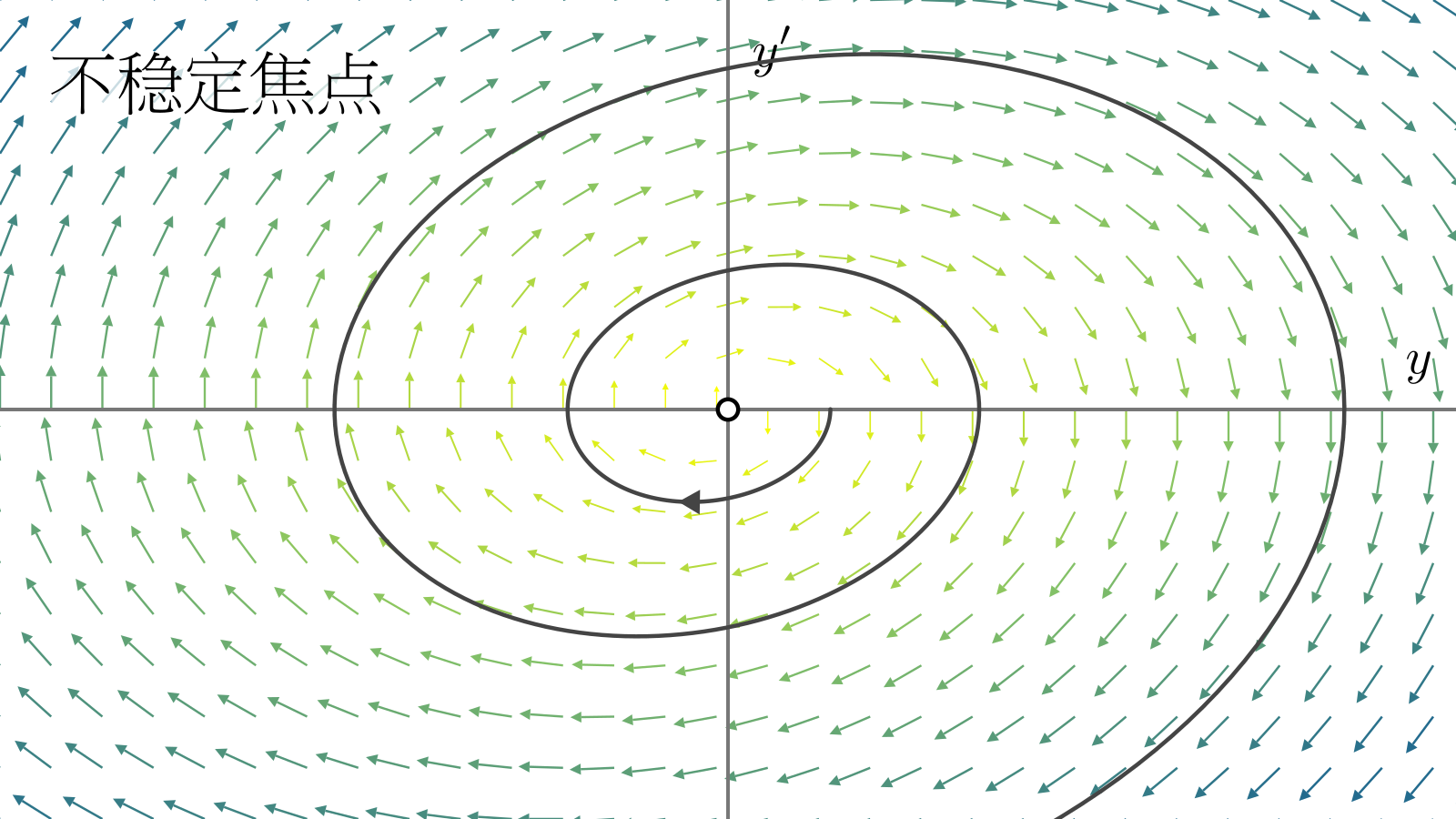
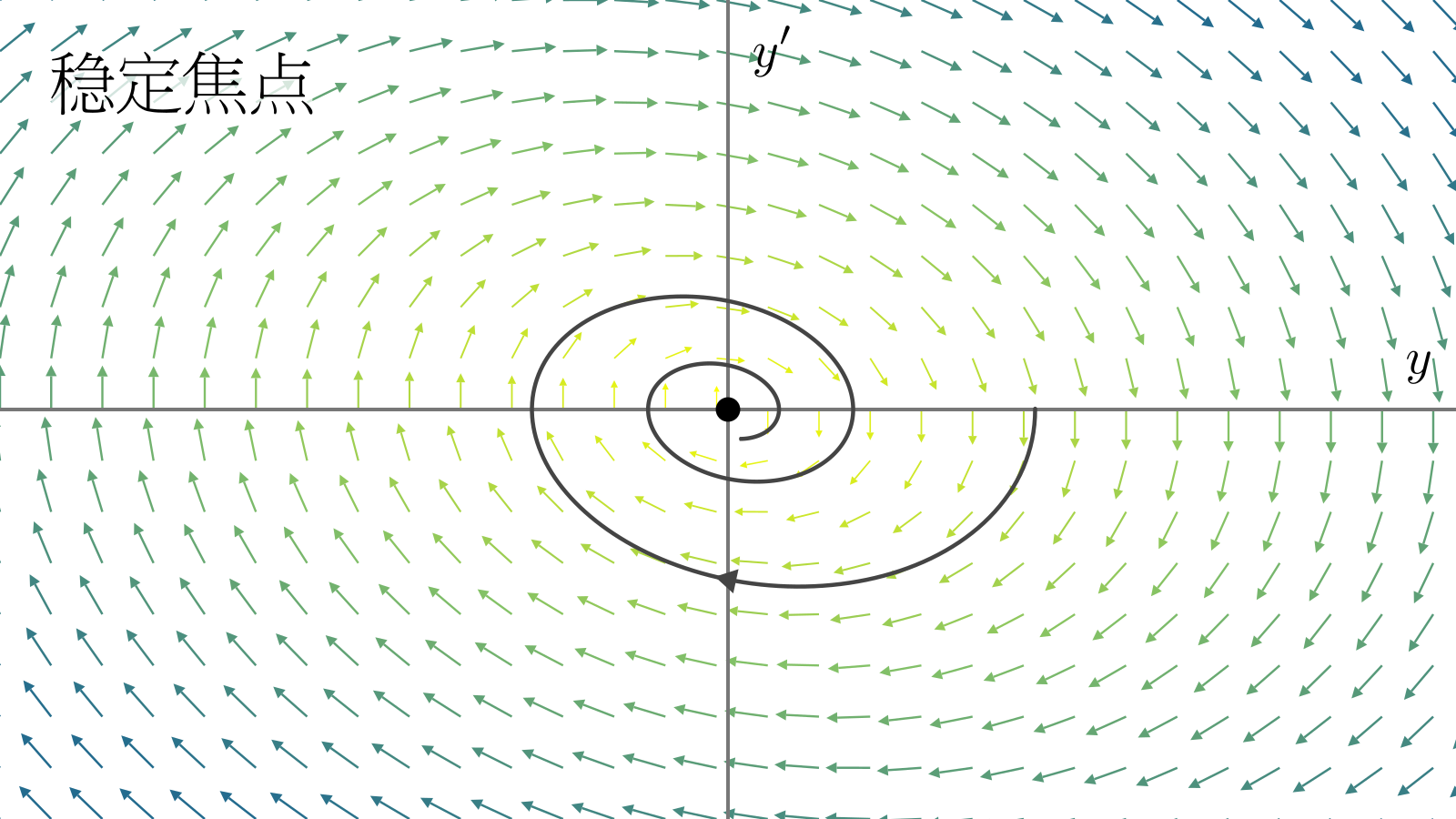
- 如果\(\lambda_1,\lambda_2\)的实部大于零，那么\(\vb{y}\)会在转圈时远离不动点（不稳定焦点）；如果实部小于零则会靠近不动点（稳定焦点），例如小阻尼的简谐振子.
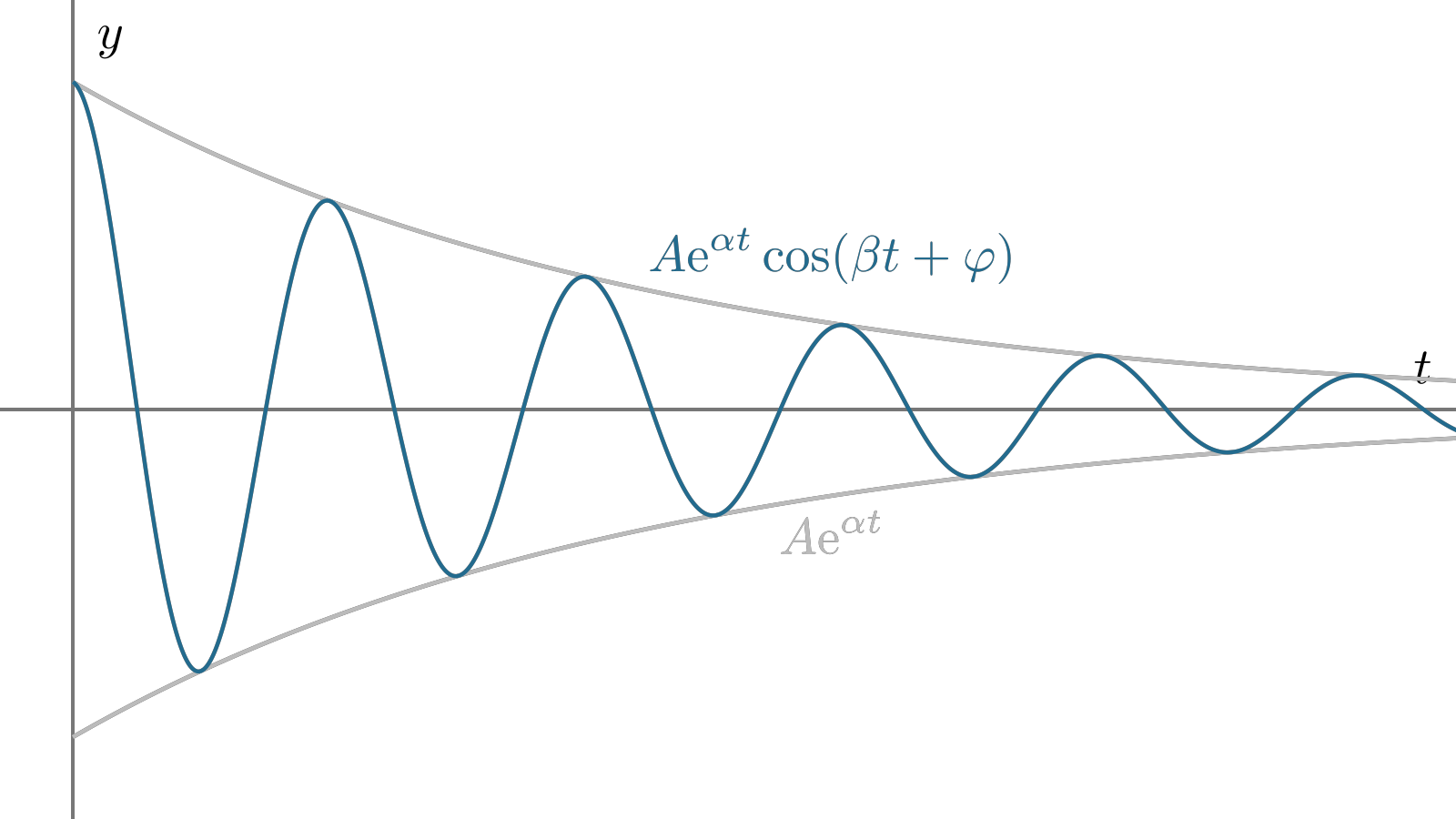
利用Euler公式（\(\e^{\i t}=\cos{t}+\i\sin{t}\)），可以把通解\(A_1\e^{\lambda_1t}+B_1\e^{\lambda_2t}\)中的虚指数转化为三角函数：

设\(\lambda_{1,2}=\alpha\pm\i\beta\)，于是方程的通解可以化为\(y=A\e^{\alpha t}\cos(\beta t+\varphi)\)，\(A,\varphi\)是待定常数（与\(A_1,B_1\)有关）. y是周期性振动的，其振幅按照指数增/减：

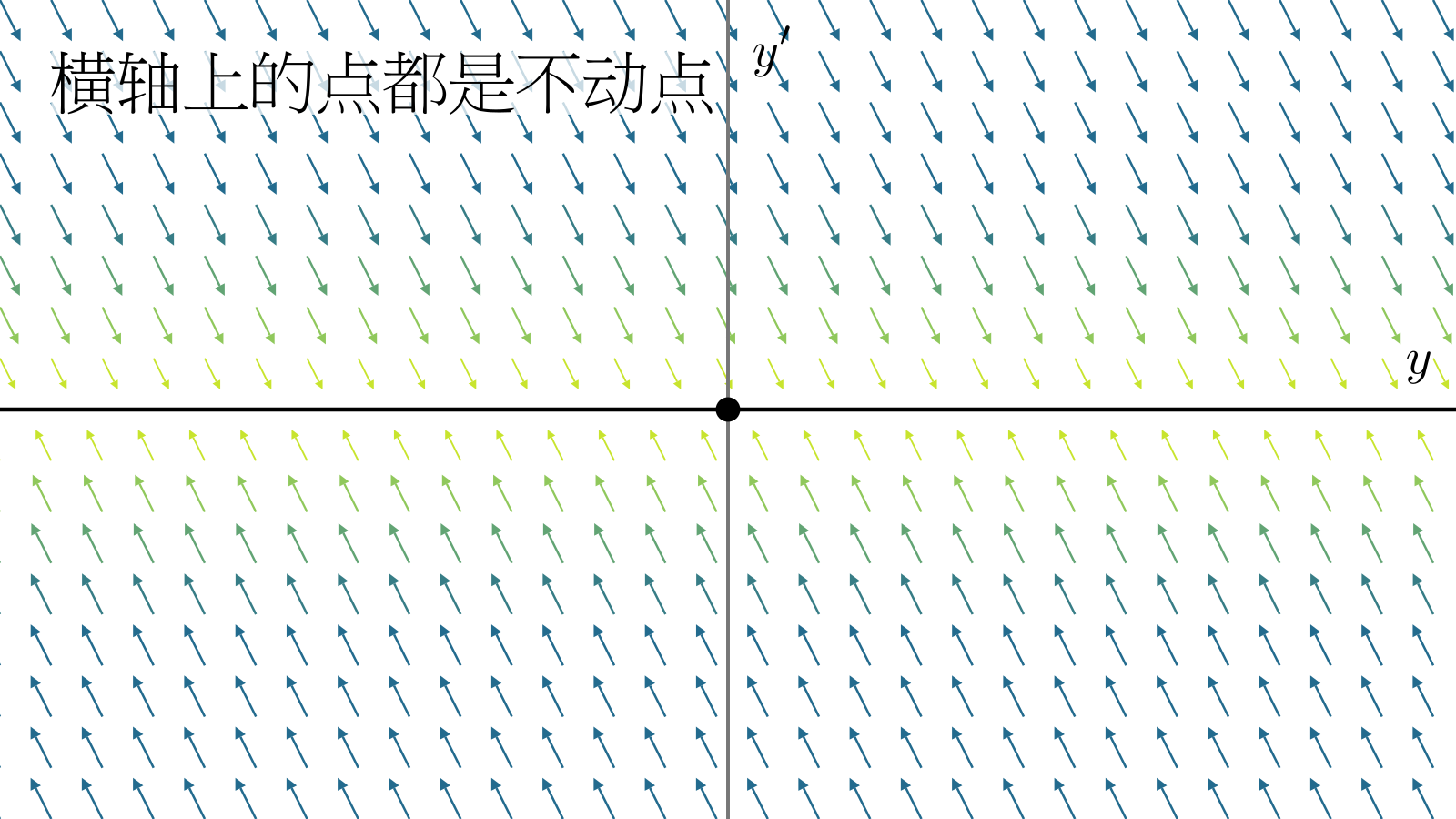
如果\(\lambda_1\lambda_2=0\)，那么某条直线上的所有点都是不动点.

由于此时\(q=0\)，那么方程化为\(y''-py'=0\)，做替换：\(Y=y'\)，可以把方程降至一阶：\(Y'-pY=0\). 可以解得\(Y=C_0\e^{pt}\)，从而\(y=C_1\e^{pt}+C_2\)，和一阶（齐次）方程的解只相差一个常数. 从图中可以看出，方程的轨线是直线.

此时，方程表现了和低阶方程相似的性质，称为退化微分方程.

这一节关于不动点（奇点）的讨论是Poincaré（庞加莱）在《微分方程所定义的积分曲线》（1881-1886）中首次给出的.

2 单摆

2.1 线性化

一个理想单摆的运动方程是 \[ \theta''+\frac gl\sin\theta=0 \] 由于含有\(\sin\theta\)项，这是一个二阶非线性微分方程. 非线性的微分方程求解起来非常非常非常难，所以我们希望化非线性为线性. 当\(\theta\)非常小的时候（约在\(\pm10^\circ\)范围内），有\(\sin\theta\approx\theta\)（如下图所示），

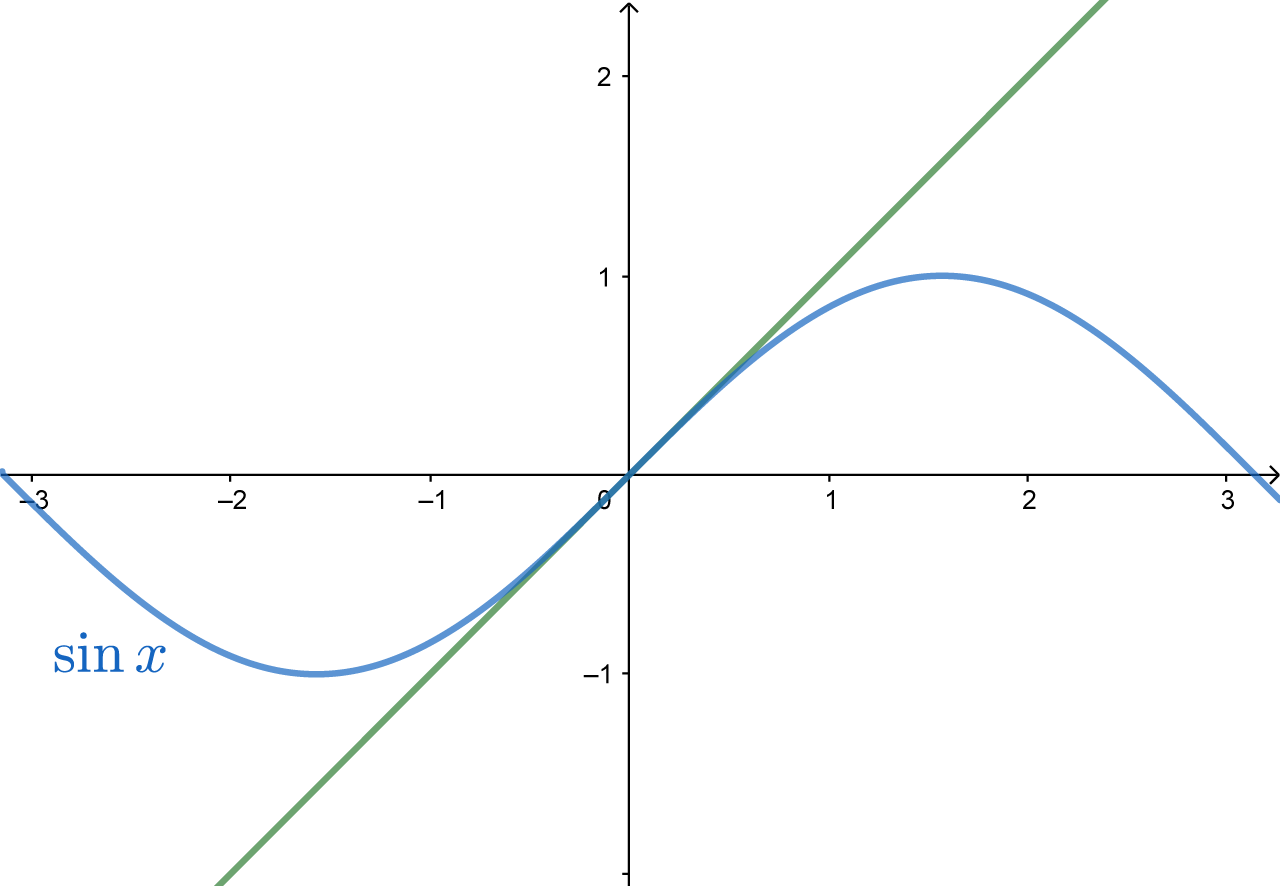
于是可以把方程化为 \[ \theta''+\frac gl\theta=0 \] 这是线性的，描述了单摆的简谐运动：\(\theta=A\cos(\sqrt{\dfrac gl}\cdot t+\varphi)\). 我们也可以给方程加入一个阻尼项\(\mu\theta'\)，讨论起来和\(\S1\)是一模一样的.

不过，当\(\theta\)很大时，近似解会有巨大的误差. 下图中，初始角度为\(\dfrac\pi2\)，深色为精确解，浅色为近似解.

2.2 向量场

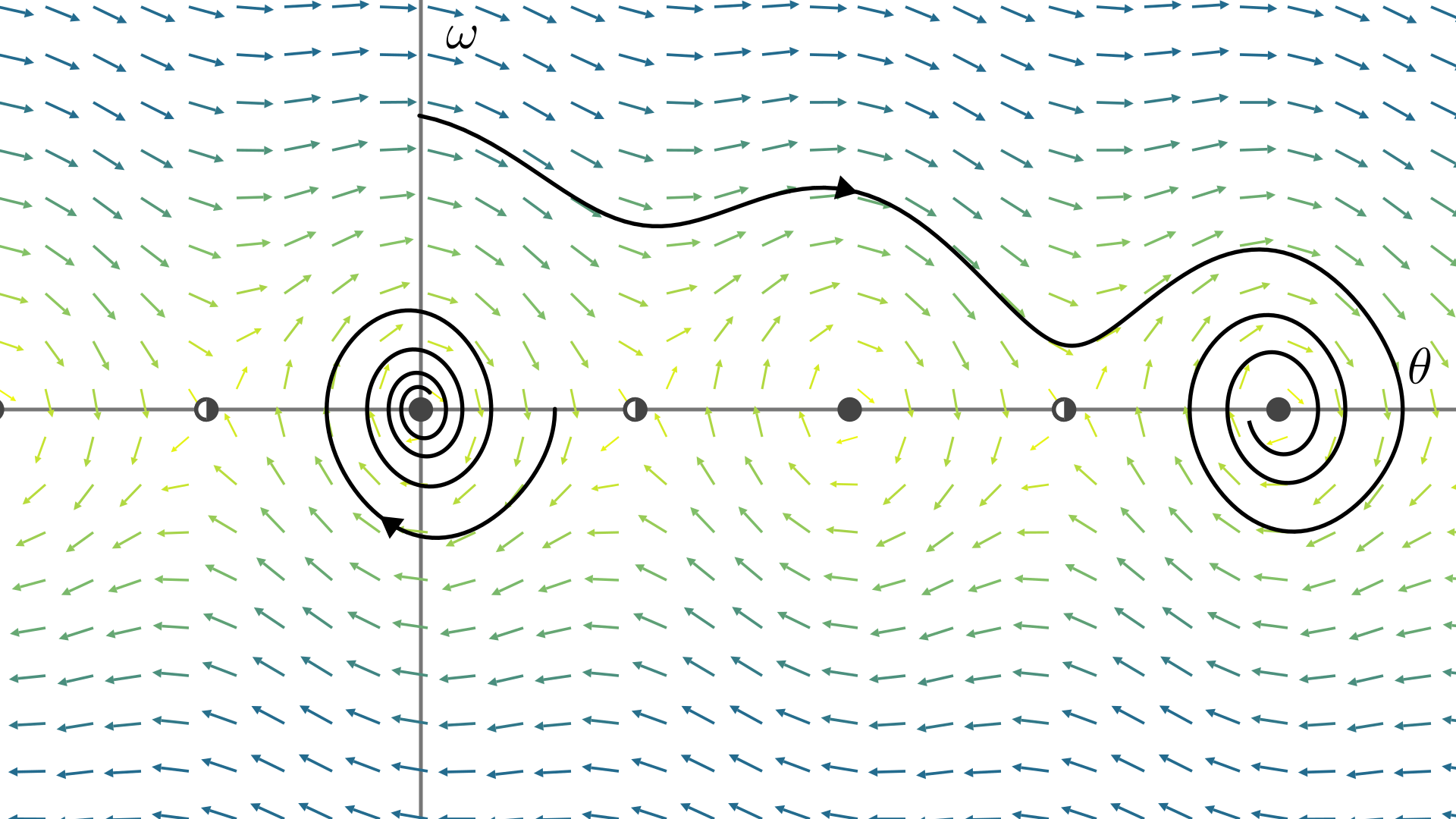
如果要研究\(\theta\)较大时系统的演化规律，我们确实可以解出精确的\(\theta(t)\)关系，不过是用复杂的非初等函数表示的. 所以我们考虑几何方法——向量场：令\(\omega=\theta'\)，再在方程左边加入阻尼项\(\mu\theta'\)， \[ \dv{}{t}\pmqty{\theta\\\omega} = \pmqty{\omega\\-\dfrac gl\sin\theta-\mu\omega} \] 当\(\mu=0\)，如下图，向量场是呈周期性变化的；系统不会有能量损失. 当初始能量较小时，质点会在平衡位置附近振动（轨线是封闭曲线）；当初始能量较大时，质点能越过平衡位置，一圈一圈不停转下去（轨线向\(\theta\)正方向无限延伸）. 分布在\(\theta\)轴上有无穷多个不动点，它们一半是稳定的（位于\(\theta=2n\pi,n\in\Z\)，质点在最底部的平衡位置），一半是不稳定的（鞍点，位于\(\theta=(2n+1)\pi,n\in\Z\)，质点位于最顶部）.

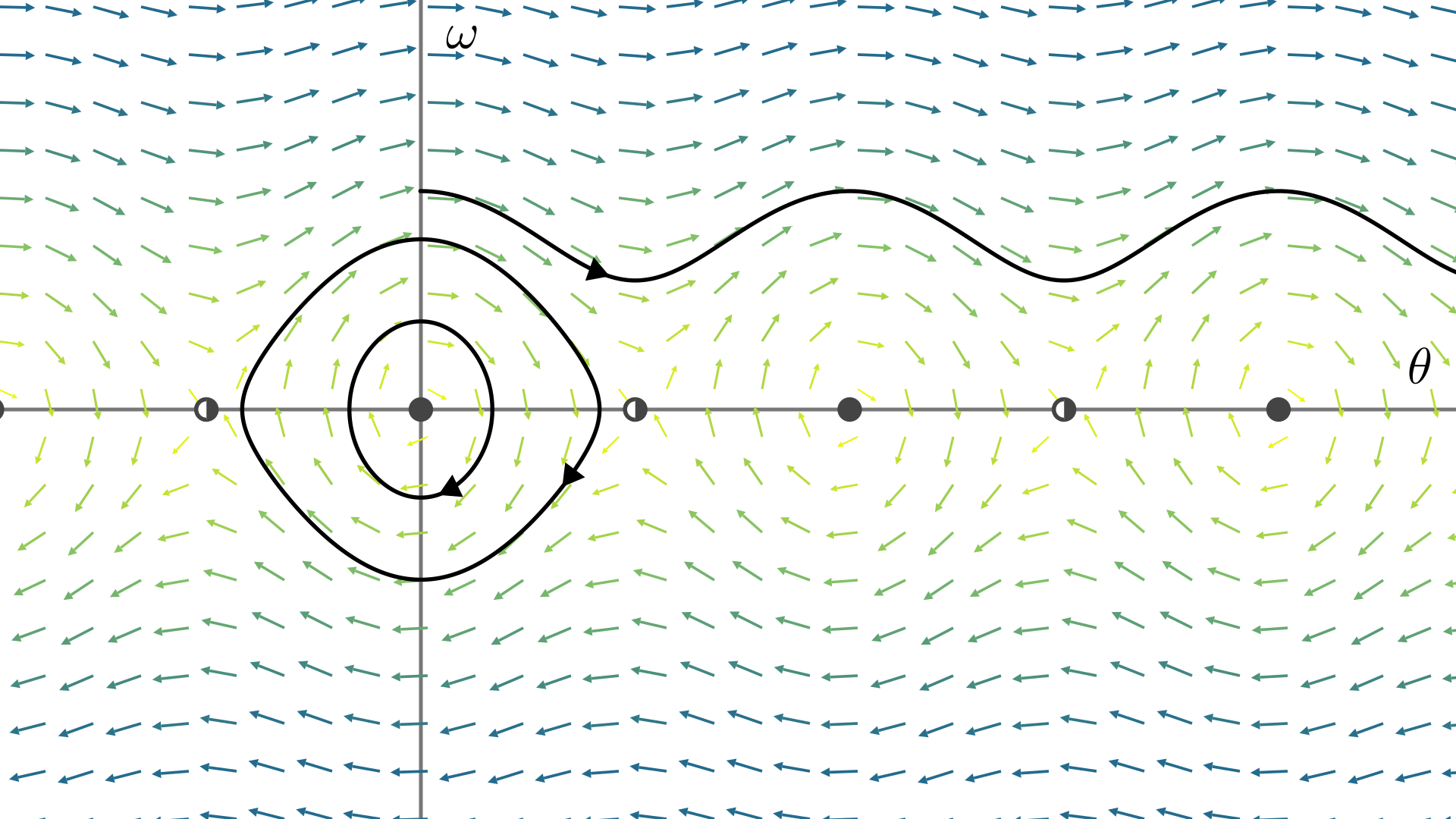
观察图中两个绕着原点的闭轨，可以注意到：当\(\theta\)初始值较小时，轨线近似为一个椭圆（即简谐振子的轨线）；当初始值较大时，轨线变成了一个近似菱形的曲线.

当\(\mu>0\)，如下图，向量场会向不动点"偏转"，有能量损失. 此时不论初始值如何（只要不在鞍点上），轨线都会向\(\theta\)轴靠近，最终陷入一个稳定不动点.

2.3 数值法

利用向量场，我们可以发展出一种数值求解微分方程的方法.

选定一个初始点\((\theta_0,\omega_0)\). 在向量场中，沿着此处的向量\(\vb{v}_1\)走很小的一步\(\vb{v}_1\Delta t\)，得到下一个点\((\theta_1,\omega_1)\)，再沿着此处的向量\(\vb{v}_2\)走很小一步\(\vb{v}_2\Delta t\)，得到\((\theta_2,\omega_2)\)……这样，我们可以大致地描绘出系统的轨线（一条折线）：

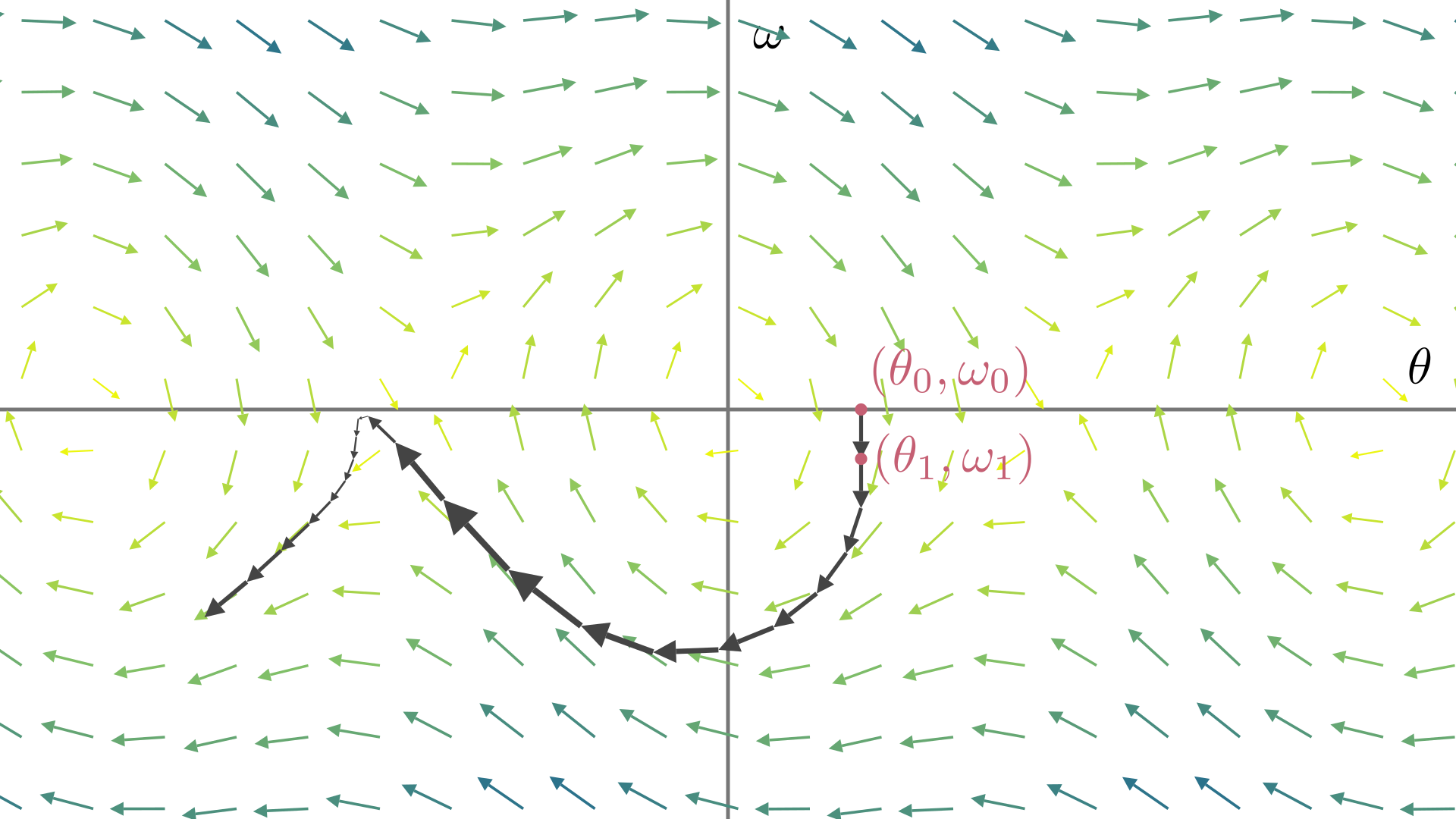
这种方法把的核心就是把"瞬时变化率"近似为"平均变化率"（与上一篇中推导指数函数\(\e^{aT}\)的思想是类似的）： \[ y'(t)=\lim_{h\to0} \frac{y(t+h)-y(t)}{h} \approx \frac{y(t+\Delta t)-y(t)}{\Delta t} \] 于是微分方程\(\Cases{\theta'=\omega\\\omega'=-\dfrac{g}l\sin\theta-\mu\omega}\)变成了差分方程： \[ \Cases{ \dfrac{ \orange{ \theta_{n+1}}- \blue{ \theta_n} }{\Delta t} = \blue{ \omega_n} \\ \dfrac{ \orange{ \omega_{n+1}}- \blue{ \omega_n} }{\Delta t} = -\dfrac{g}l\sin\blue{\theta_n} - \mu\blue{\omega_n} } \quad (n\in\N) \] 根据某一时刻的\((\blue{\theta_n},\blue{\omega_n})\)，就可以得到下一时刻的\((\orange{\theta_{n+1}},\orange{\omega_{n+1}})\)，于是可以得到离散序列 \[ (\theta_0,\omega_0),(\theta_1,\omega_1),\dots,(\theta_N,\omega_N) \] 即数值解. 但是当\(\Delta t\)比较大的时候，误差会快速叠加，造成的结果就是轨线完全偏离了应有的趋势，如上图. \(\Delta t\)越小，数值解与精确解就越接近，如下所示.