ODE2 一阶微分方程

1 人口模型

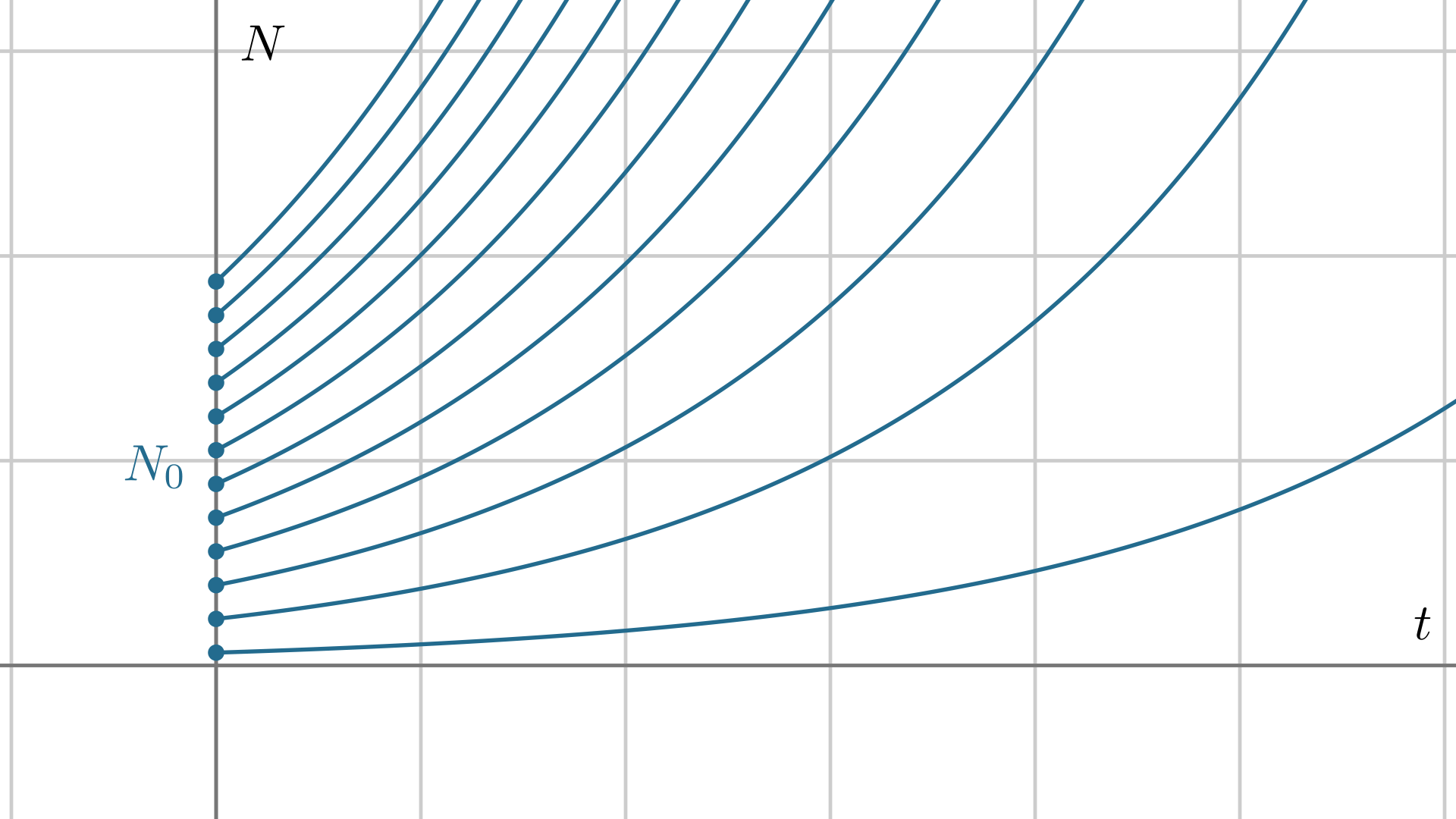
设想某个地区的人口增长情况：总人口为\(N(t)\)；人口的增长速度，即\(N'(t)\)，正比于人口总数： \[ N'(t)=rN(t) \] 增长率\(r\)是一个正的常数. 这个方程是一个一阶线性微分方程，它表示函数\(N(t)\)的导数正比于它自身，很容易让我们想到指数函数：\(\displaystyle\dv{\e^{kt}}{t}=k\e^{kt}\)，所以方程的一个解是\(N(t)=\e^{rt}\)，此时初始人口为\(N(0)=1\). 如果我们规定初始人口数量为\(N(0)=N_0\)，那么解就是 \[ N(t)=N_0\e^{rt} \] 可以代入验证：它仍然满足原方程. 一个微分方程的解是不唯一的，需要根据初始条件来确定. 下面画出了不同\(N_0\)时的解：

微分方程有多解，这是因为在求导数的过程中"消去"了一些信息： \[ y(t)=2t+C(C\textsf{是常数}) \xrightarrow{求导数} y'(t)=2 \] 在这个过程中，常数被抹去了，导致我们不能由一个函数的的导数来唯一确定它.

这就像平方和开平方： \[ \pm2 \xrightarrow{平方} 4 \] 正负号被抹去了，所以由一个实数的平方并不能唯一确定它.

一个\(n\)阶的微分方程最高涉及到\(n\)阶导数，所以解的表达式中含有\(n\)个待定的常数，需要\(n\)个条件来确定它们.

2 电源单杆

另外一个例子.

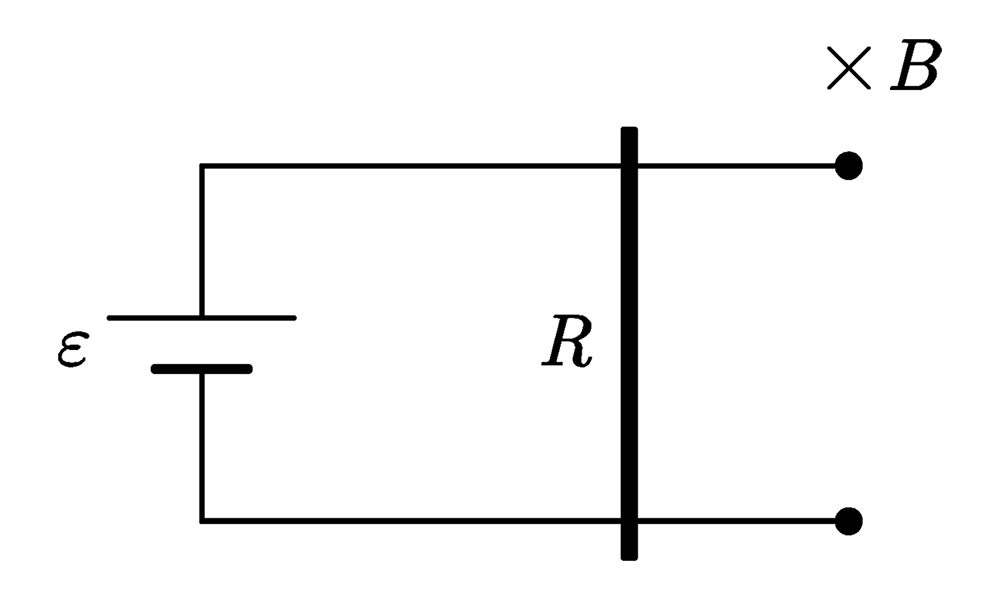
电源电动势为\(\varepsilon\)，空间中有垂直向里的匀强磁场\(B\)，水平平行光滑导轨（足够长）上有一个导体棒，电阻为\(R\). 不计阻力和其他电阻. 由物理学知识，我们知道电路中会出现顺时针的电流，导体棒会向右运动，产生的反电动势又会阻碍运动……设导体棒的速度为\(v(t)\)，加速度为\(a(t)\)，电路中电流为\(i(t)\)（速度向右为正方向、电流顺时针为正方向），那么有：\(\Cases{ v(t)BL+i(t)R = \varepsilon \\ mv'(t) = i(t)LB }\)

从而有 \[ v'(t)+\frac{B^2L^2}{mR}{v(t)}=\frac{\varepsilon LB}{mR} \] 这也是一个一阶线性微分方程，但是和人口方程不同的是，它多了一个常数项，是一个非齐次的微分方程.

2.1 向量场

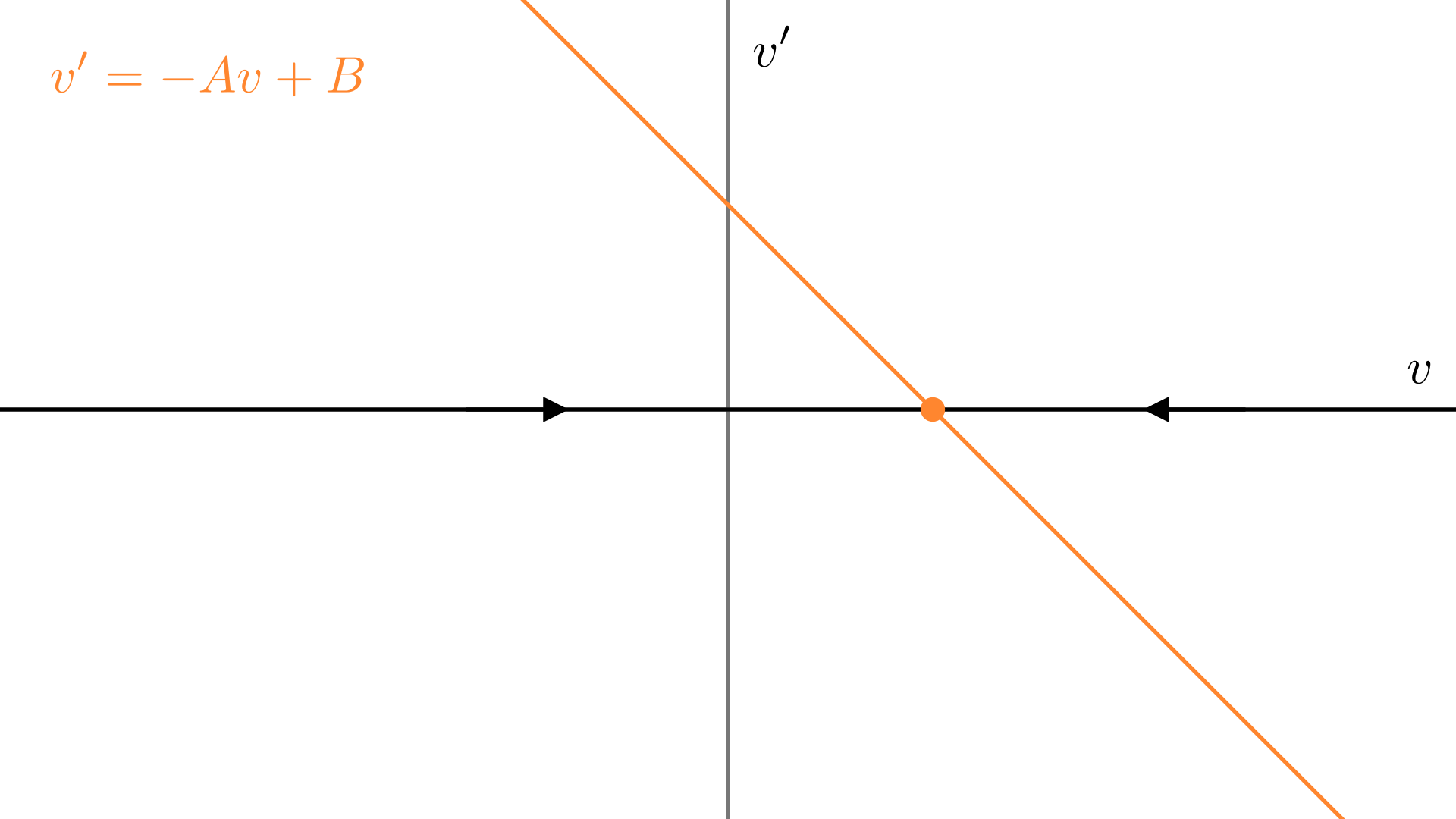
我们先不去解这个方程，而是采用几何方法. 原方程移项后变为\(v'=-Av+B\)（\(A,B\)是系数），想象一条横轴\(v\)表示速度，上面的每个点\(v\)都长出来了一根向量\(v'\)，表示加速度，即速度的变化率.

这构成了一个向量场. 为了画出它，可以先画出\(v'-v\)图像，再在横轴上的每个点画出对应的加速度向量.（当\(v'<0\)，箭头向左；\(v'>0\)，箭头向右.）

在数学中，场(field)\(f\)是一个从几何空间\(M\)到集合\(S\)的映射. "向量场"和"标量场"指的是\(S\)中的元素是向量还是标量. 例如，电场\(\vb{E}\)给三维空间\(\R^3\)中的每个点赋予了一个电场强度\(\vb{E}(x,y,z)\)，是向量场；电势场\(\varphi\)给\(\R^3\)中的每个点赋予了一个电势\(\varphi(x,y,z)\)，是标量场.

这个例子中的向量场把直线上的点映射到了一个向量.

可以把横轴想象成一种流体在流动. 在\(v'<0\)（箭头向左）的地方，流体向左流动；在\(v'>0\)（箭头向右）的地方，流体向右流动. 在\(v'=0\)的地方，流体不流动，所以把这个点叫做不动点(fixed point). 上图中，不动点两侧的流体都流向不动点，不动点两侧所有的\(v\)都会趋近于这个不动点.

所以可以得出结论：当初始速度\(v_0\ne\dfrac\varepsilon{BL}\)时，速度会逐渐趋近于\(\dfrac\varepsilon{BL}\)；当\(v_0=\dfrac\varepsilon{BL}\)，速度会保持不变.

最后看看要怎么解这个方程. \[ v'+\frac{B^2L^2}{mR} v=\frac{\varepsilon LB}{mR} \] 回想一下\(\S1\)的例子，我们希望\(v'\)能和\(v\)成正比，也就是\(v'-v\)图像是一条过原点的直线. 所以只需要把图像向左平移\(\dfrac\varepsilon{BL}\)就行，也就是作替换：\(V=v-\dfrac\varepsilon{BL}\)，代入方程后有 \[ V'=-\frac{B^2L^2}{mR} V \] 所以\(V=C\e^{\large-\frac{B^2L^2}{mR}t}\)，从而\(v=C\e^{\large-\frac{B^2L^2}{mR}t}+\dfrac\varepsilon{BL}\)，其中\(C\)是一个与初始速度有关的常数.

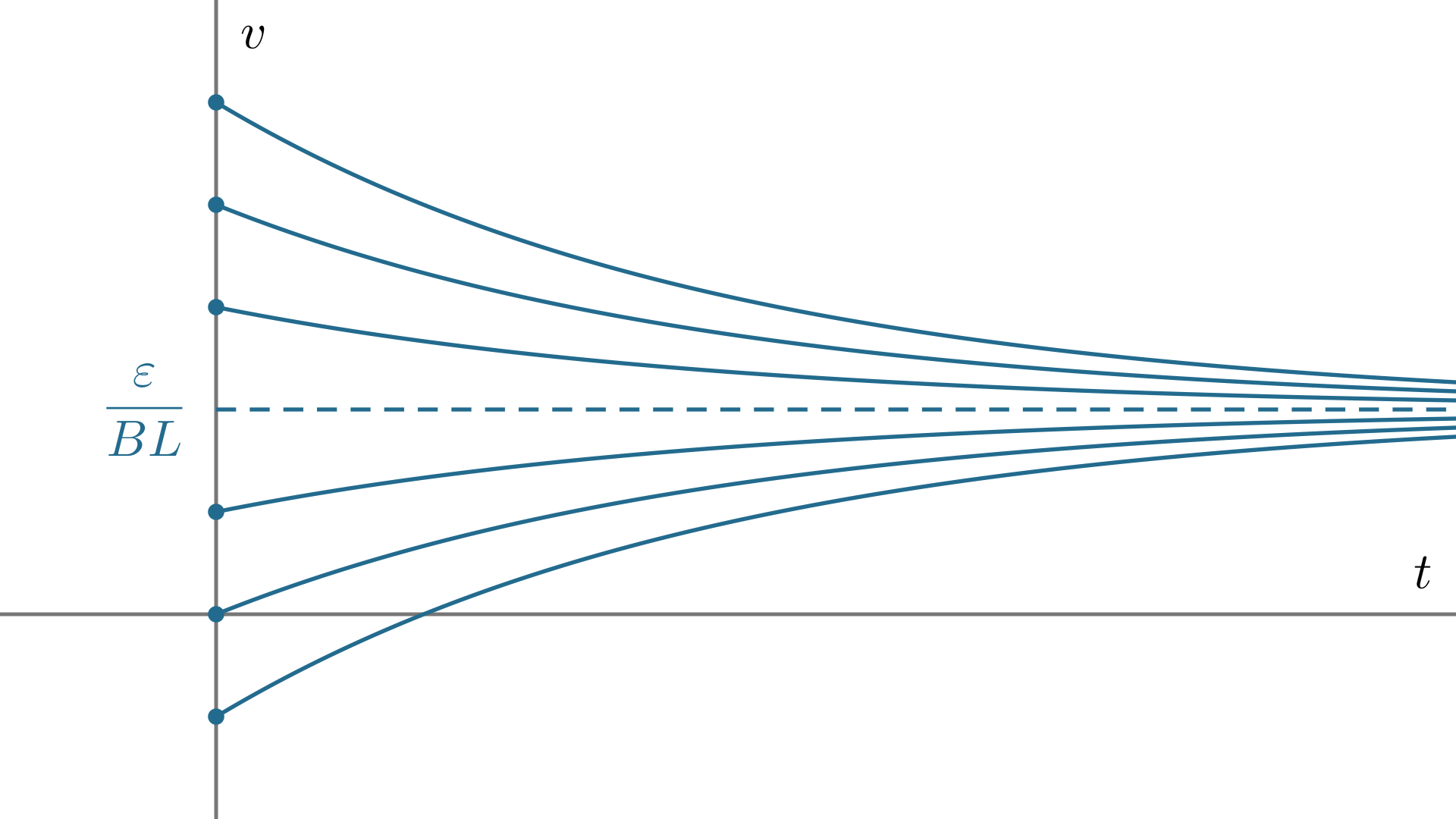
当\(t\to+\infty\)时，\(\e^{\large-\frac{B^2L^2}{mR}t}\to0\)，所以\(v\to\dfrac\varepsilon{BL}\). 以及从图像中也可以看出，不论初始值如何，速度总是会趋向于不动点\(\dfrac\varepsilon{BL}\).

2.2 不动点

现在对不动点做更深入的研究. 对于一个关于函数\(y(t)\)的一阶微分线性方程 \[ y'=py+q \] 如果\(p,q\)与是\(t\)无关的常数，那么我们称方程是自治的（也就是系统的演化规律与时间无关），此时我们可以画出它的向量场.

如果\(p\ne0\)，那么\(y'-y\)图像与横轴有一个交点，称为不动点，一般用\(y^*\)表示. 不动点满足\(y'=0\)，也就是\(y(t)\)不发生变化（不动了）. 当图像的斜率\(p\)小于零，这个不动点是稳定的，不动点两侧的解都会趋向于此（下图左）；否则是不稳定的，不动点两侧的点都会远离（下图中）.

这些概念也可以自然地推广到任意的一阶自治微分方程. 对于一个更一般的方程，也有可能存在"混合"的情况：不动点一侧的解靠近，一侧的解远离（下图右）.

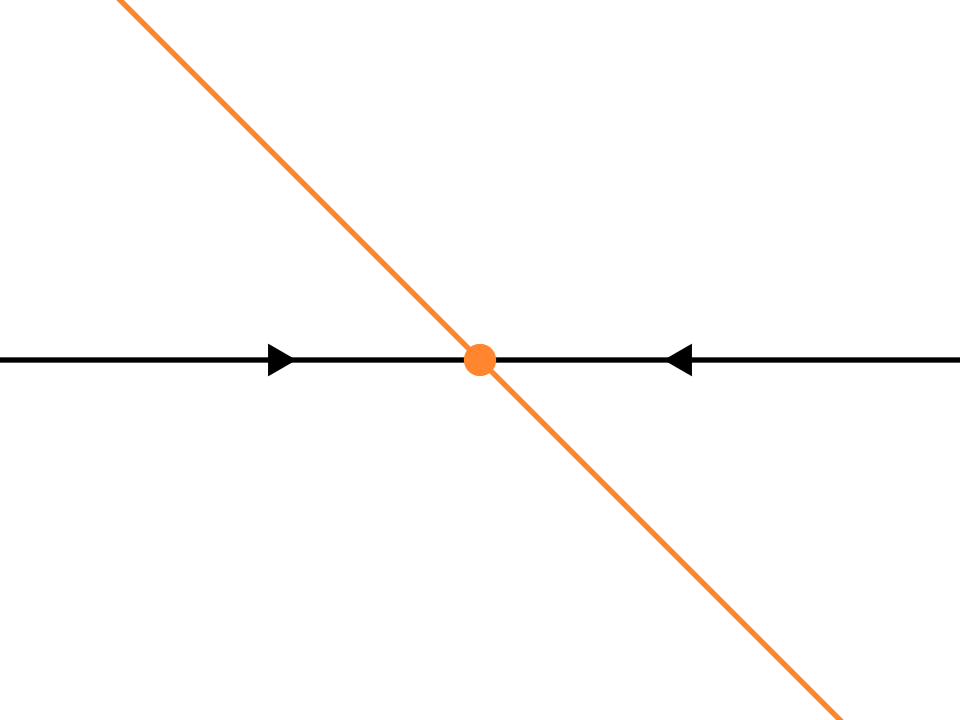
稳定

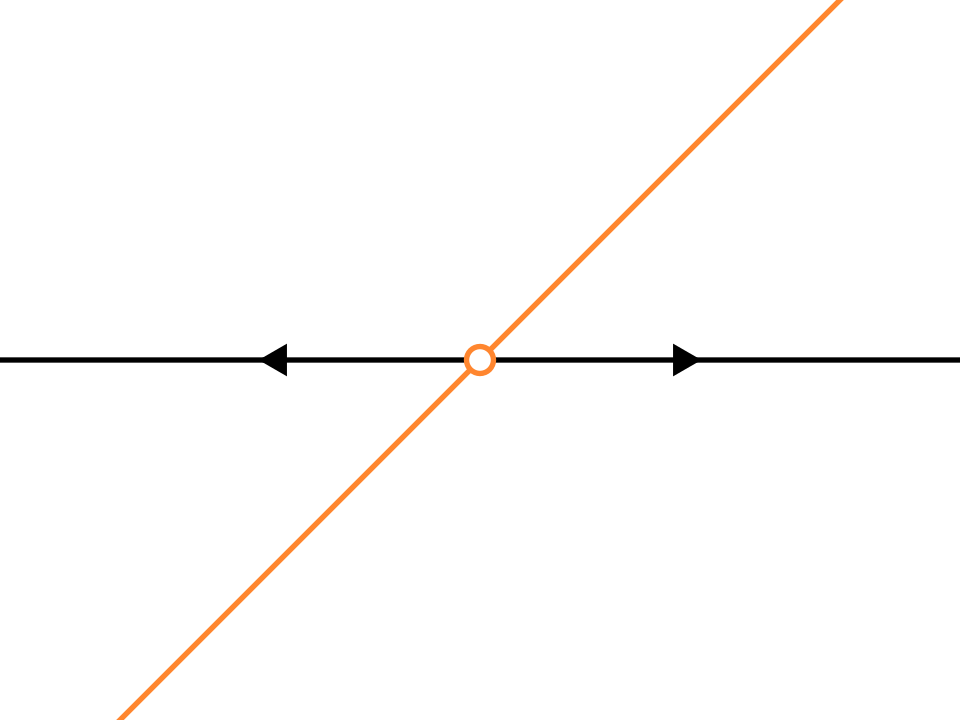
不稳定

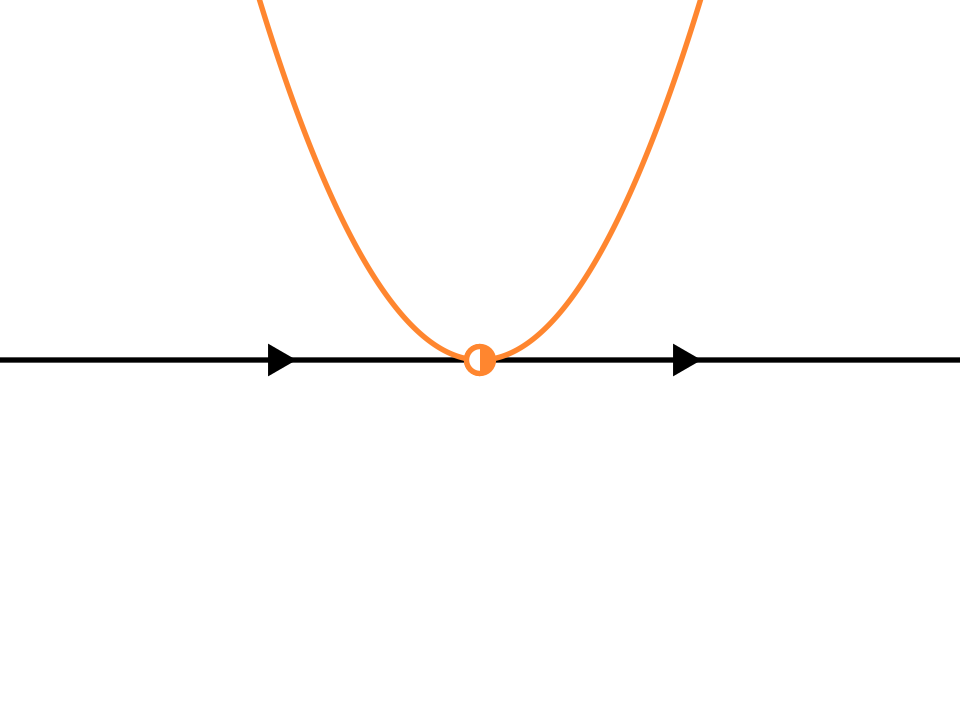
半稳定

图中，稳定、不稳定、半稳定的不动点分别用实心、空心、半实心的点表示.

怎样理解"稳定"与"不稳定"？假设不动点为\(y^*\)，在某一时刻\(t\)，有\(y(t)=y^*\)，现在给\(y\)一个很小的扰动，使得\(y(t+\Delta t)=y^*+\Delta y\)，

如果不动点是稳定的，\(y\)会逐渐回到\(y^*\)；
如果不动点是不稳定的，\(y\)会远离\(y^*\).
如果不动点是半稳定的，需要分情况讨论.

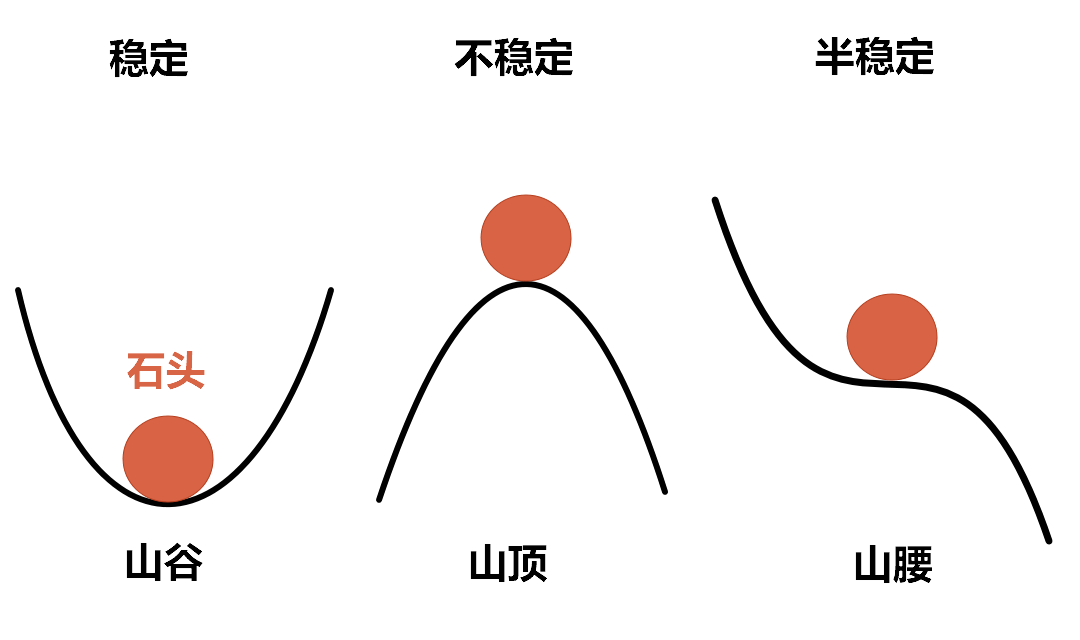
下面的图示非常直观. 石头处于静止状态，给它一个很小的力，石头可能会：

回到原来的稳定状态（下左）；
离开原来的稳定状态（下中）；
以上情况都有可能（下右）.

3 Logistic人口模型

现在让我们看一个非线性的系统，体会一下向量场和不动点的强大用途.

在第一节，我们给出了一个简单的人口模型，其中人口增长率是一个定值\(r\)，这使得人口呈指数增长：\(N(t)=N_0\e^{at}\)，但实际情况下，由于资源是有限的，人口不可能无限制增长下去. 所以，我们把增长率修改为\(r\pqty{1-\dfrac NK}\) ，其中常数\(K\)表示环境资源承载能力，\(N\)很小时，增长率接近\(r\)，\(N\)越大，增长率越小，当\(N>K\)时，增长率是负的，表示人口减少.

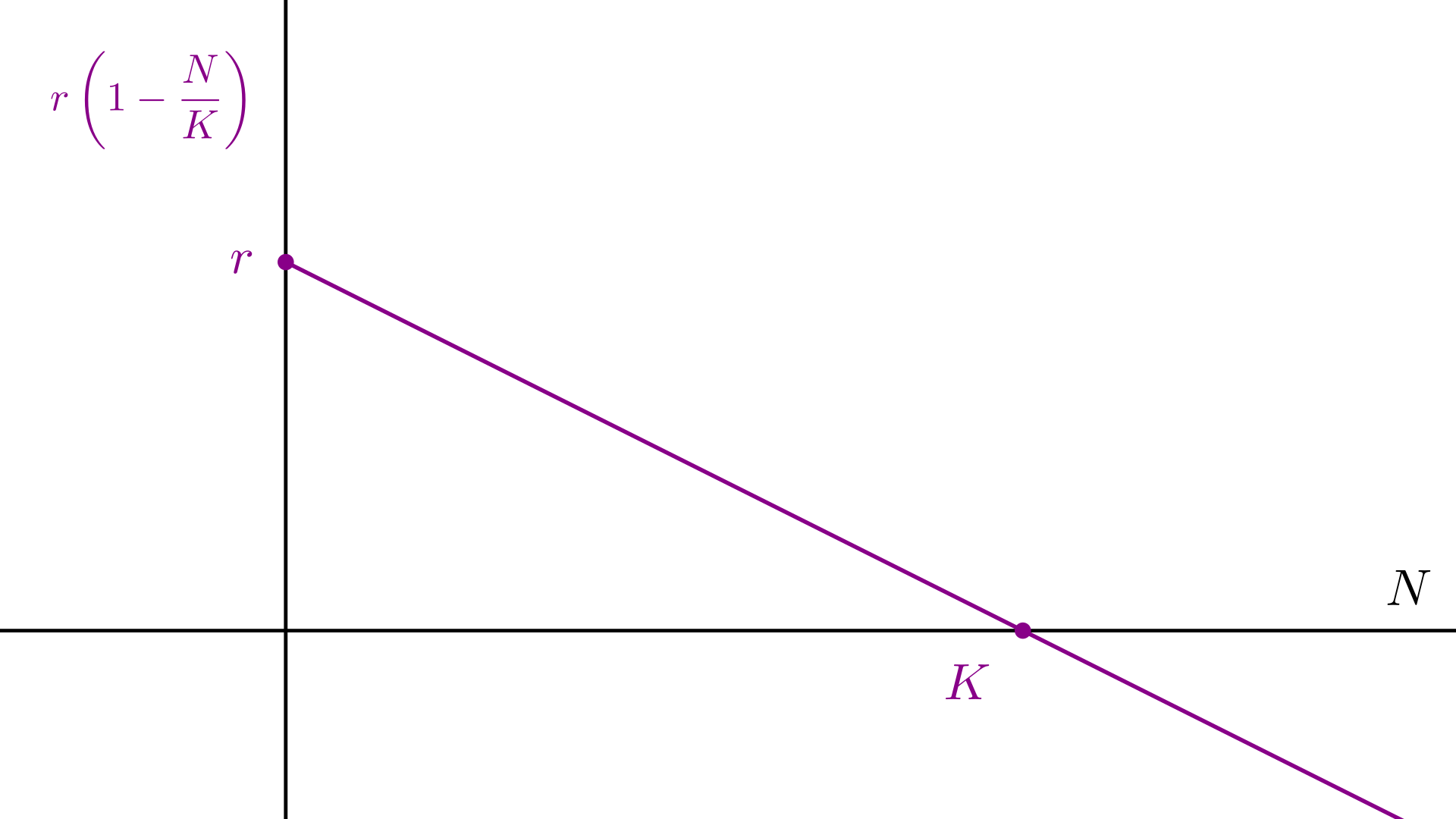
这样，我们得到了Logistic方程： \[ {N'}=rN\pqty{1-\frac NK} \] 注意到展开后方程有\(N^2\)项，所以这是一个非线性的一阶微分方程. 不妨把它的向量场画出来，

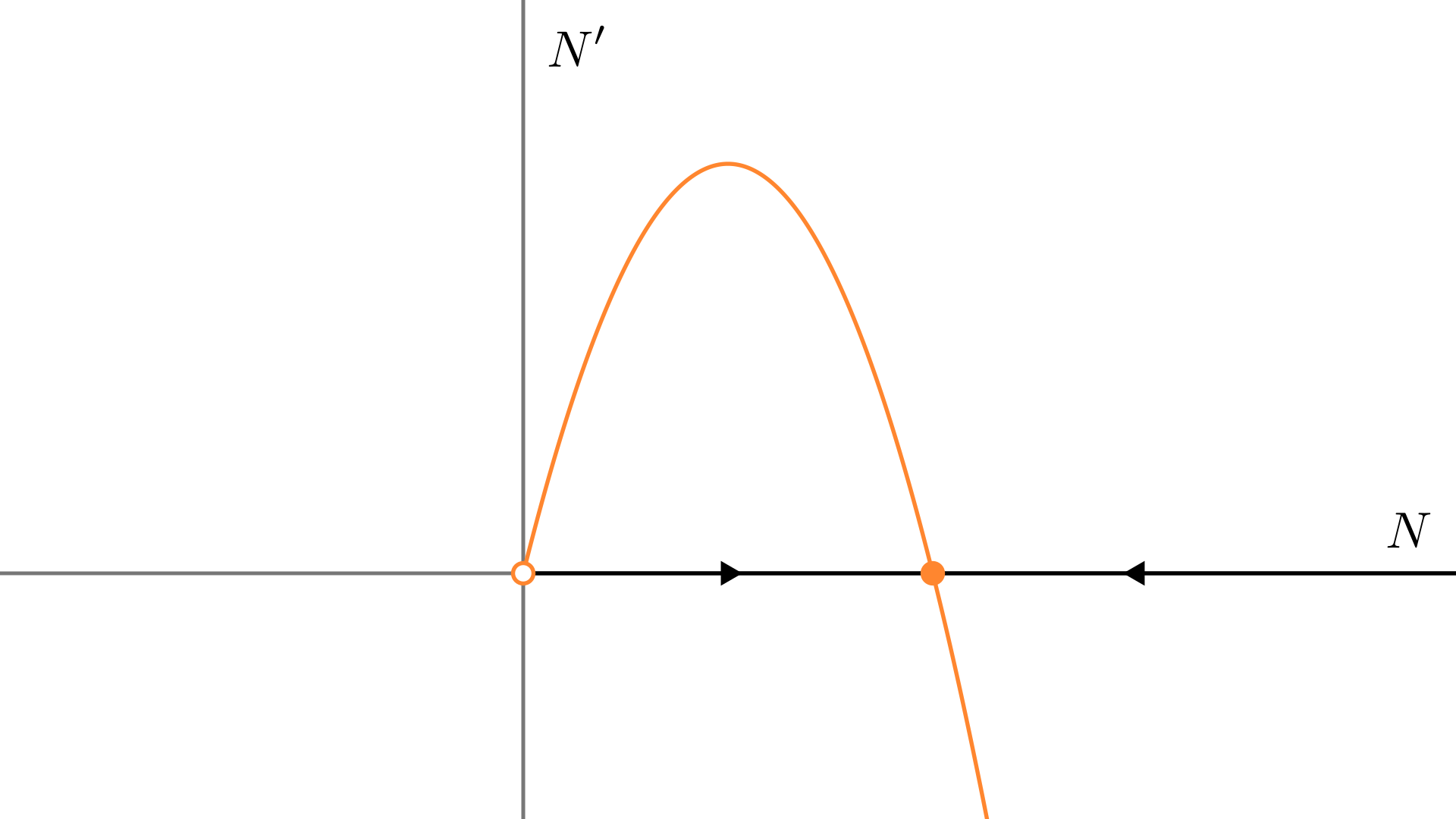
有两个不动点，\(N^*=0\)是不稳定的，\(N^*=K\)是稳定的. 所以，只要\(N_0>0\)，人口总数就会趋向于\(K\)；如果\(N_0=0\)，那么永远也不会有人.

我们也可以根据上图，预测解曲线\(N(t)\)的形状. 考虑初始人口\(0<N_0<\dfrac K2\)的情况：当\(N<\dfrac K2\)时，\(N'\)逐渐变大，图像逐渐变陡；当\(\dfrac K2<N<K\)时，\(N'\)逐渐变小，图像逐渐平缓，所以此时\(N-t\)曲线是一个类似"S"的弧形（也就是下图中最下方的一条曲线）.

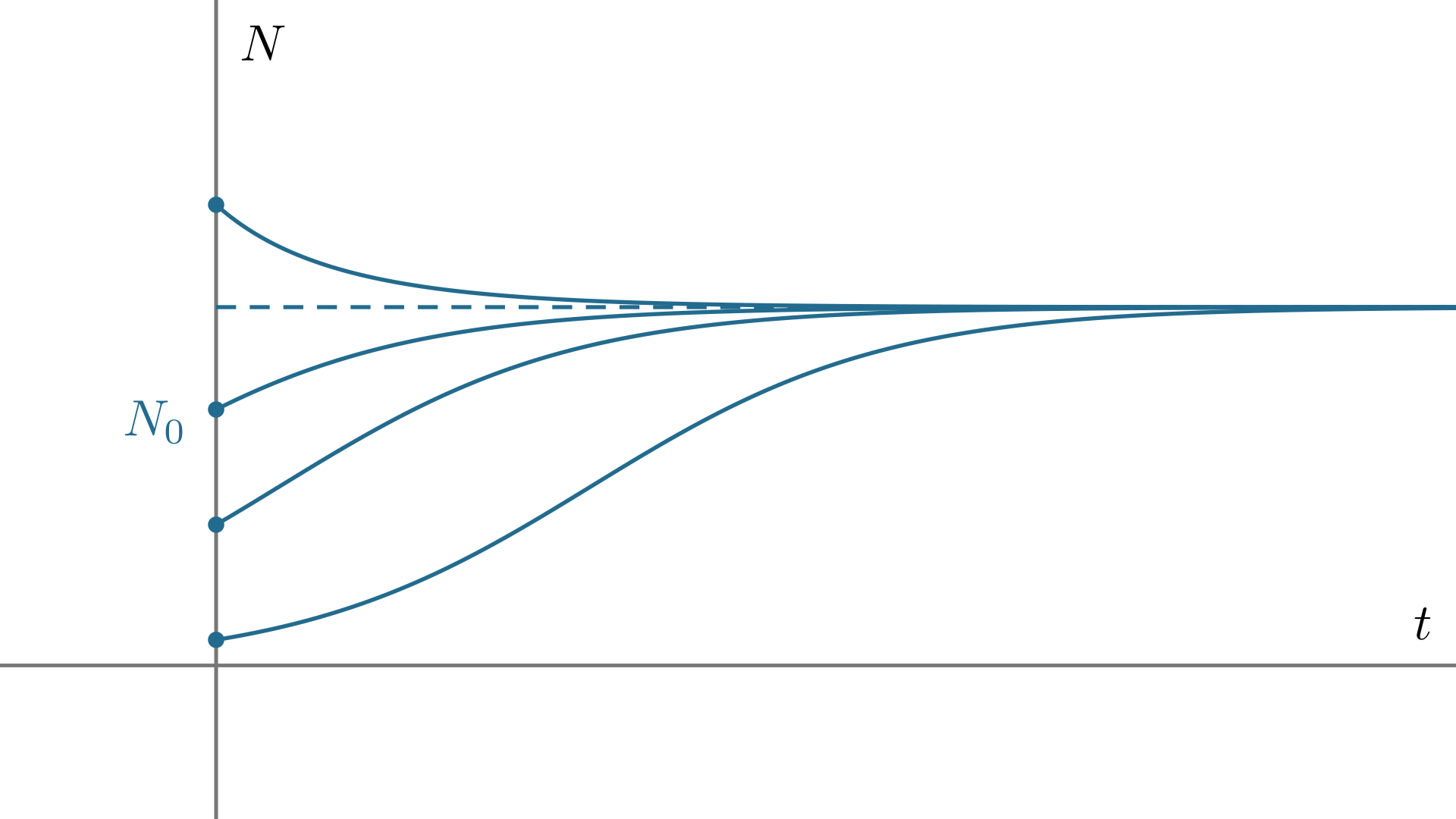
尽管这个非线性方程不好解，我们还是有很多办法来分析这个系统的演化状态的.

4 为什么是e？

下面进行一些简单的计算推导.

在\(\S1\)中，我们提到了：指数函数的变化率正比于自身，即\(\displaystyle\dv{\e^{at}}{t}=\e^{at}\). 很多人在高中时学过导数，知道这一点，却不知为何. 实际上高中课本里连\(\e\)的定义都没有，我们只知道他是一个无理数\(2.718\dots\) 现在我们来简略推导一下.

一个一阶齐次线性微分方程 \[ \dv{y}{t}=a{y} \] 描述了一个连续变化的过程中，\(y\)本身与\(y\)的变化率之间的关系，我们可以把它离散化：设\(T>0\)，把区间\([0,T]\)平均分成\(n\)份，每一份的长度是\(\Delta t\)，于是\(T=n\Delta t\).

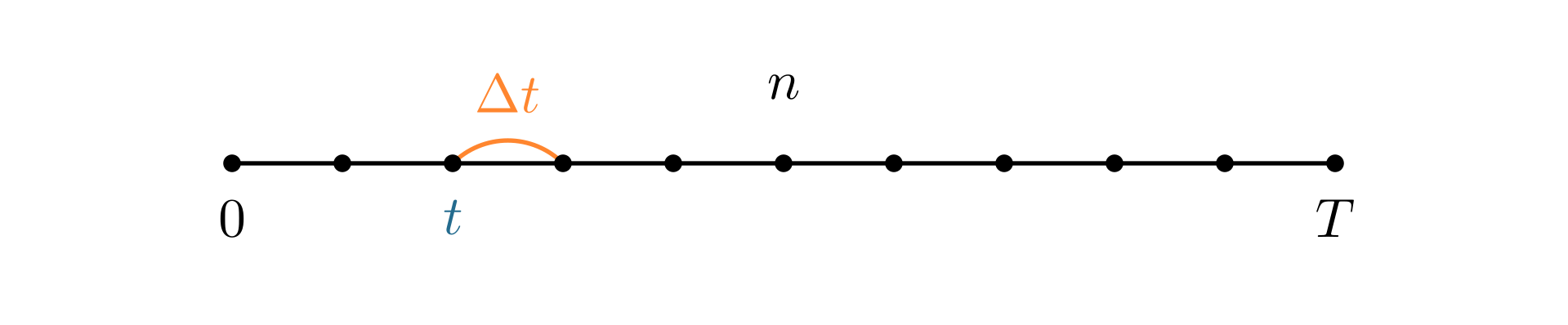
用平均变化率\(\dfrac{\Delta y}{\Delta t}=\dfrac{y(t+\Delta t)-y(t)}{\Delta t}\)来代替瞬时变化率\(\displaystyle\dv{y}{t}\)，可以得到 \[ \Align{ \dfrac{y(t+\Delta t)-y(t)}{\Delta t} \approx \dv{y}{t}= ay(t) \\ \Rightarrow y(t+\Delta t) \approx y(t)\cdot\orange{ (1+a\Delta t)} } \] 这是一个递推关系式，它表示：从\(t=0\)开始，\(t\)每前进一个\(\Delta t\)，\(y(t)\)就会乘以一个固定的倍数\(\orange{ (1+a\Delta t)}\).

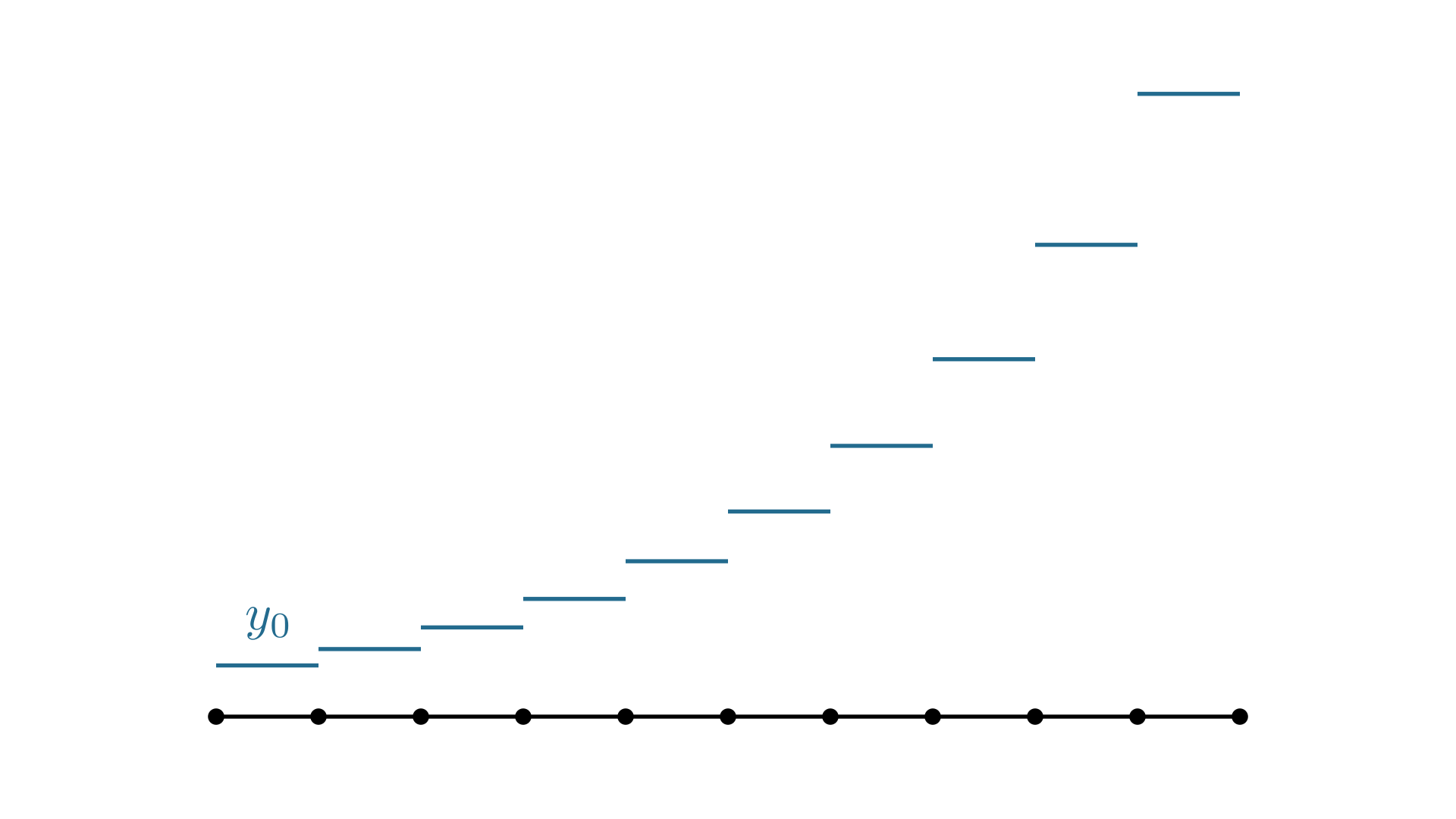
所以，\(y(t)\)的值取决于从\(0\)到\(t\)有多少个\(\Delta t\). 对于\(y(T)\)，因为\([0,T]\)中有\(n\)个\(\Delta t\)，所以 \[ y(T) \approx y(0) \cdot \orange{ (1+a\Delta t)^n} \] 为了方便，令\(y(0)=1\)，\(m=a\Delta t=\dfrac{aT}{n}\)，代入上式，有 \[ y(T) \approx \pqty{1+m} ^ {\large\frac{aT}{m}} = \bqty{{ \color{salmon} \pqty{1+m}^{\large\frac1{m}} }} ^ {aT} \] 这是\(y(T)\)的近似式. \(\Delta t\)越小（即\(m\)越小），近似效果越好，如果我们让\(\Delta t\)无限地趋于\(0\)（也即\(m\to0\)），那么近似值就变成了精确值，这是一个取极限的过程： \[ y(T) = \lim_{m\to0} \bqty{{ \color{salmon} \pqty{1+m} ^ {\large\frac1{m}} }} ^ {aT} \] \(m\to0\)的过程中，函数由离散变得连续，就像：

从图像上看，似乎确实是一个指数函数. 实际上，我们定义自然常数 \[ \e = \lim_{m\to0} {\color{salmon} \pqty{1+m} ^ {\large\frac1{m}}} = 2.71828\dots \] 于是 \[ y(T)=\e^{aT} \]

\(T\)的范围可以拓展到实数域.

还有最后一个问题，\(\e\)为什么要叫"自然"常数？

在自然界中，许多量的变化速度是和它自身呈比例关系的，这时，指数函数\(y=\e^{\alpha t}\)就会参与进来. 举几个具体的例子：

种群演化、病毒传播、细胞分裂等：合适的条件下，这些东西繁衍传播的速度和它们的数量呈正比.
复合利率：在银行存钱\(y_0\)，如果年利率为\(r\)，且按照复利计算，那么\(n\)年后的存款为\((1+r)^{n} \cdot y_0\).
链式反应：在核裂变中，一个铀原子裂变并且放出多个中子，每个中子又可以被一个铀原子吸收进而裂变，放出更多的中子…… 反应的进程是呈指数爆炸的.

还有一个几何上的例子，等角螺线\(r=\e^{k\theta}\)（极坐标方程），它从原点附近向外螺旋伸展，而且任意一点处的切线与径向夹角相等（夹角\(\alpha=\abs{\arctan{k}}\)），如下图.

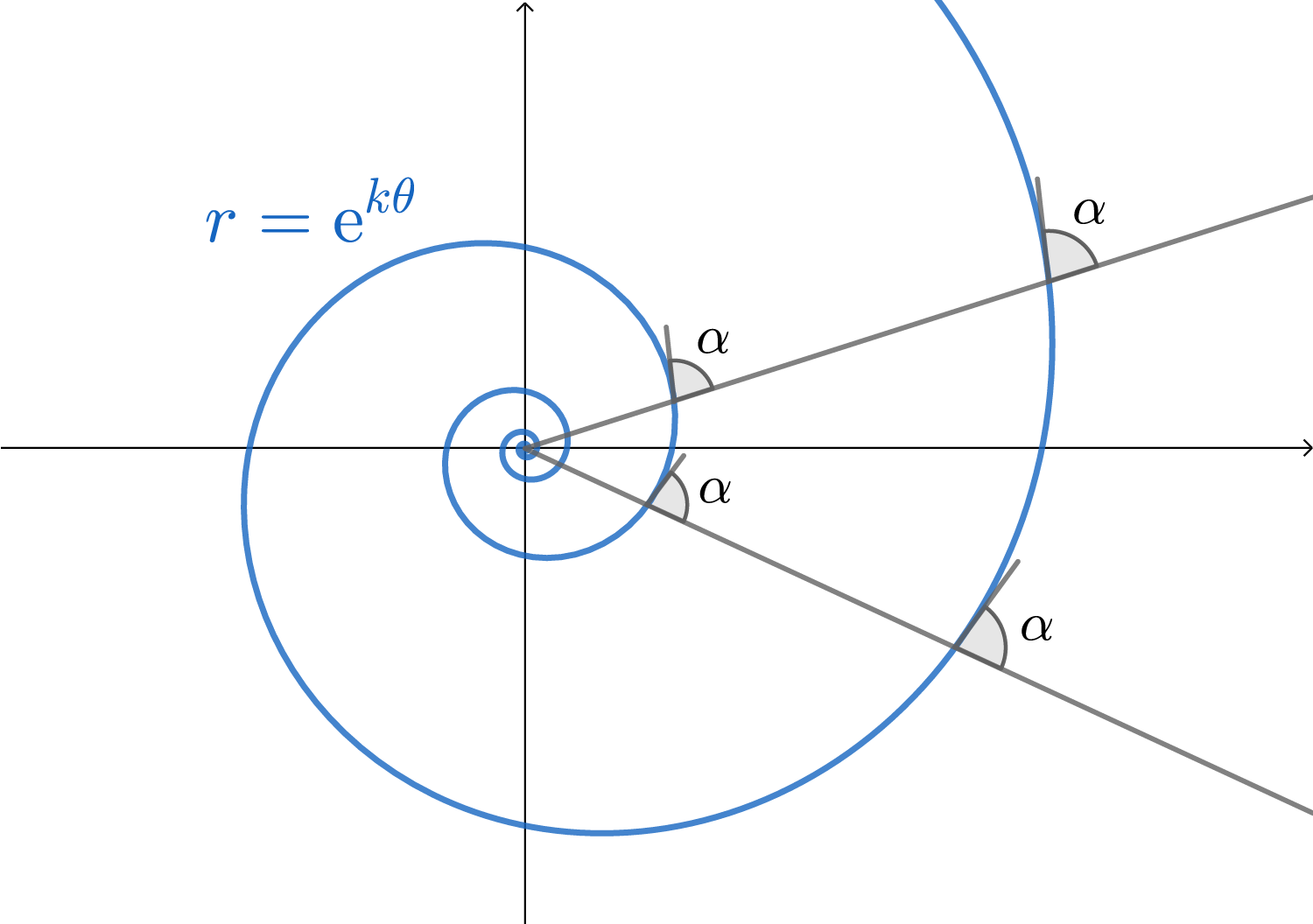
自然界中的等角螺线有很多，如：

鹦鹉螺壳：壳内每个"小房间"都是相似的. 从最里面开始，每一个房间都是上一个房间的放大版，使得半径\(r\)随着角度\(\theta\)呈指数放大，形成了一条等角螺线.
气旋：气团的速度方向与径向夹角是定值，从而气旋的臂形成了一条等角螺线.
银河系：银河系的旋臂大致是一条等角螺线，\(\alpha\approx12^\circ\).