ODE1 动力系统

这是一个关于微分方程的系列，会有4篇文章：

• ODE1 动力系统：这个领域的研究对象和历史，以及一些概念.
• ODE2 一阶微分方程：人口模型、向量场与不动点.
• ODE3 二阶微分方程：简谐运动、单摆、相空间与不动点.
• ODE4 线性微分方程：一些关于线性微分方程的讨论.

你需要有一些预备知识：

• 高中导数.
• 简单的线性代数（可参考系列视频: 线性代数的本质）.

1 动力系统

万物都在运动. 动力系统(dynamical system)指的是随着时间变化的系统：振动的弹簧振子、变化的人口、四处流动的大气气团都是动力系统的例子. 一个动力系统的状态可以由一个关于时间\(t\)的函数\(y(t)\)描述.

动力学(dynamics)是研究动力系统的学科：具体地说，就是研究系统的状态怎样演化. 这个领域的研究从17世纪的牛顿开始. 牛顿提出了力学三定律、发明了微积分，而最简单的动力系统莫过于一个运动的质点了. 在无阻尼弹簧振子中，把质点在某处自由释放，利用牛顿第二定律可以列出 \[ mx''(t)=-kx(t) \tag{a} \] 其中\(x(t)\)表示质点（在\(t\)时刻）的位置，\(x''(t)\)为加速度. 上式是一个关于未知函数\(x\)和它的（2阶）导数\(x''\)的方程，称为关于\(x\)的二阶微分方程(differential equation). 牛顿最先对微分方程做了系统的研究，如在《原理》中建立并求解了行星运动方程，从而验证了开普勒三定律. 解决了太阳-地球系统的运动问题（二体问题）后，牛顿又将目光转向三体问题. 但是问题忽然变得非常复杂；几十年后，人们发现三体问题是无解的（无法求出解析式）.

Poincaré（庞加莱）在1881年发表论文，提出了定性研究微分方程的思想，即从方程本身出发，利用几何工具来定性地分析，例如：这个系统随时间（定性的）的变化趋势如何？是趋向于平衡稳定、呈现出周期变化，或者是呈现出更复杂的模式？……

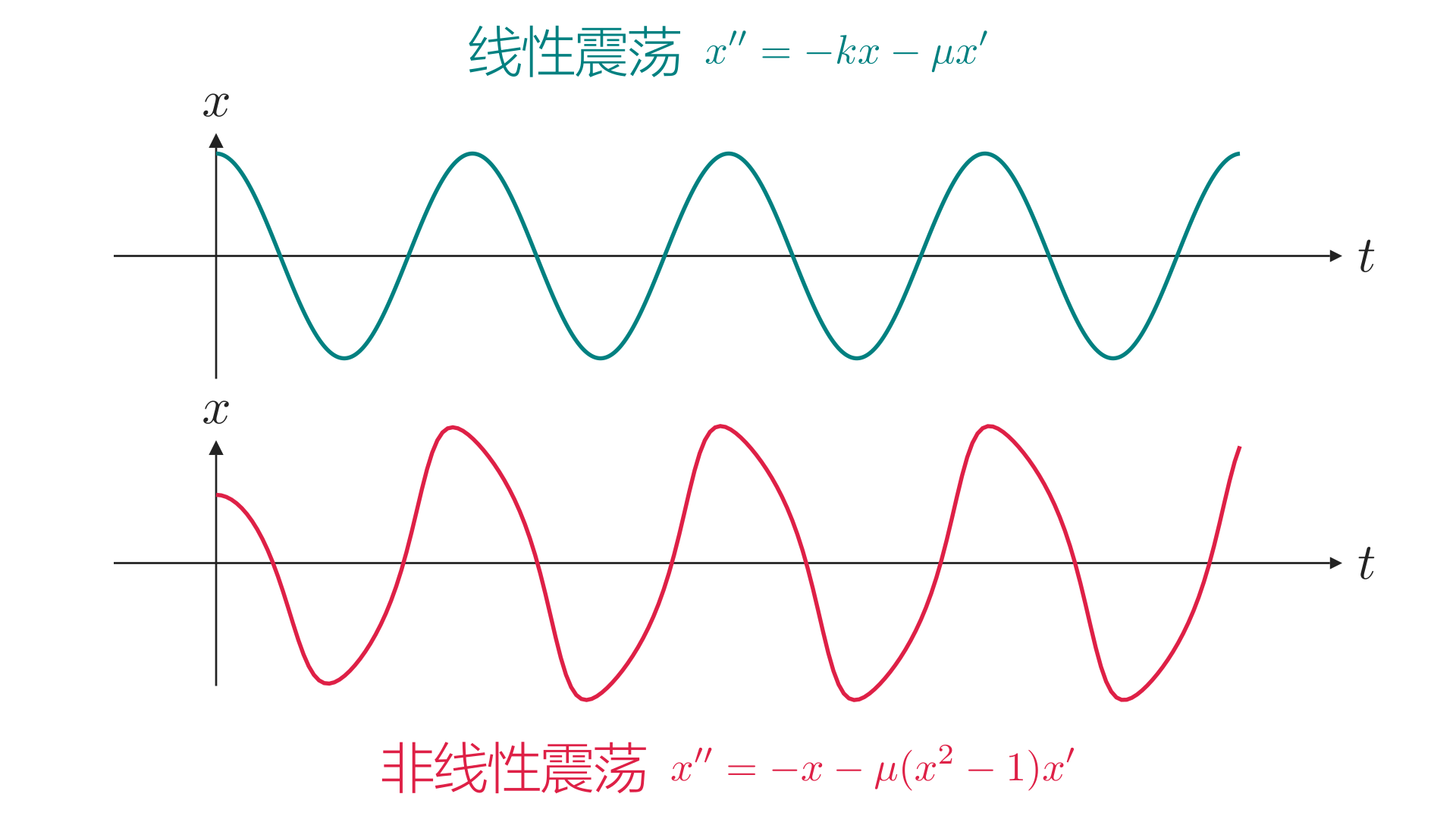
二十世纪初，非线性的震荡（与之相对的是简谐运动这类线性震荡）被广泛应用于雷达、收音机等电子设备中；五十年代，随着高速计算机的发明，我们可以用数值模拟的方法，得到微分方程的数值近似解.

1963年，气象学家Lorenz（洛伦兹）在计算机上模拟了一个简单的气流模型. 他发现气流没有呈现出周期性或者趋于稳定状态，而是不停地做无规律、非周期的震荡；并且初始状态的微小改变能使得演化趋势截然不同. 这个现象称为混沌(chaos)，这也是为什么难以预测天气的原因——大气初始状态的微小改变和误差会让模拟结果与真实情况大相径庭.

之后，人们在流体流动、种群演化、化学反应、神经网络、经济学等诸多方面发现了混沌的影子. 举一个简单的例子，一个人口演化模型：\(p_n\)表示第\(n\)年的人口规模（\(n\in\N\)，\(p_n\)在\(0\)到\(1\)之间），\(r\)是一个正常数，方程 \[ p_{n+1}=rp_n(1-p_n) \tag{b} \] 描述了人口的迭代规律（称为Logistic迭代）. 上式是一个迭代映射(iterated map)或者差分方程(difference equation). 和微分方程相似，差分方程也是一个关于未知函数的方程，不过它的未知函数是离散变化的. 1976年，生物学家Robert May发现了（这个看似简单的）Logistic迭代映射背后的混沌现象.

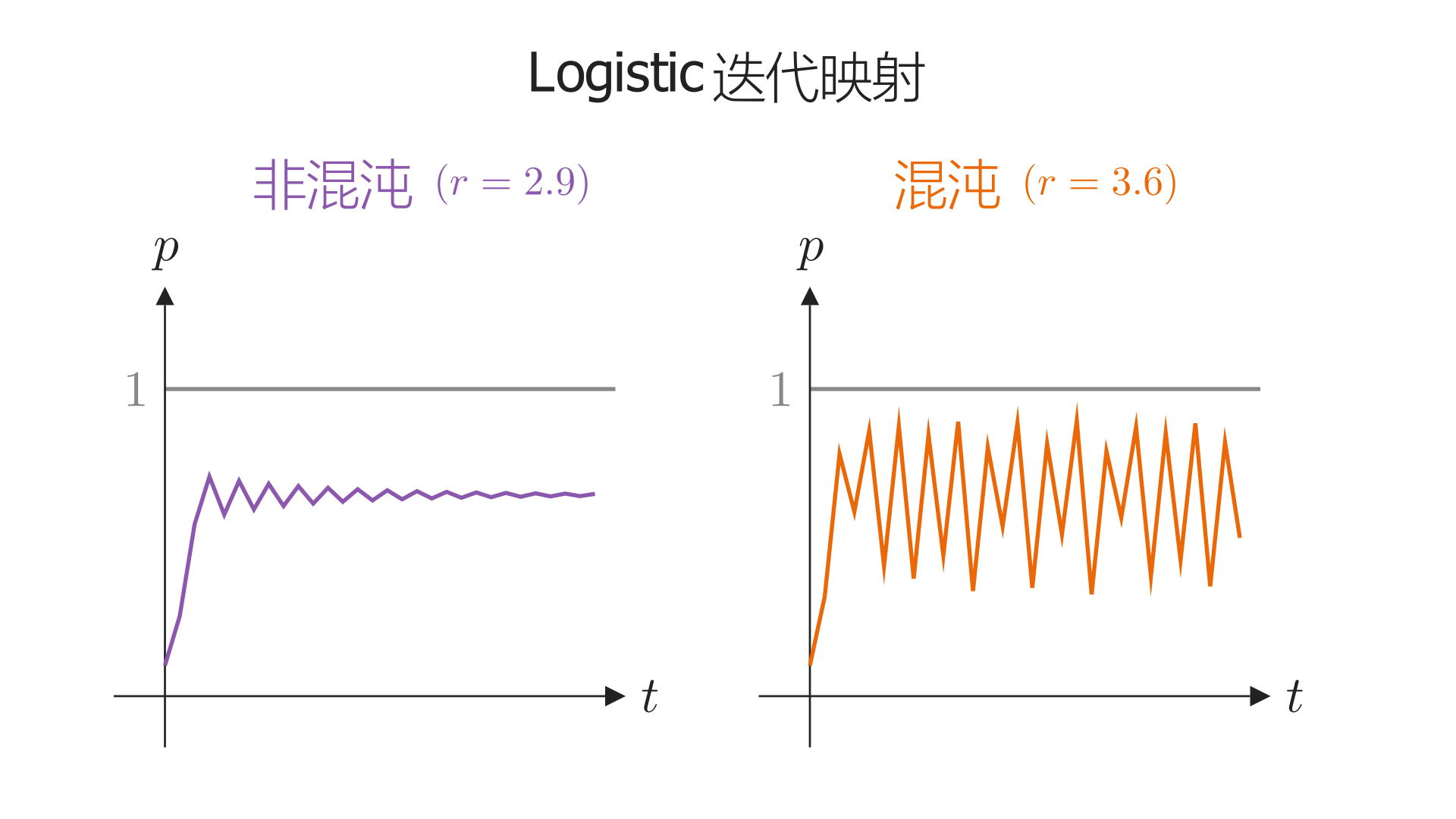
之后，数学物理学家Feigenbaum（费根鲍姆）发现了一个系统从常规转变为混沌的规律；同时，Mandelbrot（曼德博）关于分形的研究也正普及于世. 总而言之，动力学，尤其是非线性动力学，是一个年轻而有活力的学科.

下面介绍一下上面提及的几组概念.

2 差分与微分

首先来简单回顾导数的相关概念.

差分(difference)，顾名思义，就是函数\(y(t)\)的"差别"，即"改变量"： \[ \orange{\Delta y(t)} = y(t+\blue{\Delta t}) - y(t) \] 其中，\(\Delta t\)和\(\Delta y\)分别是自变量、因变量的差分，如下面视频中一开始的情形.（当然，这里的\(y(t)\)可以是离散的：\(t\in\N\)，\(\Delta t=1\)，但是这样就没有下面"微分"的概念了.）

当\(\Delta t\)非常非常小，趋近于\(0\)的时候，上面动画中的割线趋于一条切线，这条切线能够较好拟合\(y(t)\)，所以\(\Delta y\)与\(\Delta t\)的关系也可以用线性关系来近似： \[ \orange{\Delta y(t)} \approx \alpha \blue{\Delta t} \quad (\blue{\Delta t}\to0) \] \(\alpha\)是切线的斜率. 当\(\Delta t\)足够小的时候，上式的偏差是微乎其微的，所以认为\(\Delta y\)就等于\(\alpha \Delta y\)，写作： \[ \orange{\dd{y}(t)}=\alpha\blue{\dd{x}} \] 其中\(\dd{x},\dd{y}\)分别称为自变量、因变量的微分(differential)，即"微小"（\(\Delta t\)趋近于\(0\)时）的改变量，\(\alpha\)就是\(y(t)\)在\(t\)处的导数(derivative)，也可以写作\(\displaystyle\alpha = \dv{y}{t}\)，是因变量与自变量微分的商，所以也叫做微商. 此外，自变量与因变量差分的商\(\dfrac{\Delta y}{\Delta t}\)叫做差商，或者平均变化率. 导数是平均变化率的极限，或者叫瞬时变化率： \[ \dv{y}{t} =\lim_{\Delta t\to0}\frac{\Delta y}{\Delta t} =\lim_{\Delta t\to0}\frac{y(t+\Delta t)-y(t)}{\Delta t} \] "\(\dd{}\)"是微分符号，它本身带有"改变量趋近于\(0\)"的含义. 微分的本质，就是对\(y(t)\)在\(t\)附近的线性近似，以直代曲.

对于每一点\(t\)，都有一个对应的导数\(\alpha(t)\)，记函数\(y'(t)=\alpha(t)\)为\(y(t)\)的导函数.

不过，\(\Delta y\approx\alpha\Delta t\)（\(\Delta t\to0\)）这种关系不是任何时候都存在的. 如果\(y(t)\)在\(t\)附近满足 \[ \orange{\Delta y}=\alpha\blue{\Delta t}+o(\blue{\Delta t}) \] 其中，

• 误差项\(o(\Delta t)\)表示\(\Delta t\)的高阶小量，比\(\Delta t\)小得多，于是可以被忽略.
• \(\alpha\)是一个只\(t\)有关、与\(\Delta t\)趋于\(0\)的方式无关的实数.

如果满足上面的条件，那么称\(y(t)\)在\(t\)可微.

顾名思义，微分方程就是关于未知函数\(\color{SteelBlue}y(t)\)以及它的导数（微分之商）的方程，例如 \[ {\color{SteelBlue}y''}+2{\color{SteelBlue}y'}+{\color{SteelBlue}y}^2=0 \qquad x+2{\color{SteelBlue}y}=\sin{\color{SteelBlue}y'} \quad \dots \] 而差分方程是关于未知数列\(\set{ {\color{SeaGreen}y_n} }\)（离散的函数）以及它的差分的方程，例如 \[ {\color{SeaGreen}\Delta y_n} + 2{\color{SeaGreen}y_n}^2 - {\color{SeaGreen}y_n} = 0 \qquad {\color{SeaGreen}\Delta y_n} + {\color{SeaGreen}\Delta(\Delta y_n)} = {\color{SeaGreen}y_n} \quad \dots \] 不过由于数列的差分可以写成两项之差，\(\Delta y_n=y_{n+1}-y_n\)，上面的方程一般也等价地写成 \[ {\color{SeaGreen}y_{n+1}} =2{\color{SeaGreen}y_n}(1-{\color{SeaGreen}y_n}) \qquad {\color{SeaGreen}y_{n+2}} ={\color{SeaGreen}y_{n+1}}+{\color{SeaGreen}y_n} \quad \dots \] 在这几篇文章中，我们主要研究微分方程.

3 线性与非线性

一个微分方程是线性(linear)的，如果方程两边都是关于\(\color{SteelBlue}y,y',y'',\dots\)的一次多项式，例如 \[ \Align{ {\color{SteelBlue}y''}-{\color{SteelBlue}y'}+2{\color{SteelBlue}y}=\cos{x}, && x^2{\color{SteelBlue}y'''}-4{\color{SteelBlue}y}=0, && {\color{SteelBlue}y'}=3{\color{SteelBlue}y} } \] 以及前面提到的\({\color{SteelBlue}x''}=-k{\color{SteelBlue}x}-\mu{\color{SteelBlue}x'}\)（简谐振子）都是线性微分方程，而 \[ \Align{ {\color{SteelBlue}y''}+2\sin{\color{SteelBlue}y}=0, && \pqty{{\color{SteelBlue}y'}}^2+x=0, && \frac{x+2{\color{SteelBlue}y}}{x-{\color{SteelBlue}y}}={\color{SteelBlue}y'} } \] 以及前面提到的\({\color{SteelBlue}x''}=-{\color{SteelBlue}x}-\mu({\color{SteelBlue}x}^2-1)\)（Van de Pol非线性振子）都是非线性微分方程.

微分方程的阶数(order)是方程中\(\color{SteelBlue}y\)的最高阶导数的阶数.

对于线性微分方程，我们已经有了比较完善的理论. 线性方程描述了一个"理想"的世界：系统总是等于部分的总和，误差总是会被按照确定的倍率放大，不会有难以预测的混沌…… 随着讨论的深入，你对"线性"微分方程的理解会逐渐深入.

不过，生活中大部分事物都是非线性的（例如，同时听两首你喜欢的歌不会给你双倍的快乐），大部分非线性微分方程我们无法求解，不过可以把它们近似成线性方程来求解，或者是从方程直接来分析动力系统的演化. 接下来我们会探讨微分方程，首先利用直观的几何工具来分析，最后会讨论方程的求解以及解的特点等.