GTM218 | 7 子流形
GTM218 (Introduction to Smooth Manifolds) Chapter 5 的笔记.
"光滑子流形" 指的是作为光滑流形的子集的光滑流形. 光滑子流形上有两种拓扑, 一种是其自身作为光滑流形的拓扑, 一种是子空间拓扑.
最重要的一类光滑子流形是 "嵌入子流形", 即上述两种拓扑相同的子流形. 正如其名, 嵌入子流形恰好是光滑嵌入的像集. 另一类更一般的光滑子流形是 "浸入子流形", 它不要求两种拓扑相同. 浸入子流形恰好是单射浸入的像; 其在局部和嵌入子流形一样, 但整体上与子空间拓扑不同.
需要注意的是, 在有些书中, "光滑子流形" 特指 "嵌入子流形".
9 Embedded Submanifolds
9.1 Embedded submanifolds
设光滑流形 \(M\) 的子集 \(S\subset M\). 若 \(S\) 在子空间拓扑以及适当光滑结构下构成无边光滑流形, 使得包含映射 \(S\hookrightarrow M\) 是光滑嵌入, 则称 \(S\) 是 \(M\) 的一个嵌入子流形 (embedded submanifold) 或正则子流形 (regular submanifold). 此时, 称 \(\dim M-\dim S\) 为 \(S\) 在 \(M\) 中的余维数 (codimension). 余维数为 \(1\) 的嵌入子流形也称为嵌入超曲面 (embedded hypersurface).
最简单的嵌入子流形就是余维数为 \(0\) 的嵌入子流形. 回顾: (带边) 光滑流形 \(M\) 的开子流形指的是开子集 \(U\), 其拓扑为子空间拓扑, 光滑结构为 \(M\) 的坐标卡在 \(U\) 上的限制.
Proposition 9.1 (余维数 \(0\) 的嵌入子流形) 设光滑流形 \(M\), 则 \(M\) 的余维数为 \(0\) 的子流形恰为其开子流形.
Pf 设开子流形 \(U\subset M\), 则 \(U\) 是光滑流形且与 \(M\) 维数相等. 在局部坐标系下, 包含映射 \(\iota\) 是恒等映射, 因此是光滑浸入; 又 \(U\) 具有子空间拓扑, \(\iota\) 是拓扑嵌入, 进而是光滑嵌入.
反之, 设 \(U\subset M\) 是余维数 \(0\) 的嵌入子流形, 则包含映射 \(\iota\) 是光滑嵌入. 由 Corollary 7.4 的 2, \(\iota\) 是局部微分同胚, 进而是开映射, 故 \(U\) 是 \(M\) 的开子集.
下面的几个定理给出了构造嵌入子流形的其他办法.
Proposition 9.2 (作为光滑嵌入的像) 设 (带边) 光滑流形 \(M\), 光滑流形 \(N\), 光滑嵌入 \(F:N\to M\), 记 \(S=F(N)\). 则在子空间拓扑下, \(S\) 是拓扑流形, 且其上存在唯一的光滑结构, 使得 \(S\) 是 \(M\) 的嵌入子流形, 且 \(F\) 是 \(N\to S\) 的微分同胚.
Pf \(F\) 是光滑嵌入意味着 \(N\to S\) 是同胚, 进而将 \(N\) 的拓扑流形结构带到 \(S\). 要让 \(F\) 是到 \(S\) 的微分同胚, 可以这样定义 \(S\) 上的光滑结构: \({\cal A}_S:=\{(F(U),\varphi\circ F^{-1})\}\), 其中 \((U,\varphi)\) 是 \(N\) 的光滑图册; \({\cal A}_S\) 的光滑相容性由 \(N\) 的图册的光滑相容性保证. 显然 \(F\) 在该光滑结构下是一个微分同胚, 且这样的 \({\cal A}_S\) 是唯一的. 此时, 包含映射 \(\iota:S\hookrightarrow M\) 等于复合映射 \[ S \overset{F^{-1}}\longrightarrow N \overset{F}\longrightarrow M, \] 即微分同胚与光滑嵌入的复合, 因此 \(\iota\) 是光滑嵌入.
由定义, 任意嵌入子流形都是光滑嵌入的像 (考虑包含映射), 上面的定理表明反之亦然.
Proposition 9.3 (作为积流形的切片) 设光滑流形 \(M,N\), 点 \(p\in M\). 则 \(M\cong M\times\{p\}\) 是 \(M\times N\) 的嵌入子流形.
Pf \(M\times\{p\}\) 是光滑嵌入 \(x\mapsto(x,p)\) 的像.
Proposition 9.4 (作为光滑映射的图像) 设 \(m\) 维光滑流形 \(M\), \(n\) 维 (带边) 光滑流形 \(N\), 开集 \(U\subset M\), 光滑映射 \(f:U\to N\). 则 \(f\) 的图像 \[ \Gamma(f)=\{(x,y)\in M\times N\mid x\in U,y=f(x)\} \] 是 \(M\times N\) 的 \(m\) 维嵌入子流形.
Pf 定义映射 \(\gamma_f:U\to M\times N\), \(\gamma_f(x)=(x,f(x))\), 则 \(\gamma_f\) 是光滑的, 其像集等于 \(\Gamma(f)\). 注意到自然投射 \(\pi_M:M\times N\to M\) 是 \(\gamma_f\) 的光滑左逆, 因此对 \(x\in U\), 切映射 \((\gamma_f)_{*,x}\) 有左逆, 因此是单射, 故 \(\gamma_f\) 是光滑浸入. 此外, \(\pi_M|_{\Gamma(f)}\) 是 \(\gamma_f:U\to\Gamma(f)\) 的连续左逆, 因此 \(\gamma_f:U\to M\times N\) 是拓扑嵌入. 因此 \(\gamma_f\) 是光滑嵌入, 由 Proposition 9.2, \(\Gamma(f)\) 是嵌入子流形.
有时我们需要一种更强的嵌入子流形. 嵌入子流形 \(S\subset M\) 称为逆紧嵌入的 (properly embedded), 若包含映射 \(S\hookrightarrow M\) 是逆紧映射.
Proposition 9.5 (逆紧嵌入的充要条件) 设 (带边) 光滑流形 \(M\), 嵌入子流形 \(S\subset M\). 则 \(S\) 是逆紧嵌入的当且仅当 \(S\) 是 \(M\) 的闭子集. 特别地, 紧的嵌入子流形是逆紧嵌入的.
Pf 若 \(S\) 是逆紧嵌入, (到紧生成的 Hausdorff 空间的) 连续逆紧映射是闭映射, 故 \(S\) 是闭子集. 反之, 若 \(S\) 是闭子集, 像集闭的拓扑嵌入是逆紧的, \(\iota\) 是逆紧映射.
对于最后一句话, 只需注意到 Hausdorff 空间的紧子集是闭的.
Proposition 9.6 (整体光滑映射的图像是逆紧嵌入的) 设光滑流形 \(M\), (带边) 光滑流形 \(N\), 光滑映射 \(f:M\to N\), 则 \(\Gamma(f)\) 是 \(M\times N\) 的逆紧嵌入子流形.
Pf 自然投射 \(\pi_M:M\times N\to M\) 是嵌光滑入 \(\gamma_f:M\to M\times N\) 的光滑左逆, 故 \(\gamma_f\) 逆紧.
9.2 Slice charts
局部来看, 嵌入子流形就像欧氏空间 \(\R^k\) 到 \(\R^n\) 的标准嵌入, 即线性方程组的解集. 具体来说, 设 \(\R^n\) 的开子集 \(U\), 整数 \(k\in\{0,\dots,n\}\), 则子集 \[ S=\{(x^1,\dots,x^k,x^{k+1},\dots,x^n)\in U\mid x^{k+1}=c^{k+1},\dots,x^n=c^n\} \] 称为 \(U\) 的一个 \(k\) 维切片 (slice), 其中 \(c^{k+1},\dots,c^n\) 是常数. 切片 \(S\) 同胚于 \(\R^k\) 的开子集. 特别地, 当 \(k=n\) 时, \(S=U\).
对于光滑流形 \(M\) 的坐标卡 \((U,\varphi)\), 子集 \(S\subset U\) 称为该坐标卡的一个 \(k\) 维切片, 若 \(\varphi(S)\) 是 \(\varphi(U)\subset\R^n\) 的 \(k\) 维切片.
Theorem 9.7 (嵌入子流形的局部刻画) 设光滑流形 \(M\), 子集 \(S\subset M\).
- 若 \(S\) 是 \(k\) 维嵌入子流形, 则 \(S\) 中任意一点附近存在 \(M\) 的坐标卡 \((U,\varphi)\), 使得 \(S\cap U\) 是 \(U\) 的 \(k\) 维切片. 此时我们称 \(S\) 满足局部 \(k\)-切片条件, 坐标卡 \((U,\varphi)\) 称为 \(S\) 在 \(M\) 中的切片坐标卡.
- 若 \(S\) 满足局部 \(k\)-切片条件, 则 \(S\) 在子空间拓扑下构成拓扑流形, 且在适当光滑结构下构成嵌入子流形.
Pf 一, 设 \(S\) 是 \(k\) 维嵌入子流形. 任取 \(p\in S\). 因为 \(\iota:S\hookrightarrow M\) 是光滑浸入, 故存在 \(S\) 的以 \(p\) 为中心的坐标卡 \((U,\varphi)\) 和 \(M\) 的以 \(p\) 为中心的坐标卡 \((V,\psi)\), 使得 \(\iota|_U:U\to V\) 有标准形式 \[ (x^1,\dots,x^k)\mapsto(x^1,\dots,x^k,0,\dots,0). \] 因为 \(S\) 有子空间拓扑且 \(U\) 开, 则存在 \(M\) 的开子集 \(W\) 使得 \(U=S\cap W\). 令 \(V_0=W\cap V\), 则 \((V_0,\psi|_{V_0})\) 是一个以 \(p\) 为中心的坐标卡, 且 \(S\cap V_0=U\) 是 \(V\) 的切片.
二, 设 \(S\) 满足局部切片条件. 子空间 \(S\) 继承 \(M\) 的 Hausdorff 性与第二可数性. 对于局部欧氏性, 我们能利用 \(S\) 的局部 \(k\)-切片构造一个光滑图册.
任取 \(p\in S\), 存在 \(M\) 的以 \(p\) 为中心的坐标卡 \((U,\varphi)\), 使得 \(S\cap U\) 是 \(U\) 的 \(k\) 维切片. 设 \(\pi:\R^n\to\R^k\) 是向前 \(k\) 个坐标的自然投射. 令 \[ \Align{ V&=U\cap S, & \hat{V}&=(\pi\circ\varphi)(V), & \psi=\pi\circ\varphi|_V:V\to\hat{V}. } \] 要说明 \((V,\psi)\) 构成 \(S\) 的一个坐标卡, 我们要证明:
\(\hat{V}\) 是 \(\R^k\) 的开集. 注意到 \(\varphi\) 是同胚, 而 \(\pi\) 是开映射, 故 \(\hat{V}\) 是开的.
\(\psi\) 是同胚. 设 \(\varphi(V)\) 在 \(\varphi(U)\) 中由方程 \(x^{k+1}=c^{k+1},\dots,x^n=c^n\) 给出, 则 \(\psi:V\to\hat{V}\) 具有连续的逆映射 \(\varphi^{-1}\circ j|_{\hat V}:\hat{V}\to V\), 其中 \(j:\R^k\to\R^n\), \[ (x^1,\dots,x^k)\mapsto(x^1,\dots,x^k,c^{k+1},\dots,c^n). \]
接着验证这些坐标卡的光滑相容性. 设 \((U,\varphi)\) 和 \((U',\varphi')\) 是两个切片坐标卡, \((V,\psi)\) 和 \((V',\psi')\) 分别是对应的 \(S\) 的坐标卡, 则转移映射 (如下图) \[ \Align{ \psi'\circ\psi^{-1} &=(\pi\circ\varphi')\circ(\varphi^{-1}\circ j|_{\hat V}) \\ &=\pi\circ(\varphi'\circ\varphi^{-1})\circ j|_{\hat V} } \] 是三个光滑映射的复合, 故光滑.
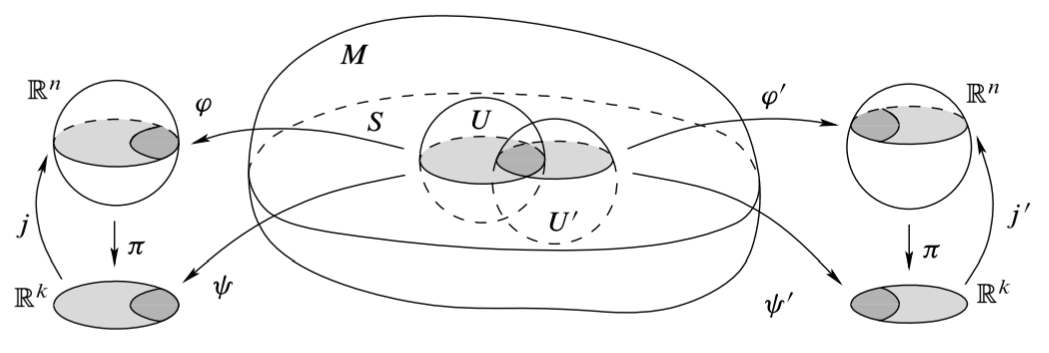
在如上定义的光滑结构下, \(S\) 构成光滑流形. 并且在 \((U,\varphi)\) 与相应的 \((V,\psi)\) 下, 包含映射 \(\iota:S\hookrightarrow M\) 有形式 \((x^1,\dots,x^k)\mapsto(x^1,\dots,x^k,c^{k+1},\dots,c^n)\), 因此是一个光滑浸入. 又因为 \(S\) 有子空间拓扑, 所以 \(\iota\) 是拓扑嵌入, 因此是光滑嵌入. 故 \(S\) 是嵌入子流形.
后面我们将证明, 上面的证明中构造的光滑结构是唯一的 (只有它能让 \(S\) 成为 \(M\) 的嵌入子流形).
Theorem 9.8 (边界是逆紧嵌入的) 设带边光滑流形 \(M\), 则 \(\partial M\) 在子空间拓扑下构成 \((n-1)\) 维无边拓扑流形, 且在适当光滑结构下构成 \(M\) 的逆紧嵌入子流形.
Pf 我们已经知道 \(\partial{M}\) 是 \((n-1)\) 维子流形, 且为 \(M\) 的闭子集. 我们只需再证明 \(\partial{M}\) 是嵌入子流形, 进而由逆紧嵌入的充要条件 (Proposition 9.5), \(\partial{M}\) 是逆紧嵌入的.
根据边界的定义, 任给 \(p\in\partial{M}\), 存在以 \(p\) 为中心的界坐标卡 \((U,\varphi)\), 满足 \[ \partial{M}\cap U =\{(x^1,\dots,x^{n-1},x^n)\in\varphi(U)\mid x^n=0\}, \] 这恰恰说明 \(\partial{M}\) 满足局部 \((n-1)\)-切片条件. 由 Theorem 9.7, \(\partial{M}\) 是嵌入子流形.
9.3 Level sets
嵌入子流形可以由光滑映射的水平集给出. 在第一节的例子中, 我们看到光滑函数 \(\Phi:\R^n\supset U\to\R\) 的水平集 (满足某些条件) 构成光滑流形. 下面的定理是这个例子的强化版本.
Theorem 9.9 (常秩水平集定理) 设光滑流形 \(M,N\), 光滑映射 \(\Phi:M\to N\) 有常秩 \(r\). 则任意水平集 \(\Phi^{-1}(c)\) 都是 \(M\) 的逆紧嵌入子流形, 其余维数为 \(r\).
Pf 设 \(\dim{M}=m\), \(\dim N=n\). 任取 \(p\in\Phi^{-1}(c)\), 根据秩定理, 存在以 \(p\) 为中心的坐标卡 \((U,\varphi)\) 和以 \(c\) 为中心的坐标卡 \((V,\psi)\), 使得 \(\Phi\) 有局部标准型. 于是 \(\Phi^{-1}(c)\cap U\) 是切片 \[ \{ (x^1,\dots,x^r,x^{r+1},\dots,x^m)\in U\mid x^1=0,\dots,x^r=0 \}, \] 因此 \(\Phi^{-1}(c)\) 是余维数 \(r\) 的嵌入子流形. 因为 \(\{c\}\subset N\) 是闭子集, \(\Phi\) 连续, 因此 \(\Phi^{-1}(c)\) 是闭子集. 由逆紧嵌入的充要条件, \(\Phi^{-1}(c)\) 是逆紧嵌入的.
常秩水平集定理可以看作线性映射 "秩-零化度定理" 的推广. 设线性映射 \(L:\R^m\to\R^n\) 的秩为 \(r\), 则零空间 \(\ker{L}=L^{-1}(0)\) 是 \(\R^m\) 的线性子空间, 其余维数为 \(r\). 从解方程的角度看, 线性方程组 \(Lx=0\) 一共有 \(r\) 个线性无关的方程, 每个方程使 \(x\in\R^m\) 的自由度减少 \(1\), 因此总共减少了 \(r\) 自由度, 即 \(\ker{L}\) 的余维数为 \(r\). 对于常秩光滑映射 \(\Phi:M\to N\), 在局部上看, 方程 \(\Phi(x)=c\) 一共有 \(r\) 个线性无关的坐标分量, 在 \(\dim{M}\) 的基础上减少了 \(r\) 自由度.
常秩映射的两个特殊情况是光滑浸入和光滑淹没.
- 对于光滑浸入, \(r=\dim{M}\), 因此水平集是 \(M\) 的 \(0\) 维子流形, 即一些离散的点, 这当然没什么好研究的.
- 对于光滑淹没, \(r=\dim{N}\), 因此水平集是 \(M\) 的余维数等于 \(\dim{N}\) 的逆紧嵌入子流形.
实际上, 光滑淹没的条件是可以放松的. 因为我们只关心水平集 \(\Phi^{-1}(c)\) 上的 "淹没性", 因此 \(\Phi\) 不必是整体上的光滑淹没, 而只需在 \(\Phi^{-1}(c)\) 上是光滑淹没即可. 先引入几个概念. 对于光滑映射 \(\Phi:M\to N\), 点 \(p\in M\) 称为 \(\Phi\) 的正则点 (regular point), 若 \(\Phi_{*,p}:T_pM\to T_{\Phi(p)}N\) 是满射; 否则称为临界点 (critical point).
- 根据 Proposition 7.1, 正则点集是 \(M\) 的开子集.
- 若 \(\dim{M}<\dim{N}\), 则 \(M\) 的每个点都是临界点.
- \(M\) 的每个点都是正则点, 当且仅当 \(\Phi\) 是光滑淹没.
点 \(c\in N\) 称为正则值 (regular value), 若 \(\Phi^{-1}(c)\) 只包含正则点 (此时称 \(\Phi^{-1}(c)\) 为正则水平集); 否则称 \(c\) 为临界值 (critical value). 特别地, 若 \(\Phi^{-1}(c)=\emptyset\), 则 \(c\) 也是正则值.
Corollary 9.10 (正则水平集定理) 设光滑流形 \(M,N\), 光滑映射 \(\Phi:M\to N\). 若 \(c\in N\) 是 \(\Phi\) 的正则值, 则 \(\Phi^{-1}(c)\) 是 \(M\) 的逆紧嵌入子流形, 其余维数为 \(\dim{N}\).
Pf 由 Proposition 7.1, 满足 \(\rank{F_{*,p}}=\dim{N}\) 的点 \(p\) 组成的集合 \(U\) 是 \(M\) 的开子集. 根据假设, \(\Phi^{-1}(c)\subset U\). 因为 \(\Phi|_U:U\to N\) 是光滑淹没, 所以水平集 \(\Phi^{-1}(c)\) 是 \(U\) 的嵌入子流形. 又因为光滑嵌入的复合 \(\Phi^{-1}(c)\hookrightarrow U\hookrightarrow M\) 仍是光滑嵌入, 因此 \(\Phi^{-1}(c)\) 是 \(M\) 的嵌入子流形. \(\Phi^{-1}(c)\) 的闭性由 \(\Phi\) 的连续性保证.
正则水平集定理的应用:
(球面) \(\mathbb{S}^n\) 是 \(\R^{n+1}\) 上的函数 \(f:\R^{n+1}\to\R\), \(f(x)=\|x\|^2\) 的水平集 \(f^{-1}(1)\). 计算 \(f\) 的切映射 \[ f_{*,x}(v) = 2\sum_i x^iv^i, \] 可见只要 \(x\neq0\), \(f_{*,x}\) 便是满射, 故对于任意 \(r>0\), 球面 \(S_r(0)=f^{-1}(r)\) 是 \(\R^{n+1}\) 的逆紧嵌入子流形.
(嵌入超曲面) 设光滑流形 \(M\) 上的光滑函数 \(f:M\to\R\), 则 \(0\in\R\) 是 \(f\) 的正则值, 当且仅当 \(f\) 的 Jacobi 矩阵在 \(f^{-1}(0)\) 上处处秩为 \(1\), 也即 \(f_{*,p}\neq0\). 此时 \(f^{-1}(0)\) 是 \(M\) 的余维数 \(1\) 的逆紧嵌入子流形.
还有一些反例:
- (X 形曲线) 方程 \(x^2-y^2=0\) 的图像是 \(\R^2\) 中的两条相交直线, 它可以视作 \(f(x,y)=x^2-y^2\) 的水平集 \(f^{-1}(0)\). 计算 Jacobi 矩阵: \(DF|_{(x,y)}=(2x,-2y)\), 因此 \(DF\) 在 \((0,0)\) 处为零, 故原点是不是正则点, \(f^{-1}(0)\) 不是正则水平集.
- (尖曲线) 方程 \(x^2-y^3=0\) 的图像是 \(\R^2\) 中的一个带 "尖" 曲线. 计算表明 \(f(x,y)=x^2-y^3\) 在原点处的秩为零, 故 \(f^{-1}(0)\) 不是正则水平集.
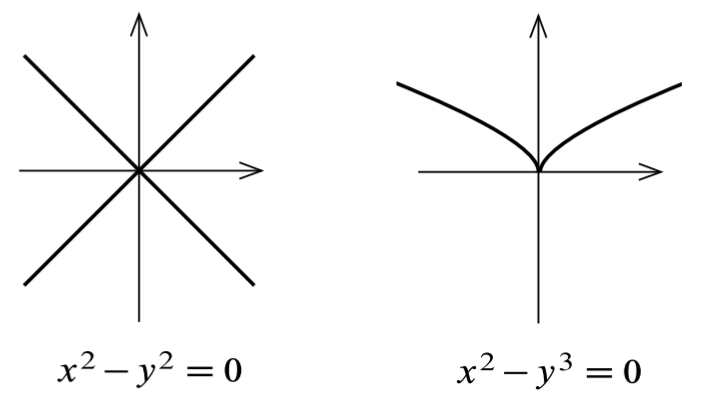
光滑淹没的水平集是嵌入子流形. 反之, 嵌入子流形在局部上是光滑淹没的水平集.
Proposition 9.11 (嵌入子流形局部为水平集) 设 \(m\) 维光滑流形 \(M\) 的子集 \(S\), 则 \(S\) 是 \(k\) 维嵌入子流形, 当且仅当对 \(S\) 中任意一点 \(p\), 存在 \(p\) 在 \(M\) 中的邻域 \(U\), 使得 \(U\cap S\) 是某光滑淹没 \(\Phi:U\to\R^{m-k}\) 的水平集.
Pf 设 \(S\) 是 \(k\) 维嵌入子流形, 则 \(p\in S\) 的 \(M\)-邻域 \(U\) 上有切片坐标 \((x^1,\dots,x^m)\). 若定义光滑淹没 \(\Phi:U\to\R^{m-k}\), \(\Phi(x)=(x^{k+1},\dots,x^m)\), 则 \(U\cap S\) 由 \(\Phi^{-1}(0)\) 给出.
反之, 设 \(S\cap U\) 是光滑淹没 \(\Phi:U\to\R^{m-k}\) 的水平集, 根据常秩水平集定理, \(S\cap U\) 是 \(U\) 的 \(k\) 维嵌入子流形, 因而满足局部 \(k\)-切片条件, 进而也在 \(M\) 中满足局部 \(k\)-切片条件 (关键, \(U\) 是 \(M\) 的开子集).