GTM218 | 6 光滑映射的局部性态

GTM218 (Introduction to Smooth Manifolds) Chapter 4 的笔记.

8 Embeddings, Submersions & Smooth Covering Maps

本节中, 我们研究三种特殊的满秩映射: 光滑嵌入, 光滑淹没, 光滑覆叠映射.

光滑流形范畴中一些特殊的映射 (橙色), 及其在拓扑空间范畴中的类比 (灰色) 如下图:

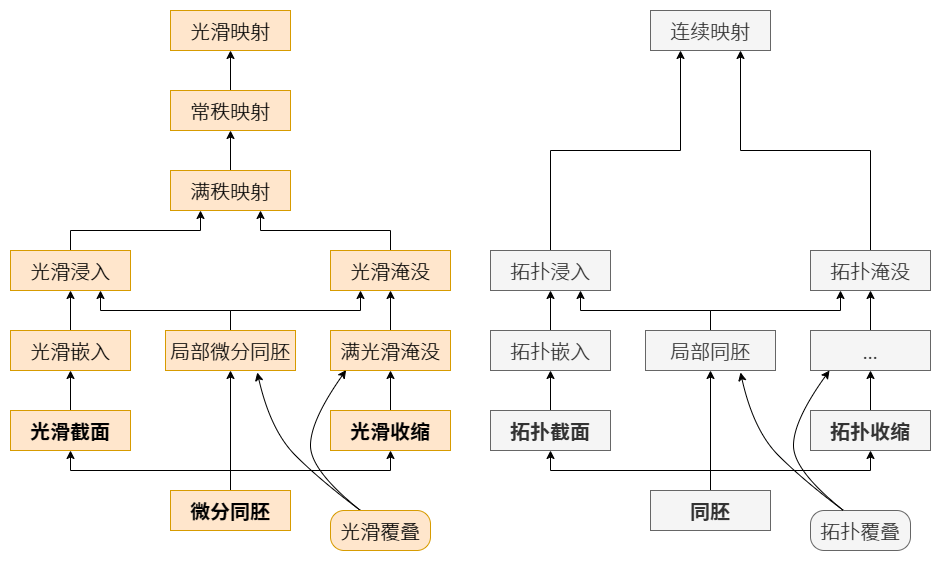
• 其中, 加粗的是那些拥有单侧/双侧逆的态射.
• 拓扑/光滑覆叠比较特殊, 因为它们对拓扑空间有额外的要求.

8.1 Embeddings

嵌入是一种特殊的光滑浸入. 若 \(M,N\) 为 (带边) 光滑流形, 光滑嵌入 (smooth embedding) 指的是同时为拓扑嵌入的光滑浸入 \(F:M\to N\) (即 \(F\) 应当是 \(M\to F(M)\) 的同胚).

• 应当注意, 光滑嵌入不等于 "光滑的拓扑嵌入", 而是 "光滑浸入 \(+\) 拓扑嵌入". 两者不相同. 例如, 映射 \(\gamma:\R\to\R^2\), \(\gamma(t)=(t^3,0)\) 是光滑的拓扑嵌入, 但它不是光滑嵌入, 因为 \(\gamma'(0)=0\).
• 复合保持光滑浸入与拓扑嵌入, 因此光滑嵌入的复合是光滑嵌入.

光滑嵌入的例子:

• (开子流形) 开子流形 \(U\hookrightarrow M\) 是光滑嵌入.

• (积) 设光滑流形 \(M_1,\dots,M_k\), 取定 \(p_i\in M_i\), 则 \(\iota_j:M_j\to\prod M_i\), \[ \iota_j(q) = (p_1,\dots,p_{j-1},q,p_{j+1},\dots,p_k) \] 是光滑嵌入. 特别地, \(\R^n\hookrightarrow\R^{n+k}\) 是光滑嵌入.

反例:

• 拓扑嵌入要求 \(f:M\to f(M)\) 是同胚, 也就是说: ① \(f\) 是单射, ② \(f\) 是保持拓扑. 因此, 光滑嵌入要比单射浸入更强.

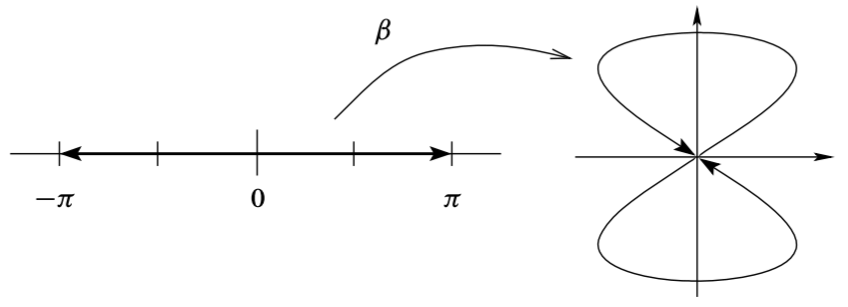
• (\(8\) 字形空间) 曲线 \(\beta:(-\pi,\pi)\to\R^2\), \[ \beta(t)=(\sin{2t},\sin{t}) \] 是一个单射浸入 (如下图). 然而它不是拓扑嵌入, 因为 \(\beta\) 的像在子空间拓扑下是紧的, 但 \((-\pi,\pi)\) 非紧.

  

• (环面上的稠密曲线) 设环面 \(\mathbb{T}^2=\mathbb{S}^1\times\mathbb{S}^1\in\C^2\), 无理数 \(\alpha\), 曲线 \(\gamma:\R\to\mathbb{T}^2\), \[ \gamma(t) = (\e^{2\pi\i t},\e^{2\pi\i\alpha t}) \] 是一个单射浸入. 然而它也不是拓扑嵌入. 可以证明, 像集 \(\gamma(\R)\) 在 \(\mathbb{T}^2\) 中稠密.

Proposition 8.1 (光滑嵌入判断) 设 (带边) 光滑流形 \(M,N\), 单射光滑浸入 \(F:M\to N\). 若 \(F\) 满足下列条件之一, 则 \(F\) 是光滑嵌入.

1. \(F\) 是开映射或闭映射.
2. \(F\) 是逆紧映射.
3. \(M\) 紧.
4. \(M\) 无边, 且 \(\dim{M}=\dim{N}\).

Pf 1, 因为开/闭的连续单射是拓扑嵌入, 因此 \(F\) 是拓扑嵌入, 进而是光滑嵌入. 2, (拓扑流形上) 连续的逆紧映射是闭映射. 3, 由闭映射引理, \(F\) 是闭映射. 4, 此时 \(F_{*,p}\) 处处可逆, Theorem 7.3 后的讨论表明 \(F(M)\subset{\rm Int}N\); Corollary 7.4 表明 \(F:M\to{\rm Int}N\) 是局部微分同胚, 进而是开映射. 因此, \(F\) 作为开映射 \(M\to{\rm Int}N\) 与 \({\rm Int}N\hookrightarrow N\) 的复合, 是开的.

• (球面) 球面的包含映射 \(\iota:\mathbb{S}^n\to\R^{n+1}\) 是光滑的 (可以计算其局部坐标表示), 并且在每一点都是单射, 因此是单射浸入. 因为 \(\mathbb{S}^n\) 紧, 所以 \(\iota\) 是嵌入.
• 光滑嵌入可以既不开又不闭, 比如曲线 \(\gamma:(0,1)\to\R^2\), \(\gamma(t)=(t,0)\). 实际上, 光滑嵌入是开/闭映射, 当且仅当像集是陪域的开/闭子集.

Theorem 8.2 (局部嵌入定理) 设 (带边) 光滑流形 \(M,N\), 光滑映射 \(F:M\to N\). TFAE:

1. \(F\) 是光滑浸入.
2. 对任意 \(p\in M\), 存在邻域 \(U\) 使得 \(F|_U:U\to N\) 是光滑嵌入.

Pf 2 \(\Rightarrow\) 1 比较简单: 此时 \(F\) 在每一点的邻域满秩, 故为满秩映射.

1 \(\Rightarrow\) 2. 我们先证明 \(F\) 在某邻域 \(U_1\) 上是单射.

• 若 \(F(p)\) 不是边界点, 则秩定理与 "带边流形的浸入标准型" (Theorem 7.9) 都表明 \(F\) 在 \(p\) 的某邻域 \(U_1\) 上有浸入标准形式, 因此 \(F|_{U_1}\) 是单射.
• 若 \(F(p)\) 是边界点, 设 \((W,\psi)\) 是以 \(F(p)\) 为中心的边界坐标卡, 此时 \(U_0=F^{-1}(W)\) 是 \(p\) 的邻域. 记包含映射 \(\iota:\H^n\hookrightarrow\R^n\), 则复合映射 \(\iota\circ\psi\circ F|_{U_0}:U_0\to\R^n\) 是到无边流形的光滑浸入, 根据上面一种情况, 存在邻域 \(U_1\subset U_0\) 使得 \(\iota\circ\psi\circ F|_{U_1}\) 单, 于是 \(F|_{U_1}\) 单.

\(M\) 局部紧, 因此存在 \(p\) 的预紧邻域 \(U\) 满足 \(\overline{U}\subset U_1\). 则 \(F|_{\overline U}\) 连续的单射, 根据闭映射引理, \(F|_{\overline{U}}\) 是拓扑嵌入. 其进一步限制 \(F|_U\) 也是拓扑嵌入; 光滑浸入 \(F\) 在开集 \(U\) 上的限制也是光滑浸入. 因此 \(F|_U\) 是光滑嵌入.

实际上, 我们可以定义拓扑浸入 (topological immersion) 为连续映射 \(F:X\to Y\) 满足任意 \(p\in X\) 存在邻域 \(U\), 使得 \(F|_U:U\to Y\) 是拓扑嵌入.

• 光滑浸入都是拓扑浸入; 光滑浸入不等于 "光滑的拓扑浸入", 例如 \(\gamma(t)=(t^3,0)\) 是后者, 却不是前者.
• 单射拓扑浸入 \(=\) 拓扑嵌入.

8.2 Submersions

设连续映射 \(\pi:M\to N\), 它的一个截面 (section) 指的是连续的右逆 \(\sigma:N\to M\), 满足 \(\pi\circ\sigma={\rm id}_N\). 开集 \(U\subset N\) 上的一个局部截面指的是连续映射 \(\sigma:U\to M\), 满足 \(\pi\circ\sigma={\rm id}_U\). 局部截面使得我们能将 \(N\) 上的构造 "局部地" 提升到 \(M\) 上.

以下定理给出了光滑淹没的刻画.

Theorem 8.3 (局部截面定理) 设光滑流形 \(M,N\), 光滑映射 \(\pi:M\to N\), TFAE:

1. \(\pi\) 是光滑淹没.
2. \(M\) 中任意一点都是光滑局部截面的像.

Pf 1 \(\Rightarrow\) 2, 任给 \(p\in M\), \(q=\pi(p)\). 根据秩定理, 存在以 \(p,q\) 为中心的坐标系 \((U,\varphi)\), \((V,\psi)\), 使得 \(\pi\) 的坐标表示为 \(\hat\pi(x^1,\dots,x^n,\dots,x^m)=(x^1,\dots,x^n)\). 取足够小邻域, 便可使 \(\pi\) 是满射. 实际上, 对于足够小的 \(\varepsilon>0\), 坐标立方体 \[ C_\varepsilon=\{x\in U\mid|x^i|<\varepsilon\} \] 在 \(\pi\) 下的像为立方体 \[ C'_\varepsilon=\{y\in V\mid |y^i|<\varepsilon\}. \] 定义映射 \(\sigma:C'_\varepsilon\to C_\varepsilon\), \(\hat\sigma(x^1,\dots,x^n)=(x^1,\dots,x^n,0,\dots,0)\), 则 \(\sigma\) 是 \(\pi\) 的局部光滑截面, 满足 \(\sigma(q)=p\).

2 \(\Rightarrow\) 1, 任取 \(p\in M\), 设 \(\sigma:U\to M\) 使得 \(\pi\circ\sigma={\rm id}_U\) 且存在 \(q\in N\), 满足 \(\sigma(q)=p\), 于是 \(\pi_{*,p}\circ\sigma_{*,q}={\rm id}_U\), 即 \(\pi_{*,p}\) 存在右逆, 是满射.

该定理启发出拓扑淹没 (topological submersion) 的定义: 即连续映射 \(\pi:X\to Y\) 满足 \(X\) 中任意一点都是连续局部截面的像.

• 同样地, 光滑淹没不等于 "光滑的拓扑淹没". 例如, \(\R^2\to\R\), \((x,y)\mapsto x^3\) 是后者, 却不是前者.
• 满射拓扑淹没 \(=\) 开的商映射.

Proposition 8.4 (光滑淹没的性质) 设光滑流形 \(M,N\), 光滑淹没 \(\pi:M\to N\). 则 \(\pi\) 是开映射; 若 \(\pi\) 还是满射, 则它是商映射.

Pf 只需证明 \(\pi\) 是开映射. 任取开集 \(W\subset M\), \(q\in\pi(W)\). 设 \(p\in W\) 满足 \(\pi(p)=q\), 则存在局部截面 \(\sigma:U\to M\) 满足 \(\sigma(q)=p\). 可以证明, \(\sigma^{-1}(W)\) 是 \(q\) 在 \(\pi(W)\) 中的邻域, 因此 \(\pi(W)\) 开.

下面三个定理表明, "满射淹没" 在光滑范畴中的角色相当于 "商映射" 在拓扑范畴中的角色.

Theorem 8.5 (满射淹没的特征性质) 设光滑流形 \(M,N\), 满射淹没 \(\pi:M\to N\). 则对任意 (带边) 光滑流形 \(P\), 映射 \(F:N\to P\) 光滑当且仅当 \(F\circ\pi\) 光滑: \[ \xymatrix{ M \ar[d]_\pi \ar[rd]^{F\circ\pi} \\ N \ar[r]_F & P. } \]

Pf 若 \(F\) 光滑, 则复合映射 \(F\circ\pi\) 光滑. 反之, 若 \(F\circ\pi\) 光滑. 任取 \(q\in N\), \(p\in\pi^{-1}(q)\), 则存在 \(q\) 的邻域 \(U\) 和光滑局部截面 \(\sigma:U\to M\) 满足 \(\sigma(q)=p\). 则 \[ F|_U = F|_U\circ{\rm id}_U = F|_U\circ(\pi\circ\sigma) = (F\circ\pi)\circ\sigma \] 是光滑映射 \((F\circ\pi)\) 与 \(\sigma\) 的复合, 于是 \(F\) 在邻域 \(U\) 光滑. 由 \(p\) 的任意性, \(F\) 光滑.

Theorem 8.6 (唯一下降/泛性质) 设光滑流形 \(M,N\), 满射淹没 \(\pi:M\to N\). 设 (带边) 光滑流形 \(P\), 光滑映射 \(F:M\to P\) 在 \(\pi\) 的纤维上常值, 则存在唯一光滑映射 \(\tilde{F}:N\to P\), 使得 \(\tilde{F}\circ\pi=F\): \[ \xymatrix{ M \ar[d]_\pi \ar[rd]^{F} \\ N \ar@{.>}[r]_{\tilde F} & P. } \]

Pf 根据连续商映射的性质, 存在唯一连续映射 \(\tilde{F}\) 满足交换图. 根据 Theorem 8.5, \(\tilde{F}\) 光滑.

Theorem 8.7 (商空间的唯一性) 设光滑流形 \(M,N_1,N_2\), 满射淹没 \(\pi_i:M\to N_i\). 若 \(\pi_1\) 在 \(\pi_2\) 的纤维上常值, 且反之亦然, 则存在唯一微分同胚 \(F:N_1\to N_2\), 使得 \(F\circ\pi_1=\pi_2\): \[ \xymatrix@C=1em{ & M \ar[dl]_{\pi_1} \ar[dr]^{\pi_2} \\ N_1 \ar@{.>}[rr]_{F} && N_2. } \]

8.3 Smooth covering maps

光滑覆叠映射是拓扑空间上覆叠映射的光滑版本. 拓扑空间的覆叠映射指的是连续满射 \(\pi:E\to M\) 满足 \(M\) 中每个点都有均匀覆叠邻域 \(U\) (即 \(\pi^{-1}(U)\) 的每个分量同胚地映到 \(U\)). 一般还要求 \(E,M\) 连通且局部道路连通.

类似地, 设 \(E,M\) 是连通 (带边) 光滑流形, 光滑满射 \(\pi:E\to M\) 称为光滑覆叠映射 (smooth covering map), 若 \(M\) 的每一点存在均匀覆叠邻域 \(U\), 满足 \(\pi^{-1}(U)\) 的每个分量微分同胚地映到 \(U\). 流形 \(M\) 称为覆叠的底 (base), \(E\) 称为覆叠流形 (covering manifold).

为了与光滑覆叠区分, 今后将拓扑空间的覆叠称为拓扑覆叠.

Proposition 8.8 (光滑覆叠的性质)

1. 光滑覆叠是局部微分同胚, 满射淹没, 开映射, 商映射.
2. 单射的光滑覆叠是微分同胚.
3. 拓扑覆叠成为光滑覆叠, 当且仅当它是局部微分同胚.

光滑覆叠映射既是局部微分同胚, 又是满射淹没. 上一节关于满射淹没的理论可以应用于光滑覆叠. 特别地, 局部截面定理可以加强:

Proposition 8.9 (光滑覆叠的局部截面定理) 设 (带边) 光滑流形 \(E,M\), 光滑覆叠 \(\pi:E\to M\). 任给均匀覆叠开集 \(U\subset M\), \(q\in U\), \(p\in\pi^{-1}(q)\), 则存在唯一光滑局部截面 \(\sigma:U\to E\), 满足 \(\sigma(q)=p\).

Pf 设 \(\tilde{U}_0\) 是 \(\pi^{-1}(U)\) 的包含 \(p\) 的分量. 因为 \(\pi\) 在 \(\tilde{U}_0\) 上的限制是微分同胚, 只需取 \(\sigma=(\pi|_{\tilde{U}_0})^{-1}\).

对于唯一性, 设另一个光滑截面 \(\sigma':U\to E\) 满足 \(\sigma'(q)=p\). 因为 \(U\) 连通, \(\sigma(U)\) 包含于 \(\tilde{U}_0\). 因为 \(\sigma'\) 是双射 \(\pi|_{\tilde U_0}\) 的右逆, 它一定等于其双侧逆, 因此等于 \(\sigma\).

Proposition 8.10 (光滑流形的拓扑覆叠) 设连通 \(n\) 维光滑流形 \(M\), 拓扑覆叠 \(\pi:E\to M\). 则 \(E\) 是 \(n\) 维拓扑流形, 且存在唯一光滑结构使 \(\pi\) 成为光滑覆叠.

Proposition 8.11 (光滑流形的拓扑覆叠, 带边) 设连通 \(n\) 维带边光滑流形 \(M\), 拓扑覆叠 \(\pi:E\to M\). 则 \(E\) 是 \(n\) 维带边拓扑流形, 满足 \(\partial{E}=\pi^{-1}(\partial{M})\), 且 \(E\) 上存在唯一光滑结构使 \(\pi\) 成为光滑覆叠.

结合以上定理, 万有 (拓扑) 覆叠的存在性定理导致如下推论:

Corollary 8.12 (万有覆叠流形的存在性) 设连通光滑流形 \(M\), 则存在单连通光滑流形 \(\tilde M\) 与光滑覆叠 \(\pi:\tilde M\to M\), 满足:

• 对于任意单连通光滑流形 \(\tilde M'\) 与光滑覆叠 \(\pi':\tilde M'\to M\), 存在微分同胚 \(\Phi:\tilde M\to\tilde M'\), 使得 \(\pi'\circ\Phi=\pi\).

光滑流形 \(\tilde M\) 称为 \(M\) 的万有覆叠流形 (universal covering manifold).

Corollary 8.13 (万有覆叠流形的存在性, 带边) 设连通带边光滑流形 \(M\), 则存在单连通带边光滑流形 \(\tilde M\) 与光滑覆叠 \(\pi:\tilde M\to M\), 满足:

• 对于任意单连通带边光滑流形 \(\tilde M'\) 与光滑覆叠 \(\pi':\tilde M'\to M\), 存在微分同胚 \(\Phi:\tilde M\to\tilde M'\), 使得 \(\pi'\circ\Phi=\pi\).

带边光滑流形 \(\tilde M\) 称为 \(M\) 的万有覆叠流形 (universal covering manifold).

下面的定理给出了光滑覆叠的一个判断条件:

Proposition 8.14 设连通 (带边) 光滑流形 \(E,M\), 若 \(\pi:E\to M\) 是逆紧的局部微分同胚, 则 \(\pi\) 是光滑覆叠映射.