GTM218 | 3 切空间

GTM218 (Introduction to Smooth Manifolds) Chapter 3 的笔记.

4 The Tangent Space

4.1 Geometric tangent vectors

欧氏空间 \(\R^n\) 中 "切向量" 的概念是很直观的. 比如, \(\R^3\) 中的光滑曲面 \(\mathbb{S}^2\) 在点 \(p\) 处的切向量 \(v\) 是 \(p\) 处切平面上的一个二维向量. 然而光滑流形的定义是比较抽象的, 并不依赖于 \(\R^n\) 中具体的几何图像. 为了将切向量的概念推广到光滑流形上, 我们先从代数角度刻画 \(\R^n\) 中的切向量.

一个思路是考虑沿着 \(v\) 的 "方向导数".

首先将 \(\R^n\) 切向量的定义明确化. 对于 \(a\in\R^n\), 定义 \(\R^n\) 在 \(a\) 处的几何切空间为 \(\R^n_a:=\{a\}\times\R^n\). 几何切空间上有 \(\R^n\) 的标准线性结构, 其中的元素 \(v_a:=(a,v)\in\R^n_a\) 称为几何切向量. \(\R^n_a\) 有标准基底 \(\{e_i|_a\}\), 其中 \(e_i=(0,\dots,1,\dots,0)\). 对于 \(v_a\in\R^n_a\), 我们有方向导数 \(D_v|_a:C^\infty(\R^n)\to\R\), 定义为 \[ D_v|_af \equiv D_vf(a) := \eval{\dv{t}}_{t=0} f(a+tv). \] 容易验证, 这是一个 \(\R\)-线性映射, 并且满足 Leibniz 律: \[ D_v|_a(fg)=f(a)D_v|_ag+g(a)D_v|_af,\quad f,g\in C^\infty(\R^n). \] 下面我们将这种映射抽象出来. 对于 \(a\in\R^n\), \(C^\infty(\R^n)\) 在 \(a\) 处的一个导子 (derivation) 指的是 \(\R\)-线性映射 \(w:C^\infty(\R^n)\to\R\), 满足 Leibniz 律: \[ w(fg)=w(f)g(a) + f(a)w(g),\quad f,g\in C^\infty(\R^n). \] 不难证明导子的如下性质:

1. 若 \(f\) 常值, 则 \(w(f)=0\).
2. 若 \(f(p)=g(p)=0\), 则 \(w(fg)=0\). (Leibniz 律的直接推论.)

记 \(T_a\R^n\) 是 \(C^\infty(\R^n)\) 的在 \(a\) 处的导子的全体. \(T_a\R^n\) 在线性映射的加法与数乘下构成 \(\R\)-线性空间. 下面我们还要证明, \(T_a\R^n\) 是有限维的, 并且自然地同构于 \(\R^n_a\), 因此能够作为几何切空间 \(\R^n_a\) 的代数刻画.

Proposition 4.1 (几何切向量的代数刻画) 设 \(a\in\R^n\). 任给几何切向量 \(v_a\in\R^n_a\), 方向导数 \(D_v|_a\) 是 \(C^\infty(\R^n)\) 在 \(a\) 处的导子, 并且映射 \[ \Align{ \Phi:\R^n_a\to T_a\R^n,\quad v_a\mapsto D_v|_a } \] 是线性同构.

Pf \(\Phi\) 的线性性不难看出. 单射性: 设 \(D_v|_a\) 是零映射, 取 \(x^i:\R^n\to\R\) 为第 \(i\) 个坐标函数, 则 \[ 0 = D_v|_ax^i = \eval{\dv{t}}_0 x^i(a+tv) = v^i \] 为 \(v\) (在 \(\R^n_a\) 的标准基底 \(\{e_i|_a\}\) 下) 的第 \(i\) 分量. 故 \(v=0\).

满射性: 任给 \(w\in T_a\R^n\), 我们定义 \(v:=v^ie_i|_a\), 其中 \(v^i=w(x^i)\). 下面证明 \(w=D_v|_a\). 为此, 取 \(f\in C^\infty(\R^n)\), 由 Taylor 公式, \[ \Align{ f(x) = f(a) &+{} \sum_{i=1}^n (x^i-a^i) \eval{\pdv{f}{x^i}}_a \\ &+{} \sum_{i,j=1}^n (x-a^i)(x-a^j) \int_0^1 (1-t) \pdv{^2f}{x^i\partial{x^j}}(a+t(x-a))\dd{t}. } \] 注意上面的双重求和中, 每一项可以写成两个在 \(x=a\) 为零的光滑函数之积: 一个是 \((x-a^i)\), 另一个是 \((x-a^j)\) 乘以定积分. 对求和中的每一项应用 \(w\), 由 Leibniz 律可得结果为 \(0\). 因此, \[ \Align{ w(f) &= w(f(a)) + \sum_{i=1}^m w\pqty{(x^i-a^i) \eval{\pdv{f}{x^i}}_a} \\ &= 0 + \eval{\pdv{f}{x^i}}_a (w(x^i)-w(a^i)) \\ &= \eval{\pdv{f}{x^i}}_a v^i = D_v|_af. } \]

取 \(\R^n_a\) 的标准基底在 \(\Phi\) 下的像, 即得到 \(T_a\R^n\) 的一个基底 \[ \qty{\eval{\pdv{x^1}}_a,\dots,\eval{\pdv{x^n}}_a},\textsf{ 其中 } \eval{\pdv{x^i}}_af:=\eval{\pdv{f}{x^i}}_a, \]

称为 \(T_a\R^n\) 的标准基底.

4.2 Tangent vectors

现在我们能将切向量的概念推广到光滑流形 \(M\) 了. 点 \(p\in M\) 处的一个导子指的是 \(\R\)-线性映射 \(v:C^\infty(M)\to\R\), 满足 \[ v(fg)=v(f)g(p)+f(p)v(g),\quad f,g\in C^\infty(M). \] 所有 \(C^\infty(M)\) 在 \(p\) 处的导子组成的 \(\R\)-线性空间称为 \(M\) 在 \(p\) 处的切空间 (tangent space). 切空间中的元素称为切向量 (tangent vector). 不难证明切向量的如下性质:

1. 若 \(f\) 常值, 则 \(v(f)=0\).
2. 若 \(f(p)=g(p)=0\), 则 \(v(fg)=0\). (Leibniz 律的直接推论.)

Proposition 4.2 (切向量的局部性) 设 (带边) 光滑流形 \(M\), \(v\in T_pM\). 若 \(f\) 在 \(p\) 的某邻域 \(U\) 上恒为 \(0\), 则 \(v(f)=0\).

Pf 取 \(\psi\in C^\infty(M)\) 是鼓包函数, 其在 \(\supp{f}\) 上恒为 \(1\), 且 \(\supp\psi\subset M\setminus\{p\}\). 注意到 \[ \psi f \equiv f, \] (在 \(\supp{f}\) 上, \(\psi\equiv1\), 有 \(\psi f\equiv f\); 在 \(\supp{f}\) 的补集上, \(f\equiv0\), 有 \(\psi f\equiv f\).) 因为 \(\psi(p)=f(p)=0\), 利用上面切向量的性质 2 即得.

"局部性" 即 \(v\) 只关心 \(f\) 在 \(p\) 的某个局部 (邻域) 上的行为, 不关心全局的行为. 换言之, 若 \(U\) 上有 \(f\equiv g\), 则 \(v(f)=v(g)\). 局部性的好处是可以将 \(v\) "限制" 到开子集上: 若 \(U\) 是开子流形, \(f\in C^\infty(U)\), 定义 \[ v(f) := v(\tilde{f}), \] 其中 \(\tilde{f}\in C^\infty(M)\) 是任意延拓 \(f\) 的光滑函数 (存在性由扩张引理保证). 局部性保证 \(v(\tilde{f})\) 与 \(\tilde{f}\) 的选择无关. 因此, \(v\in T_pM\) 也能视作 \(T_pU\) 中的切向量. 我们马上会证明, \(T_pM\) 和 \(T_pU\) 是自然同构的.

Note 一般地, 若 \(A\) 是域 \(F\) 上的代数, \(B\) 是 \(A\) 上的双模. \(F\)-线性映射 \(d:A\to B\) 若满足 Leibniz 律 \[ d(uv)=(du)v+u(dv), \] 则称 \(d\) 为 \(A\) 的一个导子 (derivation).

4.3 The differential of a map

欧氏空间中的光滑映射 \(F:U\to\R^k\) 在几何切空间上的作用体现为 Jacobi 矩阵 \((\partial F^j/\partial x^i)\), 可以视作 \(F\) 的 "最佳线性近似". 光滑流形间的光滑映射 \(F:M\to N\) 也有 "最佳线性近似", 它是切空间之前的线性映射.

设光滑流形 \(M,N\), 光滑映射 \(F:M\to N\), 点 \(p\in M\) 处的切映射 (tangent map) 是映射 \[ F_{*,p}:T_pM \to T_{F(p)}N \] 对 \(v\in T_pM\), \(F_{*,p}v\) 是 \(T_{F(p)}N\) 中的切向量, 其在 \(f\in C^\infty(N)\) 上的作用定义为 \[ (F_{*,p}v)(f) := v(f\circ F). \] 需要验证的是, \(F_{*,p}v\) 的确构成一个导子. 一方面, 其 \(\R\)-线性性由 \(v\) 的 \(\R\)-线性性保证. 另一方面, 若 \(f,g\in C^\infty(N)\), 则 \[ \Align{ (F_{*,p}v)(fg) &= v((fg)\circ F) \\ &= v((f\circ F)(g\circ F)) \\ &= v(f\circ F)(g\circ F)(p) + (f\circ F)(p)v(g\circ F) \\ &= (F_{*,p}v)f\cdot g(F(p)) + f(F(p))\cdot(F_{*,p}v)g. } \] 切映射也叫做微分 (differential).

Proposition 4.3 (切映射的性质) 设 (带边) 光滑流形 \(M,N,P\), 光滑映射 \(F:M\to N\), \(G:N\to P\), 点 \(p\in M\).

1. \(F_{*,p}:T_pM\to T_{F(p)}N\) 是 \(\R\)-线性映射.
2. (函子性之一) \((G\circ F)_{*,p}=G_{*,F(p)}\circ F_{*,p}\). (也称为 "链式法则".)
3. (函子性之二) \(({\rm id}_M)_{*,p}={\rm id}_{T_pM}\).
4. (同构映到同构) 若 \(F\) 是微分同胚, 则 \(F_{*,p}\) 是同构, 且 \((F_{*,p})^{-1}=(F^{-1})_{*,F(p)}\).

Pf 1 是切向量 \(\R\)-线性性的推论: \[ \Align{ F_{*,p}(cv+w)(f) &= (cv+w)(f\circ F) \\ &= cv(f\circ F)+w(f\circ F) \\ &= c(F_{*,p}v)f+(F_{*,p}w)f. } \] 2 的证明是直接的: \[ \Align{ \big((G_{*,F(p)}\circ F_{*,p})v\big)f &= (F_{*,p}v)(f\circ G) \\ &= v((f\circ G)\circ F) \\ &= v(f\circ(G\circ F)) \\ &= ((G\circ F)_{*,p}v)f. } \] 3, \((({\rm id}_M)_{*,p}v)f=v(f\circ{\rm id}_M)=v(f)\).

4 是函子性的直接推论.

Proposition 4.4 (开子流形的切空间) 设 (带边) 光滑流形 \(M\), 开子流形 \(\iota:U\hookrightarrow M\), 则对任意 \(p\in U\), \(\iota_{*,p}:T_pU\to T_pM\) 是同构.

Pf 单射性: 设 \(\iota_{*,p}v=0\in T_pM\). 任给 \(f\in C^\infty(U)\), 我们要证明 \(v(f)=0\). 根据扩张引理, \(f\) 扩张到光滑函数 \(\tilde{f}\in C^\infty(M)\), 满足 \(\tilde{f}|_U=f\), 即 \(\tilde{f}\circ\iota=f\), 于是 \[ v(f) = v(\tilde{f}\circ\iota) = (\iota_{*,p}v)\tilde{f} = 0. \] 满射性: 任给 \(w\in T_pM\), 我们这样定义一个 \(v\in T_pU\): 对于 \(f\in C^\infty(U)\), 记 \(\tilde{f}\in C^\infty(M)\) 是其扩张, 定义 \(v(f):=w(\tilde{f})\). 根据切向量的局部性, \(v\) 是良定义的. 容易验证 \(v\) 满足切向量的定义, 并且 \(v\) 在切映射下的像正是 \(w\): \[ (\iota_{*,p}v)g = v(g\circ\iota) = w(\widetilde{g\circ\iota}) = w(g). \]

从证明过程中可以看出, \(v\in T_pU\) 和 \(\iota_{*,p}v\in T_pM\) 其实是同一个导子, 前者无非是后者在 \(C^\infty(U)\) 上的限制. 因此, 我们通常将 \(T_pU\) 和 \(T_pM\) 认同.

根据函子性, 切空间与切映射构造可以看作 \({\sf Diff}_*\) (带点光滑流形范畴) 到 \(\sf Vect_\R\) (实线性空间范畴) 的函子, 将 \((M,p)\) 映到 \(T_pM\), 将 \(F:(M,p)\to(N,q)\) 映到 \(F_{*,p}:T_pM\to T_qN\). 这个函子称为切空间函子 (tangent space functor).

函子性的一些推论:

Proposition 4.5 (切空间的维数) 若 \(M\) 是 \(n\) 维光滑流形, \(p\in M\), 则 \(T_pM\) 是 \(n\) 维实线性空间.

Pf 设包含 \(p\) 的坐标卡 \((U,\varphi)\), 因为 \(\varphi\) 是 \(U\) 到 \(\varphi(U)\subset\R^n\) 的微分同胚, 所以 \(\varphi_{*,p}\) 是 \(T_pU\) 到 \(T_p\varphi(U)\) 的线性同构. Proposition 4.4 给出 \(T_pU\cong T_pM\), \(T_p\varphi(U)\cong T_p\R^n\), 因此 \(T_pM\cong T_p\R^n\) 是 \(n\) 维的.

Theorem 4.6 (维数的微分同胚不变性) 若 \(M,N\) 微分同胚, 则它们维数相等.

Pf 可知 \(M,N\) 的某切空间同构, 进而维数相等, 故流形的维数也相等.

下面我们来研究带边光滑流形的切空间. 从几何上看, 边界处的切空间似乎有许多种可能: 它可能像 \(\partial{M}\) 一样是 \((n-1)\) 维的, 也可能是 \(n\) 维的, 也可能是 \(n\) 维线性空间的一半... 实际上, 我们对切空间的代数定义保证了边界点的切空间其实和内部点一样, 都是 \(n\) 维线性空间.

Proposition 4.7 (带边流形切空间的维数) 若 \(M\) 是 \(n\) 维带边光滑流形, \(p\in M\), 则 \(T_pM\) 是 \(n\) 维实线性空间.

Pf 设 \(p\) 是内部点, 因为 \({\rm Int}M\) 是 \(M\) 的开子流形, 所以 \(T_p({\rm Int}M)\cong T_pM\). 注意 \({\rm Int}M\) 是一个 \(n\) 维无边流形, 所以 \(T_p({\rm Int}M)\) 是 \(n\) 维的, \(T_pM\) 也是 \(n\) 维的.

对于边界点 \(p\in\partial{M}\), 我们先研究 \(\H^n\) 边界点 \(a\in\partial\H^n\) 处的切空间, 有如下引理:

Lemma 包含映射 \(\iota:\H^n\to\R^n\) 在边界处的切映射 \(\iota_{*,a}:T_a\H^n\to T_a\R^n\) 是同构.

单射性: 设 \(\iota_{*,a}v=0\). 任取 \(f\in C^\infty(\H^n)\), 将它扩张到 \(\tilde{f}\in C^\infty(\R)\), 则 \(\tilde{f}\circ\iota=f\), 于是 \[ v(f)=v(\tilde{f}\circ\iota)=(\iota_{*,a}v)f=0. \] 满射性: 任给 \(w\in T_a\R^n\), 定义 \(v\in T_a\H^n\), \(v(f):=w(\tilde{f})\), 其中 \(\tilde{f}\) 是 \(f\) 的任意光滑扩张. 我们需要验证定义与 \(\tilde{f}\) 的选取无关: 设在 \(T_a\R^n\) 的标准基底下展开为 \(w=w^i\partial/\partial x^i|_a\), 则 \[ v(f)=w^i\eval{\pdv{\tilde{f}}{x^i}}_a, \] 根据连续性, \(\tilde{f}\) 的偏导数由 \(f\) 在 \(\H^n\) 中的 (单侧) 偏导数确定, 因而与 \(\tilde{f}\) 的选取无关. 容易验证 \(v\) 满足导子的定义, 并且 \(w=\iota_{*,a}v\), 因此 \(\iota_{*,a}\) 满. 这便证明了引理.

回到原命题. 设 \(p\in\partial{M}\), 取包含 \(p\) 的边界坐标系 \((U,\varphi)\), 记 \(\hat{U}=\varphi(U)\subset\H^n\).

• \(U\) 作为 \(M\) 的开子流形有 \(T_pM\cong T_pU\);
• 微分同胚有 \(T_pU\cong T_{\varphi(p)}\hat{U}\);
• \(\hat{U}\) 作为 \(\H^n\) 的开子流形有 \(T_{\varphi(p)}\hat{U}=T_{\varphi(p)}\H^n\);
• 根据引理有 \(T_{\varphi(p)}\H^n\cong T_{\varphi(p)}\R^n\).

综上, \(T_pM\cong T_{\varphi(p)}\R^n\), 即得.

和 \(\R^n\) 类似, 任意有限维实线性空间 \(V\) 的切空间 \(T_aV\) 都自然同构于 \(V\) (线性空间上有标准光滑结构). 先在 \(V\) 上定义方向导数: 对点 \(a\in V\), 向量 \(v\in V\), \(f\in C^\infty(V)\), 定义 \[ D_v|_af := \eval{\dv{t}}_{t=0}f(a+tv). \]

Proposition 4.8 (线性空间的切空间) 设有限维实线性空间 \(V\) 配以标准光滑结构. 任给 \(a\in V\), 方向导数映射 \(v\mapsto D_v|_a\) 是 \(V\) 与 \(T_aV\) 间的自然同构. 对任意线性映射 \(L:V\to W\), 下图交换: \[ \xymatrix{ V \ar[r]^(.45)\cong \ar[d]_L & T_aV \ar[d]^{L_{*,a}} \\ W \ar[r]_(.45)\cong & T_{La}W. } \]

Proposition 4.9 (积流形的切空间) 设光滑流形 \(M_1,\dots,M_k\), 自然投射 \(\pi_i:\prod_jM_j\to M_i\). 对任意 \(p=(p_1,\dots,p_k)\in\prod_jM_j\), 映射 \[ \Align{ \alpha: T_p(M_1\times\dots\times M_k) &\to T_{p_1}M_1\oplus\dots\oplus T_{p_k}M_k, \\ v &\mapsto ((\pi_1)_{*,p}v,\dots,(\pi_k)_{*,p}v) } \] 是线性同构. 此外, 若 \(M_i\) 中有一个是带边流形, 则命题也成立.

4.4 Computations in coordinates

切空间的基底.

设 \((U,\varphi)\) 是包含 \(p\) 的坐标卡. 因为 \(\varphi_{*,p}\) 是同构, \(T_{\varphi(p)}\R^n\) 的标准基底 \(\{\partial/\partial x^i|_{\varphi(p)}\}\) 在同构下的原像构成了 \(T_pM\) 的一个基底, 记作 \[ \eval{\pdv{x^i}}_p := (\varphi_{*,p})^{-1} \eval{\pdv{x^i}}_{\varphi(p)} = (\varphi^{-1})_{*,\varphi(p)} \eval{\pdv{x^i}}_{\varphi(p)}. \] 该基底 \(\{\partial/\partial x^i|_p\}\) 称为 \(T_pM\) 的坐标基底 (coordinate basis), 即坐标系 \((U,(x^i))\) 诱导出的基底. 坐标基向量作用于 \(f\in C^\infty(U)\) 给出 \[ \eval{\pdv{x^i}}_pf = \eval{\pdv{x^i}}_{\varphi(p)} (f\circ\varphi^{-1}) = \eval{\pdv{\hat{f}}{x^i}}_{\hat{p}}, \] 无非是求 \(f\) 关于第 \(i\) 个坐标的偏导数. 特别地, 坐标向量作用于坐标函数 \(x^j\) 给出 \[ \eval{\pdv{x^j}{x^i}}_p = \eval{\pdv{x^i}}_{\varphi(p)}(x^j\circ\varphi^{-1}) = \delta^j_i. \]

• 对于带边流形边界点处的切向量, 坐标基底应当是求取 "单侧偏导数".

切向量 \(v\in T_pM\) 在坐标基底下展开为 \[ v = v^i \eval{\pdv{x^i}}_p, \] 其中 \(v^i=v(x^i)\), 即作用于第 \(i\) 个坐标函数得到的实数. 我们将上面的讨论总结为如下定理:

Proposition 4.10 (切空间的基底) 设 (带边) 光滑流形 \(M\), 点 \(p\in M\) 附近有坐标系 \((U,(x^i))\), 则 \(T_pM\) 的一个基底是 \(\{\partial/\partial x^i|_p\}\). 切向量 \(v=T_pM\) 在该基底下的分量 \(v^i=v(x^i)\).

切映射在坐标基底下的矩阵.

设光滑映射 \(F:M\to N\), 其中 \(M,N\) 分别为 \(m,n\) 维光滑流形. 取 \(p\in M\) 附近的坐标系 \((U,(x^i))\) 和 \(F(p)\) 附近的坐标系 \((V,(y^j))\). 设切映射 \(F_{*,p}\) 在坐标基底 \(\{\partial/\partial x^i|_p\}\) 和 \(\{\partial/\partial y^j|_{F(p)}\}\) 下的矩阵为 \((a^j_i)\), 则 \[ F_{*,p}\pqty{\eval{\pdv{x^i}}_p} = a^j_i \eval{\pdv{y^j}}_{F(p)}. \] 两边作用于 \(y^k\), 右边得到 \(a^k_i\), 左边得到 \[ \Align{ \eval{\pdv{x^i}}_p(y^k\circ F) &= \eval{\pdv{x^i}}_{\hat{p}}(y^k\circ F\circ\varphi^{-1}) \\ &= \eval{\pdv{\hat{F}^k}{x^i}}_{\hat{p}}, } \] 其中 \(\hat{F}^k=y^k\circ F\circ\varphi^{-1}:\hat{U}\to\R\) 是 \(F\) 在坐标系下的第 \(k\) 个分量. 因此, 切映射的矩阵 \[ (a^j_i) = \pqty{\eval{\pdv{\hat{F}^j}{x^i}}_{\hat{p}}} = \pmqty{ \displaystyle\eval{\pdv{\hat{F}^1}{x^1}}_{\hat{p}} & \cdots & \displaystyle\eval{\pdv{\hat{F}^1}{x^n}}_{\hat{p}} \\ \vdots & \ddots & \vdots \\ \displaystyle\eval{\pdv{\hat{F}^m}{x^1}}_{\hat{p}} & \cdots & \displaystyle\eval{\pdv{\hat{F}^m}{x^n}}_{\hat{p}} \\ } \] 即坐标式 \(\hat{F}\) 的 Jacobi 矩阵.

Proposition 4.11 (切映射的矩阵) 设光滑映射 \(F:M\to N\), 点 \(p\in M\) 附近有坐标系 \((U,(x^i))\), \(F(p)\) 附近有坐标系 \((V,(y^j))\), 则切映射 \(F_{*,p}\) 在 \(T_pM\) 和 \(T_{F(p)}N\) 的坐标基底下的矩阵为坐标式 \(\hat{F}\) 的 Jacobi 矩阵 \((\partial\hat{F}^j/\partial x^i|_{\varphi(p)})\).

实际上, 切映射的概念正是为了给出 Jacobi 矩阵的一个无关坐标的定义, 可以看作 \(\R^n\) 中光滑映射的 "导数" 概念的推广. 在微分几何中, 切映射的名字很多, 比如微分, 导数, 推前, 记号也五花八门, 比如 \[ F'(p),\quad DF(p),\quad \dd{F_p},\quad T_pF,\quad F_{*,p}. \] 我们只使用 \(F_{*,p}\) 记号. 在没有歧义的情况下 (比如点 \(p\) 明确), 可以简写作 \(F_*\).

坐标变换.

设 \(p\in M\) 附近有两个坐标卡 \((U,\varphi)\), \((V,\psi)\). 切向量在这两个坐标系下的分量有何关联?

记 \(\varphi\) 的坐标函数为 \((x^i)\), \(\psi\) 的坐标函数为 \((\tilde{x}^i)\), 将转移映射 \(\psi\circ\varphi^{-1}\) 记作 \[ (\psi\circ\varphi^{-1})(x)=(\tilde{x}^1(x),\dots,\tilde{x}^n(x)). \] (其中 \(x\) 理解为 \(\varphi(U\cap V)\) 中的点.) 转移映射的微分 \[ (\psi\circ\varphi^{-1})_{*,\varphi(p)}\pqty{\eval{\pdv{x^i}}_{\varphi(p)}} = \eval{\pdv{\tilde{x}^j}{x^i}}_{\varphi(p)} \eval{\pdv{\tilde{x}^j}}_{\psi(p)}. \] 坐标基底的变换律 \[ \Align{ \eval{\pdv{x^i}}_p &= (\varphi^{-1})_{*,\varphi(p)} \eval{\pdv{x^i}}_{\varphi(p)} \\ &= (\psi^{-1})_{*,\psi(p)} (\psi\circ\varphi^{-1})_{*,\varphi(p)} \eval{\pdv{x^i}}_{\varphi(p)} \\ &= (\psi^{-1})_{*,\psi(p)} \eval{\pdv{\tilde{x}^j}{x^i}}_{\varphi(p)} \eval{\pdv{\tilde{x}^j}}_{\psi(p)} \\ &= \eval{\pdv{\tilde{x}^j}{x^i}}_{\varphi(p)} \eval{\pdv{\tilde{x}^j}}_p. } \] 于是切向量 \(v=v^i\partial/\partial x^i|_p=\tilde{v}^j\partial/\partial\tilde{x}^j|_p\) 的分量的变换律 \[ \tilde{v}^j = \eval{\pdv{\tilde{x}^j}{x^i}}_{\varphi(p)}v^i. \] 从形式上看, 坐标变换律和链式法则几乎一样, 看起来是很直接的.

Proposition 4.12 (切向量的坐标变换律) 设 (带边) 光滑流形 \(M\), 点 \(p\in M\) 附近有两个坐标卡 \((U,\varphi)\), \((V,\psi)\), 若 \(v\in T_pM\) 在两个坐标卡下的分量分别为 \(v^i\), \(\tilde{v}^j\), 则 \[ \tilde{v}^j = \eval{\pdv{\tilde{x}^j}{x^i}}_{\varphi(p)}v^i, \] 其中 \(\tilde{x}^i:\varphi(U\cap V)\to\R\) 是 \(\psi\circ\varphi^{-1}\) 的分量.

Example \(\R^3\) 中的球坐标变换.

记 \(U=\R^3\setminus\{(0,0,x^3)\mid x^3\in\R\}\), 在 \(U\) 上可以定义球坐标系 \[ \Cases{ x^1 = r\sin\theta\cos\phi, \\ x^2 = r\sin\theta\sin\phi, \\ x^3 = r\cos\theta, } \] 其中 \(\theta\in(0,\pi)\) 为向量与 \(z\) 轴正半轴的夹角, \(\theta\in[0,2\pi)\) 为经度角, \(r>0\) 为半径. 记 \(\{\partial/\partial x^i|_p\}\) 为标准坐标基底, \(\{\partial/\partial y^j|_p\}=\{\partial/\partial r|_p,\partial/\partial\theta|_p,\partial/\partial\phi|_p\}\) 为球坐标基底, 则 \[ \pqty{\eval{\pdv{y^j}}_p} = \pqty{\eval{\pdv{x^i}}_p} \pmqty{ \sin\theta\cos\phi & r\cos\theta\cos\phi & -r\sin\theta\sin\phi \\ \sin\theta\sin\phi & r\cos\theta\sin\phi & r\sin\theta\cos\phi \\ \cos\theta & -r\sin\theta & 0 }. \] 具体来说, 若有 \(p=(r,\theta,\phi)=(\sqrt2,\pi/4,\pi/2)\) 处的切向量 \[ v = 3 \eval{\pdv{r}}_p - \eval{\pdv\theta}_p + 2 \eval{\pdv\phi}_p, \] 计算得到 \[ \Align{ \eval{\pdv{r}}_p &= \frac1{\sqrt2}\eval{\pdv{x^2}}_p + \frac1{\sqrt2}\eval{\pdv{x^3}}_p, \\ \eval{\pdv\theta}_p &= \eval{\pdv{x^2}}_p - \eval{\pdv{x^3}}_p, \\ \eval{\pdv\phi}_p &= -\eval{\pdv{x^1}}_p, } \] 于是 \[ v = - 2\eval{\pdv{x^1}}_p + \pqty{\frac3{\sqrt2}-1}\eval{\pdv{x^2}}_p + \pqty{\frac3{\sqrt2}+1}\eval{\pdv{x^2}}_p. \]

4.5 Curves

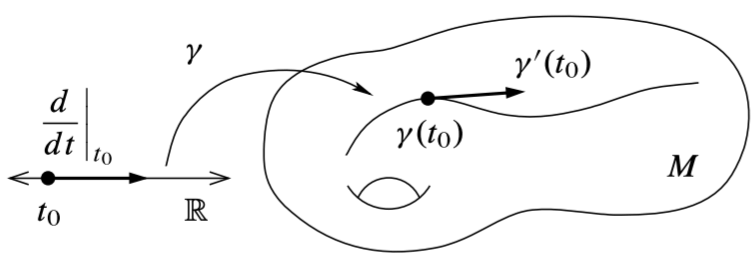
(带边) 光滑流形 \(M\) 中的一条光滑曲线 (curve) 指的是光滑映射 \(\gamma:J\to M\), 其中 \(J\subset\R\) 是区间. 曲线 \(\gamma\) 在 \(t_0\in J\) 处的切向量 / 速度 (velocity) 定义为 \[ \gamma'(t_0) := \gamma_{*}\pqty{\eval{\dv{t}}_{t_0}} \in T_{\gamma(t_0)}M, \] 其中 \(\dd/\dd t|_{t_0}\) 是 \(T_{t_0}\R\) 的标准基底. 切向量的其他记号有 \[ \dot\gamma(t_0),\quad \eval{\dv{\gamma}{t}}_{t_0}. \] 曲线的切向量对 \(f\in C^\infty(M)\) 的作用是通常的求导: \[ \gamma'(t_0)f = \gamma_{*}\pqty{\eval{\dv{t}}_{t_0}}f = \eval{\dv{t}}_{t_0}(f\circ\gamma) \equiv (f\circ\gamma)'(t_0). \] 若取 \(\gamma(t_0)\) 附近的坐标系 \((U,(x^i))\), 曲线 \(\gamma\) 有局部坐标表示 / 参数式 \[ \gamma(t) \approx (\varphi\circ\gamma)(t) = (\gamma^1(t),\dots,\gamma^n(t)), \] 此时 \(\gamma'(t_0)\) 的坐标分量就是 \(\gamma\) 参数式的导数: \[ \gamma'(t_0) = \eval{\dv{\gamma^i}{t}}_{t_0} \eval{\pdv{x^i}}_{\gamma(t_0)}. \] 这与欧氏空间中 "参数曲线" 的 "速度向量" 的定义是一致的. 利用参数式, 也可以在 \(U\) 上局部地定义一条曲线, 我们只需给出分量 \(\gamma^1(t),\dots,\gamma^n(t)\), 并定义 \(\gamma(t):=\varphi^{-1}(\gamma^1(t),\dots,\gamma^n(t))\) 即可.

若光滑曲线 \(\gamma:J\to M\) 满足 \(0\in J\), 我们称它是从 \(\gamma(0)\) 开始, 以 \(\gamma'(0)\) 为初速度的曲线.

Proposition 4.13 (切向量是都曲线的速度) 设 (带边) 光滑流形 \(M\), \(p\in M\), 则任意 \(v\in T_pM\) 都是某条光滑曲线的切向量.

Pf 先考虑内部点 \(p\in{\rm Int}M\). 取以 \(p\) 为中心的坐标卡 \((U,\varphi)\), 设 \(v\) 展开为 \(v=v^i\partial/\partial x^i|_p\), 设曲线 \(\gamma\) 在 \(U\) 下的参数式为 \[ \gamma(t) = (tv^1,\dots,tv^n),\quad-\varepsilon<t<\varepsilon, \] 对于足够小的 \(\varepsilon>0\). 显然 \(\gamma\) 是从 \(p\) 开始的, 以 \(v\) 为初速度的曲线.

对于边界点 \(p\in\partial{M}\), 同样设 \(v\) 在坐标卡下展开为 \(v=v^i\partial/\partial x^i|_p\). 完全可以仿照上式定义曲线 \(\gamma\), 唯一的问题是因为 \(U\) 只有 "一半", 所以 \(\gamma\) 可能跑出 \(U\). 如果 \(v\) "朝外", 即 \(v^n<0\), 则限制曲线的定义域为 \((-\varepsilon,0]\); 若 \(v\) "朝里", 即 \(v^n>0\), 则限制曲线的定义域为 \([0,\varepsilon)\); 如果 \(v^n=0\), 则无需限制定义域.

下面的定理表明, 曲线 "像的切向量" 等于 "切向量的像".

Proposition 4.14 (曲线的像的切向量) 设光滑映射 \(F:M\to N\), 光滑曲线 \(\gamma:J\to M\). 则对任意 \(t_0\in J\), 曲线 \(F\circ\gamma:J\to N\) 的切向量 \[ (F\circ\gamma)'(t_0) = F_*(\gamma'(t_0)). \]

Pf 直接应用定义与链式法则即可: \[ (F\circ\gamma)'(t_0) = (F\circ\gamma)_*\pqty{\eval{\dv{t}}_{t_0}} = F_* \gamma_*\pqty{\eval{\dv{t}}_{t_0}} = F_* \gamma'(t_0). \]

这给了我们一种计算 \(F_*\) 的方法, 通常要比用坐标基底计算微分好用:

Corollary 4.15 (用曲线计算微分) 设光滑映射 \(F:M\to N\), \(p\in M\), \(v\in T_pM\), 则 \[ F_{*,p}(v) = (F\circ\gamma)'(0), \] 对任意以 \(p\) 开始, 以 \(v\) 为初速度的曲线 \(\gamma:J\to M\).