GTM218 | 2 光滑映射与单位分解

GTM218 (Introduction to Smooth Manifolds) Chapter 2 的笔记.

2 Smooth Maps

2.1 Smooth functions

设 \(n\) 维光滑流形 \(M\). 函数 \(f:M\to\R^k\) 称为光滑的 (smooth), 如果对每一点 \(p\in M\), 存在包含 \(p\) 的坐标系 \((U,\varphi)\), 使得 \(f\circ\varphi^{-1}\) 是 \(\hat{U}=\varphi(U)\subset\R^n\to\R^k\) 的光滑函数.

• 对于带边流形, 定义是完全相同的, 只不过 \(f\circ\varphi^{-1}\) 是 \(\H^n\) 子集上的函数, 其光滑性的定义是: 对任意 \(p\in\hat{U}\subset\H^n\), 存在 \(r>0\), 使得 \(f\) 延拓到 \(B_r(p)\subset\R^n\) 中的光滑函数.

• 光滑性是良定义的. 若 \(f\circ\varphi^{-1}\) 光滑, 则 \[ f\circ\psi^{-1}=(f\circ\varphi^{-1})\circ(\varphi\circ\psi^{-1}) \] 作为光滑函数的复合, 也是光滑的. 这之中的关键是转移函数 \(\varphi\circ\psi^{-1}\) 的光滑性.

记 \(C^\infty(M)\) 是光滑流形 \(M\) 上所有光滑 \(\R\) 值函数的集合. 在逐点的加法与乘法下, \(C^\infty(M)\) 构成交换环以及 \(\R\)-交换代数.

我们称函数 \(\hat{f}:=f\circ\varphi^{-1}\) 是 \(f\) 在 \((U,\varphi)\) 下的坐标表示 (coordinate representation). \(f\) 是光滑函数, 当且仅当其在光滑图册下的坐标表示是光滑函数.

2.2 Smooth maps

设光滑流形 \(M,N\), 映射 \(F:M\to N\) 称为光滑的 (smooth), 如果对任意 \(p\in M\), 存在包含 \(p\) 的坐标卡 \((U,\varphi)\) 和包含 \(F(p)\) 的坐标卡 \((V,\psi)\) 满足 \(F(U)\subset V\), 且 \(\psi\circ F\circ\varphi^{-1}\) 是 \(\varphi(U)\) 到 \(\psi(V)\) 的光滑映射.

• 对于带边流形, 定义是完全相同的.

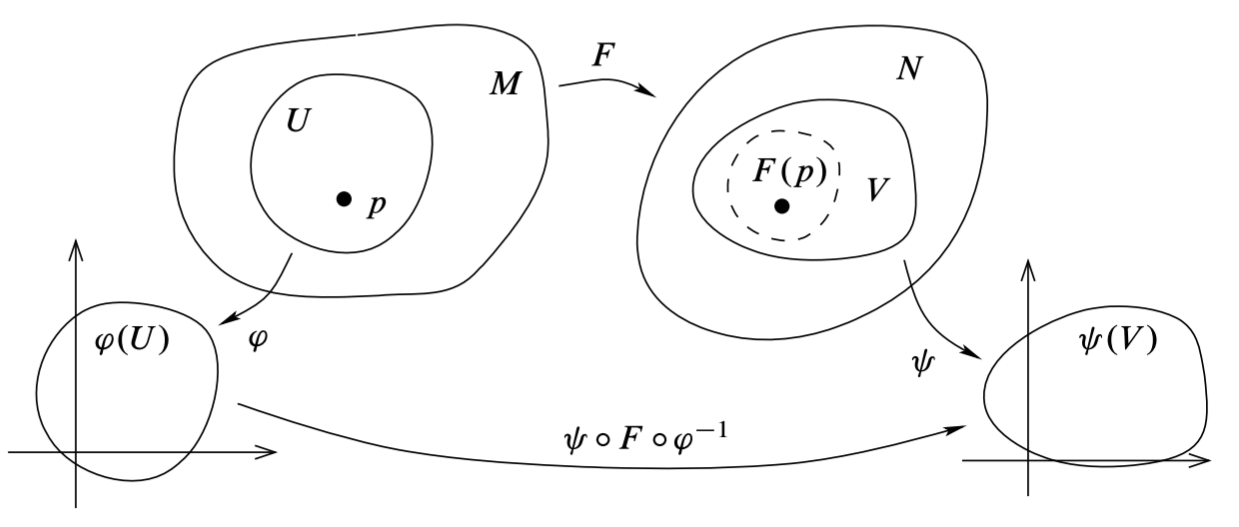
Proposition 2.1 (光滑蕴含连续) 光滑映射是连续的.

Pf 根据定义, \(F\) 在 \((U,\varphi)\) 上限制为 \[ F|_U = \psi^{-1}\circ(\psi\circ F\circ\varphi^{-1})\circ\varphi:U\to V \] 是连续映射的复合, 故 \(F|_U\) 连续. \(F\) 在每个点的某邻域连续, 有 \(F\) 连续.

Proposition 2.2 (光滑性的等价刻画) 设光滑 (带边) 流形 \(M,N\), 映射 \(F:M\to N\). TFAE:

1. \(F\) 光滑.
2. 任意 \(p\in M\), 存在包含 \(p\) 的坐标卡 \((U,\varphi)\) 和包含 \(F(p)\) 的坐标卡 \((V,\psi)\) 满足 \(U\cap F^{-1}(V)\) 是 \(M\) 中开集, 且 \(\psi\circ F\circ\varphi^{-1}\) 是 \(\varphi(U\cap F^{-1}(V))\to\psi(V)\) 的光滑映射.
3. \(F\) 连续, 且存在 \(M,N\) 的光滑图册 \(\{(U_\alpha,\varphi_\alpha)\}\), \(\{(V_\beta,\psi_\beta)\}\), 使得对任意 \(\alpha,\beta\), \(\psi_\beta\circ F\circ\varphi_\alpha^{-1}\) 是 \(\varphi_\alpha(U_\alpha\cap F^{-1}(V_\beta))\to\psi_\beta(V_\beta)\) 的光滑映射.

Pf 1 \(\Rightarrow\) 2 是显然的. 2 \(\Rightarrow\) 1, 注意到此时 \(U':=U\cap F^{-1}(V)\) 是 \(U\) 的开子集, 因此 \((U',\varphi|_{U'})\) 也是光滑坐标卡. 注意到 \(F\) 关于 \((U',\varphi|_{U'})\) 和 \((V,\psi)\) 满足光滑性的定义.

3 \(\Rightarrow\) 2 是显然的. 2 \(\Rightarrow\) 3, 显然 \(F\) 连续. 我们只需证明所有与 \((U,\varphi)\) 相容的 \((U_\alpha,\varphi_\alpha)\) 以及所有与 \((V,\psi)\) 相容的 \((V_\beta,\psi_\beta)\) 满足条件. 这是很直接的: \[ \psi_\beta\circ F\circ\varphi_\alpha^{-1} = (\psi_\beta\circ\psi^{-1}) \circ(\psi\circ F\circ\varphi^{-1}) \circ(\varphi\circ\varphi_\alpha^{-1}) \] 是光滑映射的复合, 因此是光滑映射.

Proposition 2.3 (光滑性是局部的)

1. 若任意一点 \(p\) 存在邻域 \(U\), 使得 \(F|_U\) 光滑, 则 \(F\) 光滑.
2. 若 \(F\) 光滑, 则 \(F\) 在任意开集上的限制是光滑的.

Pf 1, 因为 \(F|_U\) 光滑, 所以 \(p\) 附近有坐标卡 \((W,\varphi)\), \(F(p)\) 附近有坐标卡 \((V,\psi)\), 满足 \(p\in W\subset U\), \(F(W)\subset V\), 且 \(\psi\circ F\circ\varphi^{-1}\) 是 \(\varphi(W)\to\psi(V)\) 的光滑函数. 注意到 \(W\) 在 \(U\) 中开, \(U\) 在 \(M\) 中开, 所以 \((W,\varphi)\) 也是 \(M\) 的坐标卡. 因此 \(F\) 满足光滑性的定义.

2, 设 \(M\) 的开集 \(W\), 任取 \(p\in W\). 设 \((U,\varphi)\), \((V,\psi)\) 分别为包含 \(p,F(p)\) 的坐标卡, 且满足光滑性定义中的条件. 注意到 \((U\cap W,\varphi|_{U\cap W})\) 是开子流形 \(W\) 的光滑坐标卡, \(F\) 关于 \((U\cap W,\varphi|_{U\cap W})\) 和 \((V,\psi)\) 也满足光滑性的定义, 因此 \(F|_W\) 是光滑的.

下面的推论无非是 Proposition 2.3 的另一种表述, 但它十分有用.

Corollary 2.4 (光滑 gluing lemma) 设光滑 (带边) 流形 \(M,N\), \(\{U_\alpha\}\) 是 \(M\) 的开覆盖. 若对每个 \(\alpha\), 有光滑映射 \(F_\alpha:U_\alpha\to N\), 且它们在交集上恒等: \(F_\alpha|_{U_\alpha\cap U_\beta}=F_\beta|_{U_\alpha\cap U_\beta}\), 则存在唯一的光滑映射 \(F:M\to N\) 满足 \(F|_{U_\alpha}=F_\alpha\).

设 \((U,\varphi)\) 和 \((V,\psi)\) 分别是 \(M,N\) 的光滑坐标卡, 则 \(\hat{F}=\psi\circ F\circ\varphi^{-1}\) 称为 \(F\) 的坐标表示 (coordinate representation), 这是一个 \(\varphi(U\cap F^{-1}(V))\) 到 \(\psi(V)\) 的映射. 设 \(F\) 光滑, 结合 Proposition 2.2 与光滑结构的定义, \(F\) 在任意一对坐标卡下的表示都是光滑的. 选定一对坐标卡之后, 我们通常将 \(F\) 与 \(\hat{F}\) 认同, 不再区分.

Proposition 2.5 (光滑映射的性质)

1. 恒等映射和常值映射是光滑的.
2. 若 \(U\subset M\) 是 (带边) 开子流形, 则包含映射 \(\iota:U\hookrightarrow M\) 是光滑映射.
3. (复合映射) 若 \(F:M\to N\) 与 \(G:N\to P\) 光滑, 则 \(G\circ F:M\to P\) 光滑.

Pf 1 是显然的. 2, 对任意 \(p\in U\), \(U\) 的包含 \(p\) 的坐标卡 \((W,\varphi)\) 也是 \(M\) 的坐标卡. 包含映射 \(\iota\) 的坐标表示 \(\varphi\circ\iota\circ\varphi^{-1}={\rm id}_{\varphi(U)}\) 是光滑的.

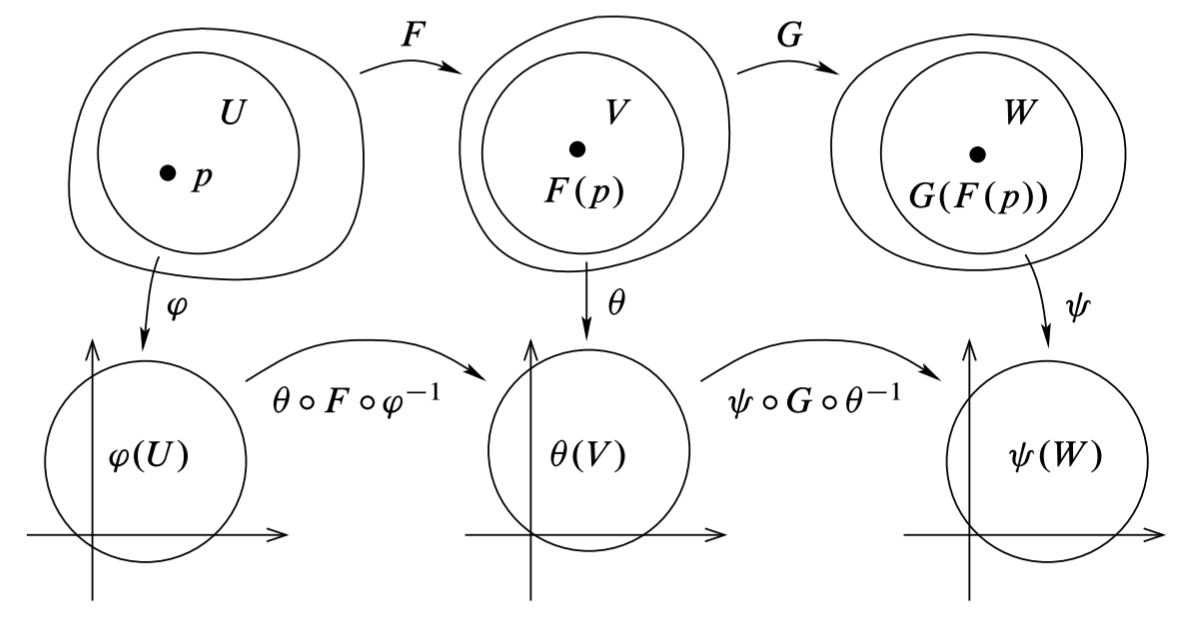
3, 任取 \(p\in M\). 由 \(G\) 的光滑性, 存在包含 \(F(p)\) 的坐标卡 \((V,\theta)\) 和包含 \(G(F(p))\) 的坐标卡 \((W,\psi)\), 满足 \(G(V)\subset W\) 且 \(\psi\circ G\circ\theta^{-1}\) 光滑. 因为 \(F\) 连续, \(F^{-1}(V)\) 是开集, 于是存在 \(M\) 的坐标卡 \((U,\varphi)\) 满足 \(p\in U\subset F^{-1}(V)\). 于是坐标表示 \(\theta\circ F\circ\varphi^{-1}\) 是光滑的, 故 \[ \psi\circ(G\circ F)\circ\varphi^{-1} = (\psi\circ G\circ\theta^{-1}) \circ (\theta\circ F\circ\varphi^{-1}) \] 作为光滑映射的复合, 也是光滑的.

Proposition 2.6 (每个分量光滑) 设 \(M_1,\dots,M_k,N\) 为带边流形, 其中 \(M_1,\dots,M_k\) 中至多一个流形的边界非空. 记 \(\pi_i:\prod_jM_j\to M_i\) 为自然投射. 则映射 \(F:N\to\prod_jM_j\) 光滑, 当且仅当每个分量 \(F_i=\pi_i\circ F\) 光滑. \[ \xymatrix{ & \prod_j M_j \ar[d]^{\pi_i} \\ N \ar[r]_{F_i} \ar[ru]^F & M_i. } \]

一些例子:

• (球面的包含映射) 球面 \(\mathbb{S}^n\) 并非 \(\R^{n+1}\) 的开子流形, 因此不能应用 Proposition 2.5. 我们用坐标表示的方法. 包含映射 \(\iota:\mathbb{S}^n\hookrightarrow\R^{n+1}\) 显然是连续的, 其在标准光滑结构下的坐标表示 \[ \Align{ \hat{\iota}(u^1,\dots,u^n) &= (\iota\circ(\varphi_i^\pm)^{-1})(u^1,\dots,u^n) \\ &= \pqty{u^1,\dots,u^{i-1},\pm\sqrt{1-\|u\|^2},u^i,\dots,u^n} } \] 在定义域上光滑. 根据 Proposition 2.2 的 3, \(\iota\) 是光滑的.

• (射影空间的商映射) 类似地, 商映射 \(\pi:\R^{n+1}\setminus\{0\}\to\mathbb{RP}^n\) 是光滑的. 射影空间的另一种商映射 \(q:\mathbb{S}^n\to\mathbb{RP}^n\) (对径认同) 是光滑的复合映射 \(q=\pi\circ\iota\).

2.3 Diffeomorphisms

拓扑流形范畴 \(\sf Man\) 中的对象是拓扑流形, 态射是连续映射, 同构是同胚映射. 类似地, 光滑流形范畴 \(\sf Diff\) 中的对象是光滑流形, 态射是光滑映射 (光滑映射的复合仍是光滑映射).

光滑流形范畴中的同构称为微分同胚 (diffeomorphism). 具体来说, 光滑映射 \(F:M\to N\) 是微分同胚, 如果存在光滑映射 \(G:N\to M\), 使得 \(F\circ G={\rm id}_N\), \(G\circ F={\rm id}_M\). (可逆且逆映射是光滑的.) 此时称 \(M,N\) 是微分同胚的 (diffeomorphic), 记作 \(M\cong N\).

Proposition 2.7 (微分同胚)

1. 微分同胚是开的同胚.
2. (复合) 微分同胚的复合是微分同胚.
3. (有限积) 微分同胚的有限积是微分同胚.
4. (限制) 微分同胚在 (带边) 开子流形上的限制是到其像的微分同胚.

• \(M\) 上的恒等映射是微分同胚, 微分同胚的逆映射是微分同胚, 结合 2, 微分同胚是等价关系.

我们已经知道, 拓扑流形上的光滑结构一般是不唯一的. 一个更深入的问题是: 在微分同胚意义下, 流形的光滑结构是否唯一?

• 考虑 \((\R,{\rm id}_{\R})\) 和 \((\R,\psi)\), \(\psi(x)=x^3\) 的例子, 这两个微分结构其实是微分同胚的! 一个微分同胚由 \(F(x)=x^{1/3}\) 给出.

实际上, 我们之后会证明, \(\R\) 上的所有微分结构都是微分同胚的.

• James Munkres 和 Edwin Moise 的工作表明, 所有维数 \(\leq3\) 的拓扑流形上有唯一的微分结构.

• 维数 \(\geq4\) 的情况十分复杂. 对于欧氏空间来说, \(n>4\) 时 \(\R^n\) 只有一种光滑结构; 但 \(\R^4\) 却有不可数多个不同的光滑结构! \(\R^4\) 上非标准光滑结构的存在性最初由 Simon Donaldson 和 Michael Freedman 在 1984 年证明.

• 对于紧流形来说, 情况更加有趣. John Milnor 在 1956 年发现了 \(\mathbb{S}^7\) 上的非标准光滑结构. 不久后, 他与 Michel Kervaire (利用 Steve Smale 的一个深刻的定理) 证明了 \(\mathbb{S}^7\) 上恰有 15 种光滑结构的微分同胚类 (若要求微分同胚保持定向的话, 则是 28 种). 球面 \(\mathbb{S}^n\) 上不同光滑结构的数量: (wikipedia)

  

  \(\mathbb{S}^4\) 上光滑结构的数量仍是未知的 (光滑 Poincaré 猜想).

  奇数维球面中, 仅有 \(\mathbb{S}^1,\mathbb{S}^3,\mathbb{S}^5,\mathbb{S}^{61}\) 具有唯一的光滑结构, 其中 \(\mathbb{S}^{61}\) 上光滑结构的唯一性是 2017 年由中国年轻数学家王国帧, 徐宙利通过计算球面的稳定同伦群而得到的. 偶数维球面的情形, 目前仅知道在维数小于 \(140\) 时, 仅有 \(\mathbb{S}^2,\mathbb{S}^6,\mathbb{S}^{12},\mathbb{S}^{56}\) (以及可能的 \(\mathbb{S}^4\)) 有唯一的光滑结构.

• 对于任意 \(n\geq3\), 都有不存在光滑结构的 \(n\) 维紧流形.

3 Partitions of Unity

光滑 gluing lemma 是一种构造光滑映射的方法: 将局部的光滑映射 "粘合" 起来. 引理的使用有两个条件: 第一, 必须选取开覆盖; 第二, 不同开集上的局部映射在交集上恒等. 本节中, 我们介绍一个更强大的工具, 即 (光滑) 单位分解, 它可以将局部的光滑映射 "融合" 在一起, 不论它们是否在交集上恒等.

我们回顾拓扑空间上单位分解的定义: 设 \(M\) 是拓扑空间, \({\cal X}=(X_\alpha)_{\alpha\in A}\) 是开覆盖. 一个从属于 \({\cal X}\) 的单位分解 指的是连续函数族 \(\psi_\alpha:M\to\R\), 满足

1. \(0\leq\psi_\alpha(x)\leq1\), 对任意 \(\alpha\in A,x\in M\).
2. \(\supp\psi_\alpha\subset X_\alpha\).
3. 支集族 \((\supp\psi_\alpha)_{\alpha\in A}\) 局部有限.
4. \(\sum_\alpha\psi_\alpha(x)=1\), 对任意 \(x\in X\).

如果 \(M\) 是 (带边) 光滑流形, 则光滑单位分解 (smooth partition of unity) 额外要求 \(\psi_\alpha\) 是光滑函数.

3.1 Smooth bump functions

一般拓扑空间 (仿紧的 Hausdorff 空间) 上单位分解的基础是 "鼓包函数", 其存在性由 Urysohn 引理保证. 对于光滑流形的光滑单位分解来说, 构造 "光滑鼓包函数" 相对简单. 我们分几步构造这样的函数.

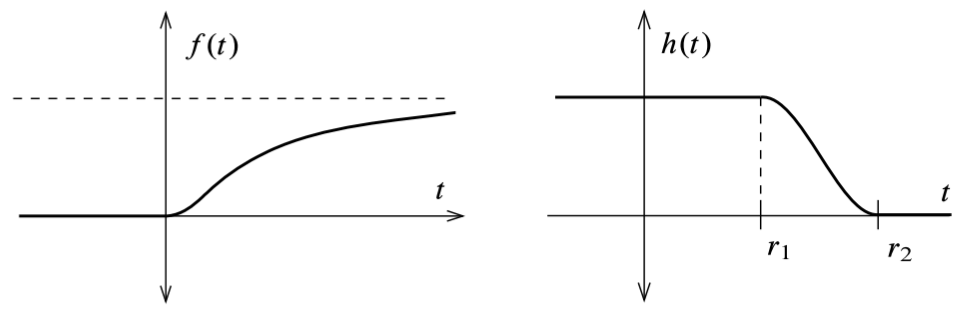
第一步, 构造函数 \(f:\R\to\R\), \[ f(t)=\Cases{ \e^{-1/t},&t>0, \\ 0, & t\leq0. } \] 这是一个光滑函数, 它在 \(t\leq0\) 时恒为零, 在 \(t>0\) 时恒正.

第二步, 构造 \(\R\) 上的截断函数 (cutoff function). 任给 \(r_1<r_2\), 考虑函数 \(h:\R\to\R\), \[ h(t) = \frac{f(r_2-t)}{f(r_2-t)+f(t-r_1)}, \] 这是一个光滑函数, 当 \(t\leq r_1\) 时, \(h(t)\equiv1\), 当 \(t\geq r_2\) 时, \(h(t)\equiv0\), 当 \(r_1<t<r_2\) 时, \(0<h(t)<1\).

第三步, 构造 \(\R^n\) 上的光滑鼓包函数 (bump function).

Lemma 3.1 (鼓包函数的存在性) 任给正实数 \(r_1<r_2\), 存在光滑函数 \(H:\R^n\to\R\) 满足 \(H\) 在 \(\overline{B_{r_1}(0)}\) 上恒为 \(1\), 在 \(\R^n\setminus B_{r_2}(0)\) 上恒为 \(0\), 在 \(B_{r_2}(0)\setminus\overline{B_{r_1}(0)}\) 上处于 \((0,1)\) 内.

Pf 取 \(h:\R\to\R\) 是上面构造的截断函数, 令 \(H(x)=h(\|x\|)\) 即可. 范数函数在 \(0\) 以外光滑, 因此 \(H\) 在 \(\R^n\setminus\{0\}\) 光滑; 因为 \(H\) 在 \(B_{r_1}(0)\) 为常值函数, 故 \(H\) 在 \(0\) 也光滑.

3.2 Existence of partions of unity

Theorem 3.2 (光滑单位分解存在性) 设 \(M\) 是 (带边) 光滑流形, \({\cal X}=(X_\alpha)_{\alpha\in A}\) 是开覆盖, 则存在从属于 \({\cal X}\) 的光滑单位分解.

Pf 开集 \(X_\alpha\) 自身构成 (带边) 光滑流形, 因此存在正则坐标 (半) 球组成的拓扑基 \({\cal B}_\alpha\). 容易验证 \({\cal B}=\bigcup_\alpha{\cal B}_\alpha\) 是 \(M\) 的拓扑基. 因为拓扑流形是仿紧的, 所以 \({\cal X}\) 存在局部有限加细, 特别地, \({\cal X}\) 可以加细到 \(\{B_i\}\), 其中 \(B_i\in{\cal B}\). 根据局部有限的闭包刻画, \(\{\overline{B_i}\}\) 是局部有限的.

(构造 \(M\) 上的鼓包函数) 对于 \(B_i\), 它是某 \(X_\alpha\) 内的正则坐标 (半) 球.

• 若 \(B_i\) 是正则坐标球, 故存在坐标球 \(B_i'\subset X_\alpha\), 满足 \(\overline{B_i}\subset B_i'\), 且有坐标映射 \(\varphi_i:B_i'\to\R^n\), 满足 \(\varphi_i(\overline{B_i})=\overline{B_{r_i}(0)}\), \(\varphi_i(B_i')=B_{r_i'}(0)\), 其中 \(r_i<r_i'\). 定义函数 \(f_i:M\to\R\), \[ f_i(x) = \Cases{ (H_i\circ\varphi_i)(x), & x\in B_i', \\ 0, & x\in M\setminus\overline{B_i}, } \] 其中 \(H_i:\R^n\to\R\) 是在 \(B_{r_i}(0)\) 严格正, 在其余地方为 \(0\) 的鼓包函数. 在 \(B_i'\setminus\overline{B_i}\) 上, \(f\) 的两个定义恒等, 根据 gluing lemma, \(f_i\) 是光滑函数, 且 \(\supp{f_i}=\overline{B_i}\).

• 若 \(B_i\) 是正则坐标半球, 操作和上面是一样的. 构造 \(H_i\) 的时候, 在完整的球上构造, 之后再限制到半球上即可.

(归一化) 定义 \(f:M\to\R\), \(f(x)=\sum_if_i(x)\). 根据 \(\{\overline{B_i}\}\) 的局部有限性, \(\sum_if_i(x)\) 在每一点都是有限和, 因此 \(f\) 是良定义的光滑函数. 由于 \(f_i(x)\) 非负且在 \(B_i\) 严格正, 而每一点 \(x\in M\) 都属于某 \(B_i\), 因此 \(f\) 严格正. 我们定义 \(g_i(x)=f_i(x)/f(x)\), 有 \(0\leq g_i(x)\leq 1\) 且 \(\sum_ig_i(x)=1\).

(重编指标) 我们需要让 \(\{g_i\}\) 以 \(\alpha\in A\) 为下标. 因为 \(\{B_i'\}\) 是 \(\cal X\) 的加细, 对每个 \(i\), 我们取 \(a(i)\in A\) 使得 \(B_i'\subset X_{a(i)}\). 对于每个 \(\alpha\in A\), 定义 \[ \psi_\alpha = \sum_{a(i)=\alpha} g_i. \] (如果不存在 \(i\) 使得 \(a(i)=\alpha\), 则 \(\psi_\alpha\) 为零函数.) 显然有 \(\sum_\alpha\psi_\alpha(x)=1\). 根据局部有限集族的性质, \[ \supp\psi_\alpha = \overline{\bigcup_{a(i)=\alpha}B_i} = \bigcup_{a(i)=\alpha}\overline{B_i} \subset X_\alpha, \] 因此 \(\psi_\alpha\) 是取值在 \([0,1]\) 内的光滑函数, 且 \((\supp\psi_\alpha)_{\alpha\in A}\) 局部有限. 总之, \(\{\psi_\alpha\}_{\alpha\in A}\) 是从属于 \(\cal X\) 的单位分解.

3.3 Applications

设拓扑空间 \(M\) 的闭子集 \(A\), 开子集 \(U\supset A\). 一个 \(A\) 的支在 \(U\) 上的鼓包函数指的是连续函数 \(\psi:M\to\R\) 满足 \(0\leq\psi(x)\leq1\), \(\supp\psi\subset U\), 且在 \(A\) 上 \(\psi(x)\equiv1\).

Proposition 3.3 (光滑鼓包函数存在性) 设 \(M\) 是 (带边) 光滑流形, 任给闭子集 \(A\), 开子集 \(U\supset A\), 存在 \(A\) 的支在 \(U\) 上的光滑鼓包函数.

Pf 令 \(U_0=U\), \(U_1=M\setminus A\), 取从属于 \(\{U_0,U_1\}\) 的光滑单位分解 \(\{\psi_0,\psi_1\}\), 其中 \(\psi_1\) 即为所求.

设 \(M,N\) 是 (带边) 光滑流形, 子集 \(A\subset M\). 一个映射 \(F:A\to N\) 称为光滑的, 如果对任意一点 \(p\in A\), 存在邻域 \(W\) 和光滑映射 \(\tilde{F}:W\to N\), 其在 \(W\cap A\) 上的限制与 \(F\) 恒等.

Lemma 3.4 (光滑映射的扩张引理) 设 (带边) 光滑流形 \(M\) 的闭子集 \(A\), 光滑函数 \(f:A\to\R^k\). 任给包含 \(A\) 的开子集 \(U\), 存在光滑函数 \(\tilde{f}:M\to\R^k\), 满足 \(\tilde{f}|_A=f\) 且 \(\supp\tilde{f}\subset U\).

Pf 对任意 \(p\in A\), 存在邻域 \(W_p\subset U\) 使得 \(\tilde{f}:W_p\to\R^k\) 是 \(f\) 的光滑扩张. \(\{W_p\mid p\in A\}\cup\{A^C\}\) 是 \(M\) 的开覆盖, 取从属于其的单位分解 \(\{\psi_p\mid p\in A\}\cup\{\psi_0\}\).

对任意 \(p\in A\), \(\psi_p\tilde{f}_p\) 是支集包含于 \(W_p\) 的光滑函数, 将其扩张到整个 \(M\): 对于 \(x\in M\setminus\supp\psi_p\), 令函数值为 \(0\). 根据 gluing lemma, 这定义了 \(M\) 上的光滑函数. 于是我们定义 \(\tilde{f}:M\to\R^k\), \[ \tilde{f}(x)=\sum_{p\in A}\psi_p(x)\tilde{f}_p(x). \] 由 \(\supp\psi_p\) 的局部有限性, 上式为有限和, 进而 \(\tilde{f}\) 是光滑的. 对于 \(x\in A\), \(\psi_0(x)=0\), 因此 \[ \tilde{f}(x) = \sum_{p\in A}\psi_p(x)\tilde{f}_p(x) = \sum_{p\in A}\psi_p(x)f_p(x) = \pqty{\psi_0(x)+\sum_{p\in A}\psi_p(x)}f(x) = f(x), \] 这验证了 \(\tilde{f}\) 是 \(f\) 的扩张. 根据局部有限集族的性质, \[ \supp\tilde{f} \subset \overline{\bigcup_{p\in A}\supp\psi_p} = \bigcup_{p\in A}\supp\psi_p \subset U. \]

单位分解可以用来构造穷竭函数. 回顾其定义: 拓扑空间 \(M\) 的穷竭函数指的是连续函数 \(f:M\to\R\), 其任意下水平集 \(f^{-1}((-\infty,c])\) 是紧的. 此时, \(f^{-1}((-\infty,n])\), \(n\in\N\) 构成 \(M\) 的紧穷竭.

Proposition 3.5 (光滑穷竭函数存在性) (带边) 光滑流形上存在正的光滑穷竭函数.

Pf 和拓扑流形的情形类似.

Theorem 3.6 (光滑函数的零点集) 设 (带边) 光滑流形 \(M\) 的闭子集 \(K\), 则存在光滑函数 \(f:M\to[0,+\infty)\), 其零点集恰为 \(K\).

Pf 先考虑 \(M=\R^n\) 的情形. 任给 \(x\in M\setminus K\), 存在 \(r\leq1\) 使得 \(B_r(x)\subset M\setminus K\). 因为 \(M\setminus K\) 第二可数, 它可以被可数多个这样的开球 \(\{B_{r_i}(x_i)\}\) 覆盖.

令 \(h:\R^n\to\R\) 是在 \(\overline{B_{1/2}(0)}\) 为 \(1\), 在 \(B_1(0)\) 外为 \(0\) 的鼓包函数. 令 \(C_i\geq1\) (\(i\in\N^+\)) 同时为 \(|h|\) 以及 \(h\) 的 \(1\) 至 \(i\) 阶各偏导数的一个上界. 定义 \(f:\R^n\to\R\) 为无穷级数 \[ f(x) = \sum_{i=1}^\infty \frac{(r_i)^i}{2^iC_i}h\pqty{\frac{x-x_i}{r_i}}, \] 级数的通项被 \(1/2^i\) 控制, 根据 Weierstrass 强级数判别法, 它一致收敛到连续函数 \(f\). 注意到第 \(i\) 项不为零 (\(>0\)) 当且仅当 \(x\in B_{r_i}(x_i)\), 因此 \(f\) 在 \(K\) 中恒为零, 在 \(M\setminus{K}\) 中恒正.

只需再证明 \(f\) 是光滑的. 归纳法. 对 \(k\geq1\), 假设我们已经证明小于 \(k\) 的各阶偏导数连续, 此时第 \(i\) 项的 \(k\) 阶偏导数为 \[ \frac{(r_i)^{i-k}}{2^iC_i} D^k h\pqty{\frac{x-x_i}{r_i}} \] (\(D^kh\) 是 \(k\) 阶某混合偏导数) 根据 \(r_i,C_i\) 的取法, 只要 \(i\geq k\), 通项就被 \(1/2^i\) 控制, 因此 \(k\) 阶偏导数的序列一致收敛, 进而 \(f\) 具有连续的 \(k\) 阶偏导数.

再考虑 \(M\) 为 \(n\) 维光滑流形的情形. 设坐标球开覆盖 \(\{B_\alpha\}\) 与从属于其的单位分解 \(\{\psi_\alpha\}\). 因为坐标开球 \(B_\alpha\cong\R^n\), 所以存在光滑函数 \(f_\alpha:B_\alpha\to\R\) 使得 \(f_\alpha^{-1}(0)=B_\alpha\cap K\). 用单位分解拼合起来 \(f=\sum_\alpha\psi_\alpha f_\alpha\) 即可.

立刻能得到推论:

Theorem 3.7 (强光滑 Urysohn 引理) 设 (带边) 光滑流形 \(M\) 的不交闭子集 \(A,B\), 则存在光滑函数 \(f:M\to[0,1]\) 使得 \(f^{-1}(0)=A\), \(f^{-1}(1)=B\).