GTM202 | 8 紧曲面

GTM202 (Introduction to Topological Manifolds) Chapter 6 的笔记.

一个 \(2\) 维流形称为一张曲面 (surface). 接下来的几节, 我们利用 CW 复形的工具来研究紧曲面的拓扑分类.

21 Compact Surfaces

21.1 Compact sufaces as quotients

在之前的章节中, 我们认识了几个紧曲面: 球面 \(\mathbb{S}^2\), 环面 \(\mathbb{T}^2\) 和实射影平面 \(\mathbb{RP}^2\).

• 在 6.2 节, 我们证明了单位球面 \(\mathbb{S}^2\) 是二维流形;
• 在 7.1 节, 我们定义了环面 \(\mathbb{T}^2=\mathbb{S}^1\times\mathbb{S}^1\). 在 13.3 节, 我们给出了另一个构造, 其等同于正方形 \(S=\{(x,y)\mid|x|+|y|\leq1\}\) 对边认同 \((x,-1)\sim(x,1),(-1,y)\sim(1,y)\) 得到的商空间, 由此得到紧性.
• 在 11.2 节, 我们定义 \(\mathbb{RP}^2\) 为 \(\R^2\setminus\{0\}\) 为 \(\R^*\) 作用的轨道空间, 并证明了它是一个二维流形. 在 13.3 节, 我们给出了另一个构造, 即对径认同的 \(\mathbb{S}^2\), 由此得到紧性.

这是三种最重要的紧曲面, 因为所有紧曲面可以由这三者构造出来 (分类定理).

就像 \(\mathbb{T}^2\) 一样, \(\mathbb{S}^2\) 和 \(\mathbb{RP}^2\) 也能实现为将正方形 \(S\) (或者闭圆盘) 的某些边认同得到的商空间.

Claim 21.1 (\(\mathbb{S}^2\) 与 \(\mathbb{RP}^2\) 作为平面区域的商)

球面 \(\mathbb{S}^2\) 同胚于下列空间:

1. 闭圆盘 \(\overline{\mathbb{B}^2}\) 模去等价关系 \((x,y)\sim(-x,y)\) (对于 \((x,y)\in\partial\overline{\mathbb{B}^2}\)) 的商.
2. 正方形 \(S\) 模去等价关系 \((x,y)\sim(-x,y)\) (对于 \((x,y)\in\partial{S}\)) 的商.

实射影平面 \(\mathbb{RP}^2\) 同胚于下列空间:

1. 闭圆盘 \(\overline{\mathbb{B}^2}\) 模去等价关系 \((x,y)\sim(-x,-y)\) (对于 \((x,y)\in\partial\overline{\mathbb{B}^2}\)) 的商.
2. 正方形 \(S\) 模去等价关系 \((x,y)\sim(-x,-y)\) (对于 \((x,y)\in\partial{S}\)) 的商.

Pf 利用商空间的唯一性, 我们只需要构造出 \(\overline{\mathbb{B}^2}\) (或 \(S\)) 到相应空间的商映射, 且与上述等价关系给出相同的 identification 便可.

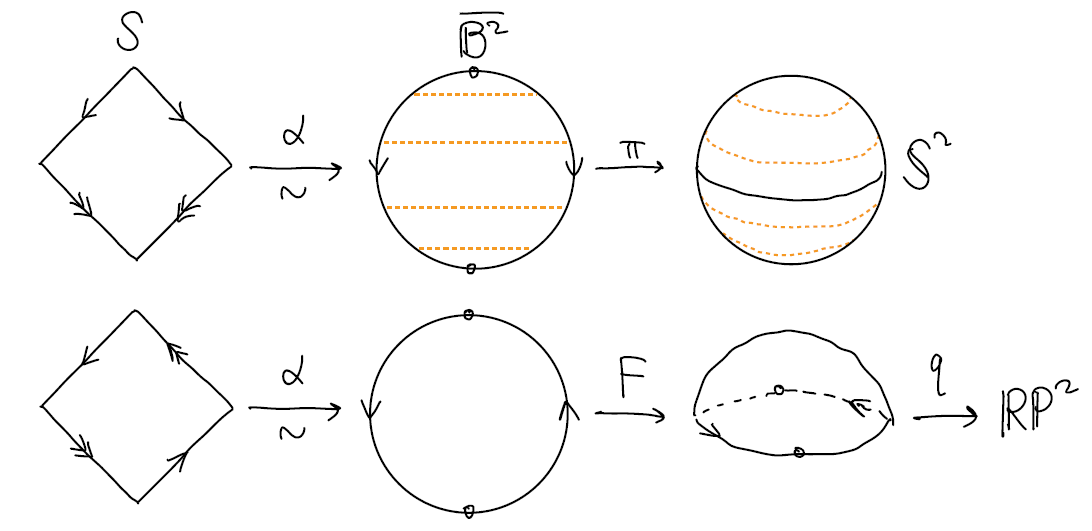
球面的 1, 考虑 "将圆盘包在球面上" 的映射 \(\pi:\overline{\mathbb{B}^2}\to\mathbb{S}^2\), \[ \pi(x,y)=\Cases{ \pqty{ -\sqrt{1-y^2}\cos\dfrac{\pi x}{\sqrt{1-y^2}}, -\sqrt{1-y^2}\sin\dfrac{\pi x}{\sqrt{1-y^2}}, y }, & y\neq\pm1, \\ (0,0,y), & y=\pm1. } \] 容易看出 \(\pi\) 是连续的, 由闭映射引理, 它是商映射. 并且 \(\pi\) 与 1 给出相同 identification.

球面的 2, 先将 \(S\) 同胚地映到 \(\overline{\mathbb{B}^2}\), 只需取 Claim 17.1 证明中构造的映射 \(\alpha:S\overset\sim\to\overline{\mathbb{B}^2}\) (将原点出发的 \(S\) 中的射线缩小到单位长射线). 最后, 考虑复合 \(\pi\circ\alpha:S\to\mathbb{S}^2\) 即可.

实射影空间的 1, 记 \(p:\mathbb{S}^2\to\mathbb{RP}^2\) 是球面对径认同的商映射, 令 \(F:\overline{\mathbb{B}^2}\to\mathbb{S}^2\) 将圆盘映到上半球面 \(F(x,y)=(x,y,\sqrt{1-x^2-y^2})\), 则 \(p\circ F:\overline{\mathbb{B}^2}\to\mathbb{RP}^2\). 根据闭映射引理, 这是商映射. 注意 \(F\) 的像是上半球面加上赤道, 在 \(p\) 下, 只有赤道对径认同, 这和 \((x,y)\sim(-x,-y)\) (\((x,y)\in\mathbb{S}^1\)) 给出相同的 identification.

实射影空间的 2, 同样考虑复合映射 \((p\circ F)\circ\alpha:S\to\mathbb{RP}^2\) 即可.

一个更一般的结论是, 任意 (满足一定条件的一个或多个) 多边形区域, 在边的认同关系下都构成 (紧) 曲面.

平面 \(\R^2\) 上的一个多边形 (polygon) 指的是同胚于 \(\mathbb{S}^1\) 的子集 \(P\subset\R^2\), 且 \(P\) 由有限个 \(1\) 维单形首尾相接组成. 因此 \(P\) 是一个 \(1\) 维单纯复形, 其 \(0\) 维单形和 \(1\) 维单形分别成为顶点和边. 多边形区域 (polygonal region) 指的是 \(\R^2\) 的紧子集, 其内部是正则坐标球 (因而是正则 \(2\) 维胞腔), 其边界是多边形. 平面中任意 \(2\) 维单形都构成多边形区域.

Claim 21.2 (曲面作为多边形区域的商) 设平面上的多边形区域 \(P_1,\dots,P_k\), \(P=\coprod_iP_i\). 若 \(P\) 上有某种等价关系: 将 \(P\) 中某些边, 通过仿射同胚, 与另外某些边认同起来. 记商映射 \(\pi:P\to M\).

1. \(M\) 是有限 \(2\) 维 CW 复形, 其 \(0\) 维骨架是 \(P\) 的顶点集在 \(\pi\) 下的像, \(1\) 维骨架是 \(P\) 的所有边之并在 \(\pi\) 下的像.
2. 如果对于 \(P_i\) 中的每条边, 有且仅有另一条边 (可以在 \(P_i\) 或其他 \(P_j\) 中) 与之认同, 则 \(M\) 是紧曲面.

Pf 1, 记 \(M_0,M_1,M_2=M\) 分别是顶点, 所有边, 多边形区域在 \(\pi\) 下的像. 根据定义, \(M_0\) 是离散空间, 且对于 \(k=1,2\), \(M_k\) 是向 \(M_{k-1}\) 粘贴有限多个 \(k\) 胞腔所得. 根据 CW 复形构造定理, \(M\) 是 \(2\) 维 CW 复形.

2, 因为 \(M\) 是有限复形, 故紧. 根据 CW 复形的流形判定, 只需证明 \(M\) 局部欧氏.

因为 \(2\) 维胞腔是开的, 其可以作为其内部点的欧氏邻域.

对于 \(1\) 维胞腔中的点 \(p\), 它恰有两个原像 \(p_1,p_2\), 各处于一条边的内部. 将 \(p_1,p_2\) 的两个边界坐标系 "拼合" 得到 \(p\) 的内部坐标系, 具体过程和 Claim 10.2 是一样的.

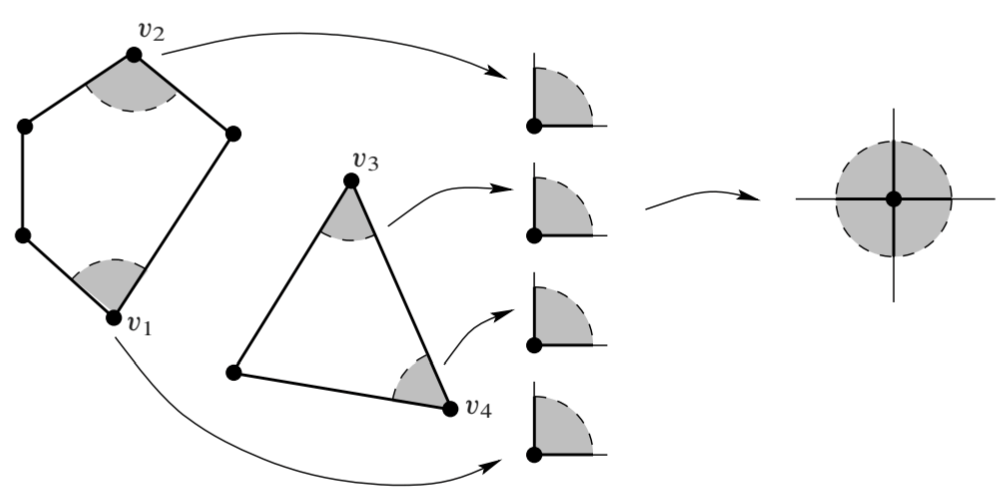
对于 \(0\) 维胞腔 \(v\), 它的原像是有限多个顶点 \(\{v_1,\dots,v_k\}\in P\). 对于每个原像点 \(v_i\), 取小开圆盘 \(B_\varepsilon(v_i)\) 只包含 \(v_i\) 一个顶点, 且只与 \(v_i\) 的两条临边相交. 因为 \(P_j\) (\(v_i\in P_j\)) 的内部都是正则坐标球, 其位于边界的一侧, 所以 \(B_\varepsilon(v_i)\cap P_j\) 是一个小扇形, 其同胚于圆心角为 \(2\pi/k\) 的扇形. 通过适当的缩放, 这些 \(2\pi/k\) 的小扇形可以拼成一个圆盘, 认同的边拼合在一起, 且认同的点重合. 由此得出 \(v\) 的邻域到圆盘的坐标映射.

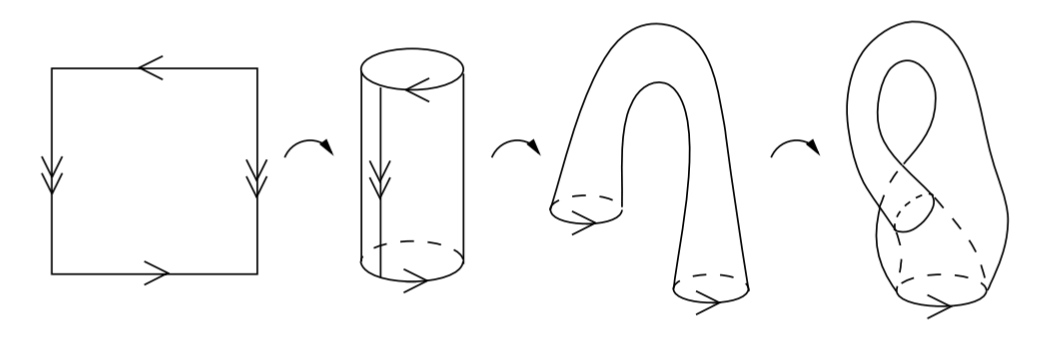
一个有趣的例子是 Klein 瓶 (Klein bottle) \(K\), 即正方形 \(I\times I\) 模去 \((0,y)\sim(1,y),(x,0)\sim(1-x,1)\) 得到的商空间. 它的几何图像见下图, 它在 \(\R^3\) 中呈现为一个自交的 "曲面" (不构成流形). 实际上, \(K\) 不同胚于 \(\R^3\) 的任何子集, 即不能被嵌入到 \(\R^3\) 中, 但其自身却是一个 \(2\) 维流形.

• \(K\) 可以嵌入到 \(\R^4\).

21.2 Connected sums

流形的连通和是将两个流形粘合起来的一种操作, 是由简单曲面构造一般曲面的工具.

Claim 21.3 (流形挖去正则坐标球) 设 \(n\geq1\) 维流形 \(M\), 正则坐标球 \(B\subset M\), 则 \(M\setminus B\) 是 \(n\) 维带边流形, 且流形边界 \(\partial{M}\cong\mathbb{S}^{n-1}\). 如果 \(n>1\) 且 \(M\) 连通, 则 \(M\setminus{B}\) 连通.

Pf 子空间 \(M\setminus{B}\) 的第二可数性与 Hausdorff 性继承 \(M\). 由正则坐标球的定义, \(\overline{B}\) 包含于某坐标球 \(B'\), 坐标映射 \(\varphi:B'\overset\sim\to B_{r'}(0)\subset\R^n\) 将 \(B\) 映到 \(B_r(0)\), 将 \(\overline{B}\) 映到 \(\overline{B_r(0)}\) (\(r<r'\)).

对于开集 \(M\setminus\overline{B}\) 中的点, 取其原本的欧氏邻域与 \(M\setminus\overline{B}\) 之交, 便得到其在 \(M\setminus{B}\) 中的欧氏邻域. 对于 \(\partial{B}\) 中的点 \(p\), 取圆环 \(B_{r'}(0)\setminus B_r(0)\) 中的包含 \(\varphi(p)\) 的一段 "扇环" \(U\) (如下图), 不难构造 \(U\) 到上半平面 \(\H^2\) 的同胚 \(\psi\). 因此 \(\varphi^{-1}(U)\) 是 \(p\) 的同胚于 \(\H^2\) 的邻域, 且 \((\psi\circ\varphi)(p)\) 是边界点.

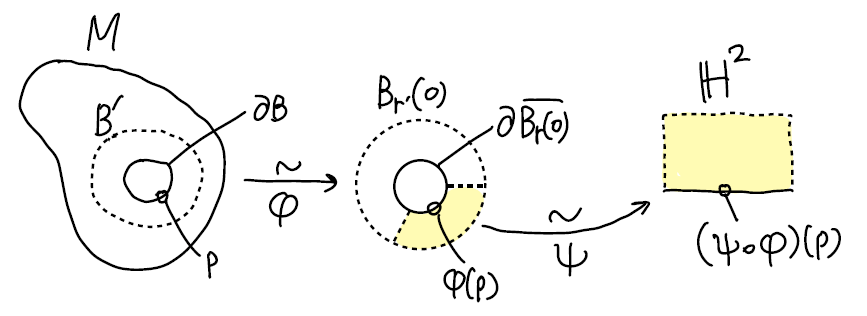
可见 (利用边界不变性), \(\partial{B}\) 中的点就是 \(M\) 的所有边界点, 故 \(\partial{M}=\partial{B}\cong\partial{\overline{B_r(0)}}\cong\mathbb{S}^1\).

最后, 设 \(n>1\) 且 \(M\) 连通, 则 \(M\) 也道路连通. 只需证明 \(M\setminus{B}\) 道路连通. 注意到对 \(n>1\), \(\partial(M\setminus B)\cong\mathbb{S}^{n-1}\) 是连通的. 任给 \(p,q\in M\setminus{B}\), 取 \(M\) 中连接 \(p,q\) 的道路 \(f\), 将其在 \(B\) 中的部分替换为 \(\partial(M\setminus B)\) 中的一条道路即可.

设 \(n\) 维流形 \(M_1,M_2\), 取正则坐标球 \(B_i\subset M_i\), 令 \(M_i'=M_i\setminus B_i\). 取同胚 \(f:\partial{M_2'}\overset\sim\to\partial{M_1'}\). 这两个流形的连通和 (connected sum) \(M_1\mathbin{\#}M_2\) 定义为黏着空间 \(M_1'\cup_fM_2'\). 简单地说, 就是两个流形分别挖掉正则坐标球, 再沿着边界贴合. 根据 Claim 10.2, \(M_1\mathbin{\#}M_2\) 是一个 \(n\) 维 (无边) 流形.

Claim 21.4 (连通和的性质) 设 \(n\) 维流形 \(M_1,M_2\).

1. 若 \(M_1,M_2\) 连通且 \(n>1\), 则 \(M_1\mathbin{\#}M_2\) 连通.
2. 若 \(M_1,M_2\) 紧, 则 \(M_1\mathbin{\#}M_2\) 紧.

Pf 1, 记 \(N=M_1\mathbin{\#}M_2\), 考虑嵌入映射 \(f_i:M_i'\hookrightarrow N\), 根据 Claim 10.2 有 \[ N=f_1(M_1)\cup f_2(M_2),\quad f_1(M_1)\cap f_2(M_2)=\partial{M_1}\neq\emptyset. \] 当 \(n>1\) 时, \(M_i'\) 连通, 进而 \(f_i(M_i')\) 连通; \(N\) 作为有公共点的连通集之并, 是连通的.

2, \(M_i'=M\setminus{B_i}\) 紧 (紧空间的闭子集); 不交并 \(M_1'\amalg M_2'\) 也紧, 商空间 \(M_1'\cup_fM_2'= M_1'\amalg M_2'/{\sim}\) 也是紧的.

连通和 \(M_1\mathbin{\#}M_2\) 依赖于正则坐标球 \(B_i\) 和同胚 \(f\) 的选择. 事实上 (我们不去证明), 在同胚意义下, \(M_1,M_2\) 至多有两种连通和 (对应 \(f\) 是否保持 \(\mathbb{S}^{n-1}\) 的定向).

特别地, 对于两个曲面来说, 这两种连通和是同胚的. 在学习完基本群与相关定理之后, 我们能证明这个结论的紧曲面版本.

• (贴上球面) \(n\) 维流形 \(M\) 与球面 \(\mathbb{S}^n\) 的连通和同胚于 \(M\).
• (贴上环面) 曲面 \(M\) 与环面 \(\mathbb{T}^2\) 的连通和相当于 "贴上一个把手".
• \(n\) 重连通和 \(\mathbb{T}^2\mathbin{\#}\cdots\mathbin{\#}\mathbb{T}^2\) 称为 带 \(n\) 个洞的环面, 可以视作贴上 \(n\) 个把手的 \(\mathbb{S}^2\).

22 Polygonal Presentation of Surfaces

22.1 Polygonal presentations

为了将紧曲面分类, 我们对曲面得有一种统一的描述方法. 接下来, 我们将曲面实现为一个多边形区域的商, 并用边的 "认同关系" 描述这张曲面.

设集合 \(S\), \(S\) 中的一个字 (word) 指的是一个有限序列 \(W\), 其中的每一项形如 \(a\) 或 \(a^{-1}\), 其中 \(a\in S\). 一个多边形表示 (polygonal presentation), 记作 \[ {\cal P}=\lr{S\mid W_1,\dots,W_k}, \] 其中 \(S\) 是一个有限集, \(W_1,\dots,W_k\) 是 \(S\) 中的字, 并且满足 ① \(W_i\) 的长度至少为 \(3\), ② \(S\) 中的每个元素至少出现在一个字中. (如果 \(k=1\), 允许字长为 \(2\).)

• 例如, 若 \(S=\{a,b\}\), 字 \(W=(a,b,a^{-1},b^{-1})\), 则一个多边形表示 \[ \lr{S\mid W}=\lr{a,b\mid aba^{-1}b^{-1}}. \] 注意我们将 \(\{\}\) 和 \(()\) 和省略了, 并且把 \(W\) 中的符号并排写在一起 (后者仅当字的个数 \(k=1\) 时).

• 当 \(S=\{a\}\), \(k=1\) 且字长为 \(2\) 时, 只有四种多边形表示: \[ \lr{a\mid aa},\lr{a\mid a^{-1}a},\lr{a\mid aa^{-1}}, \lr{a\mid a^{-1}a^{-1}}. \]

多边形表示 \({\cal P}\) 确定了一个拓扑空间 \(|{\cal P}|\), 构造过程为

1. 对于每个字 \(W_i\), 记其字长为 \(m\), 令 \(P_i\) 是 \(\R^2\) 中边长为 \(1\) 的正 \(m\) 边形区域, 且中心在原点, 一个顶点在 \(y\) 轴正半轴上.
   • 特别地, 如果 \(k=1\), 则规定 \(P_i\) 为单位圆, 其两条 "边" 分别是左半圆与右半圆, 以 \(y\) 轴分界.
2. 从 \(y\) 轴正半轴上的顶点开始, 逆时针方向走过每一条边, 将 \(W_i\) 中的符号与 \(P_i\) 中的边一一对应. 给每条边标上箭头: 如果其对应符号是 \(a\), 则箭头指向前方 (逆时针方向); 如果是 \(a^{-1}\), 则指向后方.
3. 定义 \(\coprod_iP_i\) 上的等价关系: 将符号相同的边 (通过仿射同胚) 认同, 保证拼接时箭头朝向相同. 商空间记作 \(|{\cal P}|\).

拓扑空间 \(|{\cal P}|\) 称为 \({\cal P}\) 的几何实现 (geometric realization). 多边形区域 \(P_i\) 的面, 边, 顶点边分别叫做 \({\cal P}\) 的面, 边, 顶点. 面数等于字的个数 \(k\), 边数等于所有字的长度之和. 边的两个顶点分别称为起点和终点, 保证箭头从起点指向终点.

如果 \(S\) 中的每个符号在 \(W_1,\dots,W_k\) 中都恰好出现两次, 则称 \({\cal P}\) 是一个面表示 (surface presentation). 根据 Claim 21.2, 面表示的几何实现是紧曲面.

如果 \({\cal P}\) 的几何实现同胚于某个拓扑空间 \(X\), 则称 \({\cal P}\) 是 \(X\) 的表示. 如果 \(X\) 存在面数为 \(1\) 的表示, 那么它是连通的, 因为它是连通多边形的商空间. 一些曲面的表示:

• 球面: \(\lr{a\mid aa^{-1}}\) 或 \(\lr{a\mid abb^{-1}a^{-1}}\).
• 环面: \(\lr{a,b\mid aba^{-1}b^{-1}}\).
• 实射影平面: \(\lr{a\mid aa}\) 或 \(\lr{a,b\mid abab}\).
• Klein 瓶: \(\lr{a,b\mid abab^{-1}}\).

如果多边形表示 \({\cal P},{\cal P}'\) 的几何实现同胚, 则称它们拓扑等价 (topologically equivalent), 记作 \({\cal P}\sim{\cal P}'\).

22.2 Elementary transformations

下面我们定义多边形表示 \({\cal P}\) 上的一些操作, 称为初等变换 (elementary transforms).

• 符号替换 (relabelling): 将所有 \(a\) 都换成一个未出现的新符号; 交换两个已有符号; 交换 \(a\) 和 \(a^{-1}\).

• 细分 (subdivision): 将所有 \(a\) 都换成 \(ae\), 且所有 \(a^{-1}\) 都换成 \(e^{-1}a^{-1}\), 其中 \(e\) 是未出现的新符号.

• 合并 (consolidating): 若符号 \(a,b\) 总是相邻地出现, 且以 \(ab\) 或 \(b^{-1}a^{-1}\) 形式, 则将所有 \(ab\) 换成 \(a\), 所有 \(b^{-1}a^{-1}\) 换成 \(a^{-1}\) (需保证每个字长 \(\geq3\); 若 \(k=1\), 允许字长为 \(2\)).

• 反射 (reflecting): \[ \lr{S\mid a_1\dots a_m,W_2,\dots,W_k} \mapsto \lr{S\mid a_m^{-1}\dots a_1^{-1},W_2,\dots,W_k}. \]

• 旋转 (rotating): \[ \lr{S\mid a_1a_2\dots a_m,W_2,\dots,W_k} \mapsto \lr{S\mid a_2\dots a_ma_1,W_2,\dots,W_k}. \]

• 剪切 (cutting): 若 \(W_1,W_2\) 长度都 \(\geq2\), \[ \lr{S\mid W_1W_2,\dots,W_k} \mapsto \lr{S\mid W_1e,e^{-1}W_2,\dots,W_k}. \]

• 粘合 (pasting): \[ \lr{S\mid W_1e,e^{-1}W_2,\dots,W_k} \mapsto \lr{S\mid W_1W_2,\dots,W_k}. \]

• 折叠 (folding): 若 \(W_1\) 长度 \(\geq3\), \[ \lr{S\mid W_1ee^{-1},W_2,\dots,W_k} \mapsto \lr{S\mid W_1,W_2,\dots,W_k}. \] 如果 \(k=1\), 允许 \(W_1\) 长为 \(2\).

• 展开 (unfolding): \[ \lr{S\mid W_1,W_2,\dots,W_k} \mapsto \lr{S\mid W_1ee^{-1},W_2,\dots,W_k}. \]

显然, 细分与合并, 剪切与粘合, 折叠与展开是 3 对互逆的变换.

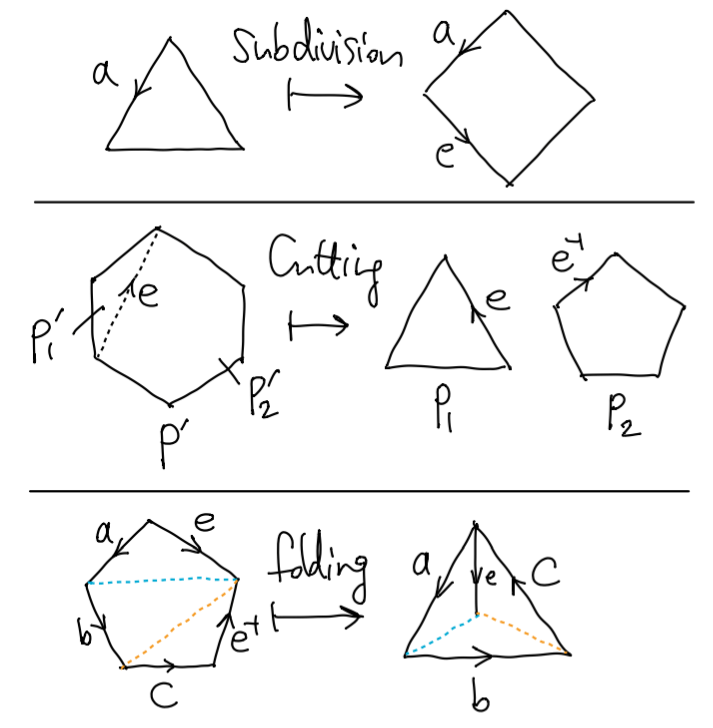
Claim 22.1 初等变换前后的多边形表示拓扑等价.

Pf 显然 "符号替换" 不改变多边形表示的几何实现. 对于互逆的一对变换, 我们只需证明其一.

(反射) 反射前后的 \(W_1\) 通过仿射同胚 \((x,y)\mapsto(-x,y)\) (关于 \(y\) 轴反射) 认同.

(旋转) 旋转前后的 \(W_1\) 通过仿射同胚 \((r,\theta)\mapsto(r,\theta-2\pi/k)\) (绕原点逆时针旋转 \(2\pi/m\)) 认同.

(剪切) 设 \(W_1e\), \(e^{-1}W_2\) 和 \(W_1W_2\) 分别对应的多边形 \(P_1,P_2,P'\). 先不考虑 \(W_3,\dots,W_k\), 记商映射 \(\pi:P_1\amalg P_2\to M\) 和 \(\pi':P'\to M'\).

记 \(e\) 为 \(P'\) 中连接 \(W_1\) 终点与 \(W_1\) 起点的线段 (根据凸性, \(e\) 一定在 \(P'\) 中). 如上图, 利用 Claim 17.2, \(P_1,P_2\) 能同胚地映到 \(P_1',P_2'\) 且保持符号相同的边重合. 将两个同胚拼合为 \(f:P_1\amalg P_2\to P'\). 显然 \(\pi\) 和 \(\pi'\circ f\) 给出相同的 identification, 其中后者 (由闭映射引理) 是商映射, 由商空间的唯一性, \(M\cong M'\).

如果还有 \(W_3,\dots,W_k\), 将 \(f\) 用恒等映射扩张到其上即可.

(细分) 记操作前后的多边形全体 \(P,P'\), 商映射 \(\pi:P\to M\), \(\pi:P'\to M'\). 利用 Claim 17.2, 存在连续映射 \(f:P\to P'\) 将每个多边形同胚地映到操作后的多边形, 保持符号相同的边重合 (如果遇到边 \(a\), 则将其等分成两端后映到边 \(a,e\); \(a^{-1}\) 同理). 同上, 商映射 \(\pi\) 和 \(\pi'\circ f\) 给出相同的 identification. 由商空间的唯一性, \(M\cong M'\).

(折叠) 同剪切, 我们可以忽略 \(W_2,\dots,W_k\). 如果 \(W_1\) 字长为 \(2\), 可先将其细分, 再折叠, 再合并. 因此我们只需考虑长度 \(\geq3\) 的字.

若 \(W_1=abc\) 长度为 \(3\), 记 \(P,P'\) 分别为 \(abcee^{-1}\) 和 \(abc\) 的多边形, 商映射 \(\pi:P\to M\), \(\pi':P'\to M'\). 如上图, 将 \(P,P'\) 各划分为三个小三角形, 利用 Claim 17.2, \(P'\) 的三个小三角可以同胚地映到 \(P\) 的三个小三角形, 保证符号相同的边重合. 同上, 由商空间的唯一性, \(M\cong M'\).

若 \(W_1\) 长度 \(\geq4\), 记 \(W_1=Xbc\), 其中字 \(X\) 长度 \(\geq2\). 剪出一条新边 \(a\), \[ \lr{S,b,c,e\mid Xbcee^{-1}} \cong \lr{S,a,b,c,e\mid Xa^{-1},abcee^{-1}}, \] 折叠第二个字, 再将两个字粘合即可.

22.3 Connected sums

在证明连通和的表示之前, 先考虑一个引理:

Claim 22.2 设曲面 \(M\) 的表示 \({\cal P}\), 其中一个多边形区域为 \(P\). 若 \(P\) 的顶点互不认同, 则 \(P\) 的内部在商映射下的像是正则坐标球.

Pf \(P\) 的顶点互不认同蕴含 \(P\) 的边互不认同, 进而商映射 \(\pi\) 将 \(P\) 单射入 \(M\), 进而 \(P\) 同胚于 \(\pi(P)\).

对于 \(\pi(P)\) 的每个顶点 \(v\), 从 \(v\) 出发的边 (非 \(\pi(P)\) 中 \(v\) 的邻边) 一定不是 \(\pi(P)\) 中的边, 否则与假设矛盾. 因此, \(\pi(P)\) 形如下图, 可以找到比 \(\pi(P)\) 稍大的坐标球 (橙色).

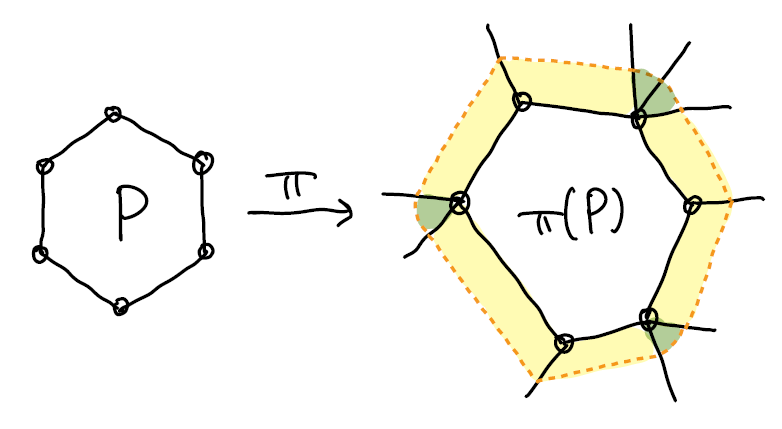
使用与 Claim 21.2 相同的技巧, 将相邻的多边形中, 绿色的小扇形与黄色的细长四边形拼起来即可.

Claim 22.3 (连通和的表示) 若 \(\lr{S_1\mid W_1},\lr{S_2\mid W_2}\) 分别是曲面 \(M_1,M_2\) 的面数为 \(1\) 的表示, 且 \(S_1,S_2\) 不交, 则 \(\lr{S_1,S_2\mid W_1W_2}\) 是连通和 \(M_1\mathbin{\#}M_2\) 的一个表示.

Pf

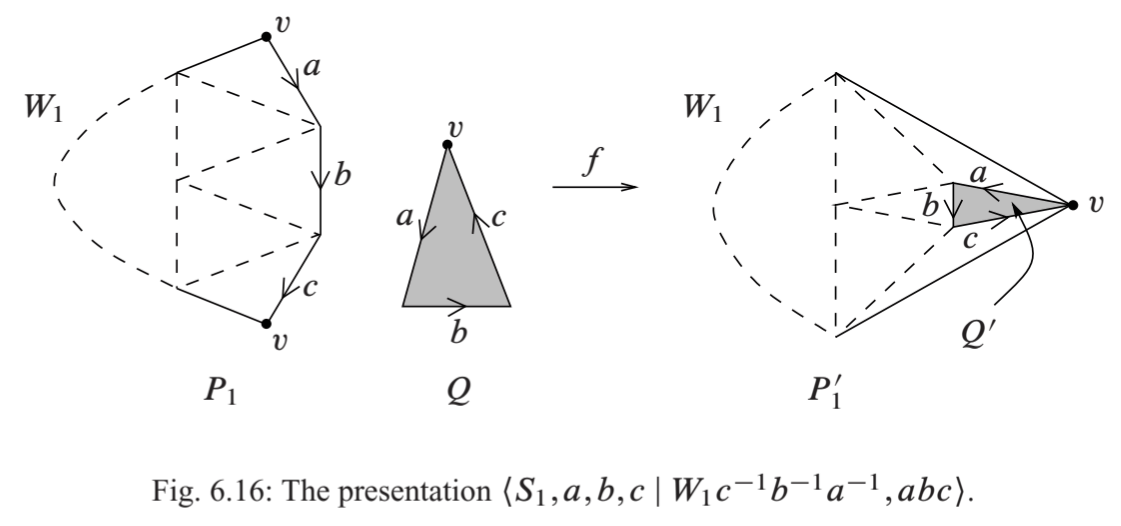
设新符号 \(a,b,c\). 考虑 \(\lr{S_1,a,b,c\mid W_1c^{-1}b^{-1}a^{-1},abc}\), 如图, 沿着 \(a\) 粘合之后再折叠两次, 这个表示等价于 \(\lr{S_1\mid W_1}\), 因此是 \(M_1\) 的表示. 记三角形 \(abc\) 的内部在 \(M_1\) 中的像为 \(B_1\), 由引理, \(B_1\) 是一个正则坐标球. 进而, \(M_1':=M_1\setminus B_1\) 的一个表示是 \[ \lr{S_1,a,b,c\mid W_1c^{-1}b^{-1}a^{-1}}, \] 其边界是边 \(c^{-1}b^{-1}a^{-1}\) 的像. 同样地, \[ \lr{S_2,a,b,c\mid abcW_2}, \] 是 \(M_2\) 挖去正则坐标球 \(B_2\) 所得 \(M_2':=M_2\setminus B_2\) 的表示, 其边界是边 \(abc\) 的像. 因此, \(M_1\mathbin{\#}M_2\) (即取 \(M_1', M_2'\) 的不交并, 再将边界认同) 的一个表示是 \[ \lr{S_1,S_2,a,b,c\mid W_1c^{-1}b^{-1}a^{-1},abcW_2}. \] 沿着 \(a\) 贴上并折叠两次, 得到 \(\lr{S_1,S_2\mid W_1W_2}\).

由此可以得到一些曲面的连通和的表示:

• 球面: \[ \lr{a\mid aa^{-1}}. \]

• \(n\) 个环面的连通和: \[ \lr{a_1,b_1,\dots,a_n,b_n\mid a_1b_1a_1^{-1}b_1^{-1} \dots a_nb_na_n^{-1}b_n^{-1} }. \]

• \(n\) 个实射影空间的连通和: \[ \lr{a_1,\dots,a_n\mid a_1a_1\dots a_na_n}. \]

这些表示称为对应曲面的标准表示 (standard presentation).