GTM202 | 7 胞腔复形

GTM202 (Introduction to Topological Manifolds) Chapter 5 的笔记.

19 Classification of 1-Manifolds

19.1 CW decomposition on 1-manifolds

Claim 19.1 \(1\) 维流形上存在正则 CW 分解.

Claim 19.2 设 \(1\) 维流形 \(M\) 上有正则 CW 分解. 则任一 \(1\) 维胞腔的边界恰好是两个 \(0\) 维胞腔; 任一 \(0\) 维胞腔恰好是两个 \(1\) 维胞腔的边界.

19.2 Classification theorems

Claim 19.3 (一维连通流形的分类) 设非空一维连通流形 \(M\). 若 \(M\) 紧, 则它同胚于 \(\mathbb{S}^1\), 若非紧, 则同胚于 \(\R\).

Claim 19.4 (一维连通带边流形的分类) 设非空一维连通带边流形 \(M\). 若 \(M\) 紧, 则它同胚于 \([0,1]\), 若非紧, 则同胚于 \([0,+\infty)\).

任意 \(n\) 维流形同胚于若干连通 \(n\) 维流形的不交并; 任意 \(n\) 维带边流形同胚于若干连通 \(n\) 维带边 (或不带边) 流形的不交并. 因此, 我们可以得到任意 \(1\) 维流形的分类.

20 Simplicial Complexes

20.1 Simplicial complexes

设欧氏空间 \(\R^n\) 的线性子空间 \(S\). 一个平行于 \(S\) 的仿射子空间指的是陪集 \(b+S\) (\(b\in\R^n\)), 其维数定义为 \(S\) 的维数.

任给 \(\R^n\) 中互异的 \(k+1\) 个点 \(v_0,\dots,v_k\). 只要 \(n\geq k\), 总存在 \(k\) 维仿射子空间包含 \(\{v_0,\dots,v_k\}\). 如果不存在小于 \(k\) 维的仿射子空间包含 \(\{v_0,\dots,v_k\}\), 则称 \(\{v_0,\dots,v_k\}\) 是仿射无关的, 或在一般位置的 (in general position).

Claim 20.1 (仿射无关的刻画) 对于 \(k+1\) 个互异的点 \(v_0,\dots,v_k\in\R^n\), TFAE:

1. \(\{v_0,\dots,v_k\}\) 仿射无关.

2. \(\{v_1-v_0,\dots,v_k-v_0\}\) 线性无关.

3. 若实数 \(c_0,\dots,c_k\) 使得 \[ \sum_{i=1}^kc_iv_i=0,\quad \sum_{i=1}^kc_i=0, \] 则 \(c_0=\dots=c_k=0\).

设仿射无关的 \(\{v_0,\dots,v_k\}\subset\R^n\), 它生成的单形/单纯形 (simplex) 定义为 \[ [v_0,\dots,v_k]:=\left\{ \sum_{i=0}^kt_iv_i \,\middle|\, t_i\geq0 \textsf{ 且 } \sum_{i=0}^kt_i=1 \right\}, \] 配以子空间拓扑. 对于 \(x=\sum t_iv_i\in[v_0,\dots,v_k]\), 非负实数 \(t_i\) 称为 \(x\) 关于 \([v_0,\dots,v_k]\) 的重心坐标 (barycentric coordinates). 点 \(v_i\) 称为单形的顶点 (vertex), 整数 \(k\) 称为单形的维数 (dimension).

• \(0\) 维单形是一个点, \(1\) 维单形是一条线段, \(2\) 维单形是一个三角形及内部, \(3\) 维单形是一个四面体及内部.

• 闭区间 \([a,b]\subset\R\) 是一个以 \(a,b\) 为顶点的单形. 单形的符号是闭区间符号的推广.

• 标准 \(k\) 维单形 (standard \(k\)-simplex) 定义为 \(\Delta_k:=[e_0,\dots,e_k]\subset\R^k\), 其中 \(e_0=0\), \(e_i\) 是 \(\R^k\) 的第 \(i\) 个标准基向量 \((0,\dots,1,\dots,0)\).

• 任何 \(k\) 维单形 \(\sigma=[v_0,\dots,v_k]\) 都同胚于 \(\Delta_k\): \[ \Align{ F:\Delta_k &\overset\sim\to \sigma, \\ (t_1,\dots,t_k) &\mapsto t_0v_0+t_1v_1+\dots+t_kv_k, } \] 其中 \(t_0=1-\sum_{i=1}^kt_i\). 这是一个连续的双射, 根据闭映射引理, \(F\) 是同胚.

对于 \(W\subset\R^n\), 它的凸包 (convex hull) 是包含 \(W\) 的所有凸集的交集, 也就是包含 \(W\) 的最小凸集.

• 集合 \(W\) 是凸集, 当且仅当它的凸包等于 \(W\) 自身.
• 根据定义容易验证, 单形是凸的, 因此其凸包等于自身.

Claim 20.2 \(k\) 维单形是一个 \(k\) 维闭胞腔.

Pf 因为任意 \(k\) 维单形都同胚于标准单形 \(\Delta_k\), 所以只需考虑后者. 因为 \(\Delta_k\) 是 \(\R^k\) 的凸紧子集, 其内部是重心坐标严格正 \(t_i>0\) 的点, 根据 Claim 17.1, \(\Delta_k\) 是 \(k\) 维闭胞腔.

接下来的一些定义也是很直观的.

设 \(k\) 维单形 \(\sigma\). 由 \(\sigma\) 的若干 (至少一个) 顶点生成的单形称为 \(\sigma\) 的一个面 (face). 真包含于 \(\sigma\) 的面称为真面 (proper face). 零维的面就是顶点, 一维的面称为边 (edge).

\(k\) 维单形 \(\sigma\) 的 \((k-1)\) 维面称为边界面 (boundary face). 因为 \(\sigma\) 是闭胞腔, 它是一个 \(k\) 维紧带边流形. 它的流形边界 \(\partial\sigma\) 是所有边界面的并 (也等于所有真面的并), 称为它的边界 (boundary); 它的内部 (interior) 是它减去它的边界. 一个 \(k\) 维开单形 (open simplex) 指的是 \(k\) 维单形的内部: (把单形定义中的 \(t_i\geq0\) 换成 \(t_i>0\)) \[ \left\{ \sum_{i=0}^kt_iv_i \,\middle|\, t_i>0 \textsf{ 且 } \sum_{i=0}^kt_i=1 \right\}, \]

• 注意, 当 \(k<n\) 时, \(k\) 维开单形并非 \(\R^n\) 中的开集, 其边界 (等于流形边界) 和内部 (等于流形内部) 不等于其拓扑边界/内部. (实际上, 其拓扑边界是它自身, 拓扑内部为空.)

欧氏空间 \(\R^n\) 中的一个 (欧氏) 单纯复形 (simplicial complex) 指的是 \(\R^n\) 中的单形族 \(K\), 满足:

1. 对 \(\sigma\in K\), 则 \(\sigma\) 的每个面都在 \(K\) 中.
2. \(K\) 中两个单形的交或者为空, 或者为它们的公共面.
3. \(K\) 是局部有限的.

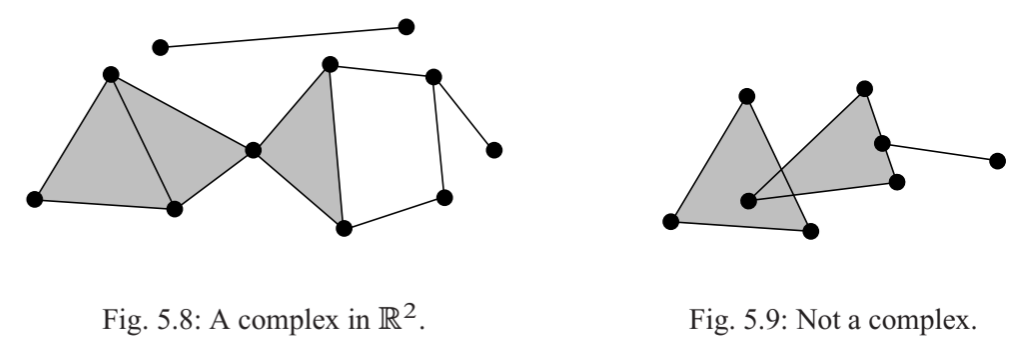
局部有限性蕴含 \(K\) 的可数性. 因为对于 \(\R^n\) 中任意一点 \(p\), 存在邻域 \(U_p\) 与有限个单形相交; 所有 \(U_p\) 组成 \(\R^n\) 的开覆盖, 它有可数子覆盖, 意味着 \(K\) 是可数的. 我们感兴趣的主要是有限单纯复形, 即只包含有限个单形的单纯复形. 此时条件 3 是多余的.

对于 \(\R^n\) 中的单纯复形 \(K\), 其维数定义为其中单形的最大维数, 这显然不超过 \(n\). 复形 \(K\) 的一个子复形指的是满足条件 1 的子集 \(S\subset K\) (它自动满足 2, 3). 对于 \(k\leq n\), \(K\) 的所有不超过 \(k\) 维的单形组成的子复形称为 \(K\) 的 \(k\) 维骨架.

对于 \(\R^n\) 中的单纯复形 \(K\), 它的承载空间 (underlying space) 定义为 \(|K|:=\bigcup_{\sigma\in K}\sigma\).

Claim 20.3 设欧氏单纯复形 \(K\), 则 \(K\) 中所有单形的内部组成的集族构成 \(|K|\) 的正则 CW 分解.

Pf 根据 Claim 17.1, 对 \(k\) 维单形 \(\sigma\in K\) (视作 \(\R^k\) 的子空间), 有同胚 \(\Phi:\overline{\mathbb{B}^k}\overset\sim\to\sigma\), 将 \(\mathbb{S}^{k-1}\) 映到 \(\sigma\) 的边界, 将 \(\mathbb{B}^k\) 映到 \(\sigma\) 的内部. 注意 \(\sigma\) 的边界由 \((k-1)\) 维单形组成, 因此 \(\Phi\) 是特征映射. 记 \(K\) 中单形的内部组成的集族为 \({\cal E}\), 根据条件 2, \({\cal E}\) 中的集合不交, 因此 \({\cal E}\) 构成 \(|K|\) 的胞腔分解.

由条件 3, \({\cal E}\) 是局部有限的, 结合 Claim 17.3, \({\cal E}\) 是 CW 分解. 因为 \(\Phi\) 将 \(\overline{\mathbb{B}^k}\) 同胚地映到 \(\sigma\) 的内部的闭包, 所以 \(\cal E\) 是正则 CW 分解.

这里有一个术语上的区别. "CW 复形" 指的是一个拥有 "CW 分解" (开胞腔族) 的拓扑空间 \(X\); 而 "单纯复形" 指的是闭胞腔族 \(K\), "承载空间" \(|K|\) 才是一个拓扑空间.

根据 Claim 20.3, 所有 CW 复形的理论可以应用于 \(|K|\) 上. 例如, \(|K|\) 紧当且仅当 \(K\) 是有限的; \(|K|\) 连通当且仅当其 \(1\) 维骨架是连通的.

• 一个 \(n\) 维单形 \(\sigma\) 及其所有面组成了一个 \(n\) 维单纯复形, 其承载空间同胚于 \(\overline{\mathbb{B}^n}\).
• \(\sigma\) 的所有真面组成的单纯复形 (即 \(\sigma\) 的边界) 是一个 \((n-1)\) 维单纯复形, 同胚于 \(\mathbb{S}^{n-1}\).
• (正多边形) 对 \(m\geq3\), 记 \(P_m\) 是平面上的正 \(m\) 边形. \(P_m\) 的所有顶点与边构成一个单纯复形, 其承载空间同胚于 \(\mathbb{S}^1\).
• (实数轴) 之前构造过 \(\R\) 的正则 CW 分解 (所有整数与单位区间 \((n,n+1)\) 组成), 而所有整数与单位闭区间 \([n,n+1]\) 则组成了一个以 \(\R\) 为承载空间的 \(1\) 为单纯复形.

设 \(X\) 是拓扑空间, \(X\) 到某单纯复形的承载空间 \(|K|\) 的同胚称为 \(X\) 的三角剖分 (triangulation). 从一维流形分类定理看出, 一维流形都是可三角剖分的.

Claim 20.4 (二维流形的三角剖分) 二维流形上存在三角剖分.

该定理的证明技术性很强. 其思想大致与 Claim 19.1 的证明相同, 即用正则坐标球覆盖流形 \(M\), 归纳地说明每个坐标球上存在三角剖分, 且与已经定义的三角剖分相容. 然而找到这样一种相容的剖分十分困难, 因为坐标球的边界可能与 (已经定义好的) 单形的边界相交无穷多次. 证明的过程需要用一些精妙的拓扑定理, 这超出了本书范围, 故略去.

根据定义, 可以得到二维流形的三角剖分 \(\varphi:M\overset\sim\to|K|\) 的一些性质:

• \(K\) 由一些 \(2\) 维单形 (三角形) 及其所有面 (边和顶点) 组成.
• \(K\) 中任两个 \(2\) 维单形的交集或者为空, 或者为其公共面 (边或顶点).
• \(K\) 中任意 \(1\) 维单形恰好是两个 \(2\) 维单形的公共面.

空间中的正多面体都能看成球面 \(\mathbb{S}^2\) 的三角剖分, 其他三角剖分的例子:

实际上, 任意三维流形也能被三角剖分 (由 Edwin Moise 在 1950 年代证明).

Claim 20.5 (三维流形的三角剖分) 三维流形上存在三角剖分.

然而, 当 \(n\geq3\) 时, 情况变得复杂. 在二十世纪末, 人们发现了不存在三角剖分的四维流形; 更高维流形上三角剖分的存在性仍是未知的. 单纯复形的拓扑信息完全地以组合的方式呈现, 因此能将拓扑问题 (对流形的研究) 简化为组合问题 (对单纯复形的研究). 单纯复形和三角剖分是组合拓扑 (combinatorial topology) 的重要研究对象.

一个流形上可能有许多三角剖分, 我们想要知道哪些剖分是 "等价" 的, 于是引入下面的概念.

设单纯复形 \(K\), 它的一个细分 (subdivision) 指的是满足如下条件的单纯复形 \(K'\):

1. \(|K'|=|K|\),
2. 对于任意 \(\sigma'\in K'\), 存在 \(\sigma\in K\), 使得 \(\sigma'\subset\sigma\).

此时, \(K\) 中的每个单形都是 \(K'\) 中的一些单形之并. 如果两个单纯复形有相同的细分, 则称它们是组合等价的 (combinatorially equivalent). Ernst Steinitz 和 Heinrich Tietze 在 1908 年提出猜想:

• 若两个单纯复形的承载空间是同胚的, 则它们是组合等价的.

它的等价表述是:

• 任意可被三角剖分的空间, 其不同的三角剖分是组合等价的.

这个猜想称为 "组合拓扑的主猜想 (Hauptvermugung)". 这个猜想的二维和三维情形是成立的, 但是对于任意更高的维数都不成立.

20.2 Simplicial maps

一个仿射映射 \(F:\R^n\to\R^m\) 是形如 \(F(x)=c+A(x)\) 的映射, 其中 \(c\in\R^m\), \(A:\R^n\to\R^m\) 为线性映射. 仿射映射是连续的.

• 仿射映射保持仿射组合: 若 \(\sum_{i=1}^kt_i=1\), 则 \(f(\sum_{i=1}^k t_iv_i)=\sum_{i=1}^kt_iF(v_i)\).

Claim 20.6 (顶点映射确定的仿射映射) 设 \(k\) 维单形 \(\sigma=[v_0,\dots,v_k]\subset\R^n\), 任给 \((k+1)\) 个点 \(w_0,\dots,w_k\in\R^m\), 对于任意仿射映射 \(F:\R^n\to\R^m\) 将 \(v_i\) 映到 \(w_i\), \(F|_\sigma\) 无关 \(F\) 的选取.

Pf 注意仿射映射 \(F\) 在 \(\sigma\) 上的限制 \(F|_\sigma\) 保持仿射组合: \[ F|_\sigma\pqty{\sum_{i=1}^k t_i v_i} =\sum_{i=1}^k t_i F|_\sigma(v_i) =\sum_{i=1}^k t_i w_i \] 这唯一确定了 \(F|_\sigma\).

我们称 \(f:=F|_\sigma:\sigma\to\R^m\) 是顶点映射 \(v_i\mapsto w_i\) 确定的仿射映射.

设单纯复形 \(K,L\), \(K_0,L_0\) 分别是其 \(0\) 维骨架 (顶点集). 一个从 \(K\) 到 \(L\) 的单纯映射 (simplicial map) 指的是连续映射 \(f:|K|\to|L|\), 满足 \(f\) 在任意单形 \(\sigma\in K\) 上的限制与某个将 \(\sigma\) 映到 \(\tau\in L\) 的仿射映射相同. (根据上面的定理, 这个 \(f|_\sigma\) 由单形 \(\sigma,\tau\) 唯一确定.) \(f\) 在 \(K_0\) 的限制 \(f_0:K_0\to L_0\) 称为 \(f\) 的顶点映射 (vertex map). 构成同胚的单纯映射称为单纯同构 (simplicial isomorphism).

Claim 20.7 (单纯映射由顶点映射唯一确定) 设单纯复形 \(K,L\), 映射 \(f_0:K_0\to L_0\) 满足:

• 若 \(\{v_0,\dots,v_k\}\) 是 \(K\) 中某单形的顶点, 则 \(\{f_0(v_0),\dots,f_0(v_k)\}\) 是 \(L\) 中某单形的顶点 (可重复).

则存在唯一以 \(f_0\) 为顶点映射的单纯映射 \(f:|K|\to|L|\). 此外, \(f\) 是单纯同构当且仅当 \(f_0\) 满足:

• \(\{v_0,\dots,v_k\}\) 是 \(K\) 中某单形的顶点, 当且仅当 \(\{f_0(v_0),\dots,f_0(v_k)\}\) 是 \(L\) 中某单形的顶点.

20.3 Abstract simplicial complexes

下面简单地介绍抽象单形, 它将一个欧氏单形的拓扑信息完全以组合方式呈现出来.

Claim 20.7 表明, 要 (在同构意义下) 确定一个单纯复形, 只需要给出两个信息: 其所有顶点以及哪些顶点张成单形. 受此启发, 我们给出如下定义.

一个抽象单纯复形 (abstract simplicial complex) 指的是非空有限集的集族 \({\cal K}\), 满足: 若 \(s\in{\cal K}\), 则 \(s\) 的任意非空子集也在 \({\cal K}\) 中. \({\cal K}\) 中的集合 \(s\) 称为抽象单形, \(s\) 中的元素称为 \(s\) 的顶点, \(s\) 的非空子集称为其面. \(s\) 的维数定义为 \(|s|-1\). 如果 \({\cal K}\) 中抽象单形的维数有上界, 则称 \({\cal K}\) 是有限维的, 其维数是 \(s\in{\cal K}\) 维数的最大值.

若 \({\cal K}\) 是有限集, 则称之为有限复形; 若每个顶点只属于有限个抽象单形, 则称 \({\cal K}\) 为局部有限复形.

抽象单形 \({\cal K}\) 的顶点集定义为 \[ {\cal K}_0 = \bigcup_{s\in{\cal K}} s. \] 设 \({\cal K},{\cal L}\) 是抽象单纯复形. 映射 \(f:{\cal K}\to{\cal L}\) 称为抽象单纯映射 (abstract simplicial map), 若存在映射 \(f_0:{\cal K}_0\to{\cal L}_0\), 使得 \[ f(\{v_0,\dots,v_k\}) = \{f_0(v_0),\dots,f_0(v_k)\} \] 其中 \(f_0\) 称为 \(f\) 的顶点映射, 需满足: 只要 \(\{v_0,\dots,v_k\}\in{\cal K}\), 则 \(\{f_0(v_0),\dots,f_0(v_k)\}\in{\cal L}\). 若 \(f_0,f\) 都是双射, 则称 \(f\) 是同构. 此时, \(f^{-1}\) 也是抽象单纯映射.

欧氏单纯复形 \(\rightarrow\) 抽象单纯复形. 给定欧氏单纯复形 \(K\), 记 \({\cal K}\) 是 \(K\) 中所有单形的顶点集组成的集族, 则 \({\cal K}\) 构成抽象单纯复形, 称为 \(K\) 的顶点概形 (vertex scheme). 根据 Claim 20.7, 两个欧氏单纯复形同构, 当且仅当其顶点概形同构.

欧氏单纯复形 \(\leftarrow\) 抽象单纯复形. 给定抽象单纯复形 \({\cal K}\), 如果某欧氏单纯复形 \(K\) 的顶点概形同构于 \({\cal K}\), 则称 \(K\) 是 \({\cal K}\) 的一个几何实现 (geometric realization).

Claim 20.8 有限的抽象单纯复形存在几何实现.

Pf 将 \({\cal K}\) 中的顶点一一列出: \(v_1,\dots,v_m\), 令 \(K\subset\R^m\) 是以 \(\{e_1,\dots,e_m\}\) 为顶点的欧氏单纯复形, 且 \([e_{i_1},\dots,e_{i_k}]\in K\) 当且仅当 \(\{e_{i_1},\dots,e_{i_k}\}\in{\cal K}\). 容易验证 \(K\) 满足欧氏单纯复形的定义, 且其顶点概形同构于 \({\cal K}\).

一些例子:

• \(\{0,1,2,\dots,n\}\) 的所有非空子集构成抽象单纯复形, 其几何实现同胚于 \(\overline{\mathbb{B}^n}\).

• \(\{0,1,2,\dots,n\}\) 的所有非空真子集构成抽象单纯复形, 其几何实现同胚于 \(\mathbb{S}^{n-1}\).

• (抽象正多边形) 对 \(n\geq3\), 记 \({\cal K}_m\) 是以 \(\{\{1\},\{2\},\dots,\{m\}\}\) 为 \(0\) 维抽象单形, 以 \[ \{\{1,2\},\{2,3\},\dots,\{m-1,m\},\{m,1\}\} \] 为 \(1\) 维抽象单形的抽象单纯复形. \({\cal K}_m\) 的几何实现同胚于 \(\mathbb{S}^1\).

• (抽象实数轴) 记 \({\cal R}\) 是所有 \(\{n\}\) 和 \(\{n,n+1\}\) (\(n\in\Z\)) 组成的集族, 它的几何实现同胚于 \(\R\).