GTM202 | 6 胞腔复形

GTM202 (Introduction to Topological Manifolds) Chapter 5 的笔记.

17 Cell Complexes & CW Complexes

胞腔复形是一类很重要也具有一般性的拓扑空间, 可以看作不断地将 \(n\) 维闭球 (更一般地, \(n\) 维胞腔) 沿着其边界粘贴到一个拓扑空间上所得. 我们最关心的一类胞腔复形是 CW 复形, 即向胞腔复形附加两个额外条件所得, 使得其拓扑性质与胞腔的拓扑性质关系更紧密.

17.1 Cells

一个同胚于 \(\mathbb{B}^n\) 的拓扑空间称为 \(n\) 维开胞腔 (open \(n\)-cell); 同胚于 \(\overline{\mathbb{B}^n}\) 的拓扑空间称为 \(n\) 维闭胞腔 (closed \(n\)-cell).

Claim 17.1 (凸紧子集是胞腔) 设内部非空的凸紧子集 \(D\subset\R^n\), 则 \(D\) 是一个 \(n\) 维闭胞腔, \({\rm Int}D\) 是一个 \(n\) 维开胞腔. 实际上, 任给 \(p\in{\rm Int}D\), 存在同胚 \(F:\overline{\mathbb{B}^n}\to D\) 将 \(0\) 映到 \(p\), 将 \(\mathbb{B}^n\) 映到 \({\rm Int}D\), 将 \(\mathbb{S}^{n-1}\) 映到 \(\partial{D}\).

Pf 通过平移 \(x\mapsto x-p\), 不妨设 \(0=p\in{\rm Int}D\). 因为 \(p\) 是内点, 开球 \(B_\varepsilon(0)\subset D\). 通过缩放 \(x\mapsto x/\varepsilon\), 有 \(\mathbb{B}^n=B_1(0)\subset D\).

核心是证明: 从原点出发的射线 \(R\) 与 \(\partial{D}\) 恰好交于一点. 因为 \(D\) 紧, 其与 \(R\) 的交是紧的, 因此存在 \(x_0\in D\cap R\) 使得 \(\|x_0\|\) 取最大值. 根据凸性, \(x_0\) 一定在 \(\partial{D}\) 中. 为了证明 \(D\cap R\) 只能有这一个点, 我们证明连接 \(0\) 与 \(x_0\) 的开线段完全在 \({\rm Int}D\) 中. 开线段上的任意一点可写作 \(\lambda x_0\), \(0<\lambda<1\). 设 \(z\in B_{1-\lambda}(\lambda x_0)\), 令 \(y=(z-\lambda x_0)/(1-\lambda)\), 直接的计算表明 \(\|y\|<1\), 即 \(y\in\mathbb{B}^n\subset D\). 注意 \(x_0,y\) 都在 \(D\) 中, 而 \(z=\lambda x_0+(1-\lambda)y\), 由凸性, \(z\) 也在 \(D\) 中. 这说明 \(B_{1-\lambda}(\lambda x_0)\subset D\), 即 \(\lambda x_0\) 是内点.

现在可以定义映射 \(f:\partial{D}\to\mathbb{S}^{n-1}\), \[ f(x) = \frac{x}{\|x\|}, \] 即将点 \(x\) 映到射线 \(R\) 与单位球面的交点, 是一个双射. \(f\) 作为连续映射在的限制, 是连续的. 因为 \(\partial{D}\) 紧, \(\mathbb{S}^{n-1}\) Hausdorff, 由闭映射引理, \(f\) 是闭映射, 因而是同胚.

最后, 定义 \(F:\overline{\mathbb{B}^n}\to D\), \[ F(x)=\Cases{ \|x\| f^{-1}\pqty{\dfrac{x}{\|x\|}}, & x\neq0, \\ 0, & x=0. } \] \(f\) 的连续性保证 \(F\) 在原点以外的连续性; 又因为 \(f^{-1}\) 有界, 所以当 \(x\to0\), \(F(x)\to0\), 即在原点连续. 从几何上看, \(F\) 将连接 \(0\) 与 \(\omega\in\mathbb{S}^{n-1}\) 的线段线性地映到连接 \(0\) 与 \(f^{-1}(\omega)\in\partial{D}\) 的线段, 根据凸性, \(F\) 的值域在 \(D\) 中. 易见 \(F\) 是双射. 根据闭映射引理, \(F\) 是同胚.

设 \(D\) 是 \(n\) 维闭胞腔, 则 \(D\cong\overline{\mathbb{B}^n}\) 是带边流形. 以 \(\partial{D},{\rm Int}D\) 分别表示 \(\mathbb{S}^{n-1}\) 和 \(\mathbb{B}^n\) 在同胚 \(F:D\overset\sim\to\overline{\mathbb{B}^n}\) 下的像. 于是 \({\rm Int}D\cong\mathbb{B}^n\) 是 \(n\) 维开胞腔, \(\partial{D}\cong\mathbb{S}^{n-1}\).

Claim 17.2 (边界映射扩张到胞腔映射) 设闭胞腔 \(D,D'\), 取定 \(p\in{\rm Int}D,p'\in{\rm Int}D'\), 连续映射 \(f:\partial{D}\to\partial{D'}\). 则 \(f\) 扩张到连续映射 \(F:D\to D'\) 满足 \(F({\rm Int}D)\subset{\rm Int}D'\) 且 \(F(p)=p'\). 如果 \(f\) 是同胚, 则 \(F\) 可以取为同胚.

Pf 设同胚 \(G:D\overset\sim\to\overline{\mathbb{B}^m}\), \(G':D'\overset\sim\to\overline{\mathbb{B}^n}\). 我们的想法是通过构造 \(\overline{\mathbb{B}^m},\overline{\mathbb{B}^n}\) 间的映射来给出 \(F\).

因为 \(\partial{D},\partial{D}'\) 分别同胚于 \(\mathbb{S}^{m-1},\mathbb{S}^{n-1}\), 所以 \(f\) 唯一确定了连续映射 \(\beta:\mathbb{S}^{m-1}\to\mathbb{S}^{n-1}\), 满足 \(\alpha\circ G = G'\circ f\). 将 \(\beta\) 拓展到连续映射 \(B:\overline{\mathbb{B}^m}\to\overline{\mathbb{B}^n}\), 定义为 \[ B(x)=\Cases{ \|x\|\beta\pqty{ \dfrac{x}{\|x\|} }, &x\neq0, \\ 0, & x=0. } \] 当 \(x\to0\) 时, \(B(x)\to0\), 因此 \(B\) 是连续的.

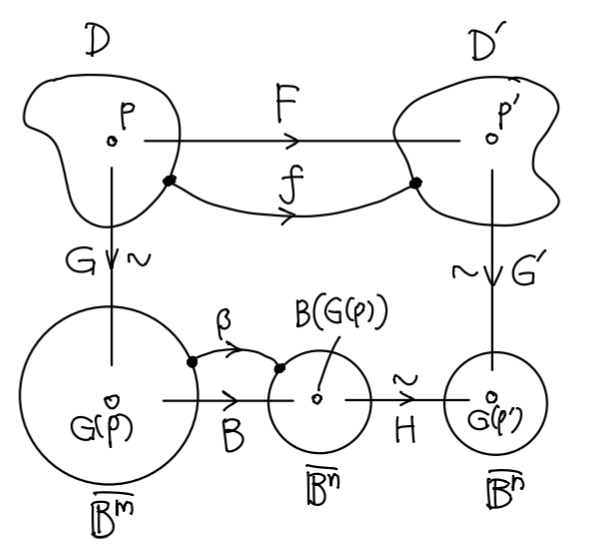
为了让 \(p,p'\) 对应, 利用 Claim 17.1, 存在 (保持边界与内部的) 同胚 \(H:\overline{\mathbb{B}^n}\overset\sim\to\overline{\mathbb{B}^n}\) 将 \(B(G(p))\) 映到 \(G'(p')\) (这两个点都在球的内部, 满足定理的假设). 复合映射 \[ F:=G' \circ H \circ B \circ G : D\to D' \] 即为所求. 如果 \(f\) 是同胚, 则 \(\beta\) 是同胚, 容易看出 \(B\) 也是同胚, 所以 \(F\) 是同胚.

17.2 Cell complexes

设 \(X\) 是非空拓扑空间, \(X\) 的一个胞腔分解 (cell decomposition) 指的是 \(X\) 的划分 \(\cal E\), 满足

1. \(\cal E\) 由开胞腔组成.
2. 对任意维数 \(n\geq1\) 的开胞腔 \(e\in\cal E\), 存在 \(n\) 维闭胞腔 \(D\) 与连续映射 \(\Phi:D\to X\), 它将 \({\rm Int}D\) 同胚地映到 \(e\), 将 \(\partial{D}\) 映到 \(\cal E\) 中维数小于 \(n\) 的所有胞腔之并. (映射 \(\Phi\) 称为 \(e\) 的特征映射.)

胞腔复形 (cell complex) 指的是拥有一个胞腔分解的 Hausdorff 空间 \(X\). 胞腔复形称为有限的, 若胞腔分解是有限集; 称为局部有限的, 若胞腔分解局部有限 (这等价于 \(\overline{\cal E}=\{\overline{e}\mid e\in{\cal E}\}\) 局部有限).

一般来说, \(X\) 的开胞腔 \(e\in\cal E\) 不一定是开集; 开胞腔的闭包 \(\overline{e}\) 也不一定是闭胞腔.

设胞腔复形 \((X,{\cal E})\). 根据闭映射引理, 特征映射 \(\Phi:D\to X\) 是闭映射. 根据连续映射的等价刻画, 特征映射的像集 \[ \Phi(D) = \Phi(\overline{{\rm Int}D}) = \overline{\Phi({\rm Int}D)} = \overline{e}, \] 因为 \(D\) 紧, 所以 \(\overline{e}\) 紧, 即 \(e\) 是预紧的.

• 特征映射的行为: \({\rm Int}D\overset\sim\rightarrow e\) 以及 \(\partial{D}\to\overline{e}\setminus e\) (由若干低维胞腔覆盖).
• 注意 \(\Phi\) 在 \(\partial{D}\) 上不一定单, 所以 \(\overline{e}\) 不一定是闭胞腔 (不一定同胚于 \(D\)).

17.3 CW complexes

回顾不交并拓扑: 设拓扑空间族 \((X_\alpha)\) 的不交并 \(\coprod X_\alpha\). 子集 \(U\subset\coprod X_\alpha\) 开, 当且仅当所有 \(U\cap X_\alpha\) 是 \(X_\alpha\) 的开子集. 不交并拓扑是满足包含映射 \(X_\alpha\hookrightarrow\coprod X_\alpha\) 连续的最强拓扑. 下面的定义可以看作不交并拓扑的推广.

设拓扑空间 \(X\), 子空间族 \({\cal B}\) 构成 \(X\) 的覆盖. 我们说 \(X\) 的拓扑与 \({\cal B}\) 连贯 (coherent), 若对任意子集 \(U\subset X\), \(U\) 是开集当且仅当对任意 \(B\in{\cal B}\), \(U\cap B\) 是 \(B\) 的开子集.

• 根据子空间拓扑的定义, 若 \(U\) 是开集, 则 \(U\cap B\) 由定义是开集. 因此, 只有反向的蕴含关系是需要验证的: 若 \(U\) 与任意 \(B\) 的交是 \(B\) 的开子集, 则 \(U\) 是开集.
• 等价地, 可将定义中的 "开" 全部换成 "闭".
• 拓扑空间 \(X\) 与其任意开覆盖, 或任意局部有限闭覆盖连贯. Gluing lemma 可以推广到任意与 \(X\) 连贯的覆盖.

Claim 17.3 (连贯拓扑的性质) 空间 \(X\) 的拓扑与子空间族 \({\cal B}\) 连贯.

1. 映射 \(f:X\to Y\) 连续, 当且仅当对任意 \(B\in\cal B\), \(f|_B\) 连续.
2. 包含映射 \(B\hookrightarrow X\) 的不交并 \(\coprod_{B\in\cal B}B\to X\) 是商映射.
3. \(X\) 的拓扑是使得包含映射 \(B\hookrightarrow X\) (\(B\in\cal B\)) 连续的最强拓扑.

CW 复形指的是满足下面两个条件的复形 \((X,{\cal E})\):

• (闭包有限, closure finiteness) 任意胞腔的闭包可被有限多个胞腔覆盖.
• (弱拓扑, weak topology) \(X\) 的拓扑与闭子集族 \(\overline{\cal E}\) 连贯.
  • 历史上, 拓扑强弱的概念曾与现在相反. 这里的 "弱拓扑" 现在看来是 "强拓扑": \(X\) 的拓扑是使得包含映射 \(\overline{e}\to X\) 连续的最强拓扑.

Claim 17.4 (局部有限复形是 CW 复形) 局部有限胞腔复形 \((X,{\cal E})\) 是 CW 复形.

Pf (C), 任给 \(e\in\cal E\), 闭包 \(\overline{e}\) 中的每一点 \(p\) 都有一个邻域 \(U_p\), 使得 \(U_p\) 只与有限个胞腔相交. 因为 \(\overline{e}\) 是紧的, 所以 \(\overline{e}\) 可以被有限个这样的 \(U_p\) 覆盖.

(W), 设 \(A\subset X\) 与任意 \(\overline{e}\) 的交是 \(\overline{e}\) 的闭子集, 要证明 \(A\) 是闭的. 任给 \(x\in X\setminus A\), (因为 \({\cal E}\) 局部有限, 所以 \(\overline{\cal E}\) 局部有限) 设 \(x\) 的 \(W\) 只与 \(\overline{\cal E}\) 中有限个闭集相交, 记为 \(\overline{e_1},\dots,\overline{e_m}\). 因为 \(A\cap\overline{e_i}\) 在 \(\overline{e_i}\) 中闭, 所以也在 \(X\) 中闭, 于是 \[ W\setminus A=W\setminus\big( (A\cap\overline{e_1})\cup\cdots\cup(A\cap\overline{e_m}) \big) \] 是 \(x\) 的包含于 \(X\setminus A\) 的邻域. 因此 \(X\setminus A\) 开, 即 \(A\) 闭.

若存在整数 \(n\), 使得 \(X\) 的任意胞腔的维数不超过 \(n\), 则称 \(X\) 是有限维的; 否则称 \(X\) 是无限维的. 对有限维的 \(X\), 它的维数定义为其胞腔的维数的最大值.

Claim 17.5 (最高维开胞腔是开集) 设 \(n\) 维 CW 复形 \(X\), 则所有 \(n\) 维胞腔都是开集.

Pf 设 \(e_0\in{\cal E}\) 是 \(n\) 为胞腔. 我们利用条件 (w) 来证明它是开集, 即证明 \(e_0\) 与任意胞腔的闭包交为开集.

一方面, 设 \(\Phi:D\to X\) 是 \(e_0\) 的特征映射, 将其视作紧空间 \(D\) 到 Hausdorff 空间 \(\overline{e_0}\) 的满射, 根据闭映射引理, 它是商映射. 因为 \(\Phi^{-1}(e_0)={\rm Int}D\) 在 \(D\) 中开, 所以 \(e_0\) 在 \(\overline{e_0}\) 中开.

另一方面, 任给其他的胞腔 \(e\in{\cal E}\), 则 \(e_0\cap e=\emptyset\), 因此 \(e_0\cap\overline{e}\) 包含于 \(\overline{e}\setminus e\), 进而被有限多个维数小于 \(n\) 的胞腔覆盖. 但 \(e_0\) 的维数为 \(n\), 所以 \(e_0\cap\overline{e}=\emptyset\) 是开集.

胞腔复形 \((X,{\cal E})\) 的子复形是一些胞腔之并 \(Y\subset X\), 满足 \(Y\) 中胞腔的闭包仍在 \(Y\) 中 (因此特征映射是有意义的). 子复形的任意交和任意并仍是子复形. 对自然数 \(n\), 定义 \(X\) 的 \(n\) 维骨架 (\(n\)-skeleton) \(X_n\) 是所有维数小于等于 \(n\) 的胞腔组成的子复形.

Claim 17.6 (子 CW 复形) 设 CW 复形 \(X\), 若 \(Y\) 是 \(X\) 的子复形, 则 \(Y\) 是闭子集, 且在子空间拓扑与继承自 \(X\) 的胞腔分解下, \(Y\) 构成 CW 复形.

Pf 作为子空间, \(Y\) Hausdorff; 由定义, \(Y\) 是其胞腔的无交并. 因为对任意胞腔 \(e\subset Y\), 有 \(\overline{e}\subset Y\), 所以 \(e\) 在 \(X\) 中的特征映射 \(\Phi\) 可以作为 \(e\) 在 \(Y\) 中的特征映射. 所以 \(Y\) 构成胞腔.

(C), 任给胞腔 \(e\subset Y\), 有 \(\overline{e}\subset Y\), 所以所有与 \(\overline{e}\) 相交的 \(X\) 的 (有限个) 胞腔也必须在 \(Y\) 中, 构成了 \(\overline{e}\) 由 \(Y\) 中胞腔的有限覆盖.

(W), 设 \(S\subset Y\) 满足 \(S\cap\overline{e}\) 是 \(\overline{e}\) 的闭集 (对任意 \(Y\) 中胞腔 \(e\)). 设 \(e\) 是 \(X\) 的胞腔且不在 \(Y\) 中, 根据 \(X\) 的闭有限性, \(\overline{e}\setminus e\) 由有限个 \(X\) 的胞腔覆盖, 其中那些也在 \(Y\) 中的胞腔记作 \(e_1,\dots,e_k\). 于是 \(\overline{e_1}\cup\cdots\cup\overline{e_k}\subset Y\), 且 \[ S\cap\overline{e} =S\cap(\overline{e_1}\cup\cdots\cup\overline{e_k})\cap\overline{e} =\big( (S\cap\overline{e_1})\cup\cdots\cup(S\cap\overline{e_k}) \big) \cap\overline{e}, \] 这是 \(\overline{e}\) 的闭子集 (首先 \(S\cap\overline{e_i}\) 是 \(\overline{e_i}\) 的闭子集, 进而也是 \(X\) 的闭子集; 其有限并也是闭子集; 再由 \(X\) 与 \(\overline{\cal E}\) 的连贯性, 这闭子集与 \(\overline{e}\) 的交是 \(\overline{e}\) 的闭集). 由连贯性, \(S\) 是 \(X\) 的闭子集, 进而是 \(Y\) 的闭子集 (子空间拓扑).

最后, 要说明 \(Y\) 是 \(X\) 的闭子集, 对 \(S=Y\) 应用前一段论证即可.

Claim 17.7 (骨架族) 设 CW 复形 \(X\), 则 \(X\) 与骨架族 \(\{X_n\mid n\in\N\}\) 连贯.

Pf 任给 \(S\subset X\) 满足 \(S\cap X_n\) 是 \(X_n\) 的闭子集. 任给 \(n\) 维胞腔 \(e\subset X_n\), 因为 \(\overline{e}\) 是 \(X\) 的闭子集, 所以也是 \(X_n\) 的闭子集, 因此 \[ S\cap\overline{e} = (S\cap X_n)\cap\overline{e} \] 作为 \(X_n\) 两个闭子集的交, 也是 \(X_n\) 的闭子集, 进而是 \(\overline{e}\) 的闭子集. 应用 \(X\) 与 \(\overline{\cal E}\) 的连贯性, \(S\) 是 \(X\) 的闭子集, 即证.

我们知道, 开胞腔 \(e\in{\cal E}\) 的特征映射 \(\Phi:D\to X\) 将 \({\rm Int}D\) 同胚地映到 \(e\); 将 \(D\) 映到 \(\overline{e}\), 但不一定同胚. 如果 存在特征映射 \(\Phi\) 将 \(D\) 同胚地映到 \(\overline{e}\), 则称 \(e\) 是一个正则胞腔 (regular cell).

• 正则胞腔 \(e\in{\cal E}\) 的内部同胚于 \(D\) 的内部; 边界同胚于 \(D\) 的边界; 闭包同胚于 \(D\) (因此 \(\overline{e}\) 是闭胞腔).
• 对于正则胞腔, 可以选包含映射 \(\overline{e}\hookrightarrow X\) 为特征映射.
• 例子:
  • \(\R^n\) 的凸紧子集的内部是正则胞腔.
  • 流形 \(M\) 的正则坐标球是正则胞腔. (闭包同胚于坐标闭球.)

如果一个 CW 复形的所有胞腔都是正则的, 且任意胞腔的闭包是有限子复形, 则称之为正则 CW 复形.

CW 复形的例子.

• (\(0\) 维 CW 复形) \(0\) 维 CW 复形是离散空间; 它是有限复形当且仅当它是有限集.

• (实数轴, 正则) \(\R\) 的一个正则胞腔分解: \(0\) 维胞腔是所有整数点; \(1\) 维胞腔是单位区间 \((n,n+1)\), \(n\in\Z\), 其特征映射 \(\Phi_n:[n,n+1]\to\R\) 是包含映射.

• (圆束) 在 \(\mathbb{S}^1\) 上取定基点 \(p\), 称楔和 \(\mathbb{S}^1\vee\cdots\vee\mathbb{S}^1\) 是一个圆束 (bouquet of circles). 可以这样构造一个胞腔分解: 基点 \(p\) 是一个 \(0\) 维开胞腔; 每个 \(\mathbb{S}^1\setminus\{p\}\) 是一个 \(1\) 维开胞腔, 配以如下复合映射作为特征映射: \[ I \overset{\omega}\to \mathbb{S}^1 \overset{i_j}\hookrightarrow \mathbb{S}^1\amalg\dots\amalg\mathbb{S}^1 \to \mathbb{S}^1\vee\dots\vee\mathbb{S}^1, \] 其中 \(\omega\) 是闭区间 \([0,1]\) 到 \(\mathbb{S}^1\) 的商映射; \(i_j\) 是第 \(j\) 个 \(\mathbb{S}^1\) 到不交并空间的包含映射. 此时, 特征映射将 \((0,1)\) 同胚地映到 \(\mathbb{S}^1\setminus\{p\}\), 将 \(\{0,1\}\) 映到 \(\{p\}\).

• (图) 维数小于等于 \(1\) 的 CW 复形称为图 (graph), 其中 \(0\) 维胞腔称为顶点 (vertex), \(1\) 维胞腔称为边 (edge).

• (球面) \(\mathbb{S}^n\) 的一个胞腔分解, 只含有两个胞腔: 一个 \(0\) 维胞腔是北极点 \((0,\dots,0,1)\); 一个 \(n\) 维胞腔是商映射 \(q:\overline{\mathbb{B}^n}\to\mathbb{S}^n\), 将 \(\partial\overline{\mathbb{B}^n}\) 坍缩到一个点. \(q\) 将 \(\mathbb{B}^n\) 同胚地映到 \(\mathbb{S}^n\), 将 \(\partial\overline{\mathbb{B}^n}\) 映到北极点.

• (球面, 正则) \(\mathbb{S}^n\) 的一种正则胞腔分解. 首先, \(\mathbb{S}^0\) 是两个点, 具有两个 \(0\) 维胞腔. 用归纳法, 现假设我们已经构造出 \(\mathbb{S}^{n-1}\) 的胞腔分解, 其包含 \(0,1,\dots,n-1\) 维胞腔各两个. 将 \(\mathbb{S}^{n-1}\) 视作 \(\mathbb{S}^n\) 的子空间 (由方程 \(x_{n+1}=0\) 确定的子集), 注意到 \(\mathbb{S}^n\) 的南北两个开半球恰好是两个 \(n\) 维正则胞腔. 这两个 \(n\) 维胞腔和 \(\mathbb{S}^{n-1}\) 的胞腔分解合起来构成 \(\mathbb{S}^n\) 的胞腔分解, 包含 \(0,\dots,n\) 维胞腔各两个.

  对于 \(k=0,\dots,n\), \(\mathbb{S}^n\) 的 \(k\) 维骨架恰为 \(\mathbb{S}^k\).

不是 CW 复形的例子.

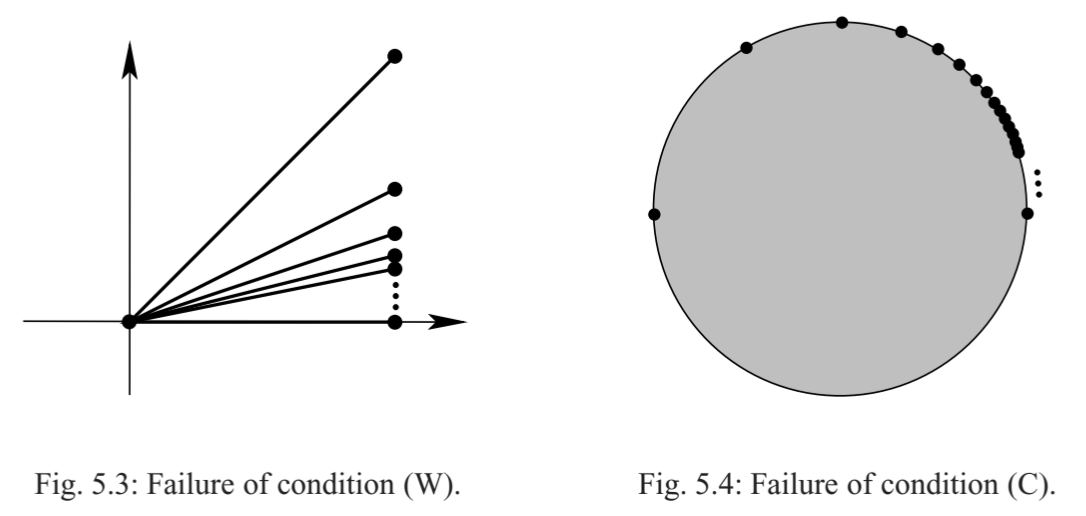
• (不满足 W) 设 \(X\subset\R^2\) 是所有连接 \((0,0)\) 与 \((0,1/n)\) (\(n\in\N^+\)) 的闭线段之并, 赋予子空间拓扑. 定义胞腔分解: \(0\) 维胞腔是点 \((0,0),(0,1),(1,1)\) 与 \((0,1/n)\) (\(n\in\N^+\)); \(1\) 维胞腔是所有线段去掉端点. 显然这个胞腔分解满足 C 条件; 但是它不满足 W 条件. 集合 \(\{(1/n,1/n^2)\mid n\in\N^+\}\) 和所有胞腔的闭包交集为闭, 但是它不是 \(X\) 的闭子集, 因为其极限点 \((0,0)\) 不在集合中.
• (不满足 C) 考虑 \(\overline{\mathbb{B}^2}\) 的一个胞腔分解: \(0\) 维胞腔是所有点 \(\e^{2\pi\i/n}\), \(n\in\N\); \(1\) 维胞腔是所有这些点间的弧; \(2\) 维胞腔是圆盘内部 \(\mathbb{B}^2\). 因为 \(2\) 维胞腔的闭包就是整个空间 \(\overline{\mathbb{B}^2}\), 所以条件 W 成立. 条件 C 不成立, 因为 \(2\) 维胞腔的闭包不能被有限多个胞腔覆盖.

18 Topological Properties of CW Complexes

18.1 Topological properties

CW 复形的连通性和道路连通性是等价的, 它们都由其骨架的连通性刻画.

Claim 18.1 (CW 复形的连通性) 设 CW 复形 \(X\), TFAE:

1. \(X\) 道路连通.
2. \(X\) 连通.
3. \(X\) 的 \(1\) 维骨架连通.
4. \(X\) 的某 \(n\) 维骨架连通.

下面讨论 CW 复形的紧性. 先给出两个引理.

Claim 18.2 (胞腔的闭包) CW 复形的任一胞腔的闭包包含于一个有限子复形.

Claim 18.3 (离散子集刻画) CW 复形 \(X\) 的子集 \(S\) 离散, 当且仅当 \(S\) 与每个胞腔的交是有限集.

Claim 18.4 (CW 复形的紧性) CW 复形 \(X\) 的子集 \(S\) 紧, 当且仅当 \(S\) 在 \(X\) 中闭, 且包含于一个有限子复形. 特别地, \(X\) 紧当且仅当它是一个有限复形.

Claim 18.5 (CW 复形的局部紧性) CW 复形局部紧当且仅当它局部有限.

18.2 Inductive construction

除了在给定的拓扑空间上选取一个胞腔分解外, 还可以归纳地来构造一个 CW 复形. 简单地说, 就是向一个离散空间上不断地粘贴 \(n\) 维胞腔 (\(n=1,2,\dots\)).

设非空拓扑空间 \(X\), 一族 \(n\) (\(n\geq1\)) 维闭胞腔 \(\{D_\alpha\}\), 且对每个 \(\alpha\), 有连续映射 \(\varphi_\alpha:\partial{D}_\alpha\to X\). 设贴映射 \[ \varphi:\coprod_\alpha \partial D_\alpha \to X, \] 其在每个 \(\partial{D}_\alpha\) 的限制是 \(\varphi_\alpha\). 我们把黏着空间 \(X\cup_\varphi(\coprod_\alpha D_\alpha)\) 叫做向 \(X\) 粘贴 \(n\) 维胞腔得到的空间.

Claim 18.6 (引理) 设 CW 复形 \(X\), 其胞腔 \(\{e_\alpha\}\) 和对应的特征映射 \(\Phi_\alpha:D_\alpha\to X\), 则特征映射的不交并 \(\Phi:\coprod_\alpha D_\alpha\to X\) 是商映射.

Claim 18.7 (骨架的构造) 设 CW 复形 \(X\), 则骨架 \(X_n\) 是向骨架 \(X_{n-1}\) 粘贴 \(n\) 维胞腔所得.

Claim 18.8 (CW 复形构造定理) 设拓扑空间链 \(X_0\subset X_1\subset X_2\subset\cdots\) 满足:

1. \(X_0\) 为非空的离散空间;
2. 对 \(n\geq1\), \(X_n\) 是向 \(X_{n-1}\) 粘贴 \(n\) 维胞腔所得;

则 \(X=\bigcup_nX_n\) 具有唯一的与 \(\{X_n\mid n\in\N\}\) 连贯的拓扑, 和唯一的胞腔分解, 使得它成为以 \(X_n\) 为骨架的 CW 复形.

• (无穷维球面) 我们知道, \(\mathbb{S}^n\) 是向 \(\mathbb{S}^{n-1}\) 粘贴两个 \(n\) 维胞腔所得的空间, 通过归纳法让这个过程一直进行下去, 我们得到了一个无穷维 CW 复形 \(\mathbb{S}^\infty=\bigcup_n\mathbb{S}^n\). 它包含有所有维数的胞腔各两个; 其骨架是所有球面 \(\mathbb{S}^n\) (\(n\in\N\)).

Claim 18.9 (CW 复形的仿紧性) CW 复形是仿紧的.

18.3 CW complexes as manifolds

Claim 18.10 (CW 复形的流形性质) 设 \(X\) 是具有可数个胞腔的 CW 复形, 若 \(X\) 局部欧氏, 则 \(X\) 是流形.

Claim 18.11 (CW 复形的流形维数) 设 \(X\) 既是 CW 复形也是流形, 则 CW 复形维数等于流形维数.