GTM202 | 5 紧致性

GTM202 (Introduction to Topological Manifolds) Chapter 4 的笔记.

15 Paracompactness

15.1 Paracompactness

仿紧的 Hausdorff 空间有一些好性质.

仿紧: \(X\) 的任意开覆盖都有局部有限的开加细.

• 局部有限: 对任意 \(x\in X\), 存在邻域 \(U_x\), 使得 \(U_x\) 只和 \({\cal A}\) 中有限个元素相交.

• 加细: 对任意 \(B\in{\cal B}\), 存在 \(A\in{\cal A}\), 满足 \(B\subset A\).

Claim 15.1 (局部有限的闭包刻画) \(X\) 的子集族 \({\cal A}\) 局部有限, 当且仅当 \(\overline{\cal A}=\{\overline{A}\mid A\in{\cal A}\}\) 局部有限.

Pf 因为 \(A\subset\overline{A}\), 所以当 \(\overline{\cal A}\) 局部有限, \(\cal A\) 也局部有限. 若 \({\cal A}\) 局部有限, 任给 \(x\in X\), 设邻域 \(W\) 只与 \({\cal A}\) 中有限个集合 \(A_1,\dots,A_n\) 相交. 因为 \(W\cap\overline{A}\) 非空蕴含 \(W\cap A\) 非空 (对任意 \(A\in{\cal A}\)), 因此满足 \(W\cap\overline{A}\) 的 \(A\) 一定在 \(A_1,\dots,A_n\) 中, 所以 \(W\) 只与 \(\overline{\cal A}\) 中有限个元素相交.

Claim 15.2 (局部有限集族的性质) 若 \({\cal A}\) 局部有限, 则 \(\overline{\bigcup_{A\in{\cal A}}A}=\bigcup_{A\in{\cal A}}\overline{A}\).

Pf 注意 \(\overline{\bigcup_{A\in{\cal A}}A}\supset\bigcup_{A\in{\cal A}}\overline{A}\) 是平凡的, 所以只证反向包含. 考虑逆否命题, 即任给 \(x\notin\bigcup_{A\in{\cal A}}\overline{A}\), 要证明 \(x\notin\overline{\bigcup_{A\in{\cal A}}A}\). 因为 \({\cal A}\) 局部有限, 所以 \(\overline{\cal A}\) 局部有限, 存在 \(x\) 的邻域 \(U\) 只与有限个 \(\overline{A}\) 相交, 记为 \(\overline{A_1},\dots,\overline{A_n}\). 则 \(U\setminus(\overline{A_1}\cup\cdots\cup\overline{A_n})\) 是 \(x\) 的邻域, 且与 \({\cal A}\) 中任意集合不交, 故 \(x\notin\overline{\bigcup_{A\in{\cal A}}A}\).

• 紧穷竭: 紧集列 \((K_i)_{i=1}^\infty\), 满足 \(X=\bigcup_iX_i\) 且 \(K_i\subset{\rm Int}K_{i+1}\).

Claim 15.3 (紧穷竭存在性) 第二可数, 局部紧的 Hausdorff 空间存在紧穷竭.

Pf 因为 \(X\) 是局部紧的 Hausdorff 空间, 存在预紧开集组成的拓扑基. 又由第二可数性, \(X\) 可以被可数多个这样的开集覆盖, 记为 \(\{U_i\}_{i=1}^\infty\).

我们只需要构造紧集列 \((K_i)_{i=1}^\infty\) 满足 \(U_j\subset K_j\) 且 \(K_j\subset{\rm Int}K_{j+1}\). 用归纳法.

令 \(K_1=\overline{U}_1\). 假设我们构造了 \(K_1,\dots,K_n\) 满足条件. 因为 \(K_n\) 紧, (能被有限个 \(U_i\) 覆盖) 所以存在正整数 \(k_n\), 使得 \(K_n\subset U_1\cup\cdots\cup U_{k_n}\). 令 \(K_{n+1}=\overline{U_1}\cup\cdots\cup \overline{U_{k_n}}\), 则 \(K_{n+1}\) 紧, 且根据 "局部有限集族的性质", \(K_{n+1}=\overline{U_1\cup\cdots\cup U_{k_n}}\), 于是 \({\rm Int}K_{n+1}=U_1\cup\cdots\cup U_{k_n}\supset K_n\). 如果我们进一步要求 \(k_n>n+1\), 则有 \(U_{n+1}\subset K_{n+1}\), 完成了归纳.

Claim 15.4 (仿紧性定理) 第二可数, 局部紧的 Hausdorff 空间是仿紧的.

Pf 设 \(X\) 是局部紧的 Hausdorff 空间, \((K_i)_{i=1}^\infty\) 是其紧穷竭. 任给开覆盖 \({\cal U}\).

对 \(j\in\N^+\), 令 \(A_j=K_{j+1}\setminus{\rm Int}K_k\) 以及 \(W_j={\rm Int}K_{j+2}\setminus K_{j-1}\) (规定 \(K_0=\emptyset\)). 则 \(A_j\) 作为紧集 \(K_{j+1}\) 的闭子集, 是紧集; \(W_j\) 是开集, 且 \(A_j\subset W_j\).

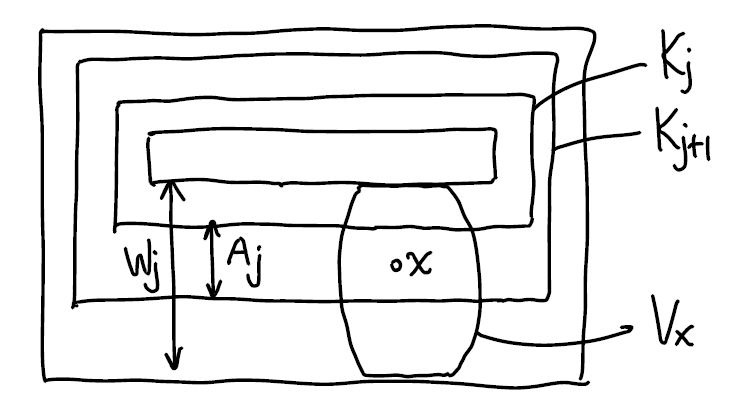
对任意 \(x\in A_j\), 取 \({\cal U}\) 中包含 \(x\) 的开集 \(U_x\), 令 \(V_x=U_x\cap W_j\). 当 \(x\) 取遍 \(A_j\), 开集 \(V_x\) 组成 \(A_j\) 的开覆盖. 因为 \(A_j\) 紧, 它有有限子覆盖 \({\cal A}_j\). 当 \(j\) 取遍 \(\N^+\), 所有 \({\cal A}_j\) 之并组成 \(M\) 的开覆盖, 且构成 \({\cal U}\) 的加细. 因为 \(W_j\) 与 \(W_{j'}\) 相交当且仅当 \(j-2\leq j'\leq j+2\), 因此上述开覆盖是局部有限的.

15.2 Normal spaces

正则空间: Hausdorff, 且闭集和其外一点可被开集分离.

正规空间: Hausdorff, 且不交的闭集可被开集分离.

• 正规 \(\Rightarrow\) 正则 \(\Rightarrow\) Hausdorff.

  • 紧 + Hausdorff \(\Rightarrow\) 正规. (Hausdorff 空间中, 紧子集可被开集分离的直接推论.)
  • (继承) 正规空间的闭子集正规.

Claim 15.5 (正规条件) Hausdorff 空间 \(X\) 正规, 当且仅当对任意闭集 \(A\subset X\) 及其邻域 \(U\), 存在 \(A\) 的邻域 \(V\) 满足 \(\overline{V}\subset U\).

Pf 若 \(X\) 正规, 则闭集 \(A\) 和 \(B=X\setminus U\) 可被开集 \(V,W\) 分离, 则 \(V\) 真包含于闭集 \(X\setminus W\), 后者包含于 \(U\), 进而 \(\overline{V}\subset U\).

反之, 若满足右侧的条件, 任给不交闭集 \(A,B\), 则 \(U=X\setminus B\) 是 \(A\) 的邻域. 存在 \(A\) 的邻域 \(V\) 满足 \(V\subset\overline{V}\subset U\), 则 \(V\) 和 \({\rm Ext}V\) 分离 \(A,B\).

Claim 15.6 (正规性定理) 仿紧的 Hausdorff 空间是正规的.

• 证明和之前的 "分离性引理" (不交紧集被开集分离) 很像.

Pf 第一步, 证明 \(X\) 是正则的. 任给不交闭集 \(A\) 和 \(B=\{q\}\). 由 Hausdorff, 任给 \(p\in A\), 存在不交邻域 \(U_p\ni p\), \(V_p\ni q\). 当 \(p\) 取遍 \(A\), 所有 \(U_p\) 连同 \(X\setminus A\) 一起构成了 \(X\) 的开覆盖. 由仿紧性, 它有局部有限的开加细 \({\cal W}\). \({\cal W}\) 中的任意元素或者是某 \(U_p\) 的子集, 或者是 \(X\setminus A\) 的子集, 令 \({\cal U}\) 是所有前者的全体. 则 \({\cal U}\) 是 \(A\) 的局部有限开覆盖, 并且, 任给 \(U\in{\cal U}\), 存在 \(q\) 的邻域 \(V\) 与 \(U\) 不交, 因此 \(\overline{U}\) 不包含 \(q\).

令 \(\mathbb{U}=\bigcup_{U\in\cal U}U\), \(\mathbb{V}=X\setminus\overline{\mathbb{U}}\). 因为 \({\cal U}\) 局部有限, 所以 \(\overline{\mathbb{U}}=\bigcup_{U\in\cal U}\overline{U}\), 进而 \(\overline{\mathbb{U}}\) 不包含 \(q\). 因此, \(\mathbb{U},\mathbb{V}\) 分别是 \(A,B\) 的不交邻域.

第二步, 证明 \(X\) 是正规的. 和第一步一样, 只不过将 Hausdorff 性换成正则性.

Claim 15.7 (Urysohn 引理) \(X\) 正规. 若 \(A,B\) 为不交闭子集, 存在连续函数 \(f:X\to[0,1]\) 满足 \(f|_A\equiv0\), \(f|_B\equiv1\).

• 正规空间中, 不交闭集可被连续函数分离. 这实际上是正规的充要条件.
• 这意味着正规空间中的函数的 "等高线" 可以足够密集. 证明中, 我们通过构造一系列密集的下水平集, 来确定一个函数 \(f\).

Pf 我们将构造 \(X\) 的开集族 \(\{U_r\}_{r\in\Q}\), 满足:

1. 当 \(r<0\), \(U_r=\emptyset\); 当 \(r>1\), \(U_r=X\).
2. \(U_0\supset A\).
3. \(U_1=X\setminus B\).
4. 对于 \(p<q\), \(\overline{U}_p\subset U_q\).

条件 1 确定了 \(r\notin[0,1]\) 时的 \(U_r\). 定义 \(U_1=X\setminus B\), 根据正规性, 存在闭集 \(A\) 的邻域 \(U_0\) 使得 \(\overline{U_0}\subset U_1\).

对于 \(r\in(0,1)\), 我们用归纳法. 将 \((0,1)\) 间的有理数 (不重不漏地) 排成序列 \((r_i)_{i\in\N^+}\).

• 首先, 根据正规性, 存在开集 \(U_{r_1}\subset X\), 使得 \(\overline{U_0}\subset U_{r_1}\) 且 \(\overline{U_{r_1}}\subset U_1\).
• 现假设我们已经对 \(i=1,\dots,n\) 构造出了开集 \(U_{r_i}\) 满足 \(\overline{U_0}\subset U_{r_i}\), \(\overline{U_{r_i}}\subset U_1\) 并且满足条件 4. 对于下一个有理数 \(r_{n+1}\), 考虑集合 \(\{0,r_1,\dots,r_n,1\}\), 令 \(p\) 是该集合中小于 \(r_{n+1}\) 的最大数; 令 \(q\) 是该集合中大于 \(r_{n+1}\) 的最小数. 根据归纳假设, \(\overline{U_p}\subset U_q\). 根据正规性, 存在 \(\overline{U_p}\) 开邻域 \(U_{r_{n+1}}\) 满足 \(\overline{U_p}\subset U_{r_{n+1}}\) 且 \(\overline{U_{r_{n+1}}}\subset U_q\). 于是 \(U_{r_{n+1}}\) 也满足条件.

根据归纳法原理, 我们构造出了满足条件 1-4 的开集族 \(\{U_r\}_{r\in\Q}\).

现在, 我们可以定义函数 \(f:X\to\R\), \[ f(x)=\inf\{r\in\Q\mid x\in U_r\}. \] 由条件 1, \(f\) 是良定义的, 且 \(f(x)\in[0,1]\). 条件 2 保证 \(f(A)=0\), 条件 3 和 4 保证 \(f(B)=1\). 只需要证明 \(f\) 是连续的.

由连续性的 subbasis criterion, 我们只需要对 \([0,1]\) 的子基, 即形如 \((-\infty,a),(a,+\infty)\) 的开集验证原像的开性. 注意以下两个观察: \[ \Align{ f(x)<a &\iff x\in U_r\textsf{ 对某 }r<a, \\ f(x)\leq a &\iff x\in\overline{U_r}\textsf{ 对任意 } r>a. } \]

• 第一条, 根据 \(f\) 的定义立刻得到.

• 第二条, 设 \(f(x)\leq a\), 任给 \(r>a\), 由 \(f\) 的定义, 存在 \(s<r\) 使得 \(x\in U_s\subset U_r\subset\overline{U_r}\).

  反之, 设 \(x\in\overline{U_r}\) 对任意 \(r>a\). 若有理数 \(s>a\), 则存在有理数 \(r\) 使得 \(s>r>a\), 根据假设, \(x\in\overline{U_r}\subset U_s\), 说明 \(f(x)\leq s\). 因为这对任意 \(s>a\) 成立, 所以 \(f(x)\leq a\).

因此, 原像集 \[ \Align{ f^{-1}((-\infty,a)) &=\bigcup_{r\in\Q_{<a}} U_r, & f^{-1}((a,+\infty)) &=X\setminus \bigcap_{r\in\Q_{>a}}\overline{U_r}, } \] (开集的任意并开; 闭集的任意交闭) 是开集.

• 支集: 连续函数 \(f:X\to\R\) 的支集指的是 \(\supp f=\overline{\{x\in X\mid f(x)\neq0\}}\).

• 鼓包函数: 设闭子集 \(A\) 及其邻域 \(U\), 满足 \(f|_A\equiv1\) 且 \(\supp f\subset U\) 的连续函数 \(f:X\to[0,1]\) 称为 \(A\) 的支在 \(U\) 上的鼓包函数.

Claim 15.8 (鼓包函数存在性) \(X\) 正规. 任给闭子集 \(A\) 及其邻域 \(U\), 存在 \(A\) 的支在 \(U\) 上的鼓包函数.

Pf 对 \(A\) 和 \(B=X\setminus U\) 应用 Urysohn 引理.

15.3 Partitions of unity

单位分解: \(X\) 的开覆盖 \({\cal U}=(U_\alpha)_{\alpha\in A}\). 一个从属于 \({\cal U}\) 的单位分解指的是一族连续函数 \(\psi_\alpha:X\to\R\), 满足

1. \(0\leq\psi_\alpha(p)\leq1\), 对任意 \(\alpha\in A,p\in X\).
2. \(\supp\psi_\alpha\subset U_\alpha\).
3. 支集族 \((\supp\psi_\alpha)_{\alpha\in A}\) 局部有限.
4. \(\sum_\alpha\psi_\alpha(p)=1\), 对任意 \(p\in X\).

Claim 15.9 (引理) \(X\) 是仿紧 Hausdorff 空间. 设开覆盖 \({\cal U}=(U_\alpha)_{\alpha\in A}\), 则 \({\cal U}\) 存在局部有限加细 \((V_\alpha)_{\alpha\in A}\) 且 \(\overline{V_\alpha}\subset U_\alpha\).

• 一个比仿紧性更强的性质.

Claim 15.10 (单位分解存在性) \(X\) 是仿紧 Hausdorff 空间. 任给开覆盖 \({\cal U}=(U_\alpha)_{\alpha\in A}\), 存在从属于其的单位分解.

Pf 应用两次引理, 我们得到了局部有限开覆盖 \({\cal V}=(V_\alpha)\) 和 \({\cal W}=(W_\alpha)\) 满足 \(\overline{W_\alpha}\subset V_\alpha\) 且 \(\overline{V_\alpha}\subset U_\alpha\). 仿紧的 Hausdorff 空间是正规的, 故存在 \(\overline{W_\alpha}\) 的支在 \(V_\alpha\) 的鼓包函数 \(f_\alpha:X\to[0,1]\).

为了得到归一化的函数, 令 \(f:X\to\R\), \(f(p)=\sum_\alpha f_\alpha(p)\). 因为 \(\supp{f}\subset V_\alpha\), \((V_\alpha)\) 局部有限, 所以 \((\supp f_\alpha)\) 局部有限, 因此每一点 \(p\in X\) 存在其邻域, 使得 \(\sum_\alpha f_\alpha(p)\) 是有限和. 因此 \(f\) 是良定义的, 且连续. 因为 \(W_\alpha\) 覆盖 \(X\), 每一点 \(p\in X\) 都属于某 \(W_\alpha\), 进而 \(f_\alpha(p)=1\), 因此 \(f\) 严格正.

因此, 定义 \(\psi_\alpha(p)=f_\alpha(p)/f(p)\), 则 \((\psi_\alpha)\) 是满足单位分解条件 1-4 的连续函数族.

单位分解的应用.

Claim 15.11 (紧流形可嵌入 \(\R^n\)) 紧带边/无边流形同胚于欧氏空间的子集.

Pf 先考虑紧无边流形 \(M\). 由紧性, 有限个坐标邻域 \(U_1,\dots,U_k\) 覆盖 \(M\), 坐标函数 \(\phi_i:U_i\overset\sim\to\R^n\). 设 \((\psi_i)\) 是从属于开覆盖 \((U_i)\) 的单位分解, 定义 \[ F_i(x) = \Cases{ \psi_i(x)\phi_i(x), & x\in U_i \\ 0, & x\in M\setminus\supp{\psi_i}. } \] 根据粘合引理, \(F_i:M\to\R^n\) 是连续的. 定义 \(F:M\to\R^{nk+k}\) 为积映射 \[ F(x)=(F_1(x),\dots,F_k(x),\psi_1(x),\dots,\psi_k(x)). \] \(F\) 是连续的, 如果还能证明它是单射, 则根据闭映射引理, \(F\) 是拓扑嵌入.

设 \(F(x)=F(y)\). 因为 \(\sum\psi_i(x)\equiv1\), 所以某 \(\psi_i(x)\neq0\), 进而 \(x\in U_i\). 注意 \(F(x)=F(y)\) 蕴含 \(\psi_i(y)=\psi_i(x)>0\), 所以 \(y\in U_i\). 进而由 \(F_i(x)=F_i(y)\) 有 \(\phi_i(x)=\phi_i(y)\). 因为 \(\phi_i\) 单, 所以 \(x=y\).

对于紧带边流形 \(M\), 双倍 \(D(M)\) 是紧无边流形, 有嵌入 \(i:D(M)\hookrightarrow\R^N\), 而 \(M\) 嵌入到 \(D(M)\) 中 (黏着空间的性质): \(i_M:M\hookrightarrow D(M)\), 两者的复合 \(i\circ i_M\) 给出了 \(M\) 到 \(\R^N\) 的嵌入.

Claim 15.12 (连续函数的零点集) 设流形 \(M\) 的闭子集 \(B\), 则存在连续函数 \(f:M\to[0,+\infty)\), 其零点集恰为 \(B\).

Pf 先考虑 \(M=\R^n\), 闭子集 \(B\subset\R^n\). 定义 \[ u(x) = \inf\{\|x-y\|\mid y\in B \}, \] 称为到 \(B\) 的距离函数. \(u\) 是非负的连续函数, 且零点集恰为 \(B\).

一般的情况, \(B\) 是流形 \(M\) 的闭子集. 设 \(M\) 的欧氏开覆盖 \({\cal U}=(U_\alpha)_{\alpha\in A}\), 其中每个开集同胚于 \(\R^n\), 设 \((\psi_\alpha)\) 是从属于 \({\cal U}\) 的单位分解. 令 \(u_\alpha\) 是到 \(B\cap U_\alpha\) 的距离函数. 定义 \[ f(x)=\sum_{\alpha\in A} \psi_\alpha(x)u_\alpha(x), \] (当 \(x\) 在 \(\supp{\psi_\alpha}\) 之外时, \(\psi_\alpha(x)u_\alpha(x)\equiv0\)) 由 \((\supp{\psi_\alpha})\) 的局部有限性, 上式在每一点都是有限和, 进而定义了一个非负连续函数. 容易验证, 这个函数的零点集恰为 \(B\): 令 \(f(x)=0\), 因为某 \(\psi_\alpha(x)\neq0\), 则 \(u_\alpha(x)=0\), 意味着 \(x\in B\cap U_\alpha\).

一个推论:

Claim 15.13 (强 Urysohn 引理) 流形 \(M\) 的不交闭子集 \(A,B\), 则存在连续函数 \(f:M\to[0,1]\) 使得 \(f^{-1}(1)=A\), \(f^{-1}(0)=B\).

Pf 根据上一个定理, 可以构造 \(u,v:M\to[0,+\infty)\), 其零点集分别为 \(A,B\). 因为 \(A,B\) 不交, 所以 \(u(x)+v(x)\) 恒正, 而函数 \(f(x)=v(x)/(u(x)+v(x))\) 就是我们想要的.

• 穷竭函数: 连续函数 \(f:X\to\R\), 满足任意下水平集 \(f^{-1}((-\infty,c])\) 是紧致的.

  • 此时, \(f^{-1}((-\infty,k])\) (\(k\in\N\)) 构成 \(M\) 的紧穷竭.

Claim 15.14 (穷竭函数存在性) 流形上存在正的穷竭函数.

Pf \(M\) 是局部紧的 Hausdorff 空间, 则存在预紧开集组成的拓扑基; 又由第二可数性, 存在可数的预紧开集覆盖 \(\{U_i\}\). 设从属于其的单位分解 \(\{\psi_i\}\). 定义 \(f:M\to\R\), \[ f(x)=\sum_{k=1}^\infty k\psi_k(x), \] 因为 \(\supp{\psi_k}\) 局部有限, 所以对任意一点 \(x\in M\), 右侧是一个有限和, 因而 \(f\) 连续. 因为 \(f(x)\geq\sum_k\psi_k(x)=1\), \(f\) 恒正.

任给 \(x\notin\bigcup_{k=1}^m\overline{U_k}\), 则对 \(1\leq k\leq m\), \(\psi_k(x)=0\), 于是 \[ f(x) = \sum_{k=m+1}^\infty k\psi_k(x) > \sum_{k=m+1}^\infty m\psi_k(x) = m. \] 因此, \(f(x)\leq m\) 蕴含 \(x\in\bigcup_{k=1}^m\overline{U_k}\).

任给 \(c\in\R\), 设 \(m\) 是任意大于 \(c\) 的正整数, 则 \(f^{-1}((-\infty,c])\) 是紧集 \(\bigcup_{k=1}^m\overline{U_k}\) 的闭子集, 故紧.

16 Proper Maps

逆紧映射: 紧集的原像是紧集.

• 序列发散到无穷: 序列 \((x_i)\subset X\) 发散到无穷, 若对任意紧集 \(K\subset X\), 只有有限个 \(x_i\) 在 \(K\) 中.

Claim 16.1 (发散到无穷的条件) \(X\) Hausdorff 且第一可数. 序列 \((x_i)\) 发散到无穷, 当且仅当它不存在收敛子列.

Pf 设 \((x_i)\) 发散到无穷, 假设存在子列 \((x_{i_j})\) 收敛到 \(x\), 则 \(\{x_{i_j}\mid j\in\N\}\cup\{x\}\) 是紧的, 且含有无穷多项 \(x_i\), 与发散到无穷矛盾. (并没有用到 Hausdorff 与第一可数性.)

设 \((x_i)\) 没有收敛子列, 假设紧集 \(K\subset X\) 含有无穷多项 \(x_i\), 则存在子列 \((x_{i_j})\subset K\). 因为第一可数的紧 Hausdorff 空间 \(K\) 是列紧的, 所以 \((x_{i_j})\) 有收敛子列, 与 \((x_i)\) 无收敛子列矛盾.

Claim 16.2 (逆紧映射保持发散到无穷大) \(F:X\to Y\) 逆紧, 则 \(F\) 将 \(X\) 中发散到无穷大的序列映到 \(Y\) 中发散到无穷大的序列.

Pf 设 \((x_i)\subset X\) 发散到无穷, 假设 \((F(x_i))\) 不发散到无穷, 则存在紧集 \(K\subset Y\) 含有无穷多项 \(F(x_i)\), 则紧集 \(F^{-1}(K)\) 也包含了无穷多项 \(x_i\), 与 \((x_i)\) 发散到无穷矛盾.

Claim 16.3 (逆紧判断) 连续映射 \(F:X\to Y\).

• 若 \(X\) 紧, \(Y\) Hausdorff, 则 \(F\) 逆紧.
• 若 \(X\) 是第二可数的 Hausdorff 空间, 且 \(F\) 将 \(X\) 中发散到无穷大的序列映到 \(Y\) 中发散到无穷大的序列, 则 \(F\) 逆紧.
• 若 \(F\) 是闭映射, 且纤维紧, 则 \(F\) 逆紧.
• 若 \(F\) 是拓扑嵌入, 且像集闭, 则 \(F\) 逆紧.
• 若 \(Y\) Hausdorff 且 \(F\) 有连续的左逆, 则 \(F\) 逆紧.
• 若 \(F\) 逆紧, 则任给 \(F\) 的饱和集 \(A\subset X\), \(F|_A:A\to F(A)\) 逆紧.

Pf 1, 设 \(K\subset Y\) 紧, 它作为 Hausdorff 空间的紧子集, 也是闭的; 由连续性, \(F^{-1}(K)\) 闭, 它作为紧空间的闭子集, 也是紧的.

4, 拓扑嵌入是闭映射, 且纤维是独点集, 当然紧. 根据 3, \(F\) 逆紧.

6, 设 \(K\subset F(A)\) 紧. \(A\) 饱和意味着 \((F|_A)^{-1}(K)=F^{-1}(K)\), 根据 \(F\) 的逆紧性, 这是紧的.

• 紧生成空间: 空间 \(X\) 紧生成, 若对任意子集 \(A\subset X\), 只要 \(A\) 与任意紧子集 \(K\subset X\) 的交在 \(K\) 中闭, 则 \(A\) 是闭集.

Claim 16.4 (紧生成判断) 第一可数空间与局部紧空间是紧生成的.

Claim 16.5 (连续的逆紧映射是闭的) 设空间 \(X\), 紧生成的 Hausdorff 空间 \(Y\), 连续的逆紧映射 \(F:X\to Y\), 则 \(F\) 闭.

• (推论) 若 \(F\) 单, 则是拓扑嵌入; 若满, 则是商映射; 若双, 则是同胚.

Pf 设 \(A\subset X\) 闭. 要证明 \(F(A)\subset Y\) 闭, 只需证明它与任意紧集的交是闭的. 设 \(K\subset Y\) 紧, 则 \(F^{-1}(K)\) 紧, 并且 \(A\cap F^{-1}(K)\) 作为紧集的闭子集, 也是紧的. 根据紧的连续不变性, \(F(A\cap F^{-1}(K))=F(A)\cap K\) 是紧的. 又因为 \(K\) Hausdorff, \(F(A)\cap K\) 在 \(K\) 中闭.

单点紧化: 设 \(X\) 是局部紧的 Hausdorff 空间. 定义 \(X^*=X\amalg\{\infty\}\) 并赋予拓扑: \[ {\cal T}={\cal T}_X \cup \{U\subset X^*\mid X^*\setminus U \textsf{ 是 $X$ 的紧子集}\}. \]

• 容易验证, \(X\) 具有子空间拓扑, 且在 \(X^*\) 中开.

Claim 16.6 (单点紧化的紧性) \(X^*\) 是紧 Hausdorff 空间.

Pf 任给 \(X^*\) 的开覆盖 \(\cal U\), 则存在开集 \(U\in{\cal U}\) 使得 \(\infty\in U\). 根据 \(X^*\) 拓扑的定义, \(X^*\setminus U\) 是 \(X\) 的紧子集. 因为 \({\cal U}\setminus\{U\}\) 覆盖 \(X^*\setminus U\), 它有有限子覆盖 \({\cal U}'\) (子空间紧性判断). \(\cal U'\) 与 \(U\) 合起来构成 \(X^*\) 的有限子覆盖.

对于 \(X^*\) 的 Hausdorff 性, 只需验证 \(\infty\) 和 \(p\in X\) 可分离. 因为 \(X\) 是局部紧的 Hausdorff 空间, 存在 \(p\) 的预紧邻域 \(U\), 满足 \(\overline{U}\) 紧. 进而 \(X^*\setminus\overline{U}\) 是 \(\infty\) 的邻域, 且与 \(U\) 不交.

Claim 16.7 (发散到无穷的序列) \(X\) 的某序列发散到无穷, 当且仅当它在 \(X^*\) 中收敛到 \(\infty\).

Pf 设 \((x_i)\) 发散到无穷. 任给 \(\infty\) 的邻域 \(U\), 则 \(X^*\setminus U\) 是 \(X\) 的紧子集. 根据发散到无穷的定义, 只有有限项 \(x_i\) 在 \(X^*\setminus U\) 中, 因此只要 \(i\) 充分大, \(x_i\in U\), 即 \(x_i\to\infty\). 反之略.

Claim 16.8 (稠密性与紧性) \(X\) 在 \(X^*\) 中稠密, 当且仅当 \(X\) 非紧.

Pf 我们证明, \(X\) 在 \(X^*\) 中非稠密, 当且仅当 \(X\) 紧.

设 \(X\) 在 \(X^*\) 中非稠密, 则存在非空开集与 \(X\) 不交. 这非空开集只能是 \(\{\infty\}\), 因此 \(X^*\setminus\{\infty\}\) 是 \(X\) 的紧子集, 即 \(X\) 紧. 反之是类似的.

单点紧化的例子.

• \(\R^n\) 的单点紧化. 记 \((\R^n)^*\) 是 \(\R^n\) 的单点紧化. 设 \(\sigma:\mathbb{S}^n\setminus\{N\}\to\R^n\) 是球极投影, 则 \(\sigma\) 可扩张到同胚 \[ \Align{ \sigma^*: \mathbb{S}^n &\to (\R^n)^*, & \sigma^*(p) &= \Cases{ \infty, & p=N, \\ \sigma(p), & p\in \mathbb{S}^n\setminus\{N\}. } } \]

  • \(\C\) 的单点紧化称为黎曼球, 它同胚于 \(\mathbb{S}^2\).