GTM202 | 3 连通性

GTM202 (Introduction to Topological Manifolds) Chapter 4 的笔记.

12 Connectedness

12.1 Connectedness

连通性: \(X\) 称为非连通的, 若 \(X\) 等于两个不交的非空开子集 \(A,B\) 之并 (此时称 \(A,B\) 间断 \(X\)). 否则 \(X\) 称为连通的. 一个子集的连通性是在子空间拓扑下的连通性.

Claim 12.1(连通的刻画) \(X\) 连通, 当且仅当既开又闭的子集只有 \(X,\emptyset\).

Pf \(X\) 非连通 \(\iff\) 存在开集 \(A,B\neq\emptyset\) 使得 \(B=A^C\iff\) 存在既开又闭的 \(A\neq X,\emptyset\).

• 非空的离散空间, 非空集的不交并空间都是非连通的. 平凡空间是连通的.

Claim 12.2 (连通与离散空间) 连通空间到离散空间的连续映射是常值的.

Pf 若 \(X\) 连通, \(Y\) 离散, 且 \(f:X\to Y\) 连续. 取 \(x\in X\), 记 \(f(x)=c\). 由于 \(\{c\}\subset Y\) 既开又闭, 所以原象 \(f^{-1}(c)\) 既开又闭, 因为 \(X\) 连通, \(f^{-1}(c)\) 又不等于 \(\emptyset\), 则只能等于 \(X\). 即 \(f\equiv c\).

Claim 12.3 (连通的连续不变性) \(f:X\to Y\) 连续, 若 \(X\) 连通, 则 \(f(X)\) 连通.

Pf 限制陪域为 \(f(X)\), 进而 \(f:X\to f(X)\) 是连续的满射.

考虑逆否. 设 \(f(X)\) 非连通, 则存在 \(f(X)\) 的开子集 \(U,V\) 间断 \(f(X)\). 由连续性, \(f^{-1}(U),f^{-1}(V)\) 是开集, 且间断 \(X\), \(X\) 非连通.

立刻得到推论:

Claim 12.4 (拓扑不变性) 同胚于连通空间的空间是连通的.

Claim 12.5 (连通的性质)

• (引理) 设不交的子集 \(U,V\subset X\). 若 \(A\subset X\) 连通且 \(A\subset U\cup V\), 则或者 \(A\subset U\), 或者 \(A\subset V\).
  • 连通集, 如果是不交并空间的子集, 不能被拆成两部分.
• 若 \(X\) 有连通稠密子集, 则 \(X\) 连通.
• (\(A\) 到 \(\overline{A}\) 连通) 若 \(A\subset X\) 连通, 则对任意 \(B\) 满足 \(A\subset B\subset\overline{A}\), \(B\) 连通.
• (并) 若 \(\{B_\alpha\}\) 是一系列有公共点的连通子集, 则 \(\bigcup B_\alpha\) 连通.
• (积) 连通空间的有限积连通.
• (商) 连通空间的商空间连通.

Pf 1, 若 \(A\) 同时具有 \(U,V\) 中的点, 则 \(A\cap U,A\cap V\) 间断 \(A\).

2, 设稠密子集 \(A\) 连通. 反证, 假设 \(U,V\) 间断 \(X\), 则 1 告诉我们 \(A\) 在 \(U,V\) 其一中, 不妨设 \(A\subset U\). 则 \(X=\overline{A}\subset\overline{U}=U\), 于是 \(V=\emptyset\), 矛盾.

3, 设 \(A\) 连通, \(A\subset B\subset\overline{A}\). 因为 \(A\) 在 \(\overline{A}\) 中稠密, 则 \(A\) 在 \(B\) 中稠密, 利用 2, \(B\) 连通.

4, 假设 \(U,V\) 间断 \(\bigcup B_\alpha\). 设 \(p\) 为 \(B_\alpha\) 的公共点, 不妨 \(p\in U\). 因为每个 \(B_\alpha\) 连通且 \(B_\alpha\subset U\cup V\), 利用 1, 得到 \(B_\alpha\subset U\), 进而 \(\bigcup B_\alpha\subset U\), 所以 \(V=\emptyset\), 矛盾.

5, 只需考虑两个空间的积, 进而用归纳法得到任意有限积.

设 \(X,Y\) 连通, 假设 \(U,V\) 间断 \(X\times Y\). 取 \((x_0,y_0)\in U\), 则 \(\{x_0\}\times Y\), 因为同胚于 \(Y\), 所以是连通的. 利用 1, 有 \(\{x_0\}\times Y\subset U\). 任给 \(y\in Y\), 则 \(X\times\{y\}\) 连通, 并且它与 \(U\) 有公共点 \((x_0,y)\), 则 \(X\times\{y\}\subset U\). 进而 \(X\times Y\subset U\), \(V\) 空, 矛盾.

6, 商映射是连续, 保持连通性. 且商映射满, 故商空间连通.

Claim 12.6 (线性连续统的连通集) 线性连续统 \(L\) 的非空子集连通, 当且仅当它是独点集/区间.

• 特别地, \(L=(-\infty,+\infty)\)是连通的.

Pf 独点集显然连通, 所以假设子集 \(J\subset L\) 至少有两个元素.

若 \(J\) 是区间, 假设非连通, 则存在开集 \(U,V\subset L\) 使得 \(U\cap J,V\cap J\) 间断 \(J\). 取 \(a\in U\cap J\), \(b\in V\cap J\), 不妨设 \(a<b\). 因为 \(J\) 是区间, 所以 \([a,b]\subset J\). 由 \(U\cap J\) 和 \(V\cap J\) 的开性, 存在 \(\varepsilon>0\), 使得 \([a,a+\varepsilon)\subset U\cap J\) 以及 \((b-\varepsilon,b]\subset V\cap J\) (\(\varepsilon\) 的存在性依赖序关系的稠密性).

(由 \(L\) 的 Dedekind 完备性) 取 \(c=\sup(U\cap[a,b])\), 则 \(a+\varepsilon\leq c\leq b-\varepsilon\), 所以 \(c\) 在 \(a,b\) 之间, 有 \(c\in J\subset U\cup V\). 如果 \(c\in U\), 则 (由 \(U\) 的开性), 某 \((c-\delta,c+\delta)\subset U\), 与 \(c\) 是上界矛盾. 如果 \(c\in V\), 则某 \((c-\delta,c+\delta)\subset V\), 与 \(U\) 不交, 与 \(c\) 是确界矛盾. 总之, \(J\) 是连通的.

若 \(J\) 不是区间, 则存在 \(a<c<b\), \(a,b\in J\) 而 \(c\notin J\), 则 \((-\infty,c)\cap J\) 和 \((c,+\infty)\cap J\) 间断 \(J\).

• 连续归纳法/连通性论证: 设区间 \(I\subset\R\). 要证明性质 \(p(x)\) 对任意 \(x\in I\) 成立, 考虑集合 \[ X=\{x\in I\mid p(x)\textsf{ 成立}\}\subset I, \] 我们只需说明 (1) \(X\neq\emptyset\), (2) \(X\) 是开子集, (3) \(X\) 是闭子集, 再由 \(I\) 的连通性, 有 \(X=I\).

Claim 12.7 (介值定理) \(X\) 连通, \(f:X\to\R\) 连续. 任给 \(p,q\in X\), \(f\) 取到 \(f(p),f(q)\) 间所有值.

Pf 连续映射保持连通性, 所以 \(f(X)\subset\R\) 连通, 所以 \(f(X)\) 只能是独点集或区间.

例: 拓扑群.

• 子集生成的子群: 子集 \(S\subset G\) 生成的子群 \(\lr{S}=\bigcup_{n=1}^\infty(S\cup S^{-1})^n\), 是包含 \(S\) 的最小子群.

Claim 12.8 (拓扑群)

• (开子群) 拓扑群的开子群也是闭的.
• (邻域生成既开又闭子群) \(e\) 的邻域 \(U\) 生成的子群 \(\lr{U}\) 既开又闭.
• (连通子集生成连通子群) 包含 \(e\) 的连通子集 \(U\) 生成的子群 \(\lr{U}\) 是连通的.
• (连通群) 若 \(G\) 连通, 则 \(e\) 的任意邻域生成 \(G\).

Pf 1, 设开子群 \(H\subset G\). 任给 \(g\in G\setminus H\), 考虑 \(gH=l_g(H)\) 作为开集 \(H\) 的同胚像, 也是开集. 并且由子群的定义知 \(gH\cap H=\emptyset\), 因此 \(H\) 闭.

2, 只需证明 \(\lr{U}\) 开. 任给 \(g\in\lr{U}\), 则 \(gU\) 是 \(g\) 的包含于 \(\lr{U}\) 的邻域.

3, 由定义, \(\lr{U}=\bigcup_{n=1}^\infty(U\cup U^{-1})^n\), 其中所有并项连通, 且有公共点 \(e\), 因此并集是连通的.

4, 设连通邻域 \(U\), 则非空子集 \(\lr{U}\) 既开又闭, 因为 \(G\) 连通, 只能有 \(\lr{U}=G\).

12.2 Path connectedness

道路连通性: 称 \(X\) 是道路连通的, 若任意两点 \(p,q\in X\) 有道路相连.

• 道路: 连续映射 \(f:I=[0,1]\to X\) 满足 \(f(0)=p\), \(f(1)=q\).

  • 道路连通性更好用, 因为映射 \(f\) 易操作.
  • 道路 \(f_1:[0,1]\to X\) 和 \(f_2:[1,2]\to Y\) 的拼接 \(f:[1,2]\to X\) 也是道路.

Claim 12.9(道路连通更强) 道路连通的空间是连通的.

Pf 给定 \(p\in X\). 对任意 \(q\in X\), 设 \(B_q\) 是连接 \(p,q\) 的道路的像. 由连通的连续不变性, \(B_q\) 是连通的. 因此, \(X=\bigcup_{q\in X}B_q\) 是连通的.

Claim 12.10 (道路连通的性质)

• (连续不变性/拓扑不变性) 道路连通在连续映射下的像道路连通.
• (并) 若 \(\{B_\alpha\}\) 是一系列有公共点的道路连通子集, 则 \(\bigcup B_\alpha\) 道路连通.
• (积) 道路连通空间的有限积道路连通.
• (商) 道路连通空间的商空间道路连通.

Pf 1, 设 \(X\) 道路连通, \(f:X\to Y\) 连续, 不妨 \(Y=f(X)\). 对于任意 \(p,q\in f(X)\), 取 \(p_0\in f^{-1}(p)\), \(q_0\in f^{-1}(q)\), 则有道路 \(\gamma:I\to X\) 连接 \(p_0,q_0\). 容易看出 \(f\circ\gamma\) 是连接 \(p,q\) 的连续道路.

2, 设公共点 \(p\). 任给 \(a\in B_\alpha\) 和 \(b\in B_\beta\), 存在分别连接 \(a,p\) 和 \(p,b\) 的路径 \(f_1:[0,1]\to B_\alpha\) 和 \(f_2:[1,2]\to B_\beta\). 将两条路首尾相接, 得到的 \(f:[0,2]\to\bigcup B_\alpha\) 是连接 \(a,b\) 的道路.

3, 同样只考虑两个空间的积. 设 \(X,Y\) 道路连通. 任给 \((x,y),(x',y')\in X\times Y\), 存在连接 \(x,x'\) 的路径 \(f_1:I\to X\) 和连接 \(y,y'\) 的路径 \(f_2:I\to Y\), 则 \(f=(f_1,f_2)\) (连续映射的积是连续的) 是连接 \((x,y),(x',y')\) 的路径.

4, 商空间作为连续映射的像, 也是道路连通的.

道路连通空间的例子.

• \(\R^n\) 和 \(\R^n\) 的凸子集 (即任意两点所连线段仍在集合内).
• \(\R^n\setminus\{0\}\) (\(n\geq2\)).
• \(\mathbb{RP}^n\), 因为它是 \(\R^{n+1}\setminus\{0\}\) 的商空间.
• \(\mathbb{S}^n\) (\(n\geq1\)), 因为它是 \(\R^{n+1}\setminus\{0\}\) 的商空间.
• \(\mathbb{T}^n\), 因为它是 \(\mathbb{S}^1\) 的有限积.

12.3 Components

分量: \(X\) 的极大非空连通子集 (不真包含于任何连通子集内).

Claim 12.12 (分量的性质)

• (划分) 所有连通分量构成 \(X\) 的划分.
• 分量是闭子集.
• 非空连通子集包含于单个分量内.

Pf 1, 要证明分量两两不交, 且并成 \(X\). 两两不交: 假设分量 \(U,V\) 有公共点, 则它们的并也是连通的, 与 \(U,V\) 的极大性矛盾. 并成 \(X\): 任取 \(x\in X\), 则独点集 \(\{x\}\) 是连通的. 设 \(U\) 是所有包含了 \(x\) 的连通子集之并, 则 \(U\) 也是连通的, 并且也是极大的, 进而是包含 \(x\) 的分量.

2, 设 \(A\) 是分量, 则 \(\overline{A}\) 也是连通的, 由极大性, \(A=\overline{A}\).

3, 设 \(A\) 是非空连通子集, 因为分量构成 \(X\) 的划分, 所以 \(A\) 与某个分量 \(B\) 有公共点. 因此 \(A\cup B\) 也连通. 由极大性, \(A\cup B\subset B\), 换言之, \(A\subset B\).

道路分量: \(X\) 的极大非空道路连通子集.

Claim 12.13 (道路分量的性质)

• (划分) 所有道路分量构成 \(X\) 的划分.
• (与连通分量) 道路分量包含于某一个分量内. 分量是道路分量的不交并.
• 非空道路连通子集包含于单个道路分量内.

Pf 1, 3 和分量的性质 1, 3 证法相同.

2 的第一句, 道路分量 \(A\) 也是连通的, 所以包含于某分量内.

2 的第二句, 和分量的性质 1 证法相同.

利用连通性, 可以证明 \(1\) 维情形的维数不变性与边界不变性.

Claim 12.14 (维数不变性, 一维情形) 非空拓扑空间 \(X\) 不能既是 \(1\) 维流形, 又是 \(n\) (\(n>1\)) 维流形.

Pf 假设 \(X\) 既是 \(1\) 维流形, 又是 \(n\) (\(n>1\)) 维流形. 取 \(p\in X\) 的 \(1\) 维欧氏邻域 \(U\cong\R\). 因为 \(X\) 存在由 \(n\) 维坐标开球组成的拓扑基, \(p\) 在 \(U\) 中的某邻域 \(V\cong\mathbb{B}^n\). 而 \(V\) 作为 \(U\) 的开子集, 也同胚于 \(\R\) 的开子集 \(A\) (同胚在开集上的限制是同胚). 于是 \(A\cong\mathbb{B}^n\), 然而这是不可能的.

证明 \(\R\) 的开子集 \(A\) 不同胚于 \(\mathbb{B}^n\). 假设有同胚 \(\psi:A\to\mathbb{B}^n\), 取 \(p\in A\), 则开子集 \(A\setminus\{p\}\) 同胚于 \(\mathbb{B}^n\setminus\{\psi(p)\}\). 然而前者非连通, 后者连通, 导致矛盾.

Claim 12.15 (边界不变性, 一维情形) 设 \(1\) 维带边流形 \(M\), 则 \(M\) 中的点不能既是边界点, 也是内部点.

Pf 假设 \(p\in M\) 既是边界点, 也是内部点, 则包含 \(p\) 的内部坐标系 \((U,\varphi)\) 和边界坐标系 \((V,\psi)\) 满足 \(\psi(p)=0\in\partial\H^1\).

记 \(U\cap V\) 的包含 \(p\) 的连通分量为 \(A\), 则 \(\varphi(A)\) 是 \(\R\) 中包含 \(\varphi(p)\) 的开区间, 而 \(\psi(A)\) 是 \(\partial\H^1=[0,+\infty)\) 中包含 \(\psi(p)=0\) 的左开右闭区间. 注意到 \((\psi\circ\varphi^{-1})|_{\varphi(A)}\) 给出了两个区间的同胚; 而 \((\psi\circ\varphi^{-1})|_{\varphi(A)\setminus\{\varphi(p)\}}\) 给出了 \(\varphi(A)\setminus\{\varphi(p)\}\) 与 \(\psi(A)\setminus\{\psi(p)\}\) 的同胚. 然而前者不连通, 后者连通, 矛盾.

12.4 Local connectedness

局部(道路)连通: \(X\) 存在由(道路)连通开集组成的拓扑基.

• 此时, 对任意 \(x\in X\) 的任意邻域 \(U\), 存在(道路)连通邻域 \(V\subset U\).

Claim 12.16 (局部连通的性质) \(X\) 局部连通.

• (继承) 任意开子集局部连通.
• 分量是开子集.

Pf 1, 设 \(X\) 的拓扑基 \({\cal B}\) 由连通开集组成. 开子集 \(U\) 的拓扑基由 \({\cal B}\) 中包含 \(U\) 的元素组成.

2, 设分量 \(A\). 任给 \(p\in A\), 由局部连通性, 存在连通邻域 \(U\). 由于连通邻域必须包含于单个分量, 所以 \(U\subset A\), 证明了 \(A\) 是开集.

Claim 12.17 (局部道路连通的性质) \(X\) 局部道路连通.

• (更强) \(X\) 局部连通.
• (继承) 任意开子集局部道路连通.
• 道路分量是开子集.
• 分量 = 道路分量.
• 若 \(X\) 连通, 则道路连通.

Pf 1 因为道路连通强于连通. 2-3 和局部连通的 1-2 的证法一样.

4, 任给 \(p\in X\), 设 \(A,B\) 分别为包含 \(p\) 的分量和道路分量, 于是 \(B\subset A\), 并且 \(A\) 可以写作若干道路分量之并, 这些道路分量在 \(X\) 中开 (由 3), 进而也在 \(A\) 中开 (因为 \(A\) 开). 如果 \(B\) 不是唯一的道路连通分量, 则 \(B\) 和 \(A\setminus B\) 间断 \(A\), 与 \(A\) 是连通分量矛盾. 因此 \(A=B\).

5, 若 \(X\) 连通, 则 \(X\) 只有一个分量, 就是 \(X\). 由 4, 这也是道路连通的.

Claim 12.18 (流形) 带边/无边流形局部道路连通 (进而局部连通).

• 因此, 流形的连通性等价于道路连通性.

Pf 流形具有由坐标开球组成的拓扑基, 而坐标开球是道路连通的.

Claim 12.19 (锥) 拓扑空间 \(X\) 的锥 \(CX\) 是道路连通的. \(CX\) 局部(道路)连通当且仅当 \(X\) 局部(道路)连通.

Pf 设商映射 \(q:X\times[0,1]\to CX\).

1, 道路连通性. 任给 \(a,a'\in CX\), 设原象 \(q^{-1}(a)=(x,t)\), \(q^{-1}(a')=(x',t')\). 考虑 \[ f:[t,1]\to X\times[0,1],\quad f(s)=(x,s), \] 我们断言这是连接 \(q^{-1}(a)=(x,t)\) 和 \((x,1)\) 的道路. 下面证明连续性. 只需对 \(X\times[0,1]\) 的拓扑基验证. 任取开集 \(U\times I\), 其中开集 \(U\subset X\), 开区间 \(I\subset[0,1]\). 若 \(x\notin U\), 则 \(f^{-1}(U\times I)\) 为空. 若 \(x\in U\), 则 \(f^{-1}(U\times I)=[t,1]\cap I\), 是 \([t,1]\) 的相对开子集, 证明了连续性.

同理可以构造连接 \(q^{-1}(a')=(x',t')\) 和 \((x',1)\) 的道路 \(f'\). 因为商映射是连续的, 所以 \(q\circ f\) 和 \(q\circ f'\) 分别是连接 \(a,q(x,1)\) 和 \(a',q(x',1)\) 的道路. 注意 \(q(x,1)=q(x',1)\), 因此两个道路可以拼合成连接 \(a,a'\) 的道路.

2, 局部的性质. TODO

流形/不是流形的例子.

• 长射线/长直线. 取不可数集 \(Y\). 根据良序原理, \(Y\) 上有良序 \(<\), 使得任意非空子集存在最小元. 特别地, \(Y\) 有最小元 \(y_0\). 更进一步, 要求 \(Y\) 满足这样的性质: 对任意 \(y\in Y\), 只有可数个元素小于 \(y\).

  令 \({\cal R}=Y\times[0,1)\), 并赋予字典序: \[ (y,s)<(y',s')\iff y<y'\textsf{ 或 }(y=y'\textsf{ 且 }s<s'). \] 拥有字典序拓扑的 \({\cal R}\) 称为长射线. 长直线 \({\cal L}\) 指的是以 \((y_0,0)\) 为基点的一点并 \({\cal R}\vee{\cal R}\).

  • 直线 \(\R\) 可数个 \([0,1)\) 拼接 (即 \(\Z\times[0,1)\)) 并赋予字典序拓扑. 而长射线/长直线是不可数个 \([0,1)\) 拼接. 长直线的局部欧氏性和 Hausdorff 性是容易验证的.

  • 不第二可数: 考虑 \({\cal R}\) 的一个不可数开覆盖 \[ {\cal U}=\{ \textsf{开区间 } ((y,0),(y',1/2)) \mid \forall y\in Y, y'\textsf{ 是大于 } y \textsf{ 最小元} \}, \] 删去 \({\cal U}\) 中任何一个开集, 剩下的集族都不能覆盖 \({\cal R}\). 因此 \({\cal U}\) 不存在可数子覆盖, 进而 \({\cal R}\) 不是第二可数的. 一点并 \({\cal L}\) 也不是第二可数的.

  • 道路连通: 道路连通空间一点并也道路连通, 所以只考虑 \({\cal R}\). 因为对于给定的 \(y\), \(\{y\}\times[0,1)\) 是道路连通的, 所以只用考虑所有形如 \((y,0)\) 的点. 任给 \((y,0),(y',0)\in{\cal R}\), 不妨设 \(y<y'\). 根据 \(Y\) 的取法, 满足 \(y\leq z\leq y'\) 的 \(z\in Y\) 只有至多可数个 (下面只考虑无穷多个的情况), 将它们从小到大排序为 \(z_1,z_2,\dots,z_{\omega+1}\), 其中 \(z_1=y\), \(z_{\omega+1}=y'\).

    构造道路 \(f:[0,1]\to{\cal R}\). 对 \(n\in\N^+\), \(f\) 将 \([(z_n,0),(z_{n+1},0))\) 同胚地映到 \([\frac12-\frac1{2^n},\frac12-\frac1{2^{n+1}})\); \(f\) 将 \([(z_\omega,0),(z_{\omega+1},0)]\) 同胚地映到 \([\frac12,1]\). 可以证明 \(f\) 是连接 \((y,0),(y',0)\) 的道路.

    • 注意如果 \(Y\) 不满足 对任意 \(y\in Y\), \(\{y'\in Y\mid y'<y\}\) 可数 的性质, 则 \({\cal R}\) 不是道路连通的: 因为它太长了.

12.5 Examples

四种连通性的例子.

• 除开下面的限制, 四种连通性的任意其他组合都是存在的.
  • (局部) 道路连通 \(\Rightarrow\) (局部) 连通; 局部道路连通 \(+\) 连通 \(\Rightarrow\) 道路连通.

例子	连通	道路连通	局部连通	局部道路连通
拓扑学家的正弦曲线 \(T\)	√
\(T\) 与 \(x\) 轴之并	√	√
字典序的单位正方形 \(S\)	√		√
\(S\) 的锥	√	√	√
\(S\amalg S\)			√
至少两个点的离散空间			√	√
非连通流形			√	√
非空连通流形	√	√	√	√

• 拓扑学家的正弦曲线. 令 \[ \Align{ T_0 &= \{(x,y)\mid x=0,y\in[-1,1]\}, \\ T_+ &= \{(x,y)\mid x\in(0,2/\pi],y=\sin(1/x)\}, } \] 则 \(T=T_0\cup T_+\) 称为拓扑学家的正弦曲线. 注意 \(T_0\) 和 \(T_+\) 都同胚于区间, 都是(道路)连通的. \(T_0\) 闭, \(T_+\) 开 (相对于 \(T\)).

  

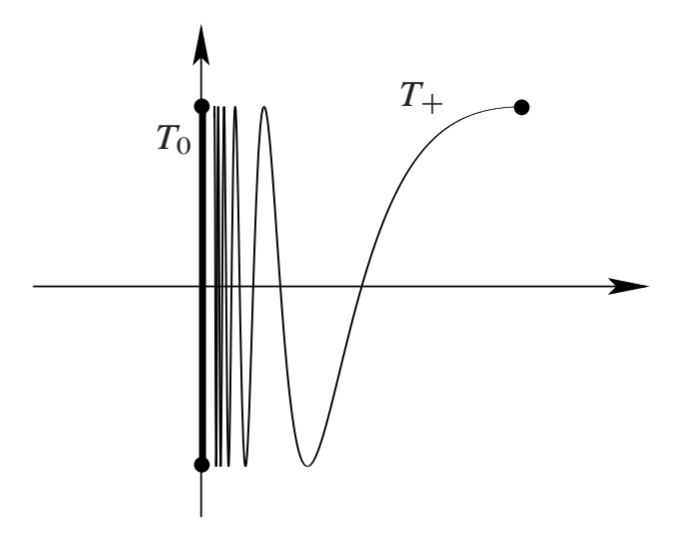
  • 连通: 假设 \(T\) 不连通, 则必定是 \(T_0,T_+\) 间断 \(T\) (因为 \(T_0,T_+\) 都连通). 任给 \(x\in T_0\), 注意到 \(x\) 的任意小邻域 \(U\) 都包含 \(T_+\) 的一些点, 即 \(U\not\subset T_0\), 因此 \(T_0\) 不开, 与假设矛盾.

  • 非道路连通: 任何 \(x\in T_0\) 与 \(y\in T_+\) 不能通过道路连接. 假设存在这样的道路 \(f:[0,1]\to T\). 不妨假设 \(t_0\) 是使得 \(f(t_0)\in T_0\) 的最大的数 (\(t_0\) 总是存在的, 因为 \(T_0\) 闭, 所以 \(f^{-1}(T_0)\) 是闭区间), 记 \(p:=f(t_0)\). 考虑 \(f\) 在 \([t_0,1]\) 上的限制 \(\tilde{f}=f|_{[t_0,1]}\), 这也是连续的.

    对于 \(p\) 的邻域 \(B_r(p)\cap T\) (\(r\) 很小, 比如 \(1/10\)), 它的原像集 \(S:=\tilde{f}^{-1}(B_r(p)\cap T)\subset[t_0,1]\) 由一个孤立点 \(t_0\) 和无穷多段小开区间组成, 不是开集. 因此 \(\tilde{f}\) 不连续, 矛盾.

  • 非局部连通: 设 \(x\in T_0\), 考虑小邻域 \(B_r(x)\) (\(r=1/10\)), 则 \(B_r(x)\) 的任意子邻域都包含无穷多段分量, 都不是连通的. 因此 \(T\) 不局部连通.

• \(T\) 与 \(x\) 轴之并. \(x\) 轴将两个道路分量 \(T_0,T_+\) 连接起来, 使之道路连通, 但仍然不是局部连通的.

• 字典序的单位正方形. 设 \(S=I\times I\) 带有字典序生成的拓扑. 这是一个线性连续统 (序的稠密性显然, 下面证明完备性), 因此是连通的.

  • Dedekind 完备性: 设非空子集 \(A\subset S\), 它在 \(x\) 轴上的投射 \(\pi_1(A)\subset I\) 具有上确界 \(c_1\). 考虑 \(x=c_1\) 截 \(A\) 所得的竖条 \(A_1:=A\times(\{c_1\}\times I)\).

    若 \(A_1\) 非空, 由于它认同于 \(I\) 的子集, 所以具有上确界 \(c_2\), 进而 \((c_1,c_2)\) 便是 \(A\) 的上确界.

    若 \(A_1\) 为空, 我们断言 \((c_1,0)\) 就是 \(A\) 的上确界. 显然它是一个上界. 任给 \((x,y)<(c_1,0)\), 则必然有 \(x<c_1\), 进而 \(x\) 不是 \(\pi_1(A)\) 的上界, \((x,y)\) 不是 \(A\) 的上界. 因此 \((c_1,0)\) 是最小上界.

    • 三个相似的例子: "拓扑流形" 一节末尾的 "不第二可数" 反例, 长直线, 本例. 其中只有后两者是线性连续统 (第一个不满足完备性; 也不是连通的).

  • 局部连通: 所有开区间组成一个拓扑基, 而线性连续统的开区间连通.

  • 非道路连通: 横坐标不同的点无法通过道路连接.

• \(S\) 的锥. 根据锥的连通性定理, \(CS\) 道路连通, 局部连通, 但不局部道路连通.

• \(S\amalg S\). 显然非连通. (不交并的拓扑基, 是原拓扑基的不交并) 局部连通性跟随 \(S\).