GTM202 | 2 构造新的拓扑空间

GTM202 (Introduction to Topological Manifolds) Chapter 3 的笔记.

6 Subspaces

6.1 The subspace topology

子空间拓扑 / 相对拓扑: \({\cal T}_S=\{V\cap S\mid V\in{\cal T}\}\).

• 开集 \(U\subset S\) 为 \(X\) 中开集与 \(S\) 的交. 闭集同理.

• (度量空间) 子空间拓扑 = 限制度量得到的拓扑.

• 注意: \(S\) 中的相对开子集, 相对闭子集.

  • \(S_1=[0,1]\cup(2,3)\), 闭子集 \([0,1]\) 是相对开子集. \(S_2=\{1/n\}_{n=1}^\infty\), 单点子集是相对开子集.

Claim 6.1 (相对开/闭子集) \(X\) 的子空间 \(S\), \(U\subset X\).

• (继承) \(U\) 在 \(S\) 中开, \(S\) 在 \(X\) 中开, 则 \(U\) 在 \(X\) 中开. (对闭同理.)
• \(U\) 在 \(X\) 中开/闭, 则 \(U\) 在 \(S\) 中开/闭.

Claim 6.2 (子空间拓扑的特征性质) 子空间 \(S\subset X\). 任给 \(f:Y\to S\), \(f\) 连续当且仅当 \(i\circ f:Y\to X\) 连续. (特别地, 包含映射 \(i:S\to X\) 是连续的.) \[ \xymatrix{ & X \\ Y \ar[r]_f \ar[ru]^{i\circ f} & S \ar@{_{(}->}[u]_i } \]

子空间拓扑是满足特征性质的唯一拓扑.

• 我们想要子空间拓扑满足: (1) 包含映射连续 (要有足够开集); (2) 若连续映射 \(f:Y\to X\) 的像集包含在 \(S\) 内, 则 \(f:Y\to S\) 也连续 (不能有太多开集). 子空间拓扑是平衡两者的唯一选择.
• 子空间拓扑是使得包含映射 \(S\hookrightarrow X\) 连续的最弱拓扑.

Pf 设 \(f\) 连续. 任给开集 \(U\subset X\), 因为 \((i\circ f)^{-1}(U)=f^{-1}(U\cap S)\), 子空间拓扑意味 \(U\cap S\) 开, 所以 \(f^{-1}(U\cap S)\) 开.

设 \(i\circ f\) 连续. 任给开集 \(U\subset S\), 存在开集 \(V\subset X\) 使得 \(U=V\cap S\), 有 \(f^{-1}(U)=(i\circ f)^{-1}(V)\) 是开集.

Claim 6.3 (连续映射的限制) \(f:X\to Y\) 连续.

• (限制定义域) \(f|_S:S\to Y\) 连续 (\(S\subset X\) 子空间).
• (限制陪域) \(f:X\to T\) 连续 (\(T\subset Y\) 子空间).
• (扩张陪域) \(f:X\to Z\) 连续 (\(Y\subset Z\) 子空间).

Claim 6.4 (子空间拓扑的性质) \(X\) 的子空间 \(S\).

• \(R\) 是 \(S\) 的子空间, 则 \(R\) 也是 \(X\) 的子空间.
• (子空间的基) \({\cal B}_S=\{B\cap S\mid B\in{\cal B}\}\).
• \(S\) 中序列在 \(S\) 下收敛到 \(p\in S\) 当且仅当在 \(X\) 下收敛到 \(p\).
• (继承) Hausdorff, 第一可数, 第二可数.

Claim 6.5 (稠密性夹逼) 设 \(A\subset B\subset X\), 则 \(A\) 在 \(X\) 中稠密, 当且仅当 \(A\) 在 \(B\) 中稠密, 且 \(B\) 在 \(X\) 中稠密.

Pf 设 \(\overline{A}=X\), 则 \(\overline{B}\supset\overline{A}=X\), 于是 \(\overline{A}=\overline{B}=X\).

设 \(A\) 在 \(B\) 中稠密, \(B\) 在 \(X\) 中稠密. 记 \(A\) 在 \(B\) 中的闭包为 \(\overline{A}^B\), 则 \[ B = \overline{A}^B = \bigcap\{(\textsf{包含 }A\textsf{ 的闭集})\cap B\} = \overline{A}\cap B. \] 因此 \(B\subset\overline{A}\), 进而 \(X=\overline{B}\subset\overline{\overline{A}}=\overline{A}\), 有 \(\overline{A}=X\).

Claim 6.6 (边界是流形) 带边 \(n\)-流形 \(M\) 的非空边界 \(\partial M\) (子空间拓扑) 是 \((n-1)\) 维无边流形.

Pf 子空间 \(\partial{M}\) 继承 Hausdorff 性与第二可数性. 下面证明局部欧氏. \(M\) 的坐标开覆盖 \({(U_\alpha,\psi_\alpha)}\) 给出了 \(\partial{M}\) 的一个开覆盖 \(\{U_\alpha\cap\partial{M}\}\). 根据边界的定义, \(\psi_\alpha(U_\alpha\cap\partial{M})=\psi(U_\alpha)\cap\partial{\H^n}\), 其中右边是 \(\partial\H^n=\R^{n-1}\) 的开子集. 因此 \(U_\alpha\cap\partial{M}\) 同胚于 \(\R^{n-1}\) 的开子集, 是欧氏邻域.

6.2 Embeddings

拓扑嵌入: \(f:A\to X\) 单射, 且 \(A\to f(A)\) 是同胚.

• 子空间的包含映射 \(i:S\hookrightarrow X\) 是嵌入.

• (刻画) 开/闭的连续单射是嵌入.

  • 拓扑嵌入 \(f\) 是开/闭映射, 当且仅当 \(f(A)\) 是 \(X\) 的开/bi

• (与同胚) 满射嵌入是同胚.

Claim 6.7 (粘合引理, gluing lemma) 设 \(X\) 的开覆盖/有限闭覆盖 \(\{A_i\}\). 连续映射 \(f_i:A_i\to Y\) 满足 \(f_i|_{A_{ij}}=f_j|_{A_{ij}}\), 则存在唯一连续映射 \(f:X\to Y\) 满足 \(f|_{A_i}=f_i\).

Pf 显然 \(f:X\to Y\) 是唯一存在的.

若 \(\{A_i\}\) 是开覆盖, 则根据连续性的局部 criterion, \(f\) 连续.

若 \(\{A_i\}\) 是有限闭覆盖. 设 \(K\subset Y\) 闭, 注意到 \(f^{-1}(K)\cap A_i=f_i^{-1}(K)\), 且这是闭集 (因为 \(f_i\) 连续, \(f_i^{-1}(K)\) 是 \(A_i\) 的闭子集, 而 \(A_i\) 是 \(X\) 的闭子集, 所有 \(f^{-1}(K)\) 是 \(X\) 的闭子集).

又因为 \(f^{-1}(K)\) 是所有 \(f^{-1}(K)\cap A_i\) 的并, 作为闭集的有限并, 也是闭集. 因此闭集的 \(f\) 原象是闭集, 故连续.

流形的例子.

• 图像: 连续映射 \(f:\R^n\supset U\to\R^k\) 的图像 \(\Gamma(f)=\{(x,y)\mid x\in U,y=f(x)\}\subset\R^{n+k}\), 赋予子空间拓扑. 实际上, \(\Gamma(f)\) 同胚于 \(U\). 考虑 \(\psi:U\to\R^{n+k}\), \(\psi(x)=(x,f(x))\), 这是一个连续单射. 连续的投射 \(\pi_1:\Gamma(f)\to U\) 是 \(\psi\) 的逆映射 (即 \(\psi\) 是开映射) 所以 \(\psi\) 是嵌入, \(\Gamma(f)\) 同胚于 \(U\).

• 单位球面: 考虑 \(\R^{n+1}\) 中的单位球面 \(\mathbb{S}^n\).

  • 作为函数图像. 可以将 \(\mathbb{S}^n\) 分成若干个函数的函数图像. 设 \(U_i^+\) 表示 \(\R^{n+1}\) 中满足 \(x_i>0\) 的子集. \(U_i^-\) 表示 \(x_i<0\) 的子集. 因为 \(\mathbb{S}^n\) 不包含原点, 所以 \(U_1^\pm,\dots,U_n^\pm\) 覆盖住 \(\mathbb{S}^n\). 在 \(U_i^\pm\) 上解方程 \(\|x\|=1\) 得到 \(x\in \mathbb{S}^n\cap U_i^\pm\) 当且仅当 \[ x_i = \pm\sqrt{1-(x_1)^2-\dots-(x_{i-1})^2-(x_{i+1})^2-\dots-(x_n)^2}. \] 因此 \(\mathbb{S}^n\cap U_i^\pm\) 是连续函数的图像, 同胚于 \(\R^n\) 中的开集. 因此 \(\mathbb{S}^n\) 是 \(n\) 维流形.

  • 球极投影 (stereographic projection). 设北极点 \(N=(0,\dots,0,1)\), 映射 \(\sigma:\mathbb{S}^n\setminus\{N\}\to\R^n\) 将 \(x\in \mathbb{S}^n\setminus\{N\}\) 映到点 \(u\in\R^n\), 满足 \(N,x,U=(u,0)\) 三点共线. 可得 \[ \sigma(x_1,\dots,x_{n+1})=\frac{(x_1,\dots,x_n)}{1-x_{n+1}}. \] 容易算出其逆映射为 \[ \sigma^{-1}(x_1,\dots,x_n) = \frac{(2u_1,\dots,2u_n,\|u\|^2-1)}{\|u\|^2+1}. \] 因为 \(\sigma,\sigma^{-1}\) 都是连续的, 所以 \(\mathbb{S}^n\setminus\{N\}\) 同胚于 \(\R^n\), 给出了 \(N\) 以外的点的欧氏邻域. 南极点的球极投影给出了 \(N\) 的欧氏邻域.

• 甜甜圈面: \(xz\)-平面中的圆周 \(C:(x-2)^2+z^2=1\) 绕 \(z\) 轴旋转一周所得曲面 \(D\). 令 \(r=\sqrt{x^2+y^2}\), 则环面由方程 \((r-2)^2+z^2=1\) 给出. 引入参数 \(\theta\) 表示以 \(z\) 为轴的经度角, \(\phi\) 表示圆 \(C\) 的圆心角, 则环面 \(D\) 的一个参数化是 \(F:\R^2\to D\), \[ F(u,v)=((2+\cos{2\pi u})\cos{2\pi v},(2+\cos{2\pi u})\sin{2\pi v}, \sin{2\pi u}). \] \(F\) 是局部同胚, 所以 \(D\) 是 \(2\)-流形.

7 Product spaces

7.1 Finite products

积拓扑: 拓扑空间 \(X_1,\dots,X_n\) 的乘积拓扑由 \({\cal B}=\{U_1\times\cdots\times U_n\mid U_i\in{\cal T}_i\}\) 生成.

• 欧氏空间 \(\R^n=\R\times\cdots\times\R\) 的乘积拓扑与度量拓扑相同.

Claim 7.1 (乘积拓扑的特征性质) 映射 \(f:Y\to\prod X_i\) 连续, 当且仅当任何分量 \(f_i=\pi_i\circ f\) 连续. \[ \xymatrix{ & \prod X_i \ar@{->>}[d]^{\pi_i} \\ Y \ar[r]_{f_i} \ar[ur]^f & X_i } \]

特别地, 自然投射 \(\pi_i:\prod X_i\to X_i\) 连续. 此外, 乘积拓扑是满足特征性质的唯一拓扑.

Claim 7.2 (乘积拓扑的性质)

• (结合性) \(X_1\times X_2\times X_3\), \((X_1\times X_2)\times X_3\), \(X_1\times(X_2\times X_3)\) 上的拓扑相同.

• (嵌入) 下面映射是拓扑嵌入 \[ \Align{ f: X_i &\to X_1\times\cdots\times X_n, \\ x &\mapsto (x_1,\dots,x_{i-1},x,x_{i+1},\dots,x_n). } \]

  • 可以证明, 这是一个闭的连续单射.

• (自然投射) 自然投射 \(\pi_i:\prod X_i\to X_i\) 是开映射.

• (基的乘积) \(X_i\) 的基 \({\cal B}_i\), 则积拓扑的基 \(\{B_1\times\cdots\times B_n\mid B_i\in{\cal B}_i\}\).

• (积与子空间拓扑) \(S_i\) 为 \(X_i\) 子空间, 则 \(\prod S_i\) 的积拓扑与作为 \(\prod X_i\) 的子空间拓扑相同.

• (继承) \(X_i\) Hausdorff/第一可数/第二可数, 则 \(\prod X_i\) 也具有相同性质.

Claim 7.3 (Hausdorff 的对角线刻画) \(X\) Hausdorff 当且仅当对角线 \(\Delta=\{(x,x)\mid x\in X\}\) 在 \(X\times X\) 中闭.

Pf 设 Hausdorff. 任给 \((x,y)\in\Delta^C\), 则 \(x\neq y\), 存在邻域 \(U_x\cap U_y=\emptyset\), 进而 \(U_x\times U_y\subset\Delta^C\), 说明 \(\Delta^C\) 开, 即 \(\Delta\) 闭.

反之, 设 \(\Delta\) 闭, 则任给 \((x,y)\in\Delta^C\), 则存在邻域 \(U_{(x,y)}\subset\Delta^C\), 自然投射 \(U_x=\pi_1(U_{(x,y)})\) 和 \(U_y=\pi_2(U_{x,y})\) 给出了 \(x,y\) 的不交邻域.

积映射: \((\prod f_i)(x_1,\dots,x_k)=(f_1(x_1),\dots,f_k(x_k))\).

Claim 7.4 连续映射的乘积是连续映射, 同胚的乘积是同胚.

Pf 设 \(f_i:X_i\to Y_i\) 连续, (连续的基 criterion) 取 \(\prod Y_i\) 的开集 \(\prod U_i\) (\(U_i\) 是 \(Y_i\) 的开集), 则 \[ \pqty{\prod f_i}^{-1}\pqty{\prod U_i} = \prod f_i^{-1}(U_i), \] 因为每一个 \(f_i^{-1}(U_i)\) 开, 所以其乘积开, \(\prod f_i\) 连续. 双射的乘积是双射; 同上可证开映射的乘积是开映射, 所以同胚的乘积是同胚.

Claim 7.5 (积流形) \(M_1,\dots,M_k\) 分别为 \(n_1,\dots,n_k\) 维流形, 则 \(\prod M_i\) 是 \(\sum n_i\) 维流形.

Pf 积空间 \(\prod M_i\) 继承第二可数和 Hausdorff 性. 设 \((x_1,\dots,x_k)\in\prod M_i\), 取 \(x_i\) 的欧氏邻域 \(U_i\in M_i\), 则 \(\prod U_i\) 也是开集, 又因为同胚的乘积还是同胚, 所以 \(\prod U_i\) 同胚于 \(\prod\R^{n_i}=\R^{\sum n_i}\) 的开集. 因此 \(\prod M_i\) 是 \(\sum n_i\) 维流形.

• 环面 (torus): \(\mathbb{T}^n=\mathbb{S}^1\times\cdots\times \mathbb{S}^1\).

7.2 Infinite products

无穷乘积: \(\prod X_\alpha\), 默认为积拓扑.

• 箱拓扑: \({\cal B}_0=\{\prod U_\alpha\mid U_\alpha\in{\cal T}_\alpha\}\) 生成.

• 积拓扑: \({\cal B}=\{\prod U_\alpha\mid U_\alpha\in{\cal T}_\alpha,\textsf{ 只有有限个 } U_\alpha\neq X_\alpha\}\) 生成.

  • 当只有有限个 \(X_\alpha\) 具有非平凡拓扑时, 积拓扑与箱拓扑相同.
  • 若有无穷多个非平凡 \(X_\alpha\), 考虑 \(U=\prod U_\alpha\), 其中无穷多个 \(U_\alpha\neq X_\alpha\). 则 \(U\) 在箱拓扑下开, 在积拓扑下不是开集.

Claim 7.6 (无穷积拓扑特征性质) 映射 \(f:Y\to\prod X_\alpha\) 连续, 当且仅当所有 \(f_\alpha=\pi_\alpha\circ f\) 连续. 积拓扑是满足特征性质的唯一拓扑.

Pf \(f\) 连续推出 \(f_i\) 连续是平凡的. 设 \(f_i\) 连续, 开集 \(\prod U_\alpha\subset \prod X_\alpha\). 因为 \[ f^{-1}\pqty{\prod U_\alpha}=\bigcap f^{-1}(U_\alpha), \] 注意, 只有有限个 \(U_\alpha\neq X_\alpha\), 所以右边实际上是有限交, 因此仍是开集.

8 Disjoint union spaces

不交并拓扑: 设不交并 \(\coprod X_\alpha\). 子集 \(U\subset\coprod X_\alpha\) 是开集, 当且仅当所有 \(U\cap X_\alpha\) 是开集.

Claim 8.1 (不交并拓扑的特征性质) 映射 \(f:\coprod X_\alpha\to Y\) 连续, 当且仅当任意限制 \(f_\alpha=f\circ i_\alpha\) 连续. 不交并拓扑是满足特征性质的唯一拓扑. \[ \xymatrix{ & \coprod X_\alpha \\ Y \ar[r]_{f_\alpha} \ar[ru]^f & X_\alpha \ar@{_{(}->}[u]_{i_\alpha} } \]

Pf 设 \(f\) 连续, 由 \(f_\alpha^{-1}(U)=X_\alpha\cap f^{-1}(U)\) 即得. 设 \(f_\alpha\) 连续, 注意到 \(f^{-1}(U) = \bigcup f_\alpha^{-1}(U)\), 开集的任意并都是开集.

Claim 8.2 (不交并拓扑的性质)

• (闭集刻画) \(U\subset\coprod X_\alpha\) 闭, 当且仅当每个 \(U\cap X_\alpha\) 闭.
• (包含映射) \(i_\alpha:X_\alpha\to\coprod X_\alpha\) 是拓扑嵌入 (连续单射, 既开又闭).
• (不交并与积拓扑) 若 \(Y\) 是离散空间, 则拓扑空间 \(X\times Y\) 与 \(\coprod_{y\in Y}X\) 认同.
• (继承) \(X_i\) Hausdorff/第一可数/第二可数(且指标集可数), 则 \(\prod X_i\) 也具有相同性质.

Claim 8.3 (不交并流形) 若干 \(n\) 维流形 \((M_\alpha)_{\alpha\in A}\) 的不交并是流形, 当且仅当 \(A\) 可数.

Pf 若 \(A\) 可数, 则 \(\coprod M_\alpha\) 第二可数且 Hausdorff. 任意 \(M_\alpha\) 的某欧氏邻域 \(U\) 也是 \(\coprod M_\alpha\) 的欧氏邻域.

若 \(A\) 不可数, 只需说明 \(\coprod M_\alpha\) 不是第二可数的. 设 \(M_\alpha\) 的开覆盖 \(\{U_\alpha\}\), 则 \(\coprod\{U_\alpha\}\) 构成了 \(\coprod M_\alpha\) 的开覆盖. 这个覆盖不可数, 且没有可数子覆盖 (不满足第二可数空间的性质).

9 Quotient spaces

9.1 The quotient topology

商拓扑: 拓扑空间 \(X\), 满射 \(q:X\to Y\). 定义 \(U\subset Y\) 为开集, 当且仅当 \(q^{-1}(U)\) 是 \(X\) 的开集. 此时 \(q\) 称为商映射. 商映射显然是连续的.

设拓扑空间 \(X\) 上的等价关系 \(\sim\), \(q:X\to X/{\sim}\), \(x\mapsto[x]\). 在 \(q\) 的商拓扑下, \(X/{\sim}\) 称为商空间.

• 商空间一般不继承 Hausdorff, 可数, 局部欧氏性质.

Claim 9.1 (商的第二可数条件) 设 \(P\) 第二可数, \(M\) 是商空间. 若 \(M\) 局部欧氏, 则它也第二可数.

• 因此, 流形的商空间, 如果局部欧氏且 Hausdorff 的话, 也是流形.

Pf 记商映射 \(q:P\to M\). 对于 \(M\) 的坐标球开覆盖 \({\cal U}\), \(q^{-1}[{\cal U}]\) 是 \(P\) 的开覆盖. 它有可数子覆盖 \(q[{\cal U}']\), 其中 \({\cal U}'\) 可数. 于是 \({\cal U}'\) 是 \(M\) 的坐标球可数开覆盖. 坐标球第二可数, 则 \(M\) 也第二可数.

Claim 9.2 (商的 Hausdorff 条件) 设开的商映射 \(q:X\to Y\), 则 \(Y\) Hausdorff 当且仅当 \[ {\cal R}=\{(x_1,x_2)\mid q(x_1)=q(x_2)\} \] 在 \(X\times X\) 中闭.

Pf 设 \(Y\) Hausdorff. 对 \((x_1,x_2)\notin{\cal R}\), 存在 \(q(x_1),q(x_2)\) 的不交邻域 \(V_1,V_2\subset Y\), 则 \(q^{-1}(V_1)\times q^{-1}(V_2)\) 是 \((x_1,x_2)\) 的邻域, 且与 \({\cal R}\) 不交, 因此 \({\cal R}\) 闭.

反之, 设 \({\cal R}\) 闭. 设不同的两点 \(y_1,y_2\in Y\), 取 \(x_i\in X\) 满足 \(q(x_i)=y_i\). 因为 \((x_1,x_2)\notin{\cal R}\), 存在邻域 \(U_1\times U_2\subset X\times X\) 与 \({\cal R}\) 不交. 因为 \(q\) 开, \(q(U_1),q(U_2)\) 是 \(y_1,y_2\) 的不交邻域.

• 若 \(q\) 是等价关系 \(\sim\) 确定的, 则定理表明, \(X/{\sim}\) 闭当且仅当 \(\sim\) 在 \(X\times X\) 闭.

9.2 Properties of the quotient map

设 \(X,Y\) 为拓扑空间, \(q:X\to Y\) 是商映射.

• 子集 \(q^{-1}(y)\) 称为 \(y\in Y\) 的纤维. 子集 \(U\subset X\) 称为关于 \(q\) 饱和, 若 \(U=q^{-1}(V)\).

  • \(U\) 饱和 \(\iff U=q^{-1}(q(U))\iff U\) 是纤维之并.

Claim 9.3 (商映射刻画) 连续满射 \(q:X\to Y\) 是商映射, 当且仅当 \(q\) 将饱和开/闭集映到开/闭集.

• 一个充分条件: 连续的开/闭满射是商映射.

Pf 设 \(q\) 商映射, 则是连续的, 显然将饱和开/闭集映到开/闭集.

设 \(q\) 将饱和开集映到开集. 任给子集 \(U\subset Y\), 注意 \(q^{-1}(U)\) 是饱和子集. 若 \(q^{-1}(U)\) 开, 则 \(U\) 开. 若 \(U\) 开, 则 \(q^{-1}(U)\) 开 (因为 \(q\) 连续). 因此 \(q\) 是商映射.

设 \(q\) 将饱和闭集映到闭集. 任给子集 \(U\subset Y\). 若 \(q^{-1}(U)\) 开, 即 \(X\setminus q^{-1}(U)=q^{-1}(Y\setminus U)\) 闭, 则 \(Y\setminus U\) 闭, 即 \(U\) 开. 若 \(U\) 开, 则 \(q^{-1}(U)\) 开 (连续性). 因此 \(q\) 是商映射.

Claim 9.4 (商映射的性质)

• 商映射的复合是商映射.
• 单射的商映射是同胚.
• \(K\subset Y\) 闭, 当且仅当 \(q^{-1}(K)\) 闭.
• (限制) 商映射在饱和开/闭集上的限制是商映射.
• 一族商映射 \(q_\alpha:X_\alpha\to Y_\alpha\), 若 \(q:\coprod X_\alpha\to\coprod Y_\alpha\) 满足 \(q|_{X_\alpha}=q_\alpha\), 则 \(q\) 也是商映射.

Claim 9.5 (连续的开/闭映射的性质总结) 设开/闭的连续映射 \(f:X\to Y\).

• 若单射, 则是拓扑嵌入.
• 若满射, 则是商映射.
• 若双射, 则是同胚.

商的特征性质.

Claim 9.6 (商映射的特征性质) 商映射 \(q:X\to Y\). 映射 \(f:Y\to Z\) 连续当且仅当 \(f\circ q\) 连续. \[ \xymatrix{ X \ar[d]_q \ar[dr]^{f\circ q} \\ Y \ar[r]_f & Z } \]

Pf 对开集 \(U\), 因为 \(q^{-1}(f^{-1}(U))=(f\circ q)^{-1}(U)\), 所以 \(f^{-1}(U)\) 开当且仅当 \((f\circ q)^{-1}(U)\) 开.

Claim 9.7 (商拓扑的唯一性) 设拓扑空间 \(X\), 集合 \(Y\), 满射 \(q:X\to Y\). 商拓扑是满足特征性质的唯一拓扑.

Claim 9.8 (唯一下降/泛性质) 设商映射 \(q:X\to Y\). 任给连续映射 \(f:X\to Z\) 满足在纤维上常值, 则存在唯一连续映射 (称为 \(f\) 在商空间的下降) \(\tilde{f}:Y\to Z\) 使得 \(f=\tilde{f}\circ q\). \[ \xymatrix{ X \ar[d]_q \ar[dr]^f \\ Y \ar@{.>}[r]_{\tilde{f}} & Z } \]

Pf 存在唯一性由商集合的泛性质保证. 连续性由商拓扑特征性质保证.

Claim 9.9 (商空间唯一性) 设商映射 \(q_1:X\to Y_1\) 和 \(q_2:X\to Y_2\) 满足 \(q_1(x)=q_1(x')\) 当且仅当 \(q_2(x)=q_2(x')\), 则存在唯一的同胚 \(\phi:Y_1\to Y_2\), 使得 \(\phi\circ q_1=q_2\).

商空间的例子.

• 单位圆. \(\R\) 上的等价关系 \(x\sim y\iff x-y\in\Z\). 商空间 \(\R/{\sim}\) 同胚于 \(\mathbb{S}^1\).

  Pf 设 \(q:\R\to \mathbb{S}^1\), \(q(t)=\e^{2\pi\i t}\). 要证明 \(q\) 开, 只需考虑 \(\R\) 的拓扑基, 即所有的开区间即可. 对于长度 \(\geq1\) 的开区间, 它映到整个 \(\mathbb{S}^1\), 当然是开的. 对于长度 \(<1\) 的开区间, 它映到 \(\mathbb{S}^1\) 上的一段弧 (不含端点), 显然是某 \(\R^2\) 开球与 \(\mathbb{S}^1\) 的交, 所以是开集. 因此 \(q\) 是开的满射, 进而是商映射.

  注意到 \(q:\R\to \mathbb{S}^1\) 和 \(\R\to\R/{\sim}\) 给出相同的 identification, 根据商映射的唯一性 \(\mathbb{S}^1\) 同胚于 \(\R/{\sim}\).

  • 连续的 \(\Z\) 周期函数 \(f:\R\to\R\) 可以唯一地下降到 \(\tilde{f}:\R/{\sim}\to\R\).

• 球面. \(\R^{n+1}\setminus\{0\}\), 定义映射 \(q:\R^{n+1}\setminus\{0\}\to \mathbb{S}^n\), \(q(x)=x/\|x\|\). 这是一个连续的满射. \(q\) 的饱和开子集是开射线之并, 显然 \(q\) 将饱和开子集映到饱和开子集, 进而是商映射.

• 实射影空间. \(\R^{n+1}\setminus\{0\}\) 上的等价关系 \(x\sim y\iff x=\lambda y\) (\(\lambda\in\R^*\)). 商空间称为实射影空间 \(\mathbb{RP}^n\).

• 将子集坍缩为一点. 设子集 \(A\subset X\). 等价关系 \(a_1\sim a_2\) 对任意 \(a_1,a_2\in A\), 而 \(x\sim x\) 对任意 \(x\notin A\). 记 \(X/A:=X/{\sim}\), 即将 \(A\) 坍缩到一点.

• 锥(cone). \(I=[0,1]\). 商空间 \((X\times I)/(X\times\{0\})\) 称为 \(X\) 上的锥, 记作 \(CX\).

  • 考虑 \(X\times I\) 的饱和子集 \(X\times\{1\}\), 商映射 \(q:X\times I\to CX\) 限制到 \(X\times\{1\}\) 仍是商映射. 记 \(X^*=q(X\times\{1\})\), 则商映射 \(X\cong X\times\{1\}\to X^*\) 是单射, 进而是同胚. 一般认同 \(X\) 和 \(X^*\), 将 \(X\) 视作 \(CX\) 的子空间.

• 楔和/一点并. 设拓扑空间 \(X_\alpha\), 给定 \(p_\alpha\in X_\alpha\) 称为基点. 楔和 \(\bigvee X_\alpha\) 定义为 \(\coprod X_\alpha\) 将 \(\{p_\alpha\}_{\alpha}\) 认同为一点的商空间. 例如, \(\R\vee\R\) 同胚于平面上的 \(xy\) 轴之并; \(\mathbb{S}^1\vee \mathbb{S}^1\) 同胚于一个 8 字.

• 两个原点的直线. 令 \(X=(\R\times\{0\})\cup(\R\times\{1\})\subset\R^2\), 等价关系 \((x,0)\sim(x,1)\) 对 \(x\neq0\). 商空间 \(X/{\sim}\) 称为两个原点的直线. 它是局部欧氏且第二可数的, 但不 Hausdorff.

10 Adjunction spaces

黏着空间: 设拓扑空间 \(X,Y\), 闭子集 \(A\subset X\), 连续映射 \(f:A\to Y\). 设 \(X\amalg Y\) 上的等价关系 \(a\sim f(a)\) 对任意 \(a\in A\), 则黏着空间 \(X\cup_fY:=(X\amalg Y)/{\sim}\). 称 \(Y\) 沿着 \(f\) 黏合到 \(X\), 映射 \(f\) 称为贴映射(attaching map). 特别地, 若 \(A\) 空, 则黏着空间是不交并.

Claim 10.1 (黏着空间的性质) 设商映射 \(q:X\amalg Y\to X\cup_fY\).

• \(q|_X\) 是拓扑嵌入, \(q(X)\) 是 \(X\cup_fY\) 的闭子空间.
• \(q|_{Y\setminus A}\) 是拓扑嵌入, \(q(Y\setminus A)\) 是 \(X\cup_fY\) 的开子空间.
• \(X\cup_fY\) 是 \(q(X)\) 和 \(q(Y\setminus A)\) 的不交并.

• 因此, \(X,Y\setminus A\) 分别认同于 \(q(X),q(Y\setminus A)\), 视作 \(X\cup_fY\) 的子空间.

Pf 先证明 \(q\) 是闭映射. 任取闭集 \(B\subset X\), 要证明 \(q(B)\) 在 \(X\cup_fY\) 中闭, 等价于 \(q^{-1}(q(B))\) 在 \(X\amalg Y\) 中闭, 即 \[ q^{-1}(q(B))\cap X,\quad q^{-1}(q(B))\cap Y \] 分别闭. 前者等于 \(B\), 根据假设是闭的. 后者等于 \(f^{-1}(B)\), 由 \(f\) 的连续性, 是闭的. 这样, \(q\) 是闭映射, 所以 \(q(X)\) 是闭集. 又 \(q|_X\) 是单的闭映射, 进而是嵌入.

注意 \(X\setminus A\subset X\amalg Y\) 是饱和子集, 所以 \(q|_{Y\setminus A}\) 是商映射, 故单射 \(q|_{X\setminus A}:X\setminus A\to q(X\setminus A)\) 是同胚. 特别地, \(q(X\setminus A)\) 开.

黏着空间的例子.

• 选定基点 \(x,y\) 的拓扑空间 \(X,Y\), 令 \(A=\{y\}\), \(f:A\to X\) 定义为 \(f(y)=x\), 则 \(X\cup_fY\) 是楔和 \(X\vee Y\).
• 令 \(A=\mathbb{S}^2\subset\overline{\mathbb{B}^2}\), 包含映射 \(f:A\hookrightarrow\overline{\mathbb{B}^2}\), 则 \(\overline{\mathbb{B}^2}\cup_f\overline{\mathbb{B}^2}\) 同胚于 \(\mathbb{S}^2\).

流形沿着边界贴合. 设 \(n\) 维带边流形 \(M,N\), 边界非空且 \(h:\partial N\to\partial M\) 同胚. 注意 \(\partial{N}\) 是 \(N\) 的闭子集, 则有黏着空间 \(M\cup_hN\).

Claim 10.2 (流形沿着边界贴合) \(M\cup_hN\) 是 \(n\) 维无边流形. 有嵌入 \(e:M\to M\cup_hN\), \(f:N\to M\cup_hN\), 其像都是闭子集, 且 \[ \Align{ e(M)\cup f(N)&=M\cup_hN \\ e(M)\cap f(N)&=e(\partial M)=f(\partial N). } \]

Pf 因为 \(h\) 是同胚, 有 \(M\cup_hN=N\cup_{h^{-1}}M\). 根据黏着空间的性质, 取 \(e=q|_M\), \(f=q|_N\) 即可满足上面的条件. 下面证明 \(M\cup_h N\) 是 \(n\) 维无边流形. 根据 Claim 9.1, 只用证明局部欧氏与 Hausdorff.

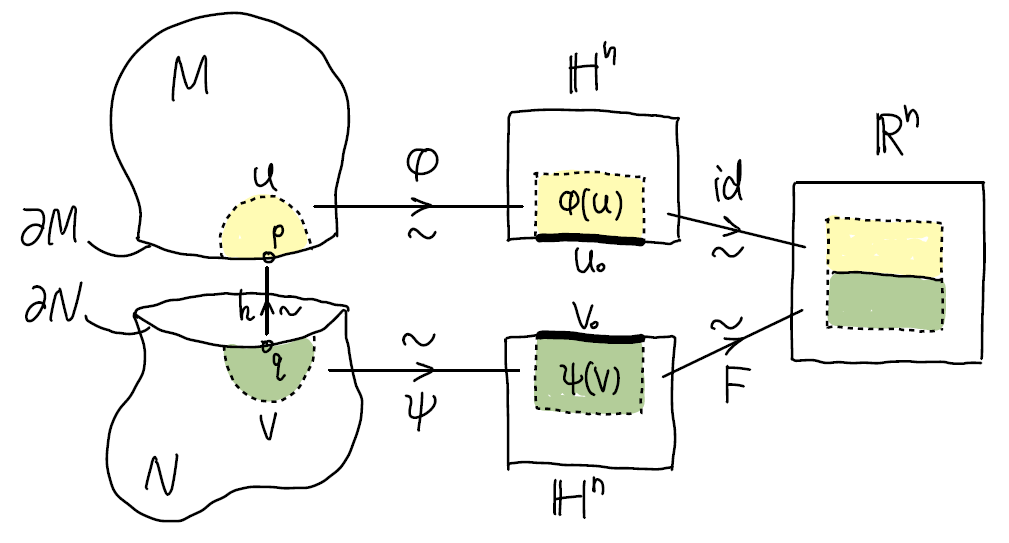
局部欧氏. 对于 \(M,N\) 的内部点, 因为内部是开子集, 故其充分小坐标球仍在内部, 可以作为 \(M\cup_h N\) 的坐标球. 对于 \(M,N\) 的一对边界点 \(x,y\) (有 \(h(x)=y\)), 记 \(s=q(x)=q(y)\), 我们的想法是将两者的边界坐标系 "拼和" 成 \(s\) 的一个内部坐系.

取 \(x,y\) 的坐标系 \(U,V\), 设 \(\varphi\) 将 \(U\) 映到 \(\H^n\) (作为上半平面) 的矩形, \(\psi\) 将 \(V\) 映到 \(\H^n\) (作为下半平面) 的矩形 (如图). 适当缩小 \(U,V\), 我们设 \(U\cap\partial{M}\) 与 \(V\cap\partial{N}\) 中的点通过 \(h\) 一一对应.

此时 \(U_0=\varphi(U)\cap\partial\H^n\) 和 \(V_0=\psi(V)\cap\partial\H^n\) 的对应点可能不在对应位置上. 因此 \(\varphi(U)\) 和 \(\psi(V)\) 不能直接拼合, 需要对 \(\psi(V)\) 进行一个变换 \(F\). 这 \(F\) 应当满足 \[ (F\circ\psi)(p) = (\varphi\circ h)(p),\quad\forall p\in V\cap\partial{N}. \] 即 \(F|_{V_0}\) 的取值是确定的, 将其延拓到 \(\psi(V)\) (取 \(F|_{V_0}\) 与恒等映射的积即可). 定义 \(\Phi:U\amalg V\to\R^n\), \[ \Phi|_U:=\varphi,\quad \Phi|_V:=F\circ\psi. \] 因为 \(U\amalg V\) 是饱和开子集, \(q\) 在其上的限制是商映射, 且 \(q(U\amalg V)\) 是 \(M\cup_hN\) 的开集. 根据 \(F\) 的取法, \(\Phi\) 可以下降到商空间 \(\tilde{\Phi}:q(U\amalg V)\to\R^n\), 它的一个逆映射是 \[ \tilde\Phi^{-1}(p) = \Cases{ (q\circ\varphi^{-1})(p), & p^n\geq0, \\ (q\circ\psi^{-1}\circ F^{-1})(p), & p^n\leq0, } \] 根据 gluing lemma, \(\tilde\Phi^{-1}\) 连续, 故 \(\tilde\Phi\) 是同胚, 即 \(s\) 的一个坐标映射.

Hausdorff. 即证明 \(q\) 的纤维可被饱和开集分离.

流形的双倍: 设带边流形 \(M\), 恒等映射 \(h={\rm id}_{\partial M}\), 则 \(D(M):=M\cup_hM\) 称为 \(M\) 的双倍. 若 \(\partial M\) 为空, 则 \(D(M)=M\amalg M\).

Claim 10.3 (带边流形 \(\cong\) 闭子集) 任意带边 \(n\) 维流形都与 \(n\) 维流形 (比如 \(D(M)\)) 的闭子集同胚.

11 Group actions

11.1 Topological groups

拓扑群: 群 \(G\) 有拓扑结构, 且 \(\mu:G\times G\to G\), \(\mu(g,h)=gh\) 和 \(\iota:G\to G\), \(\iota(g)=g^{-1}\) 都连续.

Claim 11.1 (群结构 & 拓扑结构相容) 对于拓扑群,

• (子群) 子群是拥有子空间拓扑的拓扑群.
• (直积群) 有限直积是拥有积拓扑的拓扑群.
• (闭包) 子群的闭包也是子群.

Pf 1, 设子群 \(H\) 配以子空间拓扑, 嵌入 \(i_H:H\to G\), 则 \(\mu_H=\mu\circ(i_H,i_H)\) 以及 \(\iota_H=\iota\circ i_H\) 作为连续映射的复合, 都是连续的.

2, 设直积群 \(H=\prod G_i\) 配以积拓扑. 一方面, 逆 \(\iota_H=\prod\iota_i\) 作为连续映射的积, 是连续的. 另一方面, \(H\times H\cong \prod(G_i\times G_i)\), 进而乘积 \[ \mu_H:H\times H\cong \prod(G_i\times G_i)\to\prod G_i \] 可以认同为 \(\prod \mu_i\), 所以是连续的.

3, 设子群 \(H\), 需要证明 \(\overline{H}\) 对乘积 \(\mu\) 和逆 \(\iota\) 封闭. 对于逆, \(\iota\) 连续且 \(\iota(H)=H\), 利用连续的刻画,

\(\iota(\overline{H})=\overline{\iota(H)}=\overline{H}\), 可得 \(\overline{H}\) 对逆封闭. 同理可得 \(\overline{H}\) 对 \(\mu\) 封闭.

• 左平移: \(l_g(g')=gg'\), 是连续的, 因为 \(l_g=\mu\circ i_g\), 其中嵌入 \(i_g(g')=(g,g')\). 又 \(l_g^{-1}=l_{g^{-1}}\), 所以左平移是同胚.

• 右平移 \(r_g(g')=g'g\) 也是同胚.

• 拓扑齐性: \(X\) 的任意两点 \(x,y\), 存在同胚 \(\varphi:X\to X\) 满足 \(\varphi(x)=y\). 拓扑群是拓扑齐性的.

拓扑群的例子.

• 实数加法群 \(\R\) 和直积群 \(\R^n\).
• 实数乘法群 \(\R^*\) 和子群, 正实数乘法群 \(\R^+\).
• 复数乘法群 \(\C^*\) 和子群, 单位复数乘法群 \(\mathbb{S}^1\).
• 环面 \(\mathbb{T}^n=\mathbb{S}^1\times\cdots\times \mathbb{S}^1\).
• 离散群, 拥有离散拓扑的群.
• 一般线性群 \({\rm GL}(n,\R)\), 由 \(n\times n\) 可逆实矩阵组成, 拥有 \(\R^{n^2}\) 的子空间拓扑.
• 复一般线性群 \({\rm GL}(n,\C)\).
• 正交群 \({\rm O}(n)\), 是 \({\rm GL}(n,R)\) 的子群, 由正交阵组成.

11.2 Group actions

群作用.

• 左作用: \(G\times X\to X\), 满足 \(g_1\cdot(g_2\cdot x)=(g_1g_2)\cdot x\) 和 \(e\cdot x=x\). 同理有右作用.

• 同胚作用: 若 \(X\) 是拓扑空间, 且对任意 \(g\in G\), \(x\mapsto g\cdot x\) 是同胚.

• 连续作用: \(G\times X\to X\) 是连续映射.

Claim 11.2 (连续作用 & 同胚作用)

• 连续的作用是同胚作用.
• 若 \(G\) 离散, 则作用是连续的当且仅当它是同胚作用.

Pf 设作用 \(G\times X\to X\) 连续, 这意味着 \(x\mapsto g\cdot x\) 也连续, 因为它是复合 \(x\mapsto(g,x)\mapsto g\cdot x\). 左作用的定义保证 \(x\mapsto g\cdot x\) 的逆映射是 \(x\mapsto g^{-1}\cdot x\), 它也是连续的. 因此 \(x\mapsto g\cdot x\) 是同胚.

设 \(G\) 离散, 只需证明同胚作用是连续的. 此时, 映射 \(G\times X\to X\) 限制到任意 \(\{g\}\times X\) 上是连续的. 因为 \(\{g\}\times X\) 构成 \(G\times X\) 的开覆盖, 由 gluing lemma, \(G\times X\to X\) 是连续的.

• 轨道: \(G\cdot x=\{g\cdot x\mid g\in G\}\subset X\).

• 传递作用: 任何点的轨道都是 \(X\).

• 自由作用: \(g\cdot x=x\) (存在 \(x\in X\)) 蕴含 \(g=e\).

• 轨道空间: 等价关系 \(x\sim y\iff x=g\cdot y\), 即 \(x,y\) 在同一轨道中. 商空间 \(X/{\sim}:=X/G\) 称为轨道空间. 等价关系称作轨道关系.

Claim 11.3 (轨道关系是开的) 商映射 \(q:X\to X/G\) 是开映射.

Pf 任给 \(U\subset X\), 要证明 \(q(U)\) 开, 即证 \(q^{-1}(q(U))\) 开. 根据定义, \[ q^{-1}(q(U)) = \{g\cdot x\in X\mid g\in G, x\in U\} = \bigcup_{g\in G} g\cdot U, \] 因为 \(x\mapsto g\cdot x\) 是同胚, \(U\) 开, 所以 \(g\cdot U\) 开. 作为开集之并, \(q^{-1}(q(U))\) 也开.

立刻得到推论:

Claim 11.4 (轨道空间的 Hausdorff 判定) \(X/G\) Hausdorff 当且仅当 \[ {\cal O}=\{(x_1,x_2)\mid x_1=g\cdot x_2,\exists g\in G\} \] 在 \(X\times X\) 中闭.

子群在群上的作用.

• 拓扑群 \(G\) 的子群 \(\Gamma\) 右作用于 \(G\). 轨道 \(\{g\gamma\mid\gamma\in\Gamma\}=g\Gamma\) 是 \(\Gamma\) 的左陪集. 轨道空间 \(G/\Gamma\) 称为左陪集空间.

Claim 11.5 (陪集空间的齐性) 陪集空间 \(G/\Gamma\) 是拓扑齐性的.

Pf 任取 \(g\in G\), 同胚 \(l_g:G\to G\), 考虑 \(\theta_g:G/\Gamma\to G/\Gamma\), \(\theta_g(h\Gamma)=gh\Gamma\). 显然这是双射, 且满足交换图 \[ \xymatrix{ G \ar[d]_q \ar[r]^{l_g} & G \ar[d]^q \\ G/\Gamma \ar[r]_{\theta_g} & G/\Gamma. } \] 任取开集 \(U\subset G/\Gamma\), 计算得到 \(\theta_g^{-1}(U)=(q\circ l_g\circ q^{-1})(U)\), 其中 \(q,l_g\) 都是连续的开映射, 所以右侧是开集, 故 \(\theta_g^{-1}\) 连续. 同理得到 \(\theta_g\) 是开映射, 进而同胚.

任意两个陪集 \(g\Gamma,h\Gamma\) 通过同胚 \(\theta_{hg^{-1}}\) 联系.

Claim 11.6 (商群) 若 \(\Gamma\) 是正规子群, 则商群 \(G/\Gamma\) 是拥有商拓扑的拓扑群.

Pf 只需证明 \(G/\Gamma\) 上的 \(\mu',\iota'\) 连续. 根据商群的定义, \[ \Align{ \mu'\circ(q,q) &= (q,q)\circ\mu,& \iota'\circ q &= q\circ\iota, } \] 任取开集 \(U\subset G/\Gamma\), 有 \(\mu'^{-1}(U)=(q,q)\circ\mu^{-1}\circ(q,q)^{-1}(U)\), 其中 \((q,q)\) 是连续的开映射 (是连续开映射的直积), \(\mu^{-1}\) 连续, 所以右侧是开集, 故 \(\mu'^{-1}\) 连续. 同理得到 \(\iota'\) 连续.

连续作用的例子.

• \({\rm GL}(n,\R)\) 在 \(\R^n\) (列向量空间) 上的左作用. 这是连续作用, 因为 \(g\cdot x\) 是关于 \(g,x\) 的多项式函数. 这个作用只有两条轨道: \(\R^n\setminus\{0\}\) 和 \(\{0\}\).

• \({\rm O}(n)\) 在 \(\R^n\) (列向量空间) 上的左作用. 作为上一个作用的限制, 它也是连续的. 这个作用的轨道是 \(\{0\}\) 和所有以球心在 \(0\) 的球面.

  • 轨道空间同胚于 \([0,+\infty)\): 考虑 \(f:\R^n\to[0,+\infty)\), \(f(x)=\|x\|\), 则 \(f\) 是连续的开满射, 进而是商映射. \(f\) 和轨道关系给出相同的 identification, 根据商空间的唯一性, 轨道空间同胚于 \([0,+\infty)\).

• \({\rm O}(n)\) 在 \(\R^n\) 的单位球面 \(\mathbb{S}^{n-1}\) 上的作用是传递的.

• 实射影空间. \(\R^*\) 在 \(\R^{n+1}\setminus\{0\}\) 上的左作用 (数量乘法). 这个作用是自由的, 轨道空间由所有过原点的直线 (去掉原点) 组成, 即 \(\mathbb{RP}^n\). 下面将说明, \(\mathbb{RP}^n\) 是 \(n\) 维的拓扑流形.

  • Hausdorff. 考虑 \({\cal O}=\{(x_1,x_2)\mid x_1=\lambda x_2,\lambda\neq0\}\), 将 \(x_1,x_2\) 视作列向量, 则 \((x_1,x_2)\) 是秩为 \(1\) 的 \((n+1)\times 2\) 矩阵. 秩为 \(1\) 等价于所以二阶子式为零. 因为某二阶子式的零点是闭集, 所以 \({\cal O}\) 作为有限闭集之交, 也是闭集. 这说明 \(\mathbb{RP}^n\) 是 Hausdorff 的.

  • 局部欧氏. 设开集 \(U_i=\{(x_1,\dots,x_{n+1})\mid x_i\neq0\}\), 则所有 \(q(U_i)\) 构成 \(\mathbb{RP}^n\) 的开覆盖. 定义 \[ \Align{ \psi_i:U_i &\to \R^n \\ (x_1,\dots,x_{n+1}) &\mapsto \frac1{x_i}(x_1,\dots,\widehat{x_i},\dots,x_{n+1}), } \] 是连续的开映射, 于是 \(\psi_i\circ q\) 也是连续的开映射. 注意到 \(\psi_i\circ q\) 还是双射, 进而是同胚. 因此, \(\{(q(U_i),\psi_i\circ q)\}\) 构成了 \(\mathbb{RP}^n\) 的图册.

• 复射影空间. \(\C^*\) 在 \(\C^{n+1}\setminus\{0\}\) 上的左作用. 轨道空间记作 \(\mathbb{RP}^n\), 是一个 \(2n\) 维拓扑流形.

• 环面. \(\Z\) 在 \(\R\) 上有连续的作用 \(n\cdot x=n+x\). 考虑陪集空间 \(\R/\Z\). 因为 \(x,y\) 在同一条轨道当且仅当 \(x-y\in\Z\), 所以 \(\R/\Z\) 和单位圆 \(\R/{\sim}\) 由同样的等价关系生成, 所以同胚.

  • 同样可以说明 \(\R^n/\Z^n\) 与 \(\mathbb{T}^n=\mathbb{S}^1\times\cdots\times \mathbb{S}^1\) 同胚.

  • 回忆 \(\R\to \mathbb{S}^1\) 的一个商映射是 \(q(t)=\e^{2\pi\i t}\), 则 \(\R^n\to \mathbb{T}^n\) 的一个商映射是 \[ (t_1,\dots,t_n)\mapsto(\e^{2\pi\i t_1},\dots,\e^{2\pi\i t_n}), \] 称作指数商映射.