GTM202 | 15 覆叠映射

GTM202 (Introduction to Topological Manifolds) Chapter 11 的笔记.

33 Covering Maps

33.1 Basic properties

设 \(X,E\) 是拓扑空间, \(q:E\to X\) 是连续映射. 开子集 \(U\subset X\) 被称为均匀覆叠的 (evenly covered), 如果

• \(q^{-1}(U)=\coprod_\alpha V_\alpha\), 其中 \(V_\alpha\subset E\) 是连通集.
• 对于每个\(V_\alpha\), \(q|_{V_\alpha}:V_\alpha\overset\sim\to U\) 是同胚.

注意到, 此时 \(U=q|_{V_\alpha}(V_\alpha)\) 也是连通的. 几何上, \(q^{-1}(U)\) 可以想象成 "叠在 \(U\) 上的一摞纸", 通过 \(q\) 投射到 \(U\). 容易验证, 均匀覆叠集合的连通开子集也是均匀覆叠的.

一个覆叠映射 (covering map) 是一个连续的满射 \(q:E\to X\), 其中 \(E\) 连通且局部道路连通, 且 \(X\) 中的每一点存在一个均匀覆叠的邻域. 此时, 我们称 \(E\) 是 \(X\) 的覆叠空间 (covering space), \(X\) 是覆叠的底 (base). 点 \(x\in X\) 的原像集 \(q^{-1}(x)\) 称为 \(x\) 处的纤维 (fiber).

• \(E\) 连通, 局部道路连通 \(\Rightarrow E\) 道路连通 \(\Rightarrow X\) 道路连通. 此外, \(X,E\) 的子集连通, 当且仅当道路连通.

Claim 33.1 (覆叠映射的基本性质) 设 \(q:E\to X\) 是覆叠映射.

1. \(q\) 是局部同胚, 开映射, 商映射.
2. 若 \(q\) 单, 则是同胚.
3. 若 \(V\subset E\) 是连通的饱和开子集, 则 \(q|_V:V\to q(V)\) 是覆叠映射.
4. 覆叠映射的有限积是覆叠映射.

Pf 1, 任给 \(y\in E\), 取 \(q(y)\) 的均匀覆叠邻域 \(U\), 记 \(q^{-1}(U)\) 的包含 \(y\) 的分量为 \(V\), 则 \(q|_V:V\overset\sim\to U\) 是 \(y\) 附近的局部同胚. 局部同胚是开映射; 开的连续满射是商映射.

2, 若 \(q\) 单, 则 \(q\) 是双射. 双射的局部同胚是同胚.

3, 显然 \(V\) 连通且局部连通. 任给 \(x\in q(V)\), 取 \(x\) 关于 \(q\) 的均匀覆叠邻域 \(U\), \(q^{-1}(U)=\coprod V_\alpha\), 则 \(W:=q(V)\cap U\) 是 \(x\) 的邻域, 且 \((q|_V)^{-1}(W)=\coprod(V_\alpha\cap V)\). 由 \(V\) 的饱和性, \(q(V_\alpha\cap V)=W\), 因此 \(q|_V\) 在 \(V_\alpha\cap V\) 上的限制是到 \(W\) 的同胚. 故 \(W\) 是 \(x\) 关于 \(q|_V\) 的均匀覆叠邻域.

4, 设覆叠映射 \(q_i:E_i\to X_i\), 积映射 \(q=q_1\times\dots\times q_n:\prod E_i\to\prod X_i\), 其中乘积保持连通性, 局部道路连通性. 对于 \((x_1,\dots,x_n)\in\prod X_i\), 每个 \(x_i\) 存在均匀覆叠邻域 \(U_i\subset X_i\). 实际上, \(\prod_iU_i\) 就是 \((x_1,\dots,x_n)\) 的均匀覆叠邻域: \[ q^{-1}\pqty{\prod_i U_i} = \prod_i q_i^{-1}(U_i) = \prod_i \pqty{\coprod_\alpha V_{i,\alpha}} = \coprod_\alpha \pqty{\prod_i V_{i,\alpha}}, \] 其中 \(\prod_iV_{i,\alpha}\) 作为连通集的有限积, 是连通的; 并且 \(q\) 在 \(\prod V_{i,\alpha}\) 上的限制 \[ q|_{\prod_i V_{i,\alpha}} = q_1|_{V_{1,\alpha}}\times\dots\times q_n|_{V_{n,\alpha}} \] 是同胚的乘积, 故为同胚.

覆叠映射的例子:

• (圆的指数商映射) 根据 Claim 29.1, \(\varepsilon:\R\to\mathbb{S}^1\), \(\varepsilon(x)=\e^{2\pi\i x}\) 是覆叠映射.

  • 然而, \(\varepsilon:(0,2)\to\mathbb{S}^1\), \(\varepsilon(x)=\e^{2\pi\i x}\) 不是覆叠映射, 因为 \(1\) 没有均匀覆叠邻域.

• (环面的指数商映射) 作为覆叠映射的有限积 \[ \Align{ \varepsilon^n: \R^n &\to \mathbb{T}^n \\ (x_1,\dots,x^n)&\mapsto(\varepsilon(x_1),\dots,\varepsilon(x_n)) } \] 是覆叠映射.

• (圆上的幂映射) \(p_n:\mathbb{S}^1\to\mathbb{S}^1\), \(p_n(z)=z^n\). 点 \(z_0\in\mathbb{S}^1\) 的均匀覆叠邻域是 \(U=\mathbb{S}^1\setminus\{-z_0\}\), 它的原像集 \(\{z\in\mathbb{S}^1\mid z^n\neq-z_0\}\) 由 \(n\) 段不交的弧组成, 每段弧同胚地映到 \(U\).

• (实射影空间) \(q:\mathbb{S}^n\to\mathbb{RP}^n\) (\(n\geq1\)), \(x\mapsto[x]\). 任取 \([x_0]\in\mathbb{RP}^n\), 记 \(x_0,-x_0\) 所在开半球分别为 \(V_1,V_2\), 则 \(V_1,V_2\) 是饱和开集. 令 \(U=q(V_1)=q(V_2)\) 为开集, 则 \(q\) 将 \(V_1,V_2\) 分别同胚地映到 \(U\). 因此 \(U\) 是 \([x_0]\) 的均匀覆叠邻域.

回忆: 连续映射 \(q:E\to X\) 在 \(U\subset X\) 上的局部截面指的是连续映射 \(\sigma:U\to E\) 满足 \(q\circ\sigma={\rm id}_U\).

Claim 33.2 (局部截面存在性) 设覆叠映射 \(q:E\to X\), 任给均匀覆叠开集 \(U\subset X\), \(x\in U\), \(e_0\in q^{-1}(U)\), 则存在局部截面 \(\sigma:U\to E\) 满足 \(\sigma(x)=e_0\).

Pf 设 \(\tilde{U}_0\) 是 \(q^{-1}(U)\) 的包含 \(e_0\) 的分量. 因为 \(q\) 在 \(\tilde{U}_0\) 上的限制是同胚, 只需取 \(\sigma=(q|_{\tilde{U}_0})^{-1}\).

Claim 33.3 (纤维有相同基数) 设覆叠映射 \(q:E\to X\), 对任意 \(x\in X\), \(q^{-1}(x)\) 有相同基数.

Pf 定义 \(X\) 上的等价关系: \(x\sim x'\) 当切记的 \(q^{-1}(x),q^{-1}(x')\) 有相同的基数. 取 \(x\) 的均匀覆叠邻域 \(U\), 任取 \(x'\in U\), 则 \(q^{-1}(U)\) 的每个分量恰好包含 \(q^{-1}(x),q^{-1}(x')\) 中的各一个点, 因此有一一对应 \[ q^{-1}(x) \leftrightarrow\{q^{-1}(U)\textsf{ 的分量}\} \leftrightarrow q^{-1}(x'), \] 说明 \(x\sim x'\). 故 \(U\) 包含于 \([x]\), 说明等价类是开的. 连通空间 \(X\) 上的开等价关系只能有一个等价类 (否则不同等价类间断 \(X\)), 因此 \(X\) 中所有点都等价, 即证.

我们称纤维的基数为覆叠的叶数 (number of sheets). 若基数是正整数 \(n\), 则称 \(q\) 为 \(n\) 重覆叠 (\(n\)-fold covering).

• \(q:\mathbb{S}^n\to\mathbb{RP}^n\) 是 \(2\) 重覆叠.
• 幂映射 \(p_n:\mathbb{S}^1\to\mathbb{S}^1\) 是 \(n\) 重覆叠.
• 指数商映射 \(\varepsilon:\R\to\mathbb{S}^1\) 的叶数是可数无穷.

33.2 Lifting properties

设 \(q:E\to X\) 是覆叠映射, 连续映射 \(\varphi:Y\to X\) 的一个提升 (lift) 指的是连续映射 \(\tilde\varphi:Y\to E\), 使得 \(q\circ\tilde\varphi=\varphi\): \[ \xymatrix{ & E \ar[d]^q \\ Y \ar[ru]^{\tilde\varphi} \ar[r]_\varphi & X. } \] - 局部截面 \(\sigma:U\to E\) 可以将 \(\varphi\) "局部地提升". 如果某个子集 \(W\subset Y\) 满足 \(\varphi(W)\subset U\), 则 \(\sigma\circ\varphi|_W\) 是 \(\varphi|_W\) 的一个提升.

以下两个定理是研究覆叠映射的关键.

Claim 33.4 (唯一提升性质) 设覆叠映射 \(q:E\to X\), 连通空间 \(Y\), 连续映射 \(\varphi:Y\to X\) 的两个提升 \(\tilde{\varphi}_1,\tilde{\varphi}_2:Y\to E\). 若 \(\tilde{\varphi}_1,\tilde{\varphi_2}\) 在 \(Y\) 中某点取值相同, 则它们恒相等.

Pf 我们使用 "连通性论证". 令 \({\cal A}=\{y\in Y\mid\tilde\varphi_1(y)=\tilde\varphi_2(y)\}\). 根据假设 \({\cal A}\) 非空. 我们只需证明 \({\cal A}\) 既开又闭, 则由 \(Y\) 的连通性, \({\cal A}=Y\).

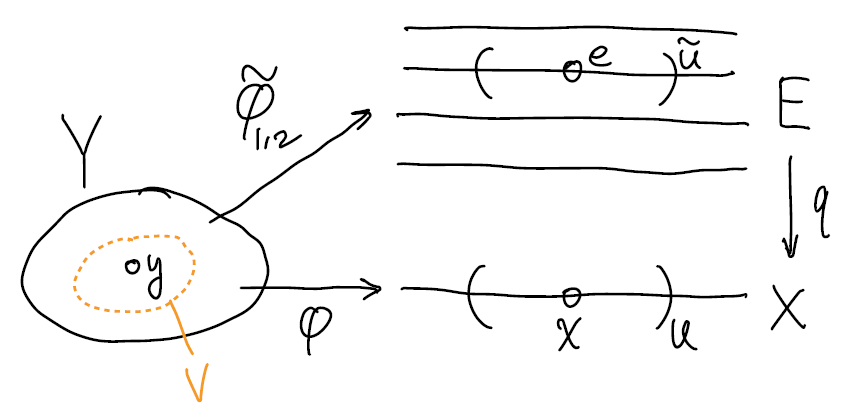
开性: 取 \(y\in{\cal A}\). 如图, 记 \(e=\tilde\varphi_1(y)=\tilde\varphi_2(y)\), \(x=\varphi(y)=q(e)\). 取 \(x\) 的均匀覆叠邻域 \(U\), 记 \(\tilde{U}\) 为 \(q^{-1}(U)\) 的包含 \(e\) 的分量. 令 \(V=\tilde\varphi_1^{-1}(\tilde{U})\cap\tilde\varphi_2^{-1}(\tilde{U})\), 则 \(V\) 是 \(y\) 的邻域, 且 \(\tilde{\varphi}_1,\tilde\varphi_2\) 在 \(V\) 上的像都包含于 \(\tilde{U}\). 根据提升的定义, \(q\circ\tilde\varphi_1|_V=q\circ\tilde\varphi_2|_V\), 注意 \(q\) 在 \(\tilde{U}\) 上是单射 (左可消), 得到 \(\tilde\varphi_1|_V=\tilde\varphi_2|_V\), 故 \(V\subset{\cal A}\). 因此 \({\cal A}\) 开.

闭性: 我们证明 \({\cal A}^C\) 开. 取 \(y\notin{\cal A}\). 记 \(e_i=\tilde\varphi_i(y)\), \(x=\varphi(y)=q(e_i)\), 有 \(e_1\neq e_2\). 取 \(x\) 的均匀覆叠邻域 \(U\), 记 \(\tilde{U}_i\) 为 \(q^{-1}(U)\) 的包含 \(e_i\) 的分量, 则 \(\tilde U_1\cap\tilde U_2=\emptyset\). 令 \(V=\tilde\varphi_1^{-1}(\tilde{U})\cap\tilde\varphi_2^{-1}(\tilde{U})\), 则 \(V\) 是 \(y\) 的邻域, 并且 \(\tilde\varphi_i(V)\subset\tilde{U}_i\), 故 \(\tilde\varphi_1|_V,\tilde\varphi_2|_V\) 像集的交集为空. 故 \(V\subset{\cal A}^C\), \({\cal A}^C\) 开.

Claim 33.5 (同伦提升性质) 设覆叠映射 \(q:E\to X\), 局部连通空间 \(Y\), 连续映射 \(\varphi_0,\varphi_1:Y\to X\) 间有同伦 \(H:Y\times I\to X\). 若 \(\tilde{\varphi}_0:Y\to E\) 是 \(\varphi_0\) 的一个提升, 则 \(H\) 有唯一提升 \(\tilde{H}:Y\times I\to E\), 满足 \(\tilde{H}_0=\tilde\varphi_0\). 若 \(H\) 保持子集 \(A\subset Y\) 不动, 则 \(\tilde{H}\) 也保持 \(A\) 不动.

Pf 证明分为 4 步.

步骤 1: \(\tilde{H}\) 的唯一性.

• 任给 \(Y\) 的子集 \(W\), 设 \(\tilde{H},\tilde{H}'\) 是 \(H\) 在 \(W\times I\) 上的提升, 且 \(\tilde{H}|_{W\times\{0\}}=\tilde{H}'|_{W\times\{0\}}\).

  任取 \(y\in Y\), 有 \(I\to E\) 的映射 \(t\mapsto\tilde{H}(y,t)\) 和 \(t\mapsto\tilde{H}'(y,t)\), 可以发现它们都是 \(I\to X\) 的映射 \(t\mapsto H(y,t)\) 的提升, 并且起点在 \(t=0\) 取值相同. 根据唯一提升性质, 两个在 \(I\) 上相等. 进而 \(\tilde{H}\) 和 \(\tilde{H}'\) 在 \(W\times I\) 上相等.

• 特别地, 取 \(W=Y\), 有满足 \(\tilde{H}_0=\tilde\varphi_0\) 的提升唯一 (如果存在的话).

步骤 2: 在局部定义 \(\tilde{H}\).

• 任取 \(y_0\in Y\), 我们在 \(W\times I\) 上定义 \(\tilde{H}\), 其中 \(W\) 是 \(y_0\) 的某邻域. 因为局部截面可以给出局部提升, 我们的想法是将 \(W\times I\) "细分", 使得每一段在 \(H\) 下映到某均匀覆叠邻域内, 进而可以提升到 \(\tilde{H}\), 再利用 gluing lemma 拼起来即可.

• 任给 \(s\in I\), 存在 \(H(y_0,s)\in X\) 的均匀覆叠邻域 \(U\). 因为 \(H^{-1}(U)\) 是 \((y_0,s)\) 的邻域, 而开集的乘积组成 \(Y\times I\) 的拓扑基, 所以存在开集 \(V\subset Y\), \(J\subset I\) 使得 \((y_0,s)\in V\times J\subset H^{-1}(U)\). 当 \(s\) 取遍 \(I\), 所有这些 \(V\times J\) 构成 \(\{y_0\}\times I\) 的开覆盖. 由紧性, \(\{y_0\}\times I\) 可以被有限个这样的开集 \(V_1\times J_1,\dots,V_m\times J_m\) 覆盖.

• 设 \(W\) 是 \(y_0\) 的包含于 \(V_1\cap\dots\cap V_m\) 的连通邻域 (由 \(Y\) 的局部连通性, 这样的邻域存在). 由 Lebesgue 数引理, \(I\) 的开覆盖 \(\{J_1,\dots,J_k\}\) 有 Lebesgue 数 \(\delta\). 设正整数 \(n\) 满足 \(1/n<\delta\). 此时, 对任意 \(j=1,\dots,n\), 集合 \(W\times[(j-1)/n,j/n]\) 在 \(H\) 下的像包含于一个均匀覆叠开集中.

• 现在可以开始定义 \(\tilde{H}\) 了. 用归纳法.

  • 取包含 \(H(W\times[0,1/n])\) 的均匀覆叠开集 \(U_1\subset X\). 令 \(\sigma_1:U_1\to E\) 是 \(q\) 的局部截面, 且满足 \(\sigma_1(\varphi_0(y_0))=\tilde\varphi_0(y_0)\). 对于 \((y,s)\in W\times[0,1/n]\), 定义 \[ \tilde{H}(y,s) := (\sigma_1\circ H)(y,s). \] 作为连续映射的复合, \(\tilde{H}\) 连续. 注意到映射 \(\tilde{H}_0:W\to E\), \(\tilde{H}_0(y)=\tilde{H}(y,0)\) 是 \(H_0=\varphi_0\) 的一个提升, 且与 \(\tilde\varphi_0\) 在 \(b_0\) 取值相同, 根据唯一提升性质, \(\tilde{H}_0=\tilde\varphi_0\).

  • 假设我们已经定义了 \(\tilde{H}:W\times[0,(j-1)/n]\) 对于某 \(j\in\{1,\dots,n\}\).

    令 \(U_j\) 是包含 \(H(W\times[(j-1)/n,j/n])\) 的均匀覆叠开集, \(\sigma_j:U_j\to E\) 是满足 \(\sigma_j(H(y_0,(j-1)/n))=\tilde{H}(y_0,(j-1)/n)\) 的局部截面. 定义连续映射 \[ \tilde{H}(y,s)=(\sigma_j\circ H)(y,s) \] 对于 \((y,s)\in W\times[(j-1)/n,j/n]\).

    

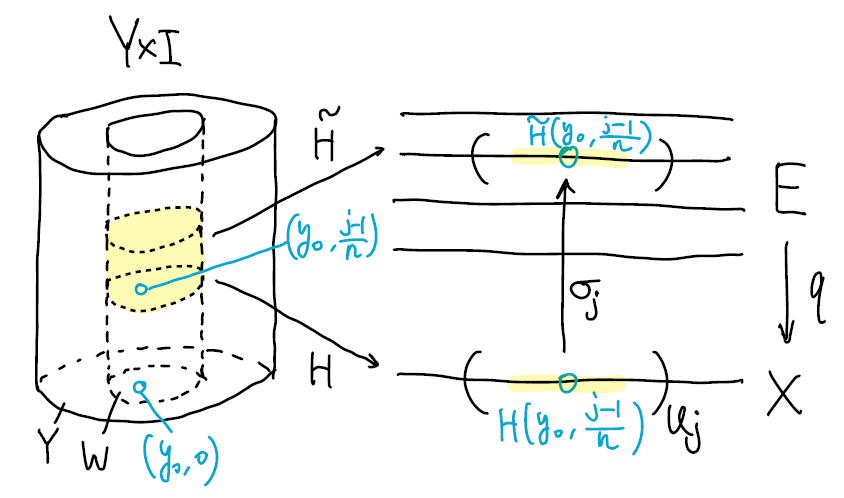
    需说明这与之前的定义相容. 对重叠部分 \(W\times\{(j-1)/n\}\) (这是连通集, 因为 \(W\) 连通), 注意新旧 \(\tilde{H}\) 在该集合上的限制都是 \(H\) 的提升, 并且在 \((y_0,(j-1)/n)\) 取值相同, 根据唯一提升性质, 新旧 \(\tilde{H}\) 在该集合上恒等. 由 gluing lemma, 我们成功将 \(\tilde{H}\) 连续延拓到 \(W\times[0,j/n]\).

• 总之, 我们定义了 \(H\) 在 \(W\times I\) 上的连续提升.

步骤 3: 整体定义 \(\tilde{H}\).

• \(Y\) 中的任意一点都存在邻域 \(W\), 使得 \(\tilde{H}\) 可以定义在 \(W\times I\) 上. 若 \(W,W'\) 是两个这样的邻域, 根据步骤 1, 两个提升 \(\tilde{H},\tilde{H}'\) 在 \((W\cap W')\times I\) 上恒相等. 根据 gluing lemma, \(\tilde{H}\) 能够连续地定义在整个 \(Y\times I\) 上. 根据构造, \(\tilde{H}_0=\tilde\varphi_0\).

步骤 4: 若 \(H\) 保持子集 \(A\subset Y\) 不动, 则 \(\tilde{H}\) 也保持 \(A\) 不动.

• 任给 \(a\in A\), 映射 \(I\to X\), \(t\mapsto H(a,t)\) 是常映射 \(t\mapsto\varphi_0(a)\), 其唯一提升是常映射 \(t\mapsto\tilde\varphi_0(a)\). 然而 \(t\mapsto\tilde{H}(a,t)\) 也是它的一个提升, 只能有 \(\tilde{H}(a,t)\equiv\tilde\varphi_0(a)\). 故 \(\tilde{H}\) 保持 \(A\) 不动.

同伦提升性质的一个推论是:

Claim 33.6 (道路提升性质) 设覆叠映射 \(q:E\to X\), 道路 \(f:I\to X\), 点 \(e\in q^{-1}(f(0))\), 则存在唯一提升 \(\tilde{f}:I\to E\), 满足 \(\tilde{f}(0)=e\).

• 我们将满足初值 \(\tilde{f}(0)=e\) 的提升记作 \(\tilde{f}_e\).

Pf 道路 \(f:I\to X\) 可以视作 \(\{*\}\to X\) 的两个映射 \(*\mapsto f(0)\) 和 \(*\mapsto f(1)\) 间的同伦. 因为 \(*\mapsto e\) 是前者的一个提升, 由同伦提升性质, \(f\) 唯一地提升到 \(\tilde{f}:I\to E\), 满足 \(\tilde{f}(0)=e\).

在研究 \(\mathbb{S}^1\) 的时候, 我们还给出了 Claim 29.6, 大致思想是: 两条道路同伦, 当且仅当其提升具有相同的终点. 证明利用了 \(\R\) 的单连通性, 所以难以推广到一般的覆叠映射. 然而, 我们有如下较弱的版本:

Claim 33.7 (单值性定理) 设覆叠映射 \(q:E\to X\), 道路 \(f,g:I\to X\) 有相同的起点和终点, 设 \(\tilde{f}_e,\tilde{g}_e\) 是两个起点相同的提升.

1. \(\tilde{f}_e\sim\tilde{g}_e\) 当且仅当 \(f\sim g\). (都是道路同伦)
2. 若 \(f\sim g\), 则 \(\tilde{f}_e(1)=\tilde{g}_e(1)\).

Pf 1, 若 \(\tilde f_e\sim\tilde g_e\), 则 \(f\sim g\), 因为复合保持道路同伦. 反之, 若 \(f\sim g\), 则同伦 \(H:I\times I\to X\) 提升到 \(\tilde{H}:I\times I\to E\), \(\tilde{H}\) 是 \(\tilde{f}_e\) 与 \(g\) 的某个提升 \(\tilde{g}\) 之间的同伦. 因为 \(\tilde{H}\) 保持 \(\{0,1\}\) 不变, 所以 \(\tilde{g}(0)=e\), 根据唯一性, \(\tilde{g}=\tilde{g}_e\).

2, 若 \(f\sim g\), 根据 1, \(\tilde{f}_e\sim\tilde{g}_e\) 道路同伦, 当然有相同的终点.

Claim 33.8 (覆叠映射的诱导同态是单射) 设覆叠映射 \(q:E\to X\). 任给 \(e\in E\), 诱导同态 \(q_*:\pi_1(E,e)\to\pi_1(X,q(e))\) 是单射.

Pf 设 \([f]\in\pi_1(E,e)\) 满足 \(q_*[f]=[c_{q(e)}]\) 映到恒等元, 即 \(q\circ f\sim c_{q(e)}\). 根据单值性定理, \(q\circ f,c_{q(e)}\) 的两个起点相同的提升道路同伦. 注意到 \(f\) 和 \(c_e\) 就是两个起点相同的提升, 有 \([f]=[c_e]\) 为恒等元.

因为 \(q_*\) 单, 所以 \(\pi_1(E,e)\) 同构于 \(\pi_1(X,q(e))\) 的子群 \(\im{q_*}\), 它被称为覆叠的诱导子群 (subgroup induced by the covering).

33.3 The general lifting problem

并非所有的连续映射 \(\varphi:Y\to X\) 都能够提升到覆叠空间 \(E\). 判断一个映射能否提升的问题叫做提升问题 (lifting problem). 下面的定理将提升问题转化为一个代数问题.

Claim 33.9 (可提升的标准) 设覆叠映射 \(q:E\to X\), 空间 \(Y\) 连通且局部道路连通, \(\varphi:Y\to X\) 连续. 取 \(y_0\in Y\), \(e_0\in E\) 满足 \(q(e_0)=\varphi(y_0)\). 则 \(\varphi\) 存在满足 \(\tilde\varphi(y_0)=e_0\) 的提升 \(\tilde\varphi:Y\to E\), 当且仅当 \[ \varphi_*\pi_1(Y,y_0) \subset q_*\pi_1(E,e_0). \]

Pf \(\Rightarrow\) 是容易证明的 (甚至不需要 \(Y\) 的任何连通性). 若 \(\tilde\varphi\) 满足假设, 根据 \(\pi_1\) 的函子性有交换图: \[ \xymatrix{ & \pi_1(E,e_0) \ar[d]^{q_*} \\ \pi_1(Y,y_0) \ar[ru]^{\tilde\varphi_*} \ar[r]_(.45){\varphi_*} & \pi_1(X,\varphi(y_0)). } \] 因此 \(\varphi_*\pi_1(Y,y_0)=q_*\tilde\varphi_*\pi_1(Y,y_0)\subset q_*\pi_1(E,e_0)\).

\(\Leftarrow\) 我们利用道路提升性质, 将 \(\varphi\) "沿着道路提升". 具体来说, 如果 \(\tilde\varphi\) 是存在的, 那么有如下观察:

• 对任意 \(y\in Y\) 与连接 \(y_0,y\) 的道路 \(f\), \(\tilde\varphi\circ f\) 是 \(\varphi\circ f\) 的提升, 其以 \(e_0\) 为起点, 以 \(\tilde\varphi(y)\) 为终点.

这启发我们这样定义 \(\tilde\varphi\): 对任意 \(y\in Y\), 取一条连接 \(y_0,y\) 的道路 \(f\), 定义 \[ \tilde\varphi(y) := (\widetilde{\varphi\circ f})_{e_0}(1). \] 其中 \((\widetilde{\varphi\circ f})_{e_0}\) 是 \(\varphi\circ f\) 的以 \(e_0\) 为起点的提升. 我们要证明: ① \(\tilde\varphi\) 良定义, 不依赖道路的选择; ② \(\tilde\varphi\) 连续. 于是根据定义, \((q\circ\tilde\varphi)(y)=(q\circ(\widetilde{\varphi\circ f})_{e_0})(1)=(\varphi\circ f)(1)=\varphi(y)\), 即 \(\tilde\varphi\) 确实是 \(\varphi\) 的提升.

① \(\tilde\varphi\) 良定义.

• 任取连接 \(y_0,y\) 的道路 \(f'\), 则 \(f'*\bar{f}\) 是以 \(y_0\) 为基点的环路. 根据假设, \[ [\varphi\circ(f'*\bar{f})] = \varphi_*[f'*\bar{f}] \in \varphi_*\pi_1(Y,y_0) \subset q_*\pi_1(E,e_0). \] 这说明, 存在 \([g]\in\pi_1(E,e_0)\) 满足 \(\varphi\circ(f'*\bar{f})\sim q\circ g\), 即 \[ (\varphi\circ f')*\overline{(\varphi\circ f)} \sim q\circ g, \] 也即 \[ (\varphi\circ f') \sim (q\circ g)*(\varphi\circ f). \] 根据单值性定理, 这两条道路的以 \(e_0\) 为起点的提升具有相同终点. 其中, \((q\circ g)*(\varphi\circ f)\) 的提升是 \(g*\widetilde{(\varphi\circ f)}_{e_0}\), 因为 \(g\) 是 \(q\circ g\) 的一个提升, 而 \(g\) 是以 \(e_0\) 为基点的环路. 因此, \[ \widetilde{(\varphi\circ f')}_{e_0}(1) = \pqty{g*\widetilde{(\varphi\circ f)}_{e_0}}(1) = \widetilde{(\varphi\circ f)}_{e_0}(1), \] 即 \(f,f'\) 定义出相同的 \(\tilde\varphi(y)\).

② \(\tilde\varphi\) 连续.

• 我们首先证明一个必要条件: \(\tilde\varphi\) 将连通集映到连通集.

  设 \(V\subset Y\) 连通, 任给 \(y_1,y_2\in V\), 存在连接 \(y_0,y_1\) 的道路 \(f\) 与连接 \(y_1,y_2\) 的道路 \(g\). 因为 \(\tilde\varphi\) 是 \(\varphi\) 的提升, \(\tilde\varphi\) 将 \(f*g\) 映到 \((\varphi\circ f)*(\varphi\circ g)\) 的提升. 特别地, \(\varphi\circ g\) 的提升是 \(\tilde\varphi(V)\) 中连接 \(\tilde\varphi(y_1),\tilde\varphi(y_2)\) 的道路. 故 \(\tilde\varphi(V)\) 道路连通.

• 最后, 要证明 \(\tilde\varphi\) 连续, 只需要证明 \(Y\) 中每一点存在邻域使得 \(\tilde\varphi\) 连续 (局部 criterion).

  

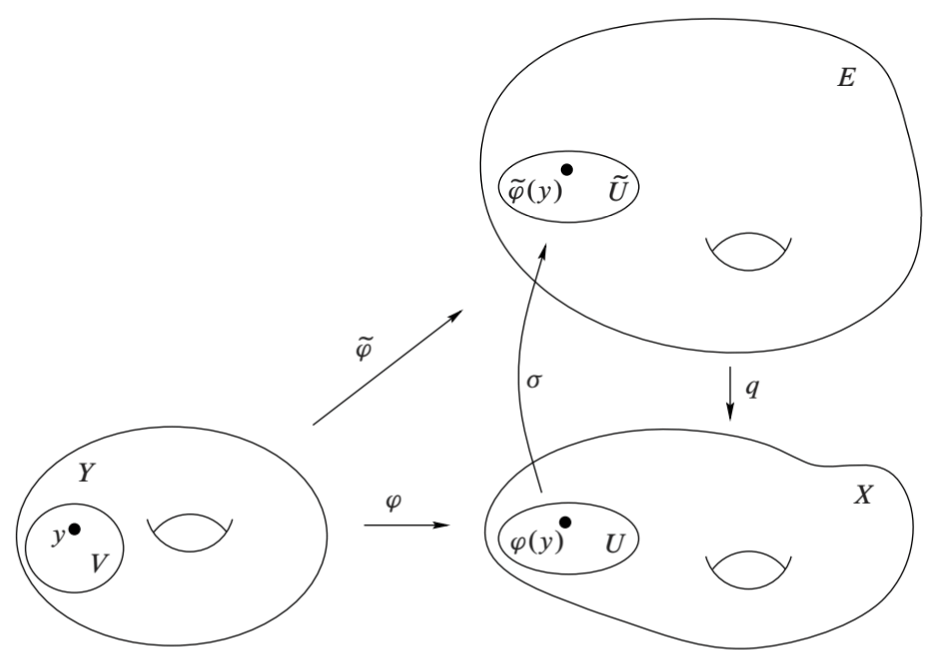
  任给 \(y\in Y\), 取 \(\varphi(y)\) 的均匀覆叠邻域 \(U\), 令 \(\tilde{U}\) 是 \(q^{-1}(U)\) 的包含 \(\tilde\varphi(y)\) 的一叶. 设 \(\sigma:U\to\tilde{U}\) 是满足 \(\sigma(\varphi(y))=\tilde\varphi(y)\) 的局部截面, 有 \(q\circ\sigma={\rm id}_U\). 取 \(V\subset Y\) 是 \(\varphi^{-1}(U)\) 的包含 \(y\) 的道路连通分量, 根据上面的性质, \(\tilde\varphi(V)\) 是 \(q^{-1}(U)\) 中的连通集, 进而 \(q^{-1}(U)\subset\tilde{U}\). 于是有下面的等式: \[ q\circ\tilde\varphi|_V = \varphi|_V = q\circ\sigma\circ\varphi|_V. \] 因为 \(\tilde\varphi|_V\) 和 \(\sigma\circ\varphi|_V\) 的像集包含于 \(\tilde{U}\), 而 \(q\) 在其上单, 消去 \(q\) 得到 \(\tilde\varphi|_V=\sigma\circ\varphi|_V\) 是连续映射的复合.

分别取 \(Y,E\) 为单连通空间, 得到两个推论:

Claim 33.10 (把定义域为单连通空间的映射提升) 设覆叠映射 \(q:E\to X\), 空间 \(Y\) 单连通且局部道路连通, \(\varphi:Y\to X\) 连续. 则 \(\varphi\) 存在提升. 此时, 任给 \(y_0\in Y\), 存在以 \(\varphi(y_0)\) 的纤维中任意一点作为 \(\tilde\varphi(y_0)\) 的提升.

Claim 33.11 (把映射提升到单连通空间) 设覆叠映射 \(q:E\to X\) 且 \(E\) 单连通. 空间 \(Y\) 连通且局部道路连通, \(\varphi:Y\to X\) 连续. 则 \(\varphi\) 存在提升, 当且仅当 \(\varphi_*\) 是平凡同态. 此时, 任给 \(y_0\in Y\), 存在以 \(\varphi(y_0)\) 的纤维中任意一点作为 \(\tilde\varphi(y_0)\) 的提升.

一个例子:

• (圆的 \(n\) 重覆叠) 考虑幂映射 \(p_n:\mathbb{S}^1\to\mathbb{S}^1\) 给出的 \(n\) 重覆叠. 容易验证, 覆叠 \(p_n\) 诱导的子群是 \([\omega]^n\) 生成的无穷循环群 (\([\omega]\) 是 \(\pi_1(\mathbb{S}^1,1)\) 的标准生成元). \[ \xymatrix{ & \mathbb{S}^1 \ar[d]^{p_n} \\ \mathbb{S}^1 \ar[r]_{p_m} \ar[ur]^f & \mathbb{S}^1 } \] 因此, 映射 \(p_m\) 存在提升 \(f\) 满足 \(p_n\circ f=p_m\), 当且仅当 \[ \lr{[\omega]^m} = \im(p_m)_* \subset \im(p_n)_* = \lr{[\omega]^n}, \] 当且仅当存在 \(k\in\Z\), 满足 \(m=kn\). 此时, 满足 \(1\mapsto1\) 的 \(f\) 由 \(p_k\) 给出.

• (圆的可数无穷覆叠) 指数商映射 \(\varepsilon:\R\to\mathbb{S}^1\) 诱导的子群是平凡群 (因为 \(\R\) 的基本群平凡). 因此, \(\varphi:X\to\mathbb{S}^1\) 能提升到 \(\R\) 当且仅当 \(\varphi_*\) 是平凡同态. 特别地, \({\rm id}_{\mathbb{S}^1}\) 不能提升; 而任意单连通空间 \(X\) 到 \(\mathbb{S}^1\) 的连续映射都能提升.