GTM202 | 14 Seifert–Van Kampen 定理

GTM202 (Introduction to Topological Manifolds) Chapter 10 的笔记.

32 The Seifert–Van Kampen Theorem

本章中, 我们介绍一个计算基本群的重要定理, 可以用来计算诸如 CW 复形, 紧曲面等空间的基本群.

这个重要定理, 即 Seifert–Van Kampen 定理, 通过考察拓扑空间 \(X\) 的子空间的基本群, 进而给出全空间的基本群.

32.1 Statement of the theorem

设拓扑空间 \(X\) 的开覆盖 \(\{U,V\}\), 设 \(U,V,U\cap V\) 道路连通, 并且我们能计算这三个子集的基本群. 我们会发现, \(X\) 中的任一环路道路同伦于若干环路的积, 积的每一项都在 \(U\) 或者 \(V\) 中. 这样的一条道路可以代表 \(\pi_1(U)*\pi_1(V)\) 中某的群元. 然而, \(\pi_1(U\cap V)\) 中的环路在自由积群中被视作不同的群元 (分别作为 \(\pi_1(U)\) 和 \(\pi_1(V)\) 的群元参与自由积), 因此我们还需要在此基础上商去某些关系.

下面我们给出定理的严谨叙述.

设 \(X\) 为拓扑空间, \(\{U,V\}\) 是 \(X\) 的开覆盖, 且 \(U\cap V\neq\emptyset\). 任取基点 \(p\in U\cap V\). 我们有四个包含映射 \[ \xymatrix@!{ & U \ar[rd]^k \\ U\cap V \ar[ru]^i \ar[rd]_j && X \\ & V \ar[ru]_l } \] 它们诱导出基本群同态 \[ \xymatrix@!{ & \pi_1(U,p) \ar[rd]^{k_*} \\ \pi_1(U\cap V,p) \ar[ru]^{i_*} \ar[rd]_{j_*} && \pi_1(X,p) \\ & \pi_1(V,p) \ar[ru]_{l_*} } \] 下面将 \(\pi_1(U)*\pi_1(V)\) 插入这个交换图. 根据自由积的泛性质, 同态 \(k_*\) 和 \(l_*\) 唯一地诱导出同态 \(\Phi:\pi_1(U)*\pi_1(V)\to\pi_1(X)\), 使得下图的右半部分交换: \[ \xymatrix@!@C=1em{ & \pi_1(U,p) \ar[rd]^{k_*} \ar@{^{(}->}[d] \\ \pi_1(U\cap V,p) \ar[ru]^{i_*} \ar[rd]_{j_*} & \pi_1(U,p)*\pi_1(V,p) \ar[r]^(.58)\Phi & \pi_1(X,p) \\ & \pi_1(V,p) \ar[ru]_{l_*} \ar@{_{(}->}[u] } \]

Claim 32.1 (Seifert–Van Kampen 定理) 设拓扑空间 \(X\) 的开覆盖 \(\{U,V\}\), 满足 \(U,V,U\cap V\) 道路连通. 令 \(p\in U\cap V\), 定义子集 \(C\subset\pi_1(U,p)*\pi_1(V,p)\), \[ C=\{(i_*\gamma)(j_*\gamma)^{-1}\mid \gamma\in\pi_1(U\cap V,p)\}. \] 则如上定义的 \(\Phi\) 是满同态, 且 \(\ker\Phi\) 等于 \(C\) 在 \(\pi_1(U,p)*\pi_1(V,p)\) 中的正规闭包. 因此, \[ \pi_1(X,p) \cong \big(\pi_1(U,p)*\pi_1(V,p)\big) \big/ \overline{C}. \] 特别地, \(\pi_1(X,p)\) 由 \(\pi_1(U,p)\) 和 \(\pi_1(V,p)\) 在 \(\Phi\) 下的像生成.

• 利用融合自由积的语言, \(\pi_1(X,p)\) 同构于 \(\pi_1(U,p)\) 和 \(\pi_1(V,p)\) 沿着 \(\pi_1(U\cap V,p)\) 的融合自由积: \[ \pi_1(X,p) \cong \pi_1(U,p) *_{\pi_1(U\cap V,p)} \pi_1(V,p), \] 其中, 融合自由积定义中的群同态由 \(i_*\) 和 \(j_*\) 给出.

• Seifert–Van Kampen 定理的证明在本章最后给出. 实际上, 该定理能推广到任意开覆盖 \(\{U_\alpha\}\) 的情形.

在后面几节的大多数应用中, 我们只需要考虑定理的特殊情况.

Claim 32.2 (Seifert–Van Kampen, 交集单连通) 假设同 Seifert–Van Kampen, 若还有 \(U\cap V\) 单连通, 则 \(\Phi\) 是 \(\pi_1(U,p)*\pi_1(V,p)\) 与 \(\pi_1(X,p)\) 的群同构. 如果 \(U,V\) 的基本群有表现 \[ \Align{ \pi_1(U,p) &\cong \lr{\alpha_1,\dots,\alpha_n\mid\rho_1,\dots,\rho_r}, \\ \pi_1(V,p) &\cong \lr{\beta_1,\dots,\beta_m\mid\sigma_1,\dots,\sigma_s}, } \] 则 \(X\) 的基本群有表现 \[ \pi_1(X,p) \cong \lr{ \alpha_1,\dots,\alpha_n,\beta_1,\dots,\beta_m \mid \rho_1,\dots,\rho_r,\sigma_1,\dots,\sigma_s }. \]

另一种特殊情况是其中一个开集 (比如 \(U\)) 单连通的情况. 此时, \(\pi_1(U,p)\) 平凡, \(i_*,k_*\) 都是平凡同态, 交换图中央的 \(\pi_1(U,p)*\pi_1(V,p)\) 变成了 \(\pi_1(V,p)\). 因此整个交换图化简为 \[ \pi_1(U\cap V,p) \overset{j_*}\longrightarrow \pi_1(V,p) \overset{l_*}\longrightarrow \pi_1(X,p). \]

Claim 32.3 (Seifert–Van Kampen, 一个开集单连通) 假设同 Seifert–Van Kampen, 若还有 \(U\) 单连通, 则包含映射 \(l:V\hookrightarrow X\) 诱导群同构 \[ \pi_1(X,p)\cong\pi_1(V,p)\Big/\overline{j_*\pi_1(U\cap V,p)}, \] 其中 \(\overline{j_*\pi_1(U\cap V,p)}\) 是 \({j_*\pi_1(U\cap V,p)}\) 在 \(\pi_1(V,p)\) 中的正规闭包. 若 \(V,U\cap V\) 的基本群有表现 \[ \Align{ \pi_1(V,p) &\cong \lr{\beta_1,\dots,\beta_m\mid\sigma_1,\dots,\sigma_s}, \\ \pi_1(U\cap V,p) &\cong \lr{\gamma_1,\dots,\gamma_p\mid\tau_1,\dots,\tau_t}, } \] 则 \(X\) 的基本群有表现 \[ \pi_1(X,p) \cong \lr{ \beta_1,\dots,\beta_m \mid \sigma_1,\dots,\sigma_s,v_1,\dots,v_p }, \] 其中 \(v_a\) 是 \(j_*\gamma_a\in\pi_1(V,p)\) 关于生成元 \(\{\beta_i\}\) 的表达式.

32.2 Applications

32.2.1 Wedge sums

回忆拓扑空间的楔和/一点并: 设带基点的拓扑空间 \((X_j,p_j)\), \(j=1,\dots,n\), 其楔和 \(X_1\vee\dots\vee X_n\) 定义为 \(\coprod_iX_i\) 商去等价关系 \(p_1\sim\dots\sim p_n\). 楔和的基点 \(*\) 是 \(p_j\) 所在的等价类. 记商映射 \(q:\coprod_jX_j\to\bigvee_jX_j\).

空间 \(X_j\) 可以视作 \(\bigvee_iX_i\) 的子空间. 考虑复合映射 \(\iota_j:X_j\hookrightarrow\coprod_iX_i\overset{q}\to\bigvee_iX_i\), 这是一个连续的单射, 容易验证它还是开映射, 因此 \(\iota_j\) 是拓扑嵌入, \(X_j\) 可以和 \(\bigvee_iX_i\) 的子空间 \(\iota_j(X_j)\) 认同.

为了利用 Seifert–Van Kampen 定理计算楔和的基本群, 我们需要对基点提出一个要求. 点 \(p\in X\) 称为非退化基点 (nondegenerate base point), 若 \(p\) 的某邻域 \(U\) 能够强形变收缩到 \(\{p\}\).

• 流形的所有点都是非退化基点, 因为坐标开球可以强形变收缩到其中任意一点.

Claim 32.4 (楔和的非退化基点) 若 \(p_j\in X_j\) 是非退化基点, 则 \(*\) 是 \(\bigvee_jX_j\) 的非退化基点.

Pf 对于 \(p_i\), 有强形变收缩 \(r_i:W_i\to\{p_i\}\), 设同伦 \({\rm id}_{W_i}\sim\iota_{\{p_i\}}\circ r_i\) 由 \(H_i:W_i\times I\to W_i\) 给出. 定义不交并空间上的同伦 \(H:(\coprod_iW_i)\times I\to\coprod_iW_i\), 定义为 \(H|_{W_i\times I}:=H_i\) (根据不交并的特征性质, 这是连续映射).

商映射 \(q\) 在饱和开集 \(\coprod_iW_i\) 上的限制是 \(\coprod_iW_i\) 到 \(W:=q(\coprod_iW_i)\) 的商映射, 其中 \(W\) 是基点 \(*\) 的一个邻域. 因为 \(I\) 局部紧, 乘积 \(q\times{\rm id}_I:(\coprod_iW_i)\times I\to W\times I\) 是商映射. 因为 \(q\circ H\) 在 \(q\times{\rm id}_I\) 的纤维上常值, 它下降到连续映射 \(\tilde{H}:W\times I\to W\), 这给出了 \(W\) 到 \(\{*\}\) 的强形变收缩.

Claim 32.5 (楔和的基本群) 设带有非退化基点的拓扑空间 \((X_j,p_j)\), \(j=1,\dots,n\), 则 \[ (\iota_j)_*:\pi_1(X_j,p_j) \to \pi_1(X_1\vee\dots\vee X_n,*) \] 诱导出的群同态 \[ \Phi: \pi_1(X_1,p_1)*\dots*\pi_1(X_n,p_n) \to \pi_1(X_1\vee\dots\vee X_n,*) \] 是群同构.

Pf 用归纳法. 下面我们证明 \(X_1\vee X_2\) 的情形. 对于 \(n>2\), 对 \(X_1\) 和 \(X_2\vee\dots\vee X_n\) 应用下面的证明 (上面的引理保证这两个空间都有非退化基点).

考虑 \(X_1\vee X_2\). 需要注意, 直接对 \(U=X_1,V=X_2\) 应用 SVK 定理是不对的, 因为它们不是开集.

取邻域 \(W_i\subset X_i\) 使得它能强形变收缩到 \(\{p_i\}\), 令 \(U=q(X_1\amalg W_2)\), \(V=q(X_2\amalg W_1)\), 其中 \(q:X_1\amalg X_2\to X_1\vee X_2\) 是商映射. 因为 \(X_1\amalg W_2\) 和 \(X_2\amalg W_1\) 都是饱和开集, \(q\) 将它们映到开集, 所以 \(U,V,U\cap V\) 是 \(X_1\vee X_2\) 中的开集.

一个关键的观察是: 由基点的非退化性, 有三组同伦等价 \[ \Align{ \{*\} &\hookrightarrow U\cap V, \\ X_1 &\hookrightarrow U, \\ X_2 &\hookrightarrow V, \\ } \] 其中每一组的左边是右边的强形变收缩.

因为 \(U\cap V\) 可缩, 进而单连通, 应用 Claim 32.2, 有群同构 \[ \Phi: \pi_1(U,*)*\pi_1(V,*) \overset\sim\to \pi_1(X,*), \] 另外, 单射 \(\iota_1:X_1\hookrightarrow U\) 和 \(\iota_2:X_2\hookrightarrow V\) 是同伦等价, 因此有基本群同构 \[ \Align{ (\iota_1)_*:\pi_1(X_1,*)&\overset\sim\to\pi_1(U,*), & (\iota_2)_*:\pi_1(X_2,*)&\overset\sim\to\pi_1(V,*), } \] 将它们复合便得到想要的结果. 具体的过程见交换图: \[ \xymatrix@!@C=1em{ \pi_1(X_1,*) \ar@[tomato][r]^{(\iota_1)_*}_{\sim} & \pi_1(U,*) \ar[rd]^{k_*} \ar@{^{(}->}@[tomato][d] \\ & \pi_1(U,*)*\pi_1(V,*) \ar@[tomato][r]^(.58)\Phi_(.58){\sim} & \pi_1(X,*) \\ \pi_1(X_2,*) \ar@[tomato][r]^{(\iota_2)_*}_{\sim} & \pi_1(V,*) \ar[ru]_{l_*} \ar@{_{(}->}@[tomato][u] } \]

一些例子:

• (圆束) \(\mathbb{S}^1\vee\dots\vee\mathbb{S}^1\) 的基本群同构于 \(\Z*\dots*\Z\). 如果记 \([\omega_i]\) 是第 \(i\) 个 \(\mathbb{S}^1\) 的基本群的生成元, 则圆束的基本群是 \([\omega_1],\dots,[\omega_n]\) 生成的自由群 \(\lr{[\omega_1],\dots,[\omega_n]}\).

  • 特别地, 8 字形空间 \(\mathbb{S}^1\vee\mathbb{S}^1\) 的基本群是由两个基本环路 \([\omega_1],[\omega_2]\) 生成的自由群, 一个群元形如 \[ [\omega_1]^{i_1}[\omega_2]^{j_1}\cdots [\omega_1]^{i_m}[\omega_2]^{j_m}. \]

• (去掉 \(n\) 个点的平面) 设 \(\R^2\setminus\{p_1,\dots,p_n\}\) 是去掉 \(n\) 的点的平面, 它可以强形变收缩到 \(\mathbb{S}^1\vee\dots\vee\mathbb{S}^1\) (每个 \(\mathbb{S}^1\) 包住一个 \(p_i\)). 因此 \(\R^2\setminus\{p_1,\dots,p_n\}\) 的基本群同构于 \(\Z^{*n}\).

• (去掉 \(n\) 个点的球面) 注意到去掉一个点的球面 \(\mathbb{S}^2\setminus\{p_0\}\) 同胚于平面 \(\R^2\) (球极投影), 因而去掉 \(n\) 个点的球面同胚于去掉 \((n-1)\) 个点的 \(\R^2\), 其基本群同构于 \(\Z^{*(n-1)}\).

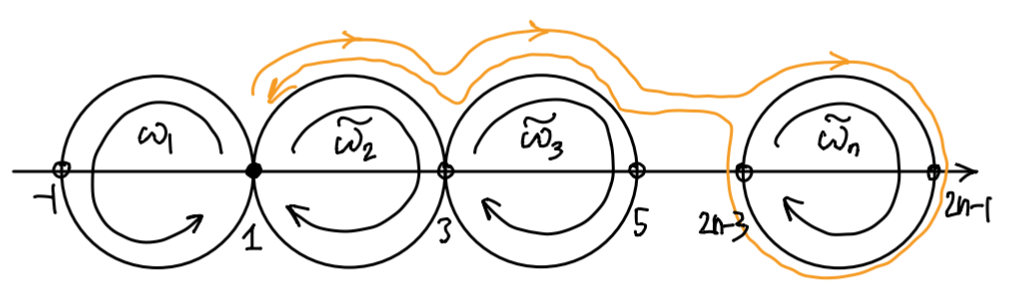
• (圆的另一种楔和) 记 \(X_n\) 是 \(\C\) 中以 \(\{0,2,\dots,2n-2\}\) 为圆心的单位元的并. \(X_{n+1}\) 可以看作 \(X_n\) 与单位圆的楔和, 基点为 \(2n-1\).

  • 记 \(\omega_k\) 是第 \(k\) 个圆周上以 \(2k-1\) 为基点, 逆时针转一圈的环路. 记 \(\tilde\omega_k\) 是第 \(k\) 个圆周上以 \(2k-3\) 为基点, 顺时针转一圈的环路.

  • 记 \(\gamma_{k,l}\) 是 \(X_n\) 中连接 \(x\) 轴上 \(k,l\) 两点的最短道路, 规定其沿着上半圆周.

  • 可以归纳地证明, \(X_n\) 以 \(1\) 为基点的基本群是 \[ \pi_1(X_n,1)=\lr{[\omega_1], [\tilde\omega_2], [\gamma_{1,3}*\tilde\omega_3*\gamma_{3,1}], \dots, [\gamma_{1,2n-3}*\tilde\omega_n*\gamma_{2n-3,1}] }. \] 生成元的几何含义是明显的: \(\gamma_{1,2n-3}*\tilde\omega_n*\gamma_{2n-3,1}\) 表示先从 \(1\) 沿着上半圆周走到 \(2n-3\), 接着绕第 \(n\) 个圆一圈, 再沿着上半圆周走回 \(1\) 的环路 (橙色).

  

32.2.2 Graphs

在 CW 复形一章中, 我们介绍了图的概念. 一个图 (graph) 是 \(0\) 或 \(1\) 维的 CW 复形. 其 \(0\) 维胞腔称为顶点 (vertices), \(1\) 维胞腔称为边 (edges). 根据定义, 对于任意一条边 \(e\), \(\overline{e}\setminus e\) 包含 \(1\) 或 \(2\) 个顶点. 对于包含于 \(\overline{e}\) 的顶点 \(v\), 我们称 \(v\) 和 \(e\) 是关联的 (incident). 一个子图 (subgraph) 是图的子复形. 因此, 若一个子图包含一条边, 则它必须包含与之关联的顶点.

只与一个顶点关联的边称为自环 (self-loop). 若顶点 \(v_1,v_2\) (可以相同) 同时与多条边关联, 则称这些边为重边 (multiple edges). 没有自环, 也没有多重边的图称为简单图 (simple graph). (有的图论文献以 "图" 代指简单图, 以 "重图" 代指这里一般意义上的图.)

一条路径 (edge path) 指的是有限序列 \((v_0,e_1,v_1,\dots,v_{k-1},e_k,v_k)\), 其中顶点和边交替出现, 以点起止, 并且满足对任意 \(i=1,\dots,k\), \(\{v_{i-1},v_i\}\) 恰好是与边 \(e_i\) 关联的顶点 (\(v_{i-1}=v_i\) 当且仅当 \(e_i\) 是自环). 顶点 \(v_0,v_k\) 分别称为起点 (initial vertex) 和终点 (terminal vertex). 平凡路径 (trivial edge path) 是单顶点的路径 \((v_0)\). 一条路径称为闭的 (closed), 若 \(v_0=v_k\); 称为简单的 (simple), 若其中的顶点 (除了 \(v_0,v_k\)) 和边都只出现一次.

• 图 \(\Gamma\) 是连通的, 当且仅当任给 \(v,v'\in\Gamma\), 存在连接 \(v,v'\) 的路径. 在连通图中, 任意两点可以由简单路径相连.

一个环 (cycle) 是非平凡的简单闭路径. 一棵树 (tree) 是不含有环的连通图.

• 一棵树中不能含有重边或自环. 若 \(e\) 是与顶点 \(v\) 关联的自环, 则 \((v,e,v)\) 是一个环. 若 \(e,e'\) 是与顶点 \(v,v'\) 关联的重边, 则 \((v,e,v',e',v)\) 是一个环. 因此, 树是一个简单图.
• 一棵树的顶点数总是比边数多 \(1\).

Claim 32.6 任意有限树都是可缩的, 因此是单连通的.

图 \(\Gamma\) 的一棵生成树 (spanning tree) 是包含了 \(\Gamma\) 的所有顶点的一棵子树. 图 \(\Gamma\) 的一棵极大子树 (maximal tree) 是不真包含于其他子树的子树.

Claim 32.7 任意有限连通图都包含一棵生成树.

设 \(\Gamma\) 是一个有限连通图, 下面我们尝试构造其基本群的一组生成元. 取顶点 \(v\) 为基点, 令 \(T\subset\Gamma\) 为一棵生成树. 设 \(e_1,\dots,e_n\) 是不在 \(T\) 中的边, 对于 \(e_i\), 记与之关联的顶点为 \(\{w_i,w_i'\}\). 我们这样构造一条以 \(v\) 为基点的环路 (如下图): ① 在 \(T\) 中选择一条从 \(v\) 到 \(w_i\) 的道路 \(g_i\), ② 沿着 \(e_i\) 从 \(w_i\) 走到 \(w_i'\), ③ 在 \(T\) 中选择一条从 \(w_i'\) 到 \(v\) 的道路 \(h_i\). 记这条环路为 \(f_i\). 注意 \([f_i]\) 与 \(g_i,h_i\) 的选取无关: 因为 \(T\) 是单连通的, 所以任意起点与终点相同的道路是道路同伦的.

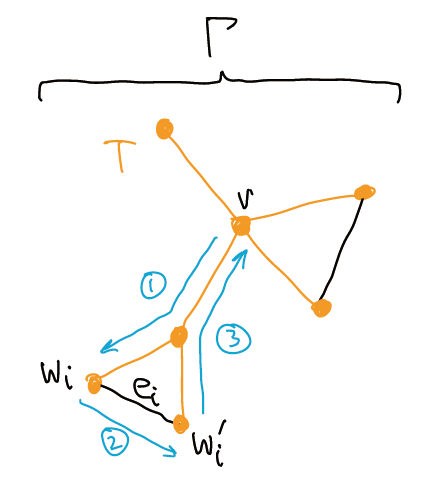
Claim 32.8 (有限图的基本群) 有限连通图 \(\Gamma\) 的基本群 \(\pi_1(\Gamma,v)\) 是以上 \([f_1],\dots,[f_n]\) 生成的自由群.

• 记 \(E,V\) 分别为 \(\Gamma\) 的边数, 顶点数, 则其生成树的边数为 \((V-1)\), 因此 \(n=E-V+1\), 于是 \[ \pi_1(\Gamma,v) \cong \underbrace{\Z*\dots*\Z}_{n=E-V+1}. \]

• 有限连通图 \(\Gamma\) 的 Euler 示性数定义为 \(\chi(\Gamma):=V-E\). 图 \(\Gamma\) 的基本群的秩为 \(1-\chi(\Gamma)\), 因此 Euler 示性数是有限连通图的同伦不变量.

Pf 对 \(n\) (即 \(\Gamma\setminus T\) 的边数) 进行归纳. 当 \(n=0\), \(\Gamma=T\) 是单连通的, 基本群平凡.

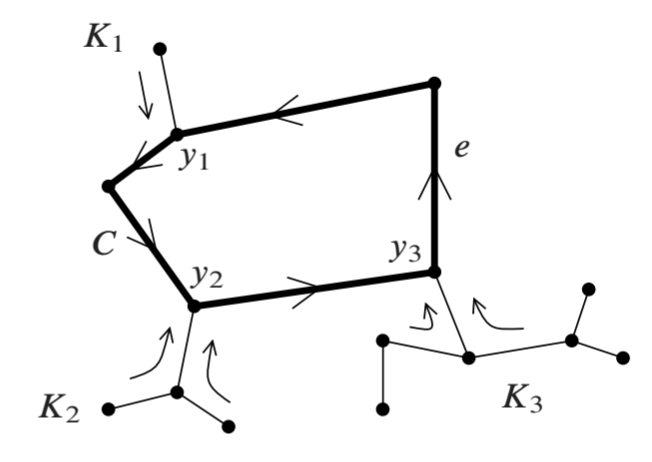
当 \(n=1\), 我们要证明 \(\pi_1(\Gamma,v)\) 是 \([f_1]\) 生成的无穷循环群. 根据假设 \(\Gamma\) 中有环 \((v_0,e_1,\dots,e_m,v_m)\), 并且 \(\Gamma\setminus{T}\) 中的唯一一条边 \(e\) 在这个环中 (否则 \(T\) 中有环). 包含 \(\{v_0,e_1,\dots,e_m,v_m\}\) 的子图 \(C\subset\Gamma\) 同胚于 \(\mathbb{S}^1\). 我们下面证明包含映射 \(C\hookrightarrow\Gamma\) 是同伦等价.

设 \(K\) 是 \(\Gamma\setminus{T}\) 中的所有边及其顶点构成的子图. \(K\) 的任一分量 \(K_i\) 是 \(\Gamma\) 的连通子图, 且包含于 \(T\), 进而是一棵树 (下图). 还需注意到 \(K_i\) 与 \(C\) 有公共顶点 \(y_i\) (因为 \(\Gamma\) 连通), 并且该 \(y_i\) 是唯一的: 假如 \(K_i\cap C\) 有两个点 \(y_i,y_i'\), 我们就能找到 \(T\) 中的一个环 (在 \(K_i\) 中从 \(y_i\) 走到 \(y_i'\), 再在 \(C\) 中从 \(y_i'\) 走到 \(y_i\), 且不穿过 \(e\)), 这是不可能的.

现在可以定义 \(\Gamma\to C\) 的强形变收缩了: 在每个 \(K_i\) 上, 令 \(K_i\) 强形变收缩到 \(y_i\); 在 \(C\) 上取恒等映射. 根据 gluing lemma, 这是强形变收缩, 进而 \(\Gamma\sim\mathbb{S}^1\).

最后我们证明 \([f_1]\) 生成 \(\pi_1(\Gamma,v)\). 取顶点 \(z\in C\), 从 \(z\) 出发, 依次遍历 \(C\) 的边的一条道路 \(a\) 显然道路同伦于 \(\mathbb{S}^1\) 的标准环路 (或其逆), 可作为 \(\pi_1(\Gamma,z)\) 的生成元. 一条从 \(v\) 到 \(z\) 的道路 \(b\) 给出了基点变换 \(\Phi_b:\pi_1(\Gamma,z)\overset\sim\to\pi_1(\Gamma,v)\), 因此 \(\pi_1(\Gamma,v)\) 的一个生成元是 \(\Phi_b[a]=[\bar{b}*a*b]\), 这是一条 ① 从 \(v\) 到 \(w_1\), ② 走过 \(e\), ③ 从 \(w_1'\) 回到 \(v\) 的环路, 所以道路同伦于 \(f_1\) (因为 \(f_1\) 的道路类不依赖于 ① 和 ③ 道路的选取). 因此我们完成了对 \(n=1\) 情形的证明.

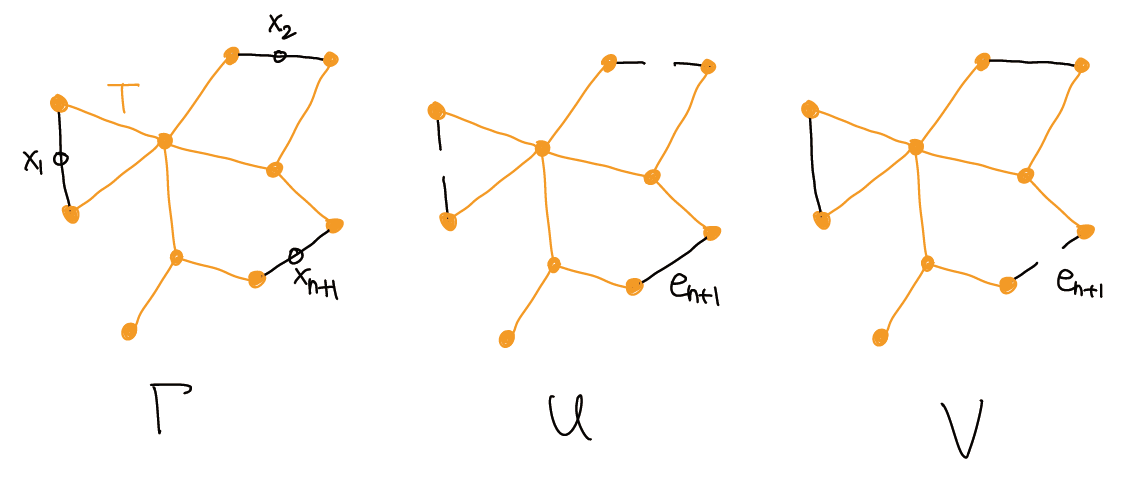
假设命题当 \(n\geq1\) 时正确, 下面考虑 \(n+1\) 的情形. 对于不在 \(T\) 中的边 \(e_1,\dots,e_{n+1}\), 取 \(x_i\in e_i\), 令 \(U=\Gamma\setminus\{x_1,\dots,x_n\}\), \(V=\Gamma\setminus\{x_{n+1}\}\) 为 \(\Gamma\) 中的开集. 容易构造强形变收缩 (如下图) \[ U\cap V\sim T,\quad U\sim T\cup e_{n+1},\quad V\sim\Gamma\setminus e_{n+1}. \] 根据 \(n=1\) 的情形, \(\pi_1(U,v)=\lr{[f_{n+1}]}\); 根据归纳假设, \(\pi_1(V,v)=\lr{[f_1],\dots,[f_n]}\). 因为 \(U\cap V\) 单连通, 由 SVK 的特殊情形, \(\pi_1(\Gamma,v)\) 同构于这两个自由群的自由积, 进而同构于 \([f_1],\dots,[f_{n+1}]\) 生成的自由群.

32.2.3 CW complexes

向拓扑空间 \(X\) 粘贴一个圆盘 \(D\), 其基本群会 "变小": 贴映射 \(\varphi:\partial{D}\to X\) 是一条环路的圆代表元, 在粘贴后, 这条环路在 \(D\) 中可以缩成一点, 是零伦的.

Claim 32.9 (粘贴一个圆盘) ...

Claim 32.10 (粘贴一个 \(n\) 维胞腔) 设 \(X\) 道路连通, \(\tilde{X}\) 是向 \(X\) 粘贴一个 \(n\geq3\) 维胞腔得到的空间. 则包含映射 \(X\hookrightarrow\tilde{X}\) 诱导出基本群同构.

Claim 32.11 (有限 CW 复形的基本群) ...

32.2.4 Compact surfaces

通过对标准曲面基本群的计算, 我们能够证明曲面分类定理中的 "唯一性" (即证明标准曲面互不同胚), 进而完成分类定理的证明.

Claim 32.12 (多边形表示的基本群) 设拓扑空间 \(M\) 有单字的多边形表示 \(\lr{a_1,\dots,a_n\mid W}\), 其中所有点都认同, 则 \(\pi_1(M)\) 有表现 \(\lr{a_1,\dots,a_n\mid W}\).

Claim 32.13 (紧曲面的基本群) 标准曲面的基本群有如下表现:

• \(\pi_1(\mathbb{S}^2)\cong\lr{\emptyset\mid\emptyset}\) (平凡群).
• \(\pi_1(\Sigma_k)\cong\lr{\beta_1,\gamma_1,\dots,\beta_k,\gamma_k\mid\beta_1\gamma_1\beta_1^{-1}\gamma_1^{-1}\cdots\beta_k\gamma_k\beta_k^{-1}\gamma_k^{-1}=e}\).
• \(\pi_1(\tilde\Sigma_l)\cong\lr{\beta_1,\dots,\beta_l\mid\beta_1^2\cdots\beta_l^2=e}\).

带边版本:

• \(\pi_1(\mathbb{S}^2_m)\cong\lr{c_1,\dots,c_m}\) (自由群).
• \(\pi_1(\Sigma_{k,m})\cong\lr{\beta_1,\gamma_1,\dots,\beta_k,\gamma_k,c_1,\dots,c_m\mid\beta_1\gamma_1\beta_1^{-1}\gamma_1^{-1}\cdots\beta_k\gamma_k\beta_k^{-1}\gamma_k^{-1}=c_1\cdots c_m}\).
• \(\pi_1(\tilde\Sigma_{l,m})\cong\lr{\beta_1,\dots,\beta_l,c_1,\dots,c_m\mid\beta_1^2\cdots\beta_l^2=c_1\cdots c_m}\).

Pf 先看无边版本. 我们之前就讨论过, \(\mathbb{S}^2\) 的基本群是平凡的, 因为它是 \(\R^3\setminus\{0\}\) 的强形变收缩. 基本曲面 \(\Sigma_k\) 和 \(\tilde\Sigma_l\) 的基本群从 Claim 32.12 立刻得到 (它们的标准表示中, 所有点都认同).

带边版本...

特别地, \(\pi_1(\mathbb{T}^2)=\pi_1(\Sigma_1)\cong\lr{\beta,\gamma\mid\beta\gamma=\gamma\beta}\cong\Z^2\), 与我们之前得到的结果一致. 对于实射影平面, 我们有 \(\pi_1(\mathbb{RP}^2)\cong\lr{\beta\mid\beta^2=e}\cong\Z/2\).

Pf (紧连通曲面分类定理, 剩下的部分) 首先注意到 \(\mathbb{S}^2\) 不可能同胚于 \(\Sigma_k,\tilde\Sigma_k\) (对任意 \(k>0\)), 因为前者基本群平凡, 而后两者基本群非平凡. 为了区分后两者, 我们考虑其基本群的交换化. 由 Claim 31.14, 我们得到 (\(k,l>0\)) \[ \Align{ {\rm Ab}(\pi_1(\Sigma_k)) &\cong \Z^{2k}, \\ {\rm Ab}(\pi_1(\tilde\Sigma_l)) &\cong \Z^{l-1}\times\Z/2. \\ } \] 注意 \(\Z^{l-1}\times\Z/2\) 含有一个非平凡的挠元, 而 \(\Z^{2k}\) 是无挠的, 因此 \(\pi_1(\Sigma_k)\) 与 \(\pi_1(\tilde\Sigma_l)\) 的交换化不同构, 它们本身也不同构. 因此 \(\Sigma_k\) 不同胚于 \(\tilde\Sigma_l\).

注意 \(\pi_1(\Sigma_k)\) 的交换化的秩为 \(2k\), 因此, 亏格 \(k\) 可以被基本群的交换化确定, 进而是拓扑不变量. 换言之, 对于 \(k\neq k'\), \(\Sigma_k\) 与 \(\Sigma_{k'}\) 不同胚.

同样地, \(\pi_1(\tilde\Sigma_l)\) 的交换化的秩为 \(l-1\), 亏格 \(l\) 也是拓扑不变量. 对于 \(l\neq l'\), \(\tilde\Sigma_l\) 与 \(\tilde\Sigma_{l'}\) 不同胚.

要证明 \(\mathbb{S}^2_m,\Sigma_{k,m},\tilde\Sigma_{k,m}\) 互不同胚, 用到 "可定向性" 是拓扑不变量这一事实. 这个事实的证明 (Claim 23.10) 没有用到分类的唯一性.

Pf (紧连通带边曲面分类定理, 剩下的部分) 注意边界的连通分量数 \(m\) 是拓扑不变量. 我们计算交换化: (\(k,l,m\geq1\)) \[ \Align{ {\rm Ab}(\pi_1(\mathbb{S}^2_m)) &\cong \Z^{m-1}, \\ {\rm Ab}(\pi_1(\Sigma_{k,m})) &\cong \Z^{2k+m-1}, \\ {\rm Ab}(\pi_1(\tilde\Sigma_{l,m})) &\cong \Z^{l+m-1}. \\ } \] 因此交换化可以被用来区分大多数情况, 唯一的例外是: \[ {\rm Ab}(\pi_1(\Sigma_{k,m})) \cong {\rm Ab}(\pi_1(\tilde\Sigma_{2k,m})). \] 此时, 可以利用可定向性来区分: \(\Sigma_{k,m}\) 可定向, \(\tilde\Sigma_{2k,m}\) 不可定向, 而可定向性是拓扑不变性!