GTM202 | 12 圆的基本群

GTM202 (Introduction to Topological Manifolds) Chapter 8 的笔记.

29 The Fundamental Group of The Circle

29.1 Lifting properties

我们仍然将 $\mathbb{S}^1$ 视作 $\C$ 的子集, 取 $1\in\C$ 作为基点. 设指数商映射 $\varepsilon:\R\to\mathbb{S}^1$, $\varepsilon(r)=\e^{2\pi\i r}$.

任给拓扑空间 $B$ 和连续映射 $\varphi:B\to\mathbb{S}^1$, $\varphi$ 的一个提升 (lift) 指的是连续映射 $\tilde{\varphi}:B\to\R$, 满足交换图 \[ \xymatrix{ & \R \ar[d]^{\varepsilon} \\ B \ar[r]_{\varphi} \ar@{.>}[ur]^{\tilde{\varphi}} & \mathbb{S}^1. } \]

Claim 29.1 (指数商映射的性质) 任意一点 $z\in\mathbb{S}^1$ 存在邻域 $U$, 满足:

$\varepsilon^{-1}(U)$ 是可数个不交的开区间 $\tilde{U}_n$ ($n\in\Z$) 之并, 并且 $\varepsilon$ 将每个 $\tilde{U}_n$ 同胚地映到 $U$.

Pf 证明是直接的. 可以用四个开半圆覆盖 $\mathbb{S}^1$: \[ \Align{ X_+&=\{x+\i y\in\mathbb{S}^1 \mid x>0\}, & Y_+&=\{x+\i y\in\mathbb{S}^1 \mid y>0\}, \\ X_-&=\{x+\i y\in\mathbb{S}^1 \mid x<0\}, & Y_-&=\{x+\i y\in\mathbb{S}^1 \mid y<0\}. } \] 这四个开半圆的原像都是一系列不交的, 长度为 $1/2$ 的开区间. 例如, \[ \varepsilon^{-1}(X_+) = \bigcup_{n\in\Z} \pqty{n-\frac14,n+\frac14}, \] 固定 $n$, 在开区间 $(n-\frac14,n+\frac14)$ 上, 连续的 (局部) 逆由下式给出: \[ \Align{ \varepsilon^{-1}: X_+ &\to\pqty{n-\frac14,n+\frac14}, \\ x+\i y &\mapsto n+\frac1{2\pi}\sin^{-1}y } \] 因为 $\mathbb{S}^1$ 的任意一点都上述四个开半圆之一, 即证.

满足上面定理中的条件的开集 $U\subset\mathbb{S}^1$ 称作被均匀覆叠的 (evenly covered). 可知, $\varepsilon^{-1}(U)$ 作为可数个 $\tilde{U}_n$ 的不交并, 其 (道路) 分量恰好就是所有 $\tilde{U}_n$.

对于连续的满射 $q:X\to Y$, 它的一个截面 (section) 指的是连续的右逆 $\sigma:Y\to X$, 即满足 $q\circ\sigma={\rm id}_Y$. 若 $U\subset Y$ 是开子集, 则 $q$ 在 $U$ 上的一个局部截面 (local section) 指的是连续映射 $\sigma:U\to X$, 满足 $q\circ\sigma={\rm id}_U$.

上面的证明中构造的 (局部) 逆映射就是 $\varepsilon$ 在 $X_+$ 与上的局部截面.

下面的定理表明, 圆的任意均匀覆叠的开子集上都存在很多截面.

Claim 29.2 ($\mathbb{S}^1$ 的局部截面) 设均匀覆叠的开子集 $U\subset\mathbb{S}^1$. 任给 $z\in U$, $r\in\varepsilon^{-1}(z)$, 存在 $\varepsilon$ 在 $U$ 上的局部截面 $\sigma:U\to\R$, 满足 $\sigma(z)=r$.

Pf 令 $\tilde{U}\subset\R$ 是 $\varepsilon^{-1}(U)$ 的包含 $r$ 的分量. 根据均匀覆叠的定义, $\varepsilon:\tilde{U}\to U$ 是同胚, $\sigma=(\varepsilon|_{\tilde{U}})^{-1}$ 即为所求.

以下两个定理是研究圆的关键. 在此我们不去证明, 因为它们是更一般的 lifting properties 的特殊情况, 在第 15 篇笔记的 33.2 节可以找到它们. (书上给出了以下两个定理的证明, 略过了更一般的 lifting properties 的证明, 这里则刚好反过来. 实际上, 除了一些符号的改动外, 两种情况的证明是一样的.)

Claim 29.3 ($\mathbb{S}^1$ 的唯一提升性质) 设 $B$ 连通, 连续映射 $\varphi:B\to\mathbb{S}^1$ 的两个提升 $\tilde{\varphi}_1,\tilde{\varphi}_2:B\to\R$. 若 $\tilde{\varphi}_1,\tilde{\varphi_2}$ 在 $B$ 中某点取值相同, 则它们恒相等.

Claim 29.4 ($\mathbb{S}^1$ 的同伦提升性质) 设 $B$ 局部连通, 连续映射 $\varphi_0,\varphi_1:B\to\mathbb{S}^1$ 间有同伦 $H:B\times I\to\mathbb{S}^1$. 若 $\tilde{\varphi}_0:B\to\R$ 是 $\varphi_0$ 的一个提升, 则 $H$ 有唯一提升 $\tilde{H}:B\times I\to\R$, 满足 $\tilde{H}_0=\tilde\varphi_0$. 若 $H$ 保持子集 $A\subset B$ 不动, 则 $\tilde{H}$ 也保持 $A$ 不动.

Claim 29.5 ($\mathbb{S}^1$ 的道路提升性质) 设道路 $f:I\to\mathbb{S}^1$, 实数 $r_0\in\varepsilon^{-1}(f(0))$, 则存在唯一提升 $\tilde{f}:I\to\R$, 满足 $\tilde{f}(0)=r_0$, 并且任意给定的另一提升与 $\tilde{f}$ 相差一个常整数.

即任给两个提升 $\tilde{f},\tilde{f}'$, 则 $\tilde{f}-\tilde{f}'$ 是常数.

Pf 一条道路 $f:I\to\mathbb{S}^1$ 可以视作两个从独点空间 $\{*\}$ 到 $\mathbb{S}^1$ 的连续映射间的同伦. 这两个连续映射是 $*\mapsto f(0)$ 和 $*\mapsto f(1)$. 根据 $\mathbb{S}^1$ 的同伦提升性质, $\tilde{f}:I\to\R$ 唯一存在.

设 $\tilde{f}'$ 是 $f$ 的另一个提升, 即 $\varepsilon(\tilde{f}(s))=f(s)=\varepsilon(\tilde{f}'(s))$, 因此对任意 $s$, $\tilde{f}(s)-\tilde{f}'(s)$ 都是整数. 又因为 $\tilde{f}-\tilde{f}'$ 是从连通空间 $I$ 到离散空间 $\Z$ 的连续映射, 其只能是常映射.

Claim 29.6 ($\mathbb{S}^1$ 上的道路同伦条件) 设 $f_0,f_1$ 是 $\mathbb{S}^1$ 上拥有相同起点与终点的道路, $\tilde{f}_0,\tilde{f}_1$ 分别是两条道路的提升, 且 $\tilde{f}_0,\tilde{f}_1$ 起点相同. 则 $f_0\sim f_1$ 当且仅当 $\tilde{f}_0,\tilde{f}_1$ 终点相同.

Pf 若 $\tilde{f}_0,\tilde{f}_1$ 终点相同 (根据假设, 它们起点也相同). 注意 $\R$ 单连通, 由单连通性的等价刻画 (Claim 25.2), $\tilde{f}_0,\tilde{f}_1$ 道路同伦, 因此 $f_0=\varepsilon\circ\tilde{f}_0$ 和 $f_1=\varepsilon\circ\tilde{f}_1$ 道路同伦.

若 $f_0\sim f_1$, 设 $H:I\times I\to\mathbb{S}^1$ 是 $f_0,f_1$ 间的道路同伦. 根据 $\mathbb{S}^1$ 的同伦提升性质, $H$ 提升到同伦 $\tilde{H}:I\times I\to\R$, 满足 $\tilde{H}_0=\tilde{f}_0$. 因为 $H$ 保持 $\{0,1\}$ 不变, $\tilde{H}$ 亦然, 意味着 $\tilde{H}$ 是一个道路同伦. 道路 $\tilde{H}_1:I\to\R$ 是 $f_1$ 的一个提升, 且它和 $\tilde{f}_1$ 有相同的起点. 根据唯一性, $\tilde{H}_1=\tilde{f}_1$. 因此 $\tilde{f}_0$ 与 $\tilde{f}_1$ 道路同伦. 特别地, 它们终点相同.

29.2 The fundamental group

现在我们将提升理论应用到 $\mathbb{S}^1$ 的环路上.

设 $f:I\to\mathbb{S}^1$ 是以 $z_0\in\mathbb{S}^1$ 为基点的环路. 任给提升 $\tilde{f}:I\to\R$, 因为 $\tilde{f}(0)$ 和 $\tilde{f}(1)$ 都在纤维 $\varepsilon^{-1}(z_0)$ 中, 所以它们相差一个整数. 注意到 $f$ 的任意两个提升的差值是常数, 所以 $\tilde{f}(1)-\tilde{f}(0)$ 是一个只与 $f$ 有关, 而与提升的选择无关的整数. 这个整数称为 $f$ 的卷绕数 (winding number), 记作 $N(f)$.

标准环路 $\omega(s)=\e^{2\pi\i s}$ 的卷绕数为 $1$. (它的一个提升是 $\tilde{\omega}(s)=s$.)
常环路的卷绕数为 $0$, 因为其任意提升都是常值映射.
道路乘法对应卷绕数加和: $N(f*g)=N(f)+N(g)$.
旋转不改变卷绕数. 映射 $\rho:\mathbb{S}^1\to\mathbb{S}^1$, $\rho(z)=\e^{\i\theta}z$ 称为旋转. 注意到 $\rho\circ\varepsilon=\varepsilon\circ\tau$, 其中 $\tau:\R\to\R$ 是平移映射 $\tau(s)=s+\theta/2{\pi}$. 因此, 若 $\tilde{f}$ 是环路 $f$ 的一个提升, 则 $\tau\circ\tilde{f}$ 是 $\rho\circ\tilde{f}$ 的一个提升. 有 \[ N(f)=N(\rho\circ f). \]

Claim 29.7 ($\mathbb{S}^1$ 的环路的同伦分类) $\mathbb{S}^1$ 中基点相同的环路道路同伦, 当且仅当它们具有相同卷绕数.

Pf 设相同基点处的环路 $f_0,f_1$. 根据道路提升性质, 存在提升 $\tilde{f}_0,\tilde{f}_1:I\to\R$, 满足 $\tilde{f}_0(0)=\tilde{f}_1(0)$. 根据道路同伦的充要条件, $f_0\sim f_1$ 当且仅当 $\tilde{f}_0$ 和 $\tilde{f}_1$ 终点相同, 即 $f_0,f_1$ 的卷绕数相同.

Claim 29.8 ($\mathbb{S}^1$ 的基本群) $\pi_1(\mathbb{S}^1,1)$ 是由 $[\omega]$ 生成的无穷循环群.

Pf 定义映射 $J:\Z\to\pi_1(\mathbb{S}^1,1)$ 和 $K:\pi_1(\mathbb{S}^1,1)\to\Z$, \[ \Align{ J(n)&=[\omega]^n,& K([f])&=N(f). } \] (因为道路同伦的环路具有相同的卷绕数, 所以 $K$ 是良定义的.) 下面证明它们是群同构. 显然 $J$ 是群同态: $[\omega]^{m+n}=[\omega]^m*[\omega]^n$. 只需要证明 $K$ 是 $J$ 的双侧逆.

我们先构造 $[\omega]^n$ 的代表元. 定义 $\alpha_n:I\to\mathbb{S}^1$, $\alpha_n(s)=\e^{2\pi\i ns}$. 显然有 $\alpha_1=\omega$, $\alpha_{-1}=\bar\omega$. 因为 $\alpha_{n-1}*\omega$ 是 $\omega$ 的一个重参数化, 所以根据归纳法, $[\alpha_n]=[\omega]^n$. 直接的计算表明, $\alpha$ 的一个提升是 $\tilde{\alpha}(s)=ns$, 因此卷绕数 $N(\alpha_n)=\tilde{\alpha}(1)-\tilde{\alpha}(0)=n$. 因为卷绕数相同, 所以 $[\omega]^n=[\alpha_n]$.

要证明 $K\circ J={\rm id}_\Z$, 任给 $n\in\Z$, 有 $K(J(n))=K([\omega]^n)=K([\alpha_n])=N(\alpha_n)=n$.

要证明 $J\circ K={\rm id}_{\pi_1(\mathbb{S}^1,1)}$, 任给 $[f]\in\pi_1(\mathbb{S}^1,1)$, 记 $n=N(f)$, 则 $f$ 与 $\alpha_n$ 具有相同的卷绕数 (且基点相同), 进而道路同伦. 因此 $J(K(f))=J(n)=[\omega]^n=[\alpha_n]=[f]$.

29.3 Some applications

$\mathbb{S}^1$ 的结论可以应用到相关的空间:

(去掉一点的平面) 因为 $\mathbb{S}^1$ 是 $\C\setminus\{0\}\cong\R^2\setminus\{0\}$ 的强形变收缩, 两者同伦等价, 故具有相同的基本群: $\pi_1(\C\setminus\{0\},1)$ 也是 $[\omega]$ 生成的无穷循环群.
- 环路 $f:I\to\C\setminus\{0\}$ 的卷绕数定义为 $r\circ f$ 的卷绕数, 其中收缩映射 $r:\C\setminus\{0\}\to\mathbb{S}^1$ 是 $r(z)=z/|z|$.
- ($\C\setminus\{0\}$ 的环路的同伦分类) $\C\setminus\{0\}$ 中的两条环路道路同伦, 当且仅当它们有相同卷绕数.
(环面) 设 $n$ 维环面 $\mathbb{T}^n=\mathbb{S}^1\times\dots\times\mathbb{S}^1$ 取定基点 $p=(1,\dots,1)$. 因为积空间的基本群是基本群的积, 所以 $\mathbb{T}^n$ 同构于 $\Z^n$.
- 记 $\omega_j(s)=(1,\dots,\e^{2\pi\i s},\dots,1)$ 是第 $j$ 个 $\mathbb{S}^1$ 中的标准环路, 则一个群同构是 \[ \Align{ \phi:\Z^n &\to \pi_1(\mathbb{T}^n,p) \\ (k_1,\dots,k_n) &\mapsto [\omega_1]^{k_1}*\dots*[\omega_n]^{k_n}. } \]
- 当 $n\geq2$ 时, $\mathbb{S}^n$ 是单连通的, $\mathbb{T}^n$ 不是, 因此两者不同胚.

Claim 29.9 (维数不变性 & 边界不变性, 二维情形)

非空拓扑空间 $X$ 不可以既是 $2$ 维流形, 也是 $n$ ($n>2$) 维流形.
设 $2$ 维带边流形 $M$, 则 $M$ 中的点不能既是内部点也是边界点.

Pf 一维的情形是利用连通性证明的. 二维情形则利用单连通性.

维数不变性. 假设 $X$ 既是 $2$ 维流形, 也是 $n$ ($n>2$) 维流形. 设 $p\in X$ 的一个 $2$ 维欧氏邻域 $U\cong\R^2$. 因为 $X$ 存在 $n$ 维坐标开球构成的拓扑基, 所以存在 $U$ 的开子集 $V\cong\mathbb{B}^n$. 与此同时 $V$ 作为 $U$ 的开子集, 同胚于 $\R^2$ 的开子集 $A$ (同胚在开集的限制是同胚), 于是 $A\cong\mathbb{B}^n$, 但这是不可能的.

证明 $A$ 不同胚于 $\mathbb{B}^n$. 重点是说明对于 $p\in A$, $A\setminus\{p\}$ 不单连通, 但 $\mathbb{B}^n\setminus\{q\}$ 是单连通的, 所以原本的两个集合不同胚. 由 $A$ 的开性, 某 $B_r(p)\subset A$. 由可以定义连续映射 \[ \Align{ r:A\setminus\{p\}&\to\partial{B}_r(p), & x&\mapsto p+r\frac{x-p}{|x-p|}. } \] 容易验证 $r|_{\partial{B}_r(p)}$ 是恒等映射, 即 $r$ 是收缩. 由于 $\partial{B}_r(p)\cong\mathbb{S}^1$ 非单连通, 所以 $A\setminus\{p\}$ 非单连通.

边界不变性. 假设 $p$ 有内部坐标邻域 $(U,\varphi)$ 和边界坐标邻域 $(V,\psi)$ 满足 $\psi(p)\in\partial\H^2$. 取 $U\cap V$ 的包含 $p$ 的连通分量 $A$, 则 $A$ 同胚于 $\R^2$ 的开子集 $\varphi(A)$ 和 $\H^2$ 的开子集 $\psi(A)$. 然而在去掉 $p$ 的像点后, $\varphi(A)\setminus\{\varphi(p)\}$ 不是单连通的, 但 $\psi(A)\setminus\{\psi(p)\}$ 是单连通的 (因为 $\psi(p)\in\partial\H^2$), 导致矛盾.

Claim 29.10 (卷绕数的复积分公式) 设 $f:I\to\C\setminus\{0\}$ 是连续可微环路, 则 \[ N(f) = \frac1{2\pi\i}\int_0^1\frac{f'(s)}{f(s)}\dd{s}. \]

Pf 根据卷绕数的定义 $N(f)=N(r\circ f)$, 其中 $r(z)=z/|z|$. 因此, 我们的思路是构造 $r\circ f$ 的提升 $H:I\to\R$, 满足 $\varepsilon\circ H=r\circ f$, 即 $\e^{2\pi\i H(t)}=f(t)/|f(t)|$.

首先令 $h:I\to\C$, \[ h(t) = \frac1{2\pi\i}\int_0^t\frac{f'(s)}{f(s)}\dd{s}, \] 有 $h(0)=0$ 以及 $h'(t)=1/2\pi\i\cdot f'(t)/f(t)$. 直接的计算表明 \[ \dv{t}(\e^{-2\pi\i h(t)}f(t)) \equiv 0, \] 因此 $\e^{-2\pi\i h(t)}f(t)$ 是常数, 代入 $t=0$, 有 $\e^{-2\pi\i h(t)}f(t)\equiv f(0)$. 于是 \[ \Align{ (r\circ f)(t) = \frac{f(t)}{|f(t)|} &= \frac{f(0)}{|f(t)|} \exp(2\pi\i h(t)) \\ &= \exp\pqty{ 2\pi\i h(t)+ \ln\frac{|f(0)|}{|f(t)|} + \i\arg f(0)}, } \] 因此一个满足条件的 $H$ 是 \[ H(t) = h(t) + \frac1{2\pi\i}\pqty{ \ln\frac{|f(0)|}{|f(t)|} + \i\arg f(0) }. \] 注意 $1/2\pi\i(\cdots)$ 中的项在 $\{0,1\}$ 上常值, 故 \[ N(f) = H(1)-H(0) = h(1)-h(0) = \frac1{2\pi\i}\int_0^1\frac{f'(s)}{f(s)}\dd{s}. \]

30 Degree Theory for the Circle

30.1 The degree of a map

基本群 $\pi_1(\mathbb{S}^1,1)$ 的信息可以用来研究 $\mathbb{S}^1$ 上连续映射的同伦分类.

设连续映射 $\varphi\in C(\mathbb{S}^1,\mathbb{S}^1)$, 我们定义其映射度 (degree) 为环路 $\varphi\circ\omega$ 的卷绕数, 记作 $\deg\varphi$.

直观上看, 映射度描述了 $\varphi$ 将 $\mathbb{S}^1$ "缠绕" 到自身的 "净圈数". 逆时针缠绕为正, 顺时针为负.
旋转 $\rho(z)=\e^{\i\theta}z$ 的映射度为 $1$, 因为 $N(\rho\circ\omega)=N(\omega)=1$.

另一种刻画映射度的方式是考察 $\varphi$ 在 $\pi_1(\mathbb{S}^1,1)$ 上的作用. 回忆循环群的自同态必定形如 $F(\gamma)=\gamma^n$, 其中 $n$ 是固定的整数. 我们称 $n$ 是自同态 $F$ 的映射度, 也记作 $\deg{F}$.

容易证明, 复合映射的映射度等于映射度的乘积.

因为 $\pi_1(\mathbb{S}^1,1)$ 是无穷循环群, 所以可以考虑其自同态的映射度: 若映射 $\varphi\in C(\mathbb{S}^1,\mathbb{S}^1)$ 满足 $\varphi(1)=1$, 则 $\varphi_*$ 是 $\pi_1(\mathbb{S}^1,1)$ 的自同态, 我们将证明 $\deg\varphi_*=\deg\varphi$.

若 $\varphi$ 不保持基点, 则 $\varphi_*$ 不再是 $\pi_1(\mathbb{S}^1,1)$ 的自同态. 一个补救措施是让 $\varphi$ 复合一个旋转 $\rho_\varphi$, 使得 $\rho_\varphi\circ\varphi$ 保持基点 $1$. 这样的旋转当然存在, 即 $\rho_\varphi(z)=z/\varphi(1)$.

Claim 30.1 (映射度的刻画) 若 $\varphi\in C(\mathbb{S}^1,\mathbb{S}^1)$, 则 $\varphi$ 的映射度等于下面自同态的映射度: \[ (\rho_\varphi\circ\varphi)_*:\pi_1(\mathbb{S}^1,1)\to\pi_1(\mathbb{S}^1,1). \] 特别地, 若 $\varphi(1)=1$, 则 $\deg\varphi_*=\deg\varphi$.

Pf 设 $\varphi$ 的映射度为 $n$, 即 $N(\varphi\circ\omega)=n$, 旋转不改变卷绕数, $N(\rho_\varphi\circ\varphi\circ\omega)=n$. 因为卷绕数相同的环路是道路同伦的, 所以 $\alpha_n\sim\rho_\varphi\circ\varphi\circ\omega$. 因此 \[ (\rho_\varphi\circ\varphi)_*[\omega] = [\rho_\varphi\circ\varphi\circ\omega] = [\alpha_n] = [\omega]^n, \] 即 $(\rho_\varphi\circ\varphi)_*$ 的映射度为 $n$.

Claim 30.2 (映射度的性质)

(同伦不变性) 同伦的连续映射具有相同的映射度.
(复合) 若 $\varphi,\psi\in C(\mathbb{S}^1,\mathbb{S}^1)$, 则 $\deg(\psi\circ\varphi)=(\deg\psi)(\deg\varphi)$.

Pf 1, 设 $\varphi,\psi\in C(\mathbb{S}^1,\mathbb{S}^1)$ 是同伦的. 根据映射度的刻画, \[ \Align{ \deg\varphi &= \deg(\rho_\varphi\circ\varphi)_*, \\ \deg\psi &= \deg(\rho_\psi\circ\psi)_*. \\ } \tag{$\#$} \] 因为旋转同伦于恒等映射 (一个同伦由 $H(z,t)=\e^{\i t\theta}z$ 给出), 复合保持同伦, 所以 $\rho_\varphi\circ\varphi\sim\rho_\psi\circ\psi$. 这两侧都是保持基点 $1$ 不变的映射, 根据 Claim 27.3, 有 \[ \rho_\psi\circ\psi = \Phi_h \circ (\rho_\varphi\circ\varphi), \] 其中 $h$ 是某条以 $1$ 为基点的环路. 因为 $\pi_1(\mathbb{S}^1,1)$ 是交换群, Claim 25.4 告诉我们 $\Phi_h$ 不依赖 $h$ 的选取. 不妨取 $h=c_1$ 为常环路, 则 $\Phi_h$ 是恒等映射, 有 $\rho_\psi\circ\psi=\rho_\varphi\circ\varphi$, 进而 $(\rho_\psi\circ\psi)_*=(\rho_\varphi\circ\varphi)_*$, 结合 $(\#)$ 式有 $\deg\varphi=\deg\psi$.

2, 设 $\varphi,\psi\in C(\mathbb{S}^1,\mathbb{S}^1)$, 计算 \[ \Align{ \deg(\psi\circ\varphi) &= \deg(\rho_{\psi\circ\varphi}\circ\psi\circ\varphi)_* \\ &= \deg(\rho_{\psi\circ\varphi}\circ\psi \circ(\rho_\varphi)^{-1} \circ\rho_\varphi \circ\varphi)_* \\ &= \deg(\rho_{\psi\circ\varphi}\circ\psi\circ(\rho_\varphi)^{-1})_* \cdot \deg(\rho_\varphi\circ\varphi)_* \\ &= \deg(\rho_{\psi\circ\varphi}\circ\psi\circ(\rho_\varphi)^{-1}) \cdot \deg(\rho_\varphi\circ\varphi). } \]

因为 $\rho_{\psi\circ\varphi}\circ\psi\circ(\rho_\varphi)^{-1}\sim\psi$ 和 $\rho_\varphi\circ\varphi\sim\varphi$, 结合 1 即证.

常见映射的映射度:

常映射的映射度为 $0$, 因为其与 $\omega$ 的复合给出常环路.
旋转 (特别地, 恒等映射) 的映射度为 $1$.
幂映射 (power map) $p_n(z)=z^n$ 的映射度为 $n$, 因为 $p_n\circ\omega=\alpha_n$.
共轭映射 (conjugation map) $c(z)=\bar{z}$ 的映射度为 $-1$, 因为 $c=p_{-1}$.
对径映射 (antipodal map) $\alpha(z)=-z$ 的映射度为 $1$, 因为它等于按 $\e^{\i\pi}$ 的旋转.

Claim 30.3 ($\mathbb{S}^1$ 上连续映射的同伦分类) $\mathbb{S}^1$ 上的两个连续映射同伦, 当且仅当其映射度相同.

Pf 同伦的映射具有相同映射度. 反之, 设 $\varphi,\psi\in C(\mathbb{S}^1,\mathbb{S}^1)$ 具有相同的映射度.

首先考虑 $\varphi(1)=\psi(1)=1$ 的情形. 映射度相同即 $\varphi\circ\omega$ 与 $\psi\circ\omega$ 卷绕数相同, 因此两条环路道路同伦, 设道路同伦由 $H:I\times I\to\mathbb{S}^1$ 给出. 根据闭映射引理, $\omega\times{\rm id}:I\times I\to\mathbb{S}^1\times I$ 是商映射, 并且注意到 $H$ 在纤维上常值, 因此 $H$ 下降到 $\tilde{H}:\mathbb{S}^1\times I\to\mathbb{S}^1$, 容易证明这给出了 $\varphi,\psi$ 间的同伦.

对于一般的情形, 则有 $\deg(\rho_\varphi\circ\varphi)=\deg(\rho_\psi\circ\psi)$ (复合同一个映射不改变映射度), 由于两侧的映射都保持 $1$ 不变, 应用上面的论证, 有 $\rho_\varphi\circ\varphi\sim\rho_\psi\circ\psi$. 因为旋转同伦于恒等映射 (因而彼此同伦), 两边分别复合旋转 $(\rho_\varphi)^{-1}$ 和 $(\rho_\psi)^{-1}$ 得到 $\varphi\sim\psi$.

Claim 30.4 (映射度决定映射的性质) 设 $\varphi\in C(\mathbb{S}^1,\mathbb{S}^1)$.

若 $\deg\varphi\neq0$, 则 $\varphi$ 是满射.
若 $\deg\varphi\neq1$, 则 $\varphi$ 有不动点.
若 $\deg\varphi\neq\pm1$, 则 $\varphi$ 不是单射.

Pf 1, 证明其逆否命题. 设 $\varphi$ 不是满射, 则 $\varphi$ 可以视作到 $\mathbb{S}^1\setminus\{p\}$ 的映射. 而 $\mathbb{S}^1\setminus\{p\}$ 同胚于 $\R$, 因此是可缩空间. 任意到可缩空间的连续映射是零伦的, 即 $\varphi$ 同伦于常映射, $\deg\varphi=0$.

2, 证明其逆否命题. 设 $\varphi$ 没有不动点, 于是连接 $\varphi(z)$ 与 $-z$ 的线段不经过原点, 进而可以定义同伦 \[ H(z,t) = \frac{(1-t)\varphi(z)-tz}{|(1-t)\varphi(z)-tz|}. \] 对径映射的映射度为 $1$, 故 $\deg\varphi=1$.

3, TODO

30.2 Some applications

先证明一个引理.

Claim 30.5 ($\mathbb{S}^1$ 上连续映射的扩张) $\varphi\in C(\mathbb{S}^1,\mathbb{S}^1)$ 可以扩张到 $\Phi\in C(\overline{\mathbb{B}^2},\mathbb{S}^1)$, 当且仅当 $\deg\varphi=0$.

Pf 回顾圆代表元的定义, 连续映射 $\varphi:\mathbb{S}^1\to\mathbb{S}^1$ 可以看作道路 $f=\varphi\circ\varepsilon$ 的圆代表元. 根据 Claim 25.5 (零伦环路的圆代表元刻画), $\varphi$ 零伦当且仅当 $\varphi$ 可扩张到连续映射 $\overline{\mathbb{B}^2}\to\mathbb{S}^1$. 而根据 $\mathbb{S}^1$ 上映射的同伦分类, $\varphi$ 零伦当且仅当 $\deg\varphi=0$.

下面是著名的 Brouwer 不动点定理的二维情形. 我们之后还会证明一般的 $n$ 维情形.

Claim 30.6 (二维 Brouwer 不动点定理) 连续映射 $f\in C(\overline{\mathbb{B}^2},\overline{\mathbb{B}^2})$ 存在不动点.

Pf 假设 $f$ 不存在不动点, 则有连续映射 $\varphi:\overline{\mathbb{B}^2}\to\mathbb{S}^1$, $\varphi(x)=(x-f(x))/|x-f(x)|$. 注意到当 $z\in\mathbb{S}^1$ 时, $\varphi(z)$ 与 $z$ 永远不为对径点, 由此可以定义 $\varphi|_{\mathbb{S}^1}$ 与 ${\rm id}_{\mathbb{S}^1}$ 间的同伦 $H:\mathbb{S}^1\times I\to\mathbb{S}^1$, \[ H(z,t) = \frac{(1-t)\varphi(z)+tz}{|(1-t)\varphi(z)+tz|}. \] 故 $\deg\varphi|_{\mathbb{S}^1}=\deg{\rm id}|_{\mathbb{S}^1}=1$. 然而 $\varphi|_{\mathbb{S}^1}$ 扩张到连续映射 $\varphi$, 上面的引理表明其映射度为 $0$, 矛盾.

Claim 30.7 (代数基本定理) $\C$ 上的非常数多项式存在零点.

Pf 设非常数多项式 $p(z)=z^n+a_{n-1}z^{n-1}+\dots+a_0$.

对 $\varepsilon>0$, 记 $p_\varepsilon(z)=\varepsilon^np(z/\varepsilon)$, 即考察 $p$ 在 "无穷远" 处的形态. 我们断言, 存在 $\varepsilon>0$, 使得对任意 $z\in\mathbb{S}^1$, 有 $|p_\varepsilon(z)-z^n|<1$. 实际上, 因为 \[ \Align{ p_\varepsilon(z)-z^n &= \varepsilon a_{n-1}z^{n-1}+\dots+\varepsilon^na_0 \\ &= \varepsilon(a_{n-1}z^{n-1}+\dots+\varepsilon^{n-1}a_0), } \] 取 $\varepsilon=(|a_{n-1}|+\dots+|a_0|+1)^{-1}$ 即可.

接下来我们证明, 作为 $\mathbb{S}^1\to\C\setminus\{0\}$ 的连续映射, $p_\varepsilon|_{\mathbb{S}^1}$ 与 $p_n(z)=z^n$ 是同伦的. 当 $z\in\mathbb{S}^1$, 根据 $\varepsilon$ 的取法, 连接 $z^n$ 与 $p_\varepsilon(z)$ 的线段不经过原点, 因此 \[ H(z,t) = \frac{(1-t)p_\varepsilon(z)+tz^n}{|(1-t)p_\varepsilon(z)+tz^n|} \] 给出了 $p_\varepsilon|_{\mathbb{S}^1}$ 与 $p_n(z)=z^n$ 间的同伦. 设 $r:\C\setminus\{0\}\to\mathbb{S}^1$, $r(z)=z/|z|$ 为收缩映射, 则 $r\circ p_\varepsilon|_{\mathbb{S}^1}$ 和 $r\circ p_n$ 也是同伦的. 作为 $\mathbb{S}^1$ 上的连续映射, 它们具有相同的映射度 $n$.

最后, 假设 $p$ 没有零点, 则 $p_\varepsilon:\C\to\C\setminus\{0\}$, 复合映射 $r\circ p_\varepsilon$ 在 $\overline{\mathbb{B}^2}$ 上的限制给出了 $r\circ p_\varepsilon|_{\mathbb{S}^1}$ 在单位圆盘上的扩张. 根据引理, $\deg(r\circ p_\varepsilon|_{\mathbb{S}^1})=0$, 矛盾.

向量场的指标.

欧氏空间 $\R^n$ 上的向量场 (vector field) 指的是连续映射 $V:\R^n\to\R^n$. 若 $V(p)=0$, 则 $p$ 称为向量场的奇点 (singular point); 若 $V(p)\neq0$, 则 $p$ 称为向量场的正则点 (regular point). 奇点 $p$ 称为孤立的 (isolated), 若它的某个邻域内不存在其他奇点.

设 $V$ 是 $\R^2$ 上的向量场, 记 ${\cal R}_V\subset\R^2$ 为其正则点全体. 对于环路 $f:I\to{\cal R}_V$, 向量场 $V$ 关于 $f$ 的卷绕数 (winding number of $V$ around $f$) 定义为环路 $V\circ f:I\to\R^2\setminus\{0\}$ 的卷绕数. 记作 $N(V,f)$.

$N(V,f)$ 只依赖于 $f$ 所在的道路类. 实际上, 若有环路同伦 $f\sim g:I\to{\cal R}_V$, 则 $V\circ f\sim V\circ g$ 也环路同伦. 根据 $\R^2\setminus\{0\}$ 上环路的同伦分类, $V\circ f$ 和 $V\circ g$ 有相同的卷绕数.
$N(V,f)$ 与映射度的关系. 由定义, $N(V,f)=N(r\circ V\circ f)$, 其中 $r:\R^2\setminus\{0\}\to\mathbb{S}^1$ 是标准的收缩映射. 取 $f$ 的圆代表元 $\tilde{f}:\mathbb{S}^1\to{\cal R}_V$, 有 $f=\tilde{f}\circ\omega$. 故 \[ N(V,f) = N(r\circ V\circ f) = N(r\circ V\circ\tilde{f}\circ\omega) = \deg(r\circ V\circ\tilde{f}), \] 即 $N(V,f)$ 是映射 $r\circ V\circ\tilde{f}:\mathbb{S}^1\to\mathbb{S}^1$ 的映射度. 所以 $N(V,f)$ 是一个同伦不变量, 同伦的 $\tilde{f}$ 给出相同的卷绕数.

设 $p$ 是向量场 $V$ 的孤立奇点, 则存在 $r>0$ 使得 $B_r(p)$ 内没有其他奇点. 对于小正数 $\varepsilon<r$, 小环路 $f_\varepsilon(s)=p+\varepsilon\omega(s)$ 不穿过奇点, 因此 $N(V,f_\varepsilon)$ 有定义. 此时, $N(V,f_\varepsilon)$ 是一个与 $\varepsilon$ 无关的整数, 称为 $V$ 在 $p$ 处的指标 (index), 记作 ${\rm Ind}(V,p)$.

注意到对于 $\varepsilon,\varepsilon'<r$, $f_\varepsilon,f_{\varepsilon'}$ 的圆代表元 $\tilde{f}_\varepsilon,\tilde{f}_{\varepsilon'}$ 是自由同伦的 (取直线同伦即可), 因此, 根据前面的讨论, $N(V,f_\varepsilon)=N(V,f_{\varepsilon'})$. 故向量场的指标是良定义的.
几个简单向量场的指标:

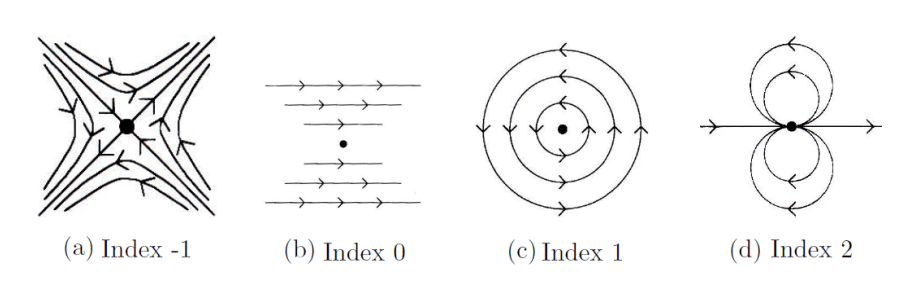
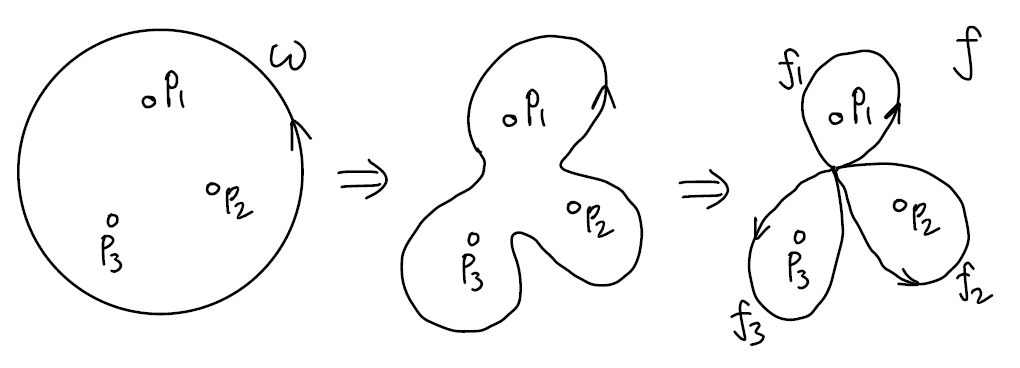
Claim 30.8 (指标和等于边界的卷绕数) 设向量场 $V$ 在 $\overline{\mathbb{B}^2}$ 内只有有限个奇点, 且都在其内部, 则 $V$ 这些奇点的指标之和等于 $N(V,\omega)$.

Pf 如下图, 根据同伦不变性, $N(V,\omega)=N(V,f)$. 因为道路乘积对应卷绕数加和, 所以 $N(V,f)$ 是所有 $N(V,f_i)$ 之和, 即 ${\rm Ind}(V,p_i)$ 之和.

$\mathbb{T}^2$ 上连续映射的同伦分类.

环面 $\mathbb{T}^2$ 在基点 $p=(1,1)$ 处的基本群 $\pi_1(\mathbb{T}^2,p)$ 由两条标准环路 \[ \Align{\omega_1(s)&=(\e^{2\pi\i s},1),&\omega_2(s)&=(1,\e^{2\pi\i s})} \] 生成. 设 $r_1,r_2$ 分别表示 $\mathbb{T}^2$ 到 $\mathbb{S}^1\times\{1\}$ 和 $\{1\}\times\mathbb{S}^1$ (这两条环路的像) 的收缩映射. 对于 $\mathbb{T}^2$ 上的连续映射 $\varphi$, 我们构造一个 $2\times2$ 矩阵 \[ D(\varphi) := \pmqty{ N{(r_1\circ\varphi\circ\omega_1)} & N{(r_1\circ\varphi\circ\omega_2)} \\ N{(r_2\circ\varphi\circ\omega_1)} & N{(r_2\circ\varphi\circ\omega_2)} }, \] 它可以视作 $\varphi$ 的 "映射度".

恒等映射 ${\rm id}_{\mathbb{T}^2}$ 和旋转映射 $\rho(z,w)=(\e^{\i\theta}z,\e^{\i\phi}w)$ 对应单位阵.
任给 $m,n,k,l\in\Z$, 定义 "幂映射" \[ \Align{ \varphi:\mathbb{T}^2 &\to\mathbb{T}^2, & \varphi(z,w)&=(z^mw^n,z^kw^l), } \] 它对应的矩阵 \[ D(\varphi) = \pmqty{m & n \\ k & l}. \]

Claim 30.9 ($\mathbb{T}^2$ 上连续映射的同伦分类) 设 $\varphi,\psi\in C(\mathbb{T}^2,\mathbb{T}^2)$.

(分类) $\varphi\sim\psi$ 当且仅当 $D(\varphi)=D(\psi)$.
(函子性) $D(\psi\circ\varphi)=D(\psi)D(\varphi)$.
(同胚) $\varphi$ 同伦于一个同伦等价映射, 当且仅当 $D(\varphi)$ 是 $\Z$ 上的可逆矩阵.

Note

#数学 #拓扑

GTM202 | 12 圆的基本群

https://disembo.github.io/Note/tp-gtm202-12/

作者

jin

发布于

2024年8月10日

许可协议

GTM218 | 光滑流形笔记上一篇

GTM202 | 11 同伦与基本群下一篇