GTM202 | 11 同伦与基本群

GTM202 (Introduction to Topological Manifolds) Chapter 7 的笔记.

26 Functoriality of Fundamental Groups

拓扑空间之间的连续映射可以诱导出基本群间的同态. 这使得基本群构造 \(\pi_1\) 成为了 "带点拓扑范畴" 到群范畴的函子, 进而导致了 \(\pi_1\) 的拓扑不变性.

26.1 The induced homomorphism

设拓扑空间 \(X\), 以 \(p\) 为基点的基本群 \(\pi_1(X,p)\). 因为连续映射保持道路同伦, \(\varphi\in C(X,Y)\) 诱导出了映射 \(\varphi_*:\pi_1(X,p)\to\pi_1(Y,\varphi(p))\), \[ \varphi_*[f] := [\varphi\circ f]. \]

• 若 \(f\sim g\), 则 \(\varphi\circ f\sim\varphi\circ g\), 说明这个映射是良定义的.

Claim 26.1 (诱导同态) 对 \(\varphi\in C(X,Y)\), \(\varphi_*\) 是群同态, 称为 \(\varphi\) 诱导的同态.

Pf 有 \[ \varphi_*([f]*[g])=\varphi_*[f*g]=[\varphi\circ(f*g)], \] 只需证明 \(\varphi\circ(f*g)=(\varphi\circ f)*(\varphi\circ g)\) (连续映射保持道路乘积), 用乘积定义直接展开即可.

26.2 Functoriality of \(\pi_1\)

Claim 26.2 (诱导同态的函子性)

1. 设 \(\varphi\in C(X,Y)\), \(\psi\in C(Y,Z)\), 则 \((\psi\circ\varphi)_*=\psi_*\circ\varphi_*\).
2. 恒等映射 \({\rm id}_X\) 诱导出的同态 \(({\rm id}_X)_*\) 是 \(\pi_1(X,p)\) 的恒等映射.

Pf 计算: \[ \Align{ \psi_*(\varphi_*[f]) &=\psi_*[\varphi\circ f]=[\psi\circ\varphi\circ f] =(\psi\circ\varphi)_*[f], \\ ({\rm id}_X)_*[f] &= [{\rm id}_X\circ f]=[f]. } \]

为了进一步阐明函子性, 我们引入带点拓扑空间范畴. 带点拓扑空间 (pointed space) 指的是二元组 \((X,p)\), 其中 \(X\) 是拓扑空间, 点 \(p\in X\). 带点拓扑空间 \((X,p),(Y,q)\) 之间的态射是连续映射 \(f\in C(X,Y)\) 满足 \(f(p)=q\). 带点拓扑空间范畴 (pointed topological category) 是由带点拓扑空间和态射组成的范畴, 记作 \({\sf Top}_*\).

基本群函子 (fundamental group functor) \(\pi_1:{\sf Top}_*\to{\sf Grp}\) 是带点拓扑空间范畴到群范畴的函子, 将 \((X,p)\) 映到基本群 \(\pi_1(X,p)\), 将态射 \(\varphi:(X,p)\to(Y,q)\) 映到诱导同态 \(\varphi_*:\pi_1(X,p)\to\pi_1(Y,q)\). 根据上面的定理, \(\pi_1\) 满足函子的条件, 是一个协变函子.

函子性的标准应用是拓扑不变性 (函子将同构映到同构).

Claim 26.3 (基本群的拓扑不变性) 若 \(\varphi:X\to Y\) 是同胚, 则有同构 \(\varphi_*:\pi_1(X,p)\to\pi_1(Y,\varphi(p))\).

基本群函子将 \({\sf Top}_*\) 的积 (积空间) 映到 \({\sf Grp}\) 的积 (直积群). 设拓扑空间 \(X_1,\dots,X_n\), 自然投射 \(p_i:X_1\times\dots\times X_n\to X_i\). 取定基点 \(x_i\in X_i\), 有诱导同态 \[ (p_i)_*:\pi_1(X_1\times\dots\times X_n,(x_1,\dots,x_n)) \to \pi_1(X_i,x_i). \] 这些同态的积是 \[ \Align{ P:\pi_1(X_1\times\dots\times X_n,(x_1,\dots,x_n)) &\to \pi_1(X_1,x_1)\times\dots\times\pi_1(X_n,x_n), \\ [f] &\mapsto ((p_1)_*[f],\dots,(p_n)_*[f]). } \]

Claim 26.4 (乘积的基本群) 如上定义的 \(P\) 是群同构.

Pf 同态的积是同态, 只需验证双射.

满: 任取 \([f_i]\in\pi_1(X_i,x_i)\), 定义积空间的环路 \(f(s)=(f_1(s),\dots,f_n(s))\), 则 \[ P[f] = ((p_1)_*[f],\dots,(p_n)_*[f]) = ([p_1\circ f],\dots,[p_n\circ f]) = ([f_1],\dots,[f_n]). \] 单: 设乘积空间的环路 \(f(s)=(f_1(s),\dots,f_n(s))\) 满足 \(P[f]\) 是直积群的恒等元, 即 \[ [c_{x_i}]=(p_i)_*[f]=[p_i\circ f]=[f_i], \] 即 \(f_i\) 道路同伦于常环路 \(c_{x_i}\), \(H_i:f_i\sim c_{x_i}\). 定义 \(H:I\times I\to X_1\times\dots\times X_n\), \[ H(s,t)=(H_1(s,t),\dots,H_n(s,t)). \] 这给出了 \(f\) 到常环路 \(c_{(x_1,\dots,x_n)}\) 的道路同伦.

实际上, 基本群函子还将 \({\sf Top}_*\) 的余积 (一点并) 映到 \({\sf Grp}\) 的余积 (自由积), 我们在后面进一步讨论.

补充一个简单的例子. 回顾拓扑齐性空间: 拓扑齐性空间 \(X\) 中, 任意两点可以由同胚联系起来. 因此任意基点的基本群 \(\pi_1(X,p)\) 都是同构的. 特别地, 拓扑群是齐性的, 因此拓扑群的基本群处处同构.

Claim 26.5 (拓扑群的基本群) 拓扑群的基本群是交换群.

Pf 因为拓扑群是齐性的, 只需考虑 \(e\in G\) 处的基本群. 任给环路 \(f,g\in\Omega(G,e)\), 考虑连续映射 \(F:I\times I\to G\), \(F(s,t)=f(s)g(t)\), 应用正方形引理, 立刻得到 \(f*g\sim g*f\).

26.3 Retraction

需要注意的是, 连续映射 \(\varphi\in C(X,Y)\) 的单射性/满射性不意味着诱导同态 \(\varphi_*\) 的单射性/满射性. 例如, \(\iota:\mathbb{S}^1\hookrightarrow\R^2\) 是单射, 然而 \(\pi_1(\mathbb{S}^1)\) 是无穷循环群, \(\pi_1(\R^2)\) 平凡, \(i_*\) 是平凡同态.

利用函子性, 要保证诱导同态的单射/满射性, 需要为连续映射找到单侧逆. 设子空间 \(A\subset X\), 包含映射 \(\iota_A:A\hookrightarrow X\). 连续映射 \(r:X\to A\) 称为收缩 (retraction), 若它是 \(\iota\) 的左逆: \(r\circ\iota_A={\rm id}_A\). 等价的说法是 \(r\) 在 \(A\) 上的限制是恒等映射. 此时称 \(A\) 是 \(X\) 的一个收缩.

Claim 26.6 (收缩的性质)

1. (道路) 连通空间的收缩是 (道路) 连通的.
2. 紧空间的收缩是紧的.
3. (传递) \(A\subset B\subset X\), 若 \(A\) 是 \(B\) 的收缩, \(B\) 是 \(X\) 的收缩, 则 \(A\) 是 \(X\) 的收缩.

Pf 收缩是连续的满射, 因此 1, 2 是显然的. 3, 设收缩 \(r_1:B\to A\), \(r_2:X\to B\), 容易验证, 复合映射 \(r_1\circ r_2:X\to A\) 给出了 \(X\) 到 \(A\) 的收缩.

Claim 26.7 (收缩的诱导同态) 设收缩 \(r:X\to A\), 则对任意一点 \(p\in A\), \((\iota_A)_*:\pi_1(A,p)\to\pi_1(X,p)\) 是单射, \(r_*:\pi_1(X,p)\to\pi_1(A,p)\) 是满射.

Pf 因为 \(r\circ\iota_A={\rm id}_A\), 利用函子性有 \(r_*\circ(\iota_A)_*={\rm id}\), 两者互为单侧逆, 即 \(r_*\) 满, \((\iota_A)_*\) 单.

Claim 26.8 (收缩保持单连通) 单连通空间的收缩是单连通的.

• (逆否命题) 若收缩不单连通, 则原空间不单连通.

Pf 因为 \((\iota_A)_*:\pi_1(A,p)\to\pi_1(X,p)\) 是单射, 如果 \(\pi_1(X,p)\) 平凡, 则 \(\pi_1(A,p)\) 平凡.

一些收缩的例子:

• (去掉一个点的平面) 对于 \(n\geq1\), 映射 \(r:\R^n\setminus\{0\}\to\mathbb{S}^n\), \(x\mapsto x/\|x\|\) 是收缩. 因为 \(\mathbb{S}^1\) 不单连通, 所以去掉一个点的平面 \(\R^2\setminus\{0\}\) 不单连通.
• (二维环面) 环面 \(\mathbb{T}^2=\mathbb{S}^1\times\mathbb{S}^1\) 到子空间 \(\mathbb{S}^1\times\{1\}\) 的收缩由 \(r(z,w)=(z,1)\) 给出. 因此 \(\mathbb{T}^2\) 不是单连通的.
• (数字 \(8\)) 数字 \(8\) 空间 \({\cal E}\subset\R^2\) 是两个单位圆 \(\mathbb{S}^1\) 的一点并, 它可以收缩到其中一个单位圆, 因此不单连通.
• (圆盘不可收缩到边界) 单位圆盘 \(\overline{\mathbb{B}^2}\) 单连通, 而其边界 \(\mathbb{S}^1\) 非单连通, 因此单位圆盘不可收缩到其边界.

27 Homotopy Equivalence

同伦等价是一个比同胚弱的等价关系. 基本群不光在同胚下保持, 还在同伦等价下保持. 这个结论让我们能够计算更多空间的基本群.

27.1 Homotopy equivalence

回顾: 拓扑空间 \(X,Y\) 称为同胚的, 记 \(X\cong Y\), 若存在 \(\varphi\in C(X,Y)\) 和 \(\psi\in C(Y,X)\) 满足 \(\psi\circ\varphi={\rm id}_X\) 且 \(\varphi\circ\psi={\rm id}_Y\). 称 \(\psi,\varphi\) 互为逆映射. 同胚是一个很强的等价关系, 同胚的空间具有相同的拓扑性质. 下面引入一个较弱的等价关系.

设 \(\varphi\in C(X,Y)\), 若存在 \(\psi\in C(Y,X)\), 满足 \(\psi\circ\varphi\sim{\rm id}_X\) 且 \(\varphi\circ\psi\sim{\rm id}_Y\), 则称 \(X,Y\) 是同伦等价的 (homotopy equivalent), 称映射 \(\varphi,\psi\) 是 \(X,Y\) 间的同伦等价 (homotopy equivalence), \(\psi\) 称为 \(\varphi\) 的一个同伦逆 (homotopy inverse). 在同伦等价下保持不变的性质称为同伦不变性.

• 同伦等价是拓扑空间之间的等价关系.

• \(X\cong Y\) 蕴含 \(X\sim Y\), 反之不然. 实际上, 很多拓扑性质 (如紧性, Hausdorff 性) 不能在同伦等价下保持. 同伦等价大致说的是两个空间具有相似的形状, 比如 "洞" 的个数. 下图中的几个拓扑空间互不同胚, 但同伦等价: (图自香蕉空间)

  

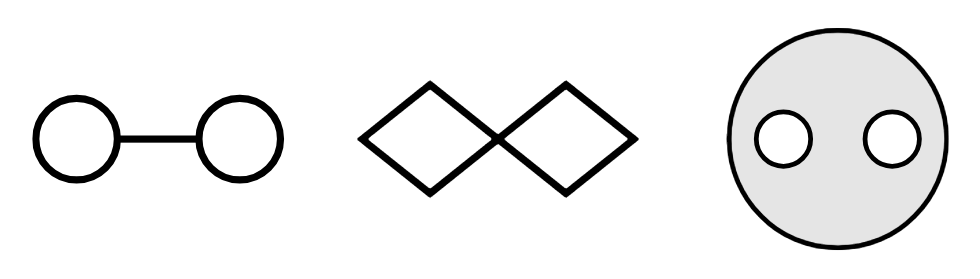
27.2 Deformation retractions

收缩映射满足 \(r\circ\iota_A={\rm id}_A\), 如果进一步还有 \(\iota_A\circ r\sim{\rm id}_X\), 则称之为形变收缩 (deformation retraction), 此时我们说 \(A\) 是 \(X\) 的一个形变收缩. 形变收缩是空间 \(X\) 与其子空间的一种同伦等价.

如果收缩映射还满足 \(\iota_A\circ r\) 相对 \(A\) 同伦于 \({\rm id}_X\), 则称之为强形变收缩 (strong deformation retraction).

• 子空间 \(A\) 是 \(X\) 的形变收缩, 当且仅当存在同伦 \(H:X\times I\to X\), 满足 \[ \Align{ H(x,0) &= x, &\forall x\in X, \\ H(x,1) &\in A, &\forall x\in X, \\ H(a,1) &= a, &\forall a\in A. } \] 强形变收缩则进一步要求 \(H(a,t)=a\), \(\forall a\in A,t\in I\). 有时, 我们也将同伦 \(H\) 称作形变收缩.

• 直观上讲, \(A\) 是 \(X\) 的形变收缩, 若 \(X\) 能够连续地形变成 \(A\), 同时 \(A\) 中的点最终回到原位. \(A\) 是 \(X\) 的强形变收缩, 若 \(X\) 能够连续地形变成 \(A\), 同时 \(A\) 中的点自始至终保持不动.

Claim 27.1 (球面是强形变收缩) 对 \(n\geq1\), \(\mathbb{S}^{n-1}\) 是 \(\R^n\setminus\{0\}\) 以及 \(\overline{\mathbb{B}^n}\setminus\{0\}\) 的强形变收缩.

Pf 定义同伦 \(H:(\R^n\setminus\{0\})\times I\to\R^n\setminus\{0\}\), \[ H(x,t)=(1-t)x + t\frac{x}{\|x\|}, \] 是恒等映射 \({\rm id}_{\R^n\setminus\{0\}}\) 与收缩映射 \(r:\R^n\setminus\{0\}\to\mathbb{S}^{n-1}\) 间的直线同伦, 并且保持 \(\mathbb{S}^{n-1}\) 不变, 因此是强形变收缩. 上式也应用于 \(\overline{\mathbb{B}^n}\setminus\{0\}\).

形变收缩最极端的情况是 \(X\) 形变收缩到一个点. 拓扑空间 \(X\) 称为可缩的 (contractible), 如果 \(X\) 同伦等价于一个独点空间.

Claim 27.2 (可缩空间的刻画) 设空间 \(X\), TFAE:

1. \({\rm id}_X\) 零伦.
2. \(X\) 可缩.
3. \(X\) 中任意一点是 \(X\) 的形变收缩.
4. 任意连续映射 \(\varphi\in C(Y,X)\) 是零伦的.

Pf 我们证明 1 \(\Rightarrow\) 2 \(\Rightarrow\) 3 \(\Rightarrow\) 4 \(\Rightarrow\) 1, 其中 4 \(\Rightarrow\) 1 是显然的.

1 \(\Rightarrow\) 2, 设 \({\rm id}_X\sim f_p\), 其中 \(f_p(x)\equiv p\in X\) 是常映射. 记同伦为 \(H:X\times I\to X\), 有 \[ \Align{ H(x,0) &= x, &\forall x\in X, \\ H(x,1) &= p, &\forall x\in X. } \] 注意到这给出了一个 \(X\) 到 \(\{p\}\) 的形变收缩, 故 \(X\sim\{p\}\).

2 \(\Rightarrow\) 3, 设同伦等价 \(\varphi:X\to\{p\}\), \(\psi:\{p\}\to X\), 满足 \(\psi\circ\varphi\sim{\rm id}_X\). 任给一点 \(x\in X\), 有唯一的映射 \(f:\{p\}\to\{x\}\). 容易证明, \(f\circ\varphi:X\to\{x\}\) 就是形变收缩: 一方面, 它保持 \(x\) 点不动; 另一方面, 注意到 \(\iota_{\{x\}}=\psi\circ f^{-1}\), 所以 \[ \iota_{\{x\}}\circ(f\circ\varphi) = (\psi\circ f^{-1})\circ(f\circ\varphi) = \psi\circ\varphi \sim {\rm id}_X. \] 3 \(\Rightarrow\) 4, 任给空间 \(Y\) 和 \(\varphi\in C(Y,X)\), 取 \(p\in\im\varphi\). 有形变收缩 \(r:X\to\{p\}\), 满足 \(\iota_{\{p\}}\circ r\sim{\rm id}_X\). 因为复合保持同伦, 两边复合 \(\varphi\) 得到 \[ \iota_{\{p\}}\circ r\circ\varphi \sim {\rm id}_X\circ\varphi. \] 上式左边是常值映射, 右边等于 \(\varphi\), 故 \(\varphi\) 是零伦的.

27.3 Homotopy invariance of \(\pi_1\)

基本群不光被同胚关系保持, 还被同伦等价保持.

在此之前, 我们先证明同伦的映射 \(\varphi,\psi\) 诱导出相同的基本群同态 \(\varphi_*,\psi_*\) (在相差一个同构的意义下).

Claim 27.3 (诱导同态的 "同伦不变性") 设 \(\varphi,\psi\in C(X,Y)\), 同伦 \(H:\varphi\sim\psi\). 对于 \(p\in X\), 记 \(h\) 是 \(Y\) 中连接 \(\varphi(p),\psi(p)\) 的道路, 定义为 \(h(t)=H(p,t)\). 令 \[ \Phi_h:\pi_1(Y,\varphi(p))\to\pi_1(Y,\psi(p)) \] 表示基点变换导出的群同构. 则下图交换: \[ \xymatrix@C=0em{ & \pi_1(Y,\varphi(p)) \ar[dd]_{\sim}^{\Phi_h} \\ \pi_1(X,p) \ar[ru]^{\varphi_*} \ar[rd]_{\psi_*} \\ & \pi_1(Y,\psi(p)). } \]

Pf 任取以 \(p\) 为基点的环路 \(f\). 我们要证明 \[ \Align{ \psi_*[f] &= \Phi_h(\varphi_*[f]) \\ \iff &\psi\circ f \sim \bar{h}*(\varphi\circ f)* h \\ \iff &h*(\psi\circ f) \sim (\varphi\circ f)* h. } \] 对连续映射 \(F:I\times I\to Y\), \(F(s,t)=H(f(s),t)\) 应用正方形引理即得 (如下图).

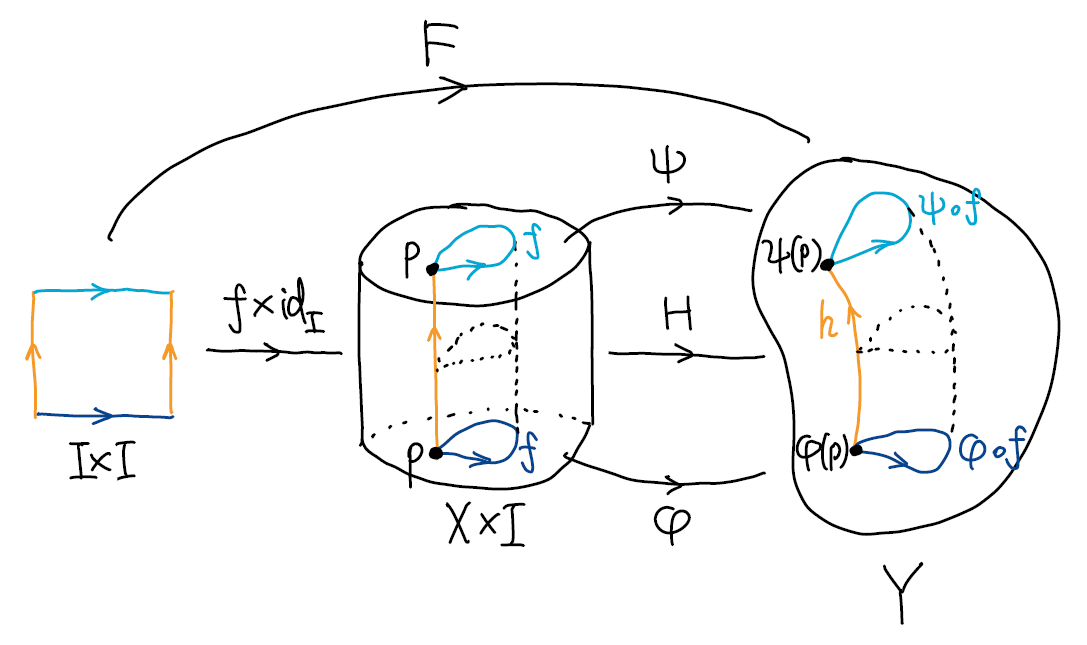
Claim 27.4 (基本群的同伦不变性) 若 \(\varphi\in C(X,Y)\) 是同伦等价, 则 \(\varphi_*:\pi_1(X,p)\to\pi_1(Y,\varphi(p))\) 是同构.

Pf 设 \(\varphi:X\to Y\) 的一个同伦逆是 \(\psi:Y\to X\), 它们满足 \(\psi\circ\varphi\sim{\rm id}_X\) 和 \(\varphi\circ\psi\sim{\rm id}_Y\). 对这两对同伦分别应用上面的定理, 得到两个交换图: \[ \xymatrix@C=0em{ & \pi_1(X,\psi(\varphi(p))) \ar[dd]_{\sim}^{\Phi_h} \\ \pi_1(X,p) \ar[ru]^(.4){\psi_*\circ\varphi_*} \ar[rd]_(.4){({\rm id}_X)_*}^{\sim} \\ & \pi_1(X,p) } \] 以及 \[ \xymatrix@C=0em{ & \pi_1(Y,\varphi(\psi(\varphi(p)))) \ar[dd]_{\sim}^{\Phi_k} \\ \pi_1(Y,\varphi(p)) \ar[ru]^(.4){\varphi_*\circ\psi_*} \ar[rd]_(.4){({\rm id}_Y)_*}^{\sim} \\ & \pi_1(Y,\varphi(p)), } \] 其中 \(\Phi_h,\Phi_k\) 是同构. 从第一个交换图看出, \(\psi_*\circ\varphi_*\) 是同构, 特别地, \(\varphi_*\) 单. 从第二个交换图看出, \(\varphi_*\circ\psi_*\) 是同构, 特别地, \(\varphi_*\) 满. 因此 \(\varphi_*\) 是双射.

作为推论, 立刻得到: 空间 \(X\) 与其形变收缩 \(A\) 的基本群同构. 特别地, 因为独点空间是单连通的, 所以可缩空间都是单连通的.

• (去掉一点的空间) 我们已经证明了, \(\mathbb{S}^{n-1}\) 是 \(\R^n\setminus\{0\}\) 以及 \(\overline{\mathbb{B}^n}\setminus\{0\}\) 的强形变收缩. 因此,
  • 当 \(n=2\) 时, \(\R^2\setminus\{0\}\) 以及 \(\overline{\mathbb{B}^2}\setminus\{0\}\) 的基本群都是无穷循环群 (之后证明);
  • 当 \(n\geq3\) 时, \(\R^n\setminus\{0\}\) 以及 \(\overline{\mathbb{B}^n}\setminus\{0\}\) 都是单连通的.
• (星形子集) \(\R^n\) 的子集 \(B\) 称为星形的 (star-shaped), 若存在 \(p_0\in B\), 使得 \(p_0\) 与 \(B\) 中任意一点所连线段包含于 \(B\) 内. 易见星形子集是可缩的 (可以强形变收缩到 \(\{p_0\}\)), 因此是单连通的.
  • \(\R^n\) 的凸子集是一种星形子集.

\(\pi_1\) 的同伦等价性使得我们能够将其视作 "带点同伦范畴" \({\sf HTop}_*\) 到群范畴 \({\sf Grp}\) 的函子.

• 同伦范畴 (homotopy category) \({\sf HTop}\) 的对象是拓扑空间 (和 \(\sf Top\) 相同), 态射是连续映射的同伦类. 因为复合映射保持同伦, 所以态射的复合是良定义的. \({\sf HTop}\) 的同构是同伦等价 (的同伦类).
• 带点同伦范畴 (pointed homotopy category) \({\sf HTop}_*\) 的对象是带点拓扑空间 (和 \({\sf Top}_*\) 相同), 态射是保持基点的连续映射的同伦类 (保持基点不变的相对同伦).

28 Higher Homotopy Groups

实际上, 基本群 \(\pi_1(X)\) 只是 \(X\) 上的一系列群中的一个.

回顾环路的圆表示: 取定基点 \(p\in X\) 和 \(0\sim 1\in\mathbb{S}^1\), 则以 \(p\) 为基点的环路 \(f:I\to X\) 与保持基点的连续映射 \(\tilde{f}:\mathbb{S}^1\to X\) (\(\tilde{f}(0)=\tilde{f}(1)=p\)) 一一对应. 因此, \(\Omega(X,p)\) 可以与 \(C((\mathbb{S}^1,1),(X,p))\) 认同.

又注意到, 环路 \(f,g\) 道路同伦, 当且仅当 \(\tilde{f},\tilde{g}\) 相对同伦 (保持 \(\{1\}\subset\mathbb{S}^1\) 不变), 因此基本群 \(\pi_1(X,p)\) 可以视作 \(C((\mathbb{S}^1,1),(X,p))\) 在 (相对) 同伦关系下的商集 \([(\mathbb{S}^1,1),(X,p)]\).

作为其自然的推广, 我们考虑 \(C((\mathbb{S}^n,x_0),(X,p))\) 在 (相对) 同伦关系下的商集 \([(\mathbb{S}^n,x_0),(X,p)]\), 记作 \(\pi_n(X,p)\).

• 当 \(n=0\) 时, \(\mathbb{S}^0=\{\pm1\}\), 连续映射 \(f\in C((\mathbb{S}^0,1),(X,p))\) 总将 \(1\) 映到 \(p\), 因此它完全决定于 \(f(-1)\) 的取值. 这样的两个连续映射 \(f,g\) 同伦, 当且仅当 \(f(-1)\) 和 \(g(-1)\) 处在相同的道路分量中. 因此, \(\pi_0(X,p)\) 是装有 \(X\) 的所有道路分量的集合. 其上没有标准的群结构.
• 当 \(n\geq1\) 时, \(\pi_n(X,p)\) 上可以定义群乘法, 称为以 \(p\) 为基点的 \(n\) 阶同伦群 (\(n\)th holonomy group based at \(p\)). (\(n=1\) 时就是熟知的基本群.)

和基本群一样, 同伦群 \(\pi_n\) 也是 \({\sf Top}_*\) 到 \({\sf Grp}\) 的协变函子. 不同的是, 高阶同伦群 \(\pi_n(X,p)\) (\(n\geq2\)) 是交换群. \(\pi_n(X,p)\) 给出了空间 \(X\) 的 "\(n\) 维洞" 的信息. 高阶同伦群极难计算, 例如, 我们对球面同伦群 \(\pi_k(\mathbb{S}^n)\) (\(n\) 远大于 \(k\)) 的理解是十分有限的. 同伦群的结构与计算是代数拓扑 (同伦论) 的重要主题.