GTM202 | 10 同伦与基本群

GTM202 (Introduction to Topological Manifolds) Chapter 7 的笔记.

连通性和紧致性是基本的拓扑不变量, 可以让我们区分一些不同胚的拓扑空间, 比如 \(\R^2\) 和 \(\mathbb{S}^2\) (前者不紧, 后者紧). 但是, 若要区分更一般的空间, 比如 \(\R^2\) 和 \(\R^2\setminus\{0\}\), 我们就得引入更强的拓扑不变量了.

基本群和高阶同伦群是一类更精妙的拓扑不变量 (更一般地, 它们还是同伦不变量), 可以探测空间的 "不同维数的洞" 的个数.

24 Homotopy

24.1 Homotopy

设拓扑空间 \(X,Y\) 间的连续映射 \(f,g:X\to Y\). 若存在连续映射 \(H:X\times I\to Y\) (单位区间 \(I=[0,1]\)), 使得 \[ H(x,0)=f(x),\quad H(x,1)=g(x), \] 我们称映射 \(f,g\) 是同伦的 (homotopic), 且称 \(H\) 是 \(f,g\) 间的一个同伦 (homotopy). 同伦的映射记作 \(f\sim g\), 同伦 \(H\) 可记作 \(H:f\sim g\).

• 同伦 \(H\) 确定了一族连续映射 \(H_t=H(-,t):X\to Y\), 其中 \(H_0=f\), \(H_1=g\). 若将参数 \(t\in[0,1]\) 理解为时间, 则 \(H\) 可理解为将 \(f\) "连续形变" 到 \(g\).

• (直线同伦) 设 \(X\) 是拓扑空间, \(B\subset\R^n\) 是凸集. 任给连续映射 \(f:X\to B\), 定义 \(H:X\times I\to B\), \[ H(x,t) = (1-t) f(x) + t g(x). \] 显然 \(H\) 良定义 (由 \(B\) 的凸性) 且连续, 因而构成 \(f,g\) 间的同伦, 称为直线同伦 (straight-line homotopy). 这说明, 任意到某凸集的连续映射彼此同伦.

  

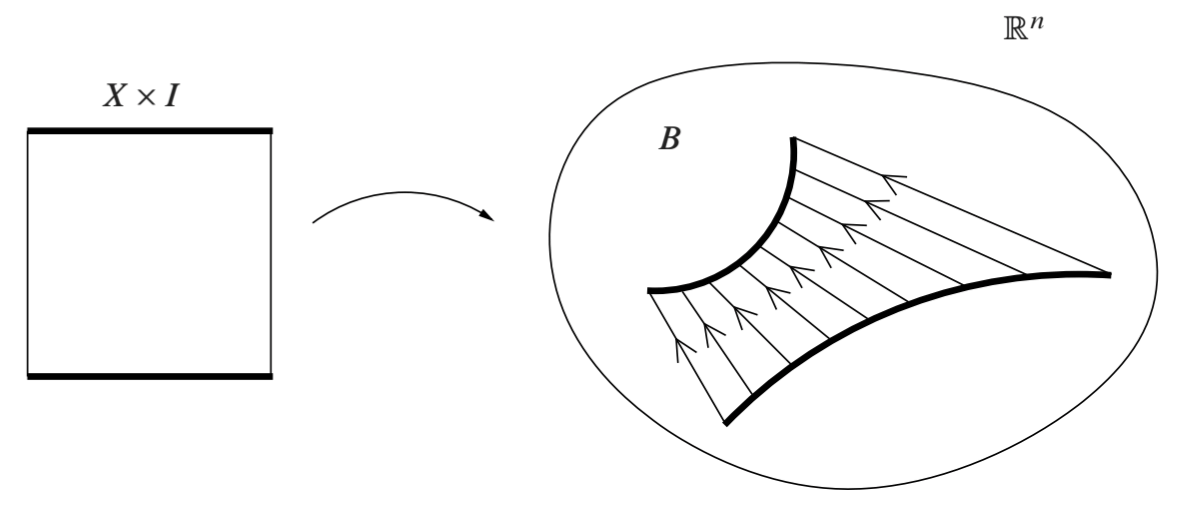
若 \(f:X\to Y\) 同伦于常值映射, 则称其为零伦的 (null-homotopic).

记 \(X\to Y\) 的所有连续映射组成的集合为 \(C(X,Y)\).

Claim 24.1 (同伦是等价关系) 同伦关系是 \(C(X,Y)\) 上的等价关系.

Pf 自反性, \(f\) 通过平凡同伦 \(H(x,t)=f(x)\) 同伦于自身.

对称性, 若 \(H:f\sim g\) 则 \(\tilde{H}(x,t)=H(x,1-t)\) 是 \(g\) 到 \(f\) 的同伦.

传递性, 若 \(F:f\sim g\), \(G:g\sim h\), 定义 \(H:X\times I\to Y\) 是将两个同伦以二倍速拼起来: \[ H(x,t)=\Cases{ F(x,2t), & 0\leq t\leq \frac12, \\ G(x,2t-1), & \frac12\leq t\leq 1. } \] 因为 \(F(x,1)=g(x)=G(x,0)\), 所以 \(H\) 定义中的两段在 \(t=1/2\) 处相容. 根据 gluing lemma, \(H\) 连续, 进而是 \(f,h\) 间的同伦.

映射 \(f\in C(X,Y)\) 在同伦关系下的等价类记作 \([f]\). 所有等价类的全体记作 \([X,Y]\).

Claim 24.2 (复合保持同伦) 设 \(f_0,f_1\in C(X,Y)\), \(g_0,g_1\in C(Y,Z)\) 且 \(f_0\sim f_1\), \(g_0\sim g_1\), 则 \(g_0\circ f_0\sim g_1\circ f_1\).

Pf 设同伦 \(F:f_0\sim f_1\), \(G:g_0\sim g_1\), 定义 \(H:X\times I\to Z\), \(H(x,t)=G(F(x,t),t)\). 于是 \[ \Align{ H(x,0) &= G(F(x,0),0) = G(f_0(x),0) = g_0(f_0(x)), \\ H(x,1) &= G(F(x,1),1) = G(f_1(x),1) = g_1(f_1(x)), } \] 因此 \(H:g_0\circ f_0\sim g_1\circ f_1\).

24.2 Path homotopy

回顾: 拓扑空间 \(X\) 中的一条道路指的是连续映射 \(f:I\to X\). 点 \(p=f(0)\) 和 \(q=f(1)\) 分别称为起点和终点, 此时我们说 \(f\) 是一条从 \(p\) 到 \(q\) 的道路.

• 作为连续映射, 道路间自然地有同伦关系. 实际上, 任给道路 \(f:I\to X\), 定义 \(H:I\times I\to X\), \[ H(s,t) = f(st). \] 这是一个连续映射, 且 \(H_1(s)=f(s)\), \(H_0\) 是常道路 \(c(s)\equiv f(0)\). 因此, 所有的道路都同伦于常道路 (即零伦的). 所以, 我们需要引入一种更强的同伦来避免这种情况.

• (记号说明) 在考虑道路的同伦时, 一般用 \(s\) 表示 "空间变量", 即道路的参数; 用 \(t\) 表示 "时间变量", 即同伦的参数.

设拓扑空间 \(X,Y\), 子空间 \(A\subset X\). 连续映射 \(f,g:X\to Y\) 间的同伦 \(H\) 称为在 \(A\) 上不变的, 若 \[ H(x,t) = f(x),\quad \forall x\in A,t\in I. \] 换言之, 所有 \(H_t\) 在 \(A\) 上与 \(f\) 相同. 此时, 称 \(H\) 是相对于 \(A\) 的同伦, 称 \(f,g\) 相对于 \(A\) 同伦. 注意 \(f,g\) 相对于 \(A\) 同伦的一个前提是它们在 \(A\) 上相同. 现在我们称不加任何限制的同伦 (即 \(A=\emptyset\)) 为自由同伦.

设 \(f,g\) 是 \(X\) 中的两条道路. \(f,g\) 间的一个道路同伦 (path homotopy) 指的是保持端点 \(\{0,1\}\subset I\) 不变的同伦, 记作 \(f\sim g\). 道路同伦的一个前提是 \(f,g\) 由相同的起点和终点.

Claim 24.3 (道路同伦是等价关系) 任给拓扑空间 \(X\) 内两点 \(p,q\), 道路同伦关系是所有连接 \(p,q\) 的道路的集合上的等价关系.

道路 \(f:I\to X\) 的一个重参数化 (reparametrization) 指的是 \(f\) 与连续映射 \(\varphi:I\to I\) 的复合 \(f\circ\varphi\), 其中 \(\varphi(0)=0\), \(\varphi(1)=1\) (保持起点和终点不变).

Claim 24.4 (重参数化是道路同伦的) 道路 \(f\) 的重参数化道路同伦于 \(f\).

Pf 将重参数化前后的道路分别写作 \(f\circ{\rm id}_I\) 和 \(f\circ\varphi\), 注意 \({\rm id}_I\) 和 \(\varphi\) 作为凸集 \(I\) 上的连续映射, 是同伦的, 根据复合保持同伦, \(f\circ{\rm id}_I\) 和 \(f\circ\varphi\) 是同伦的. 重参数化保持起点和终点, 因此它们道路同伦.

Claim 24.5 (连续映射保持道路同伦) 设 \(f_0,f_1:I\to X\) 是道路同伦的, \(\varphi\in C(X,Y)\), 则 \(\varphi\circ f_0,\varphi\circ f_1\) 道路同伦.

Pf 复合映射保持同伦, 故 \(\varphi\circ f_0,\varphi\circ f_1\) 是同伦的. 它们有相同的起点和终点, 进而道路同伦.

24.3 Path operations

设拓扑空间 \(X\), 道路同伦关系是道路集合 \(C(I,X)\) 上的等价关系. 记道路 \(f\) 所在等价类为 \([f]\), 称为道路类 (path class).

道路的积与逆的定义是很直观的:

• 设道路 \(f,g:I\to X\), 若 \(f(1)=g(0)\), 则它们的积 (product) 是 \(f*g:I\to X\), \[ (f*g)(s) = \Cases{ f(2s), & 0\leq t\leq \frac12, \\ g(2s-1), & \frac12\leq t\leq 1. \\ } \] 根据 gluing lemma, \(f\cdot g\) 是连续的. 道路的积就是两个道路的拼接.

• 道路 \(f\) 的逆 (reverse) 定义为 \(\bar{f}=f(1-s)\).

Claim 24.6 (积保持同伦) 若 \(f_0\sim f_1\), \(g_0\sim g_1\) 且 \(f_0*g_0\) 有意义, 则 \(f_1*g_1\) 有意义且 \(f_0*f_1\sim g_0*g_1\).

Pf 设道路同伦 \(F:f_0\sim f_1\), \(G:g_0\sim g_1\), 则 \(H:f_0*f_1\sim g_0*g_1\) 由下式给出: \[ H(s,t)=\Cases{ F(2s,t), & 0\leq s\leq\frac12, 0\leq t\leq 1, \\ G(2s-1,t), & \frac12\leq s\leq1, 0\leq t\leq 1, \\ } \] 根据 gluing lemma, \(H\) 连续.

根据以上定理, 道路的积可以定义在道路类上: \([f*g]:=[f]*[g]\) 是良定义的, 不依赖于代表元的选取. 下面我们给出道路类的运算性质. 记点 \(p\) 处的常道路 \(c_p(s)\equiv p\).

Claim 24.7 (道路类运算的性质) 设拓扑空间 \(X\), \(f\) 是连接 \(p,q\in X\) 的道路, \(g,h\) 是任意道路.

1. ("恒等元") \([c_p]*[f]=[f]*[c_q]=[f]\).
2. ("逆元") \([f]*[\bar{f}]=[c_p]\) 以及 \([\bar{f}]*[f]=[c_q]\).
3. ("结合律") \([f]*([g]*[h])=([f]*[g])*[h]\), 当两侧有意义时.

Pf 1, 我们只证明 \(f\sim c_p*f\). 参考下图, 道路同伦具体由下式给出: \[ H(s,t)=\Cases{ p, & t\geq 2s, \\ f\pqty{\dfrac{2s-t}{2-t}}, & t\leq 2s. } \] 2, 我们只证明 \(c_p\sim f*\bar{f}\). 参考下图, 道路同伦具体由下式给出: \[ H(s,t)=\Cases{ f(2s), & 0\leq s\leq \frac{t}2, \\ f(t), & \frac{t}2\leq s\leq1-\frac{t}2, \\ f(2-2s), & 1-\frac{t}2\leq s\leq1. \\ } \]

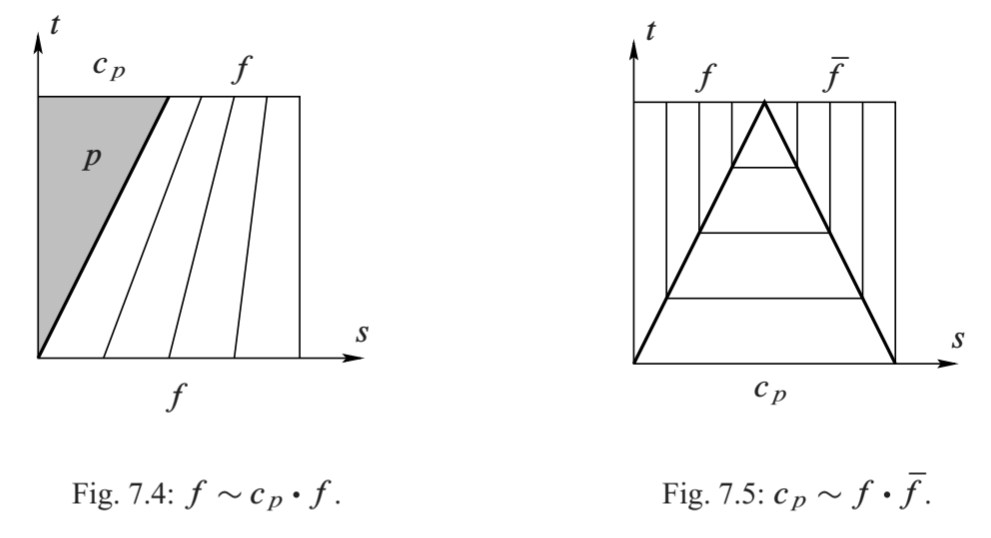
3, 结合律是比较简单的. \(f*(g*h)\) 是先以 \(2\) 倍速走完 \(f\), 再分别以 \(4\) 倍速走完 \(g,h\). 而 \((f*g)*h\) 是现以 \(4\) 倍速走完 \(f,g\), 再以 \(2\) 倍速走完 \(h\). 两者相差一个重参数化, 因此是道路同伦的.

• 注意以上三个运算性质只对道路类成立, 对道路是不成立的, 比如一般来说 \((f*g)*h\neq f*(g*h)\). 我们约定, 连乘 \(f*g*h\) 表示的是 \((f*g)*h\).

• 道路类运算具有和群乘法很像的性质, 但一个主要区别是: 不是任意两个道路类都能相乘, 只有首尾相接的道路可以 (按给定顺序) 相乘. 如果我们记 \(\Pi_1(X)\) 为 \(X\) 上所有 (任意起点与终点) 道路类的集合, 则它构成一个群胚 (groupoid), 其上有部分二元运算 \(*\) 与对所有元素都有定义的取逆运算:

  • (逆元) \(a*a^{-1}\) 和 \(a^{-1}*a\) 总有定义.
  • (恒等元) 若 \(a*b\) 有定义, 则 \(a*b*b^{-1}=a\) 且 \(a^{-1}*a*b=b\).
  • (结合律) 若 \(a*b,b*c\) 有定义, 则 \((a*b)*c=a*(b*c)\).

  我们称 \(\Pi_1(X)\) 为基本群胚 (fundamental groupoid).

• 如何才能将基本群胚变成一个群? 我们可以考虑起点, 终点重合且固定的道路 (huan'lu)

25 The Fundamental Group

25.1 The fundamental group

设拓扑空间 \(X\).

我们最关心的道路是闭合的道路, 即满足 \(f(0)=f(1)\) 的道路, 称之为环路 (loop). 环路的起点称为其基点 (base point). 所有以 \(p\) 为基点的环路的集合记作 \(\Omega(X,p)\). 常环路指的是常道路 \(c_p(s)\equiv p\). 零伦环路指的是道路同伦 (不仅是同伦) 于常环路的环路.

道路同伦关系是 \(\Omega(X,p)\) 上的等价关系, 我们称商集 \(\Omega(X,p)/{\sim}\) 为 \(X\) 的以 \(p\) 为基点的基本群 (fundamental group), 记作 \(\pi_1(X,p)\). Claim 24.6 保证了 \(\pi_1(X,p)\) 上的乘法是良定义的; Claim 24.7 则保证了乘法满足群的定义.

一个自然的问题是, 基本群 \(\pi_1(X,p)\) 是否依赖于基点的选择? 注意到以 \(p\) 为基点的环路只能待在 \(p\) 所在的道路分量里, 所以 \(\pi_1(X,p)\) 只能给出这个道路分量的信息; 不同道路分量的基本群彼此无关. 因此, 我们一般只研究道路连通空间的基本群. 实际上, 下面的定理表明, 当 \(X\) 道路连通时, 其任意基点处的基本群是同构的.

Claim 25.1 (基点变换) 设 \(X\) 道路连通, 任给 \(p,q\in X\) 和连接 \(p,q\) 的道路 \(g\). 映射 \[ \Align{ \Phi_g:\pi_1(X,p) &\to \pi_1(X,q), & \Phi_g[f] &:= [\bar{g}]*[f]*[g] } \] 是群同构, 其逆为 \(\Phi_{\bar{g}}\).

Pf 容易验证, \(\Phi_g[f]\) 的确给出了以 \(q\) 为基点的环路. 直接的计算表明 \(\Phi_g\) 是群同态: \[ \Align{ \Phi_g[f_1]*\Phi_g[f_2] &= [\bar{g}]*[f_1]*[g]*[\bar{g}]*[f_2]*[g] \\ &= [\bar{g}]*[f_1]*[c_p]*[f_2]*[g] \\ &= [\bar{g}]*([f_1]*[f_2])*[g] \\ &= \Phi_g([f_1]*[f_2]). } \] 容易看出 \(\Phi_{\bar g}\) 是 \(\Phi_g\) 的逆, 因此 \(\Phi_g\) 是同构.

因此, 当我们研究 \(X\) 的基本群时, 一般不必给出基点 \(p\), 而可以直接记其为 \(\pi_1(X)\). 我们说 \(X\) 的基本群是平凡的, 如果对于某个基点 \(p\) 有 \(\pi_1(X,p)=\{[c_p]\}\); 我们说 \(X\) 的基本群同构于 \(\Z\), 如果对于某个基点 \(p\) 有 \(\pi_1(X,p)\cong\Z\), 等等.

若 \(X\) 道路连通, 且基本群 \(\pi_1(X)\) 平凡, 则称 \(X\) 为单连通的 (simply connected). 换言之, 任意环路可以 (保持基点不动地) 连续收缩为常环路.

Claim 25.2 (单连通的等价说法) \(X\) 单连通, 当且仅当, 任意起点与终点分别相同的道路是道路同伦的.

Pf 设 \(X\) 单连通, 任给这样的道路 \(f,g\), 则 \(f*\bar{g}\) 是一条环路, 有 \([f*\bar{g}]=[c_p]\), 两边右乘 \([\bar{g}]\) 给出 \([f]=[g]\).

反之, 任给环路 \(h:I\to X\), 它的前一半 \(f(s)=h(s/2)\) 和后一半 \(g(s)=h(1-s/2)\) 满足 \(f(0)=g(0)\) 和 \(f(1)=g(1)\), 因此 \([f]=[g]\). 两边右乘 \([\bar{g}]\) 给出 \([h]=[f*\bar{g}]=[c_p]\).

Claim 25.3 (凸集的单连通性) \(\R^n\) 的凸集单连通. 特别地, \(\R^n\) 单连通.

Pf 到凸集的任意连续映射是同伦的, 因而任意起点与终点相同的道路是道路同伦的. 由 Claim 25.2, 凸集单连通.

补充. 基点变换映射 \(\Phi_g:\pi_1(X,p)\to\pi_1(X,q)\) 一般是依赖于道路 \(g\) 的选择的. 然而, 当基本群是交换群时, \(\Phi_g\) 与 \(g\) 的选取无关.

Claim 25.4 (基点变换与道路无关的充要条件) 设 \(X\) 道路连通, \(p,q\in X\). 任意连接 \(p,q\) 的道路给出相同的同构, 当且仅当 \(\pi_1(X,p)\) 是交换群.

Pf 若 \(\pi_1(X,p)\) 是交换群. 任给两条连接 \(p,q\) 的道路 \(g,h\), 取 \([f]\in\pi_1(X,p)\). 有 \[ \Align{ \Phi_{g}[f] &= [\bar{g}]*[f]*[g] \\ &= ([\bar{g}]*[f]*[h])*([\bar{h}]*[g]) \\ &= ([\bar{h}]*[g])*([\bar{g}]*[f]*[h]) \\ &= [\bar{h}]*[f]*[h] \\ &= \Phi_h[f]. } \] (其中 \([\bar{g}]*[f]*[h]\), \([h]*[\bar{g}]\), 都属于 \(\pi_1(X,p)\), 两者可交换.)

若任意连接 \(p,q\) 的道路给出相同的同构. 任取 \(f,f'\in\pi_1(X,p)\). 任给连接 \(p,q\) 的道路 \(g\), 注意到 \(h:=f*g\) 也是一条连接 \(p,q\) 的道路, 且 \(\bar{h}=\bar{g}*\bar{f}\). 根据假设, \[ \Align{ \Phi_g[f'] &= \Phi_h[f'], \\ \iff [\bar{g}]*[f']*[g] &= [\bar{g}]*[\bar{f}]*[f']*[f]*[g] \\ \iff [f'] &= [\bar{f}]*[f']*[f], } \] 两边左乘 \([f]\) 得到 \([f]*[f']=[f']*[f]\), 即 \(\pi_1(X,p)\)

25.2 Circle representatives

环路 \(f\in\Omega(X,p)\) 的特殊之处在于 \(f(0)=f(1)\), 使得我们能够将其下降到 \(\mathbb{S}^1\) 上.

考虑商映射 \(q:I\to\mathbb{S}^1\), 则 \(f\) 在纤维上取值相同, 根据唯一下降定理, 存在唯一连续映射 \(\tilde{f}:\mathbb{S}^1\to X\), 使得 \(f=\tilde{f}\circ q\). \[ \xymatrix{ I \ar[d]_q \ar[dr]^f \\ \mathbb{S}^1 \ar@{.>}[r]_{\tilde{f}} & X. } \]

映射 \(\tilde{f}\) 称为 \(f\) 的圆代表元 (circle representative). 任意环路唯一确定一个圆代表元; 反之, 任意连续映射 \(\tilde{f}:\mathbb{S}^1\to X\) 唯一确定一个环路 \(f=\tilde{f}\circ q\).

Claim 25.5 (零伦环路的圆代表元刻画) 设拓扑空间 \(X\), 以 \(p\) 为基点的环路 \(f\) 和圆代表元 \(\tilde{f}\). TFAE:

1. \(f\) 是零伦环路.
2. \(\tilde{f}\) 是零伦映射. (自由同伦于常映射.)
3. \(\tilde{f}\) 可扩张到 \(\overline{\mathbb{B}^2}\to X\) 的连续映射.

Pf 我们证明 1 \(\Rightarrow\) 2 \(\Rightarrow\) 3 \(\Rightarrow\) 1.

1 \(\Rightarrow\) 2. 设 \(H:I\times I\to X\) 给出了 \(f\) 和常环路 \(c_p\) 的道路同伦. 根据闭映射引理, 连续的满射 \(\omega\times{\rm id}:I\times I\to\mathbb{S}^1\times I\) 是商映射. 因为 \(H\) 在此商映射的纤维上常值, 所以可以下降到商空间 \(\tilde{H}:\mathbb{S}^1\times I\to X\), 给出了 \(\tilde{f}\) 与常值映射 \(x\mapsto p\) 间的同伦.

2 \(\Rightarrow\) 3. 设 \(H:\mathbb{S}^1\times I\to X\) 给出了常值映射 \(k:\mathbb{S}^1\to X\) 和 \(\tilde{f}\) 的自由同伦. 球面的锥 \(C\mathbb{S}^1=(\mathbb{S}^1\times I)/(\mathbb{S}^1\times\{0\})\) 同胚于 \(\overline{\mathbb{B}^2}\), 而 \(H\) 在纤维上常值 (它将 \(\mathbb{S}^1\times\{0\}\) 映到一点), 因此下降到商空间的连续映射 \(\tilde{H}:\overline{\mathbb{B}^2}\cong C\mathbb{S}^1\to X\), 满足 \(H=\tilde{H}\circ q\). 因为 \(q\) 在 \(\mathbb{S}^1\times\{1\}\) 上的限制是自然包含 \(\mathbb{S}^1\times\{1\}\cong\mathbb{S}^1\hookrightarrow\overline{\mathbb{B}^2}\), 所以 \(\tilde{H}\) 在 \(\mathbb{S}^1\times\{1\}\) 上的限制与 \(H\) 在 \(\mathbb{S}^1\times\{1\}\) 上的限制相同, 即 \(\tilde{f}\).

3 \(\Rightarrow\) 1. 设 \(\tilde{f}\) 扩张到连续映射 \(F:\overline{\mathbb{B}^2}\to X\). 因为 \(\overline{\mathbb{B}^2}\) 是凸集, 常环路 \(c_1\) 道路同伦于环路 \(i_{\mathbb{S}^1}\circ\omega:I\to\mathbb{S}^1\hookrightarrow\overline{\mathbb{B}^2}\), 记为 \(H:I\times I\to\overline{\mathbb{B}^2}\). 我们断言, \(F\circ H:I\times I\to X\) 给出了 \(f\) 和 \(c_p\) (其中 \(p=F(1)\)) 间的道路同伦. 实际上, 我们有 \[ \Align{ (F\circ H)(s,0) &= (F\circ c_1)(s)=p, \\ (F\circ H)(s,1) &= (F\circ i_{\mathbb{S}^1}\circ\omega)(s) = (\tilde{f}\circ\omega)(s) = f(s), \\ (F\circ H)(0,t) &= F(1) = p, \\ (F\circ H)(1,t) &= F(1) = p. } \]

Claim 25.6 (正方形引理) 设连续映射 \(F:I\times I\to X\), 道路 \(f,g,h,k\) 定义为 \[ \Align{ f(s) &= F(s,0), \\ g(s) &= F(1,s), \\ h(s) &= F(0,s), \\ k(s) &= F(s,1), \\ } \] 则 \(f*g\sim h*k\).

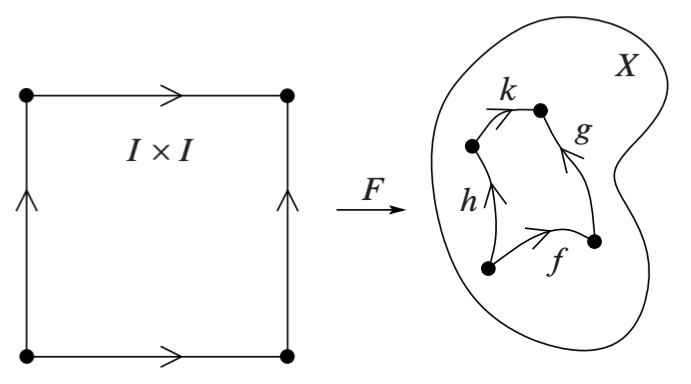
Pf 我们证明 \(c=f*g*\bar{h}*\bar{k}\) 是零伦环路, 进而得到想要的结果. 根据以上定理, 只需证明 \(\tilde{c}\) 可扩张到 \(\overline{\mathbb{B}^2}\to X\) 的连续映射. 因为 \(I\times I\) 是紧凸集, (Claim 17.1) 所以有同胚 \(\Phi:\overline{\mathbb{B}^2}\to I\times I\), 将 \(\mathbb{B}^2\) 映到 \({\rm Int}(I\times I)\), 将 \(\mathbb{S}^1\) 映到 \(\partial(I\times I)\). 复合映射 \(F\circ\Phi:\overline{\mathbb{B}^2}\to X\) 给出了 \(\tilde{c}\) 的连续扩张.

25.3 Fundamental groups of spheres and manifolds

最重要的基本群是球面的基本群. 下一章我们会证明, \(\mathbb{S}^1\) 的基本群是环路 \(\omega(s)=\e^{2\pi\i s}\) 生成的无穷阶循环群. 现在我们将目光聚焦在高维球面的基本群.

根据球极投影, 球面去掉一个点后同胚于 \(\R^n\). 因此, 只要 \(\mathbb{S}^n\) (\(n\geq2\)) 上的环路不经过某一点, 那么它便是零伦环路. 不幸的是, 空间填充曲线 (space-filling curves) 给出了连续的满射 \(f:I\to I\times I\), 因此的确存在经过 \(\mathbb{S}^n\) 中任何一点的道路. 我们的想法是将道路 "微调", 使之道路同伦于一条不经过某一点的道路.

度量空间的子集 \(S\) 的直径定义为元素距离的上确界: \({\rm diam}(S)=\sup\{d(x,y)\mid x,y\in S\}\). 设度量空间 \(X\) 的开覆盖 \({\cal U}\), 该开覆盖的 Lebesgue 数指的是正实数 \(\delta>0\), 满足: 任意直径小于 \(\delta\) 的子集和包含于某一个 \(U\in{\cal U}\) 中.

Claim 25.7 (Lebesgue 数引理) 紧度量空间的任意开覆盖具有 Lebesgue 数.

Pf 设紧度量空间 \(M\) 的开覆盖 \(\cal U\). 任一点 \(x\in M\) 处在某 \(U\in{\cal U}\) 内, 由开性, 存在 \(r(x)>0\) 使得 \(B_{2r(x)}(x)\subset U\). 开球族 \(\{B_{r(x)}(x)\mid x\in M\}\) 构成 \(M\) 的开覆盖, 它有有限子覆盖 \(\{B_{r(x_i)}(x_i)\}_{i=1}^n\).

取 \(\delta=\min\{r(x_1),\dots,r(x_n)\}\), 则 \(\delta\) 是 \({\cal U}\) 的 Lebesgue 数. 任给直径小于 \(\delta\) 的子集 \(S\), 取 \(y_0\in S\), 则 \(y_0\) 在某 \(B_{r(x_i)}(x_i)\) 中. 只需证明 \(S\subset B_{2r(x_i)}(x_i)\), 因为后者是某 \(U\in{\cal U}\) 的子集. 这是容易看出的: \(S\) 中任意一点 \(z\) 与 \(y_0\) 的距离小于 \(\delta\), 进而由三角不等式, \[ d(z,x_i)\leq d(z,y_0)+d(y_0,x_i)<\delta+r(x_i)<2r(x_i), \] 即 \(z\in B_{2r(x_i)}(x_i)\).

Claim 25.8 (微调道路使之不过某点) 设维数 \(n\geq2\) 的流形 \(M\), \(f\) 是连接 \(p_1,p_2\) 的道路, \(q\) 是 \(p_1,p_2\) 外一点, 则 \(f\) 道路同伦于一条不经过 \(q\) 的道路.

Pf 设 \(M\) 的开覆盖 \(\{U,V\}\), 其中 \(U\) 是 \(q\) 为中心的坐标球, \(V=M\setminus\{q\}\). 由连续性, \(\{f^{-1}(U),f^{-1}(V)\}\) 构成 \(I\) 的开覆盖, 记其 Lebesgue 数为 \(\delta\). 令 \(m\) 是满足 \(1/m<\delta\) 的正整数, 则在每个小区间 \([k/m,(k+1)/m]\) 上, 道路 \(f\) 的像全部在 \(U\) 内或全部在 \(V\) 内.

令 \(0=a_0<\dots<a_l=1\) 表示所有形如 \(k/m\) 的数, 且满足 \(f(a_i)\neq q\). 于是每个小段 \(f|_{[a_{i-1},a_i]}\) 完全包含于 \(U\) 或完全包含于 \(V\), 且端点不等于 \(q\). (若 \(f(k/m)=q\in U\) 对某 \(k\), 则 \([(k-1)/m,k/m]\) 和 \([k/m,(k+1)/m]\) 都映到 \(U\) 内.)

这些小段中, 完全包含于 \(V\) 的小段自然不经过 \(q\). 下面考虑完全包含于 \(U\) 的小段. 因为 \(U\setminus\{q\}\) 同胚于 \(\mathbb{B}^n\setminus\{0\}\), 是道路连通的 (这里用到维数 \(n\geq2\)), 因此对于包含于 \(U\) 的小段 \(f|_{[a_{i-1},a_i]}\), 可以用 \(U\setminus\{q\}\) 中的一段有相同端点的道路 \(g\) 替代. 因为 \(U\) 单连通, 所以 \(f|_{[a_{i-1},a_i]}\) 和 \(g\) 是道路同伦的.

Claim 25.9 (高维球面的单连通性) 对 \(n\geq2\), \(\mathbb{S}^n\) 单连通.

Pf 设北极点 \(N\in\mathbb{S}^n\), 任取另外一点 \(p\). 上面的引理表明, 以 \(p\) 为基点的任一环路 \(f\) 道路同伦于一条不经过 \(N\) 的环路 \(g\), 即 \(\mathbb{S}^n\setminus\{N\}\) 内的环路. 由球极投影, \(\mathbb{S}^n\setminus\{N\}\cong\R^n\), 所以 \(g\) 是零伦环路, 故 \(f\) 也是零伦环路.

Claim 25.10 (流形的基本群) 流形的基本群是可数的.

这里补充 Lebesgue 数的另一个应用: 一致连续. 设度量空间 \((M_1,d_1),(M_2,d_2)\), 映射 \(f:M_1\to M_2\) 称为一致连续的 (uniformly continuous), 若对任意 \(\varepsilon>0\), 存在 \(\delta>0\), 使得对任意 \(x,y\in M_1\), \[ d_1(x,y)<\delta \Rightarrow d_2(f(x),f(y))<\delta. \]

Claim 25.11 (紧度量空间上的连续函数一致连续) 若 \(M_1\) 紧, 则连续函数 \(f:M_1\to M_2\) 一致连续.

Pf 任给 \(\varepsilon>0\). 设 \(M_2\) 的开覆盖 \({\cal U}=\{B_\varepsilon(x)\mid x\in M_2\}\). 根据连续性, \(f^{-1}[{\cal U}]\) 是 \(M_1\) 的开覆盖, 由 \(M_1\) 的紧性, 它有 Lebesgue 数 \(\delta\). 对于任意 \(x,y\) 满足 \(d(x,y)<\delta\), 有 \(\{x,y\}\) 包含于 \(f^{-1}[{\cal U}]\) 中的某开集, 于是 \(\{f(x),f(y)\}\) 包含于 \({\cal U}\) 中的某开集, 即 \(d(f(x),f(y))<\varepsilon\).