机器学习: 逻辑回归
机器学习的笔记, 主要参考吴恩达的机器学习线上课, 以及"AI引论"课程.
1 Hypothesis
虽然叫做逻辑回归(logistic regression), 但是是用于分类的模型.
对于一个二分类问题, 数据集 \(D=\qty{(\boldsymbol{x}^{(i)},y^{(i)})}_{i=1}^N\), 其中 \(y^{(i)}\in\qty{0,1}\). Logistic回归假设可以用超平面 \[ \boldsymbol{\theta}\T\boldsymbol{x}=0 \] 分开两类, 即当 \(\boldsymbol{\theta}\T\boldsymbol{x}<0\) 时(负类), 标签 \(y=0\); \(\boldsymbol{\theta}\T\boldsymbol{x}\geq0\) 时(正类), 标签 \(y=1\). 我们进一步假设样本服从sigmoid函数的分布, 即标签 \(y=1\) 的概率为 \[ p(y=1|\boldsymbol{x};\boldsymbol\theta) = \operatorname{sigmoid}(\boldsymbol{\theta}\T\boldsymbol{x}) = \pqty{ 1+\exp(-\boldsymbol{\theta}\T\boldsymbol{x}) }^{-1}. \]
这个累积分布函数 \[ \operatorname{sigmoid}(x) := \frac1{1+\exp(-x)} \] 满足一些性质, 例如严格单调增加, 图像关于点\((0,\frac12)\)对称, 光滑性等.
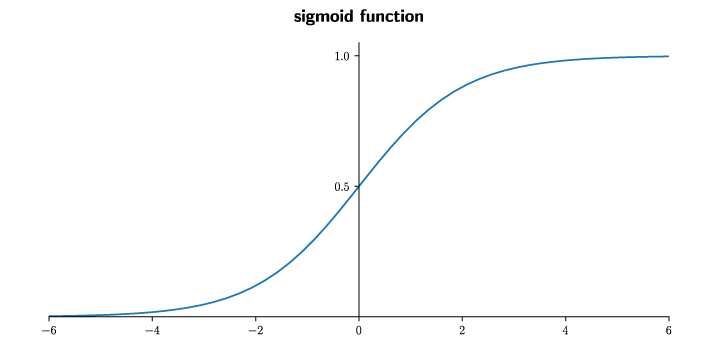
自然, 标签 \(y=0\) 的概率 \[ p(y=0|\boldsymbol{x};\boldsymbol\theta) = 1-\operatorname{sigmoid}(\boldsymbol{\theta}\T\boldsymbol{x}) = \operatorname{sigmoid}(-\boldsymbol{\theta}\T\boldsymbol{x}). \]
- 上面第二个等号用到了sigmoid函数的对称性.
- 注意到 \(p(y=1|\boldsymbol{x};\boldsymbol\theta)\geq\frac12\) 当且仅当 \(\boldsymbol{\theta}\T\boldsymbol{x}\geq0\).
假设函数: 相较于线性回归, Logistic回归的假设函数是线性函数 \(g(\boldsymbol{x})=\boldsymbol\theta\T\boldsymbol{x}\) 和sigmoid函数的复合, \[ h_\theta(\boldsymbol{x}) = \frac1{1+\exp(-\boldsymbol\theta\T\boldsymbol{x})}. \]
决策边界(decision boundary): 两类边界上的数据点构成的图形, 即超平面 \(\boldsymbol{\theta}\T\boldsymbol{x}=0\).
实际上, 可以在 \(\boldsymbol{x}\) 中引入非线性项, 使得决策边界为曲面.
例如, \(h_\theta(\boldsymbol{x}) = -1+0x_1+0x_2+1x_1^2+1x_2^2\)的决策边界 \[ \begin{align} C:-1+0x_1+0x_2+1x_1^2+1x_2^2&=0, \\ x_1^2+x_2^2&=1 \end{align} \] 是平面直角坐标系\(x_1Ox_2\)中的单位圆.
2 Maximum Likelihood Estimation
如果我们使用线性回归的方差损失函数 \[ J(\theta) = \frac1N\sum_{i=1}^N \frac12(h_\theta(\boldsymbol{x}^{(i)})-y^{(i)})^2, \] 由于假设函数非线性, 所以损失函数是非凸函数, 梯度下降不能保证收敛到全局最小值, 在这里我们采用另一种思路, 即最大似然估计(MLE).
对于模型 \(h_\theta(\boldsymbol{x})\), 把数据集 \(D\) 由这个模型生成的概率 \[ p(y|\boldsymbol{x};\boldsymbol\theta) = \prod_{i=1}^N h_\theta(\boldsymbol{x}^{(i)})^{y^{(i)}} [1-h_\theta(\boldsymbol{x}^{(i)})]^{1-y^{(i)}} \] 称为似然函数, 记作 \(L(h_\theta)\). 我们假设似然函数取最大值, 也就是说, 最终找到的模型 \(h_\theta\) 应当是最有可能生成出数据集 \(D\) 的那个模型.
为了方便计算机计算, 取对数得到对数似然, \[ \ell(h_\theta) = \log(L(h_\theta)) = \sum_{i=1}^N\bqty{ y^{(i)} \log{h_\theta(\boldsymbol{x}^{(i)})} + (1-y^{(i)}) \log{}[1-h_\theta(\boldsymbol{x}^{(i)})] }. \]
- 当预测值与真实值非常接近时, 损失接近 \(0\); 当预测值与真实值的相反类接近时, 损失趋于 \(+\infty\).
最终得到代价函数为 \[ J(h_\theta) = -\frac1N\ell(h_\theta). \] 最大似然即最小化损失函数.
Note. 线性回归的MLE方法. 对于线性回归, 一般认为确定平方差函数作为代价函数(经验风险最小化, ERM), 实际上可以用MLE解释.
模型 \(h_\theta(\boldsymbol{x})=\boldsymbol\theta\T\boldsymbol{x}\); 假设数据 \(\boldsymbol{x}^{(i)},y^{(i)}\) 服从带有(正态分布)误差的线性关系, 即 \[ y^{(i)} = h_\theta(\boldsymbol{x}^{(i)}) + \epsilon^{(i)}, \quad \epsilon\sim N(0,\sigma^2). \] 于是, 似然函数 \[ L(h_\theta) = p(y|\boldsymbol{x};\boldsymbol\theta) = \prod_{i=1}^N \frac1{\sqrt{2\pi\sigma^2}} \exp\bqty{ \frac{-1}{2\sigma^2} \pqty{ y^{(i)} - h_\theta(\boldsymbol{x}^{(i)}) }^2 }, \] 损失函数 \[ J(h_\theta) = -\frac1N\log{L(h_\theta)} = \frac1N\sum_{i=1}^N\bqty{ \frac12\log(2\pi\sigma^2) + \frac1{2\sigma^2} \pqty{ y^{(i)} - h_\theta(\boldsymbol{x}^{(i)}) }^2 }. \] 可以发现, 损失函数与平方差函数具有相同的梯度(相差一个正常数), 两者会得出相同的最优解.
3 Gradient Descent
3.1 Derivation
我们可以用梯度下降算法求得最佳参数, 首先对代价函数求导得到 \[ \pdv{J}{\boldsymbol\theta} = \frac1N \sum_{i=1}^N \pqty{ h_\theta(\boldsymbol{x}^{(i)}) - y^{(i)} } \boldsymbol{x}^{(i)}. \]
具体推导过程: 先计算
\[ \Align{ \pdv{h_\theta}{\boldsymbol\theta} = \dv{\operatorname{sigmoid}(g)}{g} \cdot \pdv{g}{\boldsymbol\theta} = h_\theta(1-h_\theta)\boldsymbol{x}. } \] (其中 \(g(\boldsymbol{x})=\boldsymbol\theta\T\boldsymbol{x}\)) 对代价函数求偏导, 有 \[ \begin{align} \pdv{J}{\boldsymbol\theta} &= -\frac1N \sum_{i=1}^N \bqty{ y^{(i)} \frac1{h_\theta(\boldsymbol{x}^{(i)})} \pdv{h_\theta}{\boldsymbol\theta} - (1-y^{(i)}) \frac1{1-h_\theta(\boldsymbol{x}^{(i)})} \pdv{h_\theta}{\boldsymbol\theta} } \\ &= -\frac1N \sum_{i=1}^N \bqty{ y^{(i)} \frac1{h_\theta(\boldsymbol{x}^{(i)})} - (1-y^{(i)}) \frac1{1-h_\theta(\boldsymbol{x}^{(i)})} } \pdv{h_\theta}{\boldsymbol\theta} \\ &= -\frac1N \sum_{i=1}^N \bqty{ y^{(i)} \frac1{h_\theta(\boldsymbol{x}^{(i)})} - (1-y^{(i)}) \frac1{1-h_\theta(\boldsymbol{x}^{(i)})} } h_\theta(\boldsymbol{x}^{(i)})(1-h_\theta(\boldsymbol{x}^{(i)})) \boldsymbol{x}^{(i)} \\ &= -\frac1N \sum_{i=1}^N \bqty{ y^{(i)} (1-h_\theta(\boldsymbol{x}^{(i)})) - (1-y^{(i)}) h_\theta(\boldsymbol{x}^{(i)}) } \boldsymbol{x}^{(i)} \\ &= -\frac1N \sum_{i=1}^N \pqty{ y^{(i)} - h_\theta(\boldsymbol{x}^{(i)}) } \boldsymbol{x}^{(i)} \\ &= \frac1N \sum_{i=1}^N \pqty{ h_\theta(\boldsymbol{x}^{(i)}) - y^{(i)} } \boldsymbol{x}^{(i)}. \end{align} \]
这样我们就可以用下面的方法来更新参数 \(\boldsymbol\theta\): \[ \begin{align} &\textsf{Repeat until convergence \{} \\ &\qquad \boldsymbol\theta := \boldsymbol\theta - \frac{\alpha}N \sum_{i=1}^N \pqty{ \frac1{1+\exp(-\boldsymbol\theta\T\boldsymbol{x}^{(i)})} - y^{(i)} } \boldsymbol{x}^{(i)} \\ &\text{\}} \end{align} \] 可以发现, 似然代价函数的偏导和线性回归中的方差代价函数的偏导看起来一样, 唯一的差异是假设函数 \(h_\theta(\boldsymbol{x})\) 不同.
3.2 Optimization
算法优化:
- Conjugate gradient
- BFGS
- L-BFGS
它们的优点:
- 不需要手动选择学习率 \(\alpha\).
- 通常比梯度下降快.
缺点: 复杂.
4 Multi-Class Classification
一对多(one-vs-all)或一对余(one-vs-rest): 将多元分类问题转化为多个二元分类问题.
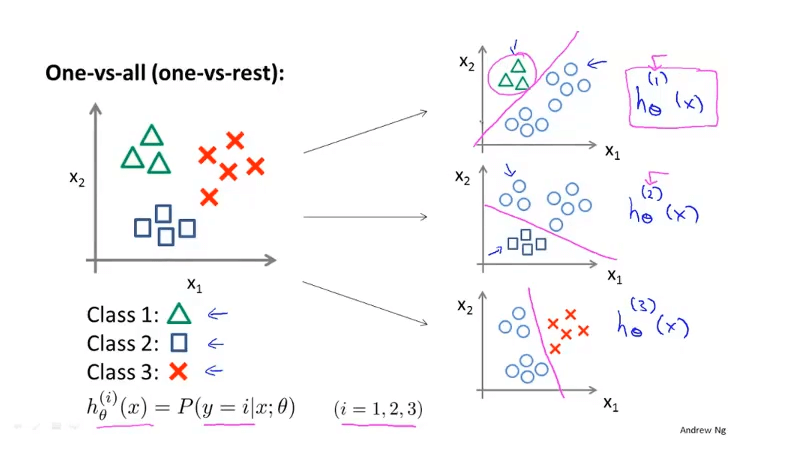
对于每个类 \(k\in\set{1,2,\dots,K}\), 将其当作正类, 其余当作负类, 训练得到一个分类器 \(h_\theta^{(k)}(\boldsymbol{x})\).
那么对于每个新的测试数据 \(\boldsymbol{x}^{(i)}\), \[ h^{(k)}_\theta(\boldsymbol{x}^{(i)}) = P(y^{(i)}=k), \] 我们只需要取概率最大的那个类, \[ \textsf{Predict: } y^{(i)} = \argmax_{k} h_\theta^{(k)}(\boldsymbol{x}^{(i)}). \]
此种方法存在一个问题, 即各个分类器是独立的, 无法统一成一个模型. 进而当类别数 \(K\) 较大时, 分别训练各个分类器的代价太高.
可以利用Softmax回归方法解决多分类问题. 共同训练 \(K\) 个模型 \(f_k(\boldsymbol{x})=\boldsymbol\theta_k\T\boldsymbol{x}\), 标签 \(y=k\) 概率 \[ p(y=k|\boldsymbol{x},\boldsymbol\theta) = \frac{\exp f_{k}(\boldsymbol{x})}{\sum_{j=1}^K \exp f_j(\boldsymbol{x})}, \]
- 这里的指数函数可以保证, 当 \(f_k(\boldsymbol{x})\) 比其他 \(f_j(\boldsymbol{x})\) 大一些时, 概率 \(p(y=k)\) 能够比 \(p(y=j)\) 大很多.
进而得到似然函数 \[ L(\boldsymbol\theta) = \prod_{i=1}^N \frac {\exp f_{y^{(i)}}(\boldsymbol{x}^{(i)})} {\sum_{j=1}^K \exp f_j(\boldsymbol{x}^{(i)})}. \]
5 Overfit & Regularization
一个模型对于测试数据需要有一定的假设, 即偏见(bias). 偏见的存在使得我们具有归纳的能力, 即对于相似的事物, 抓住主要相似点, 忽略其次要差异, 将它们归为同一类群; 如果没有偏见, 我们就缺乏归纳的能力. 模型亦如此. 由于模型的偏见不同, 造成的拟合结果也不同:
- 欠拟合(underfit): 高偏见(在训练集上代价过高).
- 合适的拟合.
- 过拟合(overfit): 高方差. 对于\(N\)个数据的回归问题, 总存在\(N-1\)次多项式函数能够穿过这些数据点, 但这通常对新的数据预测能力差(在测试集上代价明显高于训练集).
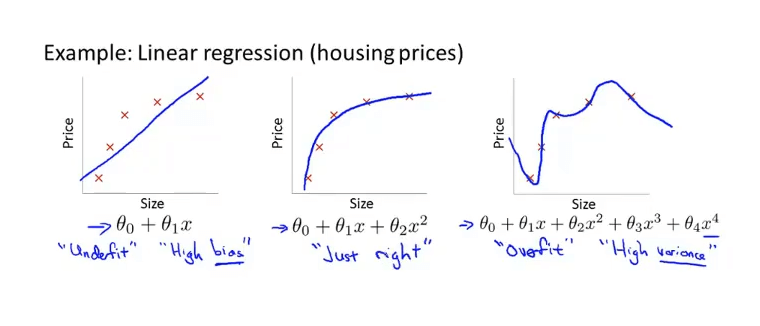
过拟合的原因一般有
- 某几个特征维度支配了预测, 即 \(\boldsymbol\theta\) 的某些分量过大.
- 存在大量无用特征, 但仍赋予了非零权重.
要解决第1个, 可以利用L2正则化(regularization)方法, 即将 \(\boldsymbol\theta\) 的L2范数添加到代价函数中(以线性回归为例), \[ J(h_\theta) = \frac1{2N} \bqty{\sum_{i=1}^N \pqty{ h_\theta(\boldsymbol{x}^{(i)})-y^{(i)} }^2 } + \color{or}\frac{\lambda}{2N}\sum_{j=1}^M\theta_j^2 \]
- 其中的 \(\theta_j^2\) 会对较大的权重给出很大的惩罚, 使得权重分配更平均.
- 注意最后的求和是从 \(j=1\) 开始的, 即不考虑 \(\theta_0\) 的大小.
- L2正则化的线性回归也称为岭回归(rindge regression).
- 式中 \(\lambda >0\), 称为正则化参数(regularization parameter). 它和学习率 \(\alpha\) 一样是在学习前预先设定的, 成为超参数 (hyperparameter). 选择哪种模型, 哪种代价函数, 哪种正则化也可看作超参数. 对于超参数的选择, 一般先找出所有可能的超参数组合, (分别训练完毕后)在验证集(validation set)上找出误差最小的超参数集.
要解决第2个, 可以手动选择要保留的特征, 或使用模型选择算法; 也可以利用L1正则化方法, 即将 \(\boldsymbol\theta\) 的L1范数添加到代价函数中(以线性回归为例), \[ J(h_\theta) = \frac1{2N} \bqty{\sum_{i=1}^N \pqty{ h_\theta(\boldsymbol{x}^{(i)})-y^{(i)} }^2 } + \color{or}\frac{\lambda}{N}\sum_{j=1}^M|\theta_j| \]
- 鼓励稀疏的 \(\boldsymbol\theta\), 即大部分维度的权重为零.
- L1正则化的线性回归也称为Lasso回归.
以线性回归+L2正则化为例, 新的代价函数的导数是 \[ \pdv{J}{\boldsymbol\theta} = \frac1N \sum_{i=1}^N \pqty{ h_\theta(\boldsymbol{x}^{(i)}) - y^{(i)} } \boldsymbol{x}^{(i)} + \frac\lambda N \boldsymbol\theta \] 迭代中更新的步骤(注意 \(\theta_0\) 要单独更新): \[ \begin{align} \boldsymbol\theta &:= \boldsymbol\theta - \alpha\bqty{ \frac1N \sum_{i=1}^N \pqty{ h_\theta(\boldsymbol{x}^{(i)}) - y^{(i)} } \boldsymbol{x}^{(i)} + \frac{\lambda}N \boldsymbol\theta } \\ &= \blue{\pqty{1-\alpha\frac{\lambda}N}}\boldsymbol\theta - \alpha \frac1N \sum_{i=1}^N \pqty{ h_\theta(\boldsymbol{x}^{(i)}) - y^{(i)} } \boldsymbol{x}^{(i)} \end{align} \] 可以关注到蓝色的部分是略小于 \(1\) 的数, 它在每次迭代的时候都把 \(\boldsymbol\theta\) 变小一点点.