梁GR | 4 微分形式及其积分
5 Differential Forms and Integration
5.1 Differential forms
微分形式.
设\(V\)为\(n\)维线性空间, \({\cal T}_V(0,l)\)中的元素\(\omega_{a_1\dots a_l}\)称为一个\(l\)次形式(\(l\)-form), 如果它是全反称的, 即 \[ \omega_{a_1\dots a_l} = \omega_{[a_1\dots a_l]}, \] 可以将\(\omega_{a_1\dots a_l}\)简记作\(\omega\). 可以证明以下结论:
- \(\omega_{a_1\dots a_l} = \omega_{[a_1\dots a_l]}\iff\omega_{\mu_1\dots\mu_l} = \omega_{[\mu_1\dots\mu_l]}\)(回推时, 存在一组基底满足条件即可.)
- \(\omega_{a_{\sigma(1)}\dots\mu_{\sigma(l)}}=(\sgn\sigma)\omega_{a_1\dots a_l}\).
\(V\)上的全体\(l\)形式的集合记作\(\Lambda(l)\), 则\(\Lambda(0)=\R\), \(\Lambda(1)=V^*\). 容易证明, \(\Lambda(l)\)是\({\cal T}_V(0,l)\)的线性子空间. 要找到其维数, 我们要求其基底, 为此先定义一种张量积. 将全凡尘化的张量积称为楔积(wedge product), 对于\(l\)形式\(\omega\)和\(m\)形式\(\mu\), 它们的楔积定义为 \[ \omega\wedge\mu = (\omega\wedge\mu)_{a_1\dots a_l b_1\dots b_m} := \frac{(l+m)!}{l!m!} \omega_{[a_1\dots a_l}\mu_{b_1\dots b_m]}. \] 楔积是映射\(\wedge:\Lambda(l)\times\Lambda(m)\to\Lambda(l+m)\), 可以证明其具有:
- 双线性性. \((\alpha\omega)\wedge\mu=\alpha(\omega\wedge\mu)=\omega\wedge(\alpha\mu)\), \(\forall\alpha\in\R\).
- 结合性. \((\omega\wedge\mu)\wedge\lambda=\omega\wedge(\mu\wedge\lambda)\).
- 分级反对称性(graded anti-symmetry). \(\omega\wedge\mu=(-1)^{lm}\mu\wedge\omega\).
设\(V^*\)的一个基底\(\qty{(e_\mu)^a}\), 通过它们之间的楔积可以构造出\(\Lambda(l)\)的一个基底: 设\(\Lambda(l)\)的一个基矢为 \[ (e^{\mu_1})_a \wedge \dots \wedge (e^{\mu_l})_a, \] 若其中有两者相等, 则由分级反对称性知, 楔积结果为零, 因此\(\mu_1,\dots,\mu_l\)互不相等. 另一方面, \(\mu_1,\dots,\mu_l\)的顺序不重要, 因为调整顺序后楔积的结果最多相差一个负号, 所以不妨有\(\mu_1,\dots,\mu_l\)递增. 因此, \(\mu_1,\dots,\mu_l\)是\((1,\dots,n)\)中选出\(l\)个数的一个组合, \(\dim\Lambda(l)=\Cases{ {n\choose l},&n\leq l\\0,&n>l }\). 一个\(l\)形式可以展开为 \[ \Align{ \omega_{a_1\dots a_l} &= \sum_{\rm C} \omega_{\mu_1\dots\mu_l} (e^{\mu_1})_{a_1} \wedge \dots \wedge (e^{\mu_l})_{a_l} \\ &= \frac1{l!} \,\omega_{\mu_1\dots\mu_l} (e^{\mu_1})_{a_1} \wedge \dots \wedge (e^{\mu_l})_{a_l}, } \] (其中\(\sum_{\rm C}\)表示对\((1,\dots,n)\)中取\(l\)个数的各种组合求和; 第二行表示对所有\(\mu_i\)求和, 其非零项数等于\(n\)取\(l\)的排列数\(l!{n\choose l}\), 可分为\({n\choose l}\)组, 每组含\(l!\)个相同的项, 除以\(l!\)便得到第二个等号) 其分量(注意没有楔积) \[ \omega_{\mu_1\dots\mu_l} = \omega_{a_1\dots a_l} (e_{\mu_1})^{a_1} \dots (e_{\mu_l})^{a_l}. \] 上面是纯代数的内容, 现在我们回到流形\(M\)上来. 若对\(M\)(或\(A\subset M\))的任意一点\(p\)指定\(V_p\)上的一个\(l\)形式, 那么就得到一个\(l\)形式场. 称光滑的\(l\)形式场为\(l\)次微分形式场(differential \(l\)-form), 也简称\(l\)形式(场). 可以用坐标基底方便地表出, \[ \Align{ \omega_{a_1\dots a_l} &= \sum_{\rm C} \omega_{\mu_1\dots\mu_l} (\dd{x}^{\mu_1})_{a_1} \wedge \dots \wedge (\dd{x}^{\mu_l})_{a_l}, \\ \omega_{\mu_1\dots\mu_l} &= \omega_{a_1\dots a_l} \pqty{\pdv{x^{\mu_1}}}^{a_1} \dots \pqty{\pdv{x^{\mu_l}}}^{a_l}. } \] \(M\)上全体(光滑)\(l\)形式场的集合记作\(\Lambda_M(l)\).
Claim 1 (楔积与行列式)
对任意\(1\)形式场\(\omega^1,\dots,\omega^n\), 有 (其中\(\omega^\mu{_\nu}\)代表\(1\)形式\(\omega^\mu\)的第\(\nu\)个分量) \[ \omega^1\wedge\cdots\wedge\omega^n =\det(\omega^\mu{_\nu})\dd{x^1}\wedge\cdots\wedge\dd{x^n}. \]
对任意矢量场\(v_1,\dots,v_n\), 有 (其中\(v_\mu{^\nu}\)代表矢量场\(v_\mu\)的第\(\nu\)个分量) \[ \dd{x^1}\wedge\cdots\wedge\dd{x^n}(v_1,\dots,v_n) = \det(v_\mu{^\nu}). \]
Pf 第1条, 利用楔积的线性性和反对称性, \[ \Align{ \omega^1\wedge\cdots\wedge\omega^n &=(\omega^1{_1}\dd{x^1}+\dots+\omega^1{_n}\dd{x^n})\wedge\cdots\wedge (\omega^n{_1}\dd{x^1}+\dots+\omega^n{_n}\dd{x^n}) \\ &=\sum_{\sigma\in S_n} (\omega^1{_{\sigma(1)}}\dd{x^{\sigma(1)}})\wedge\cdots\wedge (\omega^1{_{\sigma(n)}}\dd{x^{\sigma(n)}}) \\ &=\sum_{\sigma\in S_n} \omega^1{_{\sigma(1)}}\cdots\omega^1{_{\sigma(n)}} \dd{x^{\sigma(1)}}\wedge\cdots\wedge\dd{x^{\sigma(n)}} \\ &=\sum_{\sigma\in S_n} (\sgn\sigma)\, \omega^1{_{\sigma(1)}}\cdots\omega^1{_{\sigma(n)}} \dd{x^1}\wedge\cdots\wedge\dd{x^n} \\ &=\det(\omega^\mu{_\nu})\dd{x^1}\wedge\cdots\wedge\dd{x^n}. } \] (其中第2步是从\(n\)个因式中, 各选取一项参与乘积, 为了使得结果非零, 选取的\(n\)项中不能包含相同的对偶基底, 因此是对排列\(\sigma\in S_n\)求和.) 第2条, \[ \Align{ \dd{x^1}\wedge\cdots\wedge\dd{x^n}(v_1,\dots,v_n) &=\sum_{\sigma\in S_n}(\sgn\sigma) (\dd{x^{\sigma(1)}})_{a_1}\cdots(\dd{x^{\sigma(n)}})_{a_n} (v_1)^{a_1}\cdots(v_n)^{a_n} \\ &=\sum_{\sigma\in S_n}(\sgn\sigma) (v_1)^{\sigma(1)}\cdots(v_n)^{\sigma(n)} =\det(v_\mu{^\nu}). } \]
实际上, 这两条都可以作为行列式\(\det(A^\mu{_\nu})\)的定义.
1的推论就是 \[ (T\omega^1)\wedge\cdots\wedge(T\omega^n) =\det(T)\,\omega^1\wedge\cdots\wedge\omega^n, \] 对于任意\((1,1)\)型张量\(T_a{^b}\)(线性映射\(\Lambda_p(1)\to\Lambda_p(1)\)).
外微分.
流形\(M\)上的外微分算符(exterior differentiation operator)是一个映射\(\dd{}:\Lambda_M(l)\to\Lambda_M(l+1)\), 定义为 \[ (\dd{\omega})_{ba_1\dots a_l}:=(l+1)\nabla_{[b}\omega_{a_1\dots a_l]}. \] 无挠导数算符\(\nabla_a\)可以任取, 因为\(C^c{_{ab}}\)下标的对称性保证对\(\tilde\nabla_a\), 有\(\nabla_{[b}\omega_{\dots]}=\tilde\nabla_{[b}\omega_{\dots]}\).
对于标量场\(f\), 其外微分\((\dd{f})_a=\nabla_af\), 恰恰是之前定义的对偶矢量场\((\dd{f})_a\).
取\(\nabla_a\)为\(\partial_a\)可知, 设\(\omega_{a_1\dots a_l}=\sum_{\rm C}\omega_{\mu_1\dots\mu_l}(\dd{x}^{\mu_1})_{a_1} \wedge \dots \wedge (\dd{x}^{\mu_l})_{a_l}\), 则 \[ \Align{ (\dd\omega)_{ba_1\dots a_l} &= \sum_{\rm C} (\dd\omega_{\mu_1\dots\mu_l})_b \wedge (\dd{x}^{\mu_1})_{a_1} \wedge \dots \wedge (\dd{x}^{\mu_l})_{a_l} \\ &= \frac1{l!} (\dd\omega_{\mu_1\dots\mu_l})_b \wedge (\dd{x}^{\mu_1})_{a_1} \wedge \dots \wedge (\dd{x}^{\mu_l})_{a_l}, } \] 其中\((\dd\omega_{\mu_1\dots\mu_l})_b\)是标量场的外微分.
可知, 外微分算符是线性的; 而且对于\(l,m\)形式场\(\omega,\mu\), 有\(\dd(\omega\wedge\mu)=(\dd\omega)\wedge\mu+(-1)^l\omega\wedge(\dd\mu)\), 称为反Leibniz律(anti-Leibniz rule).
Example \(\R^2\)上的\(1\)形式场\(\omega=\omega_1\dd{x^1}+\omega_2\dd{x^2}\)的外微分 \[ \Align{ \dd{\omega} &=\dd\omega_\mu\wedge\dd{x}^\mu \\ &=\pqty{\pdv{\omega_\mu}{x^\nu}\dd{x}^\nu}\wedge\dd{x}^\mu =\pdv{\omega_1}{x^2}\dd{x}^2\wedge\dd{x}^1 +\pdv{\omega_2}{x^1}\dd{x}^1\wedge\dd{x}^2 \\ &=(\omega_{2,1}-\omega_{1,2})\dd{x}^1\wedge\dd{x}^2 } \] \(\R^3\)上的\(1\)形式场\(\omega=\omega_1\dd{x^1}+\omega_2\dd{x^2}+\omega_2\dd{x^3}\)的外微分 \[ \Align{ \dd{\omega} &=\dd\omega_\mu\wedge\dd{x}^\mu \\ &=\cdots \\ &=(\omega_{2,1}-\omega_{1,2})\dd{x}^1\wedge\dd{x}^2 +(\omega_{3,1}-\omega_{1,3})\dd{x}^1\wedge\dd{x}^3 +(\omega_{3,2}-\omega_{2,3})\dd{x}^2\wedge\dd{x}^3 } \] \(\R^3\)上的\(1\)形式场\(\omega=\omega_{12}\dd{x^1}\wedge\dd{x^2}+\omega_{13}\dd{x^1}\wedge\dd{x^3}+\omega_{23}\dd{x^2}\wedge\dd{x^3}\)的外微分 \[ \Align{ \dd{\mu} &=\sum_{\rm C} \dd\omega_{\mu_1\mu_2} \wedge\dd{x}^{\mu_1}\wedge\dd{x}^{\mu_2} \\ &=\cdots \\ &=(\mu_{23,1}-\mu_{13,2}+\mu_{12,3})\dd{x^1}\wedge\dd{x^2}\wedge\dd{x^3} } \]
设\(\omega\)为\(l\)形式场, 若\(\dd\omega=0\), 则称其为闭的(closed); 若存在\(\mu\)使得\(\omega=\dd\mu\), 则称其为恰当的(exact).
Claim 2 任意恰当形式都为闭形式, 即\(\dd{}^2=0\).
Pf 取\(\partial_a\), 有\((\dd\dd{\omega})_{cba_1\dots a_l}=(l+2)(l+1)\partial_{[c}\partial_{[b}\omega_{a_1\dots a_l]]}=(l+2)(l+1)\partial_{[(c}\partial_{b)}\omega_{a_1\dots a_l]}=0\).
- 要让该命题的逆命题成立, 需要对流形提出一些要求. 平凡流形\(\R^n\)满足这一要求, 而流形一定局部平凡. 因此若\(\omega\)为闭形式, 则\(M\)的任意一点\(p\)必有邻域\(N\), 在\(N\)上存在\(\mu\), 使得\(\dd\mu=\omega\).
Claim 3 微分形式与李导数.
- (李导数是导子) \({\cal L}_v(\omega\wedge\mu)=({\cal L}_v\omega)\wedge\mu+\omega\wedge({\cal L}_v\mu)\).
- (Cartan同伦公式) \({\cal L}_v\omega_{a_1\dots a_l}=\dd{}_{a_1}(v^b\omega_{ba_2\dots a_l})+v^b(\dd\omega)_{ba_1\dots a_l}\).
- (外微分和李导数可交换) \({\cal L}_v\dd{\omega}=\dd{ {\cal L}_v\omega}\).
5.2 Integration of forms
讨论积分之前, 先要给出流形定向的概念. 若一个\(n\)维流形\(M\)上存在一个处处非零的\(C^0\)的\(n\)形式场\(\varepsilon\), 则称为\(M\)为可定向的(orientable). 给定了一个定向的流形称为定向流形.
- 例如, \(\R^3\)是可定向的, \(\dd{x}\wedge\dd{y}\wedge\dd{z}\)就是一个定向; 莫比乌斯带(Möbius strip)是不可定向的.
对于\(M\)上的两个定向\(\varepsilon_1,\varepsilon_2\), 若存在处处为正的标量场\(h\), 使得\(\varepsilon_1=h\varepsilon_2\), 则称两者给出同一个定向.
- \(M\)的定向(orientation)是\(\varepsilon\)的等价类.
- 因为\(n\)维流形上每点的\(\Lambda(l)\)都是一维线性空间, 所以对于两个定向\(\varepsilon_1,\varepsilon_2\), 必定存在\(h\), 使\(\varepsilon_1=h\varepsilon_2\). 由定向的定义可知, \(h\)连续而且处处非零. 对于连通流形来说, \(h\)或者恒正, 或者恒负, 可见一个连通流形只有两种定向.
设\(M\)选定了定向\(\varepsilon\), 开域\(O\subset M\)上的基底场\(\qty{(e_\mu)^a}\)叫做右手的(right handed), 如果\((e^1)_{a_1}\wedge\cdots\wedge(e^n)_{a_n}\)与\(\varepsilon\)给出同一个定向; 否则叫做左手的(left handed). 一个坐标系称为右手系(左手系), 如果其坐标基底场为右手的(左手的).
- 一个有用的结论是, 若两个相交的坐标系定向相同, 则坐标变换的Jacobi行列式为正; 反之为负.
对于一个\(n\)形式场\(\omega\), 它用坐标基底展开为 \[ \omega = \omega_{1\dots n}(x^1,\dots,x^n) \dd{x^1} \wedge \dots \wedge \dd{x^n}, \] 我们定义\(\omega\)的积分就为\(n\)元函数\(\omega_{1\dots n}(x^1,\dots,x^n)\)的普通积分. 具体来说, 设\((O,\psi)\)为\(n\)维流形\(M\)上的右手系, \(\omega\)是开集\(G\subset O\)上的连续\(n\)形式场\(\omega\), 则\(\omega\)在\(G\)上的积分(integral)定义为 \[ \int_G \omega := \int_{\psi[G]} \omega_{1\dots n}(x^1,\dots,x^n) \dd{x^1}\cdots\dd{x^n}. \] 上式右边是\(n\)元函数\(\omega_{1\dots n}(x^1,\dots,x^n)\)在\(\R^n\)的开子集\(\psi[G]\)上的普通积分(Riemann或Lebesgue积分).
需要证明的是, 如上定义的积分是不依赖于坐标系\((O,\psi)\)的选取的. 为此, 选取包含\(G\)的另一个右手系\((O',\psi')\). 我们先推导\(n\)形式的坐标变换律, 设\(\omega\)在两个系的坐标分量分别为\(\omega_{1\cdots n},\omega'_{1\cdots n}\), 则由张量变换律, \[ \Align{ \omega'_{1\cdots n} &=\pdv{x^{\mu_1}}{x'^1}\cdots\pdv{x^{\mu_n}}{x'^n}\, \omega_{\mu_1\cdots\mu_n} \\ &=\sum_{\sigma\in S_n} \pdv{x^{\sigma(1)}}{x'^1}\cdots\pdv{x^{\sigma(n)}}{x'^n}\, \omega_{\sigma(1)\cdots\sigma(n)} \\ &=\sum_{\sigma\in S_n} (\sgn\sigma) \pdv{x^1}{x'^1}\cdots\pdv{x^n}{x'^n}\, \omega_{1\cdots n} \\ &=\omega_{1\dots n} \det\pqty{\pdv{x^\mu}{x'^\nu}}, } \] (第二步因为\(\mu_1,\dots,\mu_n\)互不相同, 可看作\(1,\dots,n\)的一个排列; 第三步根据分量的全反称性; 第四步由行列式的定义) 上式中\(J=\det(\pdv{x^\mu}{x'^\nu})>0\)是这个坐标变换的Jacobi行列式. 又根据多元微积分学的坐标变换法则, \[ \int_{\psi[G]}\omega_{1\dots n}\dd{x^1}\cdots\dd{x^n} =\int_{\psi'[G]}\omega_{1\dots n} |J| \dd{x'^1}\cdots\dd{x'^n} =\int_{\psi'[G]}\omega'_{1\dots n}\dd{x'^1}\cdots\dd{x'^n}, \] 即不同坐标系下\((\int_G \omega)'=\int_G \omega\).
在上述证明中, 若\((O',\psi')\)是左手系, 则Jacobi行列式\(J<0\), 取绝对值出来一个负号, 也就是说, 在左手系\((O',\psi')\)下, \(\omega\)的积分应当定义为
\[ \int_G \omega := -\int_{\psi'[G]} \omega_{1\dots n}(x'^1,\dots,x'^n) \dd{x'^1}\cdots\dd{x'^n}, \] 这样便保证积分的定义是坐标系无关的, 不论选取左手系还是右手系.
- 一个坐标系是左手系还是右手系取决于定向\(\varepsilon\), 定向改变后, 积分变号.
若\(\phi[S]\)是\(M\)的一个\(l\)维的嵌入子流形, 便可讨论\(M\)上的一个\(l\)形式场\(\mu\)在\(\phi[S]\)上的积分. 但是需要特别注意的一个点是, \(\mu\)作为\(M\)上的张量场, 其在\(\phi[S]\)上的取值不一定落在\(\phi[S]\)的切空间(的张量空间\({\cal T}_{W_q}(0,l)\))内, 有可能"支楞出去". 所以, 我们需要想出一种办法, 将\(\mu\)限制在\(\phi[S]\)上.
将\(\phi[S]\)上的\(l\)形式场\(\tilde\mu_{a_1\dots a_l}\)称为\(\mu_{a_1\dots a_l}\)在\(\phi[S]\)上的限制(restriction). 如果 \[ \tilde\mu_{a_1\dots a_l} |_q (w_1)^{a_1}\dots(w_l)^{a_l} = \mu_{a_1\dots a_l} |_q (w_1)^{a_1}\dots(w_l)^{a_l} \] 对于任意\((w_1)^{a_1}\dots(w_l)^{a_l}\in W_q\), \(q\in\phi[S]\)恒成立(即两者在\(\phi[S]\)的任意切空间作用效果相同). 今后谈及\(l\)形式场\(\mu\)在\(l\)维子流形\(\phi[S]\)上的积分时, 都应理解为其在\(\phi[S]\)的限制\(\tilde\mu\)的积分\(\int_{\phi[S]}\tilde\mu\).
5.3 Stokes' theorem
先引入带边流形的概念. \(n\)维带边流形最简单的例子是 \[ \R^{n-}:=\qty{(x^1,\dots,x^n)\in\R^n:x^1\leq0}, \] 其中\(x^1,\dots,x^n\)为自然坐标, 由\(x^1=0\)的点组成的子集叫做\(\R^{n-}\)的边界, 它是一个\((n-1)\)维流形\(\R^{n-1}\). 推广到一般情况, 一个\(n\)维带边流形(manifold with boundary)\(N\)的定义同\(n\)维流形相似, 只不过把\(\R^n\)换成\(\R^{n-}\), 即要求
- \(N\)的开覆盖\(\qty{O_\alpha}\)的每个\(O_\alpha\)都应同胚于\(\R^{n-}\)的开子集.
- 存在某些点, 它们的像在\(\R^{n-}\)的边界里. 这些点(边界点)构成的集合称为\(N\)的边界(boundary), 记作\(\partial N\). \(N\)中不是边界点的点(内点)组成的集合称为\(N\)的内部(interior), 记作\(\i(N)\).
容易验证, \(\partial N\)是一个\((n-1)\)维流形, \({\rm i}(N)\)是一个\(n\)维流形. \(\partial N\)的边界为空.
要在\(\partial N\)上积分, 首先要给出\(\partial N\)的定向. 设\(N\)的一个包含边界点的坐标域\(O\), 在该右手的正交归一坐标系下适配体元\(\varepsilon=\dd{x^1}\wedge\cdots\wedge\dd{x^n}\), 现在我们丢掉\(\dd{x^1}\), 得到一个\((n-1)\)形式\(\bar\varepsilon=\dd{x^2}\wedge\cdots\wedge\dd{x^n}\), 可以验证, \(\bar\varepsilon\)给出了边界上\(\partial N\cap O\)的一个定向. (再将若干个这样的局部定向拼合起来, 就得到了边界上的一个定向.) 将其(等价类)称为\(\partial N\)上的诱导定向(induced orientation).
- 可以证明, 若\(\qty{e_1,e_2,\dots,e_n}\)用\(\varepsilon\)衡量为右手的, 则\(\qty{e_2,\dots,e_n}\)用\(\hat\varepsilon\)衡量为右手的.
Claim 1 (Stokes定理) 设\(n\)维定向流形\(M\)的紧致子集\(N\)是\(n\)维带边流形, \(\omega\)是\(M\)上\(C^1\)的\((n-1)\)形式场, 则 \[ \int_{\i(N)}\dd{\omega} = \int_{\partial N} \omega. \]
- \(N\)和\(M\)是同维度的流形, \(M\)的定向\(\varepsilon\)自然给出了\(N\)的定向\(\varepsilon|_N\); 而\(\partial N\)上的定向是\(\varepsilon\)的诱导定向.
- \(\partial N\)是一个低维度子流形, 右边应当理解为\(\int_{\partial N} \omega = \int_{\partial N}\tilde\omega\).
- 对于流形\(M\)整体上的积分, 思想是将其分为若干坐标域, 在每个坐标域上积分, 最后拼合起来(借助单位分解).
Example 考虑\((\R^2,\delta_{ab})\)中的特例. 设矢量场\(A^a\), 光滑闭合曲线\(L\), \(S\)是\(L\)包围的开集, 笛卡尔坐标\(\qty{x,y}\). 则\(S\cup L\)可以充当\(N\), 其中\(S\)和\(L\)分别为内部和边界. \(A_a\)可以充当\(\omega\). 一方面, \[ \Align{ \dd{\omega}=(\omega_{2,1}-\omega_{1,2})\dd{x^1}\wedge\dd{x^2} =(A_{2,1}-A_{1,2})\dd{x^1}\wedge\dd{x^2}, } \] 所以Stokes定理的左边为\(\iint_S(A_{2,1}-A_{1,2})\dd{x^1}\dd{x^2}\). 另一方面, 选\(L\)的线长\(l\)为局部坐标, 将\(\tilde\omega\)用坐标基矢展开为\(\tilde\omega_a=\tilde\omega_1(l)(\dd{l})_a\), 两边与\((\pdv{l})^a\)缩并得 \[ \tilde\omega_1(l) = \tilde\omega_a\pqty{\pdv{l}}^a = \omega_a\pqty{\pdv{l}}^a = A_a\pqty{\pdv{l}}^a = A_l, \] 所以Stokes定理的右边为\(\oint_L A_l\dd{l}\). 左右两边相等, 有 \[ \iint_S\pqty{\pdv{A_2}{x^1}-\pdv{A_1}{x^2}}\dd{x^1}\dd{x^2} = \oint_L A_l\dd{l}, \] 这就是我们熟知的Green公式.
5.4 Volume elements
可定向流形\(M\)上的一个处处非零的\(C^0\)的\(n\)形式场\(\varepsilon\)称为一个体元(volume element). 如果一个体元和某个定向给出了同一个定向, 那么称体元与定向相容.
如果流形上给定了度规场\(g_{ab}\), 那么就有一个特定的选择体元的方法. 如果一个体元\(\varepsilon_{a_1\dots a_l}\)在正交归一基底\(\qty{(e^\mu)_a}\)的分量满足 \[ \varepsilon_{1\dots n} = \pm1,\quad\textsf{即}\, \varepsilon_{a_1\dots a_n} = \pm(e^1)_{a_1}\wedge\cdots\wedge(e^n)_{a_n}, \] 那么称\(\varepsilon_{a_1\dots a_l}\)为与度规适配(相容)的体元. 上式等价于 \[ \varepsilon^{a_1\dots a_n} \varepsilon_{a_1\dots a_n} = (-1)^s n!, \] 其中\(s\)是\(g_{ab}\)在(任意)正交归一基底的分量中\(-1\)的个数, 例如正定度规有\(s=0\), 洛伦兹度规有\(s=1\).
- "与度规适配"将体元确定到相差一个负号的程度, 再加上"与定向相容"便可唯一确定体元. 今后在给出度规后提到的体元, 默认是这个唯一适配的体元. 右手系下的适配体元有\(\varepsilon_{1\dots n}=(-1)^s\).
- 三维欧氏空间\((\R^3,\delta_{ab})\)中选取一个(直观含义上的)"右手系"\(\qty{x,y,z}\), 则在\(\varepsilon=\dd{x}\wedge\dd{y}\wedge\dd{z}\)给出的定向下, \(\qty{x,y,z}\)是右手系. 可知\(\varepsilon\)为适配体元.
Claim 1 设\(\varepsilon\)为适配体元, 任取基底\(\qty{(e_\mu)^a}\), 其对偶基底\(\qty{(e^\mu)_a}\), 则 \[ \varepsilon_{a_1\dots a_n} = \pm\sqrt{\abs{g}} (e^1)_{a_1}\wedge\cdots\wedge(e^n)_{a_n}, \] 其中\(+,-\)分别适用于右手和左手基底; \(g:=\det{g_{\mu\nu}}\)为度规在此基底下的分量组成的行列式(对正交归一基底有\(g=(-1)^s\)).
Pf 即证明\((\varepsilon_{\mu_1\dots\mu_n})^2=|g|\). 因为 \[ \Align{ (-1)^sn! =\varepsilon^{a_1\dots a_n}\varepsilon_{a_1\dots a_n} &=\varepsilon_{\mu_1\dots\mu_n}\varepsilon_{\nu_1\dots\nu_n} g^{\mu_1\nu_1}\cdots g^{\mu_n\nu_n} \\ &=\sum_{\sigma,\tau\in S_n} \varepsilon_{\sigma(1)\dots\sigma(n)} \varepsilon_{\tau(1)\dots\tau(n)} g^{\sigma(1)\tau(1)}\cdots g^{\sigma(n)\tau(n)} \\ &=(\varepsilon_{1\dots n})^2\sum_{\sigma,\tau\in S_n} (\sgn\sigma)(\sgn\tau)\, g^{\sigma(1)\tau(1)}\cdots g^{\sigma(n)\tau(n)} \\ &=(\varepsilon_{1\dots n})^2\sum_{\sigma,\tau\in S_n} (\sgn\tau\sigma^{-1})\, g^{1\tau(\sigma^{-1}(1))}\cdots g^{n\tau(\sigma^{-1}(n))} \\ &=n!(\varepsilon_{1\dots n})^2(\det g^{\mu\nu}), } \] 有\((\varepsilon_{1\dots n})^2=(-1)^s(\det g^{\mu\nu})^{-1}=(-1)^s(\det g_{\mu\nu})=|\!\det g_{\mu\nu}|\).
Claim 2 设\(\nabla_a\)和\(\varepsilon\)分别是与度规适配的导数算符和体元, 则\(\nabla_b\varepsilon_{a_1\dots a_n}=0\).
Claim 3 对适配体元有如下恒等式,
- \(\varepsilon^{a_1\dots a_n}\varepsilon_{b_1\dots b_n}=(-1)^sn!\delta^{[a_1}{_{b_1}}\cdots\delta^{a_n]}{_{b_n}}\).
- \(\varepsilon^{a_1\dots a_ja_{j+1}\dots a_n}\varepsilon_{b_1\dots b_jb_{j+1}\dots b_n}=(-1)^s(n-j)!j!\delta^{[a_{j+1}}{_{b_{j+1}}}\cdots\delta^{a_n]}{_{b_n}}\).
下面要介绍的Gauss定理涉及到了流形\(N\)边界\(\partial N\)上的体元, 所以在这之前, 先给出诱导体元的概念. 给定\(\varepsilon_{a_1\dots a_n}\)为\((N,g_{ab})\)的适配体元, 则\(\partial N\)上的诱导体元(induced volume form)\(\hat\varepsilon_{a_1\dots a_{n-1}}\)应当满足①与诱导定向相容, ②与诱导度规\(h_{ab}\)适配, 即 \[ \hat\varepsilon^{a_1\dots a_{n-1}} \hat\varepsilon_{a_1\dots a_{n-1}} = (-1)^{\hat s}(n-1)!, \] 其中\(\hat\varepsilon^{a_1\dots a_{n-1}}\)是用\(h^{ab}\)升指标的结果, \(\hat s\)是\(h_{ab}\)在正交归一坐标系分量中\(-1\)的个数. 可以证明, 诱导体元\(\hat\varepsilon_{a_1\dots a_{n-1}}\)与\(N\)上的体元满足如下关系, \[ \hat\varepsilon_{a_1\dots a_{n-1}} = n^b \varepsilon_{ba_1\dots a_n}. \]
- 其中\(n^b\)是外向单位法矢(\(|n^bn_b|=1\)). 若在包含边界点的坐标系下, 边界为\(x^1=0\)的点, \(N\)为\(x^1\leq0\)的点, 则"外向矢量"指的是\(v^1>0\)的矢量.
注意这个定义要求超曲面\(\partial N\)非类光, 对于类光超曲面, 诱导体元\(\hat\varepsilon_{a_1\dots a_{n-1}}\)如下定义 \[ \frac1n\varepsilon_{a_1\dots a_n} = n_{[a_1}\hat\varepsilon_{a_2\dots a_n]}. \]
5.5 Integration of functions, Gauss' law
设\(\varepsilon\)为流形\(M\)上的一个体元, \(f\)为\(M\)上的\(C^0\)标量场, 则\(f\)在\(M\)上的积分定义为 \[ \int_M f := \int_M f\varepsilon. \] 如果给定了度规, 则总选择适配体元.
Example 1 考虑\((\R^3,\delta_{ab})\)上连续函数\(f\)的积分. 先选取\(\qty{x,y,z}\), 则\(\varepsilon=\dd{x}\wedge\dd{y}\wedge\dd{z}\), 设\(f\)的坐标函数\(F(x,y,z)\), 则 \[ \int f = \int f\varepsilon = \iiint F(x,y,z)\dd{x}\dd{y}\dd{z}. \] 也可以选取(右手)球坐标系\(\qty{r,\theta,\phi}\), 则\(\sqrt{|g|}=r^2\sin\theta\), \(\varepsilon=r^2\sin\theta\dd{r}\wedge\dd{\theta}\wedge\dd{\phi}\), 设\(f\)的坐标函数\(\hat{F}(r,\theta,\phi)\), 则积分也等于 \[ \int f = \int f\varepsilon = \iiint \hat{F}(r,\theta,\phi) r^2\sin\theta\dd{r}\dd{\theta}\dd{\phi}. \]
Claim 1 设\(M\)为\(n\)维定向流形, \(N\)是\(M\)中的\(n\)维紧致带边嵌入子流形, \(g_{ab}\)为\(M\)上的度规, \(\varepsilon\)和\(\nabla_a\)分别为适配体元和适配导数算符, \(v^a\)为\(M\)上的\(C^1\)矢量场, 则 \[ \int_{\i(N)} (\nabla_bv^b)\varepsilon = \int_{\partial N} v^b\varepsilon_{ba_1\dots a_{n-1}}. \] > Pf 应用Stokes定理, 令\(\omega_{a_1\dots a_{n-1}}=v^b\varepsilon_{ba_1\dots a_{n-1}}\), 只需证明\(\dd\omega=(\nabla_bv^b)\varepsilon\). 注意到\(\dd\omega\)是\(n\)形式, 它与\(\varepsilon\)只相差一个乘子\(h\), 即\(\dd\omega_{ca_1\dots a_{n-1}}=h\varepsilon_{ca_1\dots a_{n-1}}\). 两边与\(\varepsilon^{ca_1\dots a_{n-1}}\)缩并, 右边变为\(h(-1)^sn!\), 左边变为 > \[ > \Align{ > \varepsilon^{ca_1\dots a_{n-1}} \dd\omega_{ca_1\dots a_{n-1}} > &=n\varepsilon^{ca_1\dots a_{n-1}} > \nabla_{c}(v^b\varepsilon_{ba_1\dots a_{n-1}}) \\ > &=n\varepsilon^{ca_1\dots a_{n-1}} > \varepsilon_{ba_1\dots a_{n-1}} \nabla_cv^b \\ > &=n\delta^c{_b} (-1)^s(n-1)! \nabla_cv^b \\ > &=(-1)^sn! \nabla_bv^b, > } > \] > (其中第二步因为\(\nabla\varepsilon=0\); 第三步利用了上一节Claim 3.) 因此\(h=\nabla_bv^b\), 即证.
Claim 2 (Gauss定理) 设\(M\)为\(n\)维定向流形, \(N\)是\(M\)中的\(n\)维紧致带边嵌入子流形, \(g_{ab}\)为\(M\)上的度规, \(\varepsilon\)和\(\nabla_a\)分别为适配体元和适配导数算符, \(v^a\)为\(M\)上的\(C^1\)矢量场, \(\partial N\)的外向法矢\(n^a\)满足\(|n^an_a|=1\), 则 \[ \int_{\i(N)} (\nabla_bv^b)\varepsilon = (n^cn_c) \int_{\partial N} (v^an_a)\hat\varepsilon. \]
Pf 根据Claim 2, 只需证明\(\int_{\partial N} v^b\varepsilon_{ba_1\dots a_{n-1}}=\int_{\partial N} (v^an_a)\hat\varepsilon\). 令\(\omega=v^b\varepsilon_{ba_1\dots a_{n-1}}\), 根据5.2节末关于\(\int_{\phi[S]}\omega=\int_{\phi[S]}\tilde\omega\)的讨论可知, 只需证明\(\tilde\omega_{a_1\dots a_{n-1}}=v^bn_b\hat\varepsilon_{a_1\dots a_{n-1}}\). 注意到两边均为\((n-1)\)维流形\(\partial N\)上的\((n-1)\)形式, 因此存在标量场\(K\)使得 \[ \tilde\omega_{a_1\dots a_{n-1}} = Kv^bn_b\hat\varepsilon_{a_1\dots a_{n-1}}, \] 于是只需证明\(K=n^cn_c\). 取\(V_q\)的一个右手正交归一基底\(\qty{(e_0)^a,(e_1)^a,\dots,(e_{n-1})^a}\), 其中\((e_0)^a=n^a\), 用\((e_1)^{a_1}\cdots(e_{n-1})^{a_{n-1}}\)缩并上式左右两边, 右边给出 \[ v^bn_b \hat\varepsilon_{12\dots n-1} = (n^cn_c)K v^b(e^0)_b \hat\varepsilon_{12\dots n-1} = (n^cn_c)K v^b(e^0)_b = (n^cn_c)K v^0, \] (其中第一步利用\(n_b=(n^cn_c)(e^0)_b\); 第二步利用了诱导定向的性质: 若\(\qty{(e_0)^a,\dots,(e_{n-1})^a}\)用\(\varepsilon\)衡量为右手的, 则\(\qty{(e_1)^a,\dots,(e_{n-1})^a}\)用\(\hat\varepsilon\)衡量为右手的.) 左边则给出 \[ \Align{ \tilde\omega_{a_1\dots a_{n-1}} (e_1)^{a_1}\cdots(e_{n-1})^{a_{n-1}} &=\omega_{a_1\dots a_{n-1}} (e_1)^{a_1}\cdots(e_{n-1})^{a_{n-1}} \\ &=v^b\varepsilon_{ba_1\dots a_{n-1}} (e_1)^{a_1}\cdots(e_{n-1})^{a_{n-1}} \\ &=v^\mu\varepsilon_{\mu 12\dots {n-1}} \\ &=v^0, } \] 于是\(K=\frac1{n^cn_c}=n^cn_c\), 即证.
Example 2 可以发现, 上面的Gauss定理是三维欧氏空间\((\R^3,\delta_{ab})\)中Gauss定理(如下)的推广. 设有界闭区域\(V\), 其边界\(S\)为分片光滑曲面, \(\vu{n}\)为其外向法矢, \(\vb{A}\)为\(C^1\)矢量场, 则 \[ \iiint_V(\nabla\cdot\vb{A})\dd{V} = \iint_S (\vb{A}\cdot\vu{n})\dd{S}. \]
5.6 Dual differential forms
回顾\(l\)形式场组成的线性空间的维度, 有\(\dim\Lambda_M(l)={n\choose l}={n\choose n-l}=\dim\Lambda(n-l)\). 设\(M\)为带度规\(g_{ab}\)的定向流形, \(\varepsilon\)为适配体元, 则可以构造同构映射\(\star:\Lambda_M(l)\to\Lambda_M(n-l)\), 定义如下 \[ (\star\omega)_{a_1\dots a_{n-l}} := \frac1{l!} \omega^{b_1\dots b_l} \varepsilon_{b_1\dots b_l a_1\dots a_{n-l}}. \] 称\(\star\omega\)为\(\omega\)的对偶微分形式(dual form), 也称Hodge对偶, 其中\(\star\)称为Hodge star算子.
- 可以验证, \(\star\)是线性同构映射.
- 对于\(0\)形式场\(f\), 其对偶\(\star{f}=f\varepsilon\), 再取对偶\(\star(\star{f})=(-1)^sf\).
Claim 1 对任意\(l\)形式场\(\omega\)有\(\star(\star\omega)=(-1)^{s+l(n-l)}\omega\).
Pf 根据Hodge对偶的定义, \[ \Align{ \star(\star\omega)_{c_1\dots c_l} &=\frac1{l!(n-l)!} \omega^{b_1\dots b_l} \varepsilon_{b_1\dots b_l}{^{a_1\dots a_{n-l}}} \varepsilon_{a_1\dots a_{n-l}c_1\dots c_l} \\ &=\frac{1}{l!(n-l)!}(-1)^{l(n-l)} \omega_{b_1\dots b_l} \varepsilon^{a_1\dots a_{n-l}b_1\dots b_l} \varepsilon_{a_1\dots a_{n-l}c_1\dots c_l} \\ &=(-1)^{s+l(n-l)} \omega_{b_1\dots b_l} \delta^{[b_1}{_{c_1}}\cdots\delta^{b_l]}{_{c_l}} \\ &=(-1)^{s+l(n-l)} \omega_{c_1\dots c_l}. } \]
对于两个\(l\)形式\(\omega,\mu\), 定义其内积(inner product)为 \[ \lr{\omega,\mu} := \frac1{l!}\omega^{a_1\dots a_l}\mu_{a_1\dots a_l}. \]
- 可以发现, 与定向相容\(n\)形式\(\varepsilon\)为适配体元的充要条件为\(\lr{\varepsilon,\varepsilon}=(-1)^s\).
- 正交归一右手系下, \(\lr{\omega^1\wedge\cdots\wedge\omega^n,\mu^1\wedge\cdots\wedge\mu^n}=(-1)^s\det(\omega^\mu{_\nu})\det(\mu^\rho{_\sigma})\).
Claim 2 对任意\(l\)形式场\(\omega,\mu\)和\((n-l)\)形式场\(\lambda\)有
- \(\omega\wedge\lambda=(-1)^s\lr{\star\omega,\lambda}\varepsilon\).
- \(\omega\wedge(\star\mu)=\lr{\omega,\mu}\varepsilon\).
Pf 第1条, \(\omega\wedge\lambda=\frac{n!}{l!(n-l)!}\omega_{[a_1\dots a_l}\lambda_{b_1\dots b_{n-l}]}\)作为\(n\)形式, 其与\(\varepsilon\)只相差一个乘子\(h\), 即 \[ \frac{n!}{l!(n-l)!}\omega_{[a_1\dots a_l}\lambda_{b_1\dots b_{n-l}]} = h\varepsilon_{a_1\dots a_lb_1\dots b_{n-l}}, \] 两边同时与\(\varepsilon^{a_1\dots a_lb_1\dots b_{n-l}}\)缩并, 右边变为\(h(-1)^sn!\), 左边变为 \[ \frac{n!}{l!(n-l)!} \varepsilon^{a_1\dots a_lb_1\dots b_{n-l}} \omega_{a_1\dots a_l}\lambda_{b_1\dots b_{n-l}} = \frac{n!}{(n-l)!} (\star\omega)^{b_1\dots b_{n-l}} \lambda_{b_1\dots b_{n-l}} = n!\lr{\star\omega,\lambda}, \] 所以\(h=(-1)^s\lr{\star\omega,\lambda}\), 即证.
第2条, (下面第一步利用了楔积的分级反对称性; 第二步利用了第1条; 第三步利用了Claim 1) \[ \Align{ \omega\wedge(\star\mu) &=(-1)^{l(n-l)} (\star\mu)\wedge\omega \\ &=(-1)^{l(n-l)} (-1)^s\lr{\star(\star\mu),\omega}\varepsilon \\ &=\lr{\mu,\omega} \varepsilon. } \]
下面介绍计算Hodge对偶的实用方法.
Claim 3 设右手正交归一基底\(\qty{(e^\mu)_a}\), \(\sigma\)为\(n\)阶置换, 则 \[ \star(e^{\sigma(1)}\wedge\cdots\wedge e^{\sigma(l)}) =\bar{g}\, (\sgn\sigma) (e^{\sigma(l+1)}\wedge\cdots\wedge e^{\sigma(n)}), \]
其中\(\bar{g}=g_{\sigma(1)\sigma(1)}\cdots g_{\sigma(l)\sigma(l)}=\pm1\).
- 根据Hodge对偶的线性性, 可以方便地计算任意\(l\)形式\(\omega\)的对偶形式.
Example 在欧氏空间\((\R^3,\delta_{ab})\)中, 应用Claim 3有 \[ \Align{ && \star\dd{x}&=\dd{y}\wedge\dd{z} &\star(\dd{x}\wedge\dd{y})&=\dd{z} && \\ \star1&=\dd{x}\wedge\dd{y}\wedge\dd{z} & \star\dd{y}&=\dd{z}\wedge\dd{x} & \star(\dd{y}\wedge\dd{z})&=\dd{x} & \star(\dd{x}\wedge\dd{y}\wedge\dd{z})&=1. \\ && \star\dd{z}&=\dd{x}\wedge\dd{y} & \star(\dd{z}\wedge\dd{x})&=\dd{y} && } \] 在闵氏时空\((\R^4,\eta_{ab})\)中应用Claim 3, 可以得到: 0形式和4形式的对偶, \[ \Align{ \star1 &= \dd{t}\wedge\dd{x}\wedge\dd{y}\wedge\dd{z} & \star(\dd{t}\wedge\dd{x}\wedge\dd{y}\wedge\dd{z}) &= -1. } \] 1形式的对偶, \[ \Align{ \star\dd{t} &= -\dd{x}\wedge\dd{y}\wedge\dd{z} & \star\dd{y} &= \dd{t}\wedge\dd{x}\wedge\dd{z} \\ \star\dd{x} &= -\dd{t}\wedge\dd{y}\wedge\dd{z} & \star\dd{z} &= -\dd{t}\wedge\dd{x}\wedge\dd{y}. } \] 2形式的对偶, \[ \Align{ \star(\dd{t}\wedge\dd{x}) &= -\dd{y}\wedge\dd{z} & \star(\dd{x}\wedge\dd{y}) &= \dd{t}\wedge\dd{z} \\ \star(\dd{t}\wedge\dd{y}) &= \dd{x}\wedge\dd{z} & \star(\dd{x}\wedge\dd{z}) &= -\dd{t}\wedge\dd{y} \\ \star(\dd{t}\wedge\dd{z}) &= -\dd{x}\wedge\dd{y} & \star(\dd{y}\wedge\dd{z}) &= \dd{t}\wedge\dd{x}. } \] 3形式的对偶, \[ \Align{ \star(\dd{x}\wedge\dd{y}\wedge\dd{z}) &= -\dd{t} & \star(\dd{t}\wedge\dd{x}\wedge\dd{z}) &= \dd{y} \\ \star(\dd{t}\wedge\dd{y}\wedge\dd{z}) &= -\dd{x} & \star(\dd{t}\wedge\dd{x}\wedge\dd{y}) &= -\dd{z}. } \]
应用: 欧氏空间\((\R^3,\delta_{ab})\)中的向量分析.
选定笛卡尔坐标系\(\qty{x,y,z}\), 则适配体元\(\varepsilon=\dd{x}\wedge\dd{y}\wedge\dd{z}\). 因为有度规, 所以矢量和对偶矢量自然认同, 下面不作区分.
设\(0\)形式\(f\), \(1\)形式\(F_a\), \(2\)形式\(G_{ab}\), 分别计算其外微分, 并和梯度, 旋度和散度公式(橙色)比较,
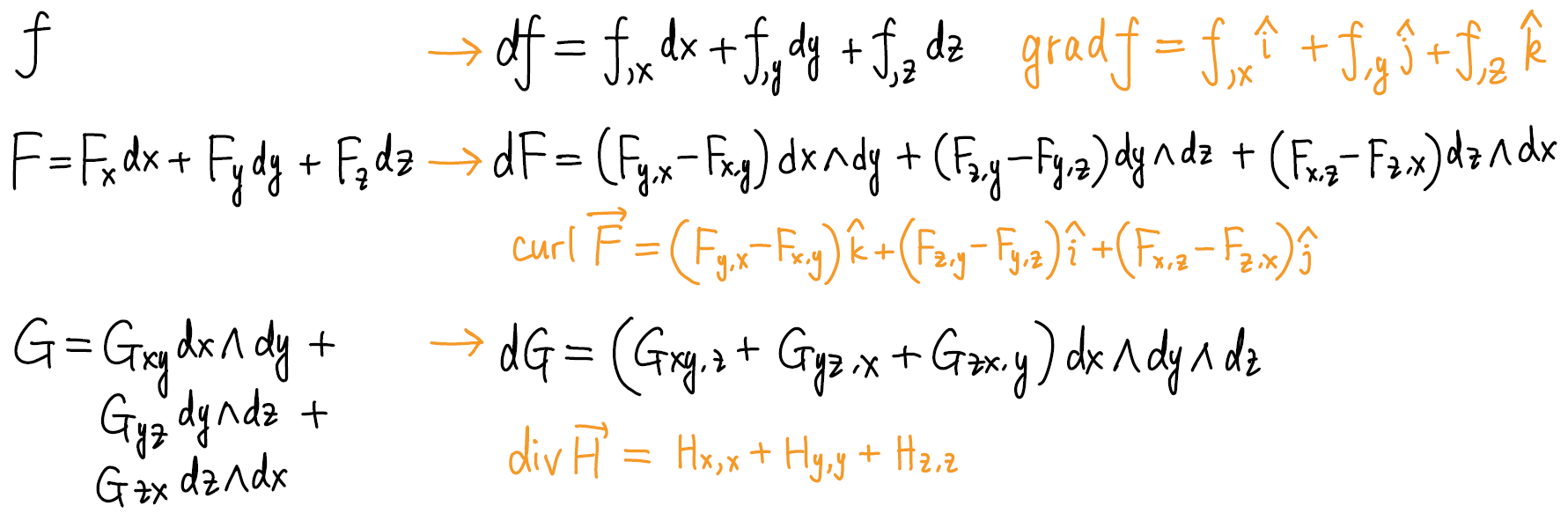
可以看到, 它们长得很像: 其的分量表达式几乎完全一样的, 只是张量类型不同. 而根据Hodge对偶的思想, \(2\)形式\(\dd{F}\)和\(1\)形式自然认同, 进而和矢量场自然认同; \(3\)形式\(\dd{G}\)和\(0\)形式, 即标量场自然认同, 所以, 外微分算符分别作用于\(0,1,2\)形式, 可以分别自然地等同于梯度, 散度, 旋度. 又根据\(\dd{\dd}=0\), 我们可以将这种关系写成正合列 \[ \Align{ 0 \xrightarrow[]{\hspace{1.5em}} \Lambda_{\R^3}(0) \xrightarrow[\orange{\rm grad}]{\dd} \Lambda_{\R^3}(1) \xrightarrow[\orange{\rm curl}]{\dd} \Lambda_{\R^3}(2) \xrightarrow[\orange{\rm div}]{\dd} \Lambda_{\R^3}(3) \xrightarrow[]{\hspace{1.5em}} 0. } \]
- 直接看出"梯度的旋度为零", "旋度的散度为0".
最后给出结论: 用上Hodge对偶, 梯度旋度散度就可以写成下面简洁的形式, \[ \Align{ {\rm grad}(f) &= \dd{f}, & {\rm curl}(F) &= \star\dd{F}, & {\rm div}(H) &= \star\dd(\star H). } \] 借助导数算符\(\partial_a\)可以写成 \[ \Align{ {\rm grad}(f)^a &= \partial^a{f}, & {\rm curl}(F)^c &= \varepsilon^{abc}\partial_a F_b, & {\rm div}(H) &= \partial^a H_a. } \]
5.7 *Computing curvatures using frames
(无挠)导数算符\(\nabla_a\)的曲率张量\(R_{abd}{^d}\)有两种求法, 一种是借用坐标基底场, 第二种是借用非坐标基底场(也称为标架(frame)). 第3.4节已经讲过第一种方法, 其中关键一步是求出\(\nabla_a\)借该坐标基底场的体现, 即克氏符\(\Gamma^\sigma{_{\mu\tau}}\); 而下面要讨论的第二种方法(借标架计算曲率)中, 首先也需要找出\(\nabla_a\)借该标架\(\qty{(e_\mu)^a}\)的体现.
之前我们提到过克氏符(也称联络系数)的等价定义\(\pqty{\pdv{x^\tau}}^b\nabla_b\pqty{\pdv{x^\mu}}^a=\Gamma^\sigma{_{\mu\tau}}\pqty{\pdv{x^\sigma}}^a\), 即一个坐标基矢沿着另一个坐标基矢的导数. 将其推广到任意标架: \[ (e_\tau)^b\nabla_b(e_\mu)^a = \gamma^\sigma{_{\mu\tau}}(e_\sigma)^a, \] 其中\(\gamma^\sigma{_{\mu\tau}}\)称为标架的联络系数(connection coefficients). 将上式用对偶基矢\((e^\sigma)_a\)缩并可以得到显示表达式: \[ \gamma^\nu{_{\mu\tau}}=(e^\nu)_a(e_\tau)^b\nabla_b(e_\mu)^a. \] 固定\(\mu,\nu\)的值, \(\tau\)可以取\(1,\dots,n\). 以它们(加负号)为分量定义的1形式\((\omega_\mu{^\nu})_a\)称为联络1形式(connection 1-form), 即 \[ (\omega_\mu{^\nu})_a := -\gamma^\nu{_{\mu\tau}}(e^\tau)_a. \] Claim 1 \((\omega_\mu{^\nu})_a=(e_\mu)^c\nabla_a(e^\nu)_c\).
就像从联络系数\(\Gamma^\sigma{}_{\mu\nu}\)计算黎曼曲率张量一样, 从联络1形式\((\omega_\mu{^\nu})_a\)也可以计算曲率张量. 由于黎曼曲率张量\(R_{abc}{^d}\)关于\(ab\)的反对称性, 可以构造2形式 \[ (\Omega_\mu{^\nu})_{ab} := R_{abc}{^d}(e_\mu)^c(e^\nu)_d, \] 称为曲率2形式(curvature 2-form). 另外, 许多文献采用\(\Omega_\mu{^\nu}=\frac12R_{\rho\sigma\mu}{^\nu}(e^\rho\wedge e^\sigma)\)作为曲率2形式的定义, 与上等价. 如果求出了曲率2形式, 就相当于求出了黎曼曲率张量的全部分量\(R_{\rho\sigma\mu}{^\nu}\), 因为 \[ R_{\rho\sigma\mu}{^\nu} = (R_\mu{^\nu})_{ab}(e_\rho)^a(e_\sigma)^b. \] 下面讲求曲率2形式的方法.
Claim 2 (Cartan第一结构方程) 引理: \[ \dd{e^\nu} = -e^\mu \wedge \omega_\mu{^\nu}. \] Claim 3 (Cartan第二结构方程) 曲率2形式与联络1形式的关系: \[ \Omega_{\mu}{^\nu} = \dd\omega_\mu{^\nu} + \omega_\mu{^\lambda}\wedge\omega_\lambda{^\nu}. \] Cartan第二结构方程等价于第3.4节的 \[ R_{abc}{^d} = \partial_{b}\Gamma^d{_{ac}}-\partial_{a}\Gamma^d{_{bc}}+ \Gamma^e{_{ca}}\Gamma^d{_{be}}+\Gamma^e{_{cb}}\Gamma^d{_{ae}}, \] 分别是黎曼曲率张量借标架和坐标基底的表达式.
由标架计算曲率可分为如下三步: ①选定标架, ②计算无挠导数算符的所有联络1形式, ③由Cartan第二结构方程计算曲率2形式. 其中第②步再展开讲解.
若流形上给定了度规\(g_{ab}\), 且导数算符与度规适配, 我们称度规分量为常数, 即满足\(\nabla_ag_{\mu\nu}=0\)的标架为刚性标架(rigid frame). 正交归一标架是最简单的刚性标架, 可以为计算带来许多方便.
引入记号 \[ \Align{ (e_\mu)_a &:= g_{ab}(e_\mu)^b, & (e^\mu)^a &:= g^{ab}(e^\mu)_b, } \] 则有 \[ \Align{ (e^\mu)^a &= g^{\mu\nu}(e_\nu)^a, & (e_\mu)_a &= g_{\mu\nu}(e^\nu)_a. } \] 这表明, 基矢的具体指标也可以用度规升降. 类似地, 可以定义\((\omega_{\mu\nu})_a:=g_{\nu\sigma}(\omega_\mu{^\sigma})_a\).
Claim 4 对刚性标架有\((\omega_{\mu\nu})_a=-(\omega_{\nu\mu})_a\).
称\((\omega_{\mu\nu})_a\)的分量\(\omega_{\mu\nu\rho}=(\omega_{\mu\nu})_a(e_\rho)^a\)为里奇旋转系数(Ricci rotation coefficients). 它共有\(n^2(n-1)/2\)个独立的数. 借用任意坐标系\(\qty{x^\mu}\), 引入符号 \[ \Lambda_{\mu\nu\rho} := [(e_\nu)_{\lambda,\tau}-(e_\nu)_{\tau,\lambda}] (e_\mu)^\lambda(e_\rho)^\tau. \] 其中\((e_\mu)_\lambda,(e_\mu)^\lambda\)分别是\((e_\mu)_a,(e_\mu)^a\)在\(\qty{x^\mu}\)的第\(\lambda\)分量. 易得\(\Lambda_{\mu\nu\rho}=-\Lambda_{\rho\nu\mu}\), 所以只有\(n^2(n-1)/2\)个独立分量. 如上求得所有\(\Lambda_{\mu\nu\rho}\)之后可以由下定理直接计算全部\(\omega_{\mu\nu\rho}\).
Claim 5 \[ \omega_{\mu\nu\rho}=\frac12( \Lambda_{\mu\nu\rho} + \Lambda_{\rho\mu\nu} - \Lambda_{\nu\rho\mu} ). \]