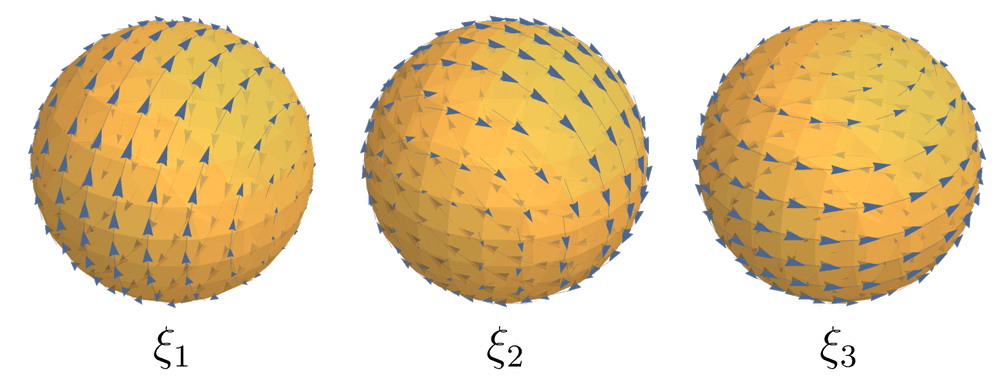梁GR | 3 李导数, Killing场和超曲面

梁灿彬, 周彬《微分几何入门与广义相对论》第四章的笔记.

4 Lie Derivatives, Killing Fields and Hypersurfaces

4.1 Maps of manifolds

2023.8.2

拉回与推前.

设$\varphi :M\to N$为微分同胚, 那么这个点的映射可以诱导出张量场${\mathcal{F}}_M(k,l)$与${\mathcal{F}}_N(k,l)$之间的映射, 即拉回(pull back)${\varphi }^{\ast }$和推前(push forward)${\varphi }_{\ast }$. 我们一步一步地来定义: (其中$f,v,\omega$是$M$上的场, $g,w,\mu$是$N$上的场, $p\in M$, $q\in N$)

• 标量场${\mathcal{F}}_M⟷{\mathcal{F}}_N$.

  • 拉回, ${\varphi }^{\ast }g:=g\circ \varphi$.
  • 推前, ${\varphi }_{\ast }f:=f\circ {\varphi }^{-1}$.

• 矢量场${\mathcal{F}}_M(1,0)⟷{\mathcal{F}}_N(1,0)$.

  • 拉回, $({\varphi }^{\ast }w){|}_p(f):=w{|}_{\varphi (p)}({\varphi }_{\ast }f)$.
  • 推前, $({\varphi }_{\ast }v){|}_q(g):=v{|}_{{\varphi }^{-1}(q)}({\varphi }^{\ast }g)$.

• 对偶矢量场${\mathcal{F}}_M(0,1)⟷{\mathcal{F}}_N(0,1)$.

  • 拉回, $({\varphi }^{\ast }\mu ){|}_p(v):=\mu {|}_{\varphi (p)}({\varphi }_{\ast }v)$.

  • 推前, $({\varphi }_{\ast }\omega ){|}_q(w):=\omega {|}_{{\varphi }^{-1}(q)}({\varphi }^{\ast }w)$.

• $(k,l)$型张量场的推拉, 很容易借助矢量场和对偶矢量场的推拉来定义, 这里仅举出一例. 对于$T^a{}_b\in {\mathcal{F}}_N(1,1)$, 其拉回定义为 $$({\varphi }^{\ast }T{)}^a{}_b{|}_p({\omega }_a{v}^b):=T^a{}_b{|}_{\varphi (p)}({\varphi }_{\ast }\omega {)}_a({\varphi }_{\ast }v{)}^b.$$

容易验证, 定义出来的${\varphi }^{\ast }v,{\varphi }_{\ast }v$等满足线性性和Leibniz律.

注: 如果$\varphi$只是光滑映射而非同胚, 那么${\varphi }^{-1}$不存在, 拉回至多延拓到${\varphi }^{\ast }:{\mathcal{F}}_N(0,l)\to {\mathcal{F}}_M(0,l)$; 推前只能逐点地定义, ${\varphi }_{\ast }:{\mathcal{T}}_{V_p}(k,0)\to {\mathcal{T}}_{V_{\varphi (p)}}(k,0)$, 而不能推前张量场. 定义如下,

• 标量场的拉回, ${\varphi }^{\ast }:{\mathcal{F}}_N\to {\mathcal{F}}_M$, $({\varphi }^{\ast }g){|}_p:=g(\varphi (p))$.

• 切空间的推前, ${\varphi }_{\ast }:V_p\to V_{\varphi (p)}$, $({\varphi }_{\ast }v)(g):=v({\varphi }^{\ast }g)$, 也称切映射(tangent map).

• 拉回的延拓, ${\varphi }^{\ast }:{\mathcal{F}}_N(0,l)\to {\mathcal{F}}_M(0,l)$, $$({\varphi }^{\ast }T{)}_{a_1\dots a_l}{|}_p(v_1{)}^{a_1}\cdots (v_l{)}^{a_l}:=T_{a_1\dots a_l}{|}_{\varphi (p)}({\varphi }_{\ast }{v}_1{)}^{a_1}\cdots ({\varphi }_{\ast }{v}_l{)}^{a_l}.$$

• 推前的延拓, ${\varphi }_{\ast }:{\mathcal{T}}_{V_p}(k,0)\to {\mathcal{T}}_{V_{\varphi (p)}}(k,0)$, $$({\varphi }_{\ast }T{)}^{a_1\dots a_k}({\omega }^1{)}_{a_1}\cdots ({\omega }^k{)}_{a_k}:=T^{a_1\dots a_k}({\varphi }^{\ast }{\omega }^1{)}_{a_1}\cdots ({\varphi }^{\ast }{\omega }^k{)}_{a_k}.$$

推前映射${\varphi }_{\ast }:V_p\to V_{\varphi (p)}$也被称为$\varphi$在$p$点的微分(differential).

设$V_p$和$V_{\varphi (p)}$的坐标基矢$\{(\frac{\partial }{\partial x^{\mu }}{)}^a\},\{(\frac{\partial }{\partial y^{\nu }}{)}^a\}$, 我们计算$(\frac{\partial }{\partial x^{\mu }}{)}^a$的推前: 一方面, 因为推前是线性的, 有${\varphi }_{\ast }{\left(\frac{\partial }{\partial x^{\mu }}\right)}^a=A^{\nu }{}_{\mu }{\left(\frac{\partial }{\partial y^{\nu }}\right)}^a$, 其中$A^{\nu }{}_{\mu }$为矩阵. 另一方面, 由推前的定义, ${\varphi }_{\ast }{\left(\frac{\partial }{\partial x^{\mu }}\right)}^a=\frac{\partial }{\partial x^{\mu }}\circ {\varphi }^{\ast }$. 于是 $$\begin{array}{}\text{(}\ast \text{)}& A^{\nu }{}_{\mu }\frac{\partial }{\partial y^{\nu }}=\frac{\partial }{\partial x^{\mu }}\circ {\varphi }^{\ast },\end{array}$$ 令${\varphi }^{\sigma }=y^{\sigma }\circ \varphi$, 即$\varphi$借坐标系的体现. 将$(\ast )$式两边作用于坐标函数$y^{\sigma }$给出 $$A^{\nu }{}_{\mu }\frac{\partial y^{\sigma }}{\partial y^{\nu }}=\frac{\partial (y^{\sigma }\circ \varphi )}{\partial x^{\mu }}\Rightarrow A^{\sigma }{}_{\mu }=\frac{\partial {\varphi }^{\sigma }}{\partial x^{\mu }},$$ 这说明, ${\varphi }_{\ast }$(作为线性映射)的矩阵恰好是$\varphi$(坐标分量式)的Jacobi矩阵. 所以, 推前可以看作是"导数"的推广.

Claim 1 推前和拉回的性质. 下面$\varphi$为微分同胚.

1. 互逆. ${\varphi }^{\ast }\circ {\varphi }_{\ast }={\mathrm{i}\mathrm{d}}_{{\mathcal{F}}_M(k,l)}$且${\varphi }_{\ast }\circ {\varphi }^{\ast }={\mathrm{i}\mathrm{d}}_{{\mathcal{F}}_N(k,l)}$.
2. 和求逆可交换. $({\varphi }^{\ast }{)}^{-1}=({\varphi }^{-1}{)}^{\ast }$.
3. 保持张量积. ${\varphi }^{\ast }(T{T}^{\prime })={\varphi }^{\ast }(T){\varphi }^{\ast }(T^{\prime })$. (推前同理.)
4. 与缩并可交换. ${\varphi }^{\ast }(\mathrm{C}T)=\mathrm{C}{\varphi }^{\ast }(T)$. (推前同理.)
5. 复合映射. $(\psi \circ \varphi {)}^{\ast }={\varphi }^{\ast }\circ {\psi }^{\ast }$, 且$(\psi \circ \varphi {)}_{\ast }={\psi }_{\ast }\circ {\varphi }_{\ast }$.
6. 于对易子. ${\varphi }_{\ast }([v,u])=[{\varphi }_{\ast }v,{\varphi }_{\ast }u]$.

坐标的变换.

一个微分同胚$\varphi :M\to N$不仅给出了点的变换, 还诱导出了:

• 坐标场和的推前和拉回(下图黄). 设$M$上的坐标卡$(O_1,\left\{x^{\mu }\right\})$, 它可以被推前为$(\varphi [O_1],\{x^{\mu }\circ {\varphi }^{-1}\})$.
• 张量场的推前和拉回(下图蓝).

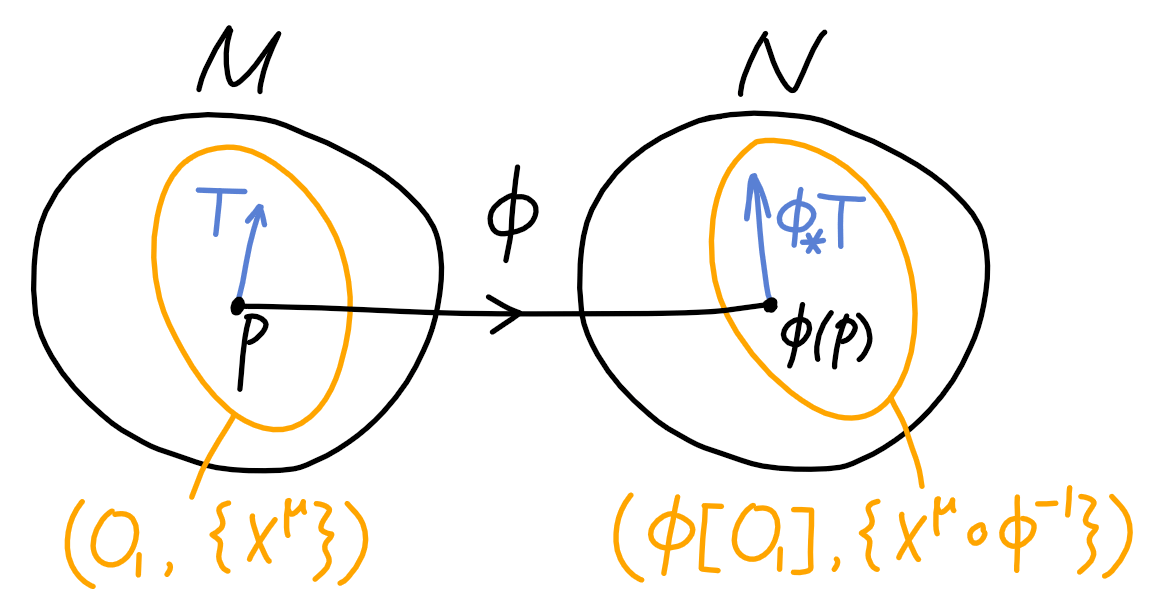
一个自然的问题就是, 以上两者的变换是否是相容的? 即, 张量场的推前${\varphi }_{\ast }T$在$\varphi [O_1]$的坐标分量, 是否等于变换前$T$在$O_1$的坐标分量?

回顾分量的定义, 要求分量就要求基矢, 而基矢是坐标线的切矢, 所以我们先证明以下引理.

Claim 2 曲线像的切矢 $=$ 切矢的推前. (等价地, 曲线原像的切矢 $=$ 像的切矢的拉回.)

Pf 对曲线$c$和微分同胚$\varphi$, 设$T$为$c(t)$在$t_0\in I$处的切矢, $T^{\prime }$为$\varphi (c(t))$在$t_0$处的切矢, 则 $$({\varphi }_{\ast }T)(f)=T({\varphi }^{\ast }f)=T(f\circ \varphi )=\frac{\mathrm{d}}{\mathrm{d}t}((f\circ \varphi )\circ c)=\frac{\mathrm{d}}{\mathrm{d}t}(f\circ (\varphi \circ c)).$$ (多次使用切矢, 推前, 拉回的定义.) 上式左边为切矢的像, 右边为像的切矢.

• 自然地有推论: $M$的坐标系推前的坐标基底 $=$ 坐标基底的推前, 即 $$\frac{\partial }{\partial x^{\prime \mu }}={\varphi }_{\ast }\frac{\partial }{\partial x^{\mu }},{\mathrm{d}x}^{\prime \mu }={\varphi }_{\ast }{\mathrm{d}x}^{\mu },$$ 其中$x^{\prime \mu }={\varphi }_{\ast }{x}^{\mu }$. (等价地, $N$中坐标系拉回的坐标基底 $=$ 坐标基底的拉回.)

Claim 3 设微分同胚$\varphi :M\to N$, $M$上坐标卡$(O_1,\left\{x^{\mu }\right\})$被推前为$(\varphi [O_1],\{x^{\mu }\circ {\varphi }^{-1}\})$, $T$是$M$上的张量场, 则 $$T^{{\mu }_1\dots {\mu }_k}{}_{{\nu }_1\dots {\nu }_l}{|}_p=({\varphi }_{\ast }T{)}^{\prime {\mu }_1\dots {\mu }_k}{}_{{\nu }_1\dots {\nu }_l}{|}_{\varphi (p)},$$ 其中左边是$T$在$O_1$上的坐标分量, 右边是${\varphi }_{\ast }T$在$\varphi [O_1]$上的坐标分量.

Pf 根据坐标分量的定义, $$\begin{array}{rl}({\varphi }_{\ast }T{)}^{\prime {\mu }_1\dots {\mu }_k}{}_{{\nu }_1\dots {\nu }_l}{|}_{\varphi (p)}& =({\varphi }_{\ast }T){|}_{\varphi (p)}(\frac{\partial }{\partial x^{\prime {\mu }_1}},\dots ,\frac{\partial }{\partial x^{\prime {\mu }_k}};\mathrm{d}{x}^{\prime {\nu }_1},\dots ,\mathrm{d}{x}^{\prime {\nu }_l})\\ & =T{|}_p({\varphi }^{\ast }\frac{\partial }{\partial x^{\prime {\mu }_1}},\dots ,{\varphi }^{\ast }\frac{\partial }{\partial x^{\prime {\mu }_k}};{\varphi }^{\ast }\mathrm{d}{x}^{\prime {\nu }_1},\dots ,{\varphi }^{\ast }\mathrm{d}{x}^{\prime {\nu }_l})\\ & =T{|}_p(\frac{\partial }{\partial x^{{\mu }_1}},\dots ,\frac{\partial }{\partial x^{{\mu }_k}};\mathrm{d}{x}^{{\nu }_1},\dots ,\mathrm{d}{x}^{{\nu }_l})\\ & =T^{{\mu }_1\dots {\mu }_k}{}_{{\nu }_1\dots {\nu }_l}{|}_p,\end{array}$$ 第三步利用了坐标基矢的变换关系.

微分同胚的两种观点.

看待微分同胚$\varphi :M\to N$向来有两种观点,

• 主动观点(active viewpoint)认为, $\varphi$表示点的变换($p\mapsto \varphi (p)$)以及张量的变换($T\mapsto {\varphi }_{\ast }T$).

• 被动观点(passive viewpoint)认为, $p$点及上所有张量都没变, $\varphi :M\to N$的结果只是坐标系发生变化:

  取$M$上的$(O_1,\left\{x^{\mu }\right\})$和$N$上的$(O_2,\left\{y^{\mu }\right\})$, 后者拉回为$({\varphi }^{-1}[O_2],\left\{x^{\prime \mu }\right\})$, 因此$M$的坐标系从$\left\{x^{\mu }\right\}$变为$\left\{x^{\prime \mu }\right\}$.

实际上, 两种观点是等价的. 在Claim 3中, 设$N$上的坐标系$O_2$, 取系$O_1$为${\varphi }^{-1}[O_2]$, 于是$\varphi [O_1]=O_2$, 因此有 $$T^{\prime {\mu }_1\dots {\mu }_k}{}_{{\nu }_1\dots {\nu }_l}{|}_p=({\varphi }_{\ast }T{)}^{{\mu }_1\dots {\mu }_k}{}_{{\nu }_1\dots {\nu }_l}{|}_{\varphi (p)}.$$ 左边是老点$p$的老张量$T$在新系${\varphi }^{-1}[O_2]$下的分量, 右边是新点$\varphi (p)$的新张量${\varphi }_{\ast }T$在老系$O_2$下的分量.

4.2 Lie derivatives

2023.8.2

有了推前和拉回, 就可以在流形上搬运张量, 进而引出导数的概念. 在第二章我们已经知道, $M$上的一个光滑矢量场$v^a$会给出一个单参数微分同胚群 $$\varphi =\{{\varphi }_t:{\varphi }_t(p)\mathsf{\text{表示}}p\mathsf{\text{点沿着}}p\mathsf{\text{处的积分曲线走}}t\mathsf{\text{单位}}\},$$ 群元${\varphi }_t$的拉回为${\varphi }_t^{\ast }$. 给定光滑张量场$T$, 则${\varphi }_t^{\ast }T$也是同型光滑张量场, 这两个场在$p$点的差值为${\varphi }_t^{\ast }T{|}_p-T{|}_p$, 这可以看作张量场$T$的(沿着$v$的)变化量, $({\varphi }_t^{\ast }T{|}_p-T{|}_p)/t$的极限则可以看作$T$在$p$点的某种导数. 于是我们定义 $${\mathcal{L}}_{v}T:=\underset{t\to 0}{lim}\frac{{\varphi }_t^{\ast }T-T}{t}$$ 为张量场$T$沿着矢量场$v$的李导数(Lie derivative), 是一个与$T$同型的张量场. ${\mathcal{L}}_v$是线性的, 而且与缩并可交换.

Claim 1 ${\mathcal{L}}_{v}f=v(f)$, 对于$f\in {\mathcal{F}}_M$.

Pf 任取$p\in M$, 设$c(t)$为矢量场$v^a$从$p$出发的积分曲线, 于是有$c(0)=p$, $c(t)={\varphi }_t(p)$, 所以 $$\begin{array}{r}{\mathcal{L}}_{v}f{|}_p=\underset{t=0}{lim}\frac{{\varphi }_t^{\ast }f{|}_p-f{|}_p}{t}=\underset{t=0}{lim}\frac{f\circ {\varphi }_t{|}_p-f{|}_p}{t}=\underset{t=0}{lim}\frac{f(c(t))-f(c(0))}{t}=\frac{\mathrm{d}(f\circ c)}{\mathrm{d}t}{|}_p\end{array}$$ 根据曲线切矢的定义, 右边就是$T(f){|}_p$, 也就是$v(f){|}_p$.

下面介绍一种对计算李导数很有用的坐标系, 称为矢量场$v^a$的适配坐标系(adapted coordinate system). 选定$v^a$的积分曲线作为$x^1$的坐标曲线(以$t$充当$x^1$), 再选定另一组与这组曲线相截(交点上切矢不平行)的曲线作为$x^2$的坐标曲线, 以此类推. 可以看出$v^a=(\frac{\partial }{\partial t}{)}^a=(\frac{\partial }{\partial x^1}{)}^a$.

Claim 2 张量场$T$沿$v$的李导数在$v$适配的坐标系下的分量 $$({\mathcal{L}}_{v}T{)}^{{\mu }_1\dots {\mu }_k}{}_{{\nu }_1\dots {\nu }_l}=\frac{\partial T^{{\mu }_1\dots {\mu }_k}{}_{{\nu }_1\dots {\nu }_l}}{\partial x^1}.$$

• 需要注意的是, 上面的等式只在适配的坐标系下成立, 不服从张量变换律, 故不能写成张量等式.

Pf 取适配坐标系包含$p,q={\varphi }_t(p)$两点, 另注意到${\varphi }_t^{\ast }=({\varphi }_t^{-1}{)}_{\ast }={\varphi }_{-t\ast }$, 有 $$\begin{array}{}\text{(a)}& ({\mathcal{L}}_{v}T{)}^{{\mu }_1\dots {\mu }_k}{}_{{\nu }_1\dots {\nu }_l}{|}_p& =\underset{t\to 0}{lim}\frac{({\varphi }_{-t\ast }T{)}^{{\mu }_1\dots {\mu }_k}{}_{{\nu }_1\dots {\nu }_l}{|}_p-T^{{\mu }_1\dots {\mu }_k}{}_{{\nu }_1\dots {\nu }_l}{|}_p}{t}.\end{array}$$ 计算第一项, 由上一节"主被动观点的等价性"(同胚映射为${\varphi }_{-t}$)有 $$\begin{array}{rl}({\varphi }_{-t\ast }T{)}^{{\mu }_1\dots {\mu }_k}{}_{{\nu }_1\dots {\nu }_l}{|}_p& =T^{\prime {\mu }_1\dots {\mu }_k}{}_{{\nu }_1\dots {\nu }_l}{|}_q\\ \text{(b)}& & =(\frac{\partial x^{\prime {\mu }_1}}{\partial x^{{\rho }_1}}\dots \frac{\partial x^{\prime {\mu }_k}}{\partial x^{{\rho }_k}}\frac{\partial x^{{\sigma }_1}}{\partial x^{\prime {\nu }_1}}\dots \frac{\partial x^{{\sigma }_l}}{\partial x^{\prime {\nu }_l}})T^{{\rho }_1\dots {\rho }_k}{}_{{\sigma }_1\dots {\sigma }_l}{|}_q.\end{array}$$ (第二步用了张量的坐标变换律) 现在要搞清楚$x$和$x^{\prime }$的变换关系, 其中$x$是$q$点老适配坐标系, $x^{\prime }$是$p$点适配坐标系推前到$q$点. 在$p,q$的邻域中任取点$\overline{q},\overline{p}={\varphi }_{-t}(\overline{q})$, 根据适配坐标系的定义有$x^1(\overline{q})=x^1(\overline{p})+t$, $x^{\tau }(\overline{q})=x^{\tau }(\overline{p})$($\tau =2,\dots ,n$). 而按照定义, ${\varphi }_{-t}$在$\overline{q}$诱导的新坐标为$x^{\prime 1}(\overline{q})=x^1(\overline{p})$, $x^{\prime \tau }(\overline{q})=x^{\tau }(\overline{p})$, 因此$x^{\prime 1}(\overline{q})=x^1(\overline{q})-t$, $x^{\prime \tau }(\overline{q})=x^{\tau }(\overline{q})$, 根据$\overline{p}$的任意性有 $$x^{\prime 1}=x^1-t,x^{\prime \tau }=x^{\tau },$$ 求导得${\displaystyle \frac{\partial x^{\prime \mu }}{\partial x^{\rho }}={\delta }^{\mu }{}_{\rho },\frac{\partial x^{\sigma }}{\partial x^{\prime \nu }}={\delta }^{\sigma }{}_{\nu }}$, 代入$(\mathrm{b})$式得到 $$\begin{array}{rl}({\varphi }_{-t\ast }T{)}^{{\mu }_1\dots {\mu }_k}{}_{{\nu }_1\dots {\nu }_l}{|}_p& =({\delta }^{{\mu }_1}{}_{{\rho }_1}\dots {\delta }^{{\mu }_k}{}_{{\rho }_k}{\delta }^{{\sigma }_1}{}_{{\nu }_1}\dots {\delta }^{{\sigma }_l}{}_{{\nu }_l})T^{{\rho }_1\dots {\rho }_k}{}_{{\sigma }_1\dots {\sigma }_l}{|}_q\\ & =T^{{\mu }_1\dots {\mu }_k}{}_{{\nu }_1\dots {\nu }_l}{|}_q,\end{array}$$ 将其代回$(\mathrm{a})$式, 再由$t=x^1$即证. $$\begin{array}{r}({\mathcal{L}}_{v}T{)}^{{\mu }_1\dots {\mu }_k}{}_{{\nu }_1\dots {\nu }_l}{|}_p=\underset{t\to 0}{lim}\frac{T^{{\mu }_1\dots {\mu }_k}{}_{{\nu }_1\dots {\nu }_l}{|}_q-T^{{\mu }_1\dots {\mu }_k}{}_{{\nu }_1\dots {\nu }_l}{|}_p}{t}=\frac{\partial T^{{\mu }_1\dots {\mu }_k}{}_{{\nu }_1\dots {\nu }_l}}{\partial x^1}{|}_p.\end{array}$$

• 推论: ${\mathcal{L}}_v$满足Leibniz律, ${\mathcal{L}}_v(ST)=({\mathcal{L}}_{v}S)T+S({\mathcal{L}}_{v}T)$.

Claim 3 与导数算符的关系. (以下${\mathrm{\nabla }}_a$为任意无挠导数算符.)

1. (矢量场) ${\mathcal{L}}_v{u}^a=[v,u{]}^a$($=v^b{\mathrm{\nabla }}_b{u}^a-u^b{\mathrm{\nabla }}_b{v}^a$).

2. (对偶矢量场) ${\mathcal{L}}_v{\omega }_a=v^b{\mathrm{\nabla }}_b{\omega }_a+{\omega }_b{\mathrm{\nabla }}_a{v}^b$.

3. (任意张量场) $$\begin{array}{rl}({\mathcal{L}}_{v}T{)}^{a_1\dots a_k}{}_{b_1\dots b_l}=v^c{\mathrm{\nabla }}_c{T}^{a_1\dots a_k}{}_{b_1\dots b_l}& -\sum _{i=1}^k{T}^{a_1\dots c\dots a_k}{}_{b_1\dots b_l}{\mathrm{\nabla }}_c{v}^{a_i}\\ & +\sum _{j=1}^l{T}^{a_1\dots a_k}{}_{b_1\dots c\dots b_l}{\mathrm{\nabla }}_{b_j}{v}^c.\end{array}$$

Pf 第1个. 只需证明两个张量在某坐标系下分量相等. 取$v^a$的适配坐标系以及普通导数算符, $$\begin{array}{rl}[v,u{]}^{\mu }& =({\mathrm{d}x}^{\mu }{)}_a[v,u{]}^a\\ & =({\mathrm{d}x}^{\mu }{)}_a(v^b{\partial }_b{u}^a-u^b{\partial }_b{v}^a)\\ & =({\mathrm{d}x}^{\mu }{)}_a(v^b{\partial }_b{u}^a)=v^b{\partial }_b{u}^{\mu }=v(u^{\mu })=\frac{\partial u^{\mu }}{\partial x^1}=({\mathcal{L}}_{v}u{)}^{\mu },\end{array}$$ 其中第三步是因为${\partial }_b{v}^a={\partial }_b(\frac{\partial }{\partial x^1}{)}^a=0$, 第五步用到了导数算符的定义.

Claim 4 设矢量场$v,u$, 则$[{\mathcal{L}}_v,{\mathcal{L}}_u]={\mathcal{L}}_{[v,u]}$作用于任意张量场都成立, 其中$[{\mathcal{L}}_v,{\mathcal{L}}_u]:={\mathcal{L}}_v{\mathcal{L}}_u-{\mathcal{L}}_u{\mathcal{L}}_v$.

4.3 Killing fields

2023.8.3

现在为流形$M$附加一个度规场$g_{ab}$. 在所有的微分同胚$\varphi :M\to M$中, 我们称那些保持度规的同胚为等度规映射, 简称等度规(isometry), 即满足${\varphi }^{\ast }{g}_{ab}=g_{ab}$的$\varphi$.

• 两边作用于矢量就是$({\varphi }^{\ast }g{)}_{ab}{v}^a{v}^b=g_{ab}{v}^a{v}^b$, 即$g_{ab}({\varphi }_{\ast }v{)}^a({\varphi }_{\ast }v{)}^b=g_{ab}{v}^a{v}^b$.
• $\varphi$等度规 $⟺{\varphi }^{-1}$等度规.

称矢量场${\xi }^a$为Killing矢量场, 如果它给出的单参微分同胚群是等度规群. 可知, ${\xi }^a$为Killing场当且仅当${\mathcal{L}}_{\xi }{g}_{ab}=0$. 根据上一节Claim 2, 如果${\displaystyle \frac{\partial g_{\mu \nu }}{\partial x^1}=0}$, 则${\displaystyle {\left(\frac{\partial }{\partial x^1}\right)}^a}$是坐标域上的Killing场.

Claim 1 ${\xi }^a$为Killing场的充要条件是满足下面的Killing方程, (其中${\mathrm{\nabla }}_c{g}_{ab}=0$) $${\mathrm{\nabla }}_a{\xi }_b+{\mathrm{\nabla }}_b{\xi }_a=0,\mathsf{\text{或}}{\mathrm{\nabla }}_{(a}{\xi }_{b)}=0,\mathsf{\text{或}}{\mathrm{\nabla }}_a{\xi }_b={\mathrm{\nabla }}_{[a}{\xi }_{b]},$$ Claim 2 设Killing场${\xi }^a$, 测地线切矢$T^a$, 则两者内积沿测地线不变, 即$T^a{\mathrm{\nabla }}_a(T^b{\xi }_b)=0$. (其中${\mathrm{\nabla }}_c{g}_{ab}=0$.)

Pf $T^a{\mathrm{\nabla }}_a(T^b{\xi }_b)=T^a{\xi }_b{\mathrm{\nabla }}_a{T}^b+T^a{T}^b{\mathrm{\nabla }}_a{\xi }_b={\xi }_b(T^a{\mathrm{\nabla }}_a{T}^b)+T^{(a}{T}^{b)}{\mathrm{\nabla }}_{[a}{\xi }_{b]}=0$.

Claim 3 (与曲率的关系) 设$(M,g_{ab})$的Killing场${\xi }^a$, 黎曼张量$R_{abc}{}^d$, 里奇张量$R_{ac}$, 则

1. ${\mathrm{\nabla }}_a{\mathrm{\nabla }}_b{\xi }_c=-R_{bca}{}^d{\xi }_d$.
2. ${\mathrm{\nabla }}^a{\mathrm{\nabla }}_a{\xi }_c=-R_{cd}{\xi }^d$.

Claim 4 设${\xi }^a,{\eta }^a$为$(M,g_{ab})$的两个Killing场, 则

1. 线性组合$\alpha {\xi }^a+\beta {\eta }^a$, 对易子$[\xi ,\eta {]}^a$也都是Killing场.
2. 推前${\varphi }_{\ast }{\xi }^a$也是Killing场, 其中$\varphi :M\to M$等度规.

Pf 第1条, $\alpha {\xi }^a+\beta {\eta }^a$的Killing性由Killing方程的线性性即得; 而利用上一节Claim 4容易得到 $${\mathcal{L}}_{[\xi ,\eta ]}{g}_{ab}=[{\mathcal{L}}_{\xi },{\mathcal{L}}_{\eta }]g_{ab}={\mathcal{L}}_{\xi }({\mathcal{L}}_{\eta }{g}_{ab})-{\mathcal{L}}_{\eta }({\mathcal{L}}_{\xi }{g}_{ab})={\mathcal{L}}_{\xi }(0)-{\mathcal{L}}_{\eta }(0)=0$$ 第2条, 设${\xi }^a$给出同胚${\psi }_t$, 先证明${\varphi }_{\ast }{\xi }^a$给出同胚$\varphi \circ {\psi }_t$, 再证明$g_{ab}$沿${\varphi }_{\ast }{\xi }^a$的李导数为零即可.

由第1条可见, 所有的Killing矢量场构成一个线性空间$\mathcal{K}$. 实际上, 作为线性空间, $\dim \mathcal{K}\le {\displaystyle \frac{n(n+1)}{2}}$. 一个Killing场等同于一类等度规变换, 也就是$(M,g_{ab})$上的一类对称性, 我们称$\dim \mathcal{K}=n(n+1)/2$的广义黎曼空间为最高对称空间.

Example 1

欧氏空间$({\mathbb{R}}^2,{\delta }_{ab})$. 坐标系$\{x,y\}$下, ${\mathrm{d}s}^2={\mathrm{d}x}^2+{\mathrm{d}y}^2$, 度规分量全部为常数, 有$\frac{\partial g_{\mu \nu }}{\partial x}=\frac{\partial g_{\mu \nu }}{\partial y}=0$, 对应两个独立的Killing场$(\frac{\partial }{\partial x}{)}^a$, $(\frac{\partial }{\partial y}{)}^a$, 它们表示平移对称性, 积分曲线是$x$和$y$坐标曲线. 为了找到第三个, 我们采用极坐标$\{r,\phi \}$, 有${\mathrm{d}s}^2={\mathrm{d}r}^2+r^2{\mathrm{d}\phi }^2$, 度规分量与$\phi$无关, 于是$(\frac{\partial }{\partial \phi }{)}^a=-y(\frac{\partial }{\partial x}{)}^a+x(\frac{\partial }{\partial y}{)}^a$也是Killing场, 它表示旋转对称性, 积分曲线是以原点为圆心的圆.

二维欧氏空间有3个独立Killing场, 是最高对称空间. 相似地, 三维欧氏空间有6个独立Killing场, 包括3个平移和3个旋转.

闵氏空间$({\mathbb{R}}^2,{\eta }_{ab})$. 坐标系$\{t,x\}$下, ${\mathrm{d}s}^2=-{\mathrm{d}t}^2+{\mathrm{d}x}^2$, 同样有两个平移场$(\frac{\partial }{\partial x}{)}^a$, $(\frac{\partial }{\partial y}{)}^a$. 现在采用新坐标$\{\psi ,\eta \}$: $$x=\psi \cosh \eta ,y=\psi \sinh \eta ,\psi \in (0,+\mathrm{\infty }),\eta \in (-\mathrm{\infty },+\mathrm{\infty }),$$ 线元${\mathrm{d}s}^2={\mathrm{d}\psi }^2-{\psi }^2{\mathrm{d}\eta }^2$, 可看出$(\frac{\partial }{\partial \eta }{)}^a$是第三个Killing场, 它表示伪转动(boost), 积分曲线是双曲线.

四维闵氏时空有10个独立的Killing场, 分为4个平移, 3个转动和3个伪转动.

Example 2 考虑二维球面$S^2$, 坐标$\{\theta ,\varphi \}$下${\mathrm{d}s}^2=R^2\mathrm{d}{\theta }^2+R^2{\sin }^2\theta \mathrm{d}{\varphi }^2$. 现在我们尝试通过解方程求出Killing场${\xi }^a$. 我们已经计算过克氏符的分量, 现在直接把公式${\mathrm{\nabla }}_a{\xi }_b={\partial }_a{\xi }_b-{\mathrm{\Gamma }}^c{}_{ab}{\xi }_c$代入Killing方程, 得到 $${\partial }_{(a}{\xi }_{b)}-{\mathrm{\Gamma }}^c{}_{(ab)}{\xi }_c=0,\mathsf{\text{即}}{\partial }_{(\mu }{\xi }_{\nu )}-{\mathrm{\Gamma }}^{\sigma }{}_{(\mu \nu )}{\xi }_{\sigma }=0,(\mu ,\nu =\theta ,\varphi )$$ 其中Killing场的分量${\xi }_{\theta }(\theta ,\varphi ),{\xi }_{\varphi }(\theta ,\varphi )$都是关于坐标的函数. 将右边的方程写开, 得到 $$\{\begin{array}{rl}& {\partial }_{\theta }{\xi }_{\theta }=0,\\ & {\partial }_{\varphi }{\xi }_{\varphi }+\sin \theta \cos \theta {\xi }_{\theta }=0,\\ & {\partial }_{\varphi }{\xi }_{\theta }+{\partial }_{\theta }{\xi }_{\varphi }-2\cot \theta {\xi }_{\varphi }=0,\end{array}$$

解得$\{\begin{array}{l}{\xi }_{\theta }=A\sin \varphi +B\cos \varphi \\ {\xi }_{\varphi }=A\sin \theta \cos \theta \cos \varphi -B\sin \theta \cos \theta \sin \varphi +C{\sin }^2\theta \end{array}$, 其中$A,B,C$为常数, 用度规升指标得到$\{\begin{array}{l}{\xi }^{\theta }=A\sin \varphi +B\cos \varphi \\ {\xi }^{\varphi }=A\cos \varphi \cot \theta -B\sin \varphi \cot \theta +C\end{array}$, 分别令$A,B,C$为$1$(其余为$0$), 可以得到三个独立的Killing场: $$\begin{array}{rl}{\xi }_1^a& =\sin \varphi {\left(\frac{\partial }{\partial \theta }\right)}^a+\cos \varphi \cot \theta {\left(\frac{\partial }{\partial \varphi }\right)}^a,\\ {\xi }_2^a& =\cos \varphi {\left(\frac{\partial }{\partial \theta }\right)}^a-\sin \varphi \cot \theta {\left(\frac{\partial }{\partial \varphi }\right)}^a,\\ {\xi }_3^a& ={\left(\frac{\partial }{\partial \varphi }\right)}^a.\end{array}$$ 可见二维球面是最高对称空间. 将${\xi }_1,{\xi }_2,{\xi }_3$画出来(如下图), 可以看出它们分别表示绕$x,y,z$轴的旋转.

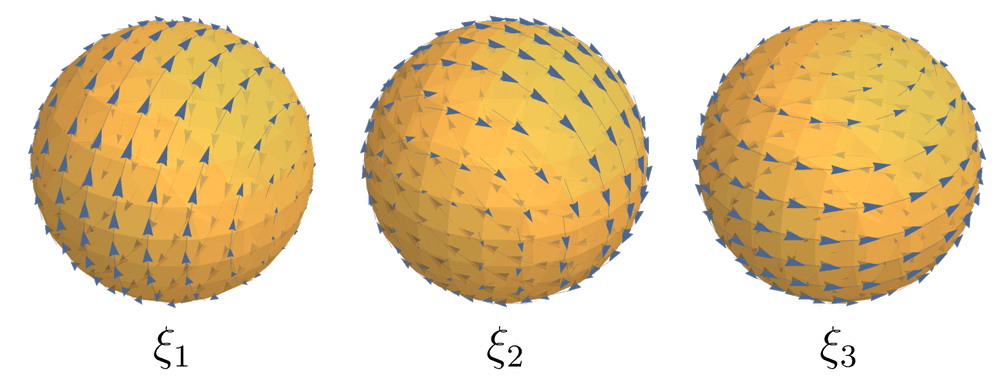
4.4 Hypersurfaces

2023.8.3

嵌入子流形, 超曲面, 法矢和法余矢.

设$M,S$为流形, $\dim S\le \dim M=n$, 映射$\varphi :S\to M$称为嵌入(embedding), 若$\varphi$是光滑的单射, 且对任意一点$p\in S$, 推前${\varphi }_{\ast }:V_p\to V_{\varphi (p)}$是非退化的(单射). $S$的拓扑和微分结构可以自然地带到$\varphi [S]$上去, 使得$\varphi :S\to \varphi [S]$成为微分同胚.

称$\varphi :S\to M$为$M$的一个嵌入子流形(embedded submanifold), 有时也称$\varphi [S]$为嵌入子流形. 若$\dim S=n-1$, 则称$\varphi [S]$为$M$的一张超曲面(hypersurface).

• 设$S^2$为${\mathbb{R}}^3$中的单位球面, 则恒等映射$\varphi :S^2\to {\mathbb{R}}^3$给出一个嵌入子流形, 而且是超曲面.
• 嵌入子流形$\varphi [S]$有两个拓扑, 一个是$\varphi$带来的, 一个是$M$的拓扑在$\varphi [S]$上诱导的, 两者不一定相同. 如果进一步要求这两个拓扑相同($\varphi$同胚), 则这样的$\varphi :S\to M$成为正则嵌入(regular embedding).
• $M$上的某些光滑函数$f$可以确定一个超曲面, 其由满足$f{|}_p=0$的点组成. 例如, 三维欧氏空间中的$f=ax+by+cz$给出一个二维平面.
  • 方程$f=0$给出一个超曲面当且仅当$\mathrm{d}f{|}_{f=0}\ne 0$恒成立.

设嵌入$\varphi :S\to M$, $p\in S$. $q=\varphi (p)$作为$M$的一点, 有切空间$V_p$, 而$\varphi [S]$在$q$处也有切空间$W_q$($W_q$是$V_q$的线性子空间, 对于$V_q$中的向量$w^a$: $w^a\in W_q$当且仅当$w^a$是$\varphi [S]$的某条曲线的切矢).

非零对偶矢量$n_a\in V_q^{\ast }$称为$\varphi [S]$在$q$点的法余矢(normal covector)为, 如果$n_a{w}^a=0,\mathrm{\forall }{w}^a\in W_q$. 如果$M$上度规$g_{ab}$, 则可以将法余矢升指标为法矢(normal vector), 即$n^a=g^{ab}{n}_b\in V_q$. 法矢与$W_q$中的所有矢量正交.

• 回顾线性代数, 法余矢和法矢分别可以看作$W_q$的零化子$W_q^0$和正交补空间$W_q^{\perp }$的(非零)元素.

Claim 1 对于超曲面$\varphi [S]$, 其上任意一点$q$都有法余矢, 且两个法余矢之间相差非零实数.

Claim 2 设$\varphi [S]$是光滑函数$f=0$给出的超曲面, 则${\mathrm{\nabla }}_{a}f{|}_q$($q\in \varphi [S]$)是该曲面的法余矢.

Pf 任取$q\in \varphi [S]$和$w^a\in W_q$, 因为$w^a$一定是超曲面上某条曲线$c(t)$的切矢, 而$c(t)$上的点总有$f=0$为常数, 所以$w^a{\mathrm{\nabla }}_{a}f=w(f)=\frac{\partial f}{\partial t}=0$.

Claim 3 设$n_a$为超曲面$\varphi [S]$的法余矢, 则$n^a\in W_q$的充要条件为$n^a{n}_a=0$.

Pf ($\Rightarrow$) 因为$n_a$为法余矢, 且$n^a\in W_q$, 所以$n^a{n}_a=0$.

($\Leftarrow$) 取$V_q$的基底$\{(e_{\mu }{)}^a\}$使得$(e_2{)}^a,\dots ,(e_n{)}^a\in W_q$, 且$(e_1{)}_a=n_a$, 因此$n^a$在该基底的第一分量$n^1=n^a(e_1{)}_a=n^a{n}_a=0$, 所以$n^a$可以被$\{(e_2{)}^a,\dots ,(e_n{)}^a\}$表出, $n^a\in W_q$.

Example 1 考虑二维闵氏空间$({\mathbb{R}}^2,{\eta }_{ab})$的超曲面的法矢, 分以下三种情况:

超曲面是$x$坐标线, 切矢$(e_2{)}^a=(\frac{\partial }{\partial x}{)}^a$, 设$(e_1{)}^a=\alpha (\frac{\partial }{\partial t}{)}^a+\beta (\frac{\partial }{\partial x}{)}^a$($\alpha \ne 0$), 因为$(e^1{)}_a(e_1{)}^a=1$且$(e^1{)}_a(e_2{)}^a=0$, 解得$(e^1{)}_a={\alpha }^{-1}(\mathrm{d}t{)}_a$, 可知$(e^1{)}_a$为法余矢, 升指标得到法矢$n^a=-{\alpha }^{-1}(\frac{\partial }{\partial t}{)}^a$.

超曲面是$t$坐标线, 同上. 法矢平行于$x$轴.

超曲面是${45}^{\circ }$斜直线, 切矢$(e_2{)}^a=(\frac{\partial }{\partial t}{)}^a+(\frac{\partial }{\partial x}{)}^a$, 设$(e_1{)}^a=\alpha (\frac{\partial }{\partial x}{)}^a+\beta (\frac{\partial }{\partial t}{)}^a$($\alpha \ne \beta$), 可以解得$(e^1{)}_a=(\alpha -\beta {)}^{-1}((\mathrm{d}t{)}_a-(\mathrm{d}x{)}_a)$, 升指标得到法矢$n^a=(\beta -\alpha {)}^{-1}((\frac{\partial }{\partial t}{)}^a+(\frac{\partial }{\partial x}{)}^a)$, 可以发现法矢与切矢$(e_2{)}^a$平行! 这就是$n^a\in W_q$的例子, 类光测地线切矢长度为零.

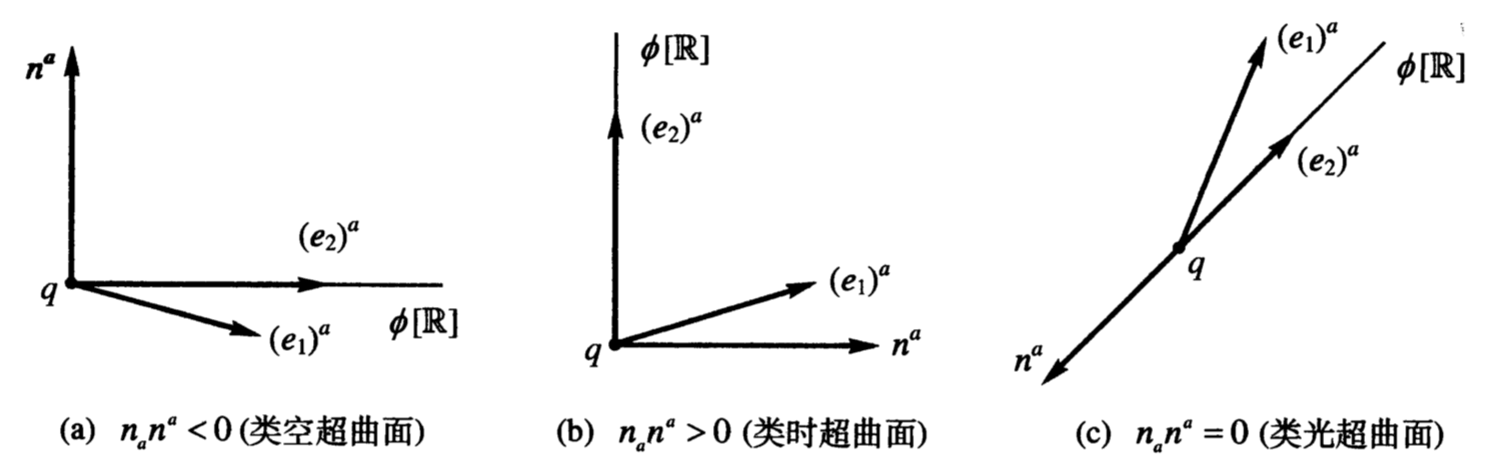
称超曲面类空, 若其法矢处处类时; 超曲面类时, 若其法矢处处类空; 超曲面类光, 若其法矢处处类光. 若$n^a{n}_a\ne 0$, 则今后谈的都是归一化法矢, 即$g_{ab}{n}^a{n}^b\equiv n^a{n}_a=\pm 1$.

诱导度规.

设$\varphi [S]$为嵌入子流形, 在$V_q$上有度规$g_{ab}$, 现在在$W_q$上找一个度规$h_{ab}$, 如果满足 $$g_{ab}{w}_1^a{w}_2^b=h_{ab}{w}_1^a{w}_2^b,(\mathrm{\forall }{w}_1^a,w_2^a\in W_q)$$ 则称$h_{ab}$为$g_{ab}$生出的诱导度规(induced metric). 诱导度规本质上就是把$V_q$的度规限制在$W_q$上的结果.

• 一个类光超曲面不存在诱导度规. 如果取法矢$n^a\in W_q$, 则$h_{ab}{n}^a{w}^b=g_{ab}{n}^a{w}^b=n_b{w}^b=0$对于$w^b\in W_q$恒成立, 于是$h_{ab}$是退化的, 不构成度规.

当$\varphi [S]$为类时或类空超曲面(或正定度规下的超曲面)时, 诱导度规可以用归一化法矢($n^a{n}_a=\pm 1$)表示为 $$h_{ab}:=g_{ab}-(n^c{n}_c)n_a{n}_b,$$ 可以验证它确实是诱导度规. 用度规$g$对其升指标得到 $$h^a{}_b=g^{ad}{h}_{db}={\delta }^a{}_b-(n^c{n}_c)n^a{n}_b.$$ 这是一个$(1,1)$型张量, 代表$V_q$上的一个线性变换, 将其作用与$v^b\in V_q$得到 $$h^a{}_b{v}^b=v^a-(n^c{n}_c)n^a(n_b{v}^b),\mathsf{\text{或}}{v}^a=h^a{}_b{v}^b+(n^c{n}_c)(n_b{v}^b)n^a,$$ 其中$(n^c{n}_c)$和$(n^b{v}_b)$都是实数, 所以右边这个式子将$v^a$写作了法向部分$(n^c{n}_c)(n_b{v}^b)n^a$和切向部分$h^a{}_b{v}^b$(因为$n_a(h^a{}_b{v}^b)=(n_b-(n^c{n}_c)(n_a{n}^a)n_b)v^b=0$, 所以$h^a{}_b{v}^b\in V_q$)的和. 称$h^a{}_b$为$V_q$到$W_q$的投影映射(projection map).

• 容易验证, $h^a{}_b$在$W_q$上是恒等算子, 从而$h^a{}_b$是满射; 而且$h^a{}_b{h}^b{}_c=h^a{}_c$, 即$h$幂等.

Example 2 考虑嵌入于$({\mathbb{R}}^3,{\delta }_{ab})$的$S^2$.

取${\mathbb{R}}^3$的球坐标$\{r,\theta ,\varphi \}$, 则度规场分量$g_{\mu \nu }=\mathrm{diag}(1,r^2,r^2{\sin }^2\theta )$. 设球面上一点$q$, 则$W_q$的基底$\{(\frac{\partial }{\partial \theta }{)}^a,(\frac{\partial }{\partial \varphi }{)}^a\}$, 由定义可以求得单位法余矢$n_a=(\mathrm{d}r{)}_a$, 升指标得到$n^a=(\frac{\partial }{\partial r}{)}^a$, 可得$n^a{n}_a=1$, 诱导度规场$h_{ab}=g_{ab}-n_a{n}_b$, 其分量 $$h_{\mu \nu }=\left(\begin{array}{}0\\ & r^2\\ & & r^2{\sin }^2\theta \end{array}\right),$$ 进而可以求得投影映射场$h^a{}_b$的分量为$h^{\mu }{}_{\nu }=\mathrm{diag}(0,1,1)$.

现在我们取笛卡尔坐标$\{x,y,z\}$, 此时可用Claim 2求法余矢: 将$S^2$看作$f=x^2+y^2+z^2-R^2=0$给出的超曲面, 计算 $${\mathrm{\nabla }}_{a}f=(\mathrm{d}f{)}_a=2x(\mathrm{d}x{)}_a+2y(\mathrm{d}y{)}_a+2z(\mathrm{d}z{)}_a$$ 可以得到归一化的法矢和法余矢(场) $$\begin{array}{rl}{n}^a& =\frac{1}{R}[x{\left(\frac{\partial }{\partial x}\right)}^a+y{\left(\frac{\partial }{\partial y}\right)}^a+z{\left(\frac{\partial }{\partial z}\right)}^a],\\ n_a& =\frac{1}{R}[x(\mathrm{d}x{)}_a+y(\mathrm{d}y{)}_a+z(\mathrm{d}z{)}_a],\end{array}$$ 其中$R=\sqrt{x^2+y^2+z^2}$. 现在可以计算诱导度规场的分量 $$h_{\mu \nu }={\delta }_{\mu \nu }-n_{\mu }{n}_{\nu }=\left(\begin{array}{}1-\frac{x^2}{R^2}& -\frac{xy}{R^2}& -\frac{xz}{R^2}\\ -\frac{xy}{R^2}& 1-\frac{y^2}{R^2}& -\frac{yz}{R^2}\\ -\frac{xz}{R^2}& -\frac{yz}{R^2}& 1-\frac{z^2}{R^2}\end{array}\right),$$ 投影映射场的分量同上.