梁GR | 1 流形与张量场

梁灿彬, 周彬《微分几何入门与广义相对论》第一章, 第二章的笔记.

1 Topology Baiscs

1.1 Topological spaces

给集合赋予一种结构(开集):

拓扑(topology)(选择集合的开子集): 有集合\(X\), \(\mathcal{T}\)中装有选定的开集(open set), 满足:

1. \(X,\varnothing\in\mathcal{T}\).
2. \(\mathcal{T}\)中任意有限个元素的交集仍在\(\mathcal{T}\)中.
3. \(\mathcal{T}\)中任意多个元素的并集仍在\(\mathcal{T}\)中.

那么\(\mathcal{T}\)称为\(X\)上的拓扑, \((X,\mathcal{T})\)是一个拓扑空间. 闭集(closed set)是开集的补集. 无关\(\mathcal{T}\)的选择, \(X,\varnothing\)既是开集也是闭集.

通常拓扑(usual topology): \(\R^n\)的通常拓扑是\(\mathcal{T}_u=\qty{\textsf{可以表示为开球之并的集合}}\). 不加声明时用它.

离散拓扑(discrete topology): 每一个子集都是开集的拓扑, \({\cal T}_d=2^X\).

诱导拓扑(induced topology): 集合\(X\)的子集\(A\)上面也可以有拓扑\(\mathcal{S}\), 它可以由\(\mathcal{T}\)诱导生成: \(\mathcal{S}=\set{V|\exists O\in X:O\cap A=V}\).

设两个拓扑空间\((X,\mathcal{T}),(Y,\mathcal{S})\), \(f:X\to Y\), 满足\(\forall O\in\mathcal{S}:f^{-1}[O]\in\mathcal{T}\)(\(Y\)的开集的逆像是\(X\)中开集的并), 那么称\(f\)连续. 如果\(f\)是一元实变函数, 那么可以证明, 这个定义和\(\varepsilon-\delta\)语言的定义是等价的.

如果两个拓扑空间间存在双射\(f\), 且它与它的逆映射都是连续的, 那么\(f\)称是同胚映射(homeomorphism), 两个空间是同胚的(homeomorphic).

• 同胚映射不能"剪开"和"粘合": 平面上的线段和圆不是同胚的.
• 在同胚映射下保持不变的性质称为拓扑性质/拓扑不变性(topological invariance).

集合\(N\subset X\)称为\(x\in X\)的一个邻域(neighborhood), 如果存在\(O\in{\cal T}\), 使得\(x\in O\subset N\). 相似的, 可以定义\(X\)的子集的邻域(将属于改成包含于即可).

若一个拓扑空间\((X,{\cal T})\)除了\(X\)和\(\emptyset\)之外没有既开又闭的子集, 那么称之为连通的(connected).

拓扑空间\((X,{\cal T})\)中, 定义

• \(A\)的闭包(closure)\(\bar{A}\)是所有包含\(A\)的闭集的交集. \[ \bar{A} := \bigcap_\alpha C_\alpha, \quad A\subset C_\alpha \textsf{ 且 } C_\alpha \textsf{ 为闭}. \]

• \(A\)的内部(interior)\(\i(A)\)是所有包含于\(A\)的开集的并集. \[ \i(A) := \bigcup_\alpha O_\alpha, \quad A\supset C_\alpha \textsf{ 且 } C_\alpha\in{\cal T}. \]

• \(A\)的边界(boundary)\(\partial A:=\bar{A}-\i(A)\). 边界中的点称为边界点.

1.2 *Properties of topological spaces

\(X\)的开子集的集合\(\qty{O_\alpha}\)称为\(A\subset X\)的一个开覆盖(open cover), 如果\(A\subset\bigcup_\alpha O_\alpha\).

• 开覆盖\(\qty{V_\alpha}\)称为\(\qty{O_\alpha}\)的加细(refinement), 如果对任意\(V_\alpha\), 存在\(O_\alpha\), 使得\(V_\alpha\subset O_\alpha\).
• 开覆盖\(\qty{O_{\alpha'}}\)称为\(\qty{O_\alpha}\)的子覆盖(subcover), 如果\(\qty{O_{\alpha'}}\subset\qty{O_{\alpha}}\).

对于\(A\)的一个覆盖\(\qty{O_\alpha}\),

• 若对任意\(p\in A\), 存在\(p\)的邻域\(W\), 使得只存在有限个\(O_\alpha\cap W\neq\emptyset\), 则称其为局部有限覆盖(locally finite cover).
• 若其为有限集, 则称其为有限覆盖(finite cover).

一个集合\(A\)称为仿紧的(paracompact), 若其任意开覆盖都有局部有限的加细. 更进一步, 若其任意开覆盖都有有限子覆盖, 则称其为紧致的(compact). 这个定义也可以拓展到\(X\)上, 此时称拓扑空间\((X,{\cal T})\)是仿紧/紧致的.

一个拓扑空间\((X,{\cal T})\)称为Hausforff的, 如果任意两点都有不相交的邻域.

一个拓扑空间\((X,{\cal T})\)称为

• 第一可数的(first countable), 如果对任意一点\(p\), 都存在可数邻域族\(\qty{O_\alpha}\), 满足对任意邻域\(N\), 都存在\(O_\alpha\), 使得\(N\supset O_\alpha\).
• 第二可数的(second countable), 如果存在可数集合族\(\qty{O_\alpha}\subset{\cal T}\), 使得\(\cal T\)中任意元素都为\(\qty{O_\alpha}\)的元素之并.

2 Differentiable Manifolds

2.1 Differentiable manifolds

在拓扑空间上增加另外的条件, 来得到一个和\(\R^n\)局部相似, 但不必整体上完全相同的空间.

拓扑流形(topological manifold): 若拓扑空间\(M\)满足如下性质,

1. Hausdorff的.
2. 第二可数的.
3. (同\(\R^n\)的局部相似性) 存在\(M\)开覆盖\(\qty{O_\alpha}\)和\(\R^n\)的开覆盖\(\qty{V_\alpha}\), 而且对于所有\(O_\alpha\), 存在同胚映射\(\psi_\alpha:O_\alpha\to V_\alpha\).

则称其为一个\(n\)维拓扑流形, 简称流形.

\(O_\alpha\)中的每个点在\(\psi_\alpha\)下都获得了一组\(\R^n\)中的坐标, 把\((O_\alpha,\psi_\alpha)\)称为一个图(chart), 或者说是坐标系. 很多个图(应当是\(M\)的一个开覆盖)放在一起组成了一个图册(atlas): \(\mathcal{A}=\set{(O_\alpha,\psi_\alpha)}\). 对图册进行更高的要求:

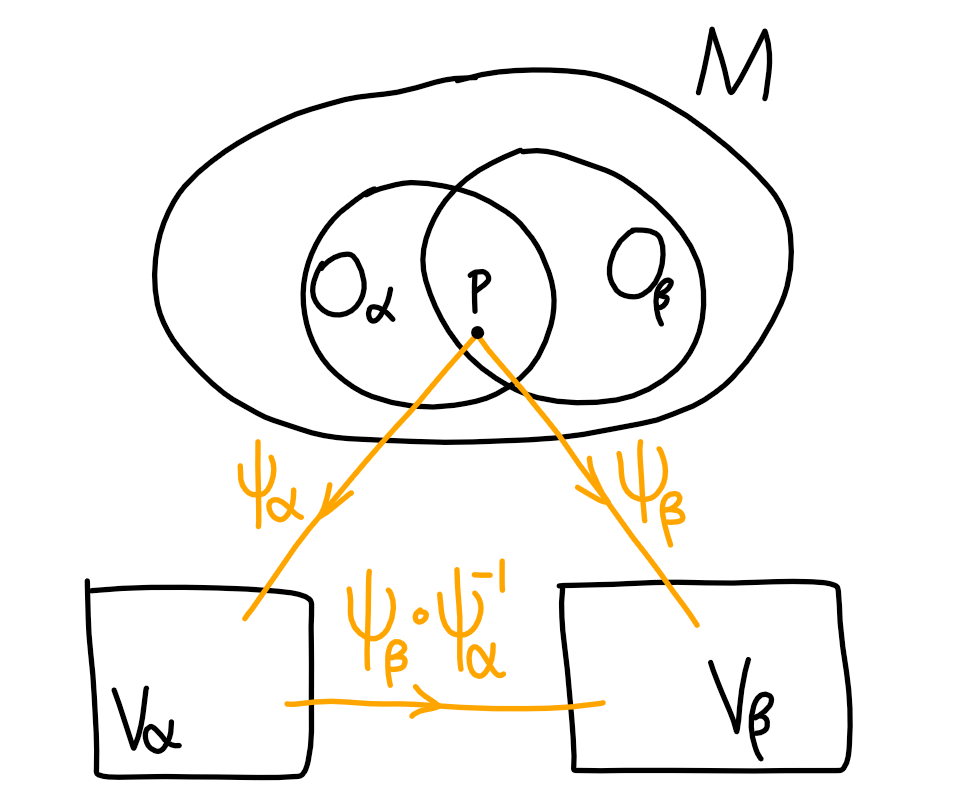
1. (\(C^r\)相容性) 如果\(O_\alpha\cap O_\beta\neq\varnothing\), 那么\(\psi_\beta\circ\psi^{-1}_\alpha\)是\(C^r\)的.
2. (图册最大化) 如果图\((\psi_0,U_0)\)满足: \(\forall(\psi_\alpha,U_\alpha)\in\mathcal{A}\)与\((\psi_0,U_0)\)相容, 那么\((\psi_0,U_0)\in\mathcal{A}\).

则称\({\cal A}\)为一个微分结构(differential structure).

微分流形(differentiable manifold)指的是具有微分结构的拓扑流形. 今后, 我们默认要求微分结构是光滑(\(C^\infty\))的, 此时微分流形\(M\)也称为光滑流形. 可以证明, 任一\(C^r\)相容的图册(也称为微分结构的一个基)都能唯一地拓展成一个最大图册, 所以指定图册时只需指定一个\(C^r\)相容的图册即可.

举例:

• \(\R^2\)和图册\(\set{(O_1,\psi_1)}\)构成了一个流形, 其中\(\psi_1\)是恒等映射. 这种只需一个图便可覆盖的流形称为平凡流形.
• 圆\(S^1\)和二维球面\(S^2\). 它们都至少需要两个图来覆盖.

映射的光滑度: 要考虑两个微分流形\(M,M'\)之间的映射\(f\), 可以借助\(\R^n\to\R^{n'}\)的映射. 设\(p\in O_\alpha\subset M\), \(f(p)\in O_\beta'\subset M'\), 当\(\psi_\beta'\circ f\circ\psi_\alpha^{-1}\)是\(C^r\)的, 那么称\(f\)是\(C^r\)的.

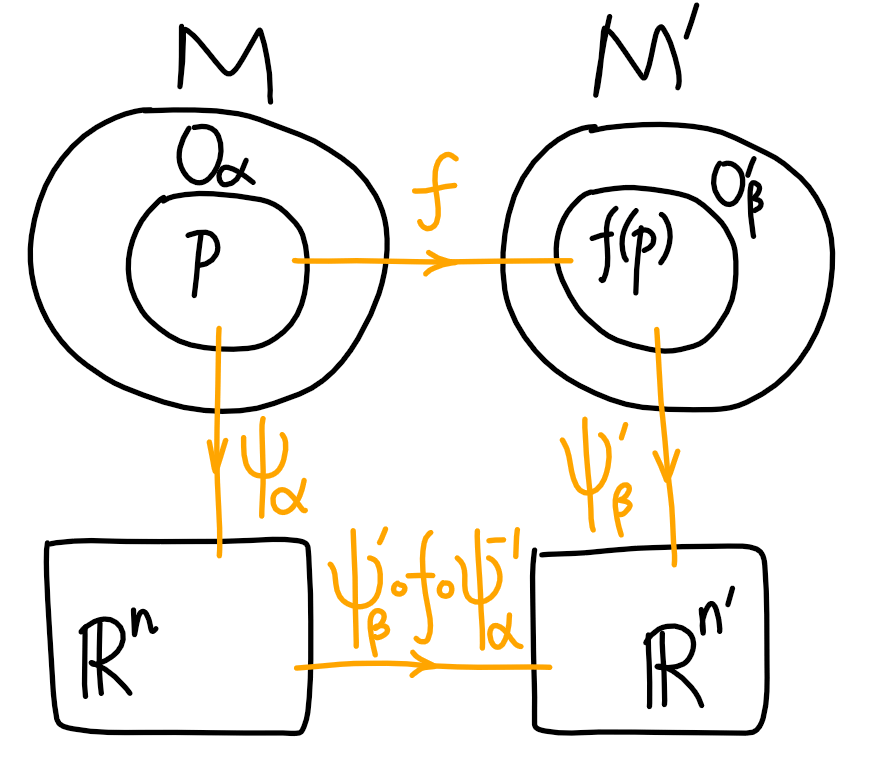
微分同胚(diffeomorphism): 如果两个微分流形间存在双射\(f\), 且它与它的逆映射都是\(C^\infty\)的, 那么\(f\)是微分同胚映射, 两个微分流形间是微分同胚的(diffeomorphic).

标量场(scalar field): \(f:M\to\R\).

• 选定坐标系\((O_0,\psi_0)\)后, 就有\(f(p)\equiv F_0(x^1,x^2,\dots,x^n)\equiv F_0(x)\).

记\(\mathcal{F}_M\)为\(M\)上全体\(C^\infty\)标量场的集合.

2.2 Tangent spaces

向量(vector): 设\(p\in M\), 映射\(v:\mathcal{F}_M\to\R\)满足: \(\forall f,g\in\mathcal{F}_M\), \(\forall\alpha,\beta\in\R\):

1. (线性性) \(v(\alpha f+\beta g)=v(\alpha f)+v(\beta g)\).
2. (Leibniz法则) \(v(fg)=f|_pv(g)+g|_pv(f)\).

则称\(v\)是流形\(M\)中, 点\(p\)的一个向量. \(p\)点的全体向量的集合记作\(V_p\).

向量可以理解为求\(f\)在\(v\)"方向"的"方向导数"(于点\(p\)).

Claim 1 \(V_p\)是一个向量空间, 且\(\dim{V_p}=\dim{M}\equiv n\).

Pf 定义加法与数乘: \((v+u)(f):=v(f)+u(f)\), \((\alpha v)(f):=\alpha v(f)\), 于是零元\(\underline{0}(f)=0\in\R\).

在\(p\)附近选定坐标系\((O_p,\psi_p)\). 定义向量\(\displaystyle X_\mu(f):=\eval{\pdv{f(x)}{x^\mu}}_p\)(\(\mu=1,2,\dots,n\)), 下证其构成\(V_p\)的一个基底.

1. 线性无关性. 设实数\(\alpha^\mu\)满足: \(\sum_\mu\alpha^\mu X_\mu=\underline0\)这是一个向量方程. 使方程两边同时作用在一个光滑函数上. 设光滑函数\(x^\nu:O_\alpha\to\R\), \(p\mapsto p\)的坐标的第\(\nu\)个分量(\(\nu=1,2,\dots,n\)). 则: \[ (\alpha^\mu X_\mu)(x^\nu)=\underline0(x^\nu). \] 又\(\rhs=0\), \(\displaystyle\lhs=\alpha^\mu X_\mu(x^\nu)=\alpha^\mu\pdv{x^\nu}{x^\mu}=\alpha^\mu\delta^\nu_\mu=\alpha^\nu\), 所以\(\alpha^\nu=0\), \(X_\mu\)线性无关.

2. 可线性表出性. 由\(\forall v\in V:v=v^\mu X_\mu\)两边作用于\(x^\nu\), 可以得到\(v^\nu=v(x^\nu)\)(\(\nu=1,2,\dots,n\)).

\(\set{X_\mu}\)称为一个坐标基底(coordinate basis), \(v^\mu\)称为\(v\)的坐标分量.

Claim 2 两个坐标基底下, \(v=v^\mu X_\mu=v'^\nu X'_\nu\), 则坐标分量满足\(\displaystyle v'^\nu=\eval{\pdv{x'^\nu}{x^\mu}}_p v^\mu\).

曲线(curve): 映射\(c:I\to M\). 如果有一个坐标系\((O,\psi)\), \(c[I]\subset O\), 那么点坐标分量\(x^\mu=x^\mu(t)\)(\(\mu=1,\dots,n\)), 这就是曲线的参数式.

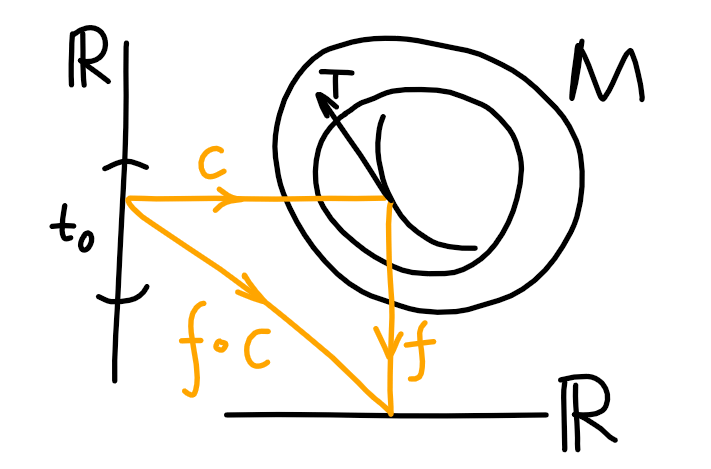
切向量(tangent vector): 在\(t_0\)处, 切向量\(T:\mathcal{F}_M\to\R\), 定义为\(\displaystyle T(f):=\eval{\dv{(f\circ c)}{t}}_{t_0}\)对任意光滑\(f\). 记\(\displaystyle T\equiv\eval{\pdv{}{t}}_{t_0}\).

\(M\)中某坐标系\(\qty{O,\psi}\)的坐标线是仅有一个分量能够自由变化的曲线. 可以验证, \(X_\mu\)是第\(\mu\)个坐标的坐标线的切向量: \(\displaystyle X_\mu\equiv\pdv{}{x^\mu}\).

应用链式法则可得, 切向量的坐标分量是该曲线的参数式之导数: \(\displaystyle \pdv{}{t}=\dv{x^\mu(t)}{t}\cdot\pdv{}{x^\mu}\).

对于\(p\)点的向量空间\(V_p\)中每个向量\(v\), 都存在一条曲线, 使得\(v\)是它的切向量, 所以\(V_p\)也称为\(p\)点的切空间(tangent space).

之前说过, \(v\in V_p\)可以理解为求取方向导数的算子: \(\displaystyle v=\alpha^\mu\pdv{}{x^\mu}\), 它是坐标基向量算子(即偏导数算子)的线性组合. 注意偏导数算子依赖于坐标系的选择.

向量场(vector field): 对每一点\(p\in M\), 都取\(V_p\)中一个向量\(v_p\), 就有了一个向量场. 给定了一个光滑映射\(f:M\to\R\)之后, \(M\)中每一点\(p\)都有\(v_p(f)\in\R\), 即一个实数与之对应, 所以\(v_p(f)\)可以看作一个标量场, 简记为\(v(f)\). 如果\(v(f)\)是\(C^r\)的, 那么称向量场\(v\)是\(C^r\)的.

对易子(commutator): 两个\(C^\infty\)向量场\(u,v\)的对易子为\([u,v](f):=u(v(f))-v(u(f))\). 可以验证, 它是一个向量场. 如果\([u,v]=\underline0\), 那么称\(u,v\)是对易的.

• 坐标基底场: \(\displaystyle v_\mu=\pdv{}{x^\mu}\), 任意\(v_\mu,v_\nu\)都是对易的.

• 对易子满足Jacobi恒等式, 即 \[ \sum_{\rm cyc}[u,[v,w]] \equiv [u,[v,w]] + [v,[w,u]] + [w,[u,v]] = \underline0. \]

积分曲线(integral curve): 设向量场\(v\), 若曲线\(c\)每一点\(t_0\)都有\(\pdv{}{t}|_{t=t_0}=v|_{c(t_0)}\), 那么称\(c\)是\(v\)的一条积分曲线. 对于\(C^\infty\)的向量场, 过任意一点\(p\)的积分曲线总是唯一存在的(在\(c(0)=p\)的条件下).

• 称一个向量场\(v\)是完备的, 如果它的每一条积分曲线的参数都可以延拓至\(\R\).

单参数微分同胚群(one-parameter group of diffeomorphisms): 含有一个参数的微分同胚映射构成的群. 设光滑映射\(\phi:\R\times M\to M\)(记\(\phi_t(\cdot)\equiv\phi(t,\cdot)\), \(\phi_p(\cdot)\equiv\phi(\cdot,p)\), \(\phi_t:M\to M\), \(\phi_p:\R\to M\)), 满足:

1. 对任意\(t\in\R\), \(\phi_t:M\to M\)是微分同胚.
2. 对任意\(s,t\in\R\), \(\phi_t\cdot\phi_s:=\phi_t\circ\phi_s\equiv\phi_{t+s}\).

那么\(G\equiv\set{\phi_t:t\in\R}\)与(2)的乘法构成单参微分同胚群. 单位元\(\phi_0(p)=p\), 逆元\(\phi_{-t}\cdot\phi_t=\phi_0\).

Claim 3 单微群\(\overset{\longrightarrow}{\underset{\text{locally}}{\longleftarrow}} C^\infty\)向量场\(v\).

Pf 给定单微群. \(\forall p\in M\), 都有\(\phi_p(0)\equiv\phi(0,p)\equiv\phi_0(p)=p\), 所以曲线\(\phi_p:\R\to M\)恒过\(p\), 便可以取它在\(p\)处的切向量\(T\). 由于\(p\)是任意的, 所以就有了一个向量场.

给定光滑向量场. \(\forall p\in M\), 都有唯一一条过\(p\)的积分曲线\(c_p:I\to M\), 定义\(\phi_t(p)\equiv c_p(t)\)(\(t\in I\)), 注意到这只对局部的参数\(t\in I\)成立.

2.3 Dual vector fields

对偶空间(dual space): 给定线性空间\(V\), 一个线性映射\(\omega:V\to\R\), 称为\(V\)的一个对偶向量(dual vector), 对偶向量构成的集合称为对偶空间, 记作\(V^*\).

Claim 1 \(V^*\)是一个线性空间, 且\(\dim{V^*}=\dim{V}\).

Pf 定义加法与数乘: \((\omega_1+\omega_2)(v):=\omega_1(v)+\omega_2(v)\), \((\alpha \omega)(v):=\alpha \omega(v)\); 零元\(\underline{0}(v):=0\in\R\).

取\(V\)的基底\(e_\mu\)(\(\mu=1,\dots,n\)), 定义\(e^{\mu*}:V\to\R\), 满足\(e^{\mu*}(e_\nu):=\delta^\mu{}_\nu\in\R\). 下面验证它们构成基底.

1. 线性无关. \(\alpha_\mu e^{\mu*}=\underline0\)有\(\forall \nu:\alpha_\mu e^{\mu*}(e_\nu)=0\)即\(\alpha_\mu\delta^\mu_\nu=0\), 则\(\alpha_\nu=0\).

2. 线性表出. 对任意\(v\in V\), 令\(\omega_\mu\equiv\omega(e_\mu)\in\R\), 那么容易证明\(\omega=\omega_\mu e^{\mu*}\).

\(\qty{e^{\mu*}}\)称为\(V\)的对偶基底(dual basis). 对\(v\in V\), 对偶基底\(e^{\mu*}\)的作用是取(基底\(e^\nu\)下)\(v\)的第\(\mu\)个分量.

若两个线性空间\(V,V'\)之间有一个线性双射\(L\), 那么称\(L\)为同构映射(isomorphism), 称\(V,V'\)是同构的(isomorphic). \(V,V'\)同构\(\iff\dim{V}=\dim{V'}\). \(V\)和\(V^*\)同构.

自然同构: \(V,V^*,V^{**}\)两两同构. 构造\(L:V\to V^{**},v\mapsto v^{**}\), 满足\(v^{**}(\omega)=\omega(v)\)(\(\forall\omega\in V^*\)), 称\(L\)是\(V,V^{**}\)的自然同构. 一般将\(V,V^{**}\)认为等同.

Claim 2 基变换. 若\(e'_\mu=A^\nu{}_\mu e_\nu\), 那么对偶基底\(e'^{\mu*}=(\tilde{A}^{-1})_\nu{}^\mu e^{\nu*}\).(\(\tilde{A}\)为转置矩阵.)

对偶向量场(dual vector field): 对每一点\(p\), 都取\(V_p^*\)中一个向量\(\omega\), 就有了一个对偶矢量场. 称一个对偶向量场\(\omega\)是\(C^\infty\)的, 若对于任何\(C^\infty\)向量场\(v\), 都有\(\omega(v)\)是\(C^\infty\)标量场.

Example 对\(f\in\mathcal{F}_M\), 设对偶向量场\(\dd{f}\)(称为\(f\)诱导的对偶向量场), 让它在\(p\)点的取值, 再作用于\(v\), 满足\(\dd{f}|_p(v):=v(f)\)(\(\forall v\in V_p\)). 对一个"方向导数算子"\(v\), 对偶向量场的效果就是把\(v\)作用在\(f\)上.

建立坐标系\((O,\psi)\), 取\(p\in O\), 坐标标量场\(x^\mu\)(取点\(p\)的第\(\mu\)坐标分量), 坐标基矢\(\displaystyle\pdv{}{x^\nu}\), 则 \[ \dd{x^\mu}\pqty{\pdv{}{x^\nu}} =\pdv{}{x^\nu}(\dd{x}^\mu)=\delta^\mu{}_\nu, \] 称\(\dd{x^\mu}\)为对偶坐标基矢.

Claim 3 \(\displaystyle\dd{f}=\pdv{f}{x^\mu}\dd{x^\mu}\), 对\(f\in\mathcal{F}_O\)(注意等式右边的\(f\)的自变量是在坐标系\((O,\psi)\)中取值的).

Claim 4 坐标变换(与2.2 Claim 2向结合; 注意指标平衡): \[ \Align{ v=v^\mu\pdv{}{x^\mu}=v'^\nu\pdv{}{x'^\nu} &\Rightarrow v'^\nu=\eval{\pdv{x'^\nu}{x^\mu}}_pv^\mu, \\ \omega=\omega_\mu\dd{x^\mu}=\omega'_\nu\dd{x}'_\nu &\Rightarrow \omega'_\nu=\eval{\pdv{x^\mu}{x'^\nu}}_p\omega_\mu. } \]

2.4 Tensor fields

张量(tensor): 多重线性的映射\(T:(\underbrace{V^*\times\dots\times V^*}_{k个})\times(\underbrace{V\times\dots\times V}_{l个})\to\R\)称为\(V\)上的一个\((k,l)\)型张量.

\(\omega\in V^*\), \(\omega:V\to\R\)是一个\((0,1)\)型张量.

\(v\in V,v^{**}\in V^{**}\), 在自然同构\(L\)下, \(v\equiv v^{**}:V^*\to\R\)是一个\((1,0)\)型张量.

\(V\)上全体\((k,l)\)型张量的集合记为\(\mathcal{T}_V(k,l)\). \(V=\mathcal{T}_V(1,0)\), \(V^*=\mathcal{T}_{V}(0,1)\).

张量面面观: 给一个\(T(\cdot;\cdot)\in T_V(1,1)\)之后, 给定一个\(\omega\in V^*\), 就有\(T(\omega;\cdot):V\to\R\), 从而\(T(\omega;\cdot)\in V^*\), 所以有\(T:V^*\to V^*\); 同样地, 也有\(T:V\to V\).

张量积(tensor product): \(T\in\mathcal{T}_V(k,l)\), \(T'\in\mathcal{T}_V(k',l')\), 则定义\(T\otimes T'\in\mathcal{T}_V(k+k',l+l')\), 且 \[ \Align{ & T \otimes T'( \omega^1,\dots,\omega^k,\omega^{k+1},\dots,\omega^{k+k'}; v_1,\dots,v_l,v_{l+1},\dots,v_{l+l'} ) \\ :={} & T(\omega^1,\dots,\omega^k;v_1,\dots,v_l) \cdot T'(\omega^{k+1},\dots,\omega^{k+k'};v_{l+1},\dots,v_{l+l'}). } \]

• 张量积不满足交换律, 但满足结合律.

Claim 1 \(\mathcal{T}_V(k,l)\)是向量空间, 且\(\dim{\mathcal{T}_V(k,l)}=n^{k+l}\)(\(n\equiv\dim{V}\)).

Example 取\(T\in\mathcal{T}_V(2,1)\), 则\(T=T^{\mu\nu}{}_\sigma e_\mu\otimes e_\nu\otimes e^{\sigma*}\), 其中\(T^{\mu\nu}{}_\sigma\equiv T(e^{\mu*},e^{\nu*};e_\sigma)\in\R\).(注意指标平衡.) 这个式子是\(T\)在基底(\(e_\mu\otimes e_\nu\otimes e^{\sigma*}\))下的展开式.

张量缩并(tensor contraction): (从矩阵的迹推广而来)\(T\in\mathcal{T}_V(k,l)\), 定义 \[ {\rm C}^i_j T := T( \underbrace{\dots,e^{\mu*}}_i,\dots; \underbrace{\dots,e_\mu}_j,\dots ) \in \mathcal{T}_V(k-1,l-1), \] 其中\(1\le i\le k\), \(1\le j\le l\). 给定线性变换, 其矩阵的迹与基底无关; 相似地, 缩并是与基底无关的.

Claim 2 \({\rm C}^1_1(v\otimes\omega)=\omega(v)\).(左边的\(v\)应理解为\(v^{**}\).) 推而广之, 有"作用\(=\)张量积\(+\)缩并".

张量场(tensor field): 每点\(p\)选取一个\(V_p\)上的\((k,l)\)型张量, 就有一个\((k,l)\)型张量场.

Claim 3 (张量变换律) 两个不同基底\(\displaystyle\qty{\pdv{}{x^\mu}},\qty{\pdv{}{x'^\mu}}\)与对应的对偶基底\(\set{\dd{x}^\mu},\set{\dd{x}'^\mu}\)下, 一个\((k,l)\)型张量\(T^{a_1\dots a_k}{_{b_1\dots b_l}}\)的分量满足变换公式 \[ T'^{\mu_1\dots\mu_k}{}_{\nu_1\dots\nu_l} = \eval{ \pdv{x'^{\mu_1}}{x^{\rho_1}}\cdots\pdv{x'^{\mu_k}}{x^{\rho_k}} \pdv{x^{\sigma_1}}{x'^{\nu_1}}\cdots\pdv{x^{\sigma_l}}{x'^{\nu_l}} }_p T^{\rho_1\dots\rho_k}{}_{\sigma_1\dots\sigma_l}. \]

2.5 Metric tensor fields

度规张量(metric tensor): \(V\)上的一个\((0,2)\)型张量\(g\)满足:

1. (对称性) \(\forall u,v\in V:g(u,v)=g(v,u)\).

2. (非退化性) \((\forall u\in V:g(v,u)=0)\Rightarrow v=\underline0\).

那么\(g\)称为\(V\)上的一个度规, 此时\(V\)有了一个度规的结构, 记作\((V,g)\). 现在可以定义:

• 模长: \(|v|:=\sqrt{|g(v,v)|}\).
• 正交(orthogonal)性: \(u\perp v\iff g(u,v)=0\).

若基底\(\set{e_\mu}\)满足: \(g_{\mu\nu}\equiv g(e_\mu,e_\nu)=\Cases{0,&\mu\ne\nu\\\pm1,&\mu=\nu}=\pm\delta^\mu{}_\nu\), 那么基底称为正交归一的(orthonormal).

号差(signature): \(g_{\mu\nu}\)组成的矩阵中\(+1\)的个数减去\(-1\)的个数, 即对角元之和. 号差与基底的选取无关.

• 正定(positive definite)度规或黎曼(Riemannian)度规: \(g_{\mu\nu}\)全是\(+1\)的度规.

• 负定(negative definite)度规: \(g_{\mu\nu}\)全是\(-1\)的度规.

• 不定(indefinite)度规.

  • 洛伦兹(Lorentzian)度规: 恰有一个\(-1\)的度规. 在洛伦兹度规下: 若\(g(v,v)>0\), 则\(v\)称为类空矢量(spacelike vector), \(<0\)称为类时矢量(timelike vector), \(=0\)称为类光矢量(lightlike/null vector).

    如果曲线\(c\)每一点的切向量都是类空向量, 那么\(c\)称为类空曲线(spacelike curve). 其他同理.

给定\(g\), 再给一个\(v\), 可以造出\(g(v,\cdot)\in V^*\), 所以有\(g:V\to V^*\), 是一个同构映射. \(V\)和\(V^*\)有度规后自然同构.

度规张量场(metric tensor field): \(V\)上的处处对称, 非退化的张量场\(g\). 只考虑号差处处相等的度规场. 度规场可以定义曲线长度.

Example \(\R^2\)中, \(\dd{l}^2=(\dd{x})^2+(\dd{y})^2\), 从而\(\displaystyle\dd{l}=\sqrt{\pqty{\dv{x}{t}}^2+\pqty{\dv{y}{t}}^2}\dd{t}=|T|\dd{t}\).

黎曼度规下, \(l:=\displaystyle\int\abs{T}\dd{t}=\int\sqrt{g(T,T)}\dd{t}\).

洛伦兹度规下, (类空, 类时, 类光曲线) \[ \Align{ l:=\displaystyle\int\abs{T}\dd{t} &=\int\sqrt{\abs{g(T,T)}}\dd{t} \\ &=\int\sqrt{\abs{g\pqty{T^\mu\pdv{}{x^\mu},T^\nu\pdv{}{x^\nu}}}}\dd{t} \\ &=\int\sqrt{\abs{T^\mu T^\nu g_{\mu\nu}}} \dd{t} =\int\sqrt{\abs{\dv{x^\mu}{t} \dv{x^\nu}{t} g_{\mu\nu}}}\dd{t} =\int\sqrt{\abs{g_{\mu\nu}\dd{x^\mu}\dd{x^\mu}}}. } \] 记\(\dd{s^2}\equiv g_{\mu\nu}\dd{x^\mu}\dd{x^\mu}\), 称为线元表达式(不过是\(g\)的另一记号), 它可能为正, 零, 负. 类光曲线的长度为零. 曲线的长度与参数的选择, 坐标系无关.

广义黎曼空间\((M,g)\). 若\(g\)正定, 则为黎曼空间(Riemannian space); 若\(g\)洛伦兹, 则为伪黎曼空间(Pseudo-Riemannian space).

黎曼空间中最简单的例子\((\R^n,\delta)\)称为\(n\)维欧氏空间(Euclidean space). 取自然坐标, 且\(\delta:=\delta_{\mu\nu}\dd{x^\mu}\otimes\dd{x^\nu}\), \(\delta_{\mu\nu}=\Cases{0,&\mu\ne\nu\\+1,&\mu=\nu}\). 可以证得, 自然坐标基底\(\displaystyle \qty{\pdv{}{x^\mu}}\)在欧氏度规下是正交归一的.

• 保持正交归一性的坐标变换: 平移, 旋转, 反射.

伪黎曼空间中最简单的例子\((\R^n,\eta)\)称为\(n\)维闵氏空间(Minkowski space). 取自然坐标, 且\(\eta:=\eta_{\mu\nu}\dd{x^\mu}\otimes\dd{x^\nu}\), \(\eta_{\mu\nu}=\Cases{0,&\mu\ne\nu,\\-1,&\mu=\nu=0,\\+1,&\mu=\nu=1,\dots,n-1}\). 自然坐标基底\(\displaystyle \qty{\pdv{}{x^\mu}}\)在闵氏度规下是正交归一的.

• 保持正交归一性的坐标变换: 平移, 伪转动(\(\set{x,t}\mapsto\set{x',t'}\): \(t'=t\cosh\alpha+x\sinh\alpha\), \(x'=t\cosh\alpha+x\sinh\alpha\)), 反射.

把一个\(S^2\)放在\((\R^3,\delta)\)里面, 欧氏度规能够诱导出球面上的度规.

\((\R^3,\delta_{ab})\)中, 笛卡尔系下线元表达式为\(\dd{s}^2=\dd{x}^2+\dd{y}^2+\dd{z}^2\), 引入球坐标系\(\qty{r,\theta,\phi}\)满足 \[ \Cases{x=r\sin\theta\cos\phi,\\y=r\sin\theta\sin\phi,\\z=r\cos\theta.} \] (\(\phi\to\) 经度, \(\theta\to\) 与\(z\)轴夹角) 于是\(\dd{s}^2=\dd{r}^2+r^2(\dd{\theta}^2+\sin^2\theta\,\dd{\phi}^2)\). 将其限制在半径为\(R\)的二维球面上, 有\(\dd{r}=0\), 于是 \[ \dd{\hat s}^2=R^2(\dd\theta^2+\sin^2\theta\,\dd\phi^2), \] 这是诱导出的度规(induced metric)在球面坐标系\(\qty{\theta,\phi}\)下的线元表达式(称为诱导线元).

2.6 Abstract index notation

2023.7.7

抽象指标记号.

1. 使用小写拉丁字母表示张量类型, 如\(v^a, \omega_b\)等; 注意指标平衡.

2. 重复代表缩并, \(T^{ab}{}_a=T(e^{\mu*},*;e_\mu)\).

3. 省略张量积记号. \(\omega\otimes\mu\to\omega_a\mu_b=\mu_b\omega_a\).

4. 抽象指标与具体指标. \(T^{ab}{}_c=T^{\mu\nu}{}_\sigma(e_\mu)^a(e_\nu)^b(e^\sigma)_c\), 其中\(T^{\mu\nu}{}_\sigma=T^{ab}{}_c(e^\mu)_a(e^\nu)_b(e_\sigma)^c\).

5. 恒等映射\(\delta^a{}_b:V\to V\), 即\(\delta^a{}_bv^b=v^a\). 可得\(\delta^a{}_b\omega_a=\omega_b\). 其分量\(\delta^a{}_b(e^\mu)_a(e_\nu)^b=\delta^\mu{}_\nu\).

6. 度规\(g_{ab}:V\to V^*\), \(V\)与\(V^*\)认同. 记\(g_{ab}v^b=v_a\)(降指标).

   • 逆映射\(g^{ab}:V^*\to V\), 满足\(g^{ca}g_{ab}=\delta^c{}_b\). 记\(g^{ab}\omega_b=\omega^a\)(升指标). 度规和逆度规在同一个基底下的分量互为逆矩阵.

   • 基矢/对偶基矢升降指标的结果, \[ \Align{ g_{ab}\pqty{\pdv{x^\mu}}^a &= g_{\mu\nu}(\dd{x^\nu})_b, & g^{ab}(\dd{x^\mu})_a &= g^{\mu\nu}\pqty{\pdv{x^\nu}}^b. } \]

   • \(g\)对称 \(\iff g_{ab}=g_{ba}\). 若\(T^a{}_b=T_b{}^a\), 则说明\(T^a{}_b\)降指标后的\(T_{ab}\)对称.

张量的对称性.

(下面讨论的对象是\((0,l)\)型张量, 对\((k,0)\)型张量是同样的.)

一个\((0,l)\)型张量\(T_{a_1\dots a_l}\)的对称部分(symmetric part)和反对称部分(antisymmetric part)分别定义为 \[ \Align{ T_{(a_1 \dots a_l)} &:= \frac1{l!}\sum_{\sigma\in S_l} T_{a_{\sigma(1)}\dots a_{\sigma(l)}}, \\ T_{[a_1 \dots a_l]} &:= \frac1{l!}\sum_{\sigma\in S_l} \sgn(\sigma) T_{a_{\sigma(1)}\dots a_{\sigma(l)}}. } \]

• 例如, \(T_{[ab]}=\dfrac12(T_{ab}-T_{ba})\), \(T_{[abc]}=\dfrac16(T_{abc}+T_{bca}+T_{cab}-T_{bac}-T_{cba}-T_{acb})\).

若\(T\)等于其对称部分, 称其为全对称的(totally symmetric); 若\(T\)等于其反对称部分, 称其为全反对称的(totally antisymmetric).

• 由定义可知, \(T_{(a_1\dots a_l)}\)中交换两个指标, 值不变; \(T_{[a_1\dots a_l]}\)中交换两个指标, 多一个负号. 因此, 有如下性质,
  • 若\(T\)对称, 则\(T_{a_1\dots a_l}=T_{a_{\sigma(1)}\dots a_{\sigma(l)}}\), 对任意置换\(\sigma\in S_n\).
  • 若\(T\)反对称, 则\(T_{a_1\dots a_l}=(\sgn\sigma)T_{a_{\sigma(1)}\dots a_{\sigma(l)}}\), 对任意置换\(\sigma\in S_n\).

Claim 1 一些很有用的运算定律,

1. 对称/反称号具有"传染性", \(T_{[a_1\dots a_l]}S^{a_1\dots a_l}=T_{[a_1\dots a_l]}S^{[a_1\dots a_l]}=T_{a_1\dots a_l}S^{[a_1\dots a_l]}\).
2. 括号内同种子括号随意增删, \(T_{[a_1\dots a_l]}=T_{[a_1\dots [a_{i+1}\dots a_j]\dots a_l]}\).
   • 嵌套括号的定义, 以\((0,3)\)型张量为例, \(T_{[a[bc]]}=\dfrac12(T_{[abc]}-T_{[bac]})\).
3. 括号内异种子括号为零, \(T_{[a_1\dots(a_i\dots a_j)\dots a_l]}=0\).
4. 异种括号缩并为零, \(T_{[a_1\dots a_l]}S^{(a_1\dots a_l)}=0\).
5. 若\(T\)反对称, 则其对称部分为零; 若\(T\)对称, 则其反对称部分为零.

Pf 1证明如下, \[ \Align{ T_{[a_1 \dots a_l]} S^{[a_1 \dots a_l]} &=\frac1{(l!)^2}\sum_{\sigma,\tau\in S_l} (\sgn\sigma)(\sgn\tau) T_{a_{\sigma(1)}\dots a_{\sigma(l)}} S^{a_{\tau(1)}\dots a_{\tau(l)}} \\ &=\frac1{(l!)^2}\sum_{\sigma,\tau\in S_l} (\sgn\sigma)(\sgn\tau)\pqty{ {\rm C}^{(\tau^{-1}\sigma)(1)}_{1} \cdots {\rm C}^{(\tau^{-1}\sigma)(l)}_{l} } (T_{a_1\dots a_l} S^{b_1\dots b_l}) \\ &=\frac1{(l!)^2}\sum_{\pi=\tau^{-1}\sigma} l! (\sgn\pi) \pqty{ {\rm C}^{\pi(1)}_{1} \cdots {\rm C}^{\pi(l)}_{l} } (T_{a_1\dots a_l} S^{b_1\dots b_l}) \\ &=\frac1{l!}\sum_{\pi\in S_l} (\sgn\pi) T_{a_1\dots a_l} S^{a_{\pi(1)}\dots a_{\pi(l)}} \\ &=T_{a_1\dots a_l} S^{[a_1\dots a_l]}. } \]

• 第3步, 注意到求和式的每一项只与\(\tau^{-1}\sigma\)有关, 因此设\(\pi=\tau^{-1}\sigma\). 对每一个\(\pi\), 有\(l!\)个\((\sigma,\tau)\)的有序对使得\(\pi=\tau^{-1}\sigma\)(对任意\(\sigma\), 都恰好有一个满足条件的\(\tau=\pi^{-1}\sigma\)), 因此多出来一个\(l!\). 又有\(\sgn\pi=(\sgn\tau)(\sgn\sigma)\), 即得.
• 圆括号的证明是一样的, 只需去掉\(\sgn\).

2证明如下, \[ \Align{ T_{[a_1\dots [a_{i+1}\dots a_j]\dots a_l]} &=\frac1{(j-i)!} \sum_{\sigma\in S_{j-i}} (\sgn\sigma) T_{[ a_1 \dots a_i a_{i+\sigma(1)} \dots a_{i+\sigma(j-i)} a_{j+1} \dots a_l]} \\ &=\frac1{(j-i)!} \sum_{\sigma\in S_{j-i}} T_{[ a_1 \dots a_i a_{i+1} \dots a_{j} a_{j+1} \dots a_l]} \\ &=T_{[a_1 \dots a_l]}, \\ T_{(a_1\dots(a_{i+1}\dots a_j)\dots a_l)} &=\frac1{(j-i)!} \sum_{\sigma\in S_{j-i}} T_{( a_1 \dots a_i a_{i+\sigma(1)} \dots a_{i+\sigma(j-i)} a_{j+1} \dots a_l)} \\ &=\frac1{(j-i)!} \sum_{\sigma\in S_{j-i}} T_{( a_1 \dots a_i a_{i+1} \dots a_{j} a_{j+1} \dots a_l)} \\ &=T_{(a_1 \dots a_l)}. } \] 3证明如下. 根据2, 只需证明\(T_{[(a_1\dots a_l)]}=0\)即可: \[ T_{([a_1\dots a_l])} = \frac1{l!} \sum_{\sigma\in S_l} (\sgn\sigma) T_{(a_{\sigma(1)} \dots a_{\sigma(l)})} = \frac1{l!} \sum_{\sigma\in S_l} (\sgn\sigma) T_{(a_1 \dots a_l)} = 0. \]

• 第3步根据\(\sum_{\sigma\in S_l} \sgn\sigma=0\).

4是1和3的推论. 5是3的推论.

Claim 2 对于任意矢量\((v_1)^a,\dots,(v_n)^a\), 有 \[ (v_1)^{[a_1}\cdots(v_n)^{a_n]}=(v_{[1})^{a_1}\cdots(v_{n]})^{a_n}. \] 对偶矢量以及圆括号亦然.

Pf (圆括号同理) \[ \Align{ (v_1)^{[a_1}\cdots(v_n)^{a_n]} &=\sum_{\sigma\in S_n} (\sgn\sigma) (v_1)^{a_{\sigma(1)}}\cdots(v_n)^{a_{\sigma(n)}} \\ &=\sum_{\sigma\in S_n} (\sgn\sigma) (v_{\sigma^{-1}(1)})^{a_1}\cdots(v_{\sigma^{-1}(n)})^{a_n} \\ &=\sum_{\sigma^{-1}\in S_n} (\sgn\sigma^{-1}) (v_{\sigma^{-1}(1)})^{a_1}\cdots(v_{\sigma^{-1}(n)})^{a_n} \\ &=(v_{[1})^{a_1}\cdots(v_{n]})^{a_n}. } \]