GTM275 | 5 测地线

GTM275 (Differential Geometry: Connections, Curvature, and Characteristic Classes) 第 16-17 节的笔记. 补充了一点完备性的内容.

13 Distance and Completeness

13.1 Distance on a Riemannian manifold

在本系列的开始, 我们定义了光滑曲线 \(c:[a,b]\to M\) 的弧长 \(l:=\int_{[a,b]}\|c'(t)\|\dd{t}\), 并证明了它不依赖于曲线的参数化. 在一个连通的黎曼流形 \(M\) (进而路径连通) 中, 任意两点 \(p,q\) 均有分段光滑的曲线相连, 定义 \(p,q\) 间的距离(distance)为这些曲线长度的下确界: \[ d(p,q) := \inf_{c}l(c). \] 如此定义的距离函数满足三个性质:

1. 正定性. \(d(p,q)\geq0\), 取等当且仅当 \(p=q\).
2. 对称性. \(d(p,q)=d(q,p)\).
3. 三角不等式. \(d(p,r)\leq d(p,q)+d(q,r)\).

于是 \((M,d)\) 构成一个度量空间. 要注意的是, 距离函数 (也叫度量, metric) \(d:M\times M\to\R\) 和黎曼度量 \(\lr{\cdot,\cdot}\) 是两个东西, 前者定义在流形上, 后者定义在切丛上.

一条连接 \(p,q\) 的分段光滑曲线 \(c\) 称为最短曲线(length-minimizing curve), 若它是所有连接 \(p,q\) 的分段光滑曲线中, 长度最短的. 此时, \(d(p,q)=l(c)\).

• 在去掉原点欧氏平面 \(\R^2-\{0\}\) 上, 两点 \((-1,0)\) 和 \((1,0)\) 的距离是 \(2\), 但是并无一条连接两点的直线段. 这说明两点间不一定有最短线.

Claim 13.1 (局部测地线是最短线) 设黎曼流形 \(M\), 测地球 \(B_\delta(p)\), \(q\in B_\delta(p)\). 则测地线 \[ \gamma:[0,1]\to B_\delta(p),\quad \gamma(0)=p,\quad\gamma(1)=q \] 是连接 \(p,q\) 的最短线. 此外, 设 \(c\) 是另一连接 \(p,q\) 的分段光滑曲线, 且 \(l(\gamma)=l(c)\), 则 \(c\) 是 \(\gamma\) 的单调重参数化.

Pf 证明的关键是将切向量 \(c'(t)\) 正交分解为径向部分 (平行于测地线的切向量) 与切向部分 (平行于测地球面的切空间), 其中正交性由高斯引理保证.

设 \(c:[a,b]\to B_\delta(p)\), \(c(a)=p\), \(c(b)=q\). 设 \(\tilde{a}\) 是最大的使得 \(c(\tilde{a})=p\) 的数; \(\tilde{b}\) (\(\tilde{a}<\tilde{b}\leq b\)) 是最小的使得 \(c(\tilde{b})\in S_\delta(p)\) 的数 (若 \(c(t)\) 始终在 \(B_\delta(p)\) 内部, 则取 \(\tilde{b}=b\)). 于是 \(l(c|_{[\tilde{a},\tilde{b}]})\leq l(c)\). 下面只考虑 \(c|_{[\tilde{a},\tilde{b}]}\).

将 \(c(t)\) 写作指数映射的像, \[ c(t)=\operatorname{Exp}_p(r(t)v(t)), \] 其中 \(r(t)>0\) 为光滑函数, \(v(t)\in S^{n-1}\subset T_pM\). 求导有 \[ \Align{ c'(t) &= (\operatorname{Exp}_p)_{*}( r'(t)v(t)+r(t)v'(t) ) \\ &= r'(t)(\operatorname{Exp}_p)_{*}(v(t)) + r(t)(\operatorname{Exp}_p)_{*}(v'(t)) } \] 注意到 \(v(t)\perp v'(t)\), 结合指数映射保持径向向量长度, 保持径向与切向的正交性 (高斯引理), 有 \[ \Align{ \|c'(t)\|^2 &= r'(t)^2 \|v(t)\|^2 + r(t)^2 \|v'(t)\|^2 \\ &\geq r'(t)^2\|v(t)\|^2 = r'(t)^2. } \] 线长 \[ \Align{ l(c) \geq l(c|_{[\tilde{a},\tilde{b}]}) &= \int_{[\tilde{a},\tilde{b}]}\|c'(t)\|\dd{t} \\ &\geq \int_{[\tilde{a},\tilde{b}]}|r'(t)|\dd{t} \\ &\geq \int_{[\tilde{a},\tilde{b}]}r'(t)\dd{t} \\ &= r(\tilde{b})-r(\tilde{a}) \\ &= r(\tilde{b}) \geq r(b) = l(\gamma). } \] 其中最后一个等号, \(r(b)\) 为 \(q\) 所在的测地球面的半径, 因为指数映射保持径向长度, \(r(b)\) 就是测地线线长. 上式取等当且仅当 \([a,b]=[\tilde{a},\tilde{b}]\), \(v'(t)\equiv0\), \(r'(t)\geq0\), 即 \(\gamma(t)\) 的单调重参数化.

正规邻域内的测地线是最短线, 但一条一般的测地线就不一定了. 球面 \(S^2\) 的大圆的一段优弧显然不是最短的 (与之相补的劣弧是最短的).

13.2 Geodesic completeness

在微分拓扑中, 一条曲线 \(c:(a,b)\to M\) 可以被光滑重参数化为 \(\bar{c}:\R\to M\), 因为 \((a,b)\) 微分同胚于 \(\R\). 但是测地线只能容许线性的重参数化 \(t=au+b\), 于是定义在有限区间上的测地线, 与定义在 \(\R\) 上的测地线无法通过重参数化互相转化. 我们称黎曼流形 \(M\) 为测地完备的(geodesic complete), 若其上每一条测地线的定义域均可延拓到 \(\R\).

• 点 \(p\) 处的测地线 \(\gamma_v(t)=\operatorname{Exp}_p(tv)\) 的定义域可以延拓到 \(t\in\R\) 意味着 \(\operatorname{Exp}_p\) 在整个 \(T_pM\) 上有定义.
• 球面和欧氏空间都是测地完备的. 去掉一点的欧氏平面 \(\R^2-\{0\}\) 不是测地完备的, 测地线 \(\gamma(t)=(t,0)\), \(t>0\) 的定义域不能延拓到 \(\R\).

连通的黎曼流形还有距离空间结构. 称一个距离空间为完备(complete)的, 若任一 Cauchy 列存在极限.

• 可以证明, 距离函数 \(d\) 诱导的拓扑与 \(M\) 作为流形的拓扑是相同的.

Claim 13.2 (Hopf-Rinow 定理) 设黎曼流形 \(M\), 则下列命题等价:

1. \((M,d)\) 是完备的距离空间.
2. 对任意 \(p\in M\), \(\operatorname{Exp}_p\) 定义在整个 \(T_pM\) 上 (\(M\) 测地完备).
3. 存在 \(p\in M\), \(\operatorname{Exp}_p\) 定义在整个 \(T_pM\) 上.
4. \(M\) 中任意有界闭子集是紧致的.

并且, 在完备的黎曼流形中, 任意两点可由最短测地线相连, 于是任意一点的指数映射 \(\operatorname{Exp}_p:T_pM\to M\) 是满射.

Pf 我们将证明 1 \(\Rightarrow\) 2 \(\Rightarrow\) 3 \(\Rightarrow\) 4 \(\Rightarrow\) 1, 其中 2 \(\Rightarrow\) 3 是显然的; 4 \(\Rightarrow\) 1 是拓扑学中的结论.

1 \(\Rightarrow\) 2. 假设一条弧长参数的最大测地线为 \(\gamma(t)\), \(a<t<b\), 其中 \(b<+\infty\). 距离空间的完备性保证当 \(t\uparrow b\) 时, \(\gamma(t)\) 趋近于某一点 \(q\in M\). 根据 Claim 11.7, 存在 \(q\) 点的邻域 \(U\) 以及 \(\varepsilon>0\), 使得对任意 \(x\in U\), \(\operatorname{Exp}_x\) 在 \(B_\varepsilon(0)\) 有定义. 取 \(\gamma(t_0)\in U\) 并且 \[ d(\gamma(t_0),q)<\frac\varepsilon2, \] 定义测地线 \(\zeta:[0,\varepsilon]\to M\), \(\zeta(0)=\gamma(t_0)\), \(\zeta'(0)=\gamma'(t_0)\), 则 \(\zeta\) 延伸了 \(\gamma\) 并超过 \(q\) 点. 这导致矛盾, 说明 \(b=+\infty\). 同样能证明 \(a=-\infty\).

对于 3 \(\Rightarrow\) 4, 引入中间命题 5: \(M\) 中任意两点可由最短测地线相连. 转而证明 3 \(\Rightarrow\) 5 \(\Rightarrow\) 4.

3 \(\Rightarrow\) 5. 结合 Claim 13.1 有 \(B_r(p)=\{ x\in M\mid d(p,x)\leq r \}\) 对任意 \(r\geq0\). 考虑 \[ \Sigma_r(p) = \{x\in B_r(p)\mid p,x\textsf{ 可用最短测地线相连}\}, \] 即要证明 \(B_r(p)=\Sigma_r(p)\). 当 \(r\) 充分小时这件事是对的, 所以若令 \[ \mathscr{T}=\{ r\in[0,+\infty)\mid B_r(p)=\Sigma_r(p)\}, \] 则 \(\mathscr{T}\) 非空且有内点. 只要证明 \(\mathscr{T}\) 既开又闭, 再由 \([0,+\infty)\) 连通便可得 \(\mathscr{T}=[0,+\infty)\). 闭性是测地线连续依赖于初始向量的直接推论. 下面证明开性. 先给出 Claim 11.7 和 Claim 13.1 的推论:

• 任给 \(q\in M\), 存在 \(q\) 的邻域 \(U\) 和 \(\varepsilon>0\), 使得 \(\operatorname{Exp}\) 定义在管状区域 \(U\times B_\varepsilon(0)\) 上, 于是 (推论) 任给 \(x\in K\), \(y\in M\), 只要 \(d(x,y)\leq\varepsilon\), 那么 \(x,y\) 就能由最短测地线连接.
• 考虑 \(B_r(p)\), 任给 \(q\in B_r(p)\), 能够找到如上的 \(U_q\) 和 \(\varepsilon_q\). 这 \(\{U_q\}\) 构成一个开覆盖. 由 \(B_r(p)\) 的紧致性, \(\{U_q\}\) 存在有限子覆盖 \(\{U_q\}_{q\in I}\). 取 \(\varepsilon:=\min_{q\in I}\varepsilon_q\), 则 \(B_r(p)\) 关于 \(\varepsilon\) 也满足如上推论.

取 \(r\in\mathscr{T}\), \(\varepsilon\) 为上面根据 \(B_r(p)\) 构造出来的值. 下面证明, 对任意 \(\varepsilon'<\varepsilon\), 有 \(r+\varepsilon'\in\mathscr{T}\). 任取 \(y\in B_{r+\varepsilon'}(p)\). 若 \(y\in B_r(p)\), 则 \(y\in\Sigma_r(p)\subset\Sigma_{r+\varepsilon'}(p)\). 若 \(y\in B_{r+\varepsilon'}(p)-B_r(p)\), 则存在 \(x\in\partial B_r(p)\), 且 \[ d(p,y) = d(p,x) + d(x,y). \]

• (注) 存在性是因为, 任意连接 \(p,y\) 的分段光滑曲线必定穿过 \(\partial B_r(p)\), 所以 \[ \Align{ d(p,y) &=\inf_{c\textsf{ 连接 }p,y} l(c) \\ &=\inf_{x\in\partial B_r(p)}\pqty{ \inf_{c_1\textsf{ 连接 }p,x}l(c_1) + \inf_{c_2\textsf{ 连接 }x,y}l(c_2) } \\ &=\inf_{x\in\partial B_r(p)}(d(p,x)+d(x,y)), } \] 由 \(\partial B_r(p)\) 的紧致性, 该下确界就等于某 \(d(p,x)+d(x,y)\).

因为 \(x\in B_r(p)\), 所以 \(p,x\) 间可以用最短测地线 \(\gamma_1\) 连接. 又因为 \[ \Align{ d(x,y) &=d(p,y)-d(p,x) \\ &=d(p,y)-r \\ &\leq(r+\varepsilon')-r=\varepsilon', } \] 所以 (根据推论) \(x,y\) 可以用最短测地线 \(\gamma_2\) 连接. 将 \(\gamma_1\), \(\gamma_2\) 连起来, 就成为连接 \(p,y\) 的最短曲线. 因为 \(y\) 在测地球里, 所以这最短曲线必然是最短测地线. 于是 \(y\in\Sigma_{r+\varepsilon'}(p)\). 总之有 \(r+\varepsilon'\in\mathscr{T}\), 所以 \(\mathscr{T}\) 是开的.

5 \(\Rightarrow\) 4. 设 \(K\subset M\) 为有界闭集. 取定 \(p\in K\), 则存在 \(A\geq0\), 使得 \[ d(p,x)\leq A,\quad x\in K. \] 又因为任给 \(x\in K\), \(p,x\) 可以用最短测地线连接, 所以 \(K\subset B_A(p)=\operatorname{Exp}_p(B_A(0))\). 注意到 \(B_A(0)\) 是紧致的, \(\operatorname{Exp}_p\) 连续, 故 \(B_A(p)\) 紧致. 集合 \(K\) 作为 \(B_A(p)\) 的闭子集, 也紧致.

Claim 13.3 完备的黎曼流形上的有界向量场是完备的. 换言之, 设向量场 \(X\), 若存在常数 \(c\) 使得 \(\|X\|\leq c\), 则 \(X\) 的每一条不可延积分曲线的定义域为 \(\R\).

Pf 反证. 假设 \(X\) 的一条积分曲线 \(\phi:[0,a)\to M\), 且不可延伸到 \(a\) (\(a<+\infty\)). 我们首先给出估计: 对于任意 \(0\leq t_1<t_2<a\), \[ \Align{ d(\phi(t_1),\phi(t_2)) &\leq \int_{[t_1,t_2]}\|\phi'(t)\|\dd{t} \\ &= \int_{[t_1,t_2]}\|X_{\phi(t)}\|\dd{t} \\ &\leq c(t_2-t_1). } \] 取 Cauchy 列 \(t_n\uparrow a\), 上面的估计意味着 \(\phi(t_n)\) 也为 Cauchy 列, 根据 \(M\) 的完备性, \(\phi(t_n)\to q\in M\). 上面的估计也意味着极限点 \(q\) 不依赖于数列 \(\{t_n\}\) 的选取. 所以当 \(t\uparrow a\), \(\phi(t)\to q\). 由 \(X\) 的连续性, 此时 \(X_{\phi(t)}\to X_q\). 设从 \(q\) 开始的积分曲线 \(\psi:[0,\varepsilon)\to M\), 则 \(\psi\) 延伸了 \(\phi\), 导致矛盾, 所以 \(a=+\infty\).

相似地, 可以证明 \(\phi\) 定义区间的下限为 \(-\infty\).

完备的黎曼流形有很好的性质, 在黎曼几何中起确定性作用. 完备黎曼流形的一些重要的例子有:

• 具有平坦度量的 \(\R^n\).
• \(\R^n\) 作为闭子集的子流形.
• 紧致黎曼流形.
• 齐性(homogeneous)黎曼流形. 黎曼流形 \(M\) 为齐性的, 当且仅当对任意 \(p,q\in M\), 存在等距同构 \(\varphi:M\to M\), 使得 \(\varphi(p)=q\).

Claim 13.4 齐性黎曼流形是完备的.

Pf 根据 Hopf-Rinow, 只需证明 \(M\) 测地完备. 设弧长参数的测地线 \(\gamma:[0,a)\to M\), 且不可延伸到 \(a\). 我们知道, 取定一个 \(p\in M\), 存在 \(\varepsilon>0\), 使得从 \(p\) 点开始的测地线的线至少在 \((-\varepsilon,\varepsilon)\) 有定义. 取 \(\delta=\min\{\varepsilon,a/2\}\), \(q=\gamma(a-\delta)\).

因为 \(M\) 是齐性流形, 所以存在等距同构 \(\varphi:M\to M\), 使得 \(\varphi(p)=q\). 由于等距同构保持测地线, 所以从 \(q\) 点出发的所有测地线至少在 \((-\delta,\delta)\) 有定义. 特别地, \(\gamma(t)\) 可以延伸到 \([0,a+\delta)\), 与假设矛盾.

14 Volume

14.1 Volume form

Claim 14.1 (对偶标架的变换律) 设开集 \(U\) 上的标架 \(\{e_i\}\), \(\{\bar{e_i}\}\) 与其对偶标架 \(\{\theta^i\}\), \(\{\bar\theta^i\}\) 分别满足 \[ \bar{e}_j=\sum_i a^i_je_i,\quad \bar\theta^i=\sum_j b^i_j\theta^j, \] (其中光滑函数 \(A=[a^i_j]:U\to{\rm GL}(n,\R)\)) 则 \(B=[b^i_j]=A^{-1}\). 此外, \[ \bar\theta^1\wedge\dots\wedge\bar\theta^n = (\det{B})\,\theta^1\wedge\dots\wedge\theta^n. \]

在一个可定向流形上, 有许多处处非零的连续 \(n\) 形式场 (即体积形式), 彼此相差一个非零函数. 若 \(M\) 为黎曼流形, 我们能挑出一个最特别的体积形式, "体积" 的概念也唯一确定下来了.

设黎曼流形 \(M\), 开集 \(U\) 上的正交归一标架 \(\{e_i\}\), 其对偶标架 \(\{\theta^i\}\), 则 \(n\) 形式 \[ \omega=\theta^1\wedge\dots\wedge\theta^n \] 在 \(U\) 处处非零. 下面说明 \(\omega\) 不依赖于正交归一标架的选取. 设有另一个正交归一标架, \(\{\bar e_i\}\), \(\{\bar\theta^i\}\), 满足变换关系 \(\bar e=eA\), \(\bar\theta=A^{-1}\theta\), 注意 \(A\) 是正交阵, \(\det{A}=\det{A}^{-1}=\pm1\), 则有 \[ \bar\omega =\bar\theta^1\wedge\dots\wedge\bar\theta^n =(\det{A}^{-1})\,\theta^1\wedge\dots\wedge\theta^n =\pm\omega. \] 当标架 \(\{e_i\}\) 与 \(\{\bar e_i\}\) 定向相同时, \(\bar\omega=\omega\). 上述 \(n\) 形式 \(\omega\) 称为 \(M\) 的黎曼体积形式(Riemannian volume form), 简称体积形式, 记作 \({\rm vol}_M\). 若 \(\int_M{\rm vol}_M\) 有限, 则称 \(\int_M{\rm vol}_M\) 为流形 \(M\) 的体积(volume).

Claim 14.2 (坐标系下的体积形式) 在正定向的坐标系 \((U,x^1,\dots,x^n)\) 下, 黎曼体积形式 \[ {\rm vol}_M = \sqrt{\det{[g_{ij}]}} \dd{x^1}\wedge\cdots\wedge\dd{x^n}. \]

Pf 设 \(U\) 上的正定向正交归一标架 \(e_1,\dots,e_n\), 对偶标架 \(\theta^1,\dots,\theta^n\), 于是存在 \([a^i_j]:U\to{\rm GL}(n,\R)\), 使得 \(\partial_j=\sum a^i_je_i\), 根据变换律, \(\dd{x}^i=\sum b^i_j\theta^i\), \(B=[b^i_j]=[a^i_j]^{-1}=A^{-1}\), 并且 \[ \dd{x^1}\wedge\dots\wedge\dd{x^n} = (\det{B})\, \theta^1\wedge\dots\wedge\theta^n. \] 所以 \[ {\rm vol}_M = \theta^1\wedge\dots\wedge\theta^n = (\det{A}) \dd{x^1}\wedge\dots\wedge\dd{x^n}. \] 为了计算 \(\det{A}\), 考虑 \[ \Align{ g_{ij} = \lr{\partial_i,\partial_j} &= \lr{ \sum a^k_ie_k, \sum a^l_je_l } \\ &= \sum a^k_ia^l_j \delta_{kl} \\ &= \sum a^k_i a^k_j = (A\T A)^i_j, } \] 于是 \([g_{ij}]=A\T A\), \(\det[g_{ij}]=\det(A\T A)=(\det{A})^2\), 或 \(\det{A}=\sqrt{\det[g_{ij}]}\).

Example 球面的体积形式. 设 \(\R^n\) 中半径为 \(r\) 的球面 \(S^{n-1}(r)\) 具有诱导黎曼度量.

在 \(\R^n\) 建立球坐标系 \[ \left\{\Align{ x_1 &= \rho\cos\theta, \\ x_2 &= \rho\sin\theta\cos\phi_1, \\ x_3 &= \rho\sin\theta\sin\phi_1\cos\phi_2, \\ &\dots \\ x_{n-1} &= \rho\sin\theta\cdots\sin\phi_{n-3}\cos\phi_{n-2}, \\ x_n &= \rho\sin\theta\cdots\sin\phi_{n-3}\sin\phi_{n-2}, \\ }\right. \] 其中 \(\rho\geq0\), \(\theta,\phi_1,\dots,\phi_{n-3}\in[0,\pi]\), \(\phi_{n-2}\in[0,2\pi]\). 根据坐标变换公式 \[ \pdv{y^j} = \pdv{x^i}{y^j}\pdv{x^i}, \] 一番计算可得 \[ \Align{ \norm{\pdv{\theta}} &= r, & \norm{\pdv{\phi_1}} &= r\sin\theta, &\dots,&& \norm{\pdv{\phi_{n-2}}} &= r\sin\theta\cdots\sin\phi_{n-3}. } \] 并且 \(\partial/\partial\theta,\partial/\partial\phi_{k}\) (\(k=1,\dots,n-2\)) 两两正交, 将其归一化便得到 \(S^{n-1}(r)\) 的正交归一标架, 其对偶标架 \[ \Align{ \omega^1 &= r\dd{\theta}, & \omega^2 &= r\sin\theta\dd{\phi_1}, &\dots,&& \omega^{n-1} &= r\sin\theta\cdots\sin\phi_{n-3}\dd{\phi_{n-2}}. } \] 于是黎曼体积形式 \[ \Align{ {\rm vol}_{S^{n-1}(r)} &= \omega^1\wedge\dots\wedge\omega^n \\ &= r^{n-1}(\sin\theta)^{n-2}(\sin\phi_1)^{n-3}\cdots(\sin\phi_{n-3})^1 \dd{\theta}\wedge\cdots\wedge\dd{\phi_{n-2}}. } \]

现在可以求球面 \(S^{n-1}(r)\) 的体积了, 不过这里的 "体积", 即体积形式在 \(S^{n-1}(r)\) 上的积分, 是我们通常所说的球的表面积(surface area). 取球坐标系下的体元, \[ \Align{ \textsf{Area} &= \int_{S^{n-1}(r)} {\rm vol}_{S^{n-1}(r)} \\ &= \int_0^\pi\dd\theta\int_0^\pi\dd\phi_1\cdots\int_0^\pi\dd\phi_{n-3} \int_0^{2\pi}\dd{\phi_{n-2}}{} \cdot r^{n-1}(\sin\theta)^{n-2}(\sin\phi_1)^{n-3}\cdots(\sin\phi_{n-3}). } \] 利用 Wallis 积分公式 \(\int_0^{\pi/2}(\sin{x})^n\dd{x}=\Cases{\frac{(n-1)!!}{n!!}\frac\pi2,&n\textsf{ 为偶数},\\\frac{(n-1)!!}{n!!},&n\textsf{ 为奇数},}\) 算得 \[ \Align{ \textsf{Area} = \Cases{ \dfrac{(2\pi)^{n/2}}{(n-2)!!}r^{n-1}, & n\textsf{ 为偶数}, \\ \dfrac{2^{(n+1)/2}\pi^{(n-1)/2}}{(n-2)!!}r^{n-1}, & n\textsf{ 为奇数}. } } \] 利用 Gamma 函数可以写作 \[ \textsf{Area} = \frac{2\pi^{n/2}}{\Gamma(\frac{n}2)} r^{n-1}. \]

14.2 Induced volume form

回忆带边流形的诱导定向. 设定向的带边流形 \(M\), 设 \(\omega\) 为 \(M\) 的体积形式, \(X\) 为 \(\partial M\) 上的光滑外向向量场, 则 \(\partial M\) 的诱导体积形式由 interior multiplication \(\iota_X\omega\) 给出.

Claim 14.3 (诱导体积形式) 设带边黎曼流形 \(M\), \(X\) 为 \(\partial M\) 上的光滑外向单位向量场, 则 \(\partial M\) 的诱导黎曼体积形式 \[ {\rm vol}_{\partial M} = \iota_X({\rm vol}_M). \]

Pf 设 \(p\in\partial{M}\). 若 \(p\) 的邻域 \(U\) 内有 \(M\) 的正定向的正交归一标架 \((X,e_2,\dots,e_n)\), 则 \((e_2,\dots,e_n)\) 为 \(\partial{M}\) 的正定向正交归一标架. 设 \(\theta^1,\dots,\theta^n\) 为 \(X,e_2,\dots,e_n\) 的对偶标架, 则 \(\theta^2,\dots,\theta^n\) 为 \(e_2,\dots,e_n\) 的对偶标架. 所以 \[ \Align{ {\rm vol}_M &= \theta^1\wedge\dots\wedge\theta^n, & {\rm vol}_{\partial M} &= \theta^2\wedge\dots\wedge\theta^n, } \] 在 \(p\) 点有 \[ \Align{ \iota_X({\rm vol}_M) &= \sum_j (-1)^{j-1}\theta^j(X)\, \theta^1\wedge\dots\wedge\widehat{\theta^j}\wedge\dots\wedge\theta^n\\ &= \theta^1(X)\,\theta^2\wedge\dots\wedge\theta^n \\ &= \theta^2\wedge\dots\wedge\theta^n = {\rm vol}_{\partial M}. } \]

单位圆的体积形式. 单位圆盘 \(D=\qty{(x,y)\in\R^2|x^2+y^2\leq1}\) 的黎曼体积形式 \({\rm vol}_D=\dd{x}\wedge\dd{y}\), 边界 \(\partial D=S^1\) 的外向单位向量场是 \[ X=x\pdv{x}+y\pdv{y}, \] 于是 \(S^1\) 的黎曼体积形式 \[ \Align{ {\rm vol}_{S^1} = \iota_X({\rm vol}_D) &= (\iota_X\dd{x})\dd{y} - \dd{x} (\iota_X\dd{y}) \\ &= (Xx)\dd{y} - \dd{x}(Xy) \\ &= x\dd{y} - y\dd{x}. } \]

Example \(\R^n\) 中超曲面的的体积形式.

设光滑函数 \(f:\R^n\to\R\), \(0\in\R\) 为 \(f\) 的正则值, 于是 \(Z(f):=\{x\in\R^n|f(x)=0\}\) 为 \(\R^n\) 的一个 \(n-1\) 维子流形, 也叫做超曲面(hypersurface). 记 \[ \operatorname{grad}f:=\sum\pdv{f}{x^i}\pdv{x^i} \] 为 \(f\) 的梯度场. 因为 \(0\) 是正则值, \(\operatorname{grad}f\) 在 \(Z(f)\) 上处处非零. 我们还断言: \(\operatorname{grad}(f)\) 是 \(Z(f)\) 的法向量场. 这是因为, 任给曲线 \(c:I\to Z(f)\), 有 \(f\circ c\equiv0\), 于是 \[ 0\equiv(f\circ c)_{*,t} = f_{*,c(t)}\cdot c'(t) = \eval{\pqty{ \pdv{f}{x^1},\dots,\pdv{f}{x^n} }}_{c(t)}\cdot c'(t) \] 即 \(\operatorname{grad}f|_{c(t)}\) 正交于 \(c'(t)\in T_{c(t)}Z(f)\).

因此 \(X=\operatorname{grad}f/\|\operatorname{grad}f\|\) 是 \(Z(f)\) 的单位法向量场.

我们如此定义 \(Z(f)\) 的定向: \(T_pZ(f)\) 的一个正交归一基底 \((e_2,\dots,e_n)\) 为正定向的, 当且仅当 \((X,e_1,\dots,e_n)\) 在 \(T_p\R^n\) 中为正定向的. 因此 \(Z(f)\) 的诱导体积形式 \[ \Align{ {\rm vol}_{Z(f)} &= \iota_X({\rm vol}_{\R^n}) \\ &= \iota_X(\dd{x^1}\wedge\cdots\wedge\dd{x^n}) \\ &= \sum_i (-1)^{i-1}\dd{x^i}(X) \dd{x^1}\wedge\dots\wedge \widehat{\dd{x^i}} \wedge\dots\wedge\dd{x^n} \\ &= \frac1{\|\operatorname{grad}f\|} \sum_i (-1)^{i-1} \pdv{f}{x^i} \dd{x^1}\wedge\dots\wedge \widehat{\dd{x^i}} \wedge\dots\wedge\dd{x^n}. } \]

Claim 14.4 (高斯映射与体积形式) 设 \(M\) 为 \(\R^{n+1}\) 中紧致定向超曲面, \(M\) 的高斯曲率 \(K\), 高斯映射 \(\nu:M\to S^n\), 则 \[ \nu^*({\rm vol}_{S^n}) = (-1)^n K {\rm vol}_M. \]

Pf 设 \(T_pM\) 的一个正交归一正定向基底 \(X_1,\dots,X_n\), 根据诱导定向的定义, 单位法向量 \(N_p\) 与此基底合起来构成 \(T_p\R^{n+1}\) 的一个正交归一正定向基底 \(N_p,X_1,\dots,X_n\). 注意 \(N_p\) 也是球面的单位法向量, 于是 \[ \Align{ (\nu^*{\rm vol}_{S^n})(X_1,\dots,X_n) &= {\rm vol}_{S^n}(\nu_{*,p}X_1,\dots,\nu_{*,p}X_n) \\ &= {\rm vol}_{\R^{n+1}}(N_p,\nu_{*,p}X_1,\dots,\nu_{*,p}X_n) \\ &= \det(N_p,\nu_{*,p}X_1,\dots,\nu_{*,p}X_n). } \] 下面计算这个行列式. 考虑有直和分解 \[ \Align{ T_{p}\R^{n+1} &= \operatorname{span}(N_p)\oplus T_pM, \\ T_{\nu(p)}\R^{n+1} &= \operatorname{span}(N_p)\oplus T_{\nu(p)}S^n, } \] 定义 \(T_{p}\R^{n+1}\to T_{\nu(p)}\R^{n+1}\) 的线性映射 \(\varphi={\rm id}\oplus\nu_{*,p}\), 满足 \[ \Align{ \varphi(N_p) &= N_p, & \varphi(X_i) &= \nu_{*,p}X_i\quad(i=1,\dots,n), } \] 根据行列式的性质, \(\det\varphi=(\det{\rm id})(\det{\nu_{*,p}})=\det\nu_{*,p}\), 所以 \[ \Align{ \det(N_p,\nu_{*,p}X_1,\dots,\nu_{*,p}X_n) &= (\det\circ\varphi^{\times n})(N_p,X_1,\dots,X_n) \\ &= (\det\varphi)\det(N_p,X_1,\dots,X_n) \\ &= (\det\nu_{*,p})\det(N_p,X_1,\dots,X_n) \\ &= (-1)^nK_p {\rm vol}_M(X_1,\dots,X_n). } \]

15 The Gauss-Bonnet Theorem

15.1 Angle function

切空间 \(T_pM\) 中任意两个向量 \(u,v\) 的夹角 \(\zeta\) 定义为 \[ \cos\zeta = \frac{\lr{u,v}}{\|u\|\cdot\|v\|}, \] 于是 \(\zeta\) 可以在相差 \(2\pi\) 的整数倍的意义下确定.

设开集 \(U\) 上有正定向的标架 \(e_1,e_2\), 光滑曲线 \(c:[a,b]\to U\). 设 \(\underline\zeta(t)\) 为 \(e_{1,c(t)}\) 与 \(c'(t)\) 的夹角, 则 \(\underline{\zeta}\) 为 \([a,b]\) 到 \(\R/2\pi\Z\) 的函数, 并且它是光滑的, 因为在局部上, \(\underline\zeta(t)\) 为 \(\cos^{-1}\lr{c'(t),e_{1,c(t)}}/\|c'(t)\|\) 的一个分支.

下面我们将 \(\underline\zeta\) 的值域提升到 \(\R\) 上. 令 \(\zeta_0\) 是满足 \[ \cos\zeta_0 = \frac{\lr{c'(a),e_{1,c(a)}}}{\|c'(a)\|} \] 的一个数. 因为 \(\R\) 是 \(\R/2\pi\Z\) 的覆叠空间且 \([a,b]\) 单连通, 根据覆叠空间的理论, 存在唯一的光滑映射 \(\zeta:[a,b]\to\R\), 满足初值 \(\zeta(a)=\zeta_0\) 且使下图交换: \[ \xymatrix{ & \R \ar@{->>}[d] \\ [a,b] \ar@{.>}[ur]^{\zeta} \ar[r]_{\underline\zeta} & \R/2\pi\Z. } \] 称 \(\zeta:[a,b]\to\R\) 是以 \(\zeta_0\) 为初值的角度函数(angle function). 标架 \(e_1,e_2\) 下, 任意两个曲线 \(c\) 的角度函数相差 \(2\pi\) 的整数倍.

Example 设单位圆 \(c:\R\to\R^2\), \(c(t)=(\cos{t},\sin{t})\), 标架 \(e_1=(1,0)\), \(e_2=(0,1)\), 则 \[ \zeta(t) = t+\frac\pi2+2k\pi, \] 是以 \(\pi/2+2k\pi\) 为初值的角度函数, 常数 \(k\in\Z\).

15.2 Geodesic curvature

考虑黎曼流形 \(M\) 上的弧长参数化的曲线 \(\gamma:[a,b]\to M\), 于是 \(T(s)=\gamma'(s)\) 的长度恒为 \(1\). 曲线 \(\gamma\) 是一条测地线, 当且仅当协变导数 \({\rm D}T/\dd{s}\equiv0\). 于是, 可以用 \(\|{\rm D}T/\dd{s}\|\) 来衡量 \(\gamma\) 偏离测地线的程度, 该值称为 \(\gamma(s)\) 的测地曲率(geodesic curvature): \[ \tilde\kappa_g := \norm{ \frac{{\rm D}T}{\dd{s}} }. \] 对于一个可定向的二维黎曼流形 \(M\), 我们可以取沿着 \(\gamma(s)\) 的法向量场 \(n(s)\) (即正交于 \(T(s)\)), 使得 \((T(s),n(s))\) 在 \(T_{\gamma(s)}M\) 中有正定向, 且正交归一. 因为 \(\lr{T,T}\equiv1\), 必然有 \[ \lr{\frac{{\rm D}T}{\dd{s}},T} = 0, \] 即 \({\rm D}T/\dd{s}\) 是法向量 \(n(s)\) 的倍数, 将这个倍数 \(\kappa_g\) 定义为 \(\gamma\) 的带符号测地曲率(signed geodesic curvature), 即 \[ \frac{{\rm D}T}{\dd{s}} = \kappa_gn, \quad\textsf{或者}\quad \kappa_g = \lr{ \frac{{\rm D}T}{\dd{s}},n }. \]

• 回顾平面曲线的无符号曲率(curvature)与有符号曲率(signed curvature), \[ \tilde\kappa = \norm{ \dv{T}{s} },\quad \kappa = \lr{ \dv{T}{s},n }, \] 可以发现, 测地曲率和有符号测地曲率分别是上面两者的推广.
• 带符号测地曲率在 \(\gamma\) 上的积分 \(\int_a^b\kappa_g\dd{s}\) 称为 \(\gamma\) 的全测地曲率(total geodesic curvature).

Claim 15.1 设定向二维黎曼流形 \(M\), 开集 \(U\) 上有正定向的正交归一标架 \(e_1,e_2\), 该标架下黎曼联络形式为 \(\omega^1_2\), 则弧长参数曲线 \(\gamma\) 的测地曲率 \[ \kappa_g = \dv{\zeta}{s} - \omega^1_2(T). \]

Pf 根据几何关系, \(T\) 和 \(n\) 在标架下展开为 \[ \Align{ T &= (\cos\zeta)e_1 + (\sin\zeta)e_2, \\ n &= (-\sin\zeta)e_1 + (\cos\zeta)e_2, } \] 于是 \[ \Align{ \frac{{\rm D}T}{\dd{s}} &= (T\cos\zeta)e_1+(\cos\zeta)\frac{{\rm D}e_1}{\dd{s}} +(T\sin\zeta)e_2+(\sin\zeta)\frac{{\rm D}e_2}{\dd{s}} \\ &= \dv{\cos\zeta}{s}e_1 + (\cos\zeta)\omega^2_1(T)e_2 +\dv{\sin\zeta}{s}e_2 + (\sin\zeta)\omega^1_2(T)e_1 \\ &=-\sin\zeta\pqty{\dv{\zeta}{s}-\omega^1_2(T)}e_1 +\cos\zeta\pqty{\dv{\zeta}{s}+\omega^2_1(T)}e_2 \\ &= \pqty{\dv{\zeta}{s}-\omega^1_2(T)}n. } \]

Claim 15.2 设定向二维黎曼流形 \(M\), 弧长参数曲线 \(\gamma:[a,b]\to M\) 的像是一个一维带边子流形 \(C\). 若 \(C\) 处在标架开集 \(U,e_1,e_2\) (正定向) 内, 联络形式 \(\omega^1_2\), 则 \[ \int_a^b\kappa_g\dd{s} = \zeta(b)-\zeta(a)-\int_C\omega^1_2. \]

Pf 注意 \(\gamma^{-1}:C\to[a,b]\) 是 \(C\) 上的坐标函数, 所以 \[ \int_C\omega^1_2 = \int_a^b\gamma^*\omega^1_2. \] 设 \(\gamma^*\omega^1_2=f(s)\dd{s}\), 其中 \(s\) 是 \([a,b]\) 的坐标. 两边作用于 \(\dv{s}\) 得到 \[ \Align{ f(s) = f(s)\dd{s}\pqty{\dv{s}} = (\gamma^*\omega^1_2)\pqty{\dv{s}} = \omega^1_2\pqty{ \gamma_*\dv{s} } = \omega^1_2(T), } \] 结合 Claim 15.1, \[ \Align{ \int_a^b\kappa_g\dd{s} &= \int_a^b\dv{\zeta}{s}\dd{s} - \int_a^b\omega^1_2(T)\dd{s} \\ &= \zeta(b)-\zeta(a)-\int_a^b\gamma^*\omega^1_2 \\ &= \zeta(b)-\zeta(a)-\int_C\omega^1_2. } \]

15.3 Gauss-Bonnet for a polygon

二维黎曼流形 \(M\) 中的一个多边形(polygon)指的是一个简单分段光滑闭曲线 \(\gamma:[a,b]\to M\); "简单"指的是不自交, "闭"指的是 \(\gamma(a)=\gamma(b)\). 多边形同样有弧长参数化的概念, \(\gamma\) 为弧长参数化的, 当且仅当其在每一个光滑小段上的切向量长度为 \(1\). 多边形的顶点(vertices)就是不光滑点 \(\gamma(s_0),\gamma(s_1),\dots,\gamma(s_m)\), 其中 \(a=s_0<\cdots<s_m=b\).

设 \(\gamma\) 为可定向二维黎曼流形 \(M\) 中的多边形, 记 \(C\) 为 \(\gamma\) 的像, \(R\) 为 \(C\) 的内部, \(K\) 为 \(M\) 的高斯曲率. 在顶点 \(\gamma(s_i)\) 处, 令 \(\gamma'(s_i^-)\) 为前一段 \(\gamma|_{[s_{i-1},s_i]}\) 在 \(s_i\) 处的切向量; \(\gamma'(s_i^+)\) 为后一段 \(\gamma|_{[s_i,s_{i+1}]}\) 在 \(s_i\) 处的切向量. \(\gamma'(s_i^-)\) 和 \(\gamma'(s_i^+)\) 所夹的在 \((-\pi,\pi)\) 间的角度 \(\varepsilon_i\) 称为 \(\gamma(s_i)\) 处的跳跃角(jumping angle), 补角 \[ \beta_i:=\pi-\varepsilon_i \] 称为 \(\gamma(s_i)\) 的内角(interior angle).

在每条边(edge) \(\gamma([s_{i-1},s_i])\) 上, 切向量 \(T\) 的角度变化为 \(\Delta\zeta_i=\zeta(s_i)-\zeta(s_{i-1})\). 在顶点处, 切向量角度跳变 \(\varepsilon_i\). 于是, 切向量在整个多边形上的角度变化为 \[ \sum_{i=1}^m\Delta\zeta_i + \sum_{i=1}^m\varepsilon_i. \] 一个多边形称称为正定向的, 若切向量 \(T\) 与 \(R\) 在边界 \(C\) 上的诱导定向相同.

Claim 15.3 (Hopf Umlaufsatz) 设定向二维黎曼流形 \(M\) 上的标架开集 \((U,e_1,e_2)\) 内有正定向的多边形 \(\gamma:[a,b]\to U\), 那么其切向量 \(T'(s)=\gamma'(s)\) 的角度变化 \[ \sum_{i=1}^m\Delta\zeta_i + \sum_{i=1}^m\varepsilon_i = 2\pi. \]

• 这说明, 尽管角度函数 \(\zeta\) 和跳跃角 \(\varepsilon_i\) 都是依赖于标架的选取的, 但是整条曲线的角度变化却不依赖于标架.

Pf 我们只证明平面曲线的情形. 要推广到 \(M\) 上的曲线, 可参考 John M. Lee 黎曼流形的 p. 272 Lemma 9.2.

设 \(\R^2\) 中弧长参数化的简单闭曲线 \(\gamma:[0,l]\to\R^2\), 不妨先假设 \(\gamma\) 是光滑的. 设 \(C=\gamma([0,l])\). 因为 \(C\) 紧, 故有界, 进而存在一条直线, 使 \(C\) 在直线的一侧. 平移直线使得其与 \(C\) 相切, 通过适当平移与旋转, 令该直线与 \(x\) 轴重合, 且切点为 \(\gamma(0)=(0,0)\).

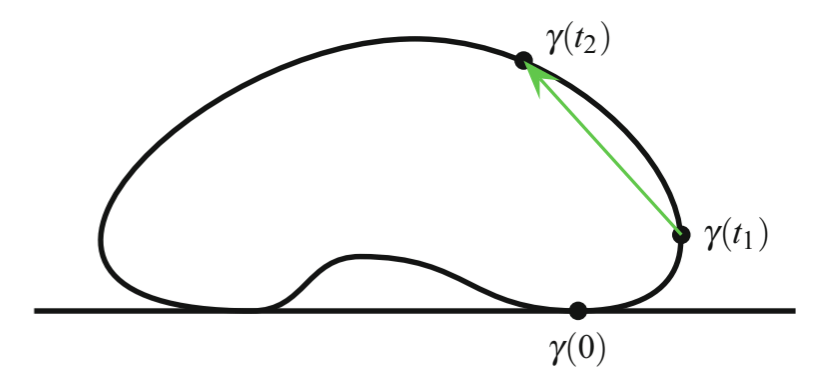
对于 \(0\leq t_1<t_2\leq l\), 记 \(\bar\alpha(t_1,t_2)\) 是向量 \(\gamma(t_2)-\gamma(t_1)\) 与 \(x\) 轴正方向的夹角. 对于 \(t_1=t_2\),记 \(\bar\alpha(t_1,t_2)\) 是切向量 \(\gamma'(t_1)\) 与 \(x\) 轴正方向的夹角.

于是我们定义出了这样一个二元函数 \(\bar\alpha\). 设 \(O=(0,0)\), \(A=(0,l)\), \(L=(l,l)\), 记 \(T\) 是 \(OAL\) 围成的闭三角形区域, 则 \(\bar\alpha:T\to\R/2\pi\Z\) 在闭三角形 \(T\) 上连续, 在开三角形上光滑. 因为 \(T\) 单连通, \(\bar\alpha\) 提升为 \(T\to\R\) 的连续函数 \(\alpha\), 且 \(\alpha\) 在开三角形上光滑.

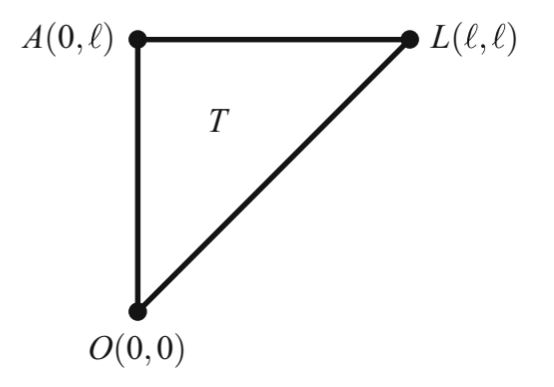
我们有 \(T\) 上的 \(1\)-形式 \(\dd\alpha\), 于是 \(\gamma\) 的角度变化由下面的积分给出: \[ \int_{\overline{OL}} \dd\alpha = \alpha(L)-\alpha(O) = \zeta(l) - \zeta(0). \] 由 Stokes 定理, \[ \int_{\partial T}\dd\alpha = \int_T\dd\dd\alpha = 0, \] 其中 \(\partial{T}=\overline{OL}+\overline{LA}+\overline{AO}\). 这意味着 \[ \Align{ \int_{\overline{OL}}\dd\alpha &= \int_{\overline{OA}}\dd\alpha + \int_{\overline{AL}}\dd\alpha \\ &= (\alpha(A)-\alpha(O)) + (\alpha(L)-\alpha(A)). } \] 其中, \(\alpha(O)=\alpha(0,0)=0\), \(\alpha(A)=\alpha(0,l)=\pi\), \(\alpha(L)=\alpha(l,l)=2\pi\), 于是 \[ \zeta(l)-\zeta(0)=\int_{\overline{OL}}\dd\alpha=2\pi. \] 最后, 对于分段光滑的曲线 \(\gamma:[0,l]\to\R^2\), 将顶点 "平滑化", 即用一段光滑弧线代替. 所得的光滑曲线和原曲线具有相同的角度改变.

Claim 15.4 (多边形的 Gauss-Bonnet 定理) 设定向二维黎曼流形 \(M\), 正交归一且正定向的标架开集 \((U,e_1,e_2)\). 设正定向的, 弧长参数的多边形 \(\gamma:[a,b]\to U\), 则 \[ \int_a^b\kappa_g\dd{s} = 2\pi - \sum_{i=1}^m\varepsilon_i - \int_R K\,{\rm vol}. \]

Pf 根据上一小节 Claim 15.2 和 Hopf Umlaufsatz, \[ \Align{ \int_a^b\kappa_g\dd{s} &= \sum_{i=1}^m\int_{s_{i-1}}^{s_i}\kappa_g\dd{s} \\ &= \sum_{i=1}^m\Delta\zeta_i - \int_C\omega^1_2 \\ &= 2\pi - \sum_{i=1}^m \varepsilon_i - \int_C\omega^1_2. } \] 回忆 "曲率与微分形式" 中, 高斯曲率的公式 \[ \Omega^1_2 = \dd\omega^1_2 = K\theta^1\wedge\theta^2, \] 因为 \(e_1,e_2\) 正交归一且正定向, 所以 \(\theta^1\wedge\theta^2\) 为 \(M\) 的黎曼体积形式. 应用 Stokes 定理有 \[ \Align{ \int_C\omega^1_2 &= \int_{\partial R}\omega^1_2 \\ &= \int_R\dd\omega^1_2 \\ &= \int_R K\theta^1\wedge\theta^2 \\ &= \int_R K\,{\rm vol}. } \] 与前式结合便证明了定理.

一类最特殊的多边形是由测地线组成的多边形, 称为测地多边形(geodesic polygon), 它们相当于平面中直线段组成的多边形. 测地线的测地曲率恒为零, 由 Claim 15.4 做出如下推论.

Claim 15.5 设定向二维黎曼流形 \(M\), 测地多边形 \(\gamma\) 处于标架开集 \(U\) 内, 则 \(\gamma\) 的内角和 \[ \sum_{i=1}^m\beta_i = (m-2)\pi + \int_RK\,{\rm vol}. \]

于是我们能得到几个关于测地三角形的有趣结论.

Claim 15.6 设定向二维黎曼流形 \(M\), 测地三角形 \(\gamma\) 处于标架开集 \(U\) 内.

1. 若 \(\gamma\) 内部高斯曲率恒为零, 则 \(\gamma\) 内角和为 \(\pi\).
2. 若 \(\gamma\) 内部高斯曲率恒正, 则 \(\gamma\) 内角和大于 \(\pi\).
3. 若 \(\gamma\) 内部高斯曲率恒负, 则 \(\gamma\) 内角和小于 \(\pi\).

Example 球面三角形与双曲三角形.

球面 \(S^2\) 具有正曲率, 其上测地三角形(球面三角形)内角和大于 \(\pi\). 设球面的半径为 \(r\), 球面三角形的三个内角分别为 \(\alpha,\beta,\gamma\), 因为球面有常曲率 \(1/r^2\), 应用 Claim 15.5, \[ \Align{ \alpha+\beta+\gamma &= \pi+\int_R\frac{1}{r^2}{\rm vol} \\ &= \pi + \frac{1}{r^2}\textsf{Area}(R), \\ \iff \textsf{Area}(R) &= (\alpha+\beta+\gamma-\pi)r^2 } \] 给出了球面三角形的面积与内角和的关系.

双曲空间具有负曲率, 测地三角形内角和小于 \(\pi\). 考虑 Poincaré 圆盘上 \(\mathbb{D}\) 的测地三角形 \(ABC\), 让 \(A,B,C\) 趋近于 \(\mathbb{D}\) 的边界, 则 \(ABC\) 的内角和趋近于 \(0\).

15.4 Gauss-Bonnet for a surface

设紧致的二维定向黎曼空间 \(M\). 根据紧致性, \(M\) 能够被划分为若干多边形, 每个多边形都处在一个标架开集 \(U_\alpha\) 内. 我们称这样的多边形划分是足够细致(sufficiently fine)的. 设 \(V,E,F\) 分别为多边形的总定点数, 总边数, 总面数, 定义欧拉示性数(Euler characteristic) \[ \chi(M) := V-E+F. \]

Claim 15.7 (Gauss-Bonnet 定理) 对于一个紧致的定向二维黎曼空间 \(M\), \[ \int_M K\,{\rm vol} = 2\pi\chi(M). \]

Pf 对多边形划分的每个多边形应用 Gauss-Bonnet, 再求和 \[ \Align{ \int_M K\,{\rm vol} = \sum\int_RK\,{\rm vol} &= \sum 2\pi - \sum\sum_{i=1}^m\varepsilon_i -\sum\int_a^b\kappa_g\dd{s} \\ &= 2\pi F - \sum\sum_{i=1}^m(\pi-\beta_i) -\sum\int_a^b\kappa_g\dd{s}. } \] 注意到每条边的测地曲率都被一正一反积了两次, 相互抵消, 即上式第三项为零. 第二项展开为 \[ \sum\sum_{i=1}^m\pi - \sum\sum_{i=1}^m\beta_i \] 第一部分, \(\pi\) 被求和了 \(2E\) 次; 第二部分为内角总和, 即每个顶点处的内角和 \(2\pi\) 乘以总顶点数 \(V\). 因此 \(\sum\sum(\pi-\beta_i)=2\pi E-2\pi V\). 代入原式, \[ \int_MK\,{\rm vol} = 2\pi F - (2\pi E-2\pi V) = 2\pi\chi(M). \]

欧拉示性数 \(\chi(M)\) 是一个拓扑不变量. 紧致定向二维流形可以根据亏格(genus) \(g\), 即 "洞的个数", 来分类. 两个曲面微分同胚, 当且仅当它们具有相同的亏格. 亏格与欧拉示性数的关系 \[ \chi = 2-2g. \] 高斯曲率与流形上的黎曼度量有关, 但是曲率在流形上的积分却只与流形的拓扑有关.

Claim 15.8 若定向紧致二维黎曼流形处处具有正曲率, 则它与球面同胚.

Pf 根据 Gauss-Bonnet, \[ 2\pi\chi(M)=\int_MK\,{\rm vol} > 0, \] 于是 \(\chi(M)=2-2g>0\), 即 \(g<1\), 只能有 \(g=0\), 即与球面同胚.

15.5 Generalizations

对于 \(\R^{2n+1}\) 中的 \(2n\) 维紧致定向超曲面 \(M\), 我们之前定义了它的高斯曲率 \(K\) (为形状算子的行列式), 高维的 Gauss-Bonnet 定理指出, \[ \int_M K\,{\rm vol}_M = \frac{{\rm vol}(S^{2n})}{2}\chi(M). \] 其中 \({\rm vol}(S^{2n})\) 是 \(2n\) 维单位球面的表面积.

设 \(n\) 维流形 \(M,N\). 一个光滑映射 \(f:M\to N\) 的映射度(degree)定义为 \[ \deg{f} := \int_M f^*\omega, \] 其中 \(\omega\) 是 \(N\) 上的 \(n\)-形式, 且满足 \(\int_N\omega=1\).

• 设 \(\R^2\) 中的光滑闭曲线 \(c:[a,b]\to\R^2\), 映射 \(\varphi:[a,b]\to S^1\) 给出每一点的单位切向量 \[ \varphi(t) = \frac{c'(t)}{\|c'(t)\|}, \] 则 \(\varphi\) 的映射度为 \[ \deg\varphi = \int_{[a,b]}\varphi^*\pqty{\frac{\dd\theta}{2\pi}} = \frac1{2\pi}\int_{[a,b]} \dd(\theta\circ\varphi) = \frac1{2\pi}\int_{[a,b]}\dd\zeta = \frac{\zeta(b)-\zeta(a)}{2\pi} \] 即曲线的切向量的角度改变除以 \(2\pi\), 可以看作切向量旋转的圈数, 称为旋转指数(rotation index).

• 设 \(\R^{2n+1}\) 中的紧致定向超曲面 \(M\), 考虑高斯映射 \(\nu:M\to S^{2n}\) 的映射度. 取 \(\omega={\rm vol}_{S^{2n}}/{\rm vol}(S^{2n})\), 则 \[ \Align{ \deg\nu &= \int_M \nu^*\pqty{\frac{{\rm vol}_{S^{2n}}}{{\rm vol}(S^{2n})}} \\ &= \frac1{{\rm vol}(S^{2n})} \int_M K{\rm vol}_M \\ &= \frac1{{\rm vol}(S^{2n})} \frac{{\rm vol}(S^{2n})}{2}\chi(M) \\ &= \frac{\chi(M)}2. } \]