GTM275 | 4 测地线

GTM275 (Differential Geometry: Connections, Curvature, and Characteristic Classes) 第 13-15 节的笔记.

10 More on Affine Connections

在研究测地线之前, 我们先补充一些关于仿射联络的内容. 先介绍克氏符, 再介绍仿射联络诱导出来的"沿着曲线的导数". 联络形式是向量丛上的联络借标架的体现, 而克氏符则是仿射联络借坐标系的体现.

10.1 Christoffel symbols

某一标架下的联络形式能够描述仿射联络, 特别地, 当我们取坐标基底为标架时, 得到的就是克氏符.

• 坐标基底场 \(\qty{\partial_i=\pdv{x^i}}\) 比切丛上的标架 \(\qty{e_i}\) 性质更好, 坐标基底的李括号为零: \([\partial_i,\partial_j]=0\).

设 \(\nabla\) 为流形 \(M\) 上的仿射联络, \((U,x^1,\dots,x^n)\) 为一坐标开集, \(\qty{\partial_i}\) 为坐标基底场. 回顾联络形式的定义, 向量场 \(\nabla_{\partial_i}\partial_j\) 能展开为 \[ \nabla_{\partial_i}\partial_j = \sum_k \omega^k_j(\partial_i)\partial_k. \] 其中 \(\omega^k_j(\partial_i)\) 是联络形式在此坐标基底下的分量, 记 \(\Gamma^k_{ij}=\omega^k_j(\partial_i)\), 这 \(n^3\) 个函数称为联络 \(\nabla\) 在该坐标系下的克氏符(Christoffel symbols). 于是 \[ \nabla_{\partial_i}\partial_j = \sum_k \Gamma^k_{ij}\partial_k. \] 设向量场 \(X=\sum X^i\partial_i\), \(Y=\sum Y^i\partial_i\), \[ \Align{ \nabla_XY &= \nabla_{X^i\partial_i}(Y^j\partial_j) \\ &= X^i \nabla_{\partial_i}(Y^j\partial_j) \\ &= X^i \partial_i(Y^j)\partial_j + X^iY^j\nabla_{\partial_i}\partial_j \\ &= [X^i \partial_i(Y^k) + X^iY^j\Gamma^k_{ij}]\partial_k. } \] 给出了向量场的联络与普通偏导数的关系.

Claim 10.1 流形 \(M\) 上的仿射联络 \(\nabla\) 无挠, 当且仅当在任意坐标系 \((U,x^1,\dots,x^n)\) 上, 克氏符的两个下标是对称的, 即 \[ \Gamma^k_{ij} = \Gamma^k_{ji}. \] 所以无挠联络也叫做对称联络.

• 由于对称性, 黎曼联络克氏符的 \(n^3\) 个分量中, 只有 \(\frac12n^2(n+1)\) 个独立分量.

Pf 设联络无挠. 在任意坐标系下, \([\partial_i,\partial_j]=0\). 由无挠性, \[ \nabla_{\partial_i}\partial_j-\nabla_{\partial_j}\partial_i = [\partial_i,\partial_j] = 0, \] 即 \[ \sum_k\Gamma^k_{ij}\partial_k + \sum_k\Gamma^k_{ji}\partial_k = 0, \] 所以 \(\Gamma^k_{ij}=\Gamma^k_{ji}\).

设任意坐标系下的克氏符对称, 于是 \(\nabla_{\partial_i}\partial_j=\nabla_{\partial_j}\partial_i\), 进而 \[ T(\partial_i,\partial_j) = \nabla_{\partial_i}\partial_j -\nabla_{\partial_j}\partial_i -[\partial_i,\partial_j] = 0. \] 由挠率的 \(\cal F\)-线性性, \(T(X,Y)=0\).

计算黎曼联络的克氏符, 既可以利用标架, 算出联络形式, 再导出克氏符; 也可以借助坐标系, 利用黎曼度量计算.

黎曼度量 \(\lr{\cdot,\cdot}\) 作为双 \({\cal F}\)-线性映射, 构成 \(M\) 上的张量场. 在标架开集 \((U,e_1,\dots,e_n)\) 下, 黎曼度量的分量记作 \(g_{ij}=\lr{e_i,e_j}\). \([g_{ij}]\) 是一个 \(n\times n\)​ 的正定矩阵, 其逆矩阵记作 \([g^{ij}]\), 两者相乘为单位阵, 即 \[ \sum_j g_{ij}g^{jk} = \delta_i^k. \]

Claim 10.2 设黎曼流形 \(M\), 坐标系 \((U,x_1,\dots,x_n)\). 度量分量 \([g_{ij}]\), 则黎曼联络的克氏符 \[ \Gamma^k_{ij} = \frac12\sum_l g^{kl}\pqty{ \pdv{g_{li}}{x^j} + \pdv{g_{lj}}{x^i} - \pdv{g_{ij}}{x^l} }. \]

Pf 下面要用到之前证明黎曼度量存在唯一性时导出的 Koszul 公式: 对 \(X,Y,Z\in{\frak X}(M)\), \[ \Align{ 2\lr{\nabla_XY,Z} = \; &X\lr{Y,Z}+Y\lr{Z,X}-Z\lr{X,Y}+{} \\ &\lr{[X,Y],Z}-\lr{[Y,Z],X}-\lr{Y,[X,Z]}. } \] 令 \(X=\partial_i\), \(Y=\partial_j\), \(Z=\partial_l\), 注意 \(X,Y,Z\) 两两对易, 有 \[ \Align{ 2\lr{\nabla_{\partial_i}\partial_j,\partial_l} &= \partial_i\lr{\partial_j,\partial_l} +\partial_j\lr{\partial_l,\partial_i} -\partial_l\lr{\partial_i,\partial_j} \\ &= \pdv{g_{lj}}{x^i}+\pdv{g_{li}}{x^j}-\pdv{g_{ij}}{x^l}. } \] 其中, 左边 \[ \Align{ 2\lr{\nabla_{\partial_i}\partial_j,\partial_l} &= 2\sum_m\lr{ \Gamma^m_{ij}\partial_m,\partial_l } \\ &= 2\sum_m\Gamma^m_{ij} g_{ml}, } \] 左右两边乘以 \([g^{kl}]\), 得到 \[ \Align{ 2\sum_{m,l}\Gamma^m_{ij} g_{ml}g^{kl} &= \sum_l g^{kl}\pqty{\pdv{g_{lj}}{x^i}+\pdv{g_{li}}{x^j}-\pdv{g_{ij}}{x^l}} \\ \iff\quad \Gamma^k_{ij} &= \frac12 \sum_l g^{kl}\pqty{\pdv{g_{lj}}{x^i}+\pdv{g_{li}}{x^j}-\pdv{g_{ij}}{x^l}}. } \]

Example 双曲模型. 在 Poincaré 圆盘 \(\mathbb{D}\) 的坐标系 \((\mathbb{D},x,y)\) 下, 度量分量 \[ \Align{ g_{11}&=g_{22}=\frac{4}{(1-|z|^2)^2}, & g_{12}&=g_{21}=0, \\ g^{11}&=g^{22}=\frac{(1-|z|^2)^2}{4}, & g^{12}&=g^{21}=0. } \] 导数 \[ \partial_1g_{11}=\partial_1g_{22}=\frac{16x}{(1-|z|^2)^3},\quad \partial_2g_{11}=\partial_2g_{22}=\frac{16y}{(1-|z|^2)^3}. \] 计算克氏符. 因为度量有两个分量为零, 所以计算过程其实没有想象中那么复杂. 这里给出结果: \[ \begin{array}{|c|c|c|} \hline k,ij & 11 & 12 & 21 & 22 \\ \hline 1 & \dfrac{2x}{1-|z|^2} & \dfrac{2y}{1-|z|^2} & \dfrac{2y}{1-|z|^2} & \dfrac{-2x}{1-|z|^2} \\ \hline 2 & \dfrac{-2y}{1-|z|^2} & \dfrac{2x}{1-|z|^2} & \dfrac{2x}{1-|z|^2} & \dfrac{2y}{1-|z|^2} \\ \hline \end{array} \] 同样, 还可以算出 Poincaré 上半平面的克氏符: \[ \begin{array}{|c|c|c|} \hline k,ij & 11 & 12 & 21 & 22 \\ \hline 1 & 0 & -1/y & -1/y & 0 \\ \hline 2 & 1/y & 0 & 0 & -1/y \\ \hline \end{array} \]

10.2 Covariant derivative along a curve

设流形 \(M\) 上的光滑曲线 \(c:[a,b]\to M\), 则沿着曲线 \(c\) 的向量场 (vector field along \(c\)) 指的是 \[ V:[a,b]\to\coprod_{t\in[a,b]} T_{c(t)}M, \] 而且 \(V(t)\in T_{c(t)}M\). 向量场 \(V(t)\) 称为光滑的, 如果对任意光滑函数 \(f:M\to\R\), \(V(t)f\) 都是光滑的. 曲线 \(c\) 上的所有光滑向量场的全体记作 \(\Gamma(TM|_{c(t)})\).

设流形 \(M\) 上的仿射联络 \(\nabla\), 光滑曲线 \(c:[a,b]\to M\). 沿着曲线 \(c\) 的协变导数(covariant derivative)指的是映射 \[ \frac{\rm D}{\dd{t}}:\Gamma(TM|_{c(t)})\to\Gamma(TM|_{c(t)}), \] 并且满足下列条件:

1. \({\rm D}V/\dd{t}\) 关于 \(V\) 是 \(\R\)-线性的.

2. (Leibniz 律) 对任意 \([a,b]\) 上的光滑函数 \(f\), \[ \frac{{\rm D}(fV)}{\dd{t}} = \dv{f}{t}V+f\frac{{\rm D}V}{\dd{t}}. \]

3. (与 \(\nabla\) 适配) 若 \(\tilde{V}\in{\frak X}(M)\) 为 \(V\in\Gamma(TM|_{c(t)})\) 的任意一个光滑延拓 (即有 \(\tilde{V}_{c(t)}=V(t)\)), 则 \[ \frac{{\rm D}V}{\dd{t}}(t) = \nabla_{c'(t)}\tilde{V}. \]

Claim 10.3 任给联络 \(\nabla\) 和光滑曲线 \(c\), 存在唯一的沿着曲线 \(c\)​ 的协变导数算子.

Pf 假设协变导数存在. 在标架开集 \((U,e_1,\dots,e_n)\) 上, 沿着 \(c\) 的向量场 \(V(t)=\sum v^i(t)e_{i,c(t)}\). 有 \[ \Align{ \frac{{\rm D}V}{\dd{t}} &= \sum_i \frac{{\rm D}(v^ie_{i,c(t)})}{\dd{t}} \\ &= \sum_i \dv{v^i}{t}e_{i,c(t)} + v^i\frac{{\rm D}e_{i,c(t)}}{\dd{t}} \\ &= \sum_i \dv{v^i}{t}e_{i,c(t)} + v^i\nabla_{c'(t)}e_{i}. } \] 因此若协变导数存在, 则它是唯一的.

我们以上式作为协变导数的定义, 容易验证其满足三个条件. 还需验证上式与标架的选取无关. 设 \(U\) 上的另一个标架 \(\bar{e}_1,\dots,\bar{e}_n\), \(V(t)=\sum\bar{v}^i(t)\bar{e}_{i,c(t)}\), 该标架下的协变导数为 \[ \frac{{\rm\bar D}V}{\dd{t}} = \sum_i \dv{\bar v^i}{t}\bar e_{i,c(t)} + \bar v^i\nabla_{c'(t)}\bar e_{i,c(t)}, \] 也满足三个条件, 根据唯一性, \({\rm\bar D}V/\dd{t}={\rm D}V/\dd{t}\). 取 \(M\) 的标架开覆盖, 能够将协变导数定义到整条曲线 \(c\) 上.

Claim 10.4 (协变导数的链式法则) 设曲线 \(c:[a,b]\to M\), 光滑函数 \(u:[a,b]\to[a,b]\). 若 \(V(t)\) 是沿着 \(c\) 的光滑向量场, 则 \(W=V\circ u\) 是沿着 \(\bar{c}=c\circ u\) 的光滑向量场. 设 \({\rm D}/\dd{t}\) 和 \({\rm\bar D}/\dd{t}\) 分别代表沿着两条曲线的协变导数, 则 \[ \eval{ \frac{{\rm\bar D}W}{\dd{t}} }_t = \eval{\frac{{\rm D}V}{\dd{t}}}_{u(t)} \eval{\dv{u}{t}}_t. \]

Pf 若 \(V(t)\) 是沿着 \(c\) 的向量场, 即 \(V(t)\in T_{c(t)}M\), 则 \(W(t)=V(u(t))=T_{c(u(t))}M\), 因此 \(W\) 是沿着重参数化后的曲线 \(\bar{c}=c\circ u\) 的向量场.

下面证明链式法则. 只需在标价开集 \((U,e_1,\dots,e_n)\) 上验证. 设 \(V(t)=\sum v^i(t)e_{i,c(t)}\), 则 \[ W(t) = \sum w^i(t) e_{i,\bar{c}(t)}, \] 其中 \(w^i=v^i\circ u\). 带入协变导数的局部定义式, \[ \Align{ \frac{{\rm\bar D}W}{\dd{t}} &= \sum_i \dv{w^i}{t}e_{i,\bar c(t)} + w^i\nabla_{\bar c'(t)}e_{i} \\ &= \sum_i \dv{v^i}{u} u'(t) e_{i,\bar c(t)} + w^i\nabla_{c'(u(t))u'(t)}e_i \\ &= \sum_i \dv{v^i}{u} u'(t) e_{i,\bar c(t)} + w^i u'(t) \nabla_{c'(u(t))}e_i \\ &= u'(t)\pqty{ \sum_i \dv{v^i}{u} e_{i,\bar c(t)} + w^i \nabla_{c'(u(t))}e_i } \\ &= u'(t) \eval{\frac{{\rm D}V}{\dd{t}}}_{u(t)}. } \] 其中, 第二个等号利用了求导的链式法则; 第三个等号利用了 \(\nabla\) 的 \({\cal F}\)-线性性将 \(u'(t)\) 拿出来.

Claim 10.5 (黎曼流形上的协变导数) 设黎曼流形 \(M\), 黎曼联络 \(\nabla\), 光滑曲线 \(c\) 上的协变导数 \({\rm D}/\dd{t}\).

1. 对任意 \(V,W\in\Gamma(TM|_{c(t)})\), \[ \dv{t}\lr{V,W} = \lr{ \frac{{\rm D}V}{\dd{t}}, W } + \lr{ V, \frac{{\rm D}W}{\dd{t}} }. \]

2. 设 \(c\) 的像在嵌入子流形 \(S\) 内. 子流形 \(S\) 的黎曼联络为 \(\nabla'={\rm pr}(\nabla)\), \(S\) 上沿着 \(c\) 的协变导数为 \[ \frac{\rm D'}{\dd{t}}:\Gamma(TS|_{c(t)})\to\Gamma(TS|_{c(t)}), \] 则 \[ \frac{{\rm D}'V}{\dd{t}} = {\rm pr}\pqty{ \frac{{\rm D}V}{\dd{t}} }. \]

Pf 第一条, 取局部正交归一标架 \(e_1,\dots,e_n\) 后不难证明. 第二条根据协变导数的公理 3 是很显然的.

我们知道, 设流形 \((M,\nabla)\), 微分同胚 \(f:M\to\tilde{M}\) 能够将 \(M\) 上的联络搬到 \(\tilde{M}\) 上去, 定义出一个 \(\tilde{M}\) 上的联络 \(\tilde\nabla\): \[ \tilde\nabla_{f_*X}f_*Y = f_*(\nabla_XY). \] 从另一个角度看, 若有流形 \((M,\nabla)\) 和 \((\tilde{M},\tilde\nabla)\), 一个满足上式的微分同胚 \(f:M\to\tilde{M}\) 称为保持联络的(connection-preserving).

• 可以证明, 黎曼流形之间的等距同构保持黎曼联络.

设 \(V\) 是一个沿着 \(c\) 的向量场, 则其在微分同胚 \(f\) 下的推前 \(f_*V\) 是一个沿着 \(f\circ c\) 的向量场, 定义为 \[ (f_*V)(t) := f_{*,c(t)}(V(t)). \]

Claim 10.6 设保持联络的微分同胚 \(f:(M,\nabla)\to(\tilde{M},\tilde\nabla)\), 光滑曲线 \(c:[a,b]\to M\) 和 \(f\circ c:[a,b]\to\tilde{M}\). 记 \({\rm D}/\dd{t}\) 和 \({\rm\tilde{D}}/\dd{t}\) 分别为沿着 \(c\) 和 \(f\circ c\) 的协变导数, 则 \[ \frac{{\rm\tilde D}(f_*V)}{\dd{t}} = f_*\pqty{ \frac{{\rm D}V}{\dd{t}} }, \quad V\in\Gamma(TM|_{c(t)}). \]

Pf 设 \(V\in\Gamma(TM|_{c(t)})\), \(\bar{V}\in\Gamma(TM)\) 为其延拓, 则 \(f_*\bar{V}\) 是 \(f_*V\) 的延拓, 这从定义直接看出: \[ (f_*\bar{V})_{f(c(t))} = f_{*,c(t)}\bar{V}_{c(t)} = f_{*,c(t)}V(t) = (f_*V)(t). \] 再由 \(f\) 保联络的定义和保持切向量的性质, \[ f_*\pqty{ \frac{{\rm D}V}{\dd{t}} } = f_*(\nabla_{c'(t)}\bar{V}) = \tilde{\nabla}_{f_*c'(t)}f_*\bar{V} = \tilde{\nabla}_{(f\circ c)'(t)}f_*\bar{V} = \frac{{\rm\tilde D}(f_*V)}{\dd{t}}. \]

最后推导协变导数的坐标表示. 设点 \(p=c(t_0)\), \(p\) 的邻域 \(U\) 上有标架 \(e_1,\dots,e_n\), 联络矩阵 \([\omega^i_j]\). 若 \(V(t)=\sum V^i(t)e_{i,c(t)}\), 则 \[ \Align{ \frac{{\rm D}V}{\dd{t}} &= \sum_i\dv{V^i}{t}e_{i,c(t)} + \sum_iV^i\frac{{\rm D}e_{i,c(t)}}{\dd{t}} \\ &= \sum_i\dv{V^i}{t}e_{i,c(t)} + \sum_jV^j\nabla_{c'(t)}e_j \\ &= \sum_i\dv{V^i}{t}e_{i,c(t)} + \sum_{i,j}V^j\omega^i_j(c'(t))e_{i,c(t)} \\ &= \sum_i\pqty{ \dv{V^i}{t} + \sum_jV^j\omega^i_j(c'(t)) } e_{i,c(t)}. } \] 特别地, 取坐标基底, 并且令 \(c'(t)=\sum T^k(t)\partial_{k,c(t)}\)​, 则有 \[ \Align{ \frac{{\rm D}V}{\dd{t}} &= \sum_i\pqty{ \dv{V^i}{t} + \sum_{j,k}V^jT^k\Gamma^i_{kj} } \partial_{i,c(t)} \\ &= \sum_k\pqty{ \dv{V^k}{t} + \sum_{i,j}\Gamma^k_{ij}T^iV^j } \partial_{i,c(t)}. } \]

11 Geodesics

11.1 Parallel translation

设流形 \(M\) 有仿射联络 \(\nabla\), 光滑曲线 \(c:I\to M\). 一个沿着曲线 \(c\) 的向量场 \(V(t)\) 若满足 \[ \frac{{\rm D}V}{\dd{t}} \equiv 0, \] 则称 \(V(t)\)​ 为沿着曲线平行(parallel)或平移的向量场.

若 \(V(t)\) 是沿着曲线 \(c:[a,b]\to M\) 平行的向量场, 则称 \(V(b)\) 是 \(V(a)\) 沿着 \(c\)​​ 平移(parallel translate / parallel transport)而来的向量.

平移的坐标表示. 在坐标系 \((U,x^1,\dots,x^n)\) 内, \(V(t)=\sum V^i(t)\partial_{i,c(t)}\), 则 \(V\) 沿着曲线平移当且仅当 \[ \dv{V^k}{t} + \sum_{i,j}\Gamma^k_{ij}T^iV^j = 0. \] 这是一个关于 \(V^i\) 的一阶线性常微分方程组. 根据解的存在唯一性定理, 给定初值 \(V(t_0)\) 后, 方程组在包含 \(t_0\) 的某区间内有唯一解. 下面还要证明, 解不仅在某个区间内存在, 还在 \(c\) 的整个定义区间 \(I\)​ 上存在. 实际上, 曲线 \(c:[a,b]\to M\)​ 也不必是光滑的, 只需要分段光滑(piecewise smooth): 存在区间 \([a,b]\) 的划分 \[ a=t_0<t_1<\cdots<t_r=b, \] 使得 \(c\) 在每个 \([t_i,t_{i+1}]\) 是光滑的 (\(i=0,\dots,r-1\)).

Claim 11.1 设流形 \((M,\nabla)\). 分段光滑曲线 \(c:[a,b]\to M\). 则任给 \(v_0\in T_{c(a)}M\), 唯一存在沿着 \(c\) 平移的向量场 \(V(t)\), 使得 \(V(a)=v_0\). 沿着 \(c\) 的平移诱导出了一个线性同构 \(\varphi_{a,b}:T_{c(a)}M\to T_{c(b)}M\)​​​.

• 平移能够将不同点处的切空间联系起来, 这也是"联络"名称的由来.

Pf 只需要考虑光滑曲线, 对于分段光滑曲线, 只需要在每一段上平移.

向量场 \(V(t)\) 的存在唯一性由常微分方程组的存在唯一性保证. 映射 \(\varphi_{a,b}\) 的线性性由线性齐次微分方程组的叠加原理保证, 其单射性由解的唯一性保证. 由于切空间维数相等, \(\varphi_{a,b}\) 为同构.

Claim 11.2 设黎曼流形 \(M\) 与黎曼联络 \(\nabla\), 则沿着曲线 \(c\) 的平移保持向量的内积. 换言之, \(\varphi_{a,b}\) 是切空间的等距同构.

Pf 设 \(V(t),W(t)\) 是沿着 \(c\) 的向量场. 根据黎曼联络的协变导数的性质, \[ \dv{t}\lr{V,W} = \lr{\frac{{\rm D}V}{\dd{t}},W} + \lr{V,\frac{{\rm D}W}{\dd{t}}} = 0, \] 既 \(\lr{V,W}\) 沿 \(c\) 为常数.

Claim 11.3 保持联络的微分同胚 \(f:(M,\nabla)\to(\tilde{M},\tilde\nabla)\) 也保持向量场沿曲线的平行性质. 换言之, 若 \(V(t)\) 沿曲线 \(c:I\to M\) 平移, 则 \(f_*V\) 沿曲线 \(c\circ f\) 平移.

11.2 Geodesics

设流形 \(M\) 有仿射联络 \(\nabla\). 若光滑曲线 \(c:I\to M\) 的切向量场 \(c'(t)\) 沿着 \(c\) 平行, 则称 \(c\) 为一条测地线(geodesic). 测地线 \(c\) 称为极大的(maximal), 若定义域 \(I\) 不能扩大到更大的区间.

• 测地线的定义不依赖于度量, 但在黎曼流形上有唯一的黎曼联络. 我们说测地线, 指的就是黎曼联络的测地线.
• 黎曼流形上的测地线切向量长度恒定. 切向量沿着曲线平移, 而平移保持内积, 自然也保持向量的长度.

Claim 11.4 设曲线 \(\gamma:I\to M\) 为(非常数)测地线, 则重参数化后的曲线 \(\bar\gamma=\gamma\circ u\) 为测地线, 当且仅当 \(u\) 为仿射变换, 即 \(u=at+b\), \(a,b\)​​​​​ 为常数.

• 若 \(\gamma(t)\) 是以 \(\gamma(0)=p\) 为起点, \(\gamma'(0)=v\) 为起始速度的测地线, 那么 \(\gamma(kt)\) 是以 \(p\) 为起点, \(kv\) 为起始速度的测地线.

Pf 设 \(\gamma'(t)=T(t)\), \(\bar\gamma'(t)=\bar{T}(t)\). 由链式法则, \[ \bar{T}=\dv{t}(\gamma\circ u)=T(u(t))u'(t). \] 利用 Leibniz 律和链式法则化简 \(\bar\gamma(t)\) 切向量的协变导数: \[ \Align{ \frac{{\rm\bar D}\bar{T}}{\dd{t}} &= \frac{{\rm\bar D}T(u(t))}{\dd{t}}u'(t) +T(u(t))u''(t) \\ &= \eval{\frac{{\rm D}T}{\dd{t}}}_{u(t)}(u'(t))^2 +T(u(t))u''(t) \\ &= T(u(t))u''(t). } \] 因为 \(T(u(t))\) 恒不为零, 因此 \({\rm D}\bar{T}/\dd{t}=0\) 当且仅当 \(u''(t)=0\), 即 \[ u(t)=at+b. \]

Claim 11.5 一个保持联络的微分同胚 \(f:(M,\nabla)\to(\tilde{M},\tilde\nabla)\)​ 将测地线映成测地线.

• 黎曼流形的等距同构保持黎曼联络, 自然也保持测地线.

根据向量场沿曲线平移的方程, 可以写出测地线切向量满足的条件, 即测地线方程(geodesic equation): \[ \dv{T^i}{t} + \sum_{i,j}\Gamma^k_{ij}T^iT^j = 0. \] 这是一个关于 \(T^i\) 的二阶非线性常微分方程组. 根据解的存在唯一性, 有下面的定理.

Claim 11.6 设流形 \((M,\nabla)\). 任给一点 \(p\in M\) 和向量 \(v\in T_pM\), 存在从 \(p\) 开始的, 以 \(v\) 为初始速度的测地线 \(c:I\to M\)​​​. 此外, 这样的测地线是唯一的, 即满足此条件的测地线必然(在定义区间的交集上)重合.

• 因此, 存在唯一的从 \(p\) 开始的, 以 \(v\) 为初速度的极大测地线, 记作 \(\gamma_v(t)\).

Claim 11.7 设黎曼流形 \(M\). 任给一点 \(p\), 总存在 \(p\) 的邻域 \(U\) 和正数 \(\delta,a>0\), 使得对任意 \(q\in U\), \(v\in T_pM\) 且 \(\|v\|\leq\delta\), 存在唯一的从 \(q\) 开始, 初速度 \(v\), 定义在区间 \((-a,a)\)​ 上的测地线 \(\gamma\).

• 一般来说, 要扩大测地线的定以区间 \((-a,a)\), 就得缩小 \(\delta\).
• 特别地, 设 \(k=a/2\), 于是 \(\bar\gamma(t):=\gamma(kt)\) 是从 \(q\) 开始的, 初速度 \(kv\), 定义在 \((-a/k,a/k)=(-2,2)\)​ 上的测地线. 于是可以断言, 对任意 \(\|kv\|\leq\varepsilon=a\delta/2\), 以 \(kv\) 为初速度的测地线, 其定义域包含 \((-2,2)\). 这个命题让我们可以定义指数函数.

Example 1 球面 \(S^2\) 的测地线. 将球面放进 \(\R^3\) 考虑. 设 \(c\) 为弧长参数化的大圆, 则 \(c''(t)\) 指向球心, 与切平面垂直, 于是 \[ \frac{{\rm D}T}{\dd{t}} = \operatorname{pr}\pqty{\dv{T}{t}} = \operatorname{pr}(c''(t)) = 0, \] 说明大圆是球面上的测地线. 又因为任给一点 \(p\in S^2\) 和 \(v\in T_pS^2\), 都存在从 \(p\) 开始, 以 \(v\) 为初速度的大圆, 由测地线的存在唯一性, 所有的测地线都是大圆.

Example 2 双曲模型的测地线.

Poincaré 上半平面. 设 \(c(t)=(x(t),y(t))\), 测地线方程 \[ \begin{gather} \ddot{x}-\dfrac2y\dot{x}\dot{y} = 0, \tag{1} \\ \ddot{y}+\dfrac1y(\dot{x}^2-\dot{y}^2) = 0. \tag{2} \end{gather} \] 测地线速度恒定, 不妨设 \(\lr{c'(t),c'(t)}=1\), 即 \[ \dot{x}^2+\dot{y}^2=y^2.\tag{3} \] 从 \((1)(3)\) 两式可以导出 \((2)\) 式, 故我们只考虑 \((1)(3)\). 设 \(\dot{x}\) 不恒为零, \((1)\) 移项后两边除以 \(\dot{x}\) 得到 \[ \frac{\ddot{x}}{\dot{x}}=\frac{2\dot{y}}{y}, \] 两边对 \(t\) 积分, \[ \ln|\dot{x}|=2\ln y+\textsf{常数}\iff \dot{x}=ky^2 \tag{4} \] 对于常数 \(k\neq0\). 代入 \((3)\) 并解出 \(\dot{y}\), \[ \dot{y} = \pm y\sqrt{1-k^2y^2},\tag{5} \] 以 \((4)\) 除 \((5)\) 得到 \[ \dv{y}{x} = \pm\frac{ky}{\sqrt{1-k^2y^2}}, \] 分离变量后积分得到 \[ x=\pm\frac1k\sqrt{1-k^2y^2}+\textsf{常数}\,d, \] 即 \[ (x-d)^2+y^2=\frac1{k^2}, \] 表示所有圆心在 \(x\) 轴上的圆. 上式要求 \(\dot{x}\) 不恒为零, 若 \(\dot{x}\) 恒为零, 则 \(c\) 是竖直的直线.

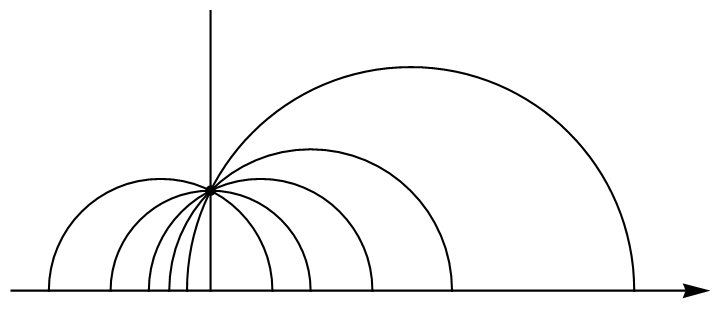
回忆上半平面到圆盘的等距同构 \(T:z\mapsto\frac{z-\i}{z+\i}\). 因为等距同构保持测地线, 所以 \(\gamma\) 是 \(\mathbb{H}\) 上的测地线当且仅当 \(T\circ\gamma\) 是 \(\mathbb{D}\) 的测地线. 根据分式线性变换的保圆性与保角性, \(\mathbb{D}\) 上的测地线是所有与单位圆正交的圆弧​.

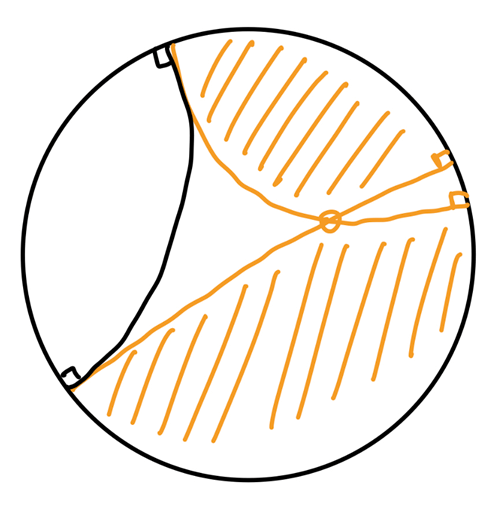
球面和 Poincaré 双曲模型是非欧几何的两个重要例子. 将极大测地线视作直线, 认为两条直线平行当且仅当它们不相交. 球面和双曲模型满足欧几里得的前四条公设, 却不满足第五条: (平行公设) 过直线外一点有且仅有一条直线与该直线平行. 这也说明, 第五公设是独立于前四条的.

• 球面上, 过直线外一点不存在直线与该支线平行. 任意两个大圆都相交于对径两点.
• 双曲空间中, 过直线外一点有无穷多条直线与之平行. 在 Poincaré 圆盘上, 任给直线 \(l\) 和直线外一点 \(p\), 对于从 \(p\) 开始的直线 \(c\), 当 \(c'(0)\) 处在某个固定的合适的范围内 (如图阴影部分), \(c\) 和 \(l\) 总是平行的.

12 Exponential Maps

12.1 The exponential map of a connection

设流形 \((M,\nabla)\). 任给一点 \(q\in M\) 和 \(v\in T_qM\), 有唯一的极大测地线 \(\gamma_v(t)\). 若 \(\gamma_v(1)\) 有定义, 记 \[ \operatorname{Exp}_q(v) := \gamma_v(1). \] 称映射 \(\operatorname{Exp}_q:T_qM\supset V\to M\) 为 \(p\) 处的指数映射(exponential map).

若 \(M\) 有黎曼度量, 则 (根据 Claim 11.7) 对于任意一点 \(p\in M\), 存在邻域 \(U\) 和 \(\varepsilon>0\), 使得对任意 \(q\in U\), 指数函数 \(\operatorname{Exp}_q(v)=\gamma_v(1)\) 在以 \(0\in T_qM\) 为中心的闭球 \(B_\varepsilon(0)\)​​ 上有定义.

• 根据常微分方程对参数的光滑依赖性可知, 指数映射是一个光滑映射.

• 设 \(s:M\to TM\) 为零截面, \(s(U)=\{(p,0)\mid p\in U\}\) 为 \(U\) 在 \(s\) 下的像. 指数函数 \(\operatorname{Exp}_p(v)\), 将其视为二元函数的话, 在 \(s(U)\) 周围的一个管状区域 \[ T_\varepsilon(U) = \{ (p,v)\in TM \mid p\in U, \|v\|\leq\varepsilon \} \] 内有定义.

Claim 12.1 在流形 \((M,\nabla)\) 上, 从任意一点 \(q\) 开始的极大测地线 \(\gamma_v(t)=\operatorname{Exp}_q(tv)\)​.

Pf \(\operatorname{Exp}_q(tv)=\gamma_{tv}(1)=\gamma_v(t)\).

Claim 12.2 (指数映射的自然性) 设 \(f:(M,\nabla)\to(M',\nabla')\) 为保联络的微分同胚, \(p\in M\). 设 \(\operatorname{Exp}_p\) 和 \(\operatorname{Exp}_{f(p)}\) 分别在 \(V\subset T_pM\) 和 \(U\subset T_{f(p)}M'\) 有定义, 则有交换图 \[ \xymatrix{ V \ar[r]^{f_{*,p}} \ar[d]_{\operatorname{Exp}_p} & U \ar[d]^{\operatorname{Exp}_{f(p)}} \\ M \ar[r]_{f} & M'. } \]

Pf 设从 \(p\) 开始的极大测地线 \(\gamma_v(t)\). 因为 \(f\) 保持测地线, 所以 \((f\circ\gamma_v)(t)\) 是从 \(f(p)\)​ 开始的极大测地线. 因为切映射保持曲线的切向量, \[ (f\circ\gamma_v)(t) = \gamma_{f_*v}(t), \] 令 \(t=1\) 得到 \[ (f\circ\operatorname{Exp}_p)(v) = (\operatorname{Exp}_{f(p)}\circ f_*)(v). \]

指数映射 \(\operatorname{Exp}_p:T_pM\supset V\to M\) 在零元处的微分是映射 \((\operatorname{Exp}_p)_{*,0}:T_0(T_pM)\to T_pM\). 因为 \(T_pM\) 是线性空间, 和自身的切空间认同, 所以 \((\operatorname{Exp}_p)_{*,0}\) 可以看作 \(T_pM\) 上的线性映射.

Claim 12.3 (指数映射的微分) 指数映射在零元的微分为恒等映射, \((\operatorname{Exp}_p)_{*,0}={\rm id}_{T_pM}\)​.

Pf 利用曲线求微分. 任给 \(v\in T_pM\), 设 \(c:I\to T_pM\) 满足 \(c(0)=0\), \(c'(0)=v\), 可以取 \(c(t)=tv\). \[ \Align{ (\operatorname{Exp}_p)_{*,0}(v) = \eval{\dv{t}}_0 (\operatorname{Exp}_p\circ\,c)(t) = \eval{\dv{t}}_0 \operatorname{Exp}_p(tv) = \eval{\dv{t}}_0 \gamma_{v}(t) = v. } \]

应用链式法则, 进一步能求出测地线的切向量与指数函数的关系 \[ \dv{t}\gamma_v(t) = (\operatorname{Exp}_p)_{*,tv}(v). \]

12.2 Normal coordinates

根据前一小节 Claim 12.3 以及反函数定理, 存在 \(0\in T_pM\) 的邻域 \(V\) 和 \(p\) 的邻域 \(U\), 使得指数映射 \(\operatorname{Exp}_p:V\to U\) 是微分同胚. 于是我们可以将 \(V\) 上的坐标搬到 \(U\) 上. 取 \(T_pM\) 的一个正交归一基底 \(\qty{e_1,\dots,e_n}\), 令 \(r^1,\dots,r^n\) 表示 \(T_pM\) 关于此基底的坐标函数. 定义 \(U\) 上的坐标函数 \[ x^i := r^i \circ \operatorname{Exp}_p^{-1}, \] 称坐标邻域 \((U,x^1,\dots,x^n)\) 为 \(p\) 的一个正规邻域(normal neighborhood), 坐标系 \(x^1,\dots,x^n\) 为正规坐标(normal coordinates). 正规坐标也叫做法坐标. 正规坐标系的原点为 \(p\). 在这个特殊的坐标系下, 许多几何对象有很简单的形式.

• \(p\) 处的坐标基底 \(\{\partial_i|_p\}\) 为正交归一的. 也就是说, \(p\) 处的度量分量 \(g_{ij}=\delta_{ij}\).

Claim 12.4

1. 正规坐标系下, 通过 \(p\) 的测地线的参数式为直线.
2. 正规坐标系下, 等距同构为正交线性变换.

Pf 第一条. 设 \(\gamma:I\to M\) 为过 \(p\) 的测地线, 且 \(\gamma'(0)=v=\sum v^ie_i\), 则 \(\gamma(t)=\operatorname{Exp}_p(tv)\), \[ x^i(\gamma(t)) = r^i(\operatorname{Exp}_p^{-1}(\gamma(t))) = tv^i. \] 第二条具体说明如下. 设等距同构 \(f:N\to M\), 则有 \(0\in T_{f(p)}M\) 的邻域 \(U'\) 和 \(f(p)\) 的邻域 \(U''\), 使得 \(\operatorname{Exp}_{f(p)}:U'\to U''\) 为微分同胚. 因为 \(f_{*,p}\) 是连续的, 存在 \(0\in T_pN\) 的邻域 \(V'\), 使 \(f(V')=U'\). 根据指数映射的自然性, 有交换图 \[ \xymatrix{ V' \ar[r]^{f_{*,p}} \ar[d]_{\operatorname{Exp}_p}^{\simeq} & U' \ar[d]^{\operatorname{Exp}_{f(p)}}_{\simeq} \\ V'' \ar[r]_{f} & U''. } \] 设 \(U'',V''\) 的正规坐标 \(\{x^i=r^i\circ\operatorname{Exp}^{-1}_p\},\{y^i=s^i\circ\operatorname{Exp}_{f(p)}^{-1}\}\), \(f\) 的坐标式 \[ \Align{ y^j\circ f\circ(x^i)^{-1} &= s^i\circ\operatorname{Exp}_{f(p)}^{-1}\circ f\circ\operatorname{Exp}_p\circ(r^i)^{-1} \\ &= s^i\circ f_{*,p}\circ(r^i)^{-1}, } \] 即等距变换 \(f_{*,p}\) 在正交归一基底下的矩阵, 为正交阵.

Claim 12.5 正规坐标下, \(p\) 处的克氏符 \(\Gamma^k_{ij}\)​ 为零, 度量分量的各偏导数 \(\partial_kg_{ij}\) 也为零.

Pf 设过 \(p\) 的测地线 \(\gamma^i(t)=v^it\), 于是 \(T^i(t)=v^i\), 带入测地线方程得到 \[ \sum_{i,j}\Gamma^k_{ij}v^iv^j = 0. \] 由于 \(v\) 是任意的, 令 \(v^i=v^j=1\), 其余分量为零, 得到 \[ \Gamma^k_{ij} + \Gamma^k_{ji} = 0, \] 结合 \(\Gamma^k_{ij}=\Gamma^k_{ji}\), 有 \(\Gamma^k_{ij}=0\)​. 此外, \[ \Align{ \partial_kg_{ij} = \partial_k\lr{\partial_i,\partial_j} = \lr{\nabla_{\partial_k}\partial_i,\partial_j} + \lr{\partial_i,\nabla_{\partial_k}\partial_j}, } \] 在 \(p\) 点克氏符为零, 所以 \(\nabla_{\partial_k}\partial_i=\nabla_{\partial_k}\partial_j=0\), 于是 \(\partial_kg_{ij}|_p=0\).

设指数映射 \(\operatorname{Exp}_p:T_pM\supset V\to U\subset M\) 为微分同胚, 闭球 \(B_\delta(0)\subset V\).

• \(T_pM\) 中半径为 \(r\leq\delta\) 的球面在 \(\operatorname{Exp}_p\) 下的像 \(S_r(p)\) 称为测地球面(geodesic sphere).
• 类似地, 半径为 \(r\leq\delta\) 的实心球的 \(\operatorname{Exp}_p\) 像 \(B_r(p)\) 称为测地球(geodesic ball).

在 \(T_pM\) 中, 从 \(0\) 出发的直线 \(tv\) 与球面 \(S_r(0)\) 是正交的 (即交点处的切向量正交). 在指数映射下, \(tv\) 映到测地线 \(\gamma_v(t)\), \(S_r(0)\) 映到 \(S_r(p)\). 下面的定理则断言此两者也正交. 换言之, 指数映射是一个局部的径向等距同构(radial isometry).

Claim 12.6 (高斯引理) 测地球面 \(S_r(p)\) 正交于所有过 \(p\) 的极大测地线.

Pf 设 \(\operatorname{Exp}_p:B_\varepsilon(0)\to M\), 记 \(S^{n-1}\) 为 \(T_pM\) 中的单位球面, \[ \Align{ \sigma:S^{n-1}\times(0,\varepsilon) &\to B_\varepsilon(p)-\{p\}, \\ (v,t) &\mapsto \operatorname{Exp}_p(tv). } \] 显然 \(t\mapsto\sigma(v_0,t)\) 是测地线 \(\gamma_{v_0}(t)\); 并且 \(v\mapsto\sigma(v,t_0)\) 是 \(S^{n-1}\to S_{t_0}(p)\) 的微分同胚.

令 \(\{\partial/\partial y^i\}\) 为 \(S^{n-1}\) 的局部坐标系, \(\partial/\partial r\) 为 \((0,\varepsilon)\) 的自然坐标, \[ \Align{ Y^i &= \sigma_*\pqty{ \pdv{y^i} }, & R &= \sigma_*\pqty{ \pdv{r} }, } \] 于是 \(Y^i\) 是测地球面之切空间的坐标系, \(R\) 是测地线 \(\gamma_v(t)\) 的切向量, 只用证明 \[ \lr{Y^i,R} = 0,\quad i=1,\dots,n-1. \] 注意到 \([\partial/\partial{y^i},R]=0\), 所以 \([Y^i,R]=0\), 进而 \[ \Align{ R\lr{Y^i,R} &= \lr{ \nabla_RY^i,R } + \lr{ Y^i,\nabla_RR } \\ &= \lr{ \nabla_RY^i,R } \\ &= \lr{ \nabla_{Y^i}R,R } \\ &= \frac12Y^i\lr{R,R} = 0. } \] (其中第二个等号是因为 \(R\) 沿测地线平移; 第三个等号根据 \(\nabla\) 无挠性和 \([Y^i,R]=0\).) 于是 \(\lr{Y^i,R}\) 沿着测地线为常数. 这常数为零, 因为当 \(p\to0\) 时, \(Y^i(p)\to0\), 有 \[ \lr{Y^i,R} \equiv \lim_{p\to0} \lr{Y^i,R}(p) = 0. \]

此外, 指数映射也保持径向向量的长度: 设 \(v\in B_\delta(0)\), \(tv\in B_\delta(0)\), 则 \[ \norm{(\operatorname{Exp}_p)_{*,v}(tv)} = \norm{t\cdot (\operatorname{Exp}_p)_{*,v}(v)} = \norm{t\cdot \eval{\dv{t}}_{1} \gamma_v(t) } = \|tv\|. \] 高斯引理在之后我们证明测地线是 (局部) 最短线中有很大用处.