GTM275 | 2 曲率与向量场

GTM275(Differential Geometry: Connections, Curvature, and Characteristic Classes)第6-9节的笔记.

3 Affine Connections

3.1 Affine connections

在一个一般的流形\(M\)上, 不一定存在一个全局的坐标系\(\qty{\pdv{x^i}}\), 所以不能像定义方向导数那样定义一个\(M\)上的导数算符. 但是我们可以采用公理化的定义, 根据一个导数算符应当满足的性质来定义它.

流形\(M\)上的仿射联络(affine connection)是一个\(\R\)-双线性映射\(\nabla:{\frak X}(M)\times{\frak X}(M)\to{\frak X}(M)\), 满足如下条件:

1. \(\nabla_XY\)关于\(X\)是\({\cal F}\)-线性的.
2. (Leibniz律) \(\nabla_X(fY)=(Xf)Y+f\nabla_XY\).

欧氏空间\(\R^n\)上的方向导数算符\(D\)是一个仿射联络, 也叫做欧氏联络(Euclidean connection). 相似地, 我们分别定义一个联络的挠率(torsion)和曲率(curvature). 挠率\(T:{\frak X}(M)\times{\frak X}(M)\to{\frak X}(M)\), \[ T(X,Y) := \nabla_XY-\nabla_YX-[X,Y], \] 曲率\(R:{\frak X}(M)\times{\frak X}(M)\times{\frak X}(M)\to{\frak X}(M)\), \[ R(X,Y)Z := [\nabla_X,\nabla_Y]Z - \nabla_{[X,Y]}Z. \]

Claim 3.1 挠率\(T\)和曲率\(R\)关于其每个变量都是\(\cal F\)-线性的.

Pf 挠率\(T\)和曲率\(R\)关于\(X,Y\)均为反对称, 因此只需验证\(T\)关于\(X\), \(R\)关于\(X,Z\)是\(\cal F\)-线性的. 具体证明略, 按照联络的性质展开即可, 需要用到引理\([fX,gY]=fg[X,Y]+f(Xg)Y-g(Yf)X\).

3.2 The Riemannian connection

黎曼联络.

在一个黎曼流形上, 我们还可以给仿射联络加上更多的条件. 一个黎曼联络(Riemannian connection)或者Levi-Civita联络, 是一个满足如下条件的仿射联络\(\nabla\),

1. (无挠性) \(T(X,Y)=0\).
2. (与度量适配) \(X\lr{Y,Z}=\lr{\nabla_XY,Z}+\lr{Y,\nabla_XZ}\).

Claim 3.2 黎曼流形上的黎曼联络存在且唯一.

Pf 与度量适配条件\(X\lr{Y,Z}=\lr{\nabla_XY,Z}+\lr{Y,\nabla_XZ}\), 循环\(X,Y,Z\), 可以写出三个恒等式: \[ \Cases{ X\lr{Y,Z}=\lr{\nabla_XY,Z}+\lr{Y,\nabla_XZ}, \\ Y\lr{Z,X}=\lr{\nabla_YZ,X}+\lr{Z,\nabla_YX}, \\ Z\lr{X,Y}=\lr{\nabla_ZX,Y}+\lr{X,\nabla_ZY}. } \] 一式加二式减三式, 并利用\(\nabla\)的无挠性, 可得 \[ X\lr{Y,Z}+Y\lr{Z,X}-Z\lr{X,Y} = \lr{\nabla_XY+\nabla_YX,Z}+\lr{[Y,Z],X}+\lr{[Y,[X,Z]]} \] 将无挠性条件\(\nabla_YX=\nabla_XY-[X,Y]\)代入上式, 移项后得 \[ \Align{ 2\lr{\nabla_XY,Z} = \; &X\lr{Y,Z}+Y\lr{Z,X}-Z\lr{X,Y}+{} \\ &\lr{[X,Y],Z}-\lr{[Y,Z],X}-\lr{Y,[X,Z]}. } \] 由此定义了一个联络\(\nabla_XY\), 由\(Z\)的任意性知\(\nabla_XY\)是唯一确定的. 可以验证, 如上定义的\(\nabla_XY\)​确实是一个黎曼联络, 所以黎曼联络存在且唯一.

• 最后的等式也叫做Koszul公式.

子流形的黎曼联络.

设\(M\)的嵌入子流形\(S\), \(p\in S\), 定义\(p\)点的正交投影(orthogonal projection)为映射\({\rm pr}_p:T_pM\to T_pS\), \[ {\rm pr}_p(X_p) := \sum_i \lr{X_p,e_i}e_i , \] 其中\(\qty{e_i}\)是\(T_pS\)的任一正交归一基底. 当\(p\)点运动, 就会得到\(S\)上的投影映射场\({\rm pr}:\Gamma(TM|_S)\to{\frak X}(S)\), \[ {\rm pr}(X)_p := {\rm pr}_p(X_p). \] 可以验证, 正交投影具有如下性质:

• \({\rm pr}\)在\({\frak X}(S)\)上为恒等映射.
• (\({\cal F}\)-线性性) \({\rm pr}(fX)=f\,{\rm pr}(X)\).
• (自伴性) \(\lr{{\rm pr}(X),Y}=\lr{X,{\rm pr}(Y)}\).

Claim 3.3 设黎曼流形\(M\)的黎曼联络\(\nabla\), 则嵌入子流形\(S\subset M\)的黎曼联络(在诱导度量下)为 \[ \nabla'_XY = {\rm pr}(\nabla_XY). \]

Pf 根据黎曼联络的唯一性知, 只需验证\(\nabla'\)确实是黎曼联络即可.

1. 关于\(X\)的\(\cal F\)-线性性: \[ \nabla'_{fX}Y ={\rm pr}(\nabla_{fX}Y) ={\rm pr}(f\nabla_XY) =f\,{\rm pr}(\nabla_XY) =f\nabla'_XY. \]

2. Leibniz律: \[ \Align{ \nabla'_X(fY) ={\rm pr}(\nabla_XfY) &={\rm pr}[(Xf)Y + f\nabla_XY] \\ &=(Xf)Y + f\,{\rm pr}(\nabla_XY) = (Xf)Y + f\nabla'_XY. } \]

3. 无挠性: \[ \nabla'_XY-\nabla'_YX = {\rm pr}(\nabla_XY-\nabla_YX) = {\rm pr}([X,Y]) = [X,Y]. \]

4. 和度量适配: \[ \Align{ X\lr{Y,Z} &= \lr{\nabla_XY,Z} + \lr{Y,\nabla_XZ} \\ &= \lr{{\rm pr}(\nabla_XY),Z} + \lr{Y,{\rm pr}(\nabla_XZ)} \\ &= \lr{\nabla'_XY,Z} + \lr{Y,\nabla'_XZ}. } \] 其中第二步利用了正交投影自伴性的推论: 若\(Y\in{\frak X}(M)\), 则\(\lr{X,Y}=\lr{{\rm pr}(X),Y}\).

3.3 Connections under a diffeomorphism

Claim 3.4 设微分同胚\(\phi:M\to\tilde M\), \(\tilde\nabla\)是\(\tilde{M}\)上的一个仿射联络, 则下式定义了\(M\)上的一个仿射联络\(\nabla:{\frak X}(M)\times{\frak X}(M)\to{\frak X}(M)\): \[ \phi_*( \nabla_XY ) = \tilde\nabla_{\phi_*X}(\phi_*Y). \]

Pf 首先应注意到, 因为\(\phi\)是微分同胚, 所以\(\phi_*\)是线性同构映射, 意味着\(\phi_*(A)=\phi_*(B)\)可推出\(A=B\). 这将在这几个命题的证明中频繁使用.

只需验证\(\nabla_XY\)关于\(X\)的\(\cal F\)-线性性和关于\(Y\)的Leibniz律即可. 一方面, \[ \Align{ \phi_*(\nabla_{fX}Y) &= \tilde\nabla_{\phi_*(fX)}(\phi_*Y) \\ &= \tilde\nabla_{\phi_*(f)\phi_*(X)}(\phi_*Y) \\ &= \phi_*(f)\tilde\nabla_{\phi_*(X)}(\phi_*Y) \\ &= \phi_*(f)\phi_*(\nabla_XY) \\ &= \phi_*(f\nabla_XY), } \] (其中第三步用到了\(\tilde\nabla\)关于\(X\)的\(\cal F\)-线性性.) 即\(\nabla_{fX}Y=f\nabla_XY\). 另一方面, \[ \Align{ \phi_*(\nabla_X(fY)) &= \tilde\nabla_{\phi_*X}(\phi_*(fY)) \\ &= \tilde\nabla_{\phi_*X}(\phi_*(f)\phi_*(Y)) \\ &= (\phi_*X)(\phi_*(f))\phi_*(Y) + \phi_*(f)\tilde\nabla_{\phi_*X}(\phi_*(Y)) \\ &= \phi_*((Xf)Y) + \phi_*(f)\phi_*(\nabla_XY) \\ &= \phi_*((Xf)Y + f\nabla_XY), \\ } \] (其中第三步用到了\(\tilde\nabla\)关于\(Y\)的Leibniz律.) 即\(\nabla_X(fY)=(Xf)Y+f\nabla_XY\).

Claim 3.5 设等距同构\(\phi:M\to\tilde M\), \(\tilde\nabla\)是\(\tilde{M}\)上的黎曼联络, 则Claim 4中定义的\(\nabla\)是\(M\)上的黎曼联络.

Pf 由等距同构的定义, 有\(\lr{X_p,Y_p}=\lr{\phi_*X_p,\phi_*Y_p}'\)对任意\(X_p,Y_p\in T_pM\), \(p\in M\)成立, 即 \[ \phi_*\lr{X,Y} = \lr{\phi_*X,\phi_*Y},\quad\forall X,Y\in{\frak X}(M). \] 下面验证\(\nabla\)满足无挠性和适配性. 一方面, \[ \Align{ \phi_*(\nabla_XY-\nabla_YX) &= \tilde\nabla_{\phi_*X}(\phi_*Y)-\tilde\nabla_{\phi_*Y}(\phi_*X) \\ &= [\phi_*X,\phi_*Y] \\ &= \phi_*[X,Y], } \] (其中第二步用了\(\tilde\nabla\)的无挠性) 即\(\nabla_XY-\nabla_YX=[X,Y]\). 另一方面, \[ \Align{ \phi_*(\lr{\nabla_XY,Z}+\lr{Y,\nabla_XZ}) &= \lr{\phi_*(\nabla_XY),\phi_*Z}+\lr{\phi_*Y,\phi_*(\nabla_XZ)} \\ &= \lr{\tilde\nabla_{\phi_*X}(\phi_*Y),\phi_*Z} + \lr{\phi_*Y,\tilde\nabla_{\phi_*X}(\phi_*Z)} \\ &= (\phi_*X)\lr{\phi_*Y,\phi_*Z} \\ &= (\phi_*X)\;\phi_*\lr{Y,Z} \\ &= \phi_*(X\lr{Y,Z}), } \] (其中第三步用了\(\tilde\nabla\)的适配性) 即\(\lr{\nabla_XY,Z}+\lr{Y,\nabla_XZ}=X\lr{Y,Z}\).

Claim 3.6 设\(R,\tilde{R}\)分别是Claim 3.5中\(\nabla,\tilde\nabla\)的曲率, 则 \[ \phi_*(R(X,Y)Z) = \tilde{R}(\phi_*X,\phi_*Y)\phi_*Z. \]

Pf \[ \Align{ \phi_*(R(X,Y)Z) &= \phi_*([\nabla_X,\nabla_Y]Z) - \phi_*(\nabla_{[X,Y]}Z) \\ &= [\tilde\nabla_{\phi_*X},\tilde\nabla_{\phi_*Y}]\phi_*Z - \tilde\nabla_{[\phi_*X,\phi_*Y]}\phi_*Z \\ &= \tilde{R}(\phi_*X,\phi_*Y)\phi_*Z. } \] 其中第二步利用了结论\(\phi_*([\nabla_X,\nabla_Y]Z)=[\tilde\nabla_{\phi_*X},\tilde\nabla_{\phi_*Y}]\phi_*Z\), 将左边展开即可证明.

4 Vector Bundles

光滑向量场间的\({\cal F}\)-线性映射是可以逐点(pointwise)定义的. 例如, 黎曼曲率\(R(X,Y)Z\)关于\(X,Y,Z\)都是\({\cal F}\)-线性的, 那么就可以定义某一点的曲率\(R_p(X_p,Y_p)Z_p:=(R(X,Y)Z)_p\), 其中\(X,Y,Z\)是任意延拓\(X_p,Y_p,Z_p\)的向量场. 这一性质固然可以在向量场的框架内证明, 但是在向量丛的框架内是最自然的.

4.1 Vector bundles

想象流形\(M\)的每一点\(p\)都附上一个\(r\)维实线性空间\(E_p\)(每一点都长出了许多向量), 将这些线性空间拼起来, 就得到了一个"向量丛".

一个光滑向量丛(smooth vector bundle)指的是光滑的满射(投影映射)\(\pi:E\to M\), 满足

1. 对任意\(p\in M\), 集合\(E_p:=\pi^{-1}(p)\)是一个\(r\)维实线性空间, 称为\(p\)点的纤维(fiber).

2. (局部平凡性) 任意一点\(p\in M\)都存在开邻域\(U\), 使得存在微分同胚 \[ \phi_U:\pi^{-1}(U) \to U\times\R^r, \] 且其在\(E_p\)的限制是一个线性同构\(E_p\to\qty{p}\times\R^r\).

其中, \(r\)称为向量丛的秩(rank), \(E\)称为总空间(total space), \(M\)称为底空间(base space), \(E\)也称为\(M\)上的一个向量丛. 定义的第2条中, 我们称\(U\)是向量丛的一个平凡化开子集(trivialization open subset), \(\phi_U\)是\(\pi^{-1}(U)\)的一个平凡化(trivialization). 一个平凡化开覆盖(trivializing open cover)指的是平凡化开集和相应的平凡化的集合\(\qty{(U_\alpha,\phi_\alpha)}\), 可以看作流形\(E\)的一个"图册".

设\(V\)是\(r\)维实线性空间, 则投影\(\pi:M\times V\to M\)是一个\(r\)秩的向量丛, 称为积丛(product bundle).

• 圆柱面\(S^1\times\R\)可以看作\(S^1\)上的\(1\)秩向量丛.
• Möbius带\([0,1]\times\R\)(认同\((0,t)\sim(1,-t)\))可以看作圆上的\(1\)秩向量丛.

设\(S\)是\(M\)的子流形, 向量丛\(\pi:E\to M\), 则\(\pi_S:\pi^{-1}(S)\to S\)也是一个向量丛, 称为\(E\)在\(S\)上的限制(restriction), 记作\(E|_S:=\pi^{-1}(S)\).

设两个光滑向量丛\(\pi_E:E\to M\), \(\pi_F:F\to N\), 一个从\(E\)到\(F\)的光滑丛映射(bundle map)或者丛同态(bundle homomorphism)指的是一组光滑映射\((\phi:E\to F,\underline\phi:M\to N)\), 满足

1. 有交换图(即先投影再映射 \(=\) 先映射再投影) \[ \xymatrix{ E \ar[r]^{\phi} \ar[d]_{\pi_E} & F \ar[d]^{\pi_F} \\ M \ar[r]_{\underline\phi} & N. } \]

2. \(\phi\)在任意纤维上的限制\(\phi_p:E_p\to F_{\underline\phi(p)}\)都是线性映射.

有时也称\(\phi:E\to F\)是一个丛映射. 当两个向量丛都在同一个流形\(M\)上时, 我们通常要求\(\underline\phi={\rm id}_M\)为恒等映射, 此时称\((\phi:E\to F,{\rm id}_M)\)为\(M\)上的一个丛映射. 若存在\(M\)上的丛映射\(\psi:F\to E\)使得\(\psi\circ\phi={\rm id}_E\)且\(\phi\circ\psi={\rm id}_F\)(\(\phi,\psi\)互逆), 则称\(\phi\)是\(M\)上的丛同构(bundle isomorphism), 称\(E,F\)是同构的(isomorphic).

• 一个同构于积丛\(M\times\R^r\to M\)的向量丛称为平凡的(trivial).

对于流形\(M\), 定义所有切向量的集合 \[ TM := \qty{(p,v): p\in M, v\in T_pM}, \] 称为\(M\)的切丛(tangent bundle). 流形间的光滑映射\(f:M\to N\)诱导出了切丛间的丛映射\(f_*:TM\to TN\),

\[ f_*(p,v) := (f(p), f_*v). \]

4.2 Sections

向量丛\(E\)在开集\(U\)上的截面(section)指的是映射\(s:U\to E\), 满足\(\pi\circ s={\rm id}_U\). 所有\(E\)在\(U\)上的光滑截面的集合记作\(\Gamma(U,E)\). 若\(U=M\), 则也记作\(\Gamma(E)\).

• 截面\(s\)将每个点\(p\in U\)对应到了一个向量\(X_p\in E_p\), 可以看作向量场概念的推广. 实际上, 切丛上的全体光滑截面\(\Gamma(TM)\)就是\({\frak X}(M)\).

• \(\Gamma(U,E)\)是光滑函数环\(C^\infty(U)\)上的模, 其"数乘"定义为 \[ (fs)(p) := f(p)s(p) \in E_p, \quad p\in U. \]

• 积丛\(M\times\R\to M\)上的光滑截面是光滑函数\(s:M\to M\times\R,p\mapsto(p,f(p))\), 因此\(\Gamma(M\times\R)\)中的截面和光滑函数\(C^\infty(M\times\R)\)具有一一对应关系.

• 设流形\(\tilde{M}\), 则"子流形\(M\)上的向量场"和"沿着子流形\(M\)的向量场", 它们指的无非就是\(\Gamma(TM)\)和\(\Gamma(T\tilde{M}|_M)\)中的元素.

开集\(U\)上的向量丛\(E\)的一个标架(frame)指的是一组\(U\)上的截面\(\qty{e_1,\dots,e_r}\), 使得对任意\(p\in U\), 向量组\(\qty{e_1(p),\dots,e_r(p)}\)都构成\(E_p\)的基底.

Claim 4.1 光滑向量丛\(\pi:E\to M\)是平凡的, 当且仅当它存在一个光滑标架.

• 向量丛必定局部平凡, 也就是说必定存在局部标架(即每个平凡化开子集\(U\)上都存在标架).

Pf 设\(E\)是平凡的, 则存在一个光滑平凡化\(\phi:E\to M\times\R^r\). 设\(\qty{v_1,\dots,v_r}\)是\(\R^r\)的标准基底, 则截面族 \[ e_i(p) := \phi^{-1}(p,v_i), \quad i=1,\dots,r \] 给出了\(E\)的一个光滑标架.

设\(\qty{e_1,\dots,e_r}\)是\(E\)的一个光滑标架, 则任意\(e\in E_p\), 都可以写作线性组合\(e=\sum a^ie_i(p)\), 于是映射 \[ \phi: E\to M\times\R^r,\quad e\mapsto(\pi(e),a^1,\dots,a^r) \] 是一个光滑映射, 其逆 \[ \psi:M\times\R^r\to E,\quad (p,a^1,\dots,a^r)\mapsto\sum a^i e_i(p) \] 也是光滑的, 意味着\(E\)同构于\(M\times\R^r\).

一个流形\(M\)上的丛映射\(\phi:E\to F\)诱导出了截面之间的映射\(\phi_\#:\Gamma(E)\to\Gamma(F)\), \[ \phi_\#(s) := \phi\circ s. \] 可以证明, 截面映射\(\phi_\#\)是\({\cal F}\)-线性的, 而接下来两节的任务就是证明任意一个\({\cal F}\)-线性映射\(\alpha:\Gamma(E)\to\Gamma(F)\)都是由某个丛映射诱导出来的, 即\(\alpha=\phi_\#\).

在此之前, 先给出一个有用的命题.

Claim 4.2 (光滑截面的延拓) 设流形\(M\)上的光滑向量丛\(E\), \(s\)是定义在开集\(U\)上的光滑截面, 点\(p\in U\), 则存在\(M\)上的光滑截面\(\bar{s}\), 使得在\(p\)的某邻域\(N\)上, \(s|_N=\bar{s}|_N\).

4.3 Local and point operators

我们说\(\R^n\)上的方向导数\(D_X\)具有"局部性": 若两个光滑函数\(f,g\)在某开集\(U\)上相等, 则两者的方向导数\(D_Xf\)和\(D_Xg\)在\(U\)上也相等. 也就是说, 方向导数\(D_X\)不关心函数在\(\R^n\)上的整体行为, 而只关心函数在某一点附近(邻域内)的行为.

下面用符号的语言描述\(D_X\)的这一性质: 设光滑函数\(f,g\)在开集\(U\)上相等, 即\(f-g=0\), 则其方向导数也相等, 即\(D_Xf=D_Xg\), 或者\(D_X(f-g)=0\). 记\(F:=f-g\), 则局部性指的是\(F=0\Rightarrow D_XF=0\)(在某开集\(U\)上).

设流形\(M\)上的光滑向量丛\(E,F\), 一个\(\R\)-线性映射\(\alpha:\Gamma(E)\to\Gamma(F)\)称为一个局部算子(local operator), 如果: 若截面\(s\in\Gamma(E)\)在某开集\(U\subset M\)上恒为零, 则\(\alpha(s)\)在\(U\)上也恒为零. \(\alpha\)称为一个点算子(point operator)(或者逐点算子), 如果\(s(p)=0\)可以推出\(\alpha(s)(p)=0\), 对任意\(p\in M\).

• 局部算子只关心截面\(s\)在某个邻域内的取值; 点算子只关心\(s\)在某点的取值.
• 联络\(\nabla_X\)是\(\Gamma(TM)\)上的局部算子; 与函数相乘的算子\(s\mapsto fs\)是\(\Gamma(TM)\)上的点算子.

Claim 4.3 设流形\(M\)上的光滑向量丛\(E,F\), 映射\(\alpha:\Gamma(E)\to\Gamma(F)\), 若\(\alpha\)是\(\cal F\)-线性的, 则\(\alpha\)是局部算子.

Pf 设\(s\in\Gamma(E)\)在开集\(U\)上恒为零, 任取\(p\in U\), 设光滑函数\(f_p:M\to\R\)满足: ①\(f(p)=1\), ②\({\rm supp}\,f\subset U\), 如下图.

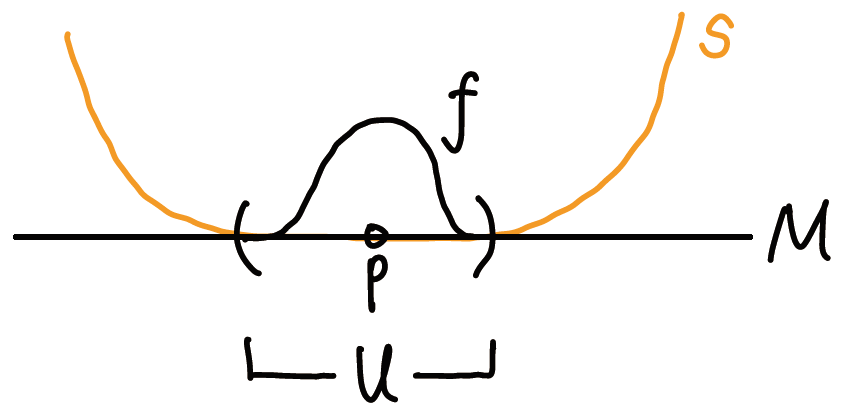
于是\(fs\in\Gamma(E)\)且\(fs\equiv0\)在\(M\)上恒成立, 于是(据\(\R\)-线性性)\(\alpha(fs)\equiv0\). 又由\(\cal F\)-线性性有 \[ 0 = \alpha(fs) = f\alpha(s), \] 在\(p\)点取值, 有\(f(p)\alpha(s)(p)=0\), 即\(\alpha(s)(p)=0\). 又根据\(p\)的任意性, 在\(U\)上有\(\alpha(s)\equiv0\).

\({\cal F}\)-线性性是\(\alpha\)局部的一个充分不必要条件. 联络\(\nabla_X:{\frak X}(M)\to{\frak X}(M)\)不具有\({\cal F}\)-线性性, 而满足Leibniz律, 可以证明它也是局部的.

局部算子的一个好处是它可以被(唯一地)限制到任意开集上.

Claim 4.4 设流形\(M\)上的向量丛\(E,F\), 局部算子\(\alpha:\Gamma(E)\to\Gamma(F)\), 则对任意开集\(U\subset M\), 唯一存在一个线性算子\(\alpha_U:\Gamma(U,E)\to\Gamma(U,F)\), 满足 \[ \alpha_U(t|_U) = \alpha(t)|_U, \quad\forall t\in\Gamma(E), \] 称为\(\alpha\)在\(U\)上的限制(restriction). 而且, 如果\(\alpha\)是\({\cal F}\)-线性的, 则\(\alpha_U\)是\({\cal F}(U)\)-线性的.

Pf 设截面\(s\in\Gamma(U,E)\), 点\(p\in U\). 根据Claim 4.2, 存在截面\(\bar{s}\in\Gamma(M,E)\), 且\(s,\bar{s}\)在\(p\)的某邻域\(W\)取值相同. 定义 \[ \alpha_U(s)(p) := \alpha(\bar{s})(p). \] 下面我们说明\(\alpha_U\)是良定义的, 即与\(\bar{s}\)的选取无关. 取另一截面\(\tilde{s}\in\Gamma(M,E)\)满足\(s,\tilde{s}\)在\(W\)取值相同, 则在\(W\)上有\(\bar{s}=\tilde{s}\), 由\(\alpha\)的局部性, \(\alpha(\bar{s})=\alpha(\tilde{s})\), 进而\(\alpha(\bar{s})(p)=\alpha(\tilde{s})(p)\), 这说明\(\alpha_U(s)(p)\)与\(\bar{s}\)的选取无关.

设全局截面\(t\in\Gamma(M,E)\), 有\(\alpha_U(t|_U)(p)=\alpha(t)(p)\)对任意\(p\in U\), 则\(\alpha_U(t|_U)=\alpha(t)|_U\), 即证.

下面的命题告诉我们: 一个\({\cal F}\)-线性的截面映射不光是局部的, 而且还是逐点的. 我们知道(Claim 4.4), 局部算子可以唯一地限制到任意开集上, 而逐点算子则可以唯一地"限制"到任意一点, 即唯一地诱导出纤维\(E_p\to F_p\)的线性映射.

Claim 4.5 设流形\(M\)上的光滑向量丛\(E,F\), 映射\(\alpha:\Gamma(E)\to\Gamma(F)\), 若\(\alpha\)是\(\cal F\)-线性的, 则\(\alpha\)是点算子. 此时, 对每个点\(p\in M\)都唯一存在线性映射\(\phi_p:E_p\to F_p\), 满足 \[ \phi_p(s(p)) = \alpha(s)(p), \quad\forall s\in\Gamma(E). \]

Pf 任给\(p\), 设\(p\)的邻域\(U\)上有标架\(\qty{e_1,\dots,e_r}\). 截面\(s\)在\(U\)上展开为\(s|_U=a^\mu e_\mu\)(其中\(a^\mu\in{\cal F}(U)\)). 设\(s(p)=0\), 则\(a^\mu(p)=0\). 由Claim 4.4, \(\alpha\)可以被限制到\(U\)上, 且 \[ \Align{ \alpha(s)(p) &= \alpha_U(s|_U)(p) \\ &= \alpha_U\pqty{\sum a^i e_i}(p) \\ &= \sum a^i(p)\cdot\alpha_U(e_i)(p) \\ &= 0. } \] (其中第三步由\(\alpha_U\)的\({\cal F}(U)\)-线性性.) 因此\(\alpha\)是逐点的.

定义算子\(\phi_p:E_p\to F_p\), \(\phi_p(e):=\alpha(s)(p)\), 其中\(s\in\Gamma(E)\)满足\(s(p)=e\). 先证明\(\phi_p\)是良定义的. 任给两个\(s,s'\)满足\(s(p)=s'(p)=e\), 则\((s-s')(p)=0\). 因为\(\alpha\)是逐点的, 有\(\alpha(s-s')(p)=0\), 即\(\alpha(s)(p)=\alpha(s')(p)\), 所以\(\phi_p(e)\)的值是唯一确定的. 再证明\(\phi_p\)是线性的: 设\(s_1,s_2\in\Gamma(E)\), \(s_1(p)=e_1,s_2(p)=e_2\), \(a\in\R\), 则 \[ \phi_p(ae_1+e_2) = \alpha(as_1+s_2)(p) = a\alpha(s_1)(p) + \alpha(s_2)(p) = a\phi_p(e_1)+\phi_p(e_2). \]

4.4 \(\cal F\)-linear section maps and bundle maps

Claim 4.5告诉我们, 一个光滑的\({\cal F}\)-线性的截面映射\(\alpha\)可以诱导出一族纤维映射\(\qty{\phi_p}_{p\in M}\), 而一个丛映射\(\psi:E\to F\)无非就是一族纤维映射\(\qty{\psi_p}_{p\in M}\)以一种"光滑"的方式组合起来, 所以说距离我们最终的目标(以截面映射\(\alpha\)构造出丛映射\(\phi\))只差"光滑"这一步. 这恰恰是下面Claim 4.6要解决的.

Claim 4.6 设流形\(M\)上的光滑向量丛\(E,F\), 映射\(\phi:E\to F\)保纤维(\(\phi(E_p)\subset F_p\)), 且在每个纤维上都是线性映射, 则 \[ \phi\,\textsf{是光滑的} \iff\phi_\#\,\textsf{将光滑截面映到光滑截面.} \]

Pf (\(\Rightarrow\)) 若\(\phi\)是光滑的, \(s\in\Gamma(E)\)是光滑的, 那么\(\phi_\#(s)=\phi\circ s\)也是光滑的.

(\(\Leftarrow\)) 任给定\(p\in M\), 设\(p\)的邻域\(U\)上有\(E,F\)的标架\(\qty{e_1,\dots,e_r},\qty{f_1,\dots,f_m}\). 设 \[ \phi_\# (e_i) = \sum A^j{_i}f_j, \] 因为\(\phi_\#\)将光滑截面\(e_\mu\)映到光滑截面, 所以\(A^\nu{_\mu}\)是\(U\)上的光滑函数. 于是对任意截面\(s=a^\mu e_\mu\in\Gamma(E|_U)\), \[ \phi_\# (s) = \sum A^j{_i} a^i f_j. \] 设\(E|_U\)的局部坐标\((x^1,\dots,x^n,a^1,\dots,a^r)\), 则 \[ \phi(x^1,\dots,x^n,a^1,\dots,a^r) = (x^1,\dots,x^n,A^1{_i}a^i,\dots,A^m{_i}a^i) \] 是\(E|_U\to F\)的光滑映射.

至此, 我们终于可以得到想要的结论.

Claim 4.7 设流形\(M\)上的光滑向量丛\(E,F\), 则存在一一对应关系: \[ \Align{ \{ \textsf{丛映射}\, E\to F \} &\longleftrightarrow \{ \mathcal{F}\textsf{-线性的截面映射}\,\alpha:\Gamma(E)\to\Gamma(F) \} \\ \phi &{}\,\longmapsto\, \phi_\#. } \]

Pf 先证明满射. 设\(\cal{F}\)-线性的截面映射\(\alpha:\Gamma(E)\to\Gamma(F)\), 根据Claim 4.5, 对任意\(p\in M\)存在\(\phi_p:E_p\to F_p\), 满足\(\phi_p(s(p))=\alpha(s)(p)\). 定义\(\phi:E\to F\), \(\phi(e):=\phi_p(e)\), 其中\(e\in E_p\). 对任意\(s\in\Gamma(E)\), \(p\in M\), \[ \phi_\# (s)(p) = \phi(s(p)) = \phi_p(s(p)) = \alpha(s)(p), \] 所以\(\phi_\#=\alpha\). 因为\(\phi_\#\)将光滑截面映到光滑截面, 由Claim 4.6, \(\phi\)是光滑的丛映射.

再证明单射. 设光滑丛映射\(\phi,\psi:E\to F\)满足\(\phi_\#=\psi_\#\). 对任意\(e\in E_p\), 取\(s\in\Gamma(E)\)满足\(s(p)=e\), 则 \[ \Align{ \phi(e) = \phi(s(p)) &= \phi_\# (s)(p) \\ &= \psi_\# (s)(p) = \psi(s(p)) = \psi(e), } \] 得到\(\phi=\psi\), 即证.

4.5 Generalization to \(\cal{F}\)-multilinear section maps

很容易将Claim 4.5推广到多线性映射, 证明是相似的.

Claim 4.8 设流形\(M\)上的光滑向量丛\(E_1,\dots,E_n,F\), 若 \[ \alpha:\Gamma(E_1)\times\cdots\times\Gamma(E_n)\to\Gamma(F) \] 关于每个变量都是\(\cal F\)-线性的, 则对任意\(p\in M\), 存在唯一\(\R\)-多线性映射 \[ \phi_p:(E_1)_p\times\cdots\times(E_n)_p \to F_p, \] 满足: 对任意\(s_1\in\Gamma(E_1),\dots,s_n\in\Gamma(E_n)\), 有 \[ \phi_p(s_1(p),\dots,s_n(p)) = \alpha(s_1,\dots,s_n)(p). \]

5 Gauss's Theorema Egregium

现在我们尝试证明高斯绝妙定理, 即证明曲面的高斯曲率是一个等距不变量, 或者说是一个内禀属性(intrinsic property). 我们已经知道, 一个黎曼流形的度量, 黎曼联络以及由此派生的黎曼曲率都是内禀属性. 于是一个自然的想法就是研究高斯曲率和黎曼曲率的联系(毕竟它们都叫"曲率").

• 等距不变量(isometric invariant)的具体含义如下: 任给黎曼流形\(M\), 设\(f_M:M\to\R\), 如果对任意等距同构\(\varphi:M\to\tilde{M}\), 都有 \[ f_M(p) = f_{\tilde{M}}(\varphi(p)),\quad\forall p\in M \] 则称\(f_M\)是等距不变量.

Claim 5.1 设\(\R^3\)的定向曲面\(M\), \(M\)的形状算子\(L\), 黎曼联络\(\nabla\)以及黎曼曲率\(R\), 则对\(X,Y,Z\in{\frak X}(M)\)有

• (高斯曲率方程) \[ R(X,Y)Z=\lr{L(Y),Z}L(X)-\lr{L(X),Z}L(Y); \]

• (Codazzi–Mainardi方程) \[ \nabla_XL(Y)-\nabla_YL(X)-L([X,Y])=0. \]

Pf 子流形\(M\)的黎曼联络\(\nabla\)是\(\R^3\)的黎曼联络\(D\)的正交投影, 也即 \[ D_YZ = \nabla_YZ + \lr{D_YZ,N}N = \nabla_YZ+\lr{L(Y),Z}N. \tag{a} \] 所以 \[ \Align{ D_XD_YZ &= D_X\nabla_YZ + D_X\lr{L(Y),Z}N \\ &= \nabla_X\nabla_YZ + \lr{L(X),\nabla_YZ}N + X\lr{L(Y),Z}N + \lr{L(Y),Z}D_XN \\ &= \nabla_X\nabla_YZ - \lr{L(Y),Z}L(X) + \lr{L(X),\nabla_YZ}N + X\lr{L(Y),Z}N. \tag{b} } \] (其中第二步根据\((\text{a})\)式和Leibniz律, 第三步根据\(L(X)\)的定义) 交换\(X,Y\)得到 \[ \Align{ D_XD_YZ &= \nabla_Y\nabla_XZ - \lr{L(X),Z}L(Y) + \lr{L(Y),\nabla_XZ}N + Y\lr{L(X),Z}N. \tag{c} } \] 由\(\text{(a)}\)式, \[ D_{[X,Y]}Z = \nabla_{[X,Y]}Z + \lr{L([X,Y]),Z}N. \tag{d} \] 将\(\text{(b)}\)式减去\(\text{(c)}\)式和\(\text{(d)}\)式得到 \[ \Align{ 0 &= R(X,Y)Z - \lr{L(Y),Z}L(X) + \lr{L(X),Z}L(Y) + \textsf{法向分量}, } \] 其中 \[ \Align{ \textsf{法向分量} = (&\lr{L(X),\nabla_YZ} + X\lr{L(Y),Z} - {} \\ &\lr{L(Y),\nabla_XZ}N - Y\lr{L(X),Z} - \lr{L([X,Y]),Z} )N. } \] 切向分量为零立刻给出高斯曲率方程.

法向分量为零, 结合\(\nabla\)与\(\lr{\cdot,\cdot}\)适配, 化简得 \[ \lr{\nabla_XL(Y),Z}-\lr{\nabla_YL(X),Z}-\lr{L([X,Y]),Z}=0. \] 由\(Z\)的任意性, 必有\(\nabla_XL(Y)-\nabla_YL(X)-L([X,Y])=0\)成立, 即Codazzi–Mainardi方程.

• 根据第4.5节的结论, 因为\(R(X,Y)Z\)是\({\cal F}\)-多线性的, 可以定义\(p\)点的曲率 \[ R_p(X_p,Y_p)Z_p := (R(X,Y)Z)_p, \] 其中\(X,Y,Z\)分别延拓\(X_p,Y_p,Z_p\). 所以高斯曲率方程对于每一点\(p\)都成立.

Claim 5.2 (高斯绝妙定理, Theorema Egregium) 设\(\R^3\)的光滑曲面\(M\), 点\(p\in M\).

1. 若\(\qty{e_1,e_2}\)是\(T_pM\)的正交归一基底, 则\(p\)点的高斯曲率 \[ K_p = \lr{R_p(e_1,e_2)e_2,e_1}. \]

2. 高斯曲率是\(\R^3\)中光滑曲面的等距不变量.

Pf 第一部分. 设\(L(e_1)=ae_1+be_2\), \(L(e_2)=be_1+ce_2\), 则(两边取内积) \[ \Align{ a &= \lr{L(e_1),e_1}, & b &= \lr{L(e_1),e_2} = \lr{L(e_2),e_1}, & c &= \lr{L(e_2),e_2}. } \] 形状算子\(L\)在\(\qty{e_1,e_2}\)下的矩阵为\(\pmqty{a&b\\c&d}\), 所以高斯曲率 \[ K_p = ac-b^2 =\lr{L(e_1),e_1}\lr{L(e_2),e_2} - \lr{L(e_1),e_2}\lr{L(e_2),e_1}. \] 另一方面, 根据高斯曲率方程, \[ R_p(e_1,e_2)e_2 = \lr{L(e_2),e_2}L(e_1)-\lr{L(e_1),e_2}L(e_2), \] 两边与\(e_1\)内积, 立刻得到\(K_p = \lr{R_p(e_1,e_2)e_2,e_1}\).

第二部分. 设\(\R^3\)中的光滑曲面\(\tilde{M}\), 等距同构\(\phi:M\to\tilde M\). 由保内积性质可知\(\qty{\phi_*e_1,\phi_*e_2}\)是\(T_{\phi(p)}\tilde{M}\)的正交归一基底, 于是\(\tilde{M}\)在\(\phi(p)\)处的高斯曲率 \[ \Align{ \tilde{K}_{\phi(p)} &=\lr{\tilde{R}_{\phi(p)}(\phi_*e_1,\phi_*e_2)\phi_*e_2,\phi_*e_1} \\ &=\lr{\phi_*[R_p(e_1,e_2)e_2],\phi_*e_1} \\ &=\lr{R_p(e_1,e_2)e_2,e_1} \\ &=K_p, } \] (其中第二步根据Claim 3.6; 第三步根据等距同构的定义) 这说明高斯曲率\(K\)是等距不变量.

Claim 5.3 (任意基底下的高斯曲率) 设\(\R^3\)的光滑曲面\(M\), 点\(p\in M\), \(\qty{u,v}\)是\(T_pM\)的基底, 则高斯曲率 \[ K_p = \frac{ \lr{R_p(u,v)v,u} }{ \lr{u,u}\lr{v,v}-\lr{u,v}^2 }. \]

Pf 设\(\qty{e_1,e_2}\)是\(T_pM\)的正交归一基底, \(u=ae_1+be_2\), \(v=ce_1+de_2\), 根据黎曼曲率的线性性和反对称性, 有\(R_p(u,v) = (ad-bc)R_p(e_1,e_2)\), 进而 \[ \lr{R_p(u,v)v,u} = (ad-bc)^2\lr{R_p(e_1,e_2)e_2,e_1}. \] 另一方面, \[ \lr{u,u}\lr{v,v}-\lr{u,v}^2 = (a^2+b^2)(c^2+d^2)-(ac+bd)^2 = (ad-bc)^2, \] 所以\(K_p = \dfrac{ \lr{R_p(u,v)v,u} }{ \lr{u,u}\lr{v,v}-\lr{u,v}^2 }\).

6 Generalization to Hypersurfaces

之前的讨论是很容易推广到高维空间的.

6.1 The shape operator

欧氏空间\(\R^{n+1}\)中的一个超曲面(hypersurface)\(M\)指的是一个\(n\)维子流形, 下文默认是光滑的. 任意超曲面\(M\)都局部存在光滑的单位法向量场\(N\). 任取\(p\in M\), \(X_p\in T_pM\), 由于\(\lr{N,N}\equiv1\), 两边求导 \[ 0=X_p\lr{N,N}=2\lr{D_{X_p}N,N}, \] 所以\(D_{X_p}N\in T_pM\). 定义形状算子\(L_p:T_pM\to T_pM\), \(L_p(X_p):=-D_{X_p}N\). 当\(p\)取遍\(M\), 就得到了全局的形状算子\(L:{\frak X}(M)\to{\frak X}(M)\), \(L(X)_p:=L_p(X_p)\). 形状算子是高斯映射 \(\nu:M\to S^n\), \(p\to N_p\) 的微分加一个负号: \[ L(X) = -\nu_*(X). \]

Claim 6.1 设\(\R^{n+1}\)的定向超曲面\(M\), \(M\)的形状算子\(L\), 则对于\(X,Y\in{\frak X}(M)\), 有

1. (形状算子给出方向导数的法向部分) \(\lr{L(X),Y}=\lr{D_XY,N}\).
2. (形状算子的自伴性) \(\lr{L(X),Y}=\lr{X,L(Y)}\).

由于自伴性, \(L_p:T_pM\to T_pM\)具有\(n\)个实特征值\(\lambda_i\)(\(i=1,\dots,n\)), 称为\(p\)点的主曲率. 定义平均曲率\(H(p)\)和高斯曲率\(K(p)\)为 \[ \Align{ H(p) &= \frac1n\sum_{i=1}^n\lambda_i = \frac1n\tr{L_p}, \\ K(p) &= \prod_{i=1}^n\lambda_i = \det{L_p}. } \]

6.2 Fundamental forms

对于任意一点\(p\in M\), 可以定义出一系列对称的双线性映射: \[ \Align{ {\rm I}(X,Y) &= \lr{X,Y}, \\ {\rm II}(X,Y) &= \lr{L(X),Y} = \lr{X,L(Y)}, \\ {\rm III}(X,Y) &= \lr{L^2(X),Y} = \lr{L(X),L(Y)} = \lr{X,L^2(Y)} \dots \\ } \] 分别称为第一, 第二, 第三...基本形式.

根据第3.2节"子流形的黎曼联络"可知, \(M\)的联络\(\nabla\)就是\(\R^{n+1}\)的方向导数\(D\)的正交投影: \[ \nabla_XY = {\rm pr}(D_XY) = D_XY - \lr{D_XY,N}N, \] 也就是说, 将\(D_XY\)分解为切向分量与法向分量: \[ \Align{ D_XY &= (D_XY)_{\rm tan} + (D_XY)_{\rm nor} \\ &= \nabla_XY + \lr{D_XY,N}N \\ &= \nabla_XY + {\rm II}(X,Y)N, \\ } \] 切向分量是超曲面的黎曼联络, 法向分量是第二基本形式.

6.3 Gauss and Codazzi equations

欧氏空间\(\R^{n+1}\)的方向导数\(D\)与超曲面的黎曼联络\(\nabla\)的关系导致了曲率\(R_D\)和\(R\)的关系. 切向分量为零给出了高斯曲率方程, 法向分量为零给出了Codazzi-Mainardi方程.

Claim 6.2 设\(\R^{n+1}\)的定向超曲面\(M\), \(M\)的形状算子\(L\), 黎曼联络\(\nabla\)以及黎曼曲率\(R\), 则对\(X,Y,Z\in{\frak X}(M)\)有

• (高斯曲率方程) \[ R(X,Y)Z=\lr{L(Y),Z}L(X)-\lr{L(X),Z}L(Y); \]

• (Codazzi–Mainardi方程) \[ \nabla_XL(Y)-\nabla_YL(X)-L([X,Y])=0. \]

Claim 6.3 设\(\R^{n+1}\)的定向超曲面\(M\), \(M\)的曲率\(R\), 则 \[ \lr{R(X,Y)Y,X} = {\rm II}(X,X)\,{\rm II}(Y,Y) - {\rm II}(X,Y)^2. \]

• 当\(M\)是\(\R^3\)中的曲面, 且\(\qty{X_p,Y_p}\)构成正交归一基底时, 上式给出了\(M\)在\(p\)点的高斯曲率.