GTM275 | 11 主丛与示性类

GTM275 (Differential Geometry: Connections, Curvature, and Characteristic Classes) 第 28-30 节的笔记.

28 Connections on a Principal Bundle

主丛 \(G\to P\to M\) 上的联络有两种等价的定义方式:

1. \(P\) 上的一个光滑右不变水平分布 \({\cal H}\).
   • 分布 \({\cal H}\) 称为右不变的, 若 \(r_{g*}(\mathcal{H}_p)=\mathcal{H}_{pg}\).
2. \(P\) 上的一个光滑等变 \({\frak g}\) 值 \(1\)-形式 \(\omega\), 满足 \(\omega(\underline{A})=A\).
   • 由于 \({\frak g}\) 与竖直子空间认同, 所以这实际上是在说 \(\omega\) 在竖直子空间上为恒等映射.

两种方式的等价性不难说明.

• 给一个右不变水平分布 \({\cal H}\), 定义一个 \({\frak g}\) 值 \(1\)-形式 \(\omega\), 使得任意一点处的 \(\omega_p\) 是从 \(T_pP\) 到 \({\cal V}_p\) 的投射, 且以 \({\cal H}_p\) 为核 (即取竖直分量的投射 \(v:T_pP\to{\cal V}_p\)).
• 给一个等变 \({\frak g}\) 值 \(1\)-形式 \(\omega\), 定义水平子空间 \({\cal H}_p\) 为 \(\ker{\omega_p}\).

换言之, 有交换图 \[ \xymatrix{ T_pP \ar[d]_{v} \ar[dr]^{\omega_p} \\ \mathcal{V}_p & \mathfrak{g}. \ar[l]^{j_{p*}}_{\sim} } \] 第一小节, 我们通过水平分布构造联络 \(\omega\). 第二小节, 我们通过联络 \(\omega\) 构造水平分布.

28.1 Ehresmann connections

设 \(G\)-主丛 \(\pi:P\to M\). 给一水平分布 \({\cal H}\), 满足 \(TP={\cal V}\oplus{\cal H}\). 此时投射 \(v:T_pP\to{\cal V}_p\) 给出切向量的竖直分量. 因为 \({\cal V}_p\) 通过 \(j_{p*}\) 与 \({\frak g}\) 认同, 考虑复合映射 \[ \omega_p := j_{p*}^{-1}\circ v:\quad T_pP \overset{v}\longrightarrow {\cal V}_p \overset{j_{p*}^{-1}}\longrightarrow {\frak g}, \] 这是一个 \(P\) 上的 \({\frak g}\) 值 \(1\)-形式.

Claim 28.1 (\({\cal H}\Rightarrow\omega\)) 若 \({\cal H}\) 是 \(P\) 上的光滑右不变水平分布, 则如上定义的 \({\frak g}\) 值 \(1\)-形式 \(\omega\) 满足

1. (恒等映射) \(\omega_p(\underline{A}_p)=A\) 对任意 \(A\in{\frak g},p\in P\).
2. (\(G\)-等变性) \(r_g^*\omega=(\operatorname{Ad}_{g^{-1}})\omega\).
3. \(\omega\) 光滑.

Pf 1, 因为 \(\underline{A}_p\) 是竖直向量, 所以 \(v(\underline{A}_p)=\underline{A}_p\), 根据 \(j_{p*}\) 的定义, \[ \omega_p(\underline{A}_p)=j_{p*}^{-1}(\underline{A}_p)=A. \] 2, 即证 \[ \omega_{pg}(r_{g*}Y_p) = (\operatorname{Ad}_{g^{-1}})\omega_p(Y_p). \] 因为两边都是 \(\R\)-线性的, 所以可以对 \(Y_p\) 为竖直向量和水平向量分别证明. 设 \(Y_p\) 为竖直向量, 则 \(Y_p=\underline{A}_p\) 对某 \(A\in{\frak g}\), 有 \[ \Align{ \omega_{pg}(r_{g*}Y_p) = \omega_{pg}(r_{g*}\underline{A}_p) &= \omega_{pg}\pqty{ \underline{\operatorname{Ad}_{g^{-1}}A}_{pg} } \\ &= \operatorname{Ad}_{g^{-1}}A \\ &= (\operatorname{Ad}_{g^{-1}})\omega_p(A_p). } \] 其中第二个等号由 Claim 26.5, 第三个和第四个等号由 1. 设 \(Y_p\) 为水平向量, 因为 \({\cal H}\) 右不变, \(r_{g*}Y_p\) 也是水平向量, 于是 \[ \omega_{pg}(r_{g*}Y_p) = 0 = (\operatorname{Ad}_{g^{-1}})\omega_p(Y_p). \] 3, 由定义, \(\omega_p(Y_p)=j_{p*}^{-1}(v(Y_p))\). 因为 \({\cal H}\) 光滑, 由 Claim 27.5, \(v(Y_p)\) 光滑. 只要证明对于光滑向量场 \(Z\in\Gamma({\cal V})\), \(j_{p*}^{-1}(Z_p)\) 也光滑依赖于 \(p\).

取 \({\cal V}\) 的光滑标架 \(\underline{B_1},\dots,\underline{B_l}\), 则 \(Z = \sum a^i\underline{B_i}\) 对于光滑函数 \(a^i\). 于是 \[ j_{p*}^{-1}(Z_p) = \sum a^i(p) B_i \] 是光滑的.

注意 \(\omega\) 的光滑性不依赖 \({\cal H}\) 的右不变性.

主丛 \(P\to M\) 上的 Ehresmann 联络, 简称联络, 指的是满足上面三个条件的 \(\omega\in\Omega^1(P,{\frak g})\).

微分形式 \(\alpha:TP\to{\frak g}\) 的 \(G\)-等变性具体解释如下. 注意到 \(TP\) 和 \({\frak g}\) 都是 \(G\)-流形: \(G\) 通过右作用的微分 \(r_{g*}\) 右作用于 \(TP\), 通过伴随表示 \(\operatorname{Ad}_{g^{-1}}\) 左作用于 \({\frak g}\). 根据等变性的定义, \[ \alpha(X_p\cdot g) = g^{-1}\cdot\alpha(X_p), \] 即 \[ \alpha(r_{g*}X_p) = (\operatorname{Ad}_{g^{-1}})\alpha(X_p) \] 换言之, \(r_g^*\alpha = (\operatorname{Ad}_{g^{-1}})\alpha\).

28.2 The horizontal distribution of a Ehresmann connection

Claim 28.2 (\(\omega\Rightarrow{\cal H}\)) 设 \(G\)-主丛 \(\pi:P\to M\) 上的 Ehresmann 联络 \(\omega\), 则 \({\cal H}_p:=\ker\omega_p\) (\(p\in P\)) 给出了 \(P\) 上的一个光滑右不变水平分布.

Pf 我们要验证三个性质:

1. \(T_pP={\cal V}_p\oplus{\cal H}_p\).
2. \(r_{g*}({\cal H}_p)\subset{\cal H}_{pg}\). (因为 \(r_{g*}\) 是可逆的, 这一条蕴含 \(r_{g*}({\cal H}_p)={\cal H}_{pg}\).)
3. \({\cal H}\) 是 \(TP\) 的光滑子丛.

1, 因为 \(\mathcal{H}_p=\ker\omega_p\), 有短正合列 \[ 0\longrightarrow \mathcal{H}_p\longrightarrow T_PP \overset{\omega_p}\longrightarrow \mathfrak{g} \longrightarrow 0. \] 映射 \(j_{p*}:{\frak g}\to\mathcal{V}_p\subset T_pP\) 提供了一个右分裂, 根据 Claim 27.6, 有同构 \[ T_pP \cong \mathfrak{g}\oplus\mathcal{H}_p \cong \mathcal{V}_p\oplus\mathcal{H}_p. \] 2, 设 \(Y_p\in{\cal H}_p=\ker\omega_p\), 需要证明 \(r_{g*}(Y_p)\in\ker\omega_{pg}\). 利用 \(\omega\) 的等变性, \[ \omega_{pg}(r_{g*}Y_p) = (r_g^*\omega)_p(Y_p) = (\operatorname{Ad}_{g^{-1}})\omega_p(Y_p) = 0. \] 3, 设 \({\frak g}\) 的基底 \(B_1,\dots,B_l\), 则 \(\omega=\sum\omega^iB_i\), 其中 \(\omega^i\in\Omega^1(P,\R)\), 因为 \(\omega_p:T_pP\to{\frak g}\) 是满射, 所以 \(\omega^1,\dots,\omega^l\) 线性无关. 根据定义, \({\cal H}_p=\bigcap_{i=1}^l\ker\omega^i_p\).

设 \(p\in P\) 的附近的坐标 \(U,x^1,\dots,x^m\), \[ \omega^i = \sum_{j=1}^l f^i_j \dd{x^j}, \] 对 \(q\in U\), 切向量 \(v_q\in T_qP\) 展开为 \[ v_q = \sum_{i=1}^m v^i \eval{\pdv{x^i}}_q. \] 于是 \[ \Align{ {\cal H}_q &= \bigcap_{i=1}^l\ker\omega^i_q \\ &= \{ v_q\in T_qP \mid \omega^i_q(v_q)=0, \forall i \} \\ &= \{ (v^1,\dots,v^m)\in\R^m \mid \textstyle\sum_{j=1}^l f^i_j(q)v^j=0, \forall i \}. \\ } \] 下面我们来求解 \((v^1,\dots,v^m)\). 令 \(F^i(q,v):=\sum_{j=1}^m f^i_j(q)v^j\), 因为 \(\omega^1,\dots,\omega^l\) 在 \(p\) 线性无关, 所以 Jacobi 矩阵 \[ \pqty{ \pdv{F^i}{v^j} }_{l\times m} = (f^i_j)_{l\times m} \] 有秩 \(l\). 不妨设左边 \(l\times l\) 的子矩阵满秩. 因为满秩性是开性质, 存在 \(p\) 的开邻域 \(W\), 使 \(l\times l\) 子矩阵满秩. 由隐函数定理, 当 \(q\in W\) 时 \(v^1,\dots,v^l\) 是 \(v^{l+1},\dots,v^m\) 的光滑函数: \[ \Align{ v^1 &= v^1(v^{l+1},\dots,v^m), \\ &\hspace{0.5em}\vdots \\ v^l &= v^l(v^{l+1},\dots,v^m). } \] 令 \[ \Align{ X_1 &= \sum_{j=1}^l v^j(1,0,\dots,0)\pdv{x^j} + \pdv{x^{l+1}}, \\ X_2 &= \sum_{j=1}^l v^j(0,1,\dots,0)\pdv{x^j} + \pdv{x^{l+2}}, \\ &\hspace{.5em}\vdots \\ X_{m-l} &= \sum_{j=1}^l v^j(0,0,\dots,1)\pdv{x^j} + \pdv{x^m}, } \] 为 \(W\) 上的光滑向量场, 且在每一点 \(q\in W\) 张成 \({\cal H}_q\), 根据 Claim 18.2, \({\cal H}\) 是光滑子丛.

在主丛 \(\pi:P\to M\) 上, 因为 \(\pi\circ r_g=\pi\), 故 \(\pi_*\circ r_{g*}=\pi_*\), 所以右平移 \(r_{g*}\) 将竖直向量映到竖直向量. 对于右不变的水平分布 \({\cal H}\), \(r_{g*}\) 将水平向量映到水平向量. 立刻有如下推论.

Claim 28.3 设光滑水平分布 \({\cal H}\) 是右不变的, 则投射 \(v,h\) 与右平移 \(r_{g*}\) 可交换.

Claim 28.4 设主丛 \(P\) 上有联络 (进而有水平分布的概念), \(\underline{A}\) 是 \(A\in{\frak g}\) 生成的基本向量场.

1. 若 \(Y\) 是 \(P\) 上的水平向量场, 则 \([\underline{A},Y]\) 是水平的.
2. 若 \(Y\) 是 \(P\) 上的右不变向量场, 则 \([\underline{A},Y]=0\).

Pf 1, 基本向量场 \(\underline{A}\) 的流是 \(\phi_t(p)=p\exp(tA)=r_{\exp(tA)}(p)\), 所以 \[ [\underline{A},Y]_p = ({\cal L}_{\underline{A}}Y)_p = \lim_{t\to 0}\frac{ (r_{\exp(-tA)})_* Y_{p\exp(tA)} - Y_p }{t} =: \lim_{t\to 0} d(t). \] 因为右平移不改变水平性, \((r_{\exp(-tA)})_* Y_{p\exp(tA)}\) 和 \(Y_p\) 都是水平向量, 因此差商 \(d(t)\) (\(t\neq0\)) 也是水平向量, 由连续性, \(\lim_{t\to 0}d(t)\) 也是水平向量.

2, 右不变性有 \[ (r_{\exp(-tA)})_* Y_{p\exp(tA)} = Y_p, \] 于是 \([\underline{A},Y]_p=({\cal L}_{\underline{A}}Y)_p=0\).

28.3 Horizontal lifts

设 \(P\) 水平分布 \({\cal H}\). 因为 \({\cal V}_p\) 定义为满射 \(\pi_*:T_pP\to T_{\pi(p)}M\) 的核, 所以有同构 \[ {\cal H}_p \cong \frac{T_pP}{{\cal V}_p} \overset{\sim}\longrightarrow T_{\pi(p)}M. \] 因此, 给一向量场 \(X\in\Gamma(TM)\), 存在唯一的水平向量 \(\tilde{X}_p\in{\cal H}_p\), 使得 \[ \pi_*(\tilde{X}_p)=X_{\pi(p)}. \] 向量场 \(\tilde{X}:P\to{\cal H}\) 称为 \(X\) 的水平提升(horizontal lift), 它满足交换图 \[ \xymatrix{ M \ar[d]_{X} & P \ar@{.>}[d]^{\tilde{X}} \ar[l]_{\pi} \\ TM & \mathcal{H}. \ar[l]^(.4){\pi_*} } \]

Claim 28.5 设 \({\cal H}\) 是 \(P\) 上的光滑右不变水平分布, \(X\in\Gamma(TM)\), 则 \(\tilde{X}\) 是 \(P\) 上的光滑右不变向量场.

Pf 右不变性. 因为 \(\pi\circ r_g=\pi\), 有 \[ \pi_*(r_{g*}\tilde{X}_p) = \pi_*(\tilde{X}_p) = X_{\pi(p)}, \] 然而 \(\pi_*(\tilde{X}_{pg})\) 也等于 \(X_{\pi(pg)}=X_{\pi(p)}\), 根据水平提升的唯一性, \(r_{g*}\tilde{X}_p=\tilde{X}_p\).

光滑性. 只需在局部验证. 设局部平凡化 \(\phi_U:P|_U\to U\times G\), 定义 \[ Z_{(x,g)} = (X_x,0) \in T_{(x,g)}(U\times G). \] 令 \(\eta:U\times G\to U\) 为自然投射. 则 \(Z\) 是 \(U\times G\) 上的光滑向量场, 且满足 \(\eta_*Z_{(x,g)}=X_x\). 定义 \(Y:=(\phi_{U*})^{-1}Z\) 是 \(P|_U\) 上的光滑向量场, 则 \[ \pi_*(Y_p) = (\pi\circ\phi_U^{-1})_*Z_{(\pi(p),g)} = \eta_*Z_{(\pi(p),g)} = X_{\pi(p)}. \] 容易验证, \(hY\) 是 \(X\) 的水平提升: \[ \pi_*(hY_p) \equiv \pi_*(Y_p) = X_{\pi(p)}. \] 根据水平提升的唯一性, \(\tilde{X}=hY\) 在 \(U\) 上光滑.

Note 更一般地, 可以在光滑纤维丛 \(\pi:E\to M\) 上定义联络的概念, 两种等价的方式是:

1. 光滑的水平分布 \({\cal H}\) 满足 \({\cal H}\oplus{\cal V}=TE\) (竖直子丛 \({\cal V}\) 同样定义为 \(\ker{\pi_*}\)).
2. \(TE\) 值光滑 \(1\)-形式 \(\omega:TE\to TE\), 满足 \(\omega^2=\omega\), \(\omega|_{\cal V}={\rm id}_{\cal V}\).
   • \(\omega\) 可以看作 \(TE\) 沿着 \({\cal H}\) 到 \({\cal V}\) 上的投射.

29 Horizontal Distributions on a Frame Bundle

向量丛 \(E\to M\) 上的联络 \(\nabla\) 可以诱导出标架丛 \({\rm Fr}(E)\) 上的联络, 即给出 \({\rm Fr}(E)\) 的一个水平分布 \({\cal H}\).

29.1 Parallel translation

设光滑向量丛 \(\eta:E\to M\).

根据 "拉回丛" 一节最后的讨论, 光滑曲线 \(c:I\to M\) 诱导出拉回丛 \(c^*E\), 即沿着曲线的向量丛, 则 \(\Gamma(c^*E)\) 表示所有沿着 \(c\) 的光滑截面. 容易证明, \(E\) 上的联络 \(\nabla\) 唯一诱导出沿着 \(c\) 的协变导数: \[ \frac{{\rm D}}{\dd{t}}: \Gamma(c^*E) \to \Gamma(c^*E), \] 满足

1. \(\R\) 线性性.
2. (Leibniz 律) \({\rm D}(fs)/\dd{t}=s\dd{f}/\dd{t}{}+f{{\rm D}s}/\dd{t}\).
3. (适配性) 对于 \(\tilde{s}\in\Gamma(M,E)\) 延拓 \(s\), 即 \(\tilde{s}(c(t))=s(t)\), 有 \({\rm D}s(t)/\dd{t}=\nabla_{c'(t)}\tilde{s}\).

截面 \(s\in\Gamma(c^*E)\) 称为沿着曲线平行的, 若 \({\rm D}s/\dd{t}\equiv0\).

和切丛 \(TM\) 的联络诱导出的协变导数一样, \(E\) 的联络 \(\nabla\) 诱导出的协变导数在局部标架下展开为 \[ \frac{{\rm D}s}{\dd{t}} = \sum_i\pqty{ \dv{s^i}{t} + \sum_js^j\omega^i_j(c'(t)) } e_{i,c(t)}. \] 同样可以得到平行移动的存在唯一性, 以及平移诱导出的线性同构 \[ \varphi_{a,b}: E_{c(a)} \overset\sim\to E_{c(b)}. \] 因此, 若光滑截面 \(e_1,\dots,e_r\in\Gamma(c^*E)\) 在 \(c(t_0)\) 处构成 \(E_{c(t_0)}\) 的一个基底, 则对任意 \(t\in I\), \(e_1,\dots,e_r\) 都构成基底, 称 \(s_1,\dots,s_r\) 为 \(c\) 上的一个平行标架(parallel frame).

设 \(E\) 的标架丛 \(\pi:{\rm Fr}(E)\to M\). 曲线 \(\tilde{c}:I\to{\rm Fr}(E)\) 称为曲线 \(c:I\to M\) 的提升(lift), 若 \[ c(t)=\pi(\tilde{c}(t)). \] 如果 \(\tilde{c}(t)\) 是沿着 \(c\) 平行的标架, 则 \(\tilde{c}(t)\) 称为水平提升.

给定 \(x=c(t_0)\in M\) 处的标架 \(e_x\) 后, 存在唯一的沿着 \(c(t)\) 的平行的标架, 说明给定初值的水平提升的存在唯一性.

29.2 Horizontal vectors

设向量丛 \(E\to M\) 配以联络 \(\nabla\), \(x\in M\) 处的标架 \(e_x\in{\rm Fr}(E_x)\). 切向量 \(v\in T_{e_x}{\rm Fr}(E)\) 称为水平的, 若存在曲线 \(c:I\to M\), \(c(0)=x\), 使得 \(v\) 是那个唯一水平提升 \[ \tilde{c}: I\to{\rm Fr}(E),\quad\tilde{c}(0)=e_x \] 的切向量 \(\tilde{c}'(0)\).

图示: 设 \(x\in M\), 标架 \(e_x\in{\rm Fr}(E_x)\). 则任给从 \(x\) 开始的曲线 \(c:I\to M\), 都存在唯一的从 \(e_x\) 开始的水平提升 \(\tilde{c}:I\to{\rm Fr}(E)\).

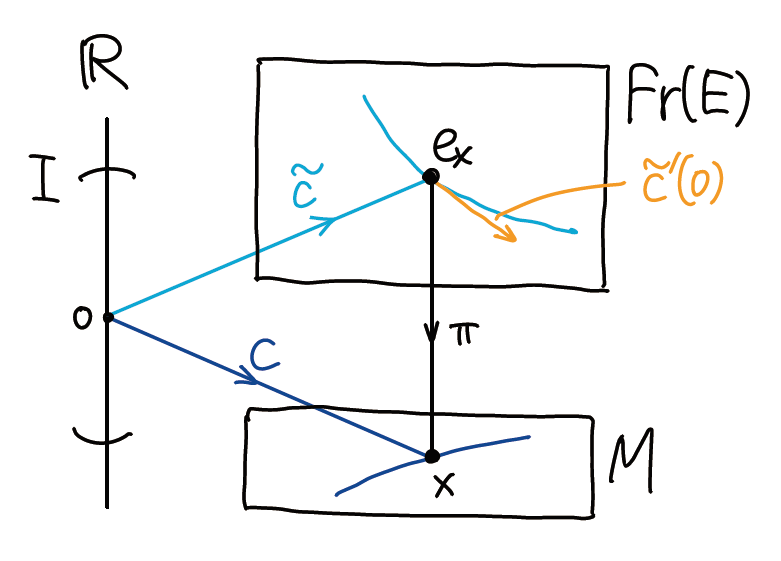
这曲线 \(\tilde{c}\) 的初始速度 \(\tilde c'(0)\in T_{e_x}{\rm Fr}(E)\) 定义为水平向量.

我们的目标是证明 \(e_x\) 处的所有水平向量的集合 \({\cal H}_{e_x}\) 是 \(T_{e_x}{\rm Fr}(E)\) 的一个线性子空间. 为此, 我们借助一个局部标架来计算水平向量 \(\tilde{c}'(0)\).

设 \(E|_U\) 的光滑标架 \(s\) (即 \({\rm Fr}(E)\) 的光滑局部截面) 满足 \(s(x)=e_x\). 显然 \(s(c(t))\) 将 \(c(t)\) 提升到 \({\rm Fr}(E)\), 当然这不一定是水平提升. 对任意 \(t\in I\), \(E_{c(t)}\) 有两个标架 \(s(c(t))\) 和 \(\tilde{c}(t)\), 设它们满足变换关系 \[ s(c(t)) = \tilde{c}(t) \cdot a(t), \] 其中光滑矩阵值函数 \(a:I\to{\rm GL}(r,\R)\). 当 \(t=0\), \(s(c(0))=e_x=\tilde{c}(0)\), 所以 \(a(0)\) 是单位阵 \(I\).

Claim 29.1 记号承上. 设 \(s_*:T_xM\to T_{e_x}{\rm Fr}(E)\) 为 \(s\) 的微分, \(\underline{a'(0)}\) 表示 \(a'(0)\in{\rm gl}(r,\R)\) 对应的 \({\rm Fr}(E)\) 上的基本向量场, 则 \[ s_*\big(c'(0)\big) = \tilde{c}'(0) + \underline{a'(0)}_{e_x}. \]

Pf 记 \(P={\rm Fr}(E)\), \(G={\rm GL}(r,\R)\), 右作用 \(\mu:P\times G\to P\), 则 \[ s(c(t)) = \mu( \tilde{c}(t), a(t) ). \] 利用微分公式 Claim 26.8, 取上式在 \(t=0\) 处的微分 (此时公式中 \(p=e_x\), \(g=I\)), \[ \Align{ s_*( c'(0) ) &= \mu_{*,(\tilde{c}(0),a(0))}(\tilde{c}'(0),a'(0)) \\ &= \mu_{*(e_x,I)}(\tilde{c}'(0),a'(0)) \\ &= \tilde{c}'(0) + \underline{a'(0)}_{e_x}. } \]

Claim 29.2 记号承上. 设 \(\nabla\) 在标架 \(s=[s_1,\dots,s_r]\) 下的联络矩阵为 \(\omega_s=[\omega^i_j]\), 则 \[ a'(0) = \omega_s(c'(0)). \]

Pf 记 \(\tilde{c}_i(0)=s_i(c(0))=e_{i,x}\), 曲线 \(\tilde{c}_i:I\to E\) 是向量 \(e_{i,x}\) 生成的沿着 \(c(t)\) 平行的向量场.

根据联络矩阵的定义, \[ \nabla_{c'(0)}s_j = \sum \omega^i_j(c'(0)) s_i(c(0)) = \sum \omega^i_j(c'(0)) e_{i,x}. \tag{$*$} \] 另一方面, 由沿曲线协变导数的性质 3, \[ \Align{ \nabla_{c'(t)}s_j = \frac{{\rm D}(s_j\circ c)}{\dd{t}}(t) &= \frac{\rm D}{\dd{t}}\sum\tilde{c}_i(t)a^i_j(t) \\ &= \sum (a^i_j)'(t)\tilde{c}_i(t) + \sum a^i_j(t) \frac{{\rm D}\tilde{c}_i}{\dd{t}}(t) \\ &= \sum (a^i_j)'(t)\tilde{c}_i(t). } \] 令 \(t=0\) 得到 \[ \nabla_{c'(0)}s_j = \sum (a^i_j)'(0)e_{i,x}, \] 结合 \((*)\) 式有 \((a^i_j)'(0)=\omega^i_j(c'(0))\).

结合以上两个引理, 我们得到了水平向量 \(\tilde{c}'(0)\) 的公式: \[ \tilde{c}'(0) = s_*\big(c'(0)\big) - \underline{\omega_s\big(c'(0)\big)}_{e_x}. \tag{$\#$} \]

Claim 29.3 设 \(n\) 为流形 \(M\) 上的光滑向量丛 \(\pi:E\to M\) 配以联络 \(\nabla\). 任给 \(x\in M\), \(e_x\in{\rm Fr}(E_x)\), 水平向量组成的集合 \({\cal H}_{e_x}\) 是 \(T_{e_x}{\rm Fr}(E)\) 的 \(n\) 维子空间, 且 \(\pi_*:{\cal H}_{e_x}\to T_xM\) 是线性同构 (\(\pi\) 是标架丛的投影).

Pf \((\#)\) 式中, \(s_*\) 和 \(\omega_s\) 显然是 \(\R\)-线性的; 操作 \(A\mapsto\underline{A}_{e_x}\) 也是 \(\R\)-线性的, 因此映射 \[ \Align{ \phi: T_xM &\to T_{e_x}{\rm Fr}(E), \\ c'(0) &\mapsto \tilde{c}'(0) } \] 是 \(\R\)-线性的. 作为线性映射 \(\phi\) 的像空间, \({\cal H}_{e_x}\) 是 \(T_{e_x}{\rm Fr}(E)\) 的线性子空间.

由提升的定义, \(\pi(\tilde{c}(t))=c(t)\), 两边微分得到 \(\pi_*(\tilde{c}'(0))=c'(0)\), 因此 \(\pi_*\) 是 \(\phi\) 的左逆, 这说明 \(\phi\) 是单射, 那么 \(\phi\) 就是到其像空间上的同构 \(\phi:T_xM\overset\sim\to{\cal H}_{e_x}\), 逆映射为 \(\pi_*:{\cal H}_{e_x}\overset\sim\to T_{e_x}M\).

29.3 Induced horizontal distribution

我们已经证明了, 向量丛 \(E\to M\) 上的联络 \(\nabla\) 给出了 \(T_pP\) (\(P={\rm Fr}(E)\)) 的水平子空间 \({\cal H}_p\), 且 \(\dim{\cal H}_p=\dim{M}\). 竖直子空间 \({\cal V}_p\) 定义为投射 \(\pi_*:T_pP\to T_{\pi(p)}M\) 的核空间, 因此 \({\cal V}_p\) 和 \({\cal H}_p\) 的维数在 \(T_pP\) 中互补. 又因为 \(\pi_*({\cal V}_p)=0\), 而 \(\pi_*:{\cal H}_p\to T_{\pi(p)}M\) 是同构, 有 \({\cal V}_p\cap{\cal H}_p=\{0\}\). 立刻得到 \[ T_p{\rm Fr}(E) = {\cal V}_p\oplus{\cal H}_p. \] 所以我们只需要再证明 \({\cal H}:=\bigcup_{p\in P}{\cal H}_p\) 的光滑性和右不变性.

因为有同构 \(\pi_*:{\cal H}_p\to T_{\pi(p)}M\), 所以 \(M\) 上的向量场 \(X\) 可以唯一地提升到 \(P\) 上去, 使得 \[ \pi_{*,p}(\tilde{X}_p) = X_{\pi(p)}. \] 称这提升为水平提升. 上一小节的 \((\#)\) 式给出了水平提升的公式: \[ \tilde{X}_p = s_{*,x}(X_x) - \underline{\omega_s(X_x)}_p, \quad p=s(x). \tag{$\clubsuit$} \]

Claim 29.4 若 \(X\) 是 \(M\) 上光滑向量场, 则 \(\tilde{X}\) 是 \({\rm Fr}(E)\) 上光滑向量场.

Pf 因为光滑性是局部性质, 所以可以在假设 \(P\) 是平凡丛 \(M\times G\) (\(G={\rm GL}(r,\R)\)). 根据水平分布的右不变性 (这是 \(\pi\circ r_a=\pi\) 的直接推论) \[ \tilde{X}_{(x,a)}=r_{a*}\tilde{X}_{(x,e)}. \] 设截面 \(s:M\to P\), \(s(x)=(x,e)\), 根据 \((\clubsuit)\) 式, \[ \tilde{X}_{(x,e)} = s_{*,x}(X_x) - \underline{\omega_s(X_x)}_{(x,e)}. \] 任给点 \(p=(x,a)\in P\) 和光滑函数 \(f\in C^\infty(P)\), 我们只需证明 \(\tilde{X}_pf\) 是光滑的. 结合以上两式, \[ \tilde{X}_pf = r_{a*}s_{*,x}(X_x)f - r_{a*}\underline{\omega_s(X_x)}_{(x,1)}f. \] 两项分开考虑. 第一项: \[ \Align{ r_{a*}s_{*,x}(X_x)f &= X_x(f\circ r_a\circ s) \\ &= X(f\circ r_a\circ s)(\pi(x)) \\ &= X\mu\Big( s(\pi(p)), \pi_2(p) \Big), } \] 其中 \(\pi_2(p)=\pi_2(x,a)=a\). 上面都是光滑函数的复合, 所以第一项是 \(P\) 上的光滑函数.

第二项: 根据 \(\omega_s\) 的右等变性, \[ \Align{ r_{a*}\underline{\omega_s(X_x)}_{(x,1)}f &= \underline{ (\operatorname{Ad}_{a^{-1}})\omega_s(X_x) }_{(x,a)}f \\ &= \underline{ (\operatorname{Ad}_{\pi_2(p)^{-1}})\omega_s(X_{\pi(p)}) }_pf, \\ } \] 其中 \(A(p):=(\operatorname{Ad}_{\pi_2(p)^{-1}})\omega_s(X_{\pi(p)})\) 显然是 \(P\to{\frak gl}(r,\R)\) 的光滑函数, 而 (根据基本向量场的定义) \(p\mapsto\underline{A(p)}_pf\) 显然也是光滑函数, 所以第二项光滑.

Claim 29.5 (\(\nabla\Rightarrow{\cal H}\)) 向量丛 \(E\to M\) 的联络 \(\nabla\) 诱导出的 \({\cal H}\) 是 \(\pi:P={\rm Fr}(E)\to M\) 上的光滑右不变水平分布.

Pf 要验证三条性质 ① \(TP={\cal V}\oplus{\cal H}\), ② \(r_{g*}({\cal H}_p)\subset{\cal H}_{pg}\), ③ 光滑性, 其中 ① 已在本小节开头验证.

③, 设 \(TM\) 在开集 \(U\) 上的标架 \(s_1,\dots,s_n\). 由 Claim 29.4, 水平提升 \(\tilde{s}_1,\dots,\tilde{s}_n\) 是 \(P|_U\) 上的光滑向量场. 因为 \(\pi_{*}:{\cal H}_p\to T_{\pi(p)}M\) 是同构, \(\tilde{s}_1,\dots,\tilde{s}_n\) 在每一点都 \(p\in P|_U\) 都张成 \({\cal H}_p\). 因此 \({\cal H}\) 是一个光滑子丛.

②, 设 \(\tilde{c}(t)=[v_1(t),\dots,v_r(t)]\) 是 \(c(t)\) 过 \(\tilde{c}(0)=p\) 的水平提升, 则 \(c'(0)\in{\cal H}_p\). 我们只需要证明 \(r_{g*}\tilde c'(0)\in{\cal H}_{pg}\). 设 \(g=[g^i_j]\in{\rm GL}(r,\R)\), \[ \tilde{c}(t)g = \bqty{ \sum g^i_1v_i(t),\dots,\sum g^i_rv_i(t) }, \] 水平性得出 \({\rm D}v_i/\dd{t}=0\), 而 \(g^i_j\) 是常数, 所以 \({\rm D}(\sum g^i_jv_i)/\dd{t}=0\). 因此, \(\tilde{c}(t)g\) 是沿着 \(c(t)\) 的以 \(\tilde{c}(0)g=pg\) 为初始点的水平提升, 初始速度 \[ {\cal H}_{pg} \ni \eval{\dv{t}}_0 \tilde{c}(t)g = r_{g*}\tilde{c}'(0). \]

29.4 Induced Ehresmann connection

向量丛上的联络 \(\nabla\) 诱导出标架丛的水平分布, 进而给出了一个 Ehresmann 联络 \(\omega\). 我们要证明, 局部标架下 \(\nabla\) 的联络矩阵正是 \(\omega\) 在标架下的拉回. 进而, 主丛的联络可以诱导出向量丛的联络.

Claim 29.6 设向量丛 \(E\to M\) 的联络 \(\nabla\) 诱导出标架丛 \({\rm Fr}(E)\to M\) 上的 Ehresmann 联络 \(\omega\). 若 \(E|_U\) 有局部标架 \(e\in\Gamma(U,{\rm Fr}(E))\), 则 \(\nabla\) 在 \(e\) 下的联络矩阵 \[ \omega_e = e^*\omega. \]

Pf 设 \(e(x)=p\), 直接应用 \((\clubsuit)\) 式, \[ \tilde{X}_p = e_*(X_x) - \underline{\omega_e(X_x)}_p, \] 其中 \(\tilde{X}\) 是水平向量场, 两边作用于 Ehresmann 联络消去 \(\tilde{X}\): \[ \Align{0 &= \omega(e_*X_x) - \omega\pqty{ \underline{\omega_e(X_x)}_p } \\ &= (e^*\omega)_xX_x - \omega_e(X_x), } \] 即 \(e^*\omega=\omega_e\).

30 Curvature on a Principal Bundle

30.1 The curvature form

Bianchi 恒等式给了我们一种定义曲率的方法. 设主丛 \(G\to P\to M\), Ehresmann 联络 \(\omega\in\Omega^1(P,{\frak g})\), 它的曲率定义为 \(\Omega\in\Omega^2(P,{\frak g})\), \[ \Omega := \dd\omega + \frac12[\omega,\omega]. \] 其中 \([\cdot,\cdot]\) 是李括号诱导的矩阵值微分形式的乘积.

Claim 30.1 设向量丛 \(E\to M\) 的联络 \(\nabla\) 诱导出标架丛 \({\rm Fr}(E)\to M\) 上的 Ehresmann 联络 \(\omega\). 若 \(E|_U\) 有局部标架 \(e\in\Gamma(U,{\rm Fr}(E))\), 则 \(\nabla\) 在 \(e\) 下的曲率矩阵 \[ \Omega_e = e^*\Omega. \]

Pf (下面第二个等号利用 Claim 19.3; 第三个等号利用 Claim 29.6) \[ \Align{ e^*\Omega &= e^*\dd\omega + \frac12e^*[\omega,\omega] \\ &= \dd e^*\omega + \frac12[e^*\omega,e^*\omega] \\ &= \dd\omega_e + \frac12[\omega_e,\omega_e] \\ &= \Omega_e. } \]

Example Maurer-Cartan 联络.

在 19.3 节, 我们知道李群 \(G\) 上有一个标准的左不变 \(1\)-形式 \(\theta\in\Omega^1(G,{\frak g})\), 称为 Maurer-Cartan 形式, 满足 ① (等变性) \(r_g^*\theta=(\operatorname{Ad}_{g^{-1}})\theta\), ② 对于 \(A\in{\frak g}\), 有 \(\theta_e(A)=A\).

Maurer-Cartan 形式可以看作积丛 \(\pi:P=M\times G\to G\) 上的联络.

设自然投射 \(\eta:P\to G\), 则 (18.5 节末 Example) \[ TP = \pi^* TM \oplus \eta^* TG \] 其中 \(\eta^*TG\) 是 \(\pi_*:TP\to TM\) 的核, 即竖直子丛. 因此 \(P\) 上有典范的水平分布 \({\cal H}=\pi^*TM\). 定义 \(P\) 上的联络 \[ \omega(X) := (\eta^*\theta)(X) = \theta(\eta_*X), \]

不难验证, 这就是 \({\cal H}\) 所确定的那个 Ehresmann 联络:

1. 恒等映射: \[ \Align{ \omega_{(x,g)}(\underline{A}_{(x,g)}) &= \theta_g(\eta_*\circ j_{(x,g)*})A \\ &= \theta_g(l_{g*}A) = \theta_e(A) = A. } \]

2. 等变性: (注意 \(\eta\circ r_g=\) 李群 \(G\) 上的 \(r_g\)) \[ \Align{ r_g^*\omega &= r_g^*(\eta^*\theta) \\ &= (\eta\circ r_g)^*\theta = r_g^*\theta = (\operatorname{Ad}_{g^{-1}})\theta = (\operatorname{Ad}_{g^{-1}})\omega. } \]

3. 与 \({\cal H}\) 适配: \(\omega(X)=0\) 只要 \(X\in\Gamma({\cal H})\).

该联络的曲率 \[ \Align{ \Omega = \dd\omega + \frac12[\omega,\omega] = \eta^*\pqty{\dd\theta + \frac12[\theta,\theta]} = 0. } \]

30.2 Properties of the curvature form

和 \(\omega\) 一样, \(\Omega\) 也具有 \(G\)-等变性. 不同的是, \(\omega\) 将水平向量映到 \(0\), 而 \(\Omega\) 将竖直向量映到 \(0\).

Claim 30.2 设 \(G\)-主丛 \(\pi:P\to M\) 上的联络 \(\omega\), 点 \(p\in P\).

1. 任意竖直向量 \(X_p\in T_pP\) 可以延拓到某 \(A\in{\frak g}\) 的基本向量场 \(\underline{A}\).
2. 任意水平向量 \(Y_p\in T_pP\) 可以延拓到某 \(B\in\Gamma(TM)\) 的水平提升 \(\tilde{B}\).

Pf 1, 因为 \(j_{p*}:{\frak g}\to{\cal V}_p\) 是满射, 所以存在 \(A\in{\frak g}\), 使 \(X_p=j_{p*}(A)=\underline{A}_p\).

2, 设 \(\pi_*(Y_p)=B_{\pi(x)}\in T_{\pi(p)}M\), 将 \(B_{\pi(x)}\) 延拓到 \(M\) 上的光滑向量场 \(B\), 则水平提升 \(\tilde{B}\) 延拓 \(Y_p\).

Claim 30.3 (曲率的性质) 设 \(G\)-主丛上的联络 \(\omega\) 和曲率 \(\Omega\).

1. (水平性) \(\Omega(X,Y)=(\dd\omega)(hX,hY)\) 对任意 \(X,Y\in\Gamma(TP)\).
2. (\(G\)-等变性) \(r_g^*\Omega=(\operatorname{Ad}_{g^{-1}})\Omega\) 对任意 \(g\in G\).
3. (第二 Bianchi 恒等式) \(\dd\Omega=[\Omega,\omega]\).

Pf 1, 我们逐点地证明. 因为 \(X_p,Y_p\) 都能分解为水平分量和竖直分量, 所以只需对水平和竖直向量证明. 分为 3 种情况.

情形 A. \(X_p,Y_p\) 都水平, 此时 \([\omega_p,\omega_p](X_p,Y_p)=0\), \[ \Omega_p(X_p,Y_p) = (\dd\omega)_p(X_p,Y_p) = (\dd\omega)_p(hX_p,hY_p). \] 情形 B. \(X_p\) 竖直, \(Y_p\) 水平, 此时也有 \([\omega_p,\omega_p](X_p,Y_p)=0\). 根据 Claim 30.2, \(X_p\) 延拓到基本向量场 \(\underline{A}\), \(Y_p\) 延拓到右不变水平向量场 \(\tilde{B}\). 因此待证等式左边 \[ \Omega(\underline{A},\tilde{B}) = \dd\omega(\underline{A},\tilde{B}) = \underline{A}\omega(\tilde{B})- \tilde{B}\omega(\underline{A})- \omega([\underline{A},\tilde{B}]). \] 其中 \(\omega(\tilde{B})\) 为零, 因为 \(\tilde{B}\) 水平; \(\tilde{B}\omega(\underline{A})=\tilde{B}A=0\), 因为 \(A\) 为常数; \([\underline{A},\tilde{B}]=0\) 根据 Claim 28.4. 因此上式为零. 另一方面, 因为 \(X_p\) 竖直, 所以待证等式右边 \((\dd\omega)_p(hX_p,hY_p)\) 也为零.

情形 C. \(X_p,Y_p\) 都竖直. 取延拓 \(X_p=\underline{A}_p\), \(Y_p=\underline{B}_p\), \[ \Align{ \Omega(\underline{A},\underline{B}) &= \dd\omega(\underline{A},\underline{B}) + \frac12\Big( [\omega(\underline{A}),\omega(\underline{B})] - [\omega(\underline{B}),\omega(\underline{A})] \Big) \\ &= \dd\omega(\underline{A},\underline{B}) + [A,B]. } \] 其中第一项 \[ \Align{ \dd\omega(\underline{A},\underline{B}) &= \underline{A}\omega(\underline{B})- \underline{B}\omega(\underline{A})- \omega([\underline{A},\underline{B}]) \\ &= \underline{A}(B)-\underline{B}(A) - \omega(\underline{[A,B]}) \\ &= 0 - 0 - [A,B], } \] 因此 \(\Omega(\underline{A},\underline{B})=-[A,B]+[A,B]=0\). 而另一方面, \((\dd\omega)_p(hX_p,hY_p)=(\dd\omega)_p(0,0)\) 也为零.

2, 由 \(\omega\) 的等变性, \[ \Align{ r_g^*\Omega &= r_g^*\dd\omega + r_g^*\frac12[\omega,\omega] \\ &= \dd{r_g^*\omega} + \frac12[r_g^*\omega,r_g^*\omega] \\ &= \dd(\operatorname{Ad}_{g^{-1}})\omega + \frac12[(\operatorname{Ad}_{g^{-1}})\omega, (\operatorname{Ad}_{g^{-1}})\omega] \\ &= (\operatorname{Ad}_{g^{-1}})\pqty{\dd\omega+\frac12[\omega,\omega]} \\ &= (\operatorname{Ad}_{g^{-1}})\Omega. } \] 其中倒数第二个等号: \(\operatorname{Ad}_{g^{-1}}=(c_{g^{-1}})_*\) 作为李群同态的微分, 是李代数同态.

3, 反复利用 Claim 19.4 及其推论, \[ \Align{ \dd\Omega &= \frac12\dd{[\omega,\omega]} \\ &= \frac12([\dd\omega,\omega]-[\omega,\dd\omega]) \\ &= [\dd\omega,\omega] \\ &= \bqty{\Omega-\frac12[\omega,\omega],\omega} \\ &= [\Omega,\omega] - \frac12[[\omega,\omega],\omega] \\ &= [\Omega,\omega]. } \]

Claim 30.4 (标架丛上推广的 Bianchi 恒等式) 标架丛上联络 \(\omega\) 的曲率 \(\Omega\) 满足 \[ \dd\Omega^k = [\Omega^k,\omega]. \] 其中 \(\Omega^k=\Omega\wedge\cdots\wedge\Omega\), \(\wedge\) 是矩阵乘法诱导出的楔积. (在一般的 \(G\)-主丛上, \({\frak g}\) 不一定是矩阵代数, 所以可能没有 \(\wedge\) 的概念.)

Pf 和向量丛的情形 (Claim 20.4) 完全一样.

Claim 30.5 设 \(G\)-主丛上的联络 \(\omega\) 和曲率 \(\Omega\). 若 \(X,Y\) 为水平向量场, 则

1. \(\Omega(X,Y)=-\omega([X,Y])\).
2. \([X,Y]\) 水平当且仅当 \(\Omega(X,Y)=0\).

Pf 1, 利用 Claim 30.3 之 1 和 \(\omega\) 的竖直性, \[ \Omega(X,Y) = \dd\omega(X,Y) = X\omega(Y)-Y\omega(X)-\omega([X,Y]) = -\omega([X,Y]). \] 2, 因为 \(\ker{\omega_p}={\cal H}_p\), 所以 \(\omega(Z)=0\) 当且仅当 \(Z\) 是水平向量场. 利用 1 即得.