GTM275 | 1 曲率与向量场

GTM275(Differential Geometry: Connections, Curvature, and Characteristic Classes)第1-5节的笔记.

1 Riemannian Manifolds

1.1 Riemannian metrics

设流形\(M\)上一点\(p\), 若\(T_pM\)上的双线性形式\(\lr{\cdot,\cdot}:T_pM\times T_pM\to\R\)满足

1. (正定性) \(\lr{X_p,X_p}\geq0\)且\(\lr{X_p,X_p}=0\)当且仅当\(X_p=0\).
2. (对称性) \(\lr{X_p,Y_p}=\lr{Y_p,X_p}\).

则称\(\lr{\cdot,\cdot}\)为\(T_pM\)上的内积(inner product). 切向量\(X_p\in T_pM\)的长度(length)为\(\norm{X_p}:=\sqrt{\lr{X_p,X_p}}\); 两个切向量正交(orthogonal), 若其内积为零.

流形\(M\)上的黎曼度量(Riemannian metric)指的就是\(M\)上的一个光滑(\(C^\infty\))内积场\(p\mapsto\lr{\cdot,\cdot}_p\). 光滑的含义如下: 若\(X,Y\)为\(M\)上的光滑向量场, 则标量场\(p\mapsto\lr{X_p,Y_p}_p\)也是光滑的. 黎曼流形(Riemannian manifold)就是配以了一个黎曼度量的流形.

若\(S\)是黎曼流形\(M\)的嵌入子流形, 则将\(M\)的黎曼度量\(\lr{\cdot,\cdot}\)限制在\(S\)上就给出了\(S\)的一个黎曼度量\(\lr{\cdot,\cdot}_S\), 称为诱导度量(induced metric).

黎曼流形\((M,\lr{\cdot,\cdot}),(N,\lr{\cdot,\cdot}')\)间的光滑映射\(F:M\to N\)称为保度量的(metric-preserving)如果 \[ \lr{u,v}_p = \lr{F_*u,F_*v}'_{F(p)},\quad \forall u,v\in T_pM,\forall p\in M. \] 保度量的微分同胚称为等距同构(isometry), 简称等距.

1.2 Existence of a Riemannian metric

流形\(M\)是局部欧氏的, 所以黎曼度量必定局部存在, 然而\(M\)整体上是否存在黎曼度量却需要进一步讨论. 为了构造\(M\)上的黎曼度量, 我们的思路是将图册开覆盖\(\qty{(O_\alpha,\psi_\alpha)}\)中的每个\(O_\alpha\)上的(局部)黎曼度量拼合起来, 需要用到的工具就是下面引入的单位分解.

流形\(M\)的开覆盖\(\qty{O_\alpha}\)称为局部有限的(locally finite), 如果每个\(p\in M\)都存在邻域\(U_p\), 使得只有有限个\(O_\alpha\)和\(U_p\)相交. 函数\(f:U\to\R\)的支集(support)指的是 \[ {\rm supp}\, f := \overline{\qty{p\in U:f(p)\neq0}}. \] 设流形\(M\)的开覆盖\(\qty{O_\alpha}_{\alpha\in A}\), 光滑函数\(\rho_\alpha: M\to\R\)的集合\(\qty{\rho_\alpha}_{\alpha\in A}\)称为从属于\(\qty{U_\alpha}\)的单位分解(partition of unity subordinate to \(\qty{U_\alpha}\)), 如果

1. \({\rm supp}\,\rho_\alpha\subset U_\alpha\), 对任意\(\alpha\in A\).
2. \(\qty{{\rm supp}\,\rho_\alpha}\)是局部有限的.
3. \(\sum_{\alpha\in A}\rho_\alpha=1\). (第2条保证, 对于任意一点\(p\), 这个求和都为有限求和.)

Claim 1.1 任何流形存在黎曼度量.

Pf 先给出一个引理: 有限个黎曼度量的非负系数线性组合仍为黎曼度量. 设\(\lr{\cdot,\cdot}_i\)(\(i=1,\dots,n\))是开集\(U\)上的黎曼度量, \(a^i\geq0\), 则\(\sum_i a^i \lr{\cdot,\cdot}_i\)也是\(U\)上的黎曼度量. 证明是比较显然的.

回到原命题. 设流形\(M\)的图册\(\qty{(O_\alpha,\psi_\alpha)}\)以及从属于\(\qty{O_\alpha}\)的单位分解\(\qty{\rho_\alpha}\).

对于每个坐标域\(O_\alpha\), 定义\(O_\alpha\)上的黎曼度量为\(\lr{X,Y}_\alpha=\delta_{ij}X^i Y^j\). 根据\(\qty{{\rm supp}\,\rho_\alpha}\)的局部有限性, 每点\(p\in M\)都有一个邻域\(U_p\), 使得只有有限个\(\rho_\alpha\)在\(U_p\)上非零, 因此 \[ \sum_\alpha \rho_\alpha\lr{\cdot,\cdot}_\alpha \] 在每一点\(p\)都是一个有限求和, 根据引理, \(\sum_\alpha \rho_\alpha\lr{\cdot,\cdot}_\alpha\)是一个黎曼度量.

1.3 Curves

流形\(M\)上的一条曲线(curve)是光滑映射\(c:[a,b]\to M\). 如果曲线\(c:[a,b]\to M\)是浸入, 则称之为正则(regular)的. 曲线\(c(t)\)在\(t\)处的切向量(tangent vector)定义为\(c'(t):=c_*(\pdv{t})\). 可知, 曲线为正则的当且仅当其切向量处处非零.

• 取坐标基底\(\qty{\pdv{x^i}}\), 则\(c(t)=x^i(t)\), 切向量作用于函数的结果: \[ c'(t)(f) =c_*\pqty{\pdv{t}}(f) =\pdv{t}(c^*f) =\dv{(f\circ c)}{t} =\dv{x^i}{t}\pdv{f}{x^i}. \] 因此, 切向量\(c'(t)\)可以展开为\(\dv{x^i}{t}\pdv{x^i}\), 切向量的分量为曲线分量的导数\(\dv{x^i}{t}\).

如果\(t=t(u)\)是闭区间的同胚, 则曲线\(\beta(u):=c(t(u))\)称为\(c(t)\)的重参数化(reparametrization). 一个重要的重参数化是弧长参数化.

黎曼流形\(M\)上的曲线\(c:[a,b]\to M\)的弧长(arc length)定义为 \[ l := \int_a^b \norm{c'(u)} \dd{u}. \]

Claim 1.2 曲线的弧长与其参数化无关.

Pf 设曲线\(c:[a,b]\to M\), 另一参数化\(c(t(u))\), \(c\leq u\leq d\), 则 \[ \Align{ \int_{[c,d]}\norm{ \dv{u}c(t(u)) }\dd{u} &= \int_{[c,d]}\norm{ c'(t(u)) } \cdot |t'(u)|\dd{u} \\ &= \int_{[a,b]}\norm{ c'(t) } \dd{t}. } \]

定义弧长函数\(s:[a,b]\to[0,l]\), 其表达式为\(s(t):=\int_a^t\norm{c'(u)}\dd{u}\). 根据Newton-Leibniz公式, 有\(s'(t)=\norm{c'(t)}>0\), 于是\(s'(t)\)严格递增, 根据反函数定理, \(s(t)\)具有光滑的反函数\(t(s)\). 因此, 我们可以定义曲线\(c(t)\)的弧长参数化(arc length parametrization)为\(\gamma(s):=c(t(s))\).

Claim 1.3 曲线\(c(t)\)为弧长参数化的, 当且仅当参数起始为\(0\), 且\(\norm{c'(t)}=1\)恒成立.

Pf "\(\Rightarrow\)", 设\(t=s(t)\), 则\(t\in[0,l]\), 且\(\norm{c'(t)}=s'(t)=1\).

"\(\Leftarrow\)", 设\(\norm{c'(t)}=1\)且\(t\)从\(0\)开始, 则 \[ s(t) = \int_0^t \norm{c'(t)}\dd{t} = \int_0^t\dd{t} = t, \] 即\(t\)为弧长参数.

2 The Euclidean Space

2.1 Curvature of curves and surfaces

平面曲线的曲率.

设弧长参数化的平面曲线\(\gamma:[0,l]\to\R^2\), 则它的切向量\(T(s)=\gamma'(s)\)为单位向量. 设\(\gamma(s)\)处的单位向量\(n(s)\)与\(T(s)\)正交且\((T(s),n(s))\)与平面的定向相同(逆时针方向), 则称 \[ \kappa(s) = \lr{T'(s),n(s)} = \lr{\gamma''(s),n(s)} \] 为\(\gamma(s)\)在\(s\)处的(带符号)曲率(curvature).

• 曲线向左弯, 曲率为正; 向右弯, 曲率为负.
• 对\(\lr{T,T}=1\)两边对\(s\)求导得到\(\lr{T,T'}=0\), 即\(T'\)与\(T\)正交, 所以\(T'\)和\(n\)平行, \(\kappa=\lr{T',n}\)就是\(T'\)的(带符号)模长.
• 法向量\(n(s)\)是切向量\(T(s)=\gamma'(s)\)逆时针旋转\(\frac\pi2\)而来的, 设\(R_{\frac\pi2}\)逆时针旋转\(\frac\pi2\)的线性变换, 则\(n(s)=R_{\frac\pi2}\gamma'(s)\).

一条曲线(固定起点和终点后)有两种弧长参数化, 分别为\(\gamma(s)\)和\(\tilde\gamma(s)=\gamma(l-s)\)(其中\(l\)为曲线长度), 它们的定向相反. 我们分别求这两个参数化下的曲率. 首先切向量 \[ T(s) = \gamma'(s),\quad \tilde{T}(s) = \gamma'(s) = -\gamma'(l-s), \] 进而有法向量 \[ \tilde{n}(s) = R_{\frac\pi2}\tilde{T}(s) = -R_{\frac\pi2}T(l-s) = -n(l-s), \] 所以两者的曲率有如下关系: \[ \tilde\kappa(s) =\lr{\tilde{T}'(s),\tilde{n}(s)} =\lr{T'(s),-n(l-s)} =-\kappa(l-s) \] 注意到\(\tilde\kappa(s)\)和\(\kappa(l-s)\)是同一点\(\tilde{\gamma}(s)=\gamma(l-s)\)的曲率. 因此, 取相反定向的参数化, 曲线的曲率相差一个负号.

空间曲面的曲率.

将曲线的曲率推广到曲面的方法有很多, 其中一种是考虑曲面截线的曲率, 另外一种是考虑曲面单位法向量场的导数(即"形状算子"). 在形状算子一节, 我们会看到两种方法的等价性. 下面我们用第一种方法来定义曲面的曲率.

设\(M\)是\(\R^3\)的二维正则子流形(曲面), \(p\in M\), \(p\)点的一个向量\(N_p\in T_p\R^3\)称为法向量(normal vector), 如果\(N_p\)与\(T_p M\)的所有向量正交. 单位法向量\(N_p\)和曲面的单位切向量\(X_p\in T_pM\)确定了一个平面\(P\). 平面\(P\)和曲面\(M\)的交线称为\(M\)的一条法截线(normal section).

正交归一向量\((X_p,N_p)\)确定了平面\(P\)的一个定向, 于是我们就可以求法截线的曲率. 设\(\gamma(s)\)是弧长参数化的法截线, 且\(\gamma(0)=p\), \(\gamma'(0)=X_p\), 则称\(\gamma(s)\)在\(s=0\)处的曲率\(\kappa(0)\)为曲面\(M\)在\(p\)点的沿\(X_p\)方向的法曲率(normal curvature), 记作 \[ \kappa(X_p) := \lr{\gamma''(0), N_p}. \]

• 注意到, 法曲率和\(N_p\)的方向有关, 如果将\(-N_p\)代入上式, 得到的法曲率就会多一个负号.
• 因为所有单位向量\(X_p\in T_pM\)构成一个圆, 所以有\(\kappa:S^1\to\R\).
• 改变曲线的定向不改变二阶导数, 所以\(\kappa(X_p)=\kappa(-X_p)\).

法曲率\(\kappa\)的最大值和最小值\(\kappa_1,\kappa_2\)称为曲面在\(p\)点的主曲率(principal curvature), 均值\(H:=(\kappa_1+\kappa_2)/2\)称为平均曲率(mean curvature), 乘积\(K:=\kappa_1\kappa_2\)称为高斯曲率(Gaussian curvature). 主曲率所对应的单位向量\(X_p\in T_pM\)称为主方向(principal direction).

• 法曲率, 主曲率, 平均曲率都与\(N_p\)的方向有关, 然而高斯曲率却与\(N_p\)的方向无关.
• 若\(X_p\)是主方向, 则\(-X_p\)也是主方向.

Example 1 考虑\(\R^3\)中的半径为\(r\)的球面, 其各个方向的法截线都是半径为\(r\)的圆, 法曲率都是\(1/r\)(取向内的单位法向量), 则平均曲率\(H=1/r\), 高斯曲率\(K=1/r^2\).

Example 2 平面\(\R^2\)的所有曲率为零. 对于半径为\(r\)的圆柱面, 其主曲率为\(0,1/r\)(取向内的单位法向量), 平均曲率为\(1/2r\), 高斯曲率为零. 平面和圆柱面是局部等距同构的, 但是其主曲率和平均曲率并不相等, 这说明主曲率和平均曲率不是等距不变量(isometric invariant), 然而可以证明的是, 高斯曲率\(K\)的确是等距不变量, 即高斯曲率在等距同构下保持不变. 这就是高斯绝妙定理(Gauss’s Theorema Egregium). 本章的一个目的就是证明高斯绝妙定理, 并尝试将其推广到高维空间.

2.2 Directional derivatives

方向导数算符.

\(\R^n\)中的向量场沿着某个切向量的导数. 光滑向量场\(Y\)在\(p\)点沿着\(X_p\)方向的方向导数(directional derivative)定义为 \[ D_{X_p} Y := X_p(Y^i) \eval{\pdv{}{x^i}}_p. \]

• 实际上, \(Y\)不必在\(p\)的某个邻域有定义, 只需要在切与\(X_p\)的某条曲线有定义即可.

• 函数\(f\)沿着\(X\)的方向导数为\(D_Xf:=X(f)\).

• 若\(X\)为光滑向量场, 则可定义\(Y\)沿着\(X\)的方向导数场\((D_XY)_p:=D_{X_p}Y\), 即 \[ D_XY = X(Y^i) \pdv{}{x^i}. \] 上式表明, 若\(X,Y\)为光滑向量场, 则\(D_XY\)也是光滑向量场, 因此\(D\)可以看作映射 \[ D:{\frak X}(\R^n)\times{\frak X}(\R^n)\to{\frak X}(\R^n), \] \(D_XY\)也记作\(D(X,Y)\).

回顾一下抽象指标: \[ (D_XY)^a = \pqty{\pdv{}{x^i}}^a X(Y^i) = \pqty{\pdv{}{x^i}}^a X^b\partial_b(Y^i) = X^b\partial_bY^a. \] (最后一步因为\(\partial_b\pqty{\pdv{}{x^i}}^a=0\)) 其中\(\partial_a\)是欧氏空间\((\R^n,\delta_{ab})\)的适配导数算符.

Claim 2.1 方向导数的性质.

1. \(D(X,Y)\)关于\(X\)是\({\cal F}\)-线性的, 关于\(Y\)是\(\R\)-线性的.
2. (Leibniz律) \(D_X(fY)=(D_Xf)Y+f(D_X Y)\).

显然, \(X,Y\)在方向导数\(D(X,Y)\)中的地位是不对称的, \(D_XY-D_YX\)一般不为零. 然而, \(D_XY-D_YX\)和向量场的对易子却有一定的关系. 衡量它和对易子差别的向量场称为导数算子的挠率(torsion), 即 \[ T(X,Y) := D_XY-D_YX-[X,Y]. \] 回顾李导数, 有\([{\cal L}_v,{\cal L}_w]={\cal L}_{[v,w]}\), 下面我们用一种新的方式来解读这个恒等式. 等式左边的\({\cal L}_v\)和\({\cal L}_w\)都是\(\R\)-线性映射\({\frak X}(\R^n)\to{\frak X}(\R^n)\), 即\({\cal L}_v,{\cal L}_w\in{\rm End}_\R({\frak X}(\R^n))\), \([{\cal L}_v,{\cal L}_w]\)是\({\rm End}_\R({\frak X}(\R^n))\)上的李括号. 等式右边的\([v,w]\)是\({\frak X}(\R^n)\)的上的李括号. 因此, 这个恒等式讲的无非是: \({\cal L}\)是一个从\({\frak X}(\R^n)\)到\({\rm End}_\R({\frak X}(\R^n))\)的李代数同态! 方向导数\(D\)当然也可以看作\({\frak X}(\R^n)\)到\({\rm End}_\R({\frak X}(\R^n))\)的线性映射(\(X\mapsto D_X\)), 所以一个自然的想法就是, \(D\)是否也是\({\frak X}(\R^n)\to{\rm End}_\R({\frak X}(\R^n))\)的李代数同态? 我们定义 \[ \Align{ R(X,Y) &:= [D_X,D_Y]-D_{[X,Y]} \\ &\hspace{0.27em} = D_XD_Y-D_YD_X-D_{[XY]} \in {\rm End}_\R({\frak X}(\R^n)) } \] 用来衡量\(D\)和李代数同态的偏差, 称为\(D\)的曲率(curvature).

Claim 2.2 方向导数的更多性质.

1. (零挠率) \(T(X,Y)=0\), 即\([X,Y]=D_XY-D_YX\).
2. (零曲率) \(R(X,Y)=0\), 即\(D_{[X,Y]}=D_XD_Y-D_YD_X\).
3. (和度量适配) \(D_X\lr{Y,Z}=\lr{D_XY,Z}+\lr{Y,D_XZ}\).

Pf 取坐标基底, 用分量展开证明.

零挠率: 即证\([X,Y](f)=(D_XY)f-(D_YX)f\)对任意光滑函数\(f\)成立. \[ \Align{ [X,Y](f) &= X(Yf) - Y(Xf) \\ &= X\pqty{Y^i \pdv{f}{x^i}} - Y\pqty{X^i \pdv{f}{x^i}} \\ &= X(Y^i) \pdv{f}{x^i} \blue{{}+Y^i X\pqty{\pdv{f}{x^i}}} - Y(X^i) \pdv{f}{x^i} \blue{{}-X^i Y\pqty{\pdv{f}{x^i}}} \\ &= X(Y^i) \pdv{f}{x^i} - Y(X^i) \pdv{f}{x^i} \\ &= (D_XY)f - (D_YX)f. } \] 其中蓝色的部分为零, 因为 \[ Y^i X\pqty{\pdv{f}{x^i}} - X^i Y\pqty{\pdv{f}{x^i}} = Y^i X^j \pdv{f}{x^j x^i} - X^i Y^j \pdv{f}{x^i x^j} = 0. \] 零曲率: 即证\(D_{[X,Y]}Z=D_XD_YZ-D_YD_XZ\)对任意光滑向量场\(Z\)成立. 由方向导数的定义, \[ D_XD_YZ = D_X\pqty{ Y(Z^i)\pdv{x^i} } = X(Y(Z^i))\pdv{x^i} \] 交换\(X,Y\)有\(D_YD_XZ=Y(X(Z^i))\pdv{x^i}\), 于是 \[ \Align{ D_XD_YZ-D_YD_XZ &= [ X(Y(Z^i)) - Y(X(Z^i)) ] \pdv{x^i} \\ &= [X,Y](Z^i)\pdv{x^i} \\ &= D_{[X,Y]}Z. } \] 和度量适配: \[ \Align{ D_X\lr{Y,Z} &= X(\delta_{ij} Y^i Z^j) \\ &= \delta_{ij} (XY^i)Z^j + \delta_{ij}Y^i(XZ^j) \\ &= \lr{D_XY,Z} + \lr{Y,D_XZ}. } \]

曲线上的方向导数.

给定曲线\(c:[a,b]\to M\), 一个沿着曲线的向量场(vector field along a curve)指的是给曲线上每个点\(c(t)\)都赋予一个向量\(V(t)\in T_{c(t)}M\). 向量场\(V(t)\)称为光滑的, 如果对于任意光滑函数\(f:M\to\R\), \(V(t)f\)都是光滑的.

• 一个\(M\)上的向量场\(X\)诱导出了沿着\(c(t)\)的向量场\(V(t):=X_{c(t)}\).

对于沿着\(c(t)\)光滑向量场\(V(t)=V^i(t)\pdv{x^i}\), 定义其沿着曲线的导数为 \[ \eval{\dv{V}{t}}_t = \dv{V^i}{t} \eval{\pdv{x^i}}_{c(t)}, \] 它也是一个沿着\(c(t)\)的光滑向量场.

实际上, \((\dv{V}{t})^a=T^b\nabla_bV^a\), 其中\(\nabla_a\)是适配导数算符.

Claim 2.3 对于两个沿着曲线的光滑向量场\(V,W\), 有 \[ \dv{}{t}\lr{V(t),W(t)} = \lr{\dv{V}{t},W} + \lr{V,\dv{W}{t}}. \]

子流形上的方向导数.

对于\(\tilde{M}\)的正则子流形\(M\), 其每点的都有两种向量, 一种是切于\(M\)的, 另一种是"支楞出去", 不切于\(M\)的. 于是我们分别定义:

• \(M\)上的向量场(vector field \(M\))指的是切于\(M\)的向量场\(X\), 满足\(X_p\in T_pM\)(\(p\in M\)).
• 沿着\(M\)的向量场(vector field along \(M\))是把\(\tilde M\)的向量场\(X\)的定义域限制在\(M\)的结果, 满足\(X_p\in T_p\tilde{M}\)(\(p\in M\)).

显然, 任何\(M\)上的向量场都是沿着\(M\)的向量场. \(M\)上的全体\(C^\infty\)向量场记作\({\frak X}(M)\), 全体沿着\(M\)的\(C^\infty\)向量场记作\(\Gamma(T\tilde{M}|_M)\). 它们都是\(C^\infty(M)\)上的模.

有了这些概念, 我们就可以求向量场沿着子流形的导数了. 给定\(\R^n\)的正则子流形\(M\)上光滑向量场\(X\)和沿着\(M\)的光滑向量场\(Y\), 我们可以求\(Y\)在\(X\)方向上的导数(以前定义的) \[ D(X,Y) \equiv D_X Y = X(Y^i) \pdv{x^i} \in \Gamma(T\R^n|_M) \] 此时, \(D\)可以看作\({\frak X}(M)\times\Gamma(T\R^n|_M)\to\Gamma(T\R^n|_M)\)的\(\R\)-双线性映射, 称为\(M\)上的方向导数算符. 因为\(X,Y\)的地位不再对称了, 所以挠率(\(T(X,Y)=D_XY-D_YX-[X,Y]\))便没有意义, 而\(D\)仍旧满足(\(\R^n\)的)方向导数算符的其他性质.

设\(\tilde{V}\)是沿着\(\R^n\)的正则子流形\(M\)的向量场, \(c:[a,b]\to M\)是\(M\)的一条光滑曲线, 则\(\tilde{V}\)诱导出了一个沿着\(c\)的向量场\(V(t)=\tilde{V}_{c(t)}\in T_{c(t)}\R^n\). 下面这个定理可以将"沿曲线的导数"和"子流形的导数"联系起来.

Claim 2.4 沿曲线的导数(关于\(t\)的导数)等于子流形上切向量方向的导数, 即 \[ \eval{\dv{V}{t}}_t = D_{c'(t)}\tilde{V}|_{c(t)}. \]

Pf 设\(V(t)=V^i(t)\pdv{x^i}\), \(\tilde{V}=\tilde{V}^i\pdv{x^i}\), 有 \[ D_{c'(t)}\tilde{V}|_{c(t)} = c'(t)(\tilde{V}^i)|_{c(t)} \pdv{x^i} = \eval{\dv{(\tilde{V}^i\circ c)}{t}}_{t} \pdv{x^i} = \eval{\dv{V}{t}}_t. \] 其中第2步由切向量的性质\(T(f)=\dv{(f\circ c)}{t}|_t\); 第3步由\((\tilde{V}\circ c)|_t=\tilde{V}_{c(t)}=V(t)\).

2.3 Gauss map and the shape operator

欧氏空间\(\R^n\)中的一张超曲面(hypersurface)\(M\)指的是光滑函数\(f:\R^n\to\R\)的零点集. 我们要求偏导数\(\pdv{f}{x^i}\)在\(M\)上不全为零(即\(\dd{f}\neq0\)), 此时\(M\)是\(\R^n\)的一个正则子流形.

• 可以证明, 若\(f=0\)给出正则超曲面\(M\), 则\(\dd{f}\)是\(M\)的一个处处非零的法向量场.

一个法向量场除以其模长就得到一个单位法向量场. 由于\(\R^3\)的任意光滑曲面在局部上都是某个坐标函数的零点集, 所以任意光滑曲面都局部存在单位法向量场. 下面我们将目光聚焦于\(\R^3\)的光滑曲面.

设\(\R^3\)中光滑曲面\(M\), \(N\)是\(M\)的光滑单位法向量场. 从某点\(p\)到该点法向量\(N_p\)的映射称为高斯映射(Gauss map), 记作 \[ \nu:M\to S^2,\quad p\mapsto N_p. \] 对于\(X_p\in T_pM\), 定义 \[ L_p(X_p) := -D_{X_p}N \] 为\(M\)在\(p\)点的形状算子(shape operator), 也叫做Weingarten映射. 对每一点都有一个形状算子, 合起来就是一个"形状算子场", 即 \[ L(X)_p := L_pX_p, \] 其中\(X\)是\(M\)上的光滑向量场.

Claim 2.5 形状算子的性质. 对于\(X,Y\in{\frak X}(M)\), 有

1. \(\lr{L(X),N}=0\), 即\(L(X)\in TM\). 因此\(L\)是\(TM\to TM\)的线性映射.
2. \(\lr{L(X),Y}=\lr{D_XY,N}\).
3. (自伴性) \(\lr{L(X),Y}=\lr{X,L(Y)}\).

Pf 第1条, 因为\(\lr{N,N}=1\), 两边同时作用\(D_X\), 有 \[ 0=D_X\lr{N,N}=\lr{D_XN,N}+\lr{N,D_XN}=-2\lr{L(X),N}. \] 第2条, 因为\(Y\in{\frak X}(M)\), 所以\(\lr{Y,N}=0\), 两边时作用\(D_X\), 有 \[ 0=D_X\lr{Y,N} =\lr{D_XY,N}+\lr{Y,D_XN} =\lr{D_XY,N}-\lr{Y,L(X)}. \] 第3条, 据2有\(\lr{L(X),Y}=\lr{D_XY,N}\)和\(\lr{L(Y),X}=\lr{D_YX,N}\), 两式相减得到 \[ \lr{L(X),Y}-\lr{X,L(Y)} =\lr{D_XY,N}-\lr{D_YX,N} =\lr{[X,Y],N}=0. \] 其中倒数第二步是根据\([X,Y]=D_XY-D_YX\); 最后一步是因为\([X,Y]\in{\frak X}(M)\).

Claim 2.6 (形状算子与高斯映射) 形状算子是Gauss映射的微分, \[ \nu_*(X_p) = -L(X_p). \]

Pf 利用曲线求映射. 设光滑曲线\(c\), \(c(0)=p\), \(c'(0)=X_p\), 则 \[ \Align{ \nu_*(X_p) = (\nu\circ c)_*\pqty{\eval{\pdv{t}}_0} &= \eval{\dv{t}}_0 (\nu\circ c) \\ &= (D_{c'(0)}N)|_p = (D_{X_p}N)_p = -L(X_p). } \]

2.4 Curvature and the shape operator

Claim 2.7 设\(\R^3\)的光滑曲面\(M\), 则\(p\in M\)的单位法向量\(N_p\)和单位切向量\(X_p\), \(\gamma(s)\)是弧长参数的法截线, 则\(\gamma(s)\)在\(p\)点的关于\(N_p\)的法曲率 \[ \kappa(X_p) = \lr{L(X_p),X_p}. \]

Pf 可知\(\gamma(0)=p\), \(\gamma'(0)=X_p\), 设\(T(t)=\gamma'(t)\)为单位切向量, 则 \[ \kappa(\gamma'(s)) = \lr{\gamma''(s), N_{\gamma(s)}} = \lr{\dv{T}{s}, N_{\gamma(s)}} = \lr{D_TT, N_{\gamma(s)}} = \lr{L(T), T}. \] (第3步依据Claim 2.4; 第4步依据Claim2.5的第2条.) 取\(t=0\)有\(\kappa(X_p)=\lr{L(X_p),X_p}\).

Claim 2.8 设\(\R^3\)的光滑曲面\(M\), 则\(p\in M\)的主方向是\(L_p\)的单位特征向量, 主曲率为\(L_p\)的特征值.

• 因此, 高斯曲率\(K=\det{L_p}\), 平均曲率\(H=\tr{L_p}/2\)​.
• 由形状算子的自伴性, 主方向相互正交.

Pf 主曲率是函数\(\kappa(X_p) = \lr{L(X_p),X_p}\)在约束条件\(\lr{X_p,X_p}=1\)下的最值, 考虑Lagrange乘数法. 选择\(T_pM\)的正交归一基底\(\qty{e_1,e_2}\), 则\(X_p=xe_1+ye_2=(x,y)\T\). 由\(L\)的自伴性知其矩阵为对称阵\(A=\pmqty{a&b\\b&c}\). 即求函数 \[ \kappa(X_p)=\lr{L(X_p),X_p}=X_p\T AX_p =ax^2+2bxy+cy^2 \] 的最值, 并有约束条件 \[ g:=\lr{X_p,X_p}=x^2+y^2=1. \] 分别求\(\kappa\)和\(g\)的梯度, \[ \Align{ {\rm grad}\,\kappa &= \pmqty{2ax+2by\\2cy+2bx} = 2AX_p, \\ {\rm grad}\,g &= \pmqty{2x\\2y} = 2X_p. } \] 由Lagrange乘数法, 在\(\kappa\)的最值处, 存在\(\lambda\in\R\)使得 \[ {\rm grad}\,\kappa = \lambda\,{\rm grad}\,g, \quad\textsf{即 } AX_p = \lambda X_p. \] 可见, \(\kappa\)的最大与最小值一定在\(A\)的单位特征向量方向处取到, 为\(p\)点的主方向. 主方向\(X_p\)(单位向量)的法曲率 \[ \kappa(X_p) = \lr{L(X_p),X_p} = \lr{AX_p,X_p} = \lambda\lr{X_p,X_p} = \lambda, \] 为\(L\)的特征向量\(X_p\)对应的特征值.

Claim 2.9 (高斯映射与总曲率) 光滑曲面\(M\)的总曲率(total curvature)指的是高斯曲率在\(M\)上的积分. 若高斯映射为单射, 则总曲率的绝对值等于高斯映射的像\(\nu(M)\)​的面积: \[ \abs{\int_M\kappa} = \textsf{Area of }\nu(M). \]

Pf 因为\(\nu:M\to\nu(M)\)为微分同胚, 应用积分换元公式, \[ \Align{ \textsf{Area of }\nu(M) = \int_{\nu(M)} 1 = \int_{\nu^{-1}(\nu(M))} \abs{\det\nu_*} = \int_M \abs{\det{L}} = \abs{\int_M\kappa}. } \]

2.5 Fundamental forms

设\(\R^3\)的光滑曲面\(M\), \(p\in M\)的欧氏度量是\(T_pM\)的一个对称的双线性形式 \[ {\rm I}(X_p,Y_p) := \lr{X_p,Y_p}, \] 称为曲面在\(p\)点的第一基本形式(first fundamental form). 设形状算子\(L:T_pM\to T_pM\), 则对称双线性形式(对称性由\(L\)的自伴性得) \[ {\rm II}(X_p,Y_p) := \lr{L(X_p),Y_p} \] 称为曲面在\(p\)点的第二基本形式(second fundamental form).

在\(T_pM\)选定基底\(\qty{e_1,e_2}\), 设 \[ \Align{ E &:= {\rm I}(e_1,e_1), & F &:= {\rm I}(e_1,e_2), & G &:= {\rm I}(e_2,e_2), \\ e &:= {\rm II}(e_1,e_1), & f &:= {\rm II}(e_1,e_2), & g &:= {\rm II}(e_2,e_2), \\ } \] (分别称为第一, 第二基本形式系数) 就可以将第一, 第二基本形式用矩阵乘法给出: \[ \Align{ {\rm I}(X_p,Y_p) &= X_p\T\pmqty{E&F\\F&G}Y_p, \\ {\rm II}(X_p,Y_p) &= X_p\T\pmqty{e&f\\f&g}Y_p. } \] 当\(p\)在坐标域\((U,\psi)\)内运动, \(E,F,G,e,f,g\)​就成为了坐标的函数.

• 结合Claim 2.7, 法曲率 \[ \kappa(X_p) = {\rm II}(X_p,X_p). \]

Claim 2.10 设\(M,M'\)为\(\R^n\)中的光滑曲面, \(\varphi:M\to M'\)为微分同胚, \(E,F,G\)为\(M\)的标架\(\qty{e_1,e_2}\)下的第一基本形式系数, \(E',F',G'\)为\(M'\)的标架\(\qty{e_1':=\varphi_*e_1,e_2':=\varphi_*e_2}\)下的第一基本形式系数, 则\(\varphi\)为等距同构当且仅当\(E|_p,F|_p,G|_p\)分别和\(E'|_{\varphi(p)},F'|_{\varphi(p)},G'|_{\varphi(p)}\)相等, 对任意\(p\in M\).

Claim 2.11 设\(\R^3\)的光滑曲面\(M\), \(p\in M\), 选定\(T_pM\)的基底, 则形状算子\(L\)的矩阵为第一基本形式矩阵的逆乘以第二基本形式矩阵, 即 \[ \pmqty{E&F\\F&G}^{-1}\pmqty{e&f\\f&g}. \]

我们使用抽象指标语言来写一写形状算子和基本形式.

• 形状算子\(L^a{_b}X^b=-X^b\nabla_bN^a\), 即\(L^a{_b}=-\nabla_bN^a\). (其中\(\nabla_a\)是适配导数算符.)

• 第一基本形式就是黎曼度量, \({\rm I}_{ab}=g_{ab}\).

• 由第二基本形式的定义, \[ {\rm II}(X_p,Y_p) = \lr{L(X_p),Y_p} = g_{cb} L^c{_a}(X_p)^c(Y_p)^b, \] 因此, \({\rm II}_{ab}=g_{cb}L^c{_a}\), 也就是形状算子张量降指标的结果! 将形状算子的表达式代入, 可得 \[ {\rm II}_{ab} = -g_{cb}\nabla_aN^c = -\nabla_aN_b. \]

结合上面两者, 有 \[ {\rm II}_{ab} = g_{cb}L^c{_a} = {\rm I}_{cb}L^c{_a},\quad\textsf{即}\, L^c{_a} = ({\rm I}^{-1})^{cb} {\rm II}_{ba}, \] 同时证明了Claim 2.11.

Example 1 计算半径为\(R\)的二维球面\(S^2\)的形状算子和第二基本形式. 利用球坐标系 \[ \Cases{ x=r\sin\theta\cos\phi, \\ y=r\sin\theta\sin\phi, \\ z=r\cos\theta, } \] (其中\(0<\theta<\pi\), \(0\leq\phi<2\pi\)), 坐标基底\(\{\pdv{\theta},\pdv{\phi}\}\), \(p\in S^2\)的单位法向量\(N_p=\pdv{r}\)(朝向外部). 我们可以借助直角坐标系计算形状算子. \(N_p\)在直角坐标系\(\{\pdv{x},\pdv{y},\pdv{z}\}\)下的分量 \[ \Align{ N_p^x &= \sin\theta\cos\phi, & N_p^y &= \sin\theta\sin\phi, & N_p^z &= \cos\theta. } \] 设切向量\(X_p=X^\theta\pdv{\theta}+X^\phi\pdv{\phi}\), 则 \[ \Align{ L(X_p) &= -D_{X_p}N = -X_p(N^i)\pdv{x^i} \\ &= (-X^\theta\cos\theta\cos\phi+X^\phi\sin\theta\sin\phi)\pdv{x}+{}\\ &\hspace{1.33em} (-X^\theta\cos\theta\sin\phi-X^\phi\sin\theta\cos\phi)\pdv{y} +(X^\theta\sin\theta)\pdv{z} \\ &=-\frac{X^\theta}{r}\pdv\theta - \frac{X^\phi}{r}\pdv\phi. } \]

(最后一步把直角坐标转换为了球坐标.) 可见\(L\)在基底\(\{\pdv{\theta},\pdv{\phi}\}\)下的矩阵为\(\pmqty{-\frac1r & 0 \\ 0 & -\frac1r}\). 进而, 球面上一点\(p\)在每个方向上的法曲率都为\(-1/r\), 高斯曲率为\(1/r^2\).

进一步可以利用\({\rm II}_{ab}=g_{cb}L^c{_a}\)算得第二基本形式矩阵 \[ \pmqty{e&f\\f&g} = \pmqty{r^2&0\\0&r^2\sin^2\theta}\pmqty{-\frac1r & 0 \\ 0 & -\frac1r} = \pmqty{-r&0\\0&-r\sin^2\theta}. \]

Example 2 \(\R^3\)中的悬链面(catenoid)和正螺面(helicoid)是两种重要的曲面.

悬链面\(U\)是悬链线绕着\(x\)轴旋转一周形成的曲面, 它的参数方程为 \[ (x,y,z) = (\cosh{u}\cos\theta,\cosh{u}\sin\theta,u),\quad u\in\R,\theta\in(0,2\pi). \] 正螺面\(V\)是一条直线一边沿着(直线上)某点匀速转动, 一边沿着垂直方向匀速前进而形成的曲面, 它的参数方程为 \[ (x,y,z) = (r\cos\theta, r\sin\theta, \theta),\quad r\in\R,\theta\in(0,2\pi). \] 下面是正螺面(\(-2<u<2\))和悬链面(\(-\sinh2<r<\sinh2\))的图片.

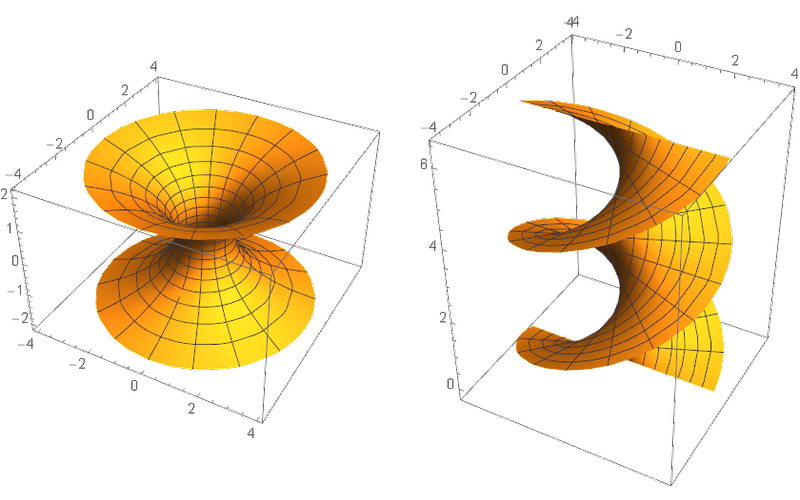
两者看起来没什么关系, 但是下面我们将证明它们是等距同构的, 更具体地说, 微分同胚\(\varphi:U\to V\),

\[ \varphi(u,\theta) := (\sinh{u}\cos\theta,\sinh{u}\sin\theta,\theta) \]

给出了一个等距同构.

证明思路: 取\(U\)的坐标基底\(\qty{\pdv{u},\pdv\theta}\), 将其推前\(\qty{\varphi_*\pdv{u},\varphi_*\pdv\theta}\)作为\(V\)的基底, 分别计算\(U,V\)在这这两个基底下的\(\rm I\)形式系数, 证明其相等(Claim 2.10).

• 如果把悬链面沿着母线剪开, 将母线拉直后挂起来, 曲面就会变成正螺面的形状.

首先, 计算\(\qty{\pdv{u},\pdv\theta}\)的推前: \[ \Align{ \varphi_*\pdv{u} &=\pdv{\varphi^j}{u}\pdv{x^j} = (\cosh{u}\cos\theta,\cosh{u}\sin\theta,0), \\ \varphi_*\pdv{\theta} &=\pdv{\varphi^j}{\theta}\pdv{x^j} = (-\sinh{u}\sin\theta,\sinh{u}\cos\theta,1). \\ } \] 其次计算\(\rm I\)形式(度量)的分量. 把\(\qty{\pdv{u},\pdv\theta}\)用\(\{\pdv{x},\pdv{y},\pdv{z}\}\)表出为 \[ \Align{ \pdv{u} &= (\sinh{u}\cos\theta,\sinh{u}\sin\theta,1), \\ \pdv{\theta} &= (-\cosh{u}\sin\theta,\cosh{u}\cos\theta,0). \\ } \] 利用定义计算\(\rm I\)形式系数: \[ \Align{ E &= \lr{\pdv{u},\pdv{u}} = \sinh^2u+1=\cosh^2u, \\ F &= \lr{\pdv{u},\pdv{\theta}} = 0, \\ G &= \lr{\pdv\theta,\pdv\theta} = \cosh^2u, \\ E'&= \lr{\varphi_*\pdv{u},\varphi_*\pdv{u}} = \cosh^2u, \\ F'&= \lr{\varphi_*\pdv{u},\varphi_*\pdv{\theta}} = 0, \\ G'&= \lr{\varphi_*\pdv\theta,\varphi_*\pdv\theta}=\sinh^2u+1=\cosh^2u. } \] 可见, \(U,V\)的\(\rm I\)形式系数系数分别相等. 根据Claim 2.10, \(\varphi\)是一个等距同构.

最后补充一个关于平均曲率的结论.

Claim 2.12 (平均曲率) 平均曲率\(H\)是法曲率的平均值, 即 \[ \frac{\kappa_1+\kappa_2}2=H=\frac1{2\pi}\int_{S^1}\kappa(X_p). \] 其中\(X_p\in S^1\)为单位向量.

Pf 设\(p\)点的主方向\(e_1,e_2\)为单位向量, 分别对应主曲率\(\kappa_1,\kappa_2\), 有 \[ \kappa_1={\rm II}(e_1,e_1),\quad \kappa_2={\rm II}(e_2,e_2). \] 任意单位向量可以展开为\(X_p=e_1\cos\theta+e_2\sin\theta\), 于是 \[ \Align{ \frac1{2\pi}\int_{S^1}\kappa(X_p) &= \frac1{2\pi}\int_{S^1} {\rm II}(X_p,X_p) \\ &= \frac1{2\pi}\int_{[0,2\pi]} {\rm II} ( e_1\cos\theta+e_2\sin\theta, e_1\cos\theta+e_2\sin\theta ) \dd{\theta} \\ &= \frac1{2\pi}\int_{[0,2\pi]} ( {\rm II}(e_1,e_1)\cos^2\theta + {\rm II}(e_2,e_2)\sin^2\theta \\ &\hspace{6em}+ 2\sin\theta\cos\theta\,{\rm II}(e_1,e_2) ) \dd{\theta} \\ &= \frac12({\rm II}(e_1,e_1) + {\rm II}(e_2,e_2)) \\ &= \frac12(\kappa_1+\kappa_2). } \]