CAIOV | 2 全纯函数初步理论
Complex Analysis in One Variable - Chapter 1 的笔记.
4 Fundamental Properties of Holomorphic Functions
设开集 \(\Omega\subset\C\), 记 \({\cal H}(\Omega)\) 为 \(\Omega\) 上所有全纯函数组成的集合. 在复数乘法、函数的加法和乘法之下, \({\cal H}(\Omega)\) 构成一个 \(\C\)-代数.
4.1 Zeros
本小节给出一些关于全纯函数的零点分布的结论.
Theorem 4.1 (解析延拓的唯一性) 设连通开集 \(\Omega\subset\C\), \(f\in{\cal H}(\Omega)\). 若存在非空开集 \(U\subset\Omega\) 使得 \(f|_U\equiv0\), 则 \(f\equiv0\).
Pf 记 \(f^{(n)}\) 为 \(f\) 的 \(n\) 阶导数, 规定 \(f^{(0)}=f\). 考虑 \(\Omega\) 的子集 \[ \Align{ E_n &= \{z\in\Omega\mid f^{(n)}(z)=0\}, & E &= \bigcap_{n\geq0} E_n. } \] 我们将证明 \(E\) 既开又闭且非空, 进而由 \(\Omega\) 的连通性, 有 \(E=\Omega\), 进而 \(f\) 在 \(\Omega\) 恒为零.
一方面, 因为 \(f^{(n)}\) 连续, \(E_n=(f^{(n)})^{-1}(0)\) 作为闭集的原像是闭集, 进而 \(E\) 是闭集.
另一方面, 因为 \(f\) 在 \(\Omega\) 全纯, 取 \(a\in\Omega\), 它在 \(a\) 的邻域 \(D\subset\Omega\) 能展开为 Taylor 级数 \[ f(z) = \sum_{n=0}^\infty \frac{1}{n!}f^{(n)}(a)(z-a)^n, \quad z\in D. \] 特别地, 令 \(a\in E\subset\Omega\), 有 \(f^{(n)}(a)=0\), 于是 \(f(z)\equiv0\) (\(z\in D\)), 进而 \(f^{(n)}\) 在 \(D\) 上处处为零, 即有 \(D\subset E\). 有 \(E\) 开.
总之, \(E\) 既开又闭. 又有 \(f|_U\equiv0\), 有 \(U\subset E\), \(E\) 非空. 得到 \(E=\Omega\).
设 \(\C\) 的连通开子集 \(U,V\) 满足 \(U\subset V\), 全纯函数 \(f\in{\cal H}(U)\), \(F\in{\cal H}(V)\). 如果 \(F|_U=f\), 则称 \(F\) 是 \(f\) 的一个解析延拓 (analytic continuation). Theorem 4.1 保证了 (当 \(V\) 连通时) 解析延拓如果存在则是唯一的.
一个比 Theorem 4.1 更强的结论是:
Theorem 4.2 (全纯函数的零点集) 设连通开集 \(\Omega\subset\C\), \(f\in{\cal H}(\Omega)\). 记零点集 \[ Z_f := \{z\in\Omega\mid f(z)=0\}. \] 若 \(f\) 不恒为零, 则 \(Z_f\) 是离散集 (即 \(Z_f\) 闭且每一点都是孤立点).
Pf 由连续性, \(Z_f\) 闭. 任取 \(a\in Z_f\), 则在邻域 \(U\) 内有 \[ f(z) = \sum_{n=0}^\infty c_n(z-a)^n,\quad z\in U. \] 因为 \(f\) 不恒为零, 由 Theorem 4.1, \(f|_U\) 不恒为零, 所以 \(\{c_n\}\) 不恒为零. 设 \(k\) 是使得 \(c_k\neq0\) 的最小整数, 则有 \[ \Align{ f(z) &= \sum_{n=k}^\infty c_n(z-a)^n \\ &= (z-a)^k \sum_{n=0}^\infty c_{k+n}(z-a)^n \\ &= (z-a)^k g(z), } \] 其中 \(g(z)=\sum_{n=0}^\infty c_{k+n}(z-a)^n\) 是 \(D\) 上的全纯函数. 因为 \(g(a)=c_k\neq0\), 由连续性, 存在 \(a\) 的邻域 \(V\subset U\) 使得 \(g|_V(z)\neq0\). 因此 \[ Z_f\cap V = \{a\}, \] 即 \(a\) 是 \(Z_f\) 的孤立点.
Theorem 4.2 表明, 连通开集 \(\Omega\) 上的全纯函数 \(f\in{\cal H}(\Omega)\) 的零点只有两种情形:
- 零点集不存在极限点, 即零点离散分布.
- 零点集存在极限点 (特别地, 若 \(f\)
在某非空开子集上为零), 则 \(f\) 在
\(\Omega\) 恒为零.
- 推论: 若 \(f,g\in{\cal H}(\Omega)\) 满足 \(\{z\in\Omega\mid f(z)=g(z)\}\) 有极限点, 则 \(f\equiv g\).
需要注意的是, 以上两个命题都要求 \(\Omega\) 连通, 因为对于非连通集 \(\Omega\) 上的全纯函数 \(f\), 其在每个连通分量上的取值是彼此无关的.
4.2 Primitives
Lemma 4.3 (原函数相差常数) 设连通开集 \(\Omega\), 全纯函数 \(f\in{\cal H}(\Omega)\) 的两个原函数 \(F,G\), 则 \(F-G\) 是常函数.
Pf 设 \(H=F-G\), 则 \(H'=F'-G'=0\), 进而 \(H^{(n)}=0\) \((n\geq1)\). 任取 \(a\in\Omega\), 设 \(H\) 的 Taylor 级数在 \(a\) 的邻域 \(U\) 收敛到 \(H\), 则对任意 \(z\in U\) 有 \[ H(z) = \sum_{n=0}^\infty \frac1{n!} H^{(n)}(a) (z-a)^n = H(a), \] 因此 \(H|_U\) 为常数. 根据解析延拓的唯一性, \(H\) 在 \(\Omega\) 上为常数.
下面我们将讨论一个一般性的问题, 即对任意开集 \(\Omega\), 函数 \(f\in{\cal H}(\Omega)\) 原函数的存在性. 与可微性不同, 原函数的存在性是一个非常复杂的问题——任何全纯函数 \(f\) 都是无穷可微的, 然而 \(f\) 可能不存在原函数. 实际上这与 \(\Omega\) 的拓扑有关.
对于拓扑平凡的开圆盘来说, 其上任意全纯函数都存在原函数 (Morera 定理证明过程的推论).
对于 \(\C\setminus\{0\}\) (非单连通), 全纯函数 \(f(z)=1/z\) 不存在原函数, 因为它在单位圆上的积分非零: \[ \int_\gamma \frac1z\dd{z} = \int_0^1 \frac1{\e^{2\pi\i t}} \dv{t}(\e^{2\pi\i t})\dd{t} = \int_0^1 2\pi\i = 2\pi\i. \]
让我们回到一般的情形.
想法: 设开集 \(\Omega\) 有一个开覆盖 \({\frak U}=\{U_i\}_{i\in I}\) (即满足 \(\bigcup_{i\in I} U_i=\Omega\)). 如果在每个 \(U_i\) 上都可以局部地构造一个 \(F\) 的原函数 \(F_i\) (假设 \(U_i\) 的拓扑足够平凡), 如果我们能把这些 \(F_i\) 以一种相容的方式 "拼合起来" 得到一个 \(\Omega\) 上整体定义的 \(F\), 岂不妙哉?
根据 Lemma, \(U_i\) 上的所有原函数都可以写成 \(F_i+c_i\) 的形式, 其中 \(c_i\) 是 \(U_i\) 上的局部常值函数 (即在每个连通分量上常值), \(F_i\) 是一个确定的函数, 满足 \(F_i'=f|_{U_i}\).
于是我们的问题就转化为了, 能否找到一族 \((c_i)_{i\in I}\), 使得这些 \((F_i+c_i)_{i\in I}\) 彼此相容? 即对任意的 \(U_i\cap U_j\neq\emptyset\), 在 \(U_i\cap U_j\) 上成立 \[ F_i + c_i = F_j + c_j. \] 下面先给出一些定义.
对任意开集 \(V\subset\C\), 记 \(\C(V)\) 为 \(V\) 上所有局部常值 (locally constant) 函数的集合.
设开集 \(\Omega\subset\C\) 的开覆盖 \({\frak U}=\{U_i\}_{i\in I}\). 设 \(J\subset I\times I\) 满足 \((i,j)\in J\) 当且仅当 \(U_i\cap U_j\neq\emptyset\).
记 \(C^0({\frak U},\C):=\prod_{i\in I}\C(U_i)\). 其中的元素称为 \({\frak U}\) 的复值 \(0\)-余链 (\(0\)-cochain).
记 \(C^1({\frak U},\C):=\prod_{(i,j)\in J}\C(U_i\cap U_j)\). 其中的元素称为 \(1\)-余链 (\(1\)-cochain).
记 \(Z^1({\frak U},\C)\) 为 \(C^1({\frak U},\C)\) 的一个子集, 定义如下: \[ Z^1({\frak U},\C) := \{(c_{ij})_{(i,j)\in J}\in C^1({\frak U},\C) \mid \textsf{在}\; U_i\cap U_j\cap U_k\neq\emptyset\;\textsf{上有}\; c_{ij}+c_{jk}+c_{ki}=0 \}. \] 其中的元素称为 \(1\)-余圈 (\(1\)-cocycle).
容易证明 \(C^0({\frak U},\C),C^1({\frak U},\C),Z^1({\frak U},\C)\) 都是是复线性空间, 且 \(Z^1({\frak U},\C)\) 是 \(C^1({\frak U},\C)\) 的子空间.
定义映射 \(\delta:C^0({\frak U},\C) \to C^1({\frak U},\C)\) 如下: 对于 \((c_i)_{i\in I}\in C^0({\frak U},\C)\) (其中 \(c_i\in\C(U_0)\)), 令 \[ (\delta c)_{ij} := (c_i|_{U_i\cap U_j}) - (c_j|_{U_i\cap U_j}) = c_i - c_j \quad\textsf{在}\;U_i\cap U_j\;\textsf{上}, \] 对于 \((i,j)\in J\). 可以验证 \(\delta c\in Z^1({\frak U},\C)\), 并且 \(\delta\) 为复线性映射, 称为余微分 (codifferential). 记 \[ B^1({\frak U},\C) := \im\delta \subset Z^1({\frak U},\C). \] 线性空间 \(B^1({\frak U},\C)\) 中的元素称为 \(1\)-余边界 (\(1\)-coboundary). 商空间 \[ H^1({\frak U},\C) := \frac{Z^1({\frak U},\C)}{B^1({\frak U},\C)} \] 称为 \({\frak U}\) 的复系数一阶上同调群 (first coholomology group).
Theorem 4.4 (原函数存在的上同调条件) 设开集 \(\Omega\subset\C\) 的开覆盖 \({\frak U}=\{U_i\}_{i\in I}\), 其中 \(U_i\) 为圆盘. 若 \(H^1({\frak U},\C)=0\), 则任意 \(f\in{\cal H}(\Omega)\) 存在原函数.
Pf 全纯函数 \(f\) 在每个圆盘 \(U_i\) 上都存在原函数 \(F_i\). 下面我们要做的就是把它们 "拼合" 起来.
对于 \((i,j)\in J\), 在 \(U_i\cap U_j\) 上定义 \(c_{ij}:=F_i-F_j\). 因为 \(U_i\cap U_j\) 连通, 由上面的 Lemma, \(c_{ij}\) 是常函数. 并且对于 \(U_i\cap U_j\cap U_k\neq\emptyset\), 有 \[ c_{ij}+c_{jk}+c_{ki} = (F_i-F_j) + (F_j-F_k) + (F_k - F_i) = 0. \] 因此函数族 \[ \xi = (c_{ij})_{(i,j)\in J} \in Z^1({\frak U},\C). \] 由于 \(H^1({\frak U},\C)=0\) 也即 \(Z^1({\frak U},\C)=B^1({\frak U},\C)\), 存在 \(c=(c_i)_{i\in I}\in C^0({\frak U},\C)\) 使得 \(\xi=\delta c\). 换言之, \((c_i)_{i\in I}\) 满足 \[ c_i - c_j = F_i - F_j,\quad\textsf{对任意}\;(i,j)\in J. \] 定义 \(\Omega\) 上的函数 \(F\) 满足 \(F|_{U_i}:=F_i-c_i\). 我们有 \(F_i-c_i=F_j-c_j\) 只要 \(U_i\cap U_j\neq\emptyset\), 因此 \(F\) 是良定义的. 由于 \(c_i\) 为常函数, 在每个 \(U_i\) 上都有 \(F'=F_i'=f\), 即 \(F\) 是 \(f\) 的原函数.
4.3 Radius of convergence
在 Section 2 中我们通过矩形的 Cauchy 积分定理、矩形的 Cauchy 公式推出了开集上的复可微函数可以做 Taylor 展开, 但它给出的收敛半径并非最优. 在本小节中, 我们将沿着相似的道路, 推出最优收敛半径.
Theorem 4.5 (圆盘的 Cauchy 积分公式) 设开集 \(\Omega\subset\C\), \(f\in{\cal H}(D)\), 开圆盘 \(D=D(a,r)\) 满足 \(\overline{D}\subset\Omega\), 则对任意 \(w\in D\), \[ f(w) = \frac{1}{2\pi\i} \int_{\gamma} \frac{f(z)}{z-w}\dd{z}, \] 其中 \(\gamma(t)=a+r\exp(2\pi\i t)\) (\(0\leq t\leq 1\)) 是圆盘的边界.
Pf 令 \[ g(z) = \Cases{ \dfrac{f(z)-f(w)}{z-w}, & z\in\Omega\setminus\{w\}, \\ f'(w), & z=w. } \] 我们断言 \(g\) 在 \(\Omega\) 全纯. 只需证明 \(g\) 在 \(w\) 附近全纯. 设 \(f\) 在 \(w\) 的邻域展开为幂级数 \(\sum_{n\geq0}c_n(z-w)^n\), 则 \(g\) 在该邻域内等于 \(\sum_{n\geq1}c_n(z-w)^{n-1}\).
取 \(\rho>r\) 满足 \(D(a,\rho)\subset\Omega\), 则 \(g\) 在 \(D(a,\rho)\) 上存在原函数 (Morera 定理证明过程的推论). 又由 Propisition 2.7, \[ \int_{\gamma} \frac{f(z)}{z-a}\dd{z}{} = f(a) \int_{\gamma} \frac{1}{z-a}\dd{z}. \] 类似于 "矩形的 Cauchy 积分公式" 的证明, 可以算出 \(\int_\gamma1/(z-a)\dd{z}=2\pi\i\).
Theorem 4.6 设开圆盘 \(D=D(a,r)\), \(f\in{\cal H}(D)\), 则 \(f\) 在在 \(a\) 处的 Taylor 级数在 \(D\) 上收敛到 \(f\).
Pf 取 \(0<\rho<r\). 在 \(D(a,\rho)\) 上应用 Cauchy 积分公式, \[ f(w) = \frac1{2\pi\i} \int_{\gamma}\frac{f(z)}{z-w}\dd{z},\quad w\in D(a,\rho). \] (其中 \(\gamma(t)=a+\rho\exp(2\pi\i t)\), \(0\leq t\leq 1\).) 将 \((z-w)^{-1}\) 展开为幂级数: \[ \Align{ \frac1{z-w} &= \frac1{z-a}\pqty{1-\frac{w-a}{z-a}}^{-1} = \frac1{z-a}\sum_{n=0}^\infty\pqty{\frac{w-a}{z-a}}^n, } \] 上式要求 \(|w-a|<|z-a|\). 注意到 \(w\in D(a,\rho)\) 而 \(z\in\partial D(a,\rho)\), 因此存在 \(0<\theta<1\) 使得 \(|w-a|\leq\theta|z-a|\), 故该级数一致收敛. 代入积分中并交换积分与求和, 得到 \[ \Align{ f(w) &= \sum_{n=0}^\infty c_n(w-a)^n, & c_n &= \frac1{2\pi\i} \int_{\gamma}\frac{f(z)}{(z-a)^{n+1}}\dd{z}. } \] 根据幂级数展开的唯一性, 有 \(c_n=f^{(n)}(a)/n!\). 因此 \(f\) 在 \(a\) 处的 Taylor 级数在 \(D(a,\rho)\) 收敛到 \(f\). 由 \(\rho<r\) 的任意性, \(f\) 在 \(a\) 处的 Taylor 级数在整个 \(D(a,r)\) 收敛到 \(f\).
立刻可以得到推论:
Corollary 4.7 (全纯函数 Taylor 级数的收敛半径) 设开集 \(\Omega\subset\C\), 点 \(a\in\Omega\). 任 \(\Omega\) 上的全纯函数 \(f\), 则 \(f\) 在 \(a\) 处的 Taylor 级数在包含于 \(\Omega\) 的最大圆盘 \(D=D(a,r)\) 上收敛到 \(f\) (换言之, \(r\) 是 \(a\) 到 \(\partial\Omega\) 的距离).
4.4 The maximum modulus principle
下面的两个小节给出了一些有关 \(f\) 及其各阶导数的模 \(|f|,|f'|,\dots\) 的结论.
我们首先给出几个极值点与二阶导数关系的结论. 设开集 \(\Omega\subset\C\), \(\Omega\) 上的实值/复值函数 \(u\) 二阶连续可微, 定义 \[ \Delta u:= \pdv{^2u}{x^2} + \pdv{^2u}{y^2}. \] 算子 \(u\mapsto\Delta u\) 称为 Laplace 算子. 此外, \[ \Delta^cu := \pdv[2]{u}{z}{\bar{z}}, \] 算子 \(u\mapsto\Delta^cu\) 称为复 Laplace 算子. 由 \(\partial/\partial z\) 和 \(\partial/\partial\bar z\) 的定义容易推出 \[ \Delta^c u = \frac14 \Delta u. \]
Proposition 4.8 (极小值点处 Hessian 半负定)
- 设开集 \(I\subset\R\), 函数 \(\phi:I\to\R\) 二阶可导. 若存在 \(t_0\in I\) 使得 \(\phi(t_0)\leq\phi(t)\) 对任意 \(t\in I\), 则 \(\phi''(t)\leq0\).
- 设开集 \(\Omega\subset\R^2\), 函数 \(u:\Omega\to\R\) 二阶连续可微. 若存在 \((x_0,y_0)\in\Omega\) 使得 \(\phi(x_0,y_0)\leq\phi(x,y)\) 对任意 \((x,y)\in\Omega\), 则 \((\Delta u)(x_0,y_0)\leq0\).
实际上, 2 可以推广为
- 设开集 \(\Omega\subset\R^n\), 函数 \(u:\Omega\to\R\) 二阶连续可微. 若存在 \(p_0\in\Omega\) 使得 \(\phi(p_0)\leq\phi(p)\) 对任意 \(p\in\Omega\), 则 Hessian \(Hu(p_0):=(\partial^2 u/\partial x_i\partial x_j(p_0))_{ij}\) 是半负定的.
Pf 只证明 1, 3.
对于 1, 注意到 \[ \phi''(t) = \lim_{h\to0}\frac{\phi(t+h)+\phi(t-h)-2\phi(t)}{h^2} \leq 0, \] 其中 \(\phi(t\pm h)\leq\phi(t)\).
对于 3, 即证明对任意 \(v=(v_1,\dots,v_n)\in\R^n\), 有 \[ \sum_{ij} \pdv{^2u}{x_i\partial x_j}(p_0) \cdot v_iv_j\leq0. \] 令 \(\phi(t)=u(p_0+tv)\), \(-\varepsilon<t<\varepsilon\). 注意到 \(\phi(0)\leq\phi(t)\), 应用 1 即得.
最大模原理 (the maximum modulus principle) 的大致意思是, 全纯函数 \(f\) 在有界闭集 \(U\) 上模长 \(|f(z)|\) 的最大值在边界 \(\partial U\) 上取到. 它基于实值函数的最大值原理 (the maximum principle).
最大模原理的一个加强版本 (强最大模原理) 进一步表明, 如果 \(|f(z)|\) 的最大值同时在 \(U\) 内部取到, 则 \(f\) 必然是常函数.
Theorem 4.9 (最大值原理) 设开集 \(\Omega\subset\C\), 实值函数 \(u\in C^2(\Omega)\). 如果 \((\Delta u)(z)\geq0\) 对任意 \(z\in\Omega\) 成立, 则对任意预紧开集 \(U\Subset\Omega\), \[ u(z) \leq \sup_{w\in\partial U} u(w), \quad z\in U. \]
Pf 先假设 \((\Delta u)(z)>0\) 对任意 \(z\in\Omega\) 成立, 记 \(z_0\in\overline{U}\) 满足 \(u(z_0)=\sup_{w\in\overline{U}}(w)\). 反证法, 假设结论不成立, 则 \(z_0\in U\), 且 \(u(z_0)\geq u(z)\) 对任意 \(z\in\overline{U}\). 由 Proposition 4.7 的 2, \((\Delta u)(z_0)\leq0\) 矛盾.
再考虑 \((\Delta u)(z)\geq0\) 的情形. 取 \(\varepsilon>0\), 令 \[ u_\varepsilon(z) := u(z) + \varepsilon|z|^2,\quad z\in\Omega. \] 则 \(\Delta u_\varepsilon=\Delta u+4\varepsilon>0\) 在 \(\Omega\) 上成立. 由上面的讨论, \[ u_\varepsilon(z)\leq\sup_{w\in\partial U} u_\varepsilon(w),\quad z\in U. \] 两边取极限 \(\varepsilon\to0\) 得到.
最大值原理中, \(U\) 预紧的条件是至关重要的. 比如取 \(U={\rm Int}H_+\) (上半平面). 对于 \(u(x,y):=y\). 有 \(\Delta u\equiv0\). 然而 \(u\) 在 \(\partial U\) 上恒为零, 在 \(U\) 上无界.
Corollary 4.10 (弱最大模原理) 设开集 \(\Omega\subset\C\), \(f\in{\cal H}(\Omega)\), 则对任意预紧开集 \(U\Subset\Omega\), \[ |f(z)| \leq \sup_{w\in\partial U} |f(w)|, \quad z\in U. \]
Pf 对 \(u(z):=|f(z)|^2=f(z)\overline{f(z)}\) 应用最大值原理即可.
下图分别展示了 \(|\cos{z}|,|\sin{z}|,|z^3-2z^2+1|\) 在单位圆盘上的图像, 我们能直观地看到其最大值都在边界处取到.

Theorem 4.11 (开映射定理) 设连通开集 \(\Omega\subset\C\), \(f\in{\cal H}(\Omega)\). 若 \(f\) 不是常函数, 则 \(f\) 是开映射 (将开集映到开集).
Pf 任取开集 \(V\subset\Omega\), 点 \(a\in V\). 通过将 \(f\) 换成 \(f-f(a)\), 不妨设 \(f(a)=0\). 取开圆盘 \(D=D(a,r)\) 满足 (1) \(\overline{D}(a,r)\subset V\), (2) 对 \(z\in\overline{D}\), \(z\neq a\) 有 \(f(z)\neq0\). (根据零点的孤立性, 这样的 \(D\) 存在.)
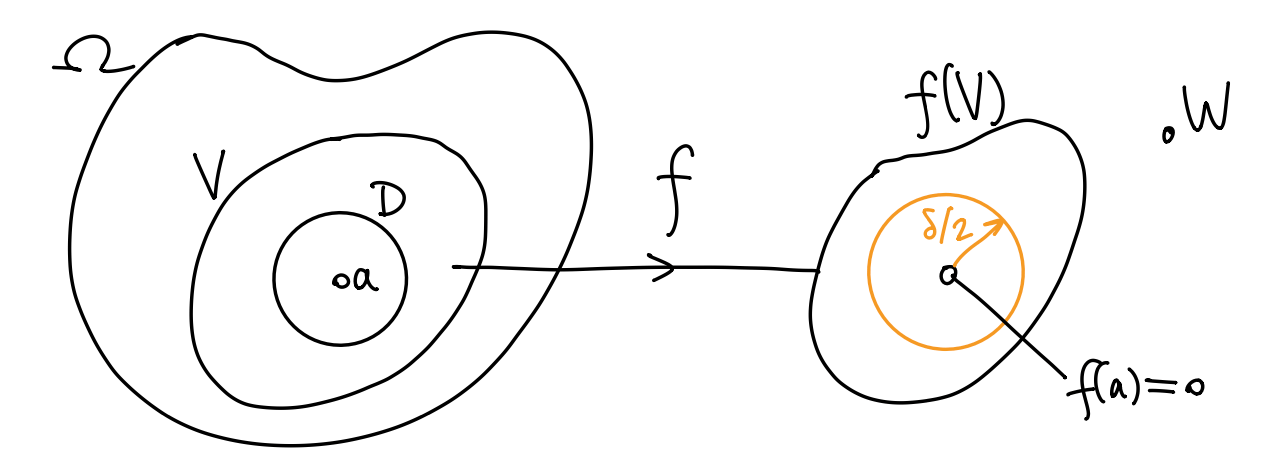
取 \(\delta=\inf\{|f(z)|\mid|z-a|=r\}\). 则 \(\delta>0\). 取点 \(w\in\C\), \(w\notin f(V)\), 我们断言 \(|w|\geq\delta/2\). 考虑函数 \(\phi(z)=1/(f(z)-w)\). 由 \(w\) 的取法, \(\phi\in{\cal H}(\Omega)\). 对 \(\phi\) 在 \(D\) 上应用弱最大模原理, \[ \frac{1}{|w|} = |\phi(a)| \leq \sup_{|z-a|=r} |\phi(z)| = \frac{1}{\inf_{|z-a|=r}|f(z)-w|}. \] 上式中 \(|f(z)-w|\geq|f(z)|-|w|\geq\delta-|w|\). 现在假设 \(|w|<\delta\), 则 \(|f(z)-w|\geq\delta-|w|>0\), 于是 \[ \frac{1}{|w|} \leq \frac{1}{\delta-|w|}, \] 即 \(|w|\geq\delta/2\). 因此, 或者有 \(|w|\geq\delta/2\), 或者有 \(|w|\geq\delta\).
总之我们证明了, 如果 \(w\notin f(V)\), 则 \(|w|\geq\delta/2\). 换言之, 开集 \(\{w\in\C\mid|w|<\delta/2\}\subset f(V)\). 注意这个开集是 \(f(a)=0\) 的邻域. 由 \(a\) 的任意性, \(f(V)\) 是开集.
Theorem 4.12 (强最大模原理) 设有界连通开集 \(\Omega\subset\C\), \(f\in{\cal H}(\Omega)\). 设 \[ M := \sup_{\zeta\in\partial\Omega} \pqty{ \limsup\limits_{\substack{z\to\zeta\\z\in\Omega}} |f(z)| }. \] 如果存在 \(z\in\Omega\), 使得 \(|f(z)|\geq M\), 则 \(f\) 是常函数.
Pf 不妨设 \(M<\infty\) (不然就没什么好证的了). 我们只需证明 \(|f(z)|\leq M\) 对任意 \(z\in\Omega\) 成立, 因为由开映射定理, \(f(\Omega)\) 是 \(\overline{D}(0,M)\) 开子集, 进而必然是 \(D(0,M)\) 的子集. 对此, 我们只用证明 \(|f(z)|\leq M+\varepsilon\) 对任意 \(\varepsilon>0\) 成立.
因为 \(\limsup_{z\to\zeta,z\in\Omega}|f(z)|\leq M\), 对任意 \(\zeta\in\partial\Omega\), 存在邻域 \(U_\zeta\), 使得 \(|f(z)|\leq M+\varepsilon\) 对任意 \(z\in U_\zeta\). 令 \(U=\bigcup_{\zeta\in\partial\Omega}U_\zeta\), \(K=\Omega-U\). 因为 \(\Omega\) 有界, \(K\) 闭, 故 \(K\) 紧.
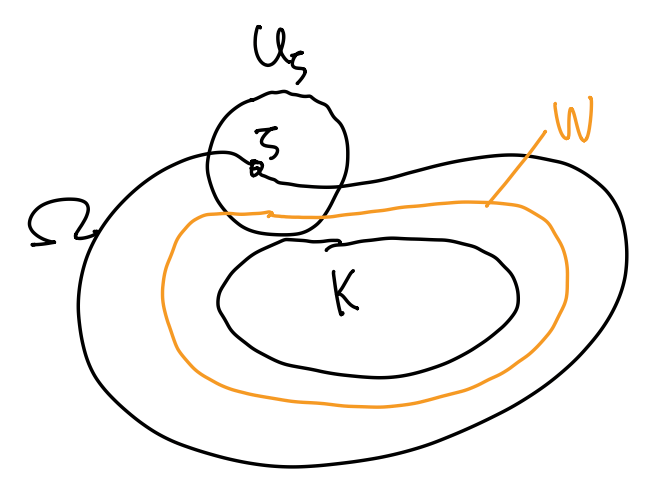
取开集 \(W\) 满足 \(K\subset W\Subset\Omega\) (如图), 则 \(\partial W\subset U\), 有 \(f(\zeta)\leq M+\varepsilon\) 对任意 \(\zeta\in\partial W\) 成立. 另一方面, 对 \(f\) 在 \(W\) 上应用弱最大模原理, 有 \[ |f(z)| \leq \sup_{\zeta\in\partial W} |f(\zeta)| \leq M+\varepsilon, \quad z\in W. \] 综上, \(|f(z)|\leq M+\varepsilon\) 在 \(U\) 和 \(W\) 上分别成立. 因为 \(\Omega\subset U\cup W\), 即证.
4.5 Cauchy's inequalities
Theorem 4.13 (Cauchy 不等式) 设 \(f\) 在圆盘 \(D(a,r)\) 上全纯, \(0<\rho<r\), 记 \(M(\rho)=\sup_{|z-a|=\rho}|f(z)|\), 则 \[ |f^{(n)}(a)| \leq n! M(\rho) \cdot \rho^{-n} \] 对 \(n\in\N\). 等价地, 若 \(f\) 在 \(a\) 处的 Taylor 级数为 \(\sum_{n\geq0}c_n(z-a)^n\), 则 \[ |c_n| \leq M(\rho)\cdot\rho^{-n}. \]
Pf 在 Theorem 4.11 的证明中, 我们得到了 \[ \Align{ c_n &= \frac1{2\pi\i} \int_{\gamma}\frac{f(z)}{(z-a)^{n+1}}\dd{z} \\ &= \frac1{2\pi\i} \int_0^1 f(a+\rho\e^{2\pi\i t}) (\rho\e^{2\pi\i t})^{-n-1} \dv{t}(\rho\e^{2\pi\i t})\dd{t} \\ &= \rho^{-n} \int_0^1 f(a+\rho\e^{2\pi\i t}) (\rho\e^{-2\pi\i nt}) \dd{t}, } \] 因此 \[ |c_n| \leq \rho^{-n} \int_0^1 \abs{f(a+\rho\e^{2\pi\i t})} \dd{t} \leq M(\rho)\rho^{-n}. \]
Theorem 4.14 (Liouville 定理) 设 \(\C\) 上的全纯函数 \(f\). 若 \(f\) 有界, 则 \(f\) 为常函数.
Pf 记 \(M(\rho)=\sup_{|z|=\rho}|f(z)|\). 如果 \(f\) 有界, 则存在常数 \(M\), 使得 \(M(\rho)\leq M\) 对任意 \(r\geq0\). 根据 Cauchy 不等式, 有 \[ |c_n| \leq M(\rho) \cdot \rho^{-n} \leq \frac{M}{\rho^n},\quad n\geq 1. \] 固定 \(n\geq 1\), 令 \(\rho\to\infty\), 得到 \(|c_n|=0\). 故 \(f(z)=c_0\).
Theorem 4.15 (代数基本定理) 复数域 \(\C\) 上的非常数多项式存在零点.
Pf 设非常数多项式 \(P(z)=a_0z^n+a_1z^{n-1}+\dots+a_n\) (\(a_0\neq0\), \(n\geq1\)). 对于 \(|z|=r\geq1\), 有 \[ \Align{ |P(z)| &= r^n\abs{a_0 + \frac{a_1}{z} + \dots + \frac{a_n}{z^n}} \\ &\geq r^n \pqty{|a_0| - \frac{|a_1|+\dots+|a_n|}{r}} \\ &\geq \frac12|a_0|r^n\quad(r\;\textsf{充分大}). } \] 如果 \(P\) 非零, 则 \(1/P\in{\cal H}(\C)\), 且对充分大的 \(|z|\) 有 \[ \frac{1}{|P(z)|} \leq \frac{2}{|a_0|r^n} \leq \frac{2}{|a_0|}, \] 则 \(1/P\) 有界. 由 Liouville 定理, \(1/P\) 为常数, 矛盾.
也可以利用开映射定理证明:
Pf 我们已经证明了当 \(r=|z|\to\infty\), 有 \(|P(z)|\to\infty\). 这实际上蕴涵了 \(P(\C)\) 是 \(\C\) 的闭集. (在第一可数空间中, \(A\) 是闭子集等价于 \(A\) 包含其中任意收敛序列的极限.) 如果 \(w_n=P(z_n)\), \(w_n\to w\in\C\), 则 \(z_n\) 有界 (否则根据 \(|P(z)|\to\infty\), \(|z|\to\infty\) 得到矛盾). 设 \(\{z_n\}\) 的子序列 \(\{z_{n_k}\}\) 收敛到 \(z\in\C\), 则 \[ P(z) = \lim P(z_{n_k}) = \lim w_{n_k} = w, \] 有 \(w\in P(\C)\).
开映射定理表明 \(P(\C)\) 既开又闭, 故 \(P(\C)=\C\).
4.6 *Roots of polynomials
5 The theorems of Weierstrass and Montel
本节我们介绍复分析中两个比较基本的定理. Weierstrass 定理表明, 全纯函数列的一致极限仍为全纯函数 (注意与光滑函数不同). Montel 定理表明, 一致有界的函数列有一致收敛子列.
Theorem 5.1 (Weierstrass) 设开集 \(\Omega\subset\C\) 上的全纯函数序列 \(\{f_n\}_{n\geq1}\). 如果 \(\{f_n\}\) 在 \(\Omega\) 内闭一致收敛到 \(f\), 则 \(f\in{\cal H}(\Omega)\). 此外, 导数序列 \(\{f_n'\}\) 在 \(\Omega\) 内闭一致收敛到 \(f'\).
Theorem 5.2 (Montel) 设开集 \(\Omega\subset\C\), 全纯函数族 \({\cal F}\subset{\cal H}(\Omega)\) 满足:
- (内闭一致有界) 对任意紧子集 \(K\subset\Omega\), 存在 \(M_K>0\), 使得对任意 \(f\in{\cal F}\) 有 \[ \abs{f(z)} \leq M_K,\quad \forall z\in K.\abs{f(z)} \leq M_K,\quad \forall z\in K. \]
则任给 \({\cal F}\) 中的函数列 \(\{f_p\}_{p\geq1}\), 存在子列 \(\{f_{p_k}\}_{k\geq1}\) 在 \(\Omega\) 内闭一致收敛.
Montel 定理的一个推论如下 (其实和 Montel 定理等价).
Theorem 5.3 (Vitali) 设连通开集 \(\Omega\subset\C\), 子集 \(A\subset\Omega\) 含有 \(\Omega\) 的极限点. 如果 \(\Omega\) 上的全纯函数序列 \(\{f_n\}_{n\geq1}\) 在 \(\Omega\) 内闭一致有界, 并且在 \(A\) 上逐点收敛, 则 \(\{f_n\}\) 在 \(\Omega\) 内闭一致收敛.