CAIOV | 1 全纯函数初步理论

Complex Analysis in One Variable - Chapter 1 的笔记.

复分析研究的是复数域 \(\C\) 上的函数. 第一章的内容是全纯函数的经典理论.

先回顾一些基础概念. 作为同构于 \(\R^2\) 的度量空间, \(\C\) 上有度量拓扑, 进而有极限的概念. 区域 (domain) 指的是 \(\C\) 的连通开子集. 开圆盘 (open disc) 和闭园盘 (closed disc) 分别指的是 \[ D(a,R)=\{z\in\C\mid|z-a|<R\},\quad \overline{D}(a,R)=\{z\in\C\mid|z-a|\leq R\}. \] 设拓扑空间 \(X\) 和子集 \(A\). 若 \(\overline{A}\) 紧, 则称 \(A\) 为预紧的 (precompact) / 相对紧的 (relative compact), 记 \(A\Subset X\).

设开子集 \(\Omega\subset\R^n\), 复值函数 \(f:\Omega\to\C\) 在某点 \(a\in\Omega\) 的各个偏导数 \((\partial f/\partial x_i)(a)\) 可以像实值函数那样定义. 记 \(\Omega\) 上的 \(k\) (\(k\in\N^*\)) 阶连续可微 (即 \(1,\dots,k\) 阶各个偏导数存在且连续) 复值函数的集合为 \(C^k(\Omega)\). 记光滑复值函数的集合为 \(C^\infty(\Omega)=\bigcap_{k\in\N^*}C^k(\Omega)\).

• 一阶连续可微 (偏导数存在且连续) 也称为实可微 (\(\R\)-differentiable).
• 对于 \(1\leq k\leq\infty\), 记 \(C^k_0(\Omega)\) 为 \(C^k(\Omega)\) 中紧支函数构成的子集合.

一维 \(\C\)-线性映射 vs 二维 \(\R\)-线性映射. 作为度量空间和实线性空间, \(\C\) 和 \(\R^2\) 是认同的. 两者的区别在于前者有一个乘法结构, 这也导致 \(\C\to\C\) 的 \(\C\)-线性映射比 \(\R^2\to\R^2\) 的 \(\R\)-线性映射有更好的性质.

设 \(\C\)-线性映射 \(f:\C\to\C\), 则存在 \(w\in\C\) 使得 \(f(z)=w\cdot z\). 记自然同构 \(\mu:\C\to\R^2\), \(x+\i y\mapsto(x,y)\), 记 \(w=a+\i b\). 则 \(f\) 等价于二维实线性映射 \[ \mu\circ f\circ\mu^{-1}:\R^2\to\R^2, \] 不难得出它的矩阵表示为 \[ \pmqty{x\\y}\mapsto\pmqty{a&-b\\b&a}\pmqty{x\\y}. \] 换言之, 作为二维实线性映射, \(f\) 的矩阵应具有 \(\pmqty{a&-b\\b&a}\) (\(a,b\in\R\)) 的形式.

1 Basic Properties of Holomorphic Functions

在本章中, \(\Omega\) 为 \(\C\) 的开子集.

1.1 Definitions

先给出两个基本定义. 设复变函数 \(f:\Omega\to\C\), 点 \(a\in\Omega\). 如果极限 \[ \lim_{\zeta\to0} \frac{f(a+\zeta)-f(a)}{\zeta} \] 存在, 我们说 \(f\) 在 \(a\) 处复可微 (\(\C\)-differentiable), 该极限称为 \(f\) 在 \(a\) 处的导数 (derivative), 记作 \(f'(a)\). 这和实变函数可微性的定义在形式上完全一样. 从定义可以直接得到:

1. 若 \(f,g\) 在 \(a\) 处复可微, 则 \(f+g,fg,\lambda f\) (\(\lambda\in\C\)) 在 \(a\) 处复可微.
2. (链式法则) 设开集 \(U,V\subset\C\). 若 \(f:U\to\C\), \(g:V\to\C\), \(f(U)\subset V\), 且 \(f\) 在 \(a\in U\) 处复可微, \(g\) 在 \(f(a)\in V\) 处复可微, 则 \(g\circ f\) 在 \(a\) 处复可微, 且 \((g\circ f)'(a)=g'(f(a))f'(a)\).

设复变函数 \(f:\Omega\to\C\). 如果对任意 \(a\in\Omega\), 存在 \(a\) 在 \(\Omega\) 中的邻域 \(U\) 以及复数列 \(\{c_n\}_{n\geq0}\), 使得 \[ f(z) = \sum_{n=0}^\infty c_n(z-a)^n,\quad\forall z\in U, \] 则称 \(f\) 在 \(\Omega\) 全纯 (holomorphic). 这个定义实际上是说 \(f\) 在 \(\Omega\) 中的每一点 \(a\) 附近都可以展开为幂级数.

• 全纯也称为解析 (anylatic). 注意应与实变函数的解析性做区分.
• 现在可以阅读 Section 3 的复幂级数理论了, 它主要探讨了复幂级数的收敛半径、复可微性, 并定义了复指数函数和三角函数. 其中关于复可微性的结论是: 若 \(f\) 在 \(\Omega\) 上全纯, 则它在 \(\Omega\) 上无穷阶复可微.

在 Section 1.2 中, 我们将用一组方程 (Cauchy-Riemann 方程) 刻画复可微性. 而在 Section 2 中, 我们将证明复可微性蕴含全纯性.

1.2 Characterizing \(\C\)-differentiability

根据 \(\C\) 与 \(\R^2\) 的同构, 复变函数 \(f(z)\) (\(z\in\C\)) 可以视作 \(f(x,y)\) (\(x,y\in\R\)). 复可微性蕴含着关于两个实变量的实可微性, 并且两个实偏导数满足一定关系.

Proposition 1.1 (复可微 \(\Rightarrow\) Cauchy-Riemann) 设 \(f:\Omega\to\C\) 在 \(a\in\Omega\) 复可微, 则偏导数 \((\partial f/\partial x)(a)\) 和 \((\partial f/\partial y)(a)\) 存在且满足 \[ \pdv{f}{x}(a) = -\i \pdv{f}{y}(a) = f'(a). \tag{a} \]

Pf 记 \(a=x+\i y\). 令 \(\zeta\in\R\), 一方面有 \[ \Align{ f'(a) &= \lim_{\zeta\to0}\frac{f(a+\zeta)-f(a)}{\zeta} \\ &= \lim_{\zeta\to0}\frac{f(x+\zeta,y)-f(x,y)}{\zeta} = \pdv{f}{x}(a). } \] 另一方面, \[ \Align{ f'(a) &= \lim_{\zeta\to0}\frac{f(a+\i\zeta)-f(a)}{\i\zeta} \\ &= \lim_{\zeta\to0}\frac{f(x,y+\zeta)-f(x,y)}{\i\zeta} = -\i\pdv{f}{y}(a). } \]

将 \(f\) 分为实部和虚部 \(f=u+\i v\), 其中 \(u,v:\Omega\to\R\), 则式 \((\text{a})\) 还可以写作 \[ \Align{ \pdv{u}{x}(a) &= \pdv{v}{y}(a), & \pdv{u}{y}(a) &= -\pdv{v}{x}(a). } \tag{b} \] 引入两个微分算子 \[ \Align{ \pdv{f}{z}(a) &:= \frac12\pqty{\pdv{f}{x}(a) - \i\pdv{f}{y}(a)}, & \pdv{f}{\bar z}(a) &:= \frac12\pqty{\pdv{f}{x}(a) + \i\pdv{f}{y}(a)}, } \] 则式 \((\text{a})\) 还可以改写成 \[ \pdv{f}{z}(a) = f'(a), \tag{c} \] 或等价地 \[ \pdv{f}{\bar z}(a) = 0. \tag{d} \] 这四个等式 \(\text{(a),(b),(c),(d)}\) 两两等价, 称为 Cauchy-Riemann 方程.

Note 关于 \(\partial/\partial z\) 和 \(\partial/\partial\bar{z}\) 的定义. 记 \(z=x+\i y\), \(\bar{z}=x-\i y\), 即 \(x=(z+\bar{z})/2\), \(y=(z-\bar{z})/(2\i)\), 将 \(f(x,y)\) 写成 \(z,\bar z\) 的函数 \(g(z,\bar{z})=f(x(z,\bar{z}),y(z,\bar{z}))\), 则 \[ \Align{ \pdv{f}{z} &= \frac12\pqty{\pdv{f}{x} - \i\pdv{f}{y}}, & \pdv{f}{\bar z} &= \frac12\pqty{\pdv{f}{x} + \i\pdv{f}{y}}, } \] 在形式上无非是链式法则.

Proposition 1.2 (Cauchy-Riemann + 连续可微 \(\Rightarrow\) 复可微) 设复变函数 \(f:\Omega\to\C\). 若 \(\partial f/\partial x\), \(\partial f/\partial y\) 在 \(a\in\Omega\) 处存在并连续, 且在 \(a\) 处满足 Cauchy-Riemann 方程, 则 \(f\) 在 \(a\) 处复可微.

Pf 记 \(f=u+\i v\), \(a=\alpha+\i\beta\). 取增量 \(\zeta=\xi+\i\eta\in\C\). 当 \(\zeta\to0\), 由连续可微性, 有 \[ \Align{ u(a+\zeta) - u(a) &= u(\alpha+\xi,\beta+\eta) - u(\alpha,\beta) \\ &= \pdv{u}{x}(a)\cdot\xi + \pdv{u}{y}(a)\cdot\eta + o(|\zeta|), } \] 同理有 \[ \Align{ v(a+\zeta) - u(a) &= \pdv{v}{x}(a)\cdot\xi + \pdv{v}{y}(a)\cdot\eta + o(|\zeta|), } \] 于是 \[ \Align{ f(a+\zeta)-f(a) &= \pdv{f}{x}(a)\cdot\xi + \pdv{f}{y}(a)\cdot\eta + o(|\zeta|). } \] 由 Cauchy-Riemann, \(\partial f/\partial y(a)=\i\partial f/\partial x(a)\), 进而 \[ \Align{ f(a+\zeta) - f(a) &= \pdv{f}{x}(a) \cdot \zeta + o(|\zeta|), } \] 即 \(f\) 在 \(a\) 复可微.

Note 需要注意的是, Proposition 1.2 不是 Proposition 1.1 的逆命题: Proposition 1.2 需要偏导数连续的条件, 但在 Proposition 1.1 中, \(f\) 在 \(a\) 复可微不能推出 \(f\) 在 \(a\) 连续可微. 一个反例是 \[ f(z) = \Cases{ z^2\sin\pqty{\dfrac1{|z|}}, & z\neq0, \\ 0, & z=0. } \] 它在 \(z=0\) 处复可微, 但不连续可微.

不同于 Proposition 1.2, 复可微的另一个准则是:

• (Looman-Menchoff) 设复变函数 \(f:\Omega\to\C\). 若 \(f\) 在 \(\Omega\) 上连续且可偏导, 且处处满足 Cauchy-Riemann 方程, 则 \(f\) 在 \(\Omega\) 复可微.

注意 "连续性" 的条件不能删去. 可以构造反例 \[ f(z) = \Cases{ \exp(-z^{-4}), & z\neq0, \\ 0, & z=0. } \] 它在 \(\C\) 上可偏导且满足 C-R 方程, 但是在 \(z=0\) 处不复可微 (注意 \(f\) 在 \(z=0\) 处不连续).

此外, "开集 \(\Omega\)" 的条件不能替换成 "点 \(a\in\Omega\)". 可以构造反例 \[ f(z) = \Cases{ \dfrac{z^5}{|z|^4} , & z\neq0, \\ 0, & z=0. } \] 它在 \(z=0\) 处连续, 且满足 C-R 方程, 但不复可微.

下面介绍 Cauchy-Riemann 方程的一种理解. 回顾切映射的概念: 设函数 \((u,v):\Omega\to\R^2\) 在 \(a\in\Omega\) 连续可微, 则它在 \(a\) 处的切映射 (tangent map) 定义为线性映射 \[ \Align{ \dd(u,v) : \R^2 &\to \R^2, & \pmqty{\xi\\\eta} &\mapsto \pmqty{ \displaystyle\pdv{u}{x}\pqty{a} & \displaystyle\pdv{u}{y}\pqty{a} \\ \displaystyle\pdv{v}{x}\pqty{a} & \displaystyle\pdv{v}{y}\pqty{a} } \pmqty{\xi\\\eta}. } \] 进而可以定义复变函数 \(f:\Omega\to\C\) 的切映射. 设自然同构 \(\mu:\C\overset\sim\to\R^2\), \(\mu(x+\i y)=(x,y)\), 定义 \[ \dd{f} := \mu^{-1}\circ\dd(u,v)\circ\mu : \C\to\C. \] 换言之, 有交换图 \[ \xymatrix{ \C \ar[r]^{\dd{f}} \ar[d]_{\mu} & \C \ar[d]^{\mu} \\ \R^2 \ar[r]_{\dd(u,v)} & \R^2. } \] 显然 \(\dd{f}\) 是一个 \(\R\)-线性映射. Cauchy-Riemann 方程 (或复可微) 则进一步保证了 \(\dd{f}\) 的 \(\C\)-线性性.

Proposition 1.3 (Cauchy-Riemann \(\iff\) 切映射 \(\C\)-线性) 连续可微的复变函数 \(f:\Omega\to\C\) 在 \(a\in\Omega\) 处满足 Cauchy-Riemann 方程当且仅当切映射 \(\dd{f}:\C\to\C\) 是 \(\C\)-线性的, 此时 \[ \dd{f}(\zeta) = \pdv{f}{z}(a)\cdot\zeta,\quad \zeta\in\C. \]

Pf 一个 \(\C\to\C\) 的 \(\C\)-线性映射就是复数乘法 \(\zeta\mapsto w\cdot\zeta\). 根据本文开头的讨论, \(\dd{f}:\C\to\C\) 的 \(\C\)-线性性等价于 \(\mu\circ\dd{f}\circ\mu^{-1}=\dd(u,v)\) 的矩阵具有 \(\pmqty{A&-B\\B&A}\) 的形式, 容易发现这等价于 Cauchy-Riemann 方程 (式 \((\text{b})\)).

2 Integration Along Curves

2.1 Curves

回顾拓扑学中曲线的相关概念. 设拓扑空间 \(X\), 则 \(X\) 上的一条曲线 (curve) 指的是连续映射 \[ \gamma: [a,b] \to X. \] 点 \(\gamma(a),\gamma(b)\) 分别称为起点和终点. 起点和终点相同的曲线称为 (在 \(\gamma(a)\) 处的) 环 (loop). 曲线的像集记作 \(\im\gamma:=\gamma([a,b])\subset X\).

对于曲线 \(\gamma:[a,b]\to X\), 它的逆 (inverse) 定义为 \[ \gamma^{-1}:[a,b]\to X, \quad \gamma^{-1}(t):=\gamma(a+b-t). \] 对于两条曲线 \(\gamma_1:[a_1,b_1]\to X\) 和 \(\gamma_2:[a_2,b_2]\to X\), 如果 \(\gamma_1(b_1)=\gamma_2(a_2)\), 则定义它们的积 (product) 为 \(\gamma_1,\gamma_2\) 按顺序拼接, 即 \[ \gamma_1\cdot\gamma_2:[a,b]\to X, \] 其中 \(a=a_1\), \(b=b_1+b_2-a_2\), \[ (\gamma_1\cdot\gamma_2)(t) = \Cases{ \gamma_1(t), & a_1\leq t\leq b_1, \\ \gamma_2(t+a_2-b_1), & b_1\leq t\leq b_1+b_2-a_2. } \] 设开集 \(\Omega\in\C\), 曲线 \(\gamma:[a,b]\to\Omega\). 我们称 \(\gamma\) 是分段可微的 (piecewise differentiable), 若存在区间 \([a,b]\) 的一个划分 \(a=a_0<a_1<\cdots<a_k=b\), 使得每一段 \[ \gamma|_{[a_{j-1},a_j]}: [a_{j-1},a_j] \to \Omega \] 都是连续可微的 (即存在开区间 \(I\supset[a_{j-1},a_j]\), 使得它是 \(I\) 上连续可微函数在闭区间上的限制). 此时, 除去某个有限集 \(S\subset[a,b]\) 后, 曲线的速度 \(\dd{\gamma}/\dd{t}\) 处处存在, 并且是有界的.

设曲线 \(\gamma_1:[a_1,b_1]\to X\) 和 \(\gamma_2:[a_2,b_2]\to X\), 我们称 \(\gamma_2\) 是 \(\gamma_1\) 的一个重参数化 (reparameterization), 如果存在严格递增的连续满射 \(\phi:[a_1,b_1]\to[a_2,b_2]\), 使得 \(\gamma_1\circ\phi=\gamma_2\). 对于两条分段可微曲线来说, 我们进一步要求 \(\phi\) 是分段可微的. 重参数化前后曲线的像相同, \(\im\gamma_1=\im\gamma_2\).

• 需要注意的是, 我们关于重参数化的定义需要其保持曲线的方向.

设开集 \(\Omega\in\C\), 对于分段可微曲线 \(\gamma:[a,b]\to\Omega\), 定义其长度 (lenght) 为 \[ L(\gamma) := \int_a^b |\gamma'(t)|\dd{t}. \] 容易证明, 重参数化不改变曲线的长度.

一些例子:

• (线段) 设 \(z,w\in\C\), 线段 \(\overrightarrow{vw}\) 为曲线 \(\gamma:[0,1]\to\C\), \[ \gamma(t) = (1-t)z + tw. \]

• (圆周) 以 \(a\in\C\) 为圆心, \(R\) 为半径的圆 (逆时针方向) 为曲线 \(\gamma:[0,1]\to\C\), \[ \gamma(t) = a + R\cdot\exp(2\pi\i t). \] (参考 Section 3.3.)

• (矩形) 矩形 \(R=[a,b]\times[c,d]\) 的边界 \(\partial R\) (逆时针方向) 为四条边 \(\gamma_1,\gamma_2,\gamma_3,\gamma_4\) 拼接而成.

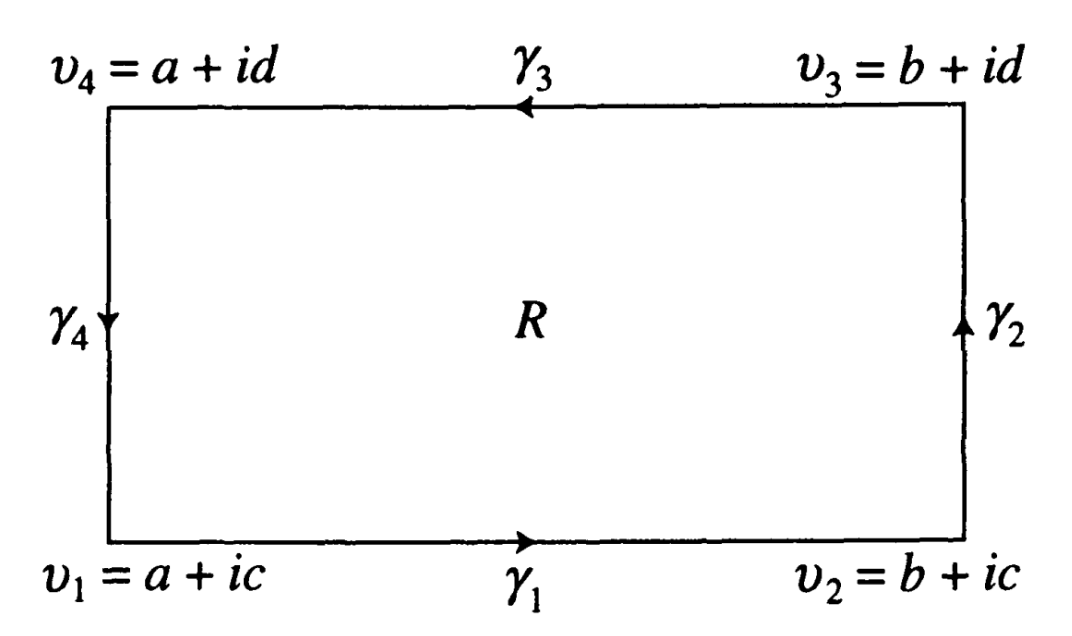
2.2 Integration along curves

现在终于可以定义复平面上的曲线积分了. 设开集 \(\Omega\in\C\), 分段可微曲线 \(\gamma:[a,b]\to\Omega\), 连续复值函数 \(f:\Omega\to\C\), 定义 \(f\) 沿着 \(\gamma\) 的曲线积分 (integral of \(f\) along \(\gamma\)) 为 \[ \int_\gamma f\dd{z} := \int_a^b f(\gamma(t)) \gamma'(t) \dd{t}. \] 从定义能直接得到 \[ \Align{ \int_{\gamma_1\cdot\gamma_2} f\dd{z} &= \int_{\gamma_1} f\dd{z} + \int_{\gamma_2} f\dd{z}, & \int_{\gamma^{-1}} f\dd{z} &= -\int_{\gamma} f\dd{z}. } \] 此外, 容易证明重参数化不改变沿曲线积分的值.

简单的放缩还可以得到如下结论: 设开集 \(\Omega\subset\C\), 连续函数 \(f:\Omega\to\C\), 分段可微曲线 \(\gamma:[a,b]\to\Omega\). 设 \(M=\sup_{z\in\im\gamma}|f(z)|\), 则 \[ \abs{\int_\gamma f\dd{z}} \leq M\cdot L(\gamma). \] 下面的定理等价于曲线积分的 Green 公式 (对于矩形).

Proposition 2.1 设开集 \(\Omega\subset\C\), 复变函数 \(f\in C^1(\Omega)\) (实可微), 闭矩形 \(R\subset\Omega\), 则 \[ \iint_R \pdv{f}{\bar{z}} \dd{x}\dd{y} = \frac1{2\i}\int_{\partial R} f\dd{z}. \]

Pf 将左边展开为定积分, 右边展开为在四条边上的积分即可.

根据 Cauchy-Riemann 方程, 如果进一步有 \(f\) 复可微, 则 \(\int_{\partial R}f\dd{z}=0\). 下面的定理表明, 若 \(f\) 复可微, 则 \(C^1\) 的条件可以删去.

Theorem 2.2 (Cauchy-Goursat 定理) 设开集 \(\Omega\subset\C\) 上的复变函数 \(f\) 复可微, 则对任意闭矩形 \(R\subset\Omega\), \[ \int_{\partial R} f\dd{z} = 0. \]

Pf 先给出一个引理:

Lemma 设开集 \(\Omega\subset\C\) 上的连续函数 \(f:\Omega\to\C\). 若存在复可微函数 \(F:\Omega\to\C\), 使得 \(F'=f\), 则对任意 \(\Omega\) 上的分段光滑闭曲线 \(\gamma\), \[ \int_\gamma f\dd{z} = 0. \] 特别地, 若 \(f\) 是复多项式, 则 \(F\) 存在, \(f\) 满足上式.

引理的证明只需借助曲线积分的定义.

回到原命题. 记 \(A:=\int_{\partial R}f\dd{z}\). 将矩形 \(R\) 沿着中位线切成四个一样的小矩形 \(R_1,\dots,R_4\) (如图), \(\partial R_i\) 的方向与 \(\partial R\) 相同, 为逆时针方向, 于是 \[ A = \sum_{\nu=1}^4\int_{\partial R_{\nu}} f\dd{z}. \] 由三角不等式有 \(|A|\leq\sum_{\nu=1}^4\abs{\int_{\partial R_\nu}f\dd{z}}\), 因此存在 \(\nu_1\), 使得 \(\abs{\int_{\partial R_{\nu_1}}f\dd{z}}\geq\frac14|A|\).

将 \(R_{\nu_1}\) 沿着中位线切成四个小矩形 \(R_{\nu_11},\dots,R_{\nu_14}\), 同理可以找到 \(\nu_2\), 使得 \(\abs{\int_{\partial R_{\nu_1\nu_2}}f\dd{z}}\geq4^{-2}|A|\). 如此归纳下去, 我们得到了矩形列 \(\{R_{\nu_1\dots\nu_k}\}_{k\geq1}\) (\(1\leq\nu_j\leq4\)), 满足

1. \(R_{\nu_1\dots\nu_{k+1}}\subset R_{\nu_1\dots\nu_k}\).
2. 周长 \(L(\partial R_{\nu_1\dots\nu_k})=2^{-k}L(\partial R)\).
3. 直径 (对角线长) \({\rm diam}(R_{\nu_1\dots\nu_k})=2^{-k}{\rm diam}(R)\).
4. \(\abs{\int_{\partial R_{\nu_1\dots\nu_k}}}\geq 4^{-k}|A|\).

由 1, 3 和闭集套定理, \(\bigcap_{k\geq1}R_{\nu_1\dots\nu_k}\) 包含唯一一个点 \(\{a\}\). 定义 \(\varepsilon(z)\) 满足 \[ f(z) = f(a) + (z-a)f'(a) + \varepsilon(z). \] 因为 \(f\) 复可微, 当 \(z-a\to0\) (\(z-a\neq0\)) 时 \(\varepsilon(z)/|z-a|\to0\). 因此任给 \(\delta>0\), 都存在 \(\eta>0\), 使得只要 \(|z-a|<\eta\), 便成立 \(|\varepsilon(z)|\leq\delta|z-a|\).

注意到 \(f(a)+(z-a)f'(a)\) 是一个多项式, 结合 Lemma, 有 \[ \int_{\partial R_{\nu_1\dots\nu_k}} f\dd{z} = \int_{\partial R_{\nu_1\dots\nu_k}} \varepsilon\dd{z}. \] 取充分大的 \(k\), 使得 \({\rm diam}(R_{\nu_1\dots\nu_k})<\eta\), 于是对 \(z\in R_{\nu_1\dots\nu_k}\), 有 \(|z-a|<\eta\), 进而 \[ \Align{ 4^{-k}|A| &\leq \abs{\int_{\partial R_{\nu_1\dots\nu_k}} f \dd{z}} = \abs{\int_{\partial R_{\nu_1\dots\nu_k}} \varepsilon \dd{z}} \\ &\leq \delta\operatorname{diam}(R_{\nu_1\dots\nu_k}) \cdot L(\partial R_{\nu_1\dots\nu_k}) \\ &= \delta\cdot 2^{-k}\operatorname{diam}(R) \cdot 2^{-k}L(\partial R), } \] 有 \(|A|\leq\delta\operatorname{diam}(R)L(\partial R)\). 由 \(\delta>0\) 的任意性, \(|A|=0\).

一个更一般的结论是:

Theorem 2.3 (矩形的 Cauchy 积分定理) 设开集 \(\Omega\subset\C\) 上的连续函数 \(f\). 若 \(f\) 在某点 \(a\in\Omega\) 之外都复可微, 则对任意闭矩形 \(R\subset\Omega\), \[ \int_{\partial R} f\dd{z} = 0. \]

Pf 情形一: \(a\) 在 \(R\) 外. 直接应用 Theorem 2.2 即可.

情形二: \(a\in\partial R\). 设 \(R=[a,b]\times[c,d]\), 取 \(R_\varepsilon=[a+\varepsilon,b-\varepsilon]\times[c+\varepsilon,d-\varepsilon]\). 则当 \(\varepsilon\to0\) 时, \(R_\varepsilon\) 的顶点收敛到 \(R\) 的顶点, 并且 \(f\) 在包含 \(R_\varepsilon\) 的开集上复可微. 应用 Theorem 2.2, \[ \int_{\partial R_\varepsilon} f\dd{z} = 0. \] 又因为 \(R\) 紧, \(f\) 在 \(R\) 上一致连续, 有 \[ \int_{\partial R_\varepsilon} f\dd{z} \to \int_{\partial R}f\dd{z}, \quad \varepsilon\to0, \] 有 \(\int_{\partial R}f\dd{z}=0\).

情形三: \(a\in{\rm Int}R\). 过 \(a\) 作平行于 \(x\) 轴的直线, 将 \(R\) 切成两个小矩形, 在每个矩形上分别应用情形二即可.

Theorem 2.4 (矩形的 Cauchy 积分公式) 设开集 \(\Omega\subset\C\) 上的复变函数 \(f\) 复可微, 闭矩形 \(R\subset\Omega\), 则对任意 \(a\in{\rm Int}R\), \[ f(a) = \frac{1}{2\pi\i} \int_{\partial R} \frac{f(z)}{z-a}\dd{z}. \]

Pf 令 \[ g(z) = \Cases{ \dfrac{f(z)-f(a)}{z-a}, & z\in\Omega\setminus\{a\}, \\ f'(a), & z=a. } \] 则 \(g(z)\) 在 \(\Omega\) 连续, 在 \(\Omega-\{a\}\) 复可微. 应用 Theorem 2.3, \[ \Align{ 0 = \int_{\partial R} g(z)\dd{z} = \int_{\partial R} \frac{f(z)}{z-a}\dd{z}{} - f(a) \int_{\partial R} \frac{1}{z-a}\dd{z}. } \] 下面只需计算 \(\int_{\partial R}1/(z-a)\dd{z}\). 考虑 \(\partial R\) 的极坐标参数化: \(r(t)=a+\rho(t)\exp(2\pi\i t)\), \(0\leq t\leq 1\), 其中 \(\rho(t)\) 是分段连续可微函数. 有 \[ \Align{ \int_{\partial R} \frac{1}{z-a}\dd{z} &= \int_0^1 \frac{1}{\rho(t)\e^{2\pi\i t}} \dv{t}\pqty{\rho(t)\e^{2\pi\i t}} \dd{t} \\ &= \int_0^1 \frac{\rho'(t)}{\rho(t)}\dd{t} + \int_0^1 2\pi\i \dd{t} \\ &= \ln\frac{\rho(1)}{\rho(0)} + 2\pi\i, } \] 因为 \(\rho(0)=\rho(1)\), 故 \(1/(z-a)\) 的积分为 \(2\pi\i\), 便证明了原命题.

2.3 Holomorphy and \(\C\)-differentiability

Theorem 2.5 (复可微 \(\Rightarrow\) 全纯) 设开集 \(\Omega\subset\C\) 上的复变函数 \(f\) 复可微, 则 \(f\) 在 \(\Omega\) 上全纯. 更进一步地, 对于 \(a\in\Omega\), 存在只与 \(a,\Omega\) 有关, 而与 \(f\) 无关的正数 \(r>0\), 以及复数列 \(\{c_n\}_{n\geq0}\), 使得 \[ f(z) = \sum_{n=0}^\infty c_n(z-a)^n,\quad z\in D(a,r). \]

Pf 取矩形 \(R\subset\Omega\) 满足点 \(a\in{\rm Int}R\). 取半径 \(r>0\) 使得开圆盘 \(\overline{D}(a,r)\subset{\rm Int}R\).

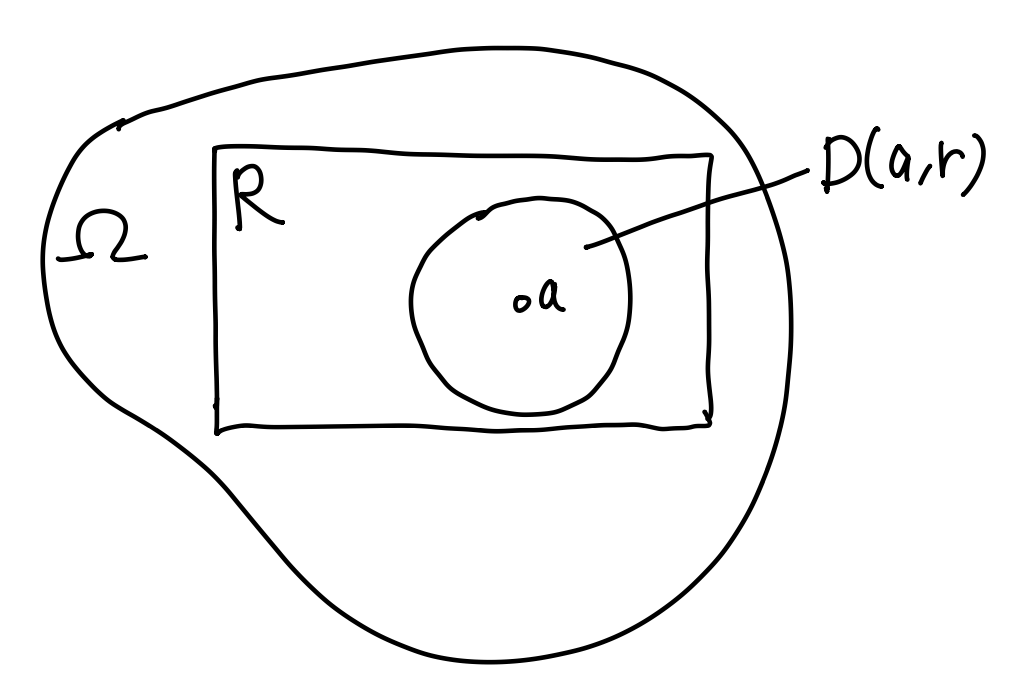
由复可微性, 在 \(R\) 上应用 Cauchy 积分公式, 得到 \[ f(w) = \frac1{2\pi\i} \int_{\partial R}\frac{f(z)}{z-w}\dd{z},\quad w\in D(a,r)\subset{\rm Int}R. \] 将 \((z-w)^{-1}\) 展开为幂级数: \[ \Align{ \frac1{z-w} &= \frac1{z-a}\pqty{1-\frac{w-a}{z-a}}^{-1} = \frac1{z-a}\sum_{n=0}^\infty\pqty{\frac{w-a}{z-a}}^n, } \] 上式要求 \(|w-a|<|z-a|\). 注意到 \(w\in D(a,r)\) 而 \(z\in\partial R\), 根据取法, 存在 \(0<\theta<1\) 使得 \(|w-a|\leq\theta|z-a|\), 故该级数一致收敛. 代入积分中, \[ \Align{ f(w) = \frac1{2\pi\i} \int_{\partial R} f(z) \sum_{n=0}^\infty\frac{(w-a)^n}{(z-a)^{n+1}} \dd{z}, } \] 因为 \(\sum_{n=0}^\infty f(z)\cdot(w-a)^n/(z-a)^{n+1}\) 一致收敛, 无穷求和与积分可以交换顺序, 即 \[ f(w) = \sum_{n=0}^\infty (w-a)^n \cdot \frac{1}{2\pi\i}\int_{\partial R} \frac{f(z)}{(z-a)^{n+1}}\dd{z}, \quad w\in D(a,r). \] 因此 \(f(w)=\sum_{n=0}^\infty c_n(w-a)^n\), 其中系数 \[ c_n = \frac1{2\pi\i} \int_{\partial R}\frac{f(z)}{(z-a)^{n+1}}\dd{z}. \]

注意以上证明中的半径 \(r\) 并不是最优的. 最优的 \(r\) 在 Section 4 中给出.

2.4 Morera's theorem

Theorem 2.6 (Morera 定理) 设开集 \(\Omega\subset\C\) 上的复变函数 \(f\) 连续. 若对任意矩形 \(R\subset\Omega\), 有 \[ \int_{\partial R}f\dd{z} = 0, \] 则 \(f\) 在 \(\Omega\) 上全纯.

Pf 只需对 \(\Omega\) 为开圆盘的情形证明. 记圆盘的中心为 \(a=\alpha+\beta\i\).

我们先构造 \(f\) 的原函数 \(F\), 再证明 \(F\) 在 \(\Omega\) 复可微, 进而 \(F\) 在 \(\Omega\) 全纯, 其导数 \(f\) 也全纯.

任取 \(z=x+\i y\in\Omega\), 记以 \(a,z\) 为对角线的矩形 \(R\) 的四个顶点为 \(a,z',z,z''\) (如图). 定义 \[ F(z) := \int_{\gamma_1} f \dd{z},\quad z\in\Omega. \] 由 \(F\) 在矩形边界 \(\partial R\) 上的积分为零, 可得 \[ \int_{\gamma_1}f\dd{z} = \int_{\gamma_2}f\dd{z}. \] 取充分小的 \(h>0\), 考虑差值 \(F(z+h)-F(z)\), 利用 \(\gamma_2\) 上的积分计算该差值, 得到的结果为 \(\int_{L_1}f\dd{z}\). 再考虑差值 \(F(z+\i h)-F(z)\), 利用 \(\gamma_1\) 上的积分计算该差值, 得到的结果为 \(\int_{L_2}f\dd{z}\).

因此有 \[ \frac{F(z+h)-F(z)}{h} = \frac1h \int_{L_1} f\dd{z} = \frac1h \int_{x}^{x+h} f(t,y)\dd{t}, \] 令 \(h\to0\), 可以得到 \((\partial F/\partial x)(z)=f(z)\). 类似地, 考虑 \[ \frac{F(z+\i h)-F(z)}{h} = \frac1h \int_{L_2} f\dd{z} = \frac{\i}h \int_{y}^{y+h} f(x,t)\dd{t}, \] 令 \(h\to0\), 可以得到 \((\partial F/\partial y)(z)=\i f(z)\). 因此 \(\partial F/\partial x=-\i\partial F/\partial y\), 由 Proposition 1.1, \(F\) 在 \(\Omega\) 复可微, 进而 \(F\) 在 \(\Omega\) 全纯. 注意到 \(F'=\partial F/\partial z=f'\), 导函数 \(f\) 也全纯.

在证明过程中, 我们利用积分路径无关的性质构造出了 \(f\) 的原函数 \(F\). 下面的定理给出了原函数存在的充要条件.

Proposition 2.7 (原函数存在性) 设连通开集 \(\Omega\subset\C\) 上的复变函数 \(f\) 连续. 则存在 \(\Omega\) 上的全纯函数 \(F\) 使得 \(F'=f\) 当且仅当对 \(\Omega\) 中的任意分段光滑闭曲线 \(\gamma\), 有 \(\int_\gamma f\dd{z}=0\).

Pf (\(\Rightarrow\)) 设存在 \(\Omega\) 上的全纯函数 \(F\) 使得 \(F'=f\), 由 Theorem 2.2 证明过程中的 Lemma 可知结论成立.

(\(\Leftarrow\)) 仿照 Morera 定理的证明即可.

Note Section 1, 2 中关于复可微性和全纯性的总结: \[ \xymatrix@C=6em{ & \textsf{$f$ 在 $\Omega$ 复可微} \ar@2{->}@<0.0ex>[ld]_{\textsf{Cauchy-Goursat}} \ar@2{->}@<0.0ex>[d]^{\textsf{Thm. 2.5}} \\ \substack{ \textstyle\textsf{$f$ 连续且在 $\Omega$ 内任意} \\ \textstyle\textsf{矩形的边界复积分为零}} \ar@2{->}[r]_(.55){\textsf{Morera}} & \textsf{$f$ 在 $\Omega$ 全纯} \ar@2{->}@<0.0ex>[d]^{\textsf{Cor. 3.6}} & \substack{ \textstyle\textsf{$f$ 在 $\Omega$ 连续,可偏导} \\ \textstyle\textsf{并满足 C-R 方程}} \ar@2{->}@<0.0ex>[lu] _{\textsf{Looman-Menchoff}} \\ & \textsf{$f$ 在 $\Omega$ 无穷阶复可微} \ar@2{->}@<0.0ex>[ru]_{\textsf{Prop. 1.1}} } \]

这里补充一点内容, 作为 Morera 定理的应用. 记上半平面 \(H_+:=\{z\in\C\mid\Im(z)\geq0\}\), 下半平面 \(H_-\{z\in\C\mid\Im(z)\leq0\}\).

Theorem 2.8 (Schwarz 反射定理) 设开集 \(\Omega\subset\C\) 关于实轴 \(\R\) 对称, 复变函数 \(f:(\Omega\cap H_+)\to\C\) 在 \(\Omega\cap H_+\) 上连续, 在 \(\Omega\cap{\rm Int}H_+\) 上全纯, 且在 \(\Omega\cap\R\) 上取实值, 则存在全纯函数 \(F:\Omega\to\C\), 满足 \[ \Align{ F|_{\Omega\cap H_+}(z) &= f(z), & F|_{\Omega\cap H_-}(z) &= \overline{f(\bar{z})}. } \]

Pf 因为 \(F\) 的两个定义在 \(\Omega\cap\R\) 上相等, 故连续. 由 Morera 定理, 任取矩形 \(R\subset\Omega\), 只需证明 \(\int_{\partial R}F\dd{z}=0\). 分三种情形:

情形一, \(R\subset{\rm Int}H_+\) 或者 \(R\subset{\rm Int}H_-\). 前者由 \(f\) 的全纯性立即得到结论; 后者有 \[ \int_{\partial R}F\dd{z} = \int_{\partial R'} \bar{f}\dd{z} = \overline{\int_{\partial R'} f\dd{z}} = 0. \] 其中 \(R'\) 是 \(R\) 沿着实轴对称的矩形.

情形二, \(R\) 的一条边与实轴 \(\R\) 重合. 不失一般性, 设 \(R\subset H_+\), 则 \(R=[a,b]\times[0,c]\). 取充分小的 \(\varepsilon>0\), 将 \(R\) 的底边向上抬升 \(\varepsilon\), 得到 \(R_\varepsilon=[a,b]\times[\varepsilon,c]\subset(\Omega\cap{\rm Int}H_+)\). 因为 \(F\) 在 \((\Omega\cap{\rm Int}H_+)\) 内全纯, 有 \(\int_{\partial R_\varepsilon}F\dd{z}=0\). 因 \(F\) 在 \(R\) 上连续, 进而一致连续, 有 \[ 0=\int_{\partial R_\varepsilon}F\dd{z} \to \int_{\partial R}F\dd{z}, \quad \varepsilon\to0. \] 即 \(\int_{\partial R}F\dd{z}=0\).

情形三, \(R\) 与 \({\rm Int}H_+\) 和 \({\rm Int}H_-\) 都交. 将 \(R\) 沿着实轴切成两个矩形, 分别应用情形二即可.

对 Schwarz 反射定理的证明略加改动, 我们能证明一个有趣的结论:

• 设 \(f:\C\to\C\) 在 \(\C\) 上连续, 在 \(\C-\R\) 上全纯, 则 \(f\) 在 \(\C\) 上全纯.

这对于 \(\R\) 或者 \(\R^2\) 上的实变函数显然是不可思议的. 这也反映出, 全纯性是比光滑性、实解析性等强的多的性质.

3 *Power Series

这个 Section 补充一些复幂级数的内容, 很大程度上和实幂级数是平行的. 这一部分可以单独拎出来, 几乎不需要复变函数的前置知识.

3.1 Radius of convergence

Lemma 3.1 (Abel 引理) 设复数列 \(\{c_n\}_{n\geq0}\), 存在 \(0\leq R\leq+\infty\), 使得幂级数 \[ \sum_{n=0}^\infty c_nz^n \] 在 \(|z|<R\) 时收敛, 在 \(|z|>R\) 时发散. 并且该幂级数在 \(D(0,R)\) 的任意紧子集上一致收敛.

Pf 令 \(R=\sup\{r\geq0\mid\exists M,\textsf{使得 }|c_n|r^n\leq M,\forall n\geq0\}\). 如果 \(|z|>R\), 则数列 \(|c_n||z|^n\) 无界, 幂级数不收敛.

任取紧子集 \(K\subset D(0,R)\), 取 \(0<\rho<R\) 满足 \(K\subset D(0,\rho)\). 取 \(r\) 满足 \(\rho<r<R\). 因为 \(r<R\), 所以存在 \(M\) 使得 \(|c_n|r^n\leq M\); 于是对于 \(z\in K\), 有 \[ |c_nz^n| = |c_n||z|^n \leq |c_n| \rho^n \leq M \pqty{\frac{\rho}{r}}^n. \] 因为 \(0<\rho/r<1\), 级数 \(\sum_{n=0}^\infty(\rho/r)^n\) 收敛, 根据 Weierstrass 判别法, 原幂级数在 \(K\) 一致收敛.

Abel 引理中的常数 \(0\leq R\leq+\infty\) 称为幂级数 \(\sum_{n=0}^\infty c_nz^n\) 的收敛半径 (radius of convergence), 开圆盘 \(D(0,R)\) 称为收敛圆盘 (disc of convergence). 需要注意的是, 幂级数在圆盘边界 (\(|z|=R\) 处) 的敛散性不能保证, 需要具体分析. 类似地, 可以定义中心不在原点的幂级数 \(\sum_{n=0}^\infty c_n(z-a)^n\) 的收敛半径和收敛圆盘.

根据一致收敛的性质, 可以得到:

Corollary 3.2 (全纯 \(\Rightarrow\) 连续) 设复变函数 \(f\) 在 \(\Omega\) 上全纯, 则 \(f\) 在 \(\Omega\) 上连续.

两个判断复级数是否收敛的方法:

Proposition 3.3 设复数列 \(\{c_n\}_{n\geq0}\).

1. (Ratio test) 记 \(l_1=\limsup_{n\to\infty}\dfrac{|c_{n+1}|}{|c_n|}\). 若 \(l_1<1\), 则级数 \(\sum_{n=0}^\infty c_n\) 绝对收敛.
2. (Root test) 记 \(l_2=\limsup_{n\to\infty}\sqrt[n]{|c_n|}\). 若 \(l_2<1\), 则级数 \(\sum_{n=0}^\infty c_n\) 绝对收敛; 若 \(l_2>1\), 则级数发散; 若 \(l_2=1\), 不能确定敛散性.
3. 若上面的 \(l_1,l_2\) 都存在 (不为无穷大), 则 \(l_1=l_2\).

上面两个 test 分别给出了两种收敛半径的计算公式:

Proposition 3.4 设复幂级数 \(\sum_{n=0}^\infty c_n(z-a)^n\).

1. 若 \(R=\dfrac{1}{\limsup|c_{n+1}|/|c_n|}\) 存在 (可为无穷大), 则级数在 \(D(a,R)\) 收敛.
2. 若 \(R=\dfrac{1}{\limsup\sqrt[n]{|c_n|}}\) 存在 (可为无穷大), 则级数的收敛半径为 \(R\).

3.2 \(\C\)-Differentiability

下面的定理告诉我们, 幂级数在收敛圆盘上可以逐项微分 / 积分.

Proposition 3.5 设幂级数 \(\sum_{n=0}^\infty c_n(z-a)^n\) 的收敛半径 \(R>0\), 且在 \(D(a,R)\) 上收敛到 \(f(z)\).

1. (幂级数的复可微性) \(f\) 在 \(D(a,R)\) 上复可微, 且 \[ f'(z) = \sum_{n=1}^\infty nc_n(z-a)^{n-1},\quad z\in D(a,R). \]

2. (幂级数的原函数) \(f\) 在 \(D(a,R)\) 上存在原函数, 它的一个原函数为 \[ F(z) = \sum_{n=0}^\infty \frac{c_n}{n+1}(z-a)^{n+1}, \quad z\in D(a,R). \]

幂级数 (在收敛圆盘内) 是复可微的, 且其导数是收敛半径相同的幂级数, 故其导数也全纯. 立刻得到推论:

Corollary 3.6 (全纯 \(\Rightarrow\) 无穷复可微) 设复变函数 \(f\) 在 \(\Omega\) 上全纯, 则 \(f\) 在 \(\Omega\) 上无穷阶复可微.

根据幂级数的逐项可微性, 我们还能得到:

Proposition 3.7 (幂级数展开的唯一性) 设 \(f:\Omega\to\C\) 在 \(a\in\Omega\) 的邻域上展开为幂级数 \(\sum_{n=0}^\infty c_n(z-a)^n\), 则 \(c_n\) 是唯一确定的. 具体来说, \[ c_n = \frac{1}{n!}f^{(n)}(a). \] 其中 \(f^{(n)}\) 为 \(f\) 的 \(n\) 阶导数.

定理中的幂级数 \(\sum_{n=0}^\infty \frac{1}{n!}f^{(n)}(a)(z-a)^n\) 称为 \(f\) 在 \(a\) 处的 Taylor 级数.

3.3 The complex \(\exp,\sin,\cos\)

我们之前用初等的方法定义并研究过 (实变) 三角函数 \(\sin(x),\cos(x)\), 这种定义具有良好的几何直观, 却不够严格, 也难以推广到复变函数. 下面我们用幂级数给出复变三角函数与指数函数的严格定义, 并反过来导出其几何直观.

复变指数、正弦、余弦函数定义为 \[ \Align{ \exp(z) &:= \sum_{n=0}^\infty \frac{z^n}{n!}, \\ \sin(z) &:= \sum_{n=0}^\infty \frac{(-1)^nz^{2n+1}}{(2n+1)!}, \\ \cos(z) &:= \sum_{n=0}^\infty \frac{(-1)^nz^{2n}}{(2n)!}. \\ } \] (规定 \(0^0=1\)) 可知其收敛半径都为无穷大, 换言之, 它们都是 \(\C\) 上的全纯函数.

Proposition 3.8 (指数函数的性质)

1. \(\exp'(z)=\exp(z)\).

2. \(\exp(z+w)=\exp(z)\exp(w)\).

3. \(\exp(z)\neq0\), 且 \(\exp(-z)=1/\exp(z)\).

4. 定义 \(\operatorname{cis}:\R\to\C\), \(\operatorname{cis}(t):=\exp(\i t)\), 则 \(\operatorname{cis}(\R)=S^1\) (单位圆), 并且 \(\operatorname{cis}\) 是一个周期函数.

   设 \(\operatorname{cis}\) 的最小正周期为 \(T\), 定义 \(\pi:=T/2\) 称为圆周率.

5. \(\exp\) 以 \(2\pi\i\) 为周期.

6. \(\exp(\R)=(0,+\infty)\).

7. \(\exp(\C)=\C^*:=\C-\{0\}\).

Pf 1 由逐项可微得到; 2 由 Cauchy 乘积得到; 3 是 2 的推论.

第 4 条. 证明分为几步.

第一步, 证明 \(\operatorname{cis}(t)\in S^1\).

• 由 2, \[ \overline{\exp(\i t)} = \exp(\overline{\i t}) = \exp(-\i t) = 1/\exp(\i t), \] 即 \(|\exp(\i t)|\equiv1\).

第二步, 证明 \(\operatorname{cis}(\R)=\Bbb{S}^1\), 需要用一些拓扑群的知识.

• 由 2, \[ \operatorname{cis}(s+t) = \exp(\i s+\i t) = \exp(\i s)\exp(\i t) = \operatorname{cis}(s)\operatorname{cis}(t). \] 换言之, \(\operatorname{cis}\) 是 \(\R\to\Bbb{S}^1\) 的群同态, \(\operatorname{cis}(\R)\) 是拓扑群 \(\Bbb{S}^1\) 的子群.

• 因为 \(|\operatorname{cis}'(t)|=1\neq0\), 由逆映射定理, \(\operatorname{cis}:\R\to\Bbb{S}^1\) 是局部微分同胚, 进而是开映射, 有 \(\operatorname{cis}(\R)\) 开. 因为拓扑群的开子群也是闭的, 故 \(\operatorname{cis}(\R)\) 既开又闭. 由 \(\Bbb{S}^1\) 的连通性, \(\operatorname{cis}(\R)=\Bbb{S}^1\).

第三步, 证明周期性.

• 设 \(T\in\R\) 满足 \[ \operatorname{cis}(t+T) = \operatorname{cis}(t)\operatorname{cis}(T) = \operatorname{cis}(t), \] 故 \(T\) 是 \(\operatorname{cis}\) 的周期当且仅当 \(\operatorname{cis}(T)=1\). 考虑所有周期的集合 \(K=\{t\in\R\mid\operatorname{cis}(t)=1\}\), 则 \(0\in K\) 且 \(K\) 为 \(\R\) 的子群.

• (\(K\) 非平凡) 假若 \(K=\{0\}\), 则任取 \(s,t\in\R\) 满足 \(\operatorname{cis}(s)=\operatorname{cis}(t)\), 即 \[ \operatorname{cis}(s-t) = 1, \] 有 \(s-t\in K=\{0\}\), 故 \(s=t\). 这说明 \(\operatorname{cis}\) 是双射. 又 \(\operatorname{cis}\) 为局部同胚, 则 \(\operatorname{cis}\) 为同胚. 然而 \(\R\) 非紧, \(\Bbb{S}^1\) 紧, 与同胚矛盾. 因此 \(K\) 至少有两个元素, 即 \(\operatorname{cis}\) 是周期函数.

• (\(K\) 的离散性) 我们证明 \(K\) 中的每个点都是孤立点.

  • 由于 \(\operatorname{cis}\) 是局部微分同胚, 存在开区间 \(I=(-\varepsilon,\varepsilon)\) 使得 \(\operatorname{cis}|_I\) 是单射, 有 \(K\cap I=\{0\}\).

  • 对任意 \(t\in T\), 记平移映射 \(\tau_t:\R\to\R\), \(x\mapsto x+t\), 则 \(\tau_t(I)\) 是 \(t\) 在 \(\R\) 中的邻域. 任取 \(s\in\tau_t(I)\cap K\), 则 \[ \Align{ \tau_t^{-1}(s) \in \tau_t^{-1}(\tau_t(I)\cap K) &\xlongequal{\tau_t^{-1}\textsf{ 单}} (\tau_t^{-1}\tau_t)(I) \cap \tau_t^{-1}(K) \\ &= I\cap K \\ &= \{0\}, } \] 即 \(s=t\), 于是 \(\tau_t(I)\cap K=\{t\}\).

• 结合以上两点, \(K\) 是 \(\R\) 的离散子集. 取 \(T:=\inf(K\cap(0,+\infty))\), 由离散性得 \(T\in K\), 故 \(T\) 即是最小正周期.

第 5 条. 结合 2 和 4, 有 \[ \exp(z+2\pi\i) = \exp(z)\exp(2\pi\i) = \exp(z)\operatorname{cis}(2\pi) = \exp(z). \] 第 6 条. 因为 \(\exp(x)\neq0\), 由连续性, \(\exp(x)\) 恒正或恒负. 注意到 \(\exp(0)=1\), 有 \(\exp(x)>0\). 又由连续性, \(\exp(\R)\) 是 \((0,+\infty)\) 的子区间.

记 \(\e=\exp(1)\), 则 \(\e=\sum_{n=0}^\infty\frac{1}{n!}>2\). 由 2 可以归纳得到 \[ \exp(n) = \e^n, \quad n\in\Z. \] 令上式中 \(n\to+\infty\), \(\exp(n)\to+\infty\); 令 \(n\to-\infty\), \(\exp(n)\to0\). 又因为 \(\exp(\R)\) 是 \((0,+\infty)\) 的子区间, 只能有 \(\exp(\R)=(0,+\infty)\).

第 7 条. 任取 \(z\in\C^*\), 则存在 \(s\in\R\) 使得 \(|z|=\exp(s)\). 又因为 \(z/|z|\in S^1\), 根据 4, 存在 \(t\in\R\) 使得 \(\exp(\i t)=z/|z|\). 于是 \[ \exp(s+\i t) = \exp(s) \exp(\i t) = |z| \cdot \frac{z}{|z|} = z. \]

指数函数的性质推出三角函数的性质.

Proposition 3.9 (三角函数的性质)

1. 指数函数和三角函数的关系: 对 \(t\in\R\), 有 \[ \Align{ \cos(t) &= \Re(\exp(\i t)) = \Re(\operatorname{cis}(t)) \\ \sin(t) &= \Im(\exp(\i t)) = \Im(\operatorname{cis}(t)) \\ } \]

2. 指数函数和三角函数的关系: 对 \(z\in\C\), 有 \[ \Align{ \cos(z) &= \frac{\exp(\i z)+\exp(-\i z)}{2}, \\ \sin(z) &= \frac{\exp(\i z)-\exp(-\i z)}{2\i}. \\ } \]

3. \(\sin(-z)=-\sin(z)\), \(\cos(-z)=\cos(z)\).

4. 和差角公式: 对 \(z,w\in\C\), 有 \[ \Align{ \cos(z+w) &= \cos(z)\cos(w) - \sin(z)\sin(w), \\ \sin(z+w) &= \sin(z)\cos(w) + \cos(z)\sin(w). } \]

5. \(\sin^2(z)+\cos^2(z)=1\).

6. \(\sin'(z)=\cos(z)\), \(\cos'(z)=-\sin(z)\).

7. \(\cos(z)\) 和 \(\sin(z)\) 都以 \(2\pi\) 为最小正周期.

Pf 1 和 2 由幂级数的运算得到. 3 ~ 6 是 2 的推论.

第 7 条. 这里只证明 \(\cos(z)\) 的周期性, 另一个是类似的. 任取 \(z=a+b\i\in\C\), 由 1 以及 \(\operatorname{cis}\) 的周期性可得 \(\cos(a+2\pi)=\cos(a)\) 以及 \(\sin(a+2\pi)=\sin(a)\), 进而 \[ \Align{ \cos(z+2\pi) &= \cos((a+2\pi)+b\i) \\ &= \cos(a+2\pi)\cos(b\i) - \sin(a+2\pi)\sin(b\i) \\ &= \cos(a)\cos(b\i) - \sin(a)\sin(b\i) \\ &= \cos(z). } \]

Proposition 3.8 中定义的 \(\pi\) 就是我们熟悉的那个 \(3.14\dots\), 它是圆的周长与直径的比值: 设半径为 \(R\) 的圆 \[ \gamma(t)=a+R\cdot\exp(2\pi\i t) = a+R\operatorname{cis}(2\pi t), \quad 0\leq t\leq 1, \] 则 \[ \frac{L(\gamma)}{2R} = \frac{1}{2R}\int_0^1 \abs{\gamma'(t)}\dd{t} = \frac{1}{2R}\int_0^1 2\pi R\dd{t} = \pi. \] 此外, 考虑从点 \((1,0)\) 开始的单位圆弧 \(\gamma(t)=\operatorname{cis}(t)\), \(0\leq t\leq \alpha\), 则 \(\alpha\) 就是 \(\gamma\) 的弧长, 而 \[ \gamma(\alpha) = (\cos\alpha,\sin\alpha), \] 这恰恰是实变三角函数的初等定义.

指数函数 / 三角函数的一个应用是复平面上的极坐标.

Proposition 3.10 (极坐标)

1. 对任意 \(z\in\C^*\), 存在 \(\rho>0\) 和 \(\theta\in[0,2\pi)\) 使得 \(z=\rho\exp(\i\theta)=\rho\cdot(\cos\theta,\sin\theta)\).
2. 对任意可微曲线 \(\gamma:[0,1]\to\C^*\), 存在可微函数 \(\rho:[0,1]\to(0,+\infty)\) 和 \(\theta:[0,1]\to\R\) 使得 \(\gamma(t)=\rho(t)\exp[\i\theta(t)]=\rho(t)\cdot(\cos\theta(t),\sin\theta(t))\).