生成模型基础 | 6 基于能量的模型

本系列的最后将讨论基于能量的模型 (energy-based model, EBM), 从这里出发可以得到很多有趣的生成模型——得分匹配、扩散模型、流匹配……

能量基模型 (EBM) 的灵感源自统计力学. 它用一个函数 $E(x)$ 来为样本空间 $x \in \mathbb{R}^N$ 中的每一点赋予一个“能量” 值. 根据物理学原理, 系统中的样本总是趋向于聚集在能量 $E(x)$ 较低的区域.

当系统孤立时, 所有样本都会聚集到 $E(x)$ 的极小值点 (基态), 形成多点分布. 这是比较无聊的情况.
为了模拟更丰富的真实世界分布, 我们需要让系统与一个恒温的 “热浴” 接触. 热浴给系统提供了温度, 在微观上表现为随机的热噪声:
- 一方面, 随机噪声让样本具有能量, 跳出局部极小值;
- 另一方面, 样本受梯度力 $-\nabla_x E(x)$, 会不断向能量低处运动;

最终, 这两种力量形成动态平衡, 样本分布密度 $p(x)$ 达到稳定状态. 这个最终稳定的分布 $p(x)$ 就是 EBM 对真实样本的建模, 它被称为 Boltzmann 分布, 由能量 $E(x)$ 和热浴温度 $T$ 唯一确定.

在训练时, EBM 使用 MLE 来优化能量函数 $E(x)$, 使得 $p(x)$ 尽量接近真实分布.
在采样时, EBM 模拟了这种弛豫过程. 先从某初始分布 $\pi(x)$ 采样, 再不断执行基于梯度的随机迭代 (即 LD-MCMC): 一边根据梯度力 $-\nabla_x E(x)$ 向能量低处移动, 一边加入随机噪声. 经过充分迭代后, 得到的样本 $x$ 便可以视为从目标分布 $p(x)$ 中采样.

注意到我们在采样中只使用了能量梯度 $\nabla_xE(x)$, 并未使用 $E(x)$ 本身, 因此训练 EBM 的另一个思路是, 我们只需要建模 $\nabla_xE(x)$, 无需建模 $E(x)$. 这种方法称为 “得分匹配”. “扩散模型” 是得分匹配的推广, 它将采样过程 LD-MCMC 推广到了更一般的形式.

之后的几节会逐一介绍上面提到的各种模型. 值得注意的是, 尽管各个模型五花八门, 但它们的核心步骤仍旧是 “将简单分布推到复杂的数据分布”. 这里使用 “推” 是因为采样的过程 (LD-MCMC) 需要若干次迭代, 是循序渐进的. 最后我们将看到, 这一采样过程与 CNF 的 “流” 有着密切联系, 进而可以用一个统一的框架涵盖所有这些模型.

13 Energy-based Models

13.1 Modeling

EBM 来自于统计物理中的 Boltzmann 分布. 这里简单介绍一下背景.

考虑一个由若干分子组成的封闭系统,

系统的体积 $V$ 和分子数 $N$ 固定. 系统可以与一个巨大的热库 (热浴) 交换能量. 当系统与热库达到热平衡时, 系统绝对温度 $T$ 和平均能量 $E$ 不变.
每个分子的能量取值范围是离散的 $\{\varepsilon_1,\dots,\varepsilon_M\}$, 一共有 $M$ 个能级. 假设某粒子处于第 $i$ 个能级的概率为 $p_i$.

现在我们想要求出 $p_i$ 具体的分布. 这看起来是一个欠定的问题, 我们的约束条件只有 \[ \sum_{i=1}^M p_i=1, \qquad \sum_{i=1}^M p_i\varepsilon_i = E. \] 有无穷多个分布 $(p_i)_{i=1}^M$ 满足这两个条件. 此时我们使用 “最大熵原理”——在所有满足条件的分布中, 选择熵最大的那个.

熵衡量了系统状态的不确定性. 我们选择最大熵分布, 相当于 (除了两个约束条件外) 给系统施加最少的假设, 得到的那个分布. 这是在已知信息最少的情况下, “最均匀、最无倾向性、最不武断” 的选择.

我们要在上面两个约束条件下最大化系统的熵 \[ S = -k_B\sum_{i=1}^M p_i\ln{p_i}. \] 使用 Lagrange 乘子法 + 一些统计力学求解该约束极值问题, 得到 \[ p_i = \frac{1}{Z} \exp(-\beta \varepsilon_i), \] 其中 $\beta=-1/k_BT$ 与系统温度成反比 ($k_B$ 是 Boltzmann 常数), 归一化系数 $Z$ 保证所有 $p_i$ 之和为 $1$, 有 $Z=\sum_{i=1}^N\exp(-\beta\varepsilon_i)$.

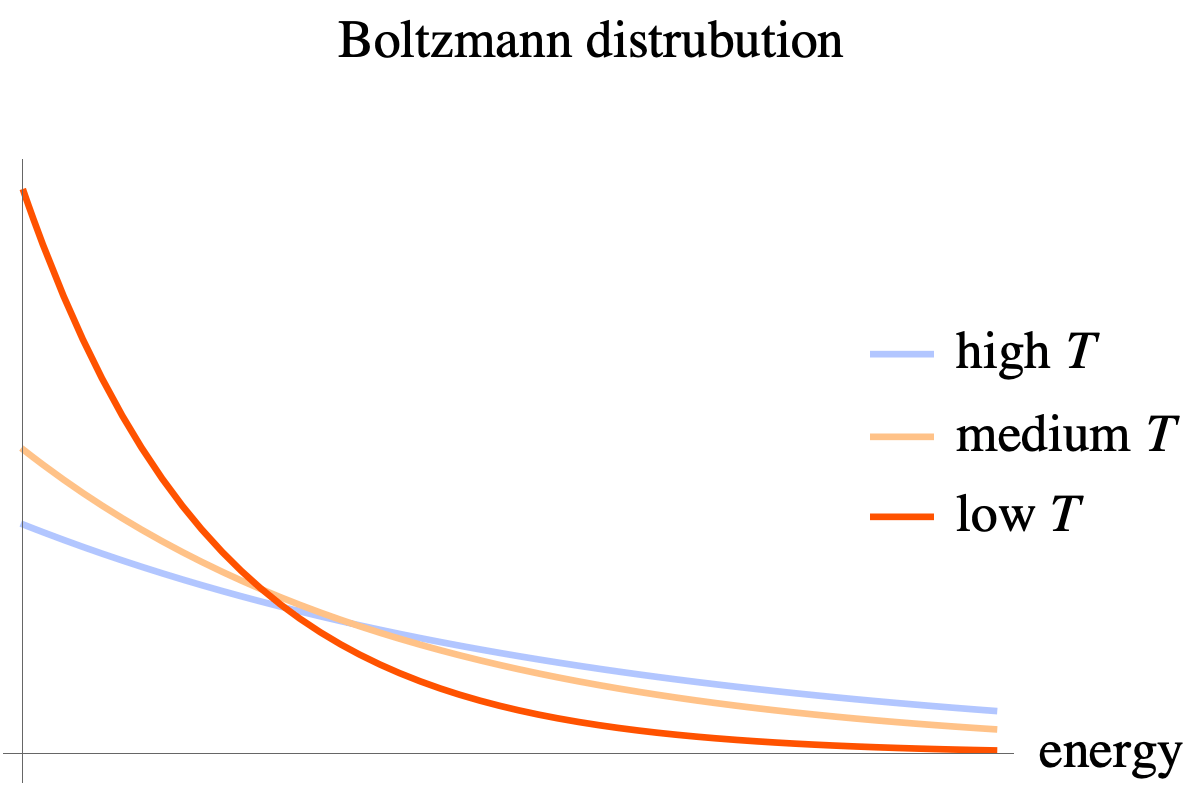
这个分布也称为 Boltzmann 分布. 下图给出了不同温度下 Boltzmann 分布的图像.

给定温度 $T$, 则分子密度随着能量的增加而下降.
当温度较低的时候, 密度曲线陡峭, 分子主要集中在能量较低的区域; 当温度较高时, 密度曲线平缓, 分子向高能量的区域移动.

EBM 将样本分布建模为 Boltzmann 分布, \[ p_\theta(x) = \frac{1}{Z_\theta} \exp(-\frac{E_\theta(x)}{\tau}), \tag{$\clubsuit$} \] 其中 $x$ 取值于 $\R^N$ 中的某开集 $\Omega$,

函数 $E_\theta:\Omega\to\R$ 称为能量函数 (给出了样本 $x$ 的 “能量”). 通常用一个神经网络建模 $E_\theta(x)$.
系数 $\tau$ 是系统的 “温度” (类比 Boltzmann 分布中的温度, 这里略去了常数 $k_B$).
归一化系数 $Z_\theta=\int_\Omega\exp(-E_\theta(x)/\tau)\dd{x}$.

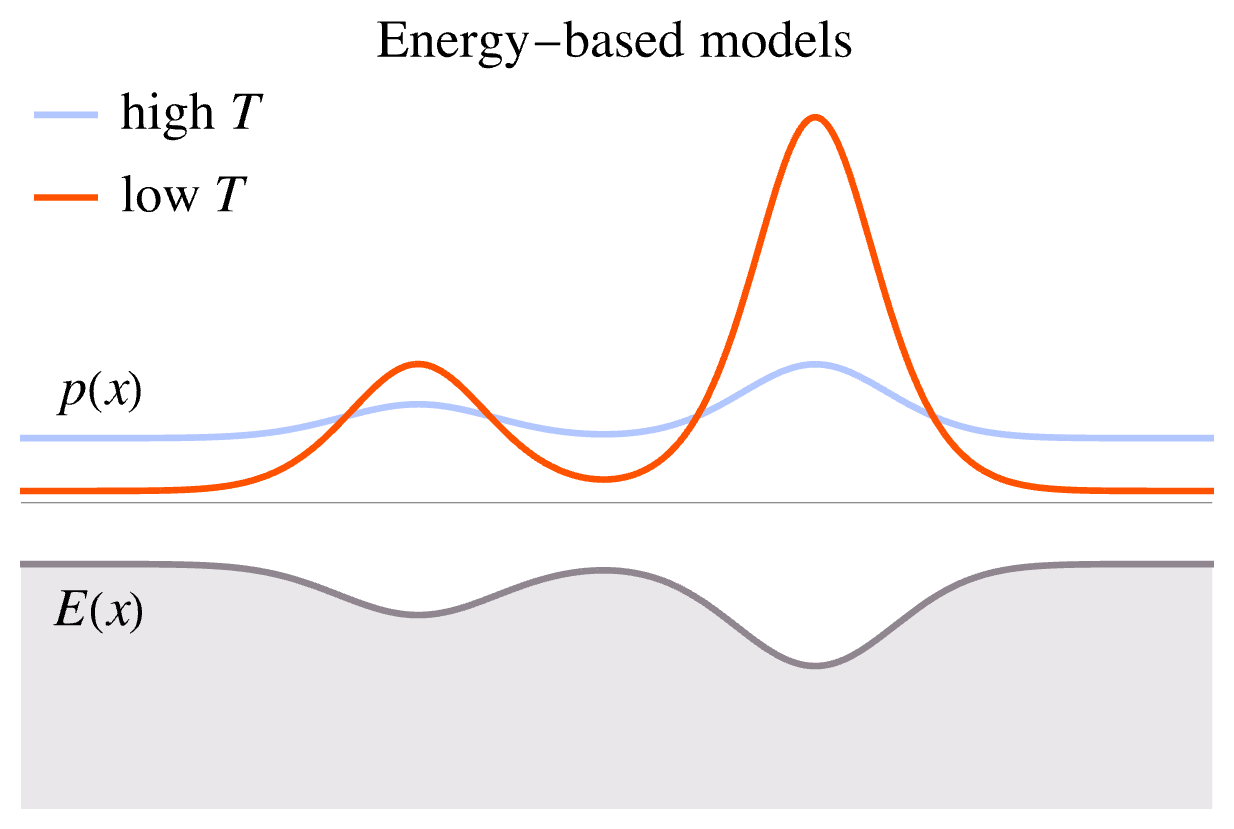
温度 $\tau$ 控制了概率密度 $p_\theta$ 的形状, 如下图所示.

在温度较低时, $p_\theta(x)$ 集中在能量 $E_\theta(x)$ 较低的区域. 此时采样 $x\sim p_\theta$ 得到的结果单一.
当温度逐渐升高时, $p_\theta$ 会逐渐分散到整个 $\Omega$. 此时采样 $x\sim p_\theta$ 得到的结果比较多样, 随机性强.

为什么我们选择将样本分布建模为 Boltzmann 分布呢? 因为很多常见分布都可以写成 $(\clubsuit)$ 式的形式, 比如下面列出的分布实际上都属于指数族分布 (exponential family).^[1]

Gauss 分布, 指数分布, beta 分布, 类别分布, $\chi^2$ 分布……

此外, 能量函数 $E_\theta(x)$ 并无任何限制, 可以灵活使用各种神经网络架构建模. 然而, EMB 的一个关键缺点是归一化系数 $Z_\theta$ 这个高维积分难以计算. 对于一般的神经网络, $E_\theta(x)$ 过于复杂, 几乎无法给出 $Z_\theta(x)$ 的闭式解; 而数值积分的计算代价又随着维度 $N$ 呈指数增长, 显然不可行.

由于无法计算 $Z_\theta$, 我们就没法使用 “标准” 的 MLE 优化 $\theta$. 主流的方法都是绕过 $Z_\theta$, 直接优化 $E_\theta(x)$, 具体方法在下一小节介绍.

Note Autoregressive as EBM.

Boltzmann 分布与我们熟知的 softmax 函数本质是同一个东西. 设 \[ (p_1,\dots,p_M) = \operatorname{softmax}(-\varepsilon_1,\dots,-\varepsilon_M), \] 则 \[ p_i = \frac {\exp(-\varepsilon_i/\tau)} {\sum_{j=1}^M \exp(-\varepsilon_j/\tau)} \] 恰好是 Boltzmann 分布. 我们一般把 softmax 的输入 $-\varepsilon_i$ 称为 logits (对数概率), 实际上可以理解为负的能量. EMB 中, 负的能量函数 $-E_\theta(x)$ 也可以叫做 logits.

从这个视角看, 自回归模型也是一种 EBM. 自回归模型对条件概率 $p_\theta(x_l\mid x_{1:l-1})$ 用 softmax 建模, 相当于一个 Boltzmann 分布. 自回归模型对每个条件概率分别归一化, 自动保证了联合概率是归一化的, \[ \Align{ &\int_{\R^L} p_\theta(x_1,\dots,x_L) \dd{x_1}\cdots\dd{x_L} \\ &= \int_{\R^{L-1}} p_\theta(x_1,\dots,x_{L-1}) \dd{x_1}\cdots\dd{x_{L-1}} \underbrace{ \int_\R p_\theta(x_L\mid x_{1},\dots,x_{L-1}) \dd{x_L} }_{{}=1\textsf{ by softmax}} \\ &= \int_{\R^{L-1}} p_\theta(x_1,\dots,x_{L-1}) \dd{x_1}\cdots\dd{x_{L-1}} \\ &= \cdots \vphantom{\int} \\ &= 1, } \] 避免了对高维分布 $p_\theta(x_1,\dots,x_L)$ 直接进行归一化.

13.2 Learning with MLE

尽管 $p_\theta(x)$ 的表达式无法计算, 我们仍然可以使用 MLE 学习参数.

设真实分布为 $p_\theta$, 我们希望最小化负对数似然 $\operatorname{NLL}(\theta):=\operatorname{E}_{x\sim p}[-\log p_\theta(x)]$. 直接计算对数似然是行不通的, 我们不妨考虑对数似然关于参数 $\theta$ 的梯度 \[ \nabla_\theta \operatorname{NLL}(\theta) = \nabla_\theta \operatorname{E}_{x\sim p}\bigl[-\log p_\theta(x)\bigr], \] 这一个定义在参数域 $\Theta$ (参数 $\theta$ 的取值范围) 上的向量场, 它永远指向 $\operatorname{NLL}$ 上升最快的方向; 在 $\operatorname{NLL}$ 的极值点处, 向量场为零. 因此, 我们可以采用梯度下降的方法——从某个初始点 $\theta_0\in\Theta$ 开始, 每次沿着梯度场下降一点, \[ \theta_{t+1} \leftarrow \theta_t - \alpha \nabla_\theta\operatorname{NLL}(\theta), \] 最终 (在合适的条件下) 可以收敛到 $\operatorname{NLL}$ 的极小值点 $\theta^*$.

将 $\nabla_\theta\operatorname{NLL}(\theta)$ 展开, \[ \Align{ \nabla_\theta \operatorname{NLL}(\theta) &= \nabla_\theta \operatorname{E}_{x\sim p}\bigl[-\log p_\theta(x)\bigr] \\ &= \operatorname{E}_{x\sim p}\bigl[ -\orange{\nabla_\theta \log p_\theta(x)} \bigr] \\ &= \operatorname{E}_{x\sim p}\biggl[ \frac{1}{\tau} \nabla_\theta E_\theta(x) + \nabla_\theta \log{Z_\theta} \biggr]. \\ } \] (第二步将积分与偏导数交换顺序.)

橙色的部分 $\orange{\nabla_\theta \log p_\theta(x)}$ 是 (单个样本的) 对数似然关于参数 $\theta$ 的梯度, 表示当观测到特定样本 $x$ 时, 如何改变参数 $\theta$ 才能使该样本的似然 $\log p_\theta(x)$ 增加得最快. 它也叫做得分 (score).

回到 $\nabla_\theta\operatorname{NLL}(\theta)$, 期望里面的第一项 $\nabla_\theta E_\theta(x)$ 是容易计算的——可以借助神经网络的自动微分器来计算梯度; 第二项与 $x$ 无关, 但计算略微复杂, 最终可以得到 (过程见后) \[ \nabla_\theta\log Z_\theta = -\frac1\tau \operatorname{E}_{x\sim p_\theta}\bigl[ \nabla_\theta E_\theta(x) \bigr], \] 因此 \[ \nabla_\theta \operatorname{NLL}(\theta) = \frac1\tau \Bigl( \underbrace{ \operatorname{E}_{x\sim p}[\nabla_\theta E_\theta(x)] }_{\textsf{positive}} - \underbrace{ \operatorname{E}_{x\sim p_\theta}[\nabla_\theta E_\theta(x)] }_{\textsf{negative}} \Bigr). \] 其中,

第一项 (positive phase) 的含义是, 从真实分布 $p(x)$ 中采样, 用于降低这些数据点的能量 $E_\theta(x)$.
第二项 (negative phase) 的含义是, 从模型 $p_\theta(x)$ 中采样, 用于提高这些样本点的能量 $E_\theta(x)$ (防止模型将所有空间都赋予高概率).

由于 $p_\theta(x)$ 是未知的, 且配分函数 $Z(\theta)$ 难以计算, MLE 训练的核心挑战在于如何高效且准确地估计第二项——也即如何从未知分布 $p_\theta(x)$ 中采样. 我们将在下面几节展开.

Pf 归一化系数 $Z_\theta$ 关于 $\theta$ 的梯度为 \[ \Align{ \blue{\nabla_\theta} \log{Z_\theta} &= \frac{1}{Z_\theta} \blue{\nabla_\theta} Z_\theta \\ &= \frac{1}{Z_\theta} \blue{\nabla_\theta} \int_\Omega\exp(-\frac{E_\theta(x)}{\tau})\dd{x} \\ &= \frac{1}{Z_\theta} \int_\Omega \blue{\nabla_\theta} \exp(-\frac{E_\theta(x)}{\tau})\dd{x} \\ &= -\frac{1}{\tau} \orange{\frac{1}{Z_\theta}} \int_\Omega \orange{\exp(-\frac{E_\theta(x)}{\tau})} \blue{\nabla_\theta} E_\theta(x) \dd{x} \\ &= -\frac{1}{\tau} \int_\Omega \orange{p_\theta(x)} \blue{\nabla_\theta} E_\theta(x) \dd{x} \\ &= -\frac{1}{\tau} \operatorname{E}_{z\sim p_\theta}[\nabla_\theta E_\theta(x)]. } \]

13.3 MCMC sampling

EBM 训练和推理的过程都需要从 $p_\theta(x)$ 中采样. MCMC (Markov chain Monte Carlo) 是从未知分布中采样的一类方法. MCMC 构造了一个 Markov 链, 其平稳分布为 $p_\theta(x)$, 进而通过多次迭代的方法让采样收敛到 $p_\theta(x)$.

Metropolis-Hastings 算法 (MH) 是最经典的 MCMC 框架. 它的流程为

从先验分布 $\pi(x)$ 中采样 $x_0$.
状态转移:
1. (提议) 从一个提议分布 (proposal distribution) $q(x'\mid x_t)$ 中采样后选状态 $x'\sim q(x'\mid x_t)$. 提议分布通常比较简单, 比如以 $x_t$ 为中心的 Gauss 分布.
2. (计算接受率) 计算接受率 \[ A(x'\mid x_t) = \min\biggl\{1, \frac{p_\theta(x')q(x_t\mid x')}{p_\theta(x_t)q(x'\mid x_t)} \biggr\}, \] 这个接受率确保了马尔可夫链满足 “细致平衡条件 (detailed balance)” , 从而保证 $p_\theta(x)$ 是平稳分布.
  
  注意计算 $A$ 时 $p_\theta(x')$ 和 $p_\theta(x_t)$ 的归一化系数 $Z_\theta$ 相互抵消, 因此即使 $Z_\theta$ 未知, 也可以计算这个接受率, 这是 MCMC 成功的关键.
3. (接受/拒绝) 采样随机数 $u\sim U[0,1]$,
  - 如果 $u \le A(x'\mid x_t)$, 则接受提议, 令 $x_{t+1}\gets x'$.
  - 如果 $u > A(x'\mid x_t)$, 则拒绝提议, 令 $x_{t+1}\gets x_t$.

MH 算法虽然通用，但在处理高维 / 复杂分布时存在显著缺点,

如果提议分布 $q$ 的步长 (如 Gauss 分布的方差) 太小, 链会像 “随机游走” 一样爬行, 探索状态空间的速度非常慢.
如果步长太大, 提议的 $x'$ 会落到目标分布 $p(x)$ 的低概率区域, 导致接受率 $A$ 极低, 大量的提议被拒绝, 链停滞在原地.
在高维空间中, 找到一个既能快速移动又具有高接受率的提议分布 $q$ 极其困难.

13.4 Langevin MCMC sampling

MH 算法在探索状态空间 $\Omega$ 时像 “无头苍蝇” 一样随机走动, 并没有利用 $p_\theta(x)$ 的已知信息 (比如能量 $E_\theta(x)$). LD-MCMC (Langevin dynamics MCMC) 的核心思想是使用 $p_\theta(x)$ 的已知信息, 从而克服 MH 效率低的问题.

LD-MCMC 启发自统计物理中的 Langevin 动力学.

EBM 的背景是 Boltzmann 分布, 即系统在平衡态时, 分子位置的分布 $p(x) \propto \exp(-E(x)/k_BT)$. Langevin 动力学则定义了系统如何通过随机热运动 (动力学) 达到或维持平衡态. 从这个角度来说, 使用 LD-MCMC 从 EBM 中采样是非常自然的.

\[ \xymatrix@=9em{ *[F-,]{\hspace{2em}\mathclap{\textsf{初始状态}}\hspace{2em}\strut} \ar@1{->}[r]^(.42){\large\textsf{Langevin 动力学}} & *[F-,]{\hspace{4.5em} \mathclap{\textsf{平衡态 (Boltzmann)}} \hspace{4.5em}\strut} } \] 由于我们刻画的是非平衡态, 分子的分布会随时间变化. 记随机变量 $x_t$ 表示 $t$ 时刻分子的位置, 其中 $t$ 取值于某区间 $I$, 则随机变量族 $\{x_t\}_{t\in I}$ 构成一个随机过程 (stochastic process). 刻画随机过程随时间演化的方程是随机微分方程 (SDE).

假设分子系统处于恒温 $T$ 的热浴中, 则 $x_t$ 的演化由 Langevin 方程刻画:这里给出的是过阻尼的 (overdamped) Langevin 方程. 具体见 https://en.wikipedia.org/wiki/Langevin_dynamics.^[2] \[ \dd{x_t} = - {\frac{1}{\gamma} \nabla_x E(x_t) \dd{t}} + {\sqrt{2 D} \dd{w_t}}, \tag{$\diamondsuit$} \] 这是一个 SDE, 其中:

第一项 $-\nabla_x E(x_t)$ 为势能梯度力, 它使得系统能量耗散, 将粒子推向低能区域.
- $\gamma$ 为摩擦系数.
第二项 $\sqrt{2D}\dd{w_t}$ 代表了周围介质对分子随机、快速的碰撞, 称为随机热涨落.
- 随机过程 $w_t$ 称为 Wiener 过程. 微分 $\dd{w_t}$ 可以理解为随机 Gauss 噪声.
- $D=k_BT/\gamma$ 为扩散系数 (diffusion coefficient).

根据物理规律 (“涨落-耗散定理”), 随机过程 $x_t$ 的稳定分布恰好为 Boltzmann 分布 \[ p(x) \propto \exp\biggl(-\frac{E(x)}{k_BT}\biggr). \] 即经过充分长时间后, $x_t$ 服从的分布与 $p(x)$ 的差距可以忽略不计.

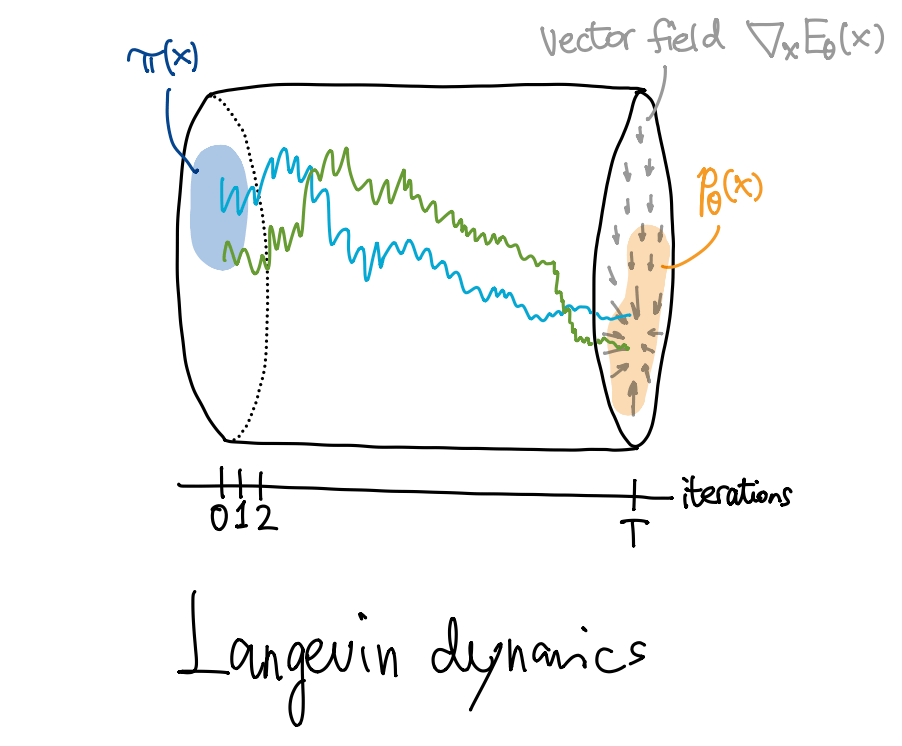
模仿物理中的 Langevin 动力学, LD-MCMC 的迭代过程设计为

从先验分布 $\pi(x)$ (例如标准 Gauss 分布) 中采样 $x_0$.
状态转移: \[ x_{t+1} \gets x_t + \alpha \nabla_x E_\theta(x_t) + \sqrt{2\alpha} \, z_t, \] 其中 $z_t\sim\mathcal{N}(0,I)$ 且相互独立, $\alpha>0$ 为步长. 这是一个离散的 Langevin 过程, 其中梯度项 $\nabla_x(\dots)$ 驱动 $x_t$ 向高概率区域移动, 随机项 $z_t$ 提供了随机探索的能力, 避免收敛到一个极值点.

LD-MCMC 使用离散的迭代过程求解连续的 SDE $(\diamondsuit)$, 称为 Euler-Maruyama 迭代法, 类似于使用 Euler 法求解 ODE.

14 Score Matching

14.1 Score matching

注意 LD-MCMC 迭代过程实际上只使用了能量梯度 $\nabla_x E_\theta(x)$, 与能量函数本身无关. 因此我们与其建模 $E_\theta(x)$, 不如直接建模 $\nabla_x E_\theta(x)$. 我们将能量梯度 $\nabla_x E_\theta(x)$ 称为得分 (score).

原论文Aapo Hyvärinen, Estimation of Non-Normalized Statistical Models by Score Matching, 2005.^[3]实际上将得分定义为 $\log{p_\theta(x)}$ 关于 $x$ 的梯度. 容易看出这等于 $\nabla_x E_\theta(x)$.
实际上, 在统计学中, 得分应当是 $\log{p_\theta(x)}$ 关于 $\theta$ (而非 $x$) 的梯度 (见前文), 这里 abuse term.

所谓得分匹配 (score matching), 就是让模型的得分函数 $\nabla_x\log p_\theta(x)$ 拟合真实的得分函数 $\nabla_x\log p(x)$. 损失函数是 $\ell^2$ 距离, \[ \mathcal{L}(\theta) := \frac12 \operatorname{E}_{x\sim p} \bigl\Vert \nabla_x{\log p(x)} - \nabla_x{\log p_\theta(x)} \bigr\Vert_2^2, \] 其中我们用一个神经网络 $s_\theta(x)$ 参数化 $\nabla_x\log{p_\theta(x)}$. 这其中有一个问题: 我们并不知道真实分布的梯度 $\nabla_x\log{p(x)}$.

假设真实分布满足某些条件包括 $\lim_{\|x\|\to\infty}p(x)s_{\theta}(x)=0$ 等.^[4], 利用分部积分的技巧重写 $\mathcal{L}(\theta)$, 我们能够得到 \[ \mathcal{L}(\theta) = \operatorname{E}_{x\sim p} \biggl[ \tr\bigl(\nabla_x s_\theta(x)\bigr) + \frac12\|s_\theta(x)\|_2^2 \biggr] + \mathsf{const.}, \] 其中第一项是向量场 $s_\theta(x)$ 的散度, 第二项为 $s_\theta(x)$ 的 $\ell^2$-范数. 这两者都是可以计算的.

得分匹配是一种隐式模型, 它不建模 $p_\theta(x)$; 然而我们不必像其他的隐式模型 (比如 GAN) 一样进行对抗学习, 大大增加了稳定性.

14.2 Denoising score matching

朴素的得分匹配在实际中会遇到一些困难. 回顾流形假设 (manifold hypothesis):

真实样本 $X$ 通常在 $\R^N$ 中十分稀疏, 即真实密度 $p(x)$ 的支集 $\supp{p}$ 构成 $\R^N$ 的低维子流形.

这意味着 $X$ 在 $\R^N$ 中是非常稀疏的——除开很小的一个区域之外, 密度 $p(x)$ 都为零! 这导致 $s_\theta(x)$ 的估计值在低样本密度区域非常不准确, 使得 Langevin 迭代初期偏离正轨, 产生差强人意的结果.

如何解决? 论文Yang Song, Stefano Ermon, Generative Modeling by Estimating Gradients of the Data Distribution, 2019.^[5]使用了 “噪声扰动” 的办法. 考虑真实分布 $p(x)$ 上叠加一个 Gauss 分布 \[ p_{\sigma}(x) := \int_{\R^N} p(y) \mathcal{N}(x;y,\sigma^2I) \dd{y}. \] 若要从 $p_\sigma(x)$ 中采样, 可以先采样真实样本 $x\sim p(x)$, 再加上 Gauss 分布 $x+\sigma z$, $z\sim\mathcal{N}(0,I)$. 这种思想的核心是下面几个观察:

Gauss 分布支在整个 $\R^N$, 这解决了流形假设带来的稀疏性.
强噪声 (较大的 $\sigma$) 让 $p_\sigma$ 更加分散, 在迭代过程中, 可以让遍布整个空间中的点移动到 $p(x)$ 的支集附近; 弱噪声 (较小的 $\sigma$) 对真实分布的扰动较小, 可以让已经处在 $p(x)$ 附近的点收敛到较精确的分布.
同时使用强噪声和弱噪声, 可以在解决稀疏性的同时提高采样准确率.

因此, 原论文采用了多个噪声层级 $\sigma_1>\sigma_2>\dots>\sigma_L$ (构成等比数列), 并对每个每个 $p_{\sigma_l}$ 进行得分匹配. 即构造一个神经网络 $s_\theta(x,l)$ (第二个参数指示噪声层级), 用来拟合不同层级的得分函数, \[ s_\theta(x,l) \approx \nabla_x \log p_{\sigma_l}(x). \] 损失函数为各个层级的 $\ell^2$ 损失的加权和, \[ \mathcal{L}(\theta) := \sum_{l=1}^L \lambda(l) \operatorname{E}_{x\sim p_{\sigma_l}} \bigl\Vert \nabla_x{\log p_{\sigma_l}(x)} - s_\theta(x,l) \bigr\Vert_2^2, \] 其中权重通常取 $\lambda(l)=\sigma_l^2$.

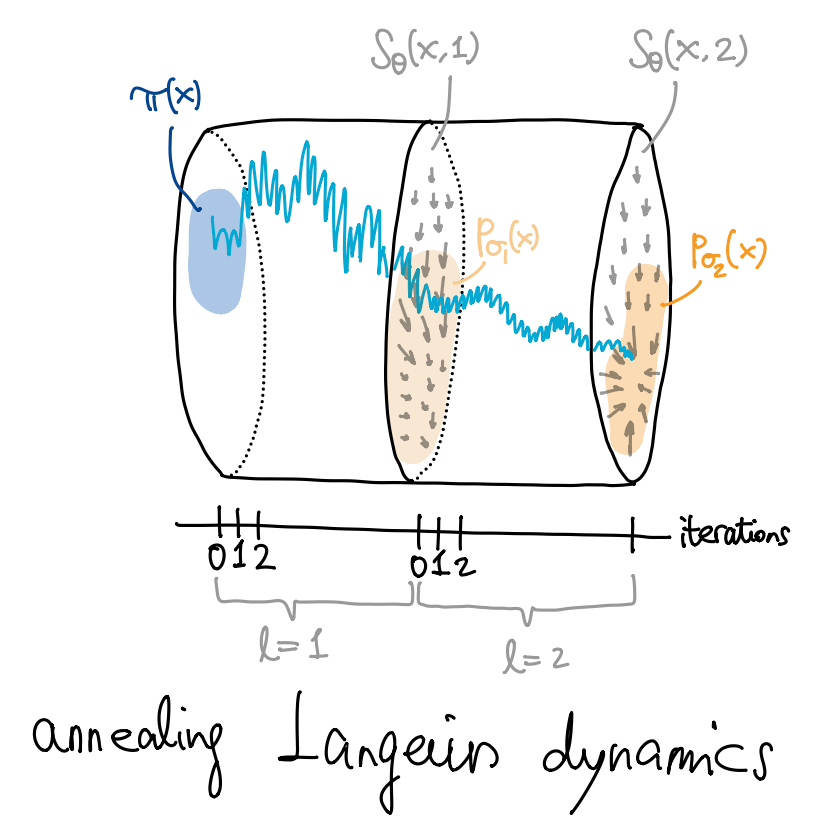
在训练好 $s_\theta(x,l)$ 之后, 我们使用退火 Langevin 动力学 (annealed Langevin dynamics) 进行采样, 步骤如下:

从先验分布 $\pi(x)$ (例如标准 Gauss 分布) 中采样 $x_0$.
对噪声层级 $l=1,2,\dots,L$,
- 迭代 $T$ 步: \[ x_{t+1} \gets x_t + \alpha_l s_\theta(x_t,l) + \sqrt{2\alpha_t}\, z_t, \] 其中随机噪声 $z_t$ 从 $\mathcal{N}(0,I)$ 中独立采样, 步长 \[ \alpha_l = \alpha_0 \cdot \frac{\sigma_l^2}{\sigma_L^2}. \] 注意 $\sigma_l^2$ 是递减的, 意味着 $\alpha_l$ 也逐级递减, 也就是所谓 “退火” (anneal).
- 将终点 $x_T$ 设为下一层级的初始值.
最终的 $x_T$ 近似服从 $p_{\sigma_L}(x)$, 当 $\sigma_L$ 充分小时约为 $p(x)$.

在采样过程中, $x$ 中的噪声被逐级消除, 因此这个模型也称为去噪得分匹配 (denoising score matching).

下面列出的分布实际上都属于指数族分布 (exponential family).↩︎
这里给出的是过阻尼的 (overdamped) Langevin 方程. 具体见 https://en.wikipedia.org/wiki/Langevin_dynamics.↩︎
Aapo Hyvärinen, Estimation of Non-Normalized Statistical Models by Score Matching, 2005.↩︎
包括 $\lim_{\|x\|\to\infty}p(x)s_{\theta}(x)=0$ 等.↩︎
Yang Song, Stefano Ermon, Generative Modeling by Estimating Gradients of the Data Distribution, 2019.↩︎

Note > Course

#机器学习

生成模型基础 | 6 基于能量的模型

https://disembo.github.io/Note/Course/gen-models/6/

作者

jin

发布于

2025年11月26日

许可协议

生成模型基础 | 5 归一化流下一篇