生成模型基础 | 5 归一化流

11 Normalizing Flows

生成模型是将随机噪声映射到复杂分布的东西. 归一化流Danilo Jimenez Rezende, Shakir Mohamed, Variational Inference with Normalizing Flows, 2015.^[1]直接模拟了这一过程.

GAN 也模拟了将噪声映射到复杂分布的过程. 不同的是, GAN 将噪声直接映射到样本 $x$, 属于隐式模型; 流模型将噪声分布映射到样本分布 $p_\theta(x)$, 属于显式模型.

Note 显式与隐式生成模型.

Explicit: 直接建模 $p_\theta(x)$, 可以计算每个样本的概率、可以通过 MLE $\argmax_\theta\,p_\theta(\mathcal{D})$ 优化.
- AR.
- VAE, 优化 ELBO (作为似然函数的下界).
- Normalizing flow.
Implicit: 不直接建模 $p_\theta(x)$, 不能计算样本概率、无法通过 MLE 优化.
- GAN, 利用判别器 / 评论家近似优化目标.

11.1 Normalizing flows

设 $\R^N$ 的非空开子集 $\Omega$ 上的随机变量 (简单分布) $Z$ 经过微分同胚本文的微分同胚都是 $C^1$ 的, 即 $g$ 可逆且 $g,g^{-1}$ 都连续可微.^[2] $g:\Omega\to\Omega$ 得到了随机变量 (复杂分布) $X$, 则根据变量替换定理, 它们的概率密度有如下关系, \[ p_X(x) = p_Z(g^{-1}(x)) \Bigl| \det(Dg^{-1}|_x) \Bigr|, \] 其中,

$D(g^{-1})$ 是 $g^{-1}$ 的 Jacobi 矩阵.
一般取 $Z$ 为标准 Gauss 分布 $\mathcal{N}(0,I)$.

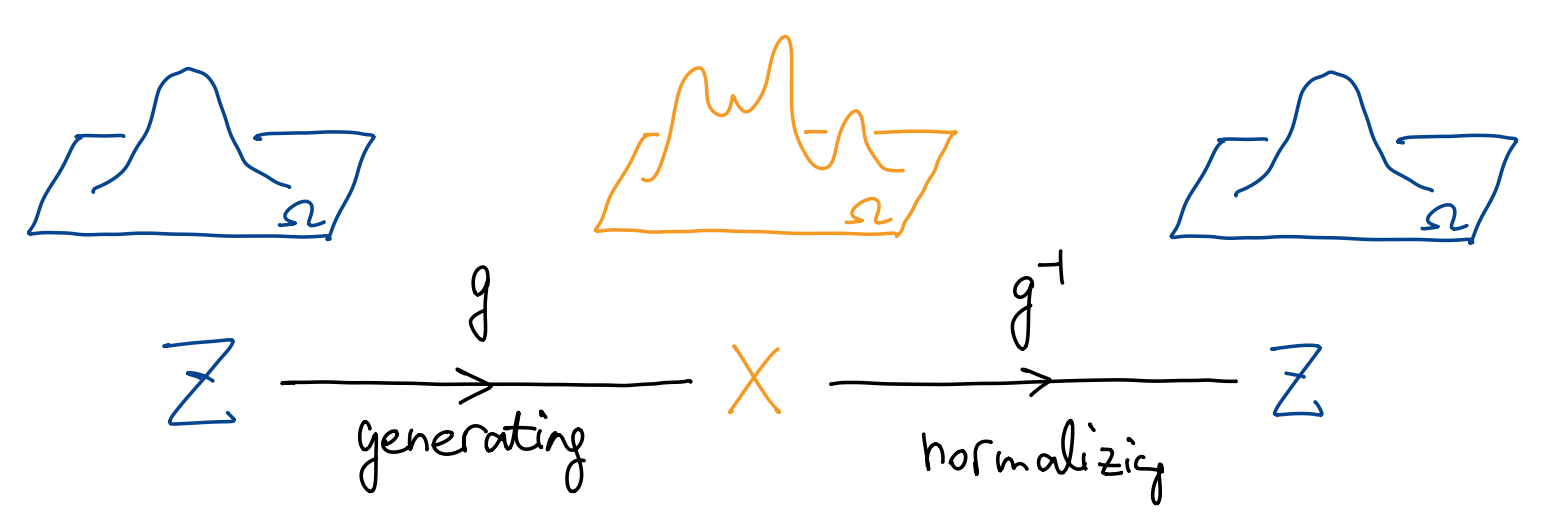
整个过程如上图所示:

$g$ 将一个简单分布 $Z$ 映射到一个复杂分布 $X$, 即生成的过程.
$g^{-1}$ 将一个复杂分布 $X$ “归一化” 到一个标准分布 $Z$. 因此这个模型也称为归一化流 (normalizing flow).

假设我们用一个神经网络 $g_\theta(x)$ 拟合这个微分同胚, 则我们可以用 MLE 来估计参数: \[ \Align{ \operatorname{NLL}(x;\theta) = -\log p_X(x_n;\theta) = -\log p_Z(\orange{g_\theta^{-1}}(x)) -\log\Bigl| \det(D\orange{g_\theta^{-1}}|_x) \Bigr|, } \]

在实际操作中, 既可以建模生成过程 $g_\theta$, 也可以建模归一化过程 $f_\theta$.

优化完成后, 生成一个随机噪声 $Z\sim p_Z$, 经过 $g_\theta$ 即可完成采样, \[ X = g_\theta(Z). \]

Note 归一化流 vs VAE.

VAE 输入样本 $X$, 输出隐空间正态分布 $\mathcal{N}(0,I)$ 的期望和方差.
归一化流输入样本 $X$, 输出服从正态分布 $\mathcal{N}(z;0,I)$ 的噪声 $Z$.

由于 VAE 是一个隐式模型, 我们不好计算似然函数, 转而去优化似然函数的下界 ELBO. 这就导致 VAE 必须使用比较浅的网络, 否则会让模型退化 (见 VAE 节). 归一化流没有这个问题, 因为它直接优化对数似然, 可以放心地使用大而深的网络.

11.2 Constructing flows

神经网络 $g_\theta$ 需要是微分同胚. 若 \[ g_\theta = g^L_\theta \circ g^{L-1}_\theta \circ \dots \circ g^1_\theta, \] 则每一层 $g^l_\theta$ 都必须是微分同胚. 在实际场景中, 我们对每个 $g^l_\theta$ 的要求是:

容易计算、容易求逆、容易求 Jacobi 矩阵.

下面看常见的几类 $g^l_\theta$.

11.2.1 MLP

Elementwise flow. 逐元素映射 $g(z)=(h(z_1),\dots,h(z_D))$, 其中 $h$ 是 $\R$ 上的微分同胚.

计算简单, 复杂度为 $O(D)$,
- $g^{-1}(x)=(h^{-1}(x_1),\dots,h^{-1}(x_D))$,
- $\det(Dg^{-1}|_x)=\prod_{i=1}^D\det(Dh^{-1}|_{x_i})$.
无法提取元素之间的关系.

Linear flow. 线性层 $g(z)=Az+b$, 其中 $A$ 可逆.

自由度为 $D^2$.
计算 $A^{-1}$ 和 $\det{A}$ 的时间复杂度为 $O(D^3)$, 代价太高了.
Linear flow with triangular matrix: 限制 $A$ 为可逆的上三角矩阵,
- 自由度为 $D(D+1)/2$.
- 计算 $\det{A}$ 的时间复杂度为 $O(D)$, 然而计算 $A^{-1}$ 的时间复杂度为 $O(D^2)$, 还是太高.
Linear flow with orthogonal matrix: 限制 $A$ 为正交阵,
- 自由度为 $D(D-1)/2$.
- 有 $\det{A}=1$ 以及 $A^{-1}=A\T$, 转置一般可以实现 $O(1)$ 时间复杂度.
- 然而这是一个带约束的优化, 即在梯度下降过程中必须保证 $A$ 一直是正交阵, 这不太容易. 一个退而求其次的办法是考虑正交阵的一个子集, 即所有 “关于超平面的反射变换” (Householder transforms), 形如 \[ R(v_1,\dots,v_D) = I - \frac{2}{v\T v}vv\T, \qquad v \in \R^D\setminus\{0\}. \] 自由度从 $D(D-1)/2$ 变成了 $D$, 但是 $(v_1,\dots,v_D)$ 可以取 (几乎) 任意向量, 是一个无约束优化问题.

11.2.2 Residual blocks

可逆 MLP 的表达能力有限. 一种更重要的模块是残差模块.

Residual flow 1. 形如 $g(z)=z+h(z)$,

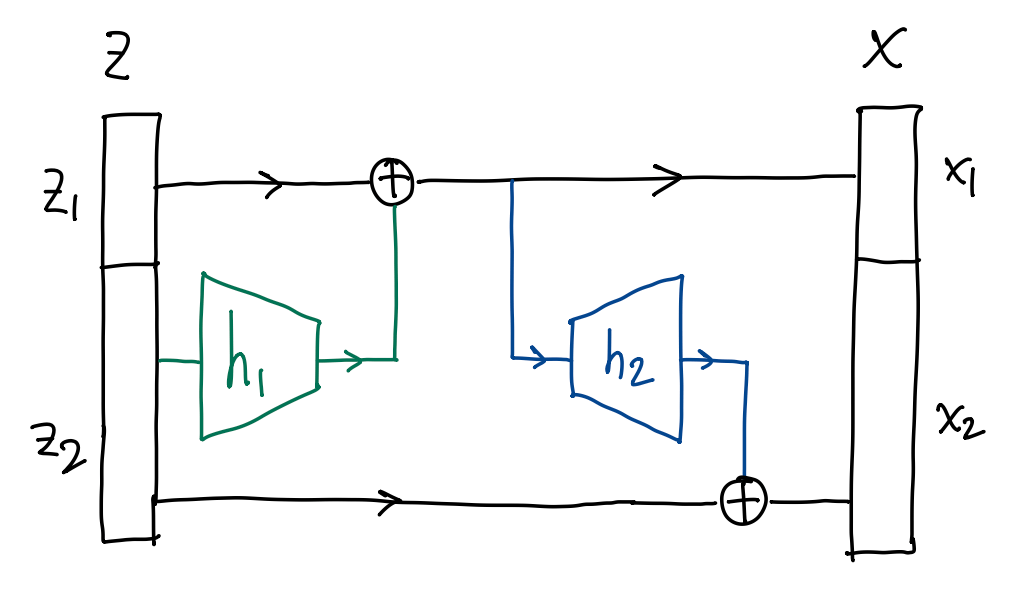
首先将输入 $z\in\R^D$ 分为两部分 $z=(z_1,z_2)$, 其中 $z_1\in\R^{d_1},z_2\in\R^{d_2}$ 且 $d_1+d_2=D$.
任取映射 $h_1:\R^{d_2}\to\R^{d_1}$ 以及 $h_2\in\R^{d_1}\to\R^{d_2}$, 构造 \[ \Align{ x_1 &= z_1 + h_1(z_2) \in\R^{d_1}, \\ x_2 &= z_2 + h_2(x_1) \in\R^{d_2}, } \] 令 $g(z):=(x_1,x_2)$ 即可. 这称为耦合层 (coupling layer), 如上图所示.
此时 $g$ 总是可逆的, 且 \[ \Align{ z_2 &= x_2 - h_2(x_1), \\ z_1 &= x_1 - h_1(z_2) = x_1 - h_1(x_2 - h_2(x_1)). } \]
Jacobi 矩阵 \[ Dg|_z = \pmqty{ I_{d_1} & Dh_1|_{z_2} \\ Dh_2|_{x_1} & I_{d_2} + Dh_2|_{x_1} Dh_1|_{z_2} }, \] 以及 \[ Dg^{-1}|_x = \pmqty{ I_{d_1} + Dh_1|_{z_2} Dh_2|_{x_1} & -Dh_1|_{z_2} \\ Dh_2|_{x_1} & I_{d_2} }. \]

Residual flow 2. 形如 $g(z)=z+h(z)$,

我们只需限制 $h$ 的 Lipschitz 常数 $L<1$ (压缩映射) 即可, 此时 $g$ 可逆.

在实操中, 通常对残差模块加入更多设计以确保计算高效. 这里举出一例.

RealNVPLaurent Dinh et al, Density estimation using Real NVP, 2017.^[3].

仍旧将输入 $z\in\R^D$ 分为两部分 $z=(z_1,z_2)$, 其中 $z_1\in\R^{d_1},z_2\in\R^{d_2}$ 且 $d_1+d_2=D$.
任取 $s,t:\R^{d_1}\to\R^{d_2}$ (原文中为仿射变换), 定义 \[ \Align{ x_1 &= z_1, \\ x_2 &= z_2 \odot \exp[s(z_1)] + t(z_1), } \] (其中 $\odot$ 是向量逐元素乘法, $\exp$ 是逐元素指数函数) 令 $g(z):=(x_1,x_2)$. 这称为仿射耦合层 (affine coupling layer).
此时 $g$ 总是可逆的, 且 \[ \Align{ z_1 &= x_1, \\ z_2 &= [x_2-t(x_1)] \odot \exp[-s(x_1)]. } \]
Jacobi 矩阵 \[ Dg|_z = \pmqty{ I_{d_1} & 0 \\ * & \diag[\exp\!\pqty{s(z_1)}] }, \qquad Dg^{-1}|_x = \pmqty{ I_{d_1} & 0 \\ * & \diag[\exp\!\pqty{-s(x_1)}] } \] 是下三角阵! 行列式就是对角元素的乘积, 非常容易计算.

12 Continuous Normalizing Flows

12.1 From discrete to continuous

上一节我们讲的是一种 “离散” 的流 (discrete normalizing flow, DNF). 从最初的随机噪声 $Z$ 开始, 一层一层地应用微分同胚 $g^l(z)$, 最终达到目标 $X$. 层数 $l=1,2,\dots,L$ 可以看作离散的时间维度, 随着层数增加, 原始分布一点一点被推到目标分布, 如下图.

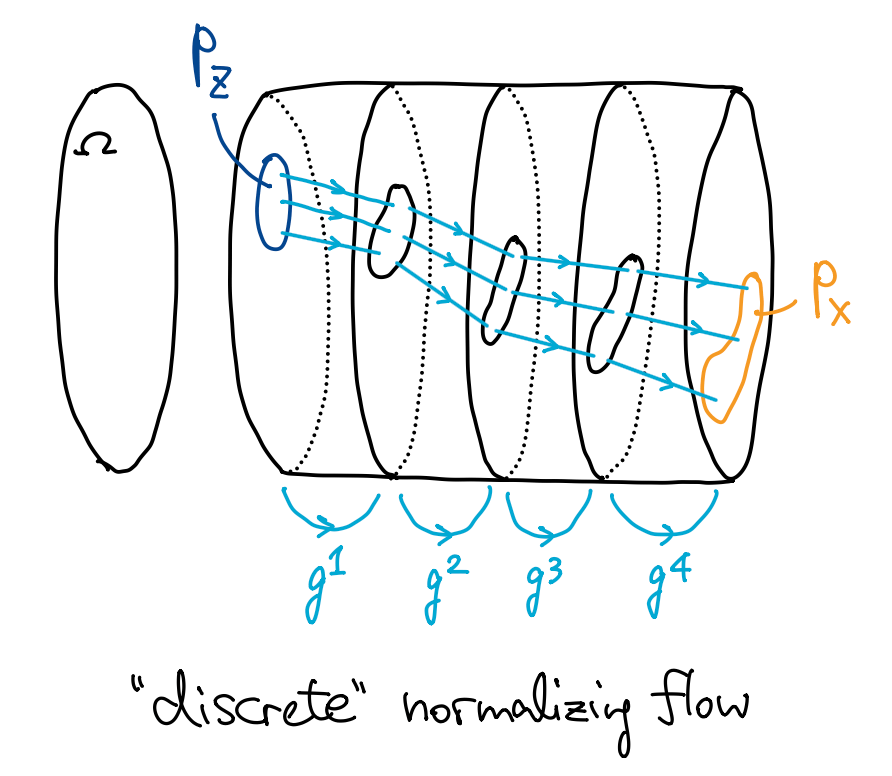
若以残差块 $g^l(z):=z+h(z;\theta^l)$ (其中每一层的结构相同, 但是参数 $\theta^l$ 不同) 作为每一层的映射, 则 DNF 可以写成一个迭代过程 \[ \Cases{ z^{l+1} = z^l + h(z^l;\theta^l), \\ z^0 \textsf{ 为给定的初始值}, } \] 当层数 $L$ 足够多且残差映射 $h$ 的输出足够小, 则该迭代过程实际上是在求解下面的初值问题: \[ \Cases{ \displaystyle \eval{\dv{z}{t}}_t = V_\theta(z(t),t), \\ z(t_0)=z_0 \textsf{ 为给定的初始值}, } \tag{$\clubsuit$} \] (使用 Euler 迭代法), 其中 $t$ 的取值范围是区间 $I\subset\R$, 映射 $V_\theta(z,t)$ 连续可微.

这里简单回顾常微分方程 (ODE) 理论. 式 $(\clubsuit)$ 是一个一阶非自治常微分方程. 映射 \[ V_\theta(-,-):\Omega\times I\to\R^N \] 称为该 ODE $(\clubsuit)$ 的向量场 (vector field), 如下图左侧.

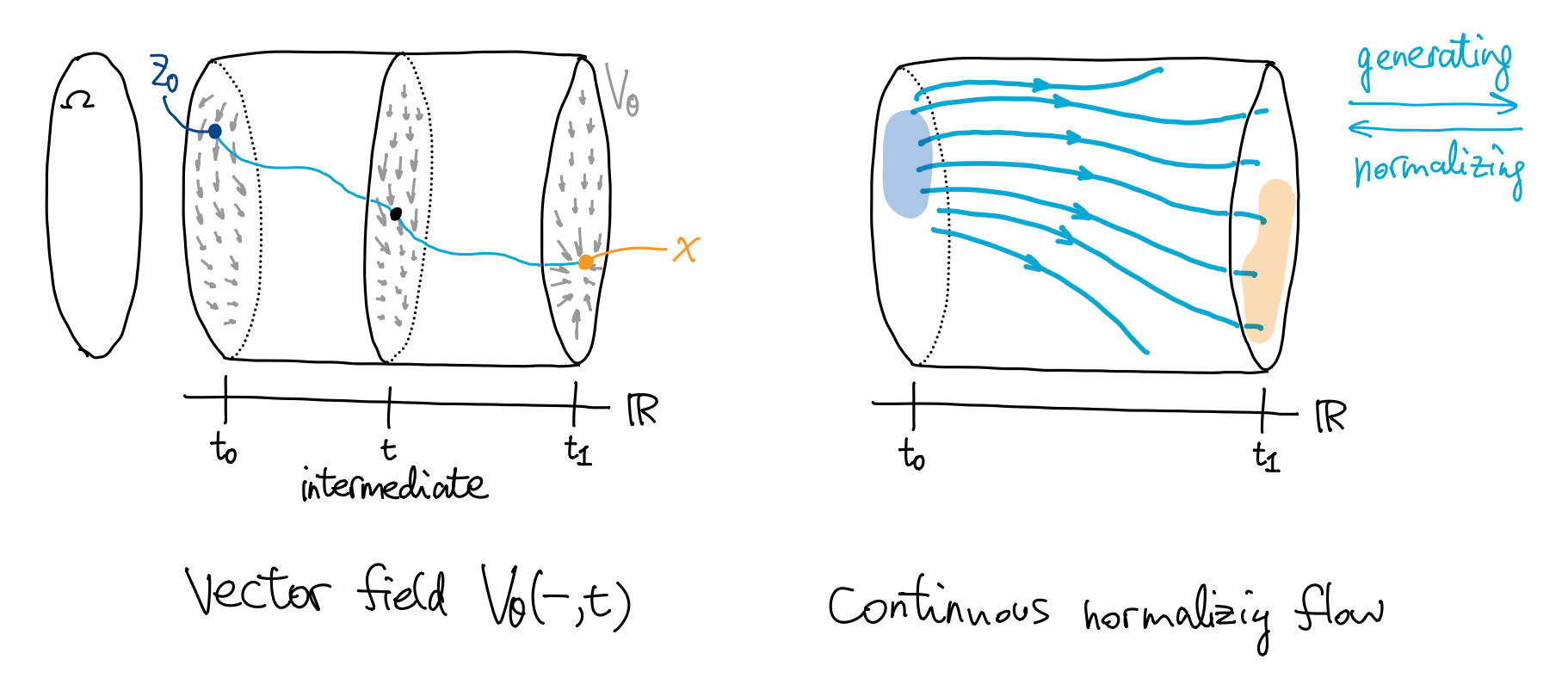
我们有如下定理: 当 $V_\theta$ 连续可微 ($C^1$) 时,

(存在性) 任给 $p\in\Omega$ 和 $t\in I$, 存在包含 $t$ 的区间 $I_0\subset I$ 以及 $p$ 的邻域 $U_0\subset\Omega$, 使得对任意初值 $z_0\in U_0$ 和初始时刻 $t_0\in I$, 存在初值问题 $(\clubsuit)$ 的解 $z:I\to\Omega$.
(唯一性) 两条积分曲线在公共部分重合.
(对初值的光滑依赖性) 记号承上, 定义 $\Phi:I_0\times I_0\times U\to\Omega$, \[ \Phi(t,t_0,z_0) := z(t), \] 其中 $z$ 是以 $z(t_0)=z_0$ 为初值的唯一积分曲线. 则 $\Phi$ 是 $C^1$ 的.

映射 $\Phi$ 称为向量场 $F_\theta$ 的流 (flow), 如上图右侧.

直观上, 固定开始时刻 $t_0$ 不变, 则随着 $t$ 变化, $\Phi(t,t_0,z_0)$ 让 $U$ 中的所有 $z_0$ 光滑地 “流动” 起来.
根据初值问题解的唯一性, 映射 $z_0\mapsto\Phi(t_1,t_0,z_0)$ 是可逆的, 逆为 $z_1\mapsto\Phi(t_0,t_1,z_1)$. 正向流表示生成过程; 逆向流表示归一化过程.

现在我们引入连续归一化流 (CNF)Ricky T. Q. Chen et al, Neural Ordinary Differential Equations, NeurIPS 2018.^[4]. DNF 建模的是 Euler 迭代过程 $h(-,\theta)$, 而 CNF 直接建模向量场 $F_\theta$. DNF 和 CNF 从不同的角度建模了同一个初值问题 $(\clubsuit)$.

Note CNF vs DNF.

CNF 建模的是迭代过程 $h(-,\theta)$, 也即流 $\Phi(t,t_0,z_0)$, 这要求神经网络必须是可逆的; 而 DNF 建模向量场 $V_\theta$, 只要它满足适当的光滑性条件, 根据存在唯一性定理, 对应的流 $\Phi$ 必定是可逆的, 因此 CNF 的网络比 DNF 灵活得多.

12.2 CNFs

CNF 的训练和采样流程与 DNF 基本相同:

	DNF	CNF
训练	① 根据 $p_Z$ 和 $V_\theta$ 计算出 $p_X$	① 根据 $p_Z$ 和 $g_\theta$ 计算出 $p_X$
	② 利用 $p_X$ 计算似然, 用 MLE 优化 $\theta$	② 利用 $p_X$ 计算似然, 用 MLE 优化 $\theta$
采样	① 从 $p_Z$ 采样噪声 $z_0\in\Omega$	① 从 $p_Z$ 采样噪声 $z_0\in\Omega$
	② 求解初值问题, 得到 $x:=\Phi(t_1,t_0,z_0)$	② 前向传播, 得到 $x:=(g^L_\theta\circ\dots\circ g^1_\theta)(z_0)$

对于 CNF, 我们有如下连续版本的 “变量替换定理” (推导见后文): \[ \pdv{\log{p_t(z(t))}}{t} = -\tr\biggl( \eval{\pdv{V_\theta}{z}}_{z(t),t} \biggr), \] 积分得到 \[ \Align{ \log{p_X(x)} = \log{p_{t_1}(z(t_1))} &= \log{p_{t_0}(t)} + \int_{t_0}^{t_1} \pdv{\log{p_t(z(t))}}{t} \dd{t} \\ &= \log{p_{Z}(z_0)} - \int_{t_0}^{t_1} \tr\biggl( \eval{\pdv{V_\theta}{z}}_{z(t),t} \biggr) \dd{t}. } \] CNF 的训练目标是最大化 $\log p_X(x)$, 即找到一个速度场 $V_\theta$, 使得:

起点密度高: $\log p_Z(z_0)$ 较高.
体积收缩: 积分项 $\int \dots \dd{t}$ 较小, 或最好为负值 (对应于体积收缩).

积分项中需要代入积分曲线 $z(t)$ 在每一时刻的值, 我们可以使用 ODE 求解器 (如 Runge-Kutta 方法) 来逼近流线 $z(t)$.

我们还需要计算 $z(t)$ 关于参数 $\theta$ 的梯度, 然而 $z(t)$ 是 ODE 求解器的输出, 不好直接进行反向传播. 原文采用了 adjoint sensitivity method.

CNF 的优势:

可以使用任何复杂网络拟合向量场 (不必是可逆的, 也不必易于计算 Jacobian), 表达能力强.
MLE 中根据 $x$ 计算 $z_0$ 的过程 (归一化) 与生成过程计算代价相同.

Pf 变量替换定理.

直观: CNF 版本的变量替换定理是 DNF 版本在 “$\Delta t\to0$” 下的 “极限”, 可以理解为在无穷小变换下, 概率密度的变化率.
迹 $\tr$ 是行列式 $\det$ 的 “微分” (改变量无穷小时的线性近似), 因此 CNF 版本中是 $\tr$ 而非 $\det$.

记 $p_t$ 是 $t_0$ 时刻的初始分布 $p_Z$ 被流 $z\mapsto\Phi(t,t_0,z)$ 推得的分布. 考虑 $p_t$ 与 $p_{t+\varepsilon}$, 满足

$p_{t+\varepsilon}$ 是 $p_t$ 被微分同胚 $T_\varepsilon:z\mapsto\Phi(t+\varepsilon,t,z)$ 推得的.

根据 (离散) 变量替换定理有 \[ \Align{ \log{p_{t+\varepsilon}(z(t+\varepsilon))} - \log{p_t(z(t))} &= \log\Biggl| \biggl( \det \eval{ \pdv{T_\varepsilon}{z} }_{z(t)} \biggr)^{\!\!-1} \Biggr| \\ &= -\log\Biggl| \det \eval{ \pdv{T_\varepsilon}{z} }_{z(t)} \Biggr|. \\ } \] 根据定义有 \[ \Align{ T_\varepsilon\bigl[z(t)\bigr] &= z(t+\varepsilon) \\ &= z(t) + \varepsilon V_\theta(z(t),t) + O(\varepsilon^2), } \] (其中 $\varepsilon\to0$) 即 $T_\varepsilon(-)=I+\varepsilon V_\theta(-,t)+O(\varepsilon^2)$. 代入变量替换定理得到 \[ \Align{ \log{p_{t+\varepsilon}(z(t+\varepsilon))} - \log{p_t(z(t))} &= -\blue{\log} \,\blue{\det} \biggl[ I + \varepsilon \eval{\pdv{V_\theta}{z}}_{z(t),t} + O(\varepsilon^2) \biggr] \\ &= -\blue{\log} \biggl[ 1 + \varepsilon \,\blue{\tr} \eval{\pdv{V_\theta}{z}}_{z(t),t} + O(\varepsilon^2) \biggr] \\ &= -\biggl[ \varepsilon \,\blue{\tr} \eval{\pdv{V_\theta}{z}}_{z(t),t} + O(\varepsilon^2) \biggr]. } \] 利用导数的定义即得.

Danilo Jimenez Rezende, Shakir Mohamed, Variational Inference with Normalizing Flows, 2015.↩︎
本文的微分同胚都是 $C^1$ 的, 即 $g$ 可逆且 $g,g^{-1}$ 都连续可微.↩︎
Laurent Dinh et al, Density estimation using Real NVP, 2017.↩︎
Ricky T. Q. Chen et al, Neural Ordinary Differential Equations, NeurIPS 2018.↩︎

Note > Course

#机器学习

生成模型基础 | 5 归一化流

https://disembo.github.io/Note/Course/gen-models/5/

作者

jin

发布于

2025年11月2日

许可协议

生成模型基础 | 6 基于能量的模型上一篇

生成模型基础 | 4 生成对抗网络下一篇

	DNF	CNF
训练	① 根据 \(p_Z\) 和 \(V_\theta\) 计算出 \(p_X\)	① 根据 \(p_Z\) 和 \(g_\theta\) 计算出 \(p_X\)
	② 利用 \(p_X\) 计算似然, 用 MLE 优化 \(\theta\)	② 利用 \(p_X\) 计算似然, 用 MLE 优化 \(\theta\)
采样	① 从 \(p_Z\) 采样噪声 \(z_0\in\Omega\)	① 从 \(p_Z\) 采样噪声 \(z_0\in\Omega\)
	② 求解初值问题, 得到 \(x:=\Phi(t_1,t_0,z_0)\)	② 前向传播, 得到 \(x:=(g^L_\theta\circ\dots\circ g^1_\theta)(z_0)\)