生成模型基础 | 4 生成对抗网络

9 GAN

回顾第一节课对生成模型的引入:

什么是生成模型? 考虑一个随机数发生器, 它可以生成出服从 \([0,1]\) 上某个分布 \(p(x)\) 的伪随机数.

• 首先它会生成 \([0,1]\) 上服从均匀分布的伪随机数 \(z\);
• 然后通过一个映射 \(f:[0,1]\to[0,1]\) 将 \(z\) 映到服从分布 \(p(x)\) 的伪随机数 \(x=f(z)\) (其中 \(f=F^{-1}\), 而 \(F\) 是 \(p(x)\) 的累积分布函数).

换言之, 随机数发生器是将随机噪声映射到服从某一 (复杂) 分布的的东西.

GAN (生成对抗网络)Ian J. Goodfellow et al, Generative Adversarial Networks.^[1] 就模拟了这个过程. 它用一个神经网络拟合 \(f:z\mapsto x\), 这个神经网络叫做生成器 (generator), 记作 \(G_\theta\).

• VAE 实际上也是将噪声 (Gauss 分布) 映射到给定分布的神经网络, 然而由于结构上的限制 (VAE 不能太宽太深, 否则会导致后验崩塌), 它只能学习很简单的分布.

Note 生成模型分为显式 (explicit) 和隐式 (implicit) 两种, 区别在于是否直接建模了样本分布 \(p(x)\).

• Explicit: 直接建模 \(p_\theta(x)\), 可以计算每个样本的概率、可以通过 MLE \(\argmax_\theta\,p_\theta(\mathcal{D})\) 优化.
  • AR.
  • VAE, 优化 ELBO (作为似然函数的下界).
• Implicit: 不直接建模 \(p_\theta(x)\), 不能计算样本概率、无法通过 MLE 优化.
  • GAN.

9.1 Metics

GAN 是一种隐式模型, 它可以采样 \(x\), 但是无法计算 \(x\) 的概率. 假设我们有一些生成器生成的数据 \(\{\hat{x}_i\}\) 和真实样本 \(\{x_i\}\), 那么我们该如何衡量 GAN 生成的好坏? 我们需要衡量 GAN 生成的分布 \(p_\theta\) 和真实分布 \(p\) 间的距离.

两个分布 \(p(x),q(x)\) 的 \(f\)-散度 (\(f\)-divergence) 定义为 \[ \Align{ D_{f}(p\parallel q) :={}& \operatorname{E}_{x\sim q(x)} f\!\pqty{\frac{p(x)}{q(x)}} \\ ={}& \int_{\R^D} f\!\pqty{\frac{p(x)}{q(x)}} q(x)\dd{x}, } \] 其中函数 \(f:(0,+\infty)\to\R\) 满足 (1) \(f\) 非负, (2) \(f\) 下凸, (3) \(f(1)=0\).

• \(f\)-散度可以衡量 \(p,q\) 间的差异:

  • 由 Jensen 不等式, \(D_f(p\parallel q)\geq0\) 且 \(D_f(p\parallel q)=0\) 当且仅当 \(p=q\).

• 取 \(f(t)=t\log{t}\), 可以得到 KL 散度 \(D_{\textsf{KL}}\).

• 取 \(f(t)=\abs{t-1}/2\), 可以得到全变差距离 (total variation distance) \[ D_f(p\parallel q) = \frac12 \int_{\R^D} \abs{p(x)-q(x)}\dd{x}. \]

取 \(f(t)=\frac{t}{2}\log{t}-\frac{t+1}{2}\log\frac{t+1}{2}\), 可得 Jensen-Shannon 散度 (JS 散度) \[ D_{\textsf{JS}}(p\parallel q) := D_f(p\parallel q) = \frac{D_{\textsf{KL}}(p\parallel m) + D_{\textsf{KL}}(q\parallel m)}{2}, \] 其中 “中间分布” \(m(x)=[p(x)+q(x)]/2\).

• JS 散度的算数平方根 \(\sqrt{D_\textsf{JS}(-,-)}\) 是对称、正定的, 且满足三角不等式, 是一个距离度量.

9.2 The discriminator

我们用 JS 散度来衡量生成的分布 \(p_\theta\) 与真实分布 \(p\) 的距离, \[ \Align{ \min_{\theta} D_{\textsf{JS}}(p\parallel p_\theta) ={}& \min_{\theta} \bqty{ D_{\textsf{KL}}(p\parallel m) + D_{\textsf{KL}}(p_\theta\parallel m) } \\ \rightsquigarrow{}& \min_{\theta}\! \bqty{ \operatorname{E}_{x\sim p}\! \pqty{ \log \orange{\frac{p(x)}{p(x)+p_\theta(x)}} } + \operatorname{E}_{x\sim p_\theta}\! \pqty{ \log \orange{\frac{p_\theta(x)}{p(x)+p_\theta(x)}} } }. } \] (略去了 \(\log\) 分子上的常数 \(2\).) 但是我们既没法计算 \(p_\theta(x)\) (因为 GAN 是一个隐式模型), 更没法计算 \(p(x)\) (否则也不需要建模了).

• 可以发现两个橙色的分式和为 \(1\). 我们来分析一下前者, \(\dfrac{p(x)}{p(x)+p_\theta(x)}\in(0,1)\),
  • 如果 \(\dfrac{p(x)}{p(x)+p_\theta(x)}\) 接近 \(1\), 那么 \(x\) 就更有可能来自于真实样本, 而非 \(G_\theta\).
  • 如果 \(\dfrac{p(x)}{p(x)+p_\theta(x)}\) 接近 \(0\), 那么 \(x\) 就更有可能来自于 \(G_\theta\), 而非真实样本.

我们不妨构造一个二分类器 \(D_\phi(x)\), 它的目的是区分 \(x\) 来源于真实样本还是 \(G_\theta\) (分别对应 \(1/0\)), 它可以近似 \(\dfrac{p(x)}{p(x)+p_\theta(x)}\). 这个 \(D_\phi\) 叫做判别器 (discriminator).

• 引入判别器的目的是计算橙色的分式, 进而计算 JS 散度.

此时生成器 \(G_\theta\) 的训练目标写作 \[ \Align{ \min_{\theta} D_{\textsf{JS}}(p\parallel p_\theta) \rightsquigarrow{}& \min_\theta \Bigl[ \operatorname{E}_{x\sim p} \log\orange{D_\phi(x)} + \operatorname{E}_{x\sim p_\theta} \log\bigl(1-\orange{D_\phi(x)}\bigr) \Bigr] \\ ={}& \min_\theta \Bigl[ \operatorname{E}_{x\sim p} \log\orange{D_\phi(x)} + \operatorname{E}_{z\sim\mathcal{N}(0,I)} \log\bigl(1-\orange{D_\phi(\purple{G_\theta(z)})}\bigr) \Bigr], \\ } \] 而判别器 \(D_\phi\) 的训练目标是最大化分类效益 (负的交叉熵) \[ \max_\phi \Bigl[ \operatorname{E}_{x\sim p} \log\orange{D_\phi(x)} + \operatorname{E}_{z\sim\mathcal{N}(0,I)} \log\bigl(1-\orange{D_\phi(\purple{G_\theta(z)})}\bigr) \Bigr]. \] 因此, 生成器和判别器实际上在进行一个对抗 (“minimax game”), \[ \min_\theta \max_\phi \Bigl[ \operatorname{E}_{x\sim p} \log\orange{D_\phi(x)} + \operatorname{E}_{z\sim\mathcal{N}(0,I)} \log\bigl(1-\orange{D_\phi(\purple{G_\theta(z)})}\bigr) \Bigr], \] 这就是 GAN (生成对抗网络) 名称的来源.

9.3 Adversial training

在实际训练中, 我们交替优化 \(D_\phi\) 和 \(G_\theta\). 重复执行:

• 从生成器中采样 \(\hat{x}_i\sim G_\theta(z_i)\), 其中 \(z_i\sim\mathcal{N}(0,I)\).

• 从真实样本中采样 \(x_i\).

• 优化判别器 (梯度上升), \[ \max_\phi \Bigl[ \sum_i \log\orange{D_\phi(x_i)} + \sum_i \log\bigl(1-\orange{D_\phi(\hat{x}_i)}\bigr) \Bigr]. \]

• 优化生成器 (梯度下降), \[ \min_\theta \sum_i \log\bigl(1-D_\phi(\purple{G_\theta(z_i)})\bigr). \]

在训练初期, 生成器比较弱, 判别器能很有信心地对 \(G_\theta(z)\) 给出 \(0\), 这就导致生成器的梯度接近零. 将梯度根据链式法则展开, \[ \eval{\pdv{\mathcal{L}}{\theta}}_\theta = -\frac{1}{1-D_\phi(G_\theta(z))} \cdot \underbrace{ \eval{\pdv{D_\phi}{x}}_{G_\theta(z)} }_{\textsf{saturates}} \cdot \eval{\pdv{G_\theta}{\theta}}_\theta, \]

注意 “saturates” 的那一项: 训练初期生成器生成的都是很烂的图, 因此在 \(G_\theta(z)\) 的小邻域内, 图片的质量都很差、判别器取值几乎恒为 \(0\) (饱和), 因此 \[ \eval{\pdv{D_\phi}{x}}_{G_\theta(z)} \approx 0, \] 进而 \(\partial\mathcal{L}/\partial\theta\approx0\). 梯度接近零的后果是 \(G_\theta\) 无法得到更新. 所以在训练初期我们转而优化 \[ \max_\theta \sum_i \log\bigl(D_\phi(\purple{G_\theta(z_i)})\bigr). \]

GAN 很难训练.

• 非凸优化问题.
• 生成器和判别器要匹配.
  • 两则必须同步学习, 并且学习速度差不多
• 模式崩溃 (mode collapse).
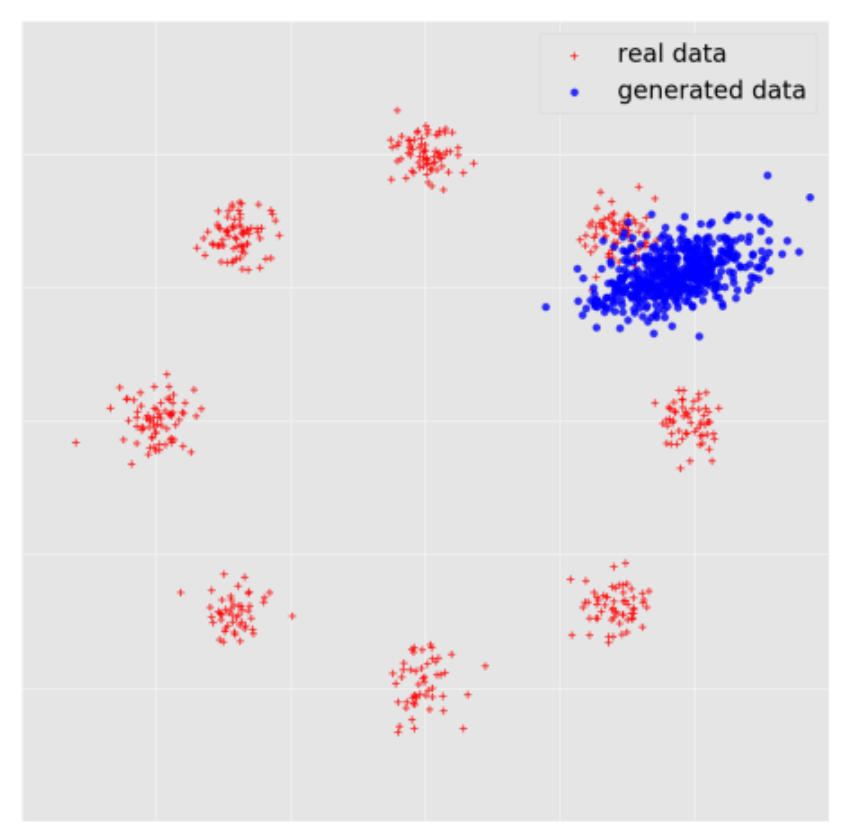
  • 生成器只能生成训练集中很少的一部分样本 (某一个 / 几个 modes), 如下图.
  • 例如在 MNIST 数据集上训练 GAN, 结果 GAN 只会生成数字 1, 尽管生成的很像 (损失很低).

10 WGAN

10.1 *Problems with GANs

在上一节末尾, 我们说了 GAN 很难训练. 下面我们详细分析一下不好训练的原因. 更细致的讨论可见这篇分析 GAN 的论文Martin Arjovsky, Léon Bottou, Towards Principled Methods for Training Generative Adversarial Networks.^[2]以及 WGAN 的论文Martin Arjovsky, Soumith Chintala, Léon Bottouu. Wasserstein GAN.^[3].

梯度消失 & 模式崩溃. 考虑均匀分布 \(p\sim U[0,1]\) 以及 \(p_\theta\sim U[\theta,\theta+1]\), 则两者的 JS 散度为 \[ D_{\textsf{JS}}(p\parallel p_\theta) = \Cases{ \abs{\theta}\ln2, & \abs{\theta}\leq1, \\ \ln{2}, & \abs{\theta}>1, } \] 可以发现, 当 \(p,p_\theta\) 的不重叠时, JS 散度饱和到了 \(\ln{2}\), 无法提供梯度. 对于模式崩溃问题, 如果 \(G_\theta\) 坍缩到一个模式, JS 散度容易像上面的例子中一样饱和.

设 \(p,p_\theta\) 的支集分别包含于 \(\R^N\) 的子流形 \(M,M_\theta\). 那么, 只要

1. \(M,M_\theta\) 在 \(\R^N\) 中是零测的;
2. 交集 \(S=M\cap M_\theta\) 在 \(M,M_\theta\) 中都为零测的,

那么 JS 散度必然是饱和的. 此时存在一个理想的判别器 \(D^*\), 它对于来自 \(p_\theta\) 的样本 (几乎) 总是给出 \(0\), 生成器的梯度消失了.

• 一般来说, 有意义的数据点组成的子流形 \(M\) 维数严格小于 \(\R^N\).
• 神经网络 \(G_\theta\) 是分片光滑嵌入. 假设生成器 \(G_\theta\) 的输入 \(z\) 是 \(Z=\R^D\) 上的随机噪声, 那么当 \(D<N\) 时, 像 \(G_\theta(Z)\) 由若干维数至多为 \(D\) 的子流形组成, 在 \(\R^N\) 中零测.
• 根据横截相交理论, 两个子流形 \(M,M_\theta\) 的交集几乎总是零测的.

换言之, 条件 1, 2 非常容易满足, 因此 GAN 的训练非常容易遇到梯度消失.

JS 散度可能不连续. 考虑一个更特殊的例子, 设 \(\eta\sim U[0,1]\), 考虑 \(\R^2\) 上平行于 \(y\) 轴的线段 \(p=(0,p_\eta)\) 以及 \(p_\theta=(\theta,p_\eta)\). 两者的 JS 散度为 \[ D_{\textsf{JS}}(p\parallel p_\theta) = \Cases{ \ln2,&\theta=0, \\ 0,&\theta\neq0, } \] 即只有两者重合时才有非零值, 在原点处不连续.

取 \(\R^N\) 的一个紧子集 \(K\) (比如图像空间 \([0,1]^N\)), 考虑 \(K\) 上的概率密度组成的集合 \(\operatorname{Prob}(K)\).

损失函数不连续的原因是 JS 散度诱导的 \(\operatorname{Prob}(K)\) 上的度量拓扑太强了, 导致参数化 \[ \theta\mapsto p_\theta \] 在 JS 散度意义下不连续. 解决办法是找一个弱一些的度量, 比如 Wasserstein 距离.

修改后的优化目标不稳定. 考虑修改后的 \(G_\theta\) 的优化目标 \[ \max_\theta \operatorname{E}_{z\sim\mathcal{N}(0,I)} \log\bigl(\orange{D_\phi(\purple{G_\theta(z)})}\bigr), \] 对 \(\log(\cdots)\) 求梯度, 并根据链式法则展开, \[ \Align{ \eval{\pdv{\mathcal{L}}{\theta}}_\theta = \frac{1}{D_\phi(G_\theta(z))} \cdot \eval{\pdv{D_\phi}{x}}_{G_\theta(z)} \cdot \eval{\pdv{G_\theta}{\theta}}_{\theta}. } \] 当判别器 \(D_\phi\) 比较接近理想判别器 \(D^*\) 时, 可以假设

• 差值 \(D_\phi-D^*\) 是一个 Gauss 过程,
• 梯度的差值 \(\partial{D_\phi}/\partial{x}-\partial{D^*}/\partial{x}\) 也是一个 Gauss 过程,

并且这两个随机过程对 \(x\) 的各个分量独立. 此时有

• 分母上的 \(D_\phi(G_\theta(z))\) 是一个均值为零的 Gauss 分布,
• 第二项 \((\partial{D_\phi}/\partial{x})|_{G_\theta(z)}\) 也是一个均值为零的 Gauss 分布,

两个 Gauss 分布无关, 因此商 \(\partial\mathcal{L}/\partial\theta\) 服从 Cauchy 分布, 均值和方差均为无穷大, 这带来了数值不稳定性.

10.2 Wasserstein distance

考虑另一种概率分布间的距离度量.

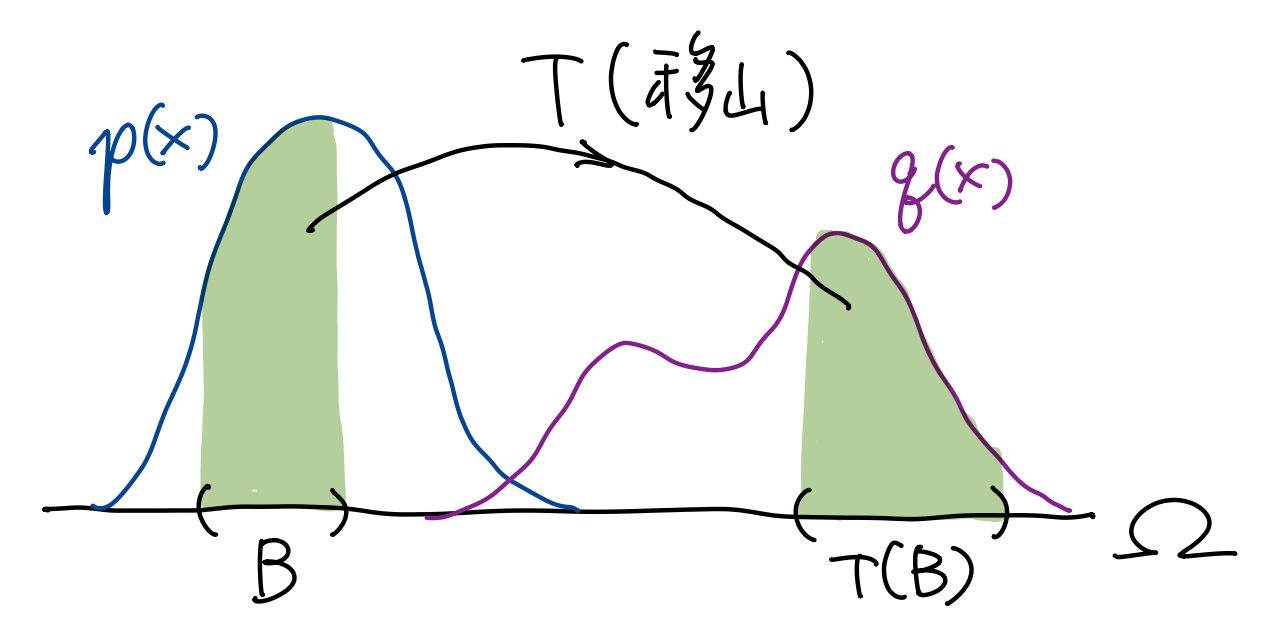
设开集 \(\Omega\subset\R^N\) 上的概率分布 \(p,q\). 一种很直接的方法是将概率密度 \(p(x)\) 全部 “搬” 到概率密度 \(q(x)\), 好比愚公移山. 考虑这个 “移山” 过程中搬运代价的最小值. 如上图, 设映射 \(T:U\to U\), 它将 \(x\) 处的质量搬到 \(T(x)\). 为了保证质量不增不减, 应有 \[ \int_B p(x)\dd{x} = \int_{T(B)}q(x)\dd{x}, \] 对于任意 Borel 集 \(B\subset\Omega\) (即绿色部分面积相等). 此时记 \(q=T_*p\)严格来说, 记号 \(T_*\) (推前) 应当作于概率测度, 而非概率密度. 这里 abuse notation 了.^[4]. 假设将 \(x\in\Omega\) 处的质量搬到 \(y\in\Omega\) 的代价为 \(c(x,y)\), 则 \(T\) 的总代价为 \[ E(T) := \int_\Omega c(x,T(x)) \, p(x) \dd{x}. \] 分布 \(p,q\) 间的距离可以用总代价的最小值刻画: \[ W(p,q) := \inf_{q=T_*p} E(T), \] 即 \(p,q\) 间的 Wasserstein 距离. 取欧氏距离 \(c(x,y)=\|x-y\|\) 时, \(W(p,q)\) 也称为推土机距离 (earth mover's distance, EMD).

Note 我们看看 EMD 是如何解决 JS 散度的几个问题的.

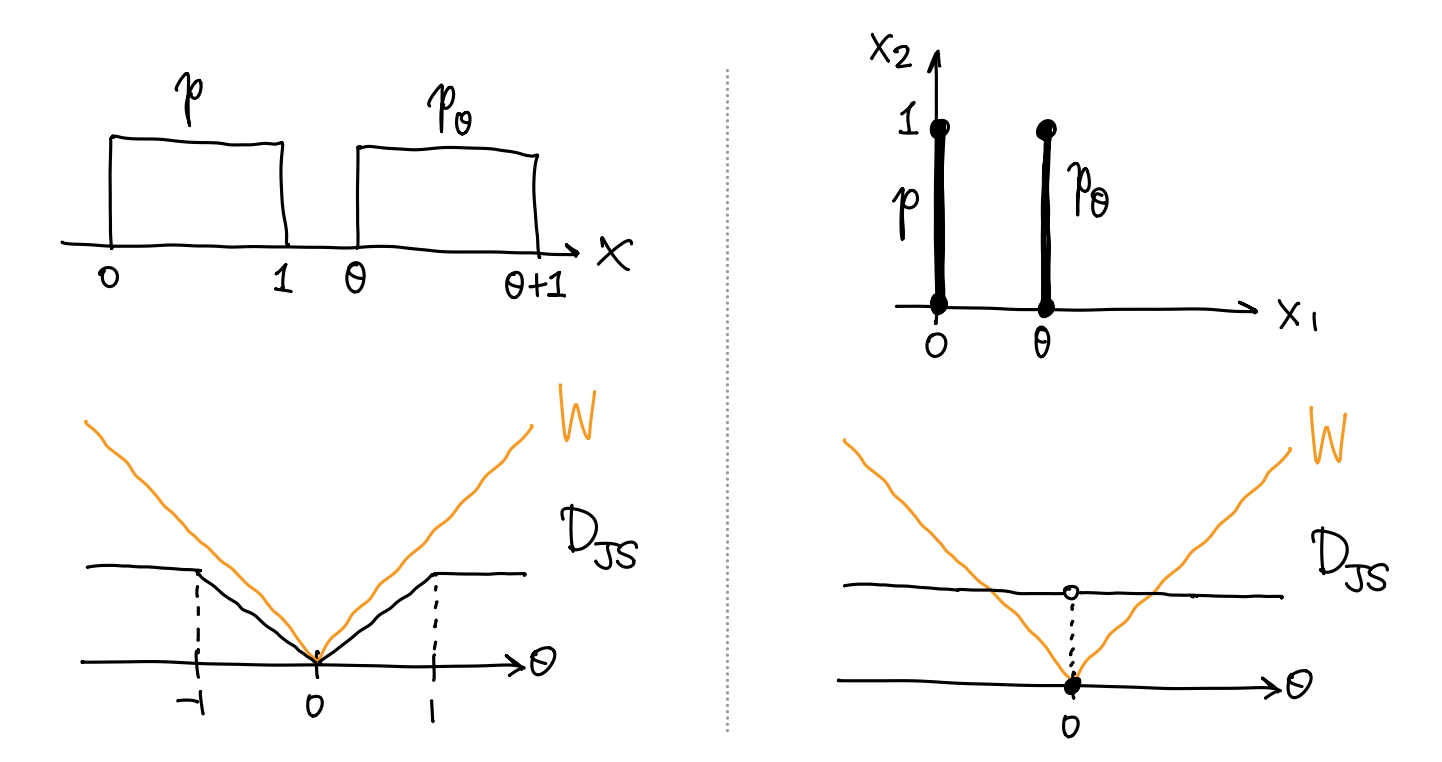
• 梯度消失 / 损失函数不连续. 对于上一小节给出的均匀分布 \(p,p_\theta\) 的例子, 均有 \[ W(p,p_\theta) = \abs{\theta}, \] 如上图. 实际上, WGAN 的论文证明了 \(W(p,p_\theta)\) 关于 \(\theta\) 连续, 且几乎处处可微后者成立当 \(p_\theta\) 关于 \(\theta\) 是局部 Lipschitz 时.^[5].

• 模式崩溃. 当 \(G_\theta\) 坍缩到一个模式时, EMD 会给出较大的惩罚, 并且这个惩罚与距离分布密度间的欧氏距离相关.

从定义来看, EMD 很难算 (满足 \(T_*p=q\) 的映射 \(T\) 不好找). 好在我们有 Kantorovich-Rubinstein 对偶, 即 \[ W(p,q) = \sup_{f\in\operatorname{Lip}(\Omega)} \Bigl( \operatorname{E}_{x\sim p} [f(x)] - \operatorname{E}_{x\sim q} [f(x)] \Bigr), \] 其中 \(\operatorname{Lip}_1(\Omega)\) 是 \(\Omega\) 上所有 \(1\)-Lipschitz 函数组成的集合若存在常数 \(L>0\) 使得 \(\|f(x)-f(y)\|\leq L\|x-y\|\) 对任意 \(x,y\in\Omega\), 则 \(f\) 称为 \(L\)-Lipschitz 的.^[6].

10.3 WGAN

我们使用 EMD 衡量生成分布 \(p_\theta\) 与真实分布 \(p\) 的距离, \[ \Align{ \min_\theta W(p,p_\theta) &= \min_\theta \sup_{f\in\operatorname{Lip}(\Omega)} \Bigl( \operatorname{E}_{x\sim p} [f(x)] - \operatorname{E}_{x\sim p_\theta} [f(x)] \Bigr) \\ &= \min_\theta \sup_{f\in\operatorname{Lip}(\Omega)} \Bigl( \operatorname{E}_{x\sim p} [f(x)] - \operatorname{E}_{z\sim\mathcal{N}(0,I)} [f(\purple{G_\theta(z)})] \Bigr). } \] 还有一个问题, 这里要取遍所有 Lipschitz 函数, 在实现上当然做不到. 所以我们引入另外一个神经网络 \(f_\phi\) 来拟合 Lipschitz 函数, \[ \Align{ \min_\theta W(p,p_\theta) \rightsquigarrow{}& \min_\theta \max_{\phi} \Bigl( \operatorname{E}_{x\sim p} [\orange{f_\phi(x)}] - \operatorname{E}_{z\sim\mathcal{N}(0,I)} [ \orange{f_\phi(\purple{G_\theta(z)})} ] \Bigr), } \] 其中 \(f_\phi\) 的优化目标是最大化括号里的东西, 当 \(f_\phi\) 达到最优时, 括号里的东西恰好就是 EMD. 因此 \(f_\phi\) 的目的就是帮我们计算 EMD. 原论文把 \(f_\phi\) 叫做评论家 (critic).

当然, 我们还需要保证 \(f_\phi\) 是 \(1\)-Lipschitz 的实际上, \(f\) 也可以是 \(L\)-Lipschitz 函数 (对于任何给定的 \(L>0\)). 此时算出来的 \(\sup_f(\cdots)\) 是 \(L\) 倍的 EMD, 与 EMD 有相同的极值点. WGAN 原论文用 weight clipping 粗暴地保证了 \(k\)-Lipschitz 性质.^[7].

• 连续可微函数 \(f_\phi\) 是 Lipschitz 连续的, 当且仅当梯度模长 \(\|\nabla_\phi f_\phi\|_2\) 处处不大于 \(1\).

因此, 可以在优化目标中加入一项梯度惩罚 (gradient penalty)Ishaan Gulrajani, Faruk Ahmed, Martin Arjovsky, Vincent Dumoulin, Aaron Courville, Improved Training of Wasserstein GANs.^[8], \[ \Align{ \min_\theta \max_{\phi} \Bigl\{ \operatorname{E}_{x\sim p} [\orange{f_\phi(x)}] - \operatorname{E}_{z\sim\mathcal{N}(0,I)} [ \orange{f_\phi(\purple{G_\theta(z)})} ] - \underbrace{ \lambda \operatorname{E}_{\zeta\sim p_\zeta} \Bigl[ \bigl( \|\orange{\nabla_\phi f_\phi(\zeta)}\|_2 - 1 \bigr)^2 \Bigr] }_{\textsf{gradient penalty}} \Bigr\}, } \] 其中 \(\zeta\sim p_\zeta\) 是随机噪声, 用来估计梯度 \(\|\nabla_\phi f_\phi\|_2\). 梯度惩罚项让 \(\|\nabla_\phi f_\phi\|_2\) 尽量接近 \(1\).

Note GAN 的设计总结.

• GAN 是一种隐式模型, 用一个神经网络 \(G_\theta\) 采样.
• 我们需要衡量 \(G_\theta\) 的分布与真实分布的差距, 作为指标.
• 引入了概率分布间的距离.
• 距离没法直接算, 需要引入另一个神经网络 (\(D_\phi,f_\phi,\dots\))
• 两个神经网络对抗训练.

---

1. Ian J. Goodfellow et al, Generative Adversarial Networks.↩︎

2. Martin Arjovsky, Léon Bottou, Towards Principled Methods for Training Generative Adversarial Networks.↩︎

3. Martin Arjovsky, Soumith Chintala, Léon Bottouu. Wasserstein GAN.↩︎

4. 严格来说, 记号 \(T_*\) (推前) 应当作于概率测度, 而非概率密度. 这里 abuse notation 了.↩︎

5. 后者成立当 \(p_\theta\) 关于 \(\theta\) 是局部 Lipschitz 时.↩︎

6. 若存在常数 \(L>0\) 使得 \(\|f(x)-f(y)\|\leq L\|x-y\|\) 对任意 \(x,y\in\Omega\), 则 \(f\) 称为 \(L\)-Lipschitz 的.↩︎

7. 实际上, \(f\) 也可以是 \(L\)-Lipschitz 函数 (对于任何给定的 \(L>0\)). 此时算出来的 \(\sup_f(\cdots)\) 是 \(L\) 倍的 EMD, 与 EMD 有相同的极值点. WGAN 原论文用 weight clipping 粗暴地保证了 \(k\)-Lipschitz 性质.↩︎

8. Ishaan Gulrajani, Faruk Ahmed, Martin Arjovsky, Vincent Dumoulin, Aaron Courville, Improved Training of Wasserstein GANs.↩︎