生成模型基础 | 3 自回归模型
7 自回归模型
设数据为高维向量 \(x=(x_1,\cdots,x_L)\in\R^L\), 我们的目的是建模 \(p(X=x)\). 这是一个很大很大的联合分布, 考虑用链式法则展开: \[ \Align{ p(X=x) &= p(X_1=x_1,\dots,X_D=x_D) \\ &= p(X_1=x_1) \prod_{i=2}^L p(X_i=x_i \mid X_1=x_1,\dots,X_{i-1}=x_{i-1}). } \] 如果我们有一个模型可以建模 \(p_\theta(x_i\mid x_2,\dots,x_{i-1})\) 以及 \(p_\theta(x_1)\), 那么就有了 \(p_\theta(x)\). 这就是自回归模型 (autoregressive models). “自回归” 指的是将当前步骤的中间结果 \((x_1,\dots,x_i)\) 再送回模型生成 \(x_{i+1}\) 的过程.
分解 (factorization) 的顺序多种多样, 对于自然语言来说, 可以是从左到右、从右到左, 甚至是随机顺序. 对于图片来说, 可以是扫描序、蛇形曲线、Z 字型曲线、随机序……
- 一些语言, 比如中文、英语, 一般用使用从左到右顺序建模 (根据前面的词预测下一个词); 另一些语言, 比如日语, 可能使用从右到左的顺序建模比较好: \(p_\theta(X_i\mid X_{i+1}=x_{i+1},\dots,X_L=x_L)\) (根据后面的词预测上一个词).
自回归模型是目前 NLP 领域最先进、最成功的范式, 后面主要介绍 NLP 领域的自回归模型.
7.1 N-gram models
N-gram 是一种远古的非参数化方法
- 一个 \((k+1)\)-gram 模型实际上需要包含所有 \(1,2,\dots,(k+1)\)-gram 的出现概率, 因为链式法则 \[ p(x_1,\dots,x_n) = \blue{p(x_1)p(x_2\mid x_1)\cdots p(x_k\mid x_{1:k-1})} \prod_{i=k+1}^L p(x_i\mid x_{1:i-1}) \] 需要起始条件.
使用 MLE 估计参数为 \[ p(x_{i:i+k}) = \frac {\textsf{数据中 }(x_{i:i+k})\textsf{ 的数量}} {\textsf{数据中所有 }k\textsf{-gram 的数量}} \] 等等.
N-gram 的问题:
- 当 \(N\) 比较小, 上下文长度太短, 生成的准确率很低.
- 当 \(N\) 比较大, 参数个数以及存储空间大幅度上升. 并且因为训练数据有限, N-gram 的概率非常稀疏, 意味着大部分概率 \(p(x_{i:i+k})\) 都为零, 生成的质量反而可能下降.
7.2 Fixed-window neural LM
自回归建模不变, Markov 假设也不变, 只不过不要数数 (counting)——而是用参数化的神经网络 \[ p_\theta(x_i\mid x_{i-k:i-1}). \]
首先将这 \(k\) 个 tokens 转化为嵌入向量 \(e_i\in\R^D\), 再经过一个隐藏层 (线性映射+激活, 视作上下文整合), 最后经过一个线性层和 softmax 转化为下一个 token \(x_i\) 的概率分布.
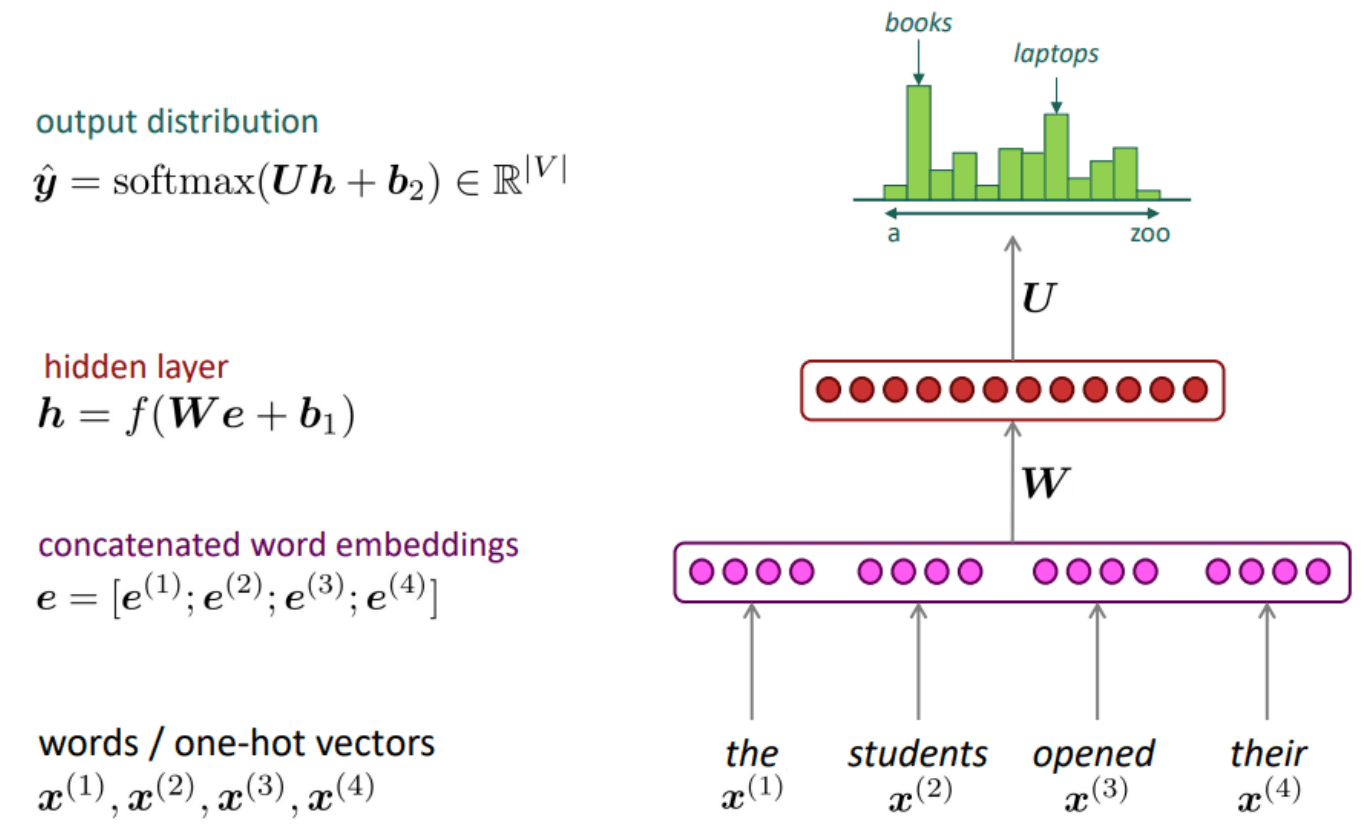
It is still an N-gram LM, but why it works better?
- 多层的结构使得特征可以组合.
- We can search through a lot more conjunctive features through high dimensional feature representations, especially for neural models the amazing word embeddings!
- 可以同时训练词嵌入和 FFNN.
然而, 该网络并未解决上下文不足的问题.
7.3 RNNs
能否构造一个神经网络, 其可以处理任意长度的上下文?
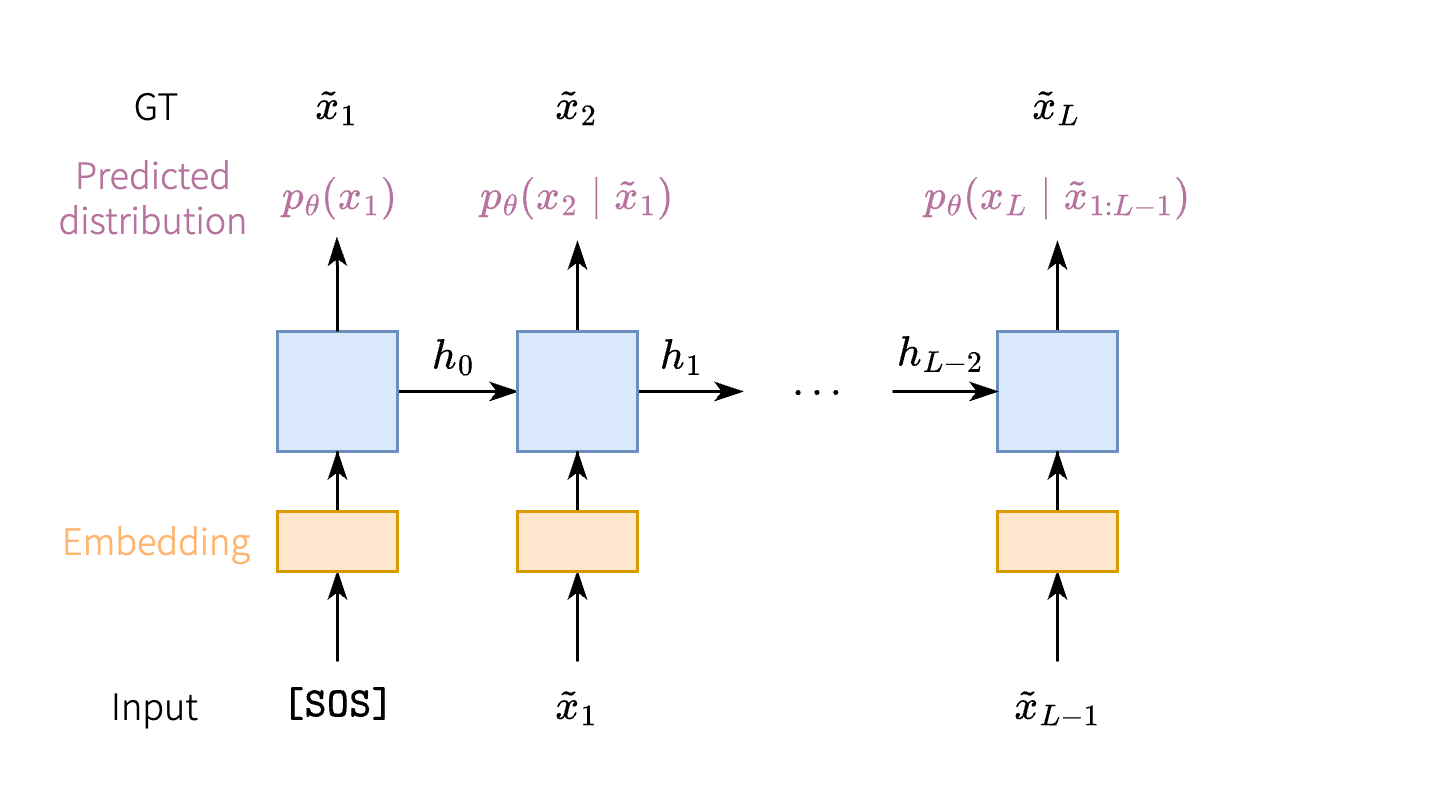
RNN (recurrent neural network) 是一个序列到序列的映射 \((x_t)\mapsto(y_t)\), 它用一个隐状态 \(\orange{h_t}\) 记忆所有的历史输入, 并不断地用当前的输入 \(x_t\) 更新这个隐状态: \[ \orange{h_t} = f_\theta(\orange{h_{t-1}},x_t), \] 更新后的隐状态经过一个映射得到当前输出, \[ y_t = g_\theta(\orange{h_t}). \] 如何用 RNN 进行自回归建模呢? 首先输入一个特殊的开始标记 \(\tilde{x}_0=\texttt{[SOS]}\) (start of sequence) 让 RNN 输出 \(x_1\), 再把 \(x_1\) 喂给 RNN 让它生成 \(x_2\), 以此类推…… 便实现了自回归生成.
如何训练 RNN? 对于一条训练数据 \((\tilde{x}_i)\in\R^L\), 依次给模型输入
\(\tilde{x}_0,\tilde{x}_1,\dots,\tilde{x}_{L-1}\),
RNN 会依次输出 token 概率分布的预测值 \(p_\theta(x_1),p_\theta(x_2\mid\tilde{x}_1),\dots,p_\theta(x_L\mid\tilde{x}_{1:L-1})\),
如下图所示. 可以使用 MLE 进行参数学习, 即最小化负对数似然 (NLL) \[
\Align{
\operatorname{NLL}(\tilde{x};\theta)
&= -\log{p_\theta(\tilde{x})} \\
&= -\log{p_\theta(x_1)}
-\sum_{i=2}^L \log{p_\theta(\tilde{x}_i \mid \tilde{x}_{1:i-1})}.
}
\]
Pros:
- 可以用于任意长度的序列
- 参数量固定 (parametric model)
- 高度非线性
Cons:
- 训练特别慢, 没办法并行化 (linearly depends on sentence length)
- 梯度爆炸、梯度消失等问题 (check papers related to LSTM)
7.4 Transformers
RNN 面临训练缓慢、长距离依赖建模不足等问题. 我们能不能构造一种神经网络, 它能一下子输入整个训练序列 \((\tilde{x}_0,\tilde{x}_1,\dots,\tilde{x}_{L-1})\), 然后对其整体加工, 再一下子输出整个预测序列 \((p_\theta(x_1),p_\theta(x_2\mid \tilde{x}_1),\dots)\)?
这不正好就是上一次讲的 Transformer 吗?
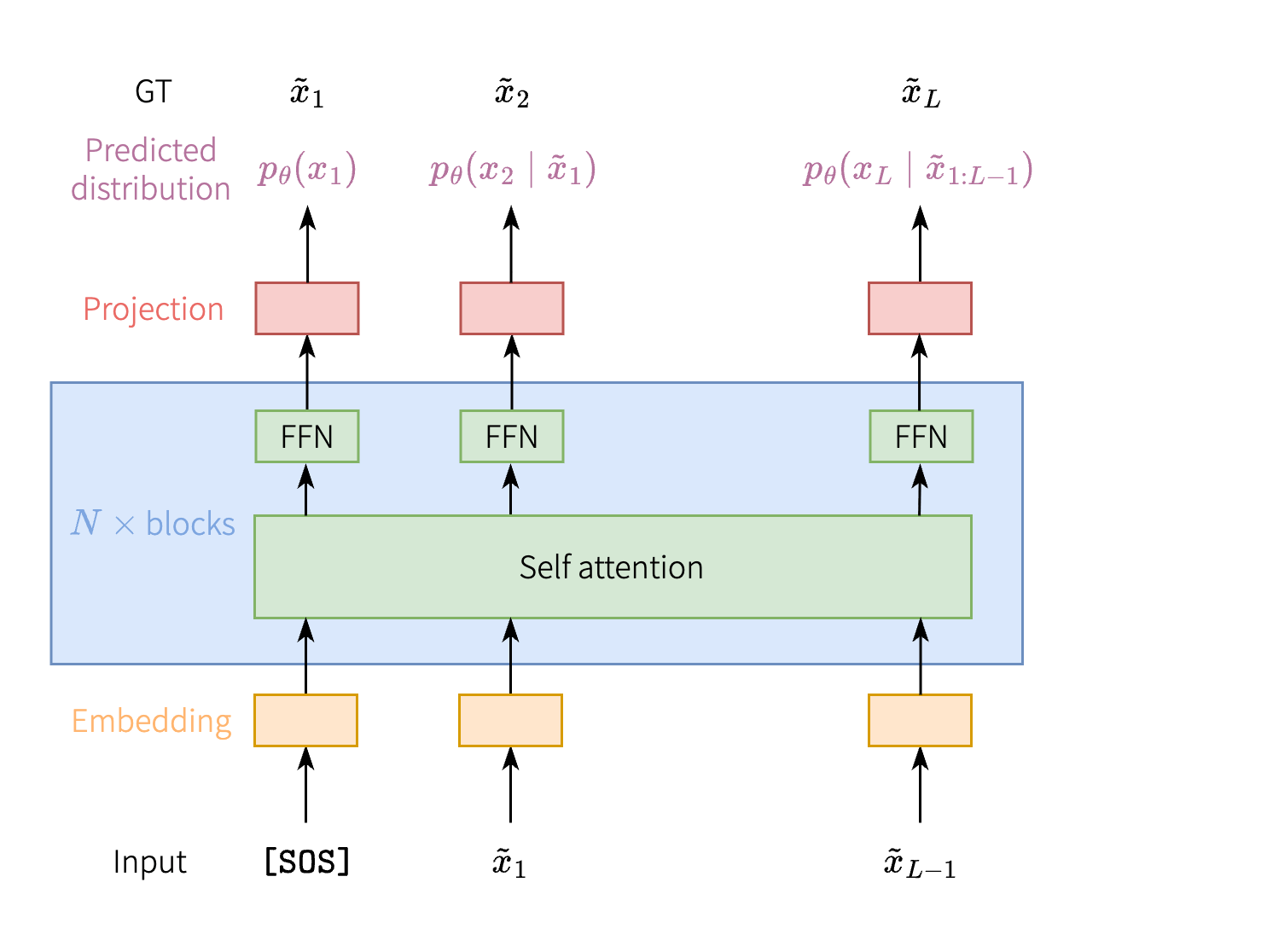
- Transformer 让输入序列 \((\tilde{x}_0,\tilde{x}_1,\dots,\tilde{x}_{L-1})\) 经过 embedding 和若干 Transformer block 之后, 输出含有上下文信息的 latent 序列 \((z_0,z_1,\dots,z_{L-1})\).
此时只需要再接一个线性层 (linear projection) 就可以将 latent \(z_i\) 转化为概率分布 \(p(x_{i+1}\mid\tilde{x}_{1:i})\), 如下图所示.
然而原生的 Transformer 不能直接用于自回归任务. 自回归任务要求模型在预测 \(x_i\) 时, 只能看见前面的 tokens \(x_1,\dots,x_{i-1}\), 然而 Transformer 的 self attention 模块却考虑了每个 token \(j\) 对 token \(i\) 的贡献: \[ a_{ij} = \frac{\exp(s_{ij})}{\sum_{k=1}^L \exp(s_{ik})}, \] 这就导致 Transformer 能找到一条 shortcut——直接将后一个输入拷贝到输出, 如下图的红色箭头.
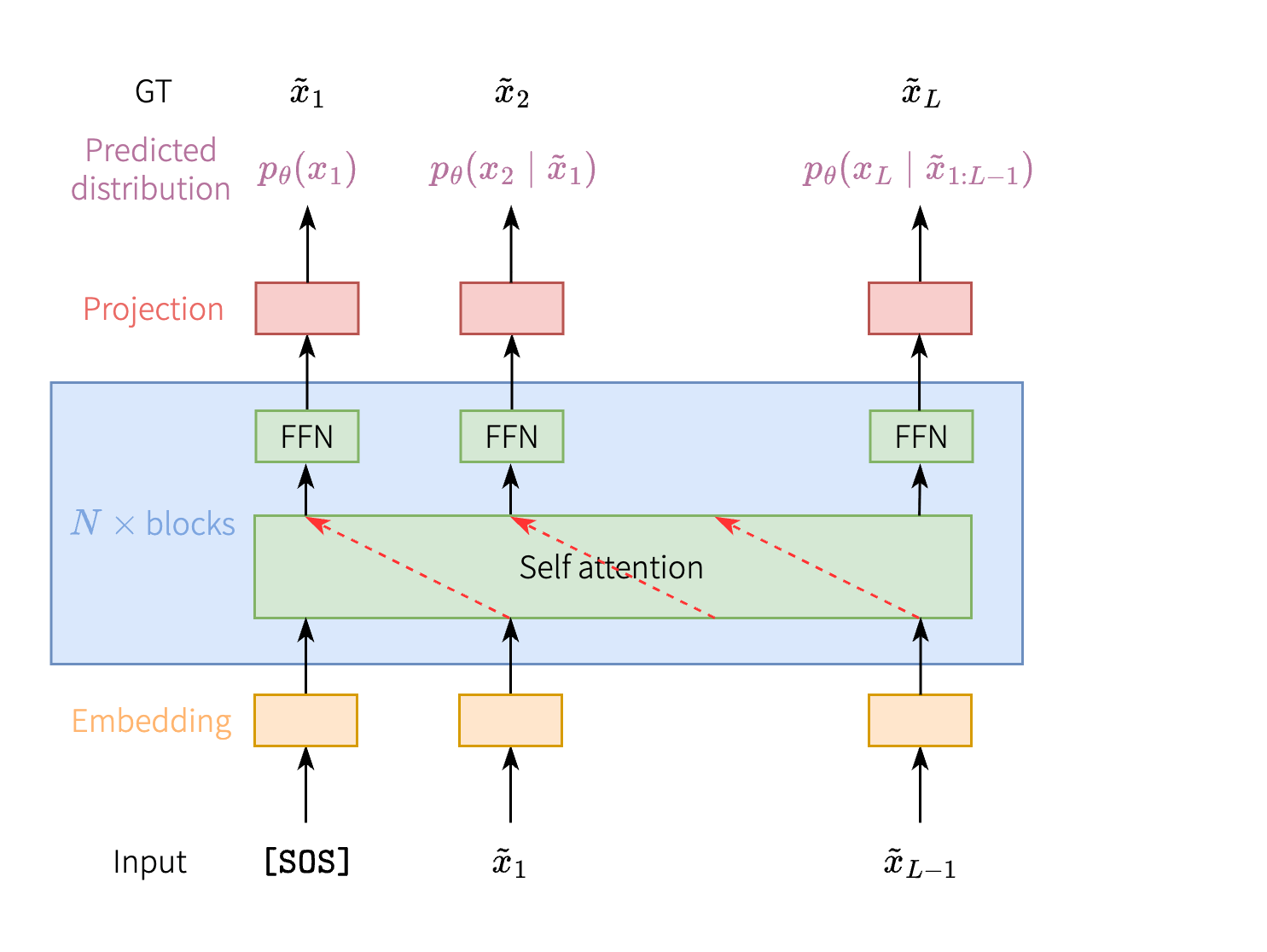
这样肯定不行.
- 模型在训练 / 测试的时候找到了作弊的捷径, 可以达到很低很低的 loss / eval metric.
- 但在真实使用的时候, 并没有 GT, 整个序列都是模型从零开始生成的, 捷径不管用了, 导致生成的结果非常差.
解决办法很简单——当 \(j>i\) 时, 强行把 \(s_{ij}\) 设为 \(-\infty\) 即可, 相应的 \(\exp(s_{ij})=0\), 也即 \(a_{ij}=0\). 用矩阵形式写出来就是 \[ A = \operatorname{softmax} \bigl( QK\T/\sqrt{D} + \orange{M} \bigr), \]
其中 \(M\in\R^{L\times L}\) 是上三角矩阵, \[ M = \pmqty{ 0 & -\infty & -\infty & \cdots & -\infty \\ 0 & 0 & -\infty & \cdots & -\infty \\ \vdots & \vdots & \ddots & \ddots & \vdots \\ 0 & 0 & \cdots & 0 & -\infty \\ 0 & 0 & \cdots & 0 & 0 }. \]
矩阵 \(M\) 也称为 causal mask (因果掩码) 或者 teacher forcing mask.
Note 所谓 teacher forcing, 指的就上面提到的 AR 模型的训练方式. 模型的输入是 GT \(\tilde{x}_{1:i}\) (正确无误的序列), 根据 GT 预测下一个 token \(p_\theta(x_{i+1}\mid\tilde{x}_{1:i})\). 因此这种 AR 模型隐含了一个假设:
- 模型在生成当前词时, 其所依赖的所有先前词都是 \(100\%\) 正确的.
虽然 teacher forcing 使得我们可以并行化输入, 但也存在问题:
- 训练环境 (的输入) 是完美无错误的, 然而在实际推理中, 模型只能以上一步的预测结果 (很可能是错误的) 作为下一步的输入.
- 模型从未在它自己的错误输出上下文下进行训练. 当推理时模型犯下第一个错误, 这个错误就会累积, 模型就会进入一个在训练中从未见过的、低概率的输入空间, 导致生成质量迅速下降或“胡言乱语”.
这称为暴露偏差 (exposure bias).
为了缓解暴露偏差, 研究人员提出了各种技巧, 如计划采样 (scheduled sampling), 它在训练过程中逐渐减少使用 GT 的频率, 转而使用模型自己的预测作为输入, 从而让模型 “适应” 真实世界的推理环境.
8 语言模型
8.1 Training
语言模型 (LM) 模型的训练目标前文已经给出, 不再赘述.
基于 Transformer 的 LM 不好训, 需要许多技巧, 尤其是工业级别的大语言模型.
- 混合精度训练:
- 除法高精度
- 矩阵乘法低精度
- Large batch 训练:
- 训练数据集 3.4B ~ 4T tokens.
- 每个 batch 至少 1M tokens (512 token/seq * 2048 seq).
- 显存有限, 没办法一下子加在这么大的 batch, 需要 gradient accumulation.
- 让训练更稳定:
- Small dropout
- 学习率 warm up
- Gradient clipping
8.2 Evaluation
自回归 LM 的训练目标是最小化负对数似然 \[ \Align{ \operatorname{NLL}(\tilde{x};\theta) = -\log{p_\theta(x_1)} -\sum_{i=2}^L \log{p_\theta(\tilde{x}_i \mid \tilde{x}_{1:i-1})}. } \] 但是由于 NLL 依赖于序列长度 \(L\) (长的句子 NLL 比较大), 所以不太适合用来评价一个 NLL 是好是坏. 将其归一化得到 per-word 的 NLL, \[ \operatorname{WNLL}(x;\theta) := \frac{1}{L} \operatorname{NLL}(x;\theta), \] 取指数得到困惑度 (perplexity) \[ \operatorname{ppl}(x;\theta) := \exp(\operatorname{WNLL}(x;\theta)). \] 困惑度是一个经典的生成模型指标.
- 给定测试集 \(\{s_i\}\), 计算模型在其上的平均困惑度 \(\frac{1}{N}\sum_{i=1}^N\operatorname{ppl}(s_i;\theta)\). 困惑度越低, 模型越好.
- 自然语言中常用的指标还包括 BLEU (机器翻译), ROUGE (信息检索)...
8.3 Inference
自回归 LM 如何采样生成一个句子?
最自然的办法:
- 输入 \(\texttt{[SOS]}\), 根据模型的输出 \(p_\theta(x_1)\) 随机采样得到 \(\hat{x}_1\).
- 把采样结果 \(\hat{x}_1\) 送进模型中, 再根据输出 \(p_\theta(x_2\mid\hat{x}_1)\) 随机采样得到 \(\hat{x}_2\).
- 以此类推, 直到输出特殊 token \(\texttt{[EOS]}\) (end of sequence), 或者达到预定长度等.
这种方法称为随机采样 (stochastic sampling). 随机采样的结果有很强的多样性 / 随机性, 但是缺点也很明显: 输出 \(\hat{x}_i\) 随机性太强, 很有可能随机到一个错误的结果, 之后模型在错误的基础上预测, 容易 “一步错步步错” (见上文 exposure bias).
为了提升准确性, 可以采用 top-\(k\) 采样, 即从 \(p_\theta(x_i\mid\hat{x}_{1:i-1})\) 中选取概率最大的 \(k\) 个 tokens, 从中随机采样.
- 当 \(k=1\) 时, 相当于取概率最大的 token, 即贪心搜索算法 (没有随机性).
另一种方法是 top-\(p\) 采样, 即从 \(p_\theta(x_i\mid\hat{x}_{1:i-1})\) 中概率大于等于 \(p\) 的 tokens 中采样.
以上的采样方法都是局部的, 即最大化每个条件概率 \(p_\theta(x_i\mid\hat{x}_{1:i-1})\). 这样容易陷入局部最优. 一个稍好些的方法是束搜索 (beam search), 即每次选取条件概率 \(p_\theta(x_i\mid\hat{x}_{1:i-1})\) 前若干名的 tokens 作为候选, 维护一个候选的集合, 最终选择联合概率最大的序列. 束搜索是贪心算法的一种改进, 但也不能保证得到联合概率 \(p_\theta(x_{1:L})\) 的最大值点.
- 束搜索在机器翻译中常用.
| 采样方法 | 随机采样 | Top-\(k\) 采样 | 贪心搜索 | 束搜索 |
|---|---|---|---|---|
| 速度 | 快 | 快 | 快 | 慢 |
| 多样性 | 😄😄😄 | 😄😄 | 🙁 | 😄 |
| 准确度 | 🙁 | 😄 | 😄 | 😄😄 |
Note 总结 RNN 和 Transformer 的训练与生成速度.
考虑在一个序列 \((x_1,\dots,x_L)\) 上训练 / 生成的时间复杂度:
| 模型 | RNN | Transformer |
|---|---|---|
| 训练 | \(O(L)\) (无法并行) | \(O(L^2)\) (可以并行) |
| 推理 | \(O(L)\) | \(O(L^2)\) |
在训练时, 尽管 RNN 计算代价低, 但它没法并行化, 效率也很低. 在推理时, 由于都是从零开始生成, 无法并行化, 所以 Transformer 计算代价高的弊端就暴露出来了.
*注: Transformer 在生成长度为 \(L\) 的序列时, 由于每次只能生成一个 token, 所以需要逐个生成长度为 \(1,2,3\dots,L-1,L\) 的序列, 总复杂度 \(O(L^3)\). 大家一般会使用 key-value cache 避免重复计算, 将总复杂度降为 \(O(L^2)\).
Non-parametric method, 参数个数不固定, 随着训练数据而变化.↩︎