生成模型基础 | 1 自编码器
现今火热的 ChatGPT, Gemini, Stable Diffusion 等等都是生成模型. 生成模型是很神奇的东西, 它似乎可以 “无中生有”, 源源不断地生出五花八门的图片、文章、视频……
什么是生成模型? 考虑一个随机数发生器, 它可以生成出服从 \([0,1]\) 上某个分布 \(p(x)\) 的伪随机数. 它具体是怎么做的呢? 首先它会生成 \([0,1]\) 上服从均匀分布的伪随机数 \(z\) (通过线性同余等方法); 然后通过一个映射 \(f:[0,1]\to[0,1]\) 将 \(z\) 映到服从分布 \(p(x)\) 的伪随机数 \(x=f(z)\) (其中 \(f=F^{-1}\), 而 \(F\) 是 \(p(x)\) 的累积分布函数).
换言之, 随机数发生器是将随机噪声 (如 \([0,1]\) 上的均匀分布随机数) 映射到服从某一分布的随机变量 (比如服从 \(p(x)\) 的随机数) 的东西. 生成模型 (generative model) 也是如此. 它将随机噪声映射为 (服从特定分布的) 语句、图片、三维形状等 (称为样本).
然而, 生成模型并没有随机数发生器那么简单:
- 样本的真实分布 \(p(x)\) 是未知的,
我们不能通过简单的公式 \(x=F^{-1}(z)\)
生成 \(x\).
- 需要利用样本集 \(\{x_i\}_i\) 训练生成模型, 让它自己学会样本的分布.
- 样本 \(x\in\R^N\) 的维数很高,
直接生成样本的计算代价很大.
- 需要一些方法处理稀疏性.
- ……
1 Autoencoders
今天讲的是最简单的生成模型, 它如此简单以至于在 CPU 上就可以训练. 当然它的表现肯定不比如今的大模型, 但已经成为了绝大多数生成模型的一部分.
1.1 Basics
一般来说, 高维空间 \({\cal X}\) (维数为 \(N\)) 中的样本分布是很稀疏的 (比如所有 \(128\times128\) 的图像中, 几乎所有图像都是噪声, 只有极少数是有意义的), 即 \(p\) 的支集 \[ \Sigma := \overline{ \{ x\in{\cal X} \mid p(x)>0 \} } \] 是一个 \(K\) 维子流形 (\(K\ll D\)). 这也称为流形假设 (manifold hypothesis). 自编码器 (autoencoder, AE) 主要的作用是学习该子流形. AE 包含两部分:
- 编码映射 (encoder) \(\varphi_\theta:{\cal
X}\to{\cal Z}\) 将数据压缩到低维空间 \({\cal Z}=\R^D\) (隐空间, latent space);
- 编码后的数据 \(\varphi_\theta(x)\) 也称为隐变量 (latent) 或者表示 (representation).
- 解码映射 (decoder) \(\psi_\theta:{\cal Z}\to\mathcal{X}\) 将压缩的数据还原.
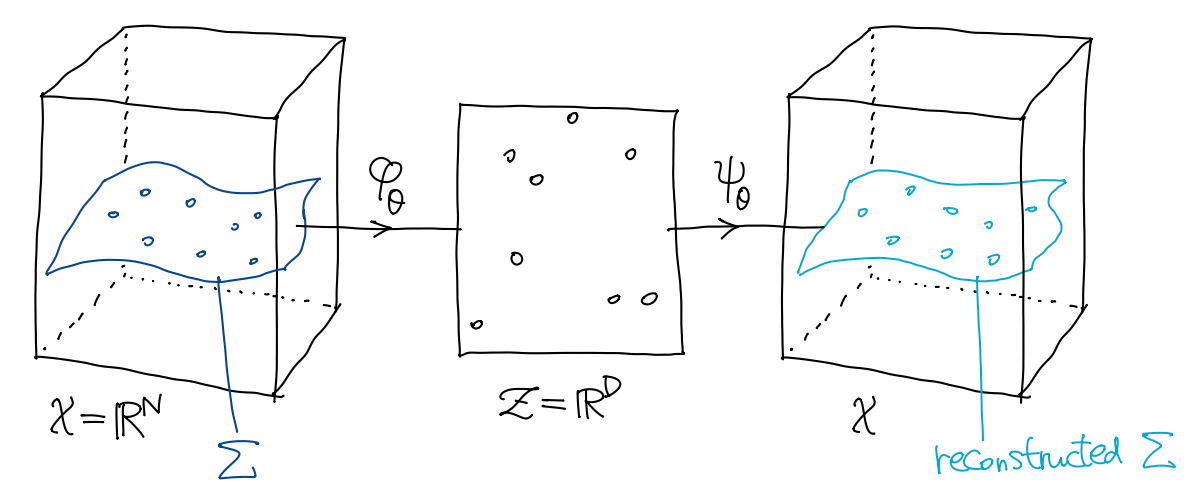
一般 encoder 和 decoder 都是 MLP (参数为 \(\theta\)), 它们组成了一个 bottleneck 的神经网络结构: 将输入 \(x\) 压缩到低维空间, 再还原回去.
我们希望压缩尽量是无损的, 即复合映射 \(\varphi_\theta\circ\psi_\theta\) 在 \(\Sigma\) 上接近恒等映射. 由此给出 \(\ell^2\) 重建损失 (reconstruction loss) \[ \Align{ \mathcal{L}_{\textsf{recon}} :={}& \operatorname{E}_{x\sim p} \| (\psi_\theta \circ \varphi_\theta) (x) - x \|_2^2. } \] AE 的一些初步应用包括:
- 将高维数据降维, 以便可视化.
- 数据压缩.
- 表示学习.
AE 的 encoder 和 decoder 映射都应当足够简单, 防止过拟合或者拟合到恒等映射.
1.2 Linear AEs
最简单的 AE, 就是取 \(\varphi_\theta\) 和 \(\psi_\theta\) 都是线性映射, 为了方便分别记作 \(U,V\). 将输入数据集 \(\{x_n\}\) (每条数据是一个列向量) 堆叠成一个矩阵 \(X\). 此时 AE 训练的优化目标为 \[ \min_{U,V} \| VUX - X \|_2^2, \] 即主成分分析 (PCA).
2 Variational Autoencoders
2.1 A naïve VAE
AE 是否是一个生成模型? 考虑隐空间中数据的分布 \[ \varphi_\theta(x) \sim (\varphi_\theta)_*p, \qquad \textsf{其中}\; x\sim p, \] (其中 \((\varphi_\theta)_*p\) 表示将概率分布 \(p\) 推到 \(\mathcal{Z}\) 上) 只要我们知道 \((\varphi_\theta)_*p\) 就可以从中采样了. 但是在一般的 AE 训练过程中, 我们并不知道 \((\varphi_\theta)_*p\) 究竟是什么, 甚至不知道它的性质.
变分自编码器 (variational autoencoder, VAE) 做的就是对隐空间的概率分布 \((\varphi_\theta)_*p\) 做了 “正则化”, 让它尽量接近一个已知的、好的分布——标准 Gauss 分布 \(\mathcal{N}(0,I)\).
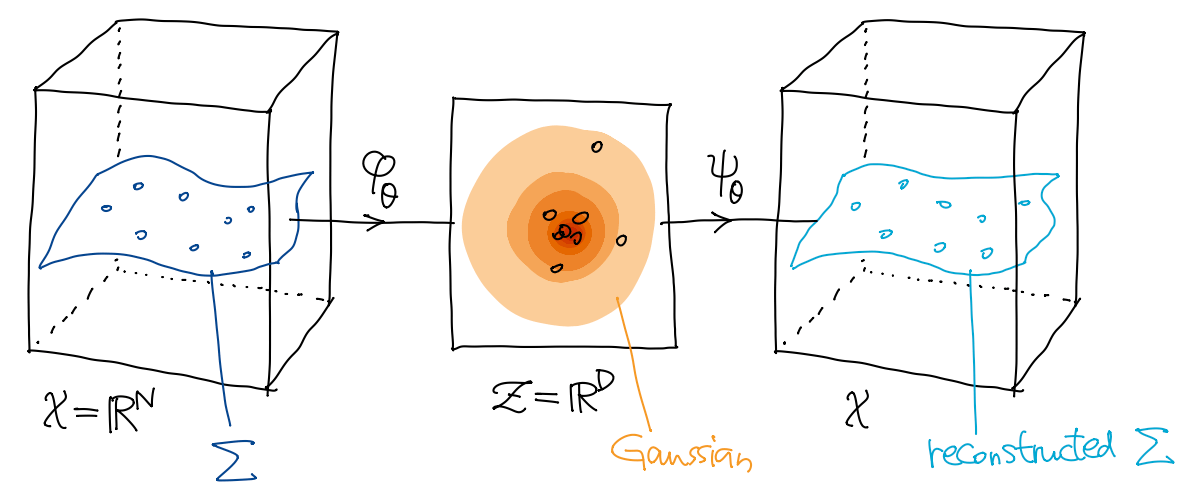
如此一来, 我们就可以从隐空间 \(\mathcal{Z}\) 上的 Gauss 分布 \(\mathcal{N}(0,I)\) 中采样 \(z\), 然后经过 decoder 就可以生成新的数据了: \[ \psi_\theta(z) \sim p. \]
在具体实现上, 我们一般将 “采样” 这个步骤放到 encoder 里: encoder \(\varphi_\theta\) 首先估计 Gauss 分布的均值和方差 \((\mu,\Sigma)\), 然后再从该 Gauss 分布 \(\mathcal{N}(\mu,\Sigma)\) 中采样一个样本作为输出的 \(z=\varphi_\theta(x)\). 换言之, encoder \(\varphi_\theta\) 并不是一个确定的函数, 而是一个随机函数 (stochastic function), 其输入是确定的 \(x\), 输出是服从某一分布的随机变量. 这种表示方法称为随机隐变量表示 (stochastic latent representation).
最后, 如何让 encoder 输出的分布接近于标准 Gauss 分布? 答案是用 KL 散度作为 “正则化”: \[ \mathcal{L}_{\textsf{reg}} := D_\textsf{KL}( \mathcal{N}(\mu,\Sigma) \parallel \mathcal{N}(0,I) ). \] VAE 的损失函数是重建损失与正则化的线性组合, \[ \mathcal{L} := \mathcal{L}_{\textsf{recon}} + \lambda \mathcal{L}_{\textsf{reg}}. \]
Note 如果不使用 KL 散度正则化会发生什么? 考虑一个极端的情况, encoder 对于所有的样本 \(\{x_i\}\) 输出的均值 \(\mu\) 都不一样, 而方差 \(\Sigma\) 接近 \(0\). 这意味着 encoder 学到了一个多点分布, 过拟合了.
Theorem (两个 Gauss 分布的 KL 散度) 设 \(p,q\) 分别为 \(n\) 维 Gauss 分布 \(\mathcal{N}(\mu_p,\Sigma_p)\) 和 \(\mathcal{N}(\mu_q,\Sigma_q)\) 的密度函数, 则 KL 散度 \[ D_{\textsf{KL}}(p\parallel q) = \frac12\bqty{ \tr(\Sigma_q^{-1}\Sigma_p) + (\mu_p-\mu_q)\T\Sigma_q^{-1}(\mu_p-\mu_q) - \log\det(\Sigma_p\Sigma_q^{-1}) - n }. \]
特别地, 若 \(q\) 为标准 Gauss 分布 \(\mathcal{N}(0,I)\), 则 \[ D_{\textsf{KL}}(p\parallel q) = \frac12\bqty{ \tr(\Sigma_p) + \mu_p\T\mu_p - \log\det(\Sigma_p) - n }. \]
2.2 The reparameterization trick
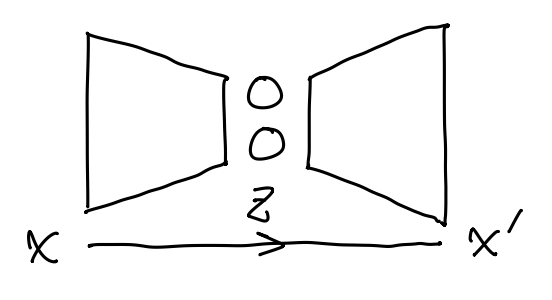
VAE 看起来好极了, 但是如果我们想要用梯度下降法训练一个 VAE, 就会发现一个致命问题——从 Gauss 分布 \(\mathcal{N}(\mu,\Sigma)\) 中采样的过程是非连续的, 导致损失函数关于 encoder 的参数不可微.
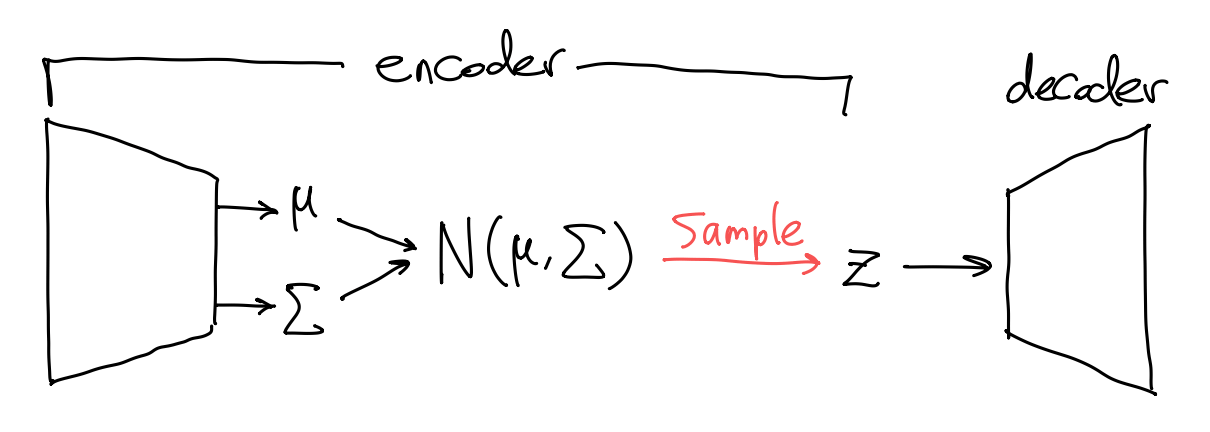
如上图, 问题的关键是 samle 步阻碍了梯度反向传播. 解决办法也很简单——只要把 sample 步挪到外面即可 (即重参数化技巧). 即先从标准 Gauss 分布采样 \(\varepsilon\sim\mathcal{N}(0,I)\), 然后根据 \((\mu,\Sigma)\) 缩放: \[ z = \sqrt{\Sigma}\cdot\varepsilon + \mu \sim \mathcal{N}(\mu,\Sigma). \] 此时计算图为
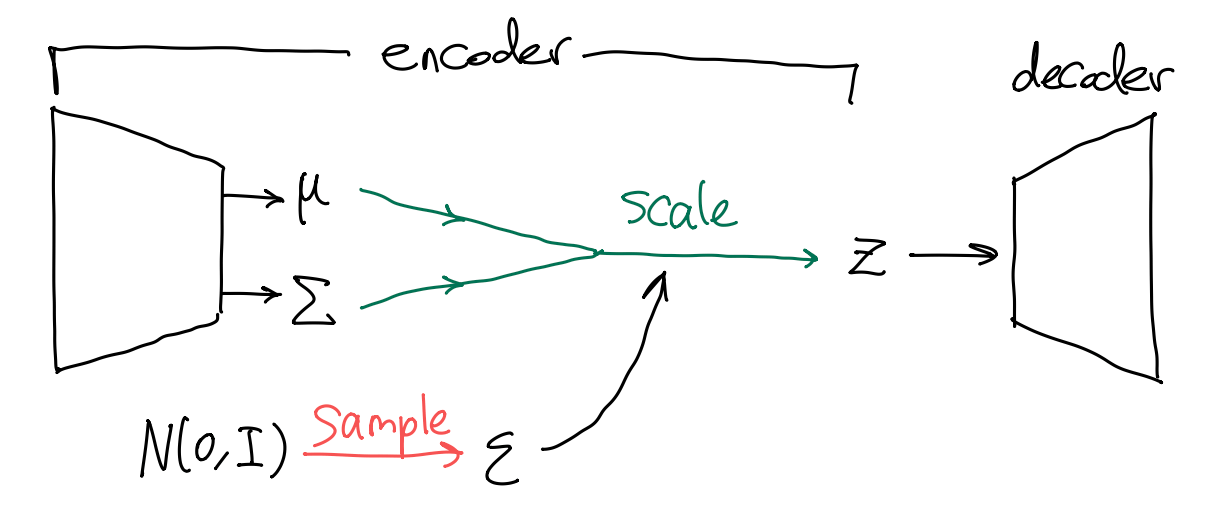
其中 sample 被挪到了支路上, 梯度可以畅通地反向传播到 encoder 的参数了.
2.3 A probabilistic view
从几何上看, VAE 学习了高维空间中子流形的局部参数化, 把数据降维了. 下面我们理论地解释 VAE 为什么能用.
统计学中有所谓参数估计问题, 即假设样本服从某一特定分布 \(p(x)\), 其参数为 \(\lambda\). 我们的任务是根据样本的观测值 \(x\) 估计分布参数 \(\lambda\). 一个常用方法是最大似然估计 (MLE).
训练 VAE 就好比一个参数估计问题, 只不过此时 \(p(x)\) 并非由参数 \(\lambda\) 指导生成, 而是由另一个分布 \(p(z)\) 指导生成 (\(z\) 就是隐变量):
首先, 从一个已知的、简单的先验分布 \(p(z)\) (比如标准 Gauss 分布 \(\mathcal{N}(0,I)\)) 中采样一个隐变量 \(z\).
然后, 利用一个复杂的条件概率分布 \(p(x\mid z)\) (即似然函数, 由 decoder 建模) 从隐变量 \(z\) 生成数据 \(x\).
(MLE) 我们的目标是最大化数据的边缘似然 (或证据) \[ p(x) = \int_{\R^n} p(x\mid z) p(z) \dd{z}. \]
这里一大难点是 \(p(x)\) 这个高维积分不好求. 解决办法是引入一个较简单的分布 \(q(z\mid x)\) 来近似 (未知的) 后验分布 \(p(z\mid x)\). 分布 \(q(z\mid x)\) 也称为近似后验分布, 由 encoder 建模.
从最大化边缘似然 (证据) 开始: \[ \Align{ \log{p(x)} &= \log\!\pqty{ \int_{\R^n} p(x\mid z)p(z) \dd{z} } \\ &= \log\!\pqty{ \int_{\R^n} \frac{p(x\mid z)p(z)}{q(z\mid x)} \cdot q(z\mid x) \dd{z} } \\ &= \log\operatorname{E}_{q(z\mid x)}\! \bqty{\frac{p(x\mid z)p(z)}{q(z\mid x)}} \\ &\geq \operatorname{E}_{q(z\mid x)}\! \bqty{ \log\frac{p(x\mid z)p(z)}{q(z\mid x)} }, } \] 其中最后一步使用了 Jensen 不等式, 注意到 \(\log\) 是上凸函数. 最后一行称为证据下界 (ELBO, evidence lower bound), 它是对数证据 \(\log{p(x)}\) 的一个下界. 我们进一步将 ELBO 展开: \[ \Align{ \log p(x) &\geq \operatorname{ELBO}(q) \\ &= \operatorname{E}_{q(z\mid x)} \bigl[\log p(x\mid z)\bigr] - \operatorname{E}_{q(z\mid x)}\! \bqty{ \log\frac{q(z\mid x)}{p(z)} } \\ &= \blue{- H( q(z\mid x),p(x\mid z) )} \purple{{}- D_{\textsf{KL}}(q(z\mid x)\parallel p(z))} \vphantom{\Bigl[} , } \] 其中第一项是负的交叉熵, 第二项是负的 KL 散度.
因为 ELBO 是边缘似然的下界, 我们只需最大化 ELBO 即可, 也就是最小化交叉熵和 KL 散度:
- 当交叉熵项取最小值时, \(q(z\mid x)\) 与 \(p(x\mid z)\) 分布相同,
- KL 散度项其实就是 VAE 的正则化损失 (令 encoder 的输出尽量接近先验分布 \(p(z)\)).
因此, 交叉熵与 KL 散度项恰好分别对应了重建损失与正则化, 这就从概率 (最大似然估计) 的角度解释了 VAE 的工作原理.
2.4 Problems in VAE
VAE usually cannot go deep (check David Wipf’s work).
The dimension of the latent code is sensitive (check David Wipf’s work).
VAE cannot do density estimation, i.e., accurately calculating \(p(x)\).
VAE is usually used as a component of a system, but not a standalone model.
Note 为什么 VAE 的网络不能太深?
强大的 decoder \(p_\theta(x\mid z)\) 可以仅凭很少的信息 (甚至忽略 \(z\)) 就能很好地完成重建任务, 即最小化交叉熵 \(H(q_\phi(z\mid x),p_\theta(x\mid z))\). 此时, 网络发现最小化 KL 散度 \(D_{\textsf{KL}}(q_\phi(z\mid x)\parallel p(z))\) 是更简单的优化路径.
因此 encoder \(q_\phi(z\mid x)\) 会忽略输入 \(x\), 直接输出一个接近先验 \(\mathcal{N}(0, I)\) 的分布, 导致隐变量 \(z\) 失去了信息量, 无法捕获数据的有效特征, 模型退化. 这也称为后验崩塌 (posterior collapse).
3 Denoising Autoencoders
VAE 根据输入数据生成了一个高斯噪声, 再从中采样, 这可以看作是在输入数据中加入了噪声. 我们不妨简化一下这个流程——直接在输入数据上加噪, 然后喂给 autoencoder, 让它重建原本的输入. 这就称为去噪自编码器 (DAE, denoising autoencoder).
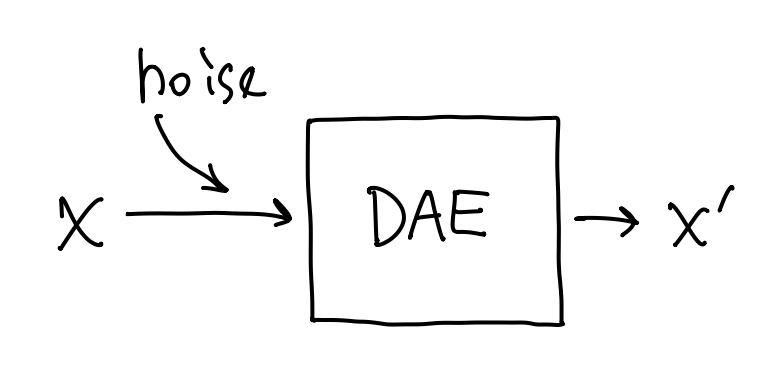
- DAE 不需要 bottleneck 设计, 因为将噪声还原为干净输入的过程显然高度不平凡, 不可能像 AE 那样, 可以用一个恒等映射糊弄过去. DAE 通常是一个很大很深的神经网络.
- DAE 不区分 encoder 和 decoder, 因为它并不是做表示学习的.
- 与 AE 一样, DAE 的损失函数是重建损失.
DAE 的加噪办法一般是 masking, 也就是把输入的 tokens 向量随机 mask
掉一些元素 (变成特定的 [MASK] token, 如下图
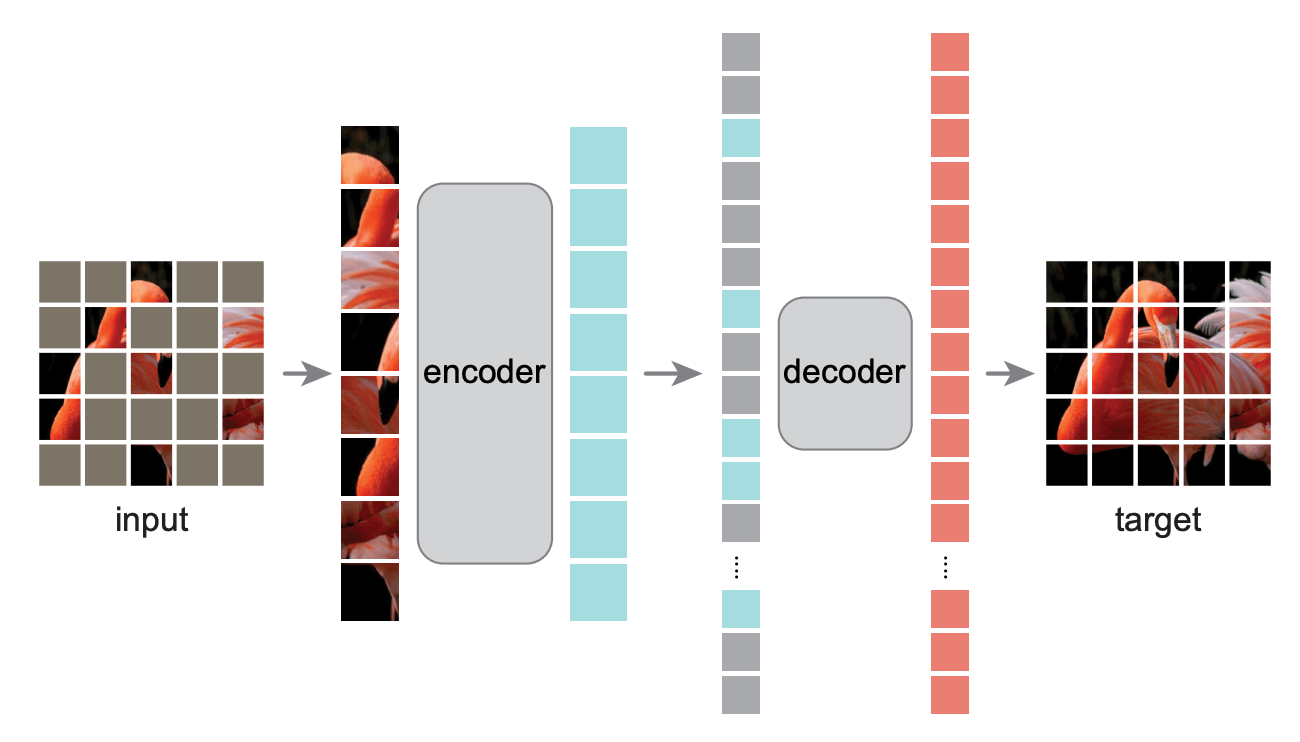
DAE is known as one of the most efficient pre-training (self-supervised) methods:
- Can be used with ANY data type
- Usually is not considered as generative model, although it can generate the missing part of the data
4 VQVAEs
VQVAE 在视觉-语言大模型中用得很多.
4.1 Quantization
AE 和 VAE 做的都是学习连续对象的连续表示 (即隐向量连续变化会使得生成结果也连续变化), 这在图像、视频、三维生成中很有用, 然而并非所有的数据都是连续的——比如自然语言中的 tokens, 它们是一个个分立的值 (categorial). 语言 tokens 和图像 latent 这一本质的不同, 使得视觉-语言大模型在实现上很困难.
为了解决这一问题, 人们提出了向量量化变分自编码器 (VQ-VAE, vector-quantized VAE), 将连续的变量编码为离散的 latent.
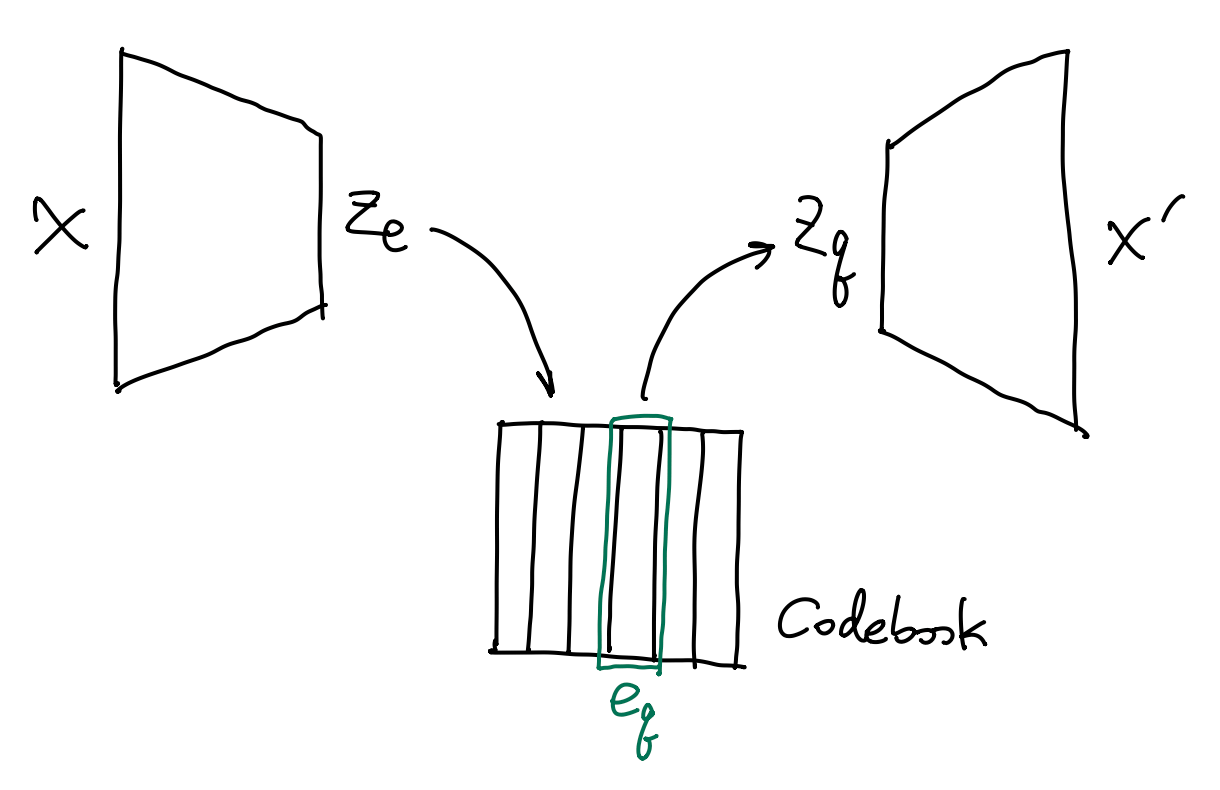
VQVAE 的架构与 VAE 相似. 为了将连续的 latent 离散化, VQVAE 引入了一个 codebook (编码表). Codebook 是有限个向量的集合 \(\{e_i\}_{i=1}^K\subset\R^D\). Encoder 的输出 \(z_e(x)\) 会与 codebook 中的向量分别计算距离, 最后选择距离最小的那个 code \(e_q\) 作为 latent \(z_q(x)\). 用公式写出来就是 \[ z_q(x) \equiv e_q := \argmin_{e_i}\, \| z_d(x) - e_i \|_2. \] 离散化的 latent \(z_q(x)\) 会作为 decoder 的输入, 重建结果为 \(\psi(z_q(x))\). 考虑重建损失 \[ \| x - \psi(z_q(x)) \|_2, \] 这里遇到了一个问题: \(z_q\) 是 \(\argmin\) 来的, 关于 \(z_d(x)\) 不连续, 导致损失函数关于 encoder 的参数不可微.
4.2 The straight-through estimator
解决办法是用一种叫做 “straight-through estimator” 的近似手段.
假设不可微函数 \(f:\R^n\to\R^n\), ST estimator 的操作为:
- 前向传播, 不作任何改动, 输出 \(f(x)\).
- 反向传播, 认为 \(\partial f/\partial x \approx \mathrm{id}_{\R^n}\), 相当于用一个最平凡的映射作为近似梯度, 让网络参数得以更新.
比如, 假设有损失函数 \(\mathcal{L}=f(g(x))\), 则梯度近似为 \[ \pdv{\mathcal{L}}{x} = \pdv{f}{g} \pdv{g}{x} \approx 1 \cdot \pdv{g}{x} = \pdv{g}{x}. \] 这等价于引入 “stop gradient” 操作: \[ \mathcal{L} = g(x) + \orange{\operatorname{StopGradient}}\bigl[f(g(x)) - g(x)\bigr], \]
正向传播时, \({\operatorname{StopGradient}}\) 为恒等映射, 因此 \(\mathcal{L}=g(x)+[f(g(x))-g(x)]=f(g(x))\).
反向传播时, \({\operatorname{StopGradient}}\) 的梯度恒为零, 因此 \[ \pdv{\mathcal{L}}{x} = \pdv{g}{x} + 0 = \pdv{g}{x}. \] 这和上面的结果是一样的.
总之, 我们引入 “stop gradient” 操作: \[ \mathcal{L}_{\textsf{recon}} := \Bigl\| x - \psi\bigl( z_e + \orange{\operatorname{StopGradient}}(z_q - z_e) \bigr) \Bigr\|. \]
- 正向传播时, 可以计算出正确的结果.
- 反向传播时, 损失关于 decoder 参数的梯度是正确的, 关于 encoder 参数的梯度是近似的 (相当于认为 codebook lookup 的梯度为恒等映射), 可以相对合理地更新 encoder 的参数.
为了减少梯度近似的误差, VQVAE 还引入了 codebook loss.
4.3 Codebook loss
引入 stop gradient 后, 我们发现损失函数关于 \(z_q\) 的梯度恒为零, 也就是说 codebook 永远不会更新了, 这显然不太好. 为了让 codebook 能够更新, 同时为了拉近 \(z_q\) 与 \(z_e\) 的距离 (以减少梯度近似的误差), 我们引入另外两个损失:
Codebook 损失, \[ \mathcal{L}_{\textsf{codebook}} := \| z_q - \operatorname{StopGradient}(z_e) \|, \] 只会更新 \(z_q\), 让 codebook 被选中的向量靠近 encoder 的输出 \(z_e\).
Commitment 损失, \[ \mathcal{L}_{\textsf{commitment}} := \| z_e(x) - \operatorname{StopGradient}(z_q) \|, \] 只会更新 \(z_e\), 让 encoder 的输出向 codebook 中的向量靠近.
总损失是三个损失的和: \[ \mathcal{L} := \mathcal{L}_{\textsf{recon}} + \mathcal{L}_{\textsf{codebook}} + \beta\mathcal{L}_{\textsf{commitment}}. \]
4.4 Improving capacity
一般令 VQVAE 的 codebook 容量 \(K=8192\), 那岂不是意味着它只能生成 \(8192\) 种不同的结果?
一种解决办法是多头 (multi-head) 量化, 即一共构造 \(L\) 个 codebooks, 把 encoder 输出的 \(z_e(x)\) 平均切分成 \(L\) 个子向量, 每个子向量算得一个最近邻 code, 在将这 \(L\) 个 codes 拼起来, 作为 decoder 的输入.
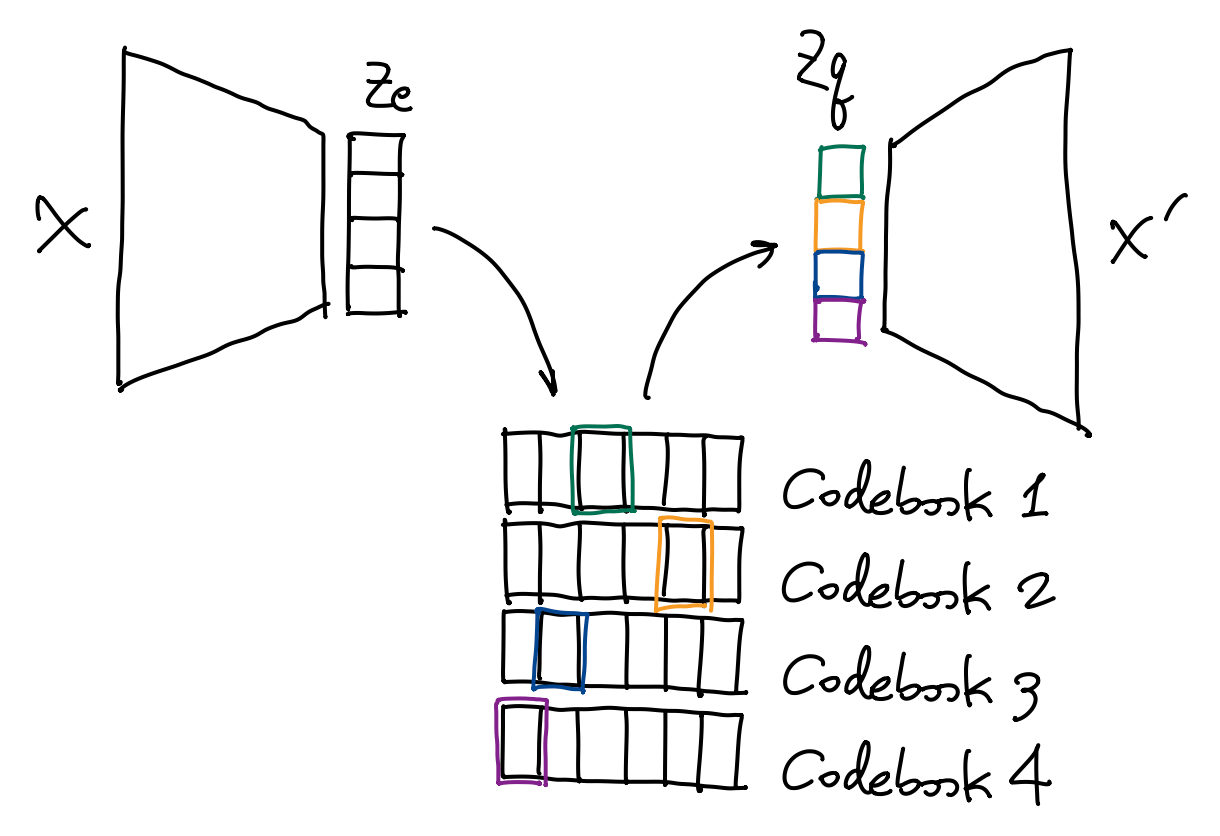
多头量化可以实现输出结果种类的指数级增长——比如当 \(L=16\) 时, 所有可能的生成结果有 \[ K^L = 8192^{16} \approx 4.11\times10^{62} \] 这么多种!
来自 Kaiming He et al, Masked Autoencoders are Scalable Vision Learners, CVPR 2022. 其中的 decoder 就是一个 DAE, 灰色的是 [MASK].↩︎