自然语言处理基础 | 4 语法分析

6 Syntactic Analysis

We have talked about different levels of analysis word level:

• analyzing the senses of a target word (点)
• sequence of words (线性)
  • evaluating a word sequence
  • segmenting phrases from a sentence
  • tagging each word in a sequence

Beyond sequences, language actually follows/obeys certain implicit rules of grammar, which carries meaning. (句法分析, 树和图)

对于一句话 I like eating green apples, 从微观到宏观:

• Constituents (短语结构):
  • S, NP, VP, PP, ...
  • apples, green apples, eating green apples, ...
• Dependency (依存结构):
  • I - like
  • like - apples
  • apples - eating
  • apples - green
  • ...

6.1 Structured prediction problems

一般来说, 求解一个结构 (线性, 树, 图等) 有两种思路:

• 离散优化: 定义一个 score 函数, 求出 score 最高的结构.
  • Viterbi 算法
  • CYK 算法
• 增量式算法: 迭代地构建一个结构.
  • 基于转移的依存解析 (贪心)

6.2 Context-free grammars

6.2.1 CFGs

形式语言 (formal language) \(L\) 指的是有限字母表 \(\Sigma\) 上的一些有限序列的集合 \(L\subset\Sigma^*\).

• Kleene star 定义为 \(\Sigma^*:=\bigcup_{n\geq0}\Sigma^n\).

上下文无关语法 (context-free grammar) 指的是四元组 \(G=(V,\Sigma,R,S)\), 其中:

• 非终结符集 \(V\).
• 终结符集 \(\Sigma\) (字母表 / 单词表), 与 \(V\) 不交.
• 有限产生规则 \(R\subset V\times(V\cup\Sigma)^*\), 给出了由非终结符生成 (非终结符或终结符) 序列的关系.
• 起始符 \(S\in V\).

该语法生成的形式语言是 \(S\) 导出的所有可能的非终结符序列的集合: \[ L(G) := \{ w\in\Sigma^* \mid S \overset{*}\Rightarrow w \}, \] 称为上下文无关语言 (CFL).

• Weak Equivalence: 两个 CFG 生成相同的 CFL.
• Strong Equivalence: 两个 CFG 生成相同的 CFL, 并且对每句话产生结构相同的分析树.

任何一个 CFG 都可以转化为 Chomsky 范式 (CNF). 在 CNF 下, \(R\) 中的元素只有两种形式:

• \(X\to YZ\) (\(X,Y,Z\in V\)).
• \(X\to x\) (\(X\in V\), \(x\in\Sigma\)).

以后我们都在 CNF 下进行语法分析.

6.2.2 Probabilistic CFGs

假设我们有一个 CFG 和一个句子, 如何判断该句子是否能由该 CFG 生成, 并给出分析树? 一般来说, 语法分析树并不是唯一的, 我们需要选择概率最大的那个语法分析树.

Probabilistic CFG 给每个产生规则赋予一个概率. 具体来说, 一个 PCFG 是五元组 \(G=(V,\Sigma,R,S,P)\), 其中映射 \(P:R\to[0,1]\) 将每个产生规则 \(A\to\beta\) 映到一个条件概率 (即给定 \(A\) 的条件下, \(A\) 生成 \(\beta\) 的概率), 满足: \[ \sum_{\beta} P(A\to\beta) = 1,\quad\textsf{对所有非终结符 $A$}. \] 记可以生成 \(s\in L(G)\) 的语法分析树的集合为 \({\cal T}(s)\), 则 \(s\) 最有可能的语法分析树为 \[ t^* = \argmax_{t\in{\cal T}(s)} p(t) = \argmax_{t\in{\cal T}(s)} \prod_{i=1}^n q(A_i\to\beta_i). \] 给定一些已经解析好的句子的集合 (即解析树的集合, treebank), 如何估计 PCFG 的参数? 考虑最大似然估计: \[ P_{\sf ML}(A\to\beta) := \frac{\textsf{$A\to\beta$ 出现的次数}}{\textsf{$A$ 出现的次数}}. \]

6.2.3 Parsing with PCFGs

现在我们已经估计好了 PCFG 的参数, 可以用 PCFG 解析一个新句子了.

Cocke-Kasami-Younger 算法 (CYK) 是一种动态规划算法. 该算法维护一个表格 \(\pi\), 其中 \(\pi(i,j,X)\) 表示非终结符 \(X\) 可以生成句子 \(s=(w_i)_{i=1}^n\) 中第 \(i\) ~ \(j\) 个单词的概率. 自底向上地计算:

• 对 \(i=1,\dots,n\) 和 \(X\in V\), 填入初始条件 \[ \pi(i,i,X)=P(X\to w_i). \]

• 对 \(i=1,\dots,n-1\), \(j=i+1,\dots,n\) 和 \(X\in V\), 计算 \[ \pi(i,j,X) = \max_{\substack{X\to YZ\\i+1\leq m\leq j}} P(X\to YZ) \cdot \pi(i,m,Y) \cdot \pi(m+1,j,Z). \]

最终的概率是 \(\pi(1,n,S)\) (如果概率为零, 说明 \(s\) 不能由该 PCFG 生成). 在计算时同时记录 path 可以复原语法分析树.

例子: PCFG 参数如下:

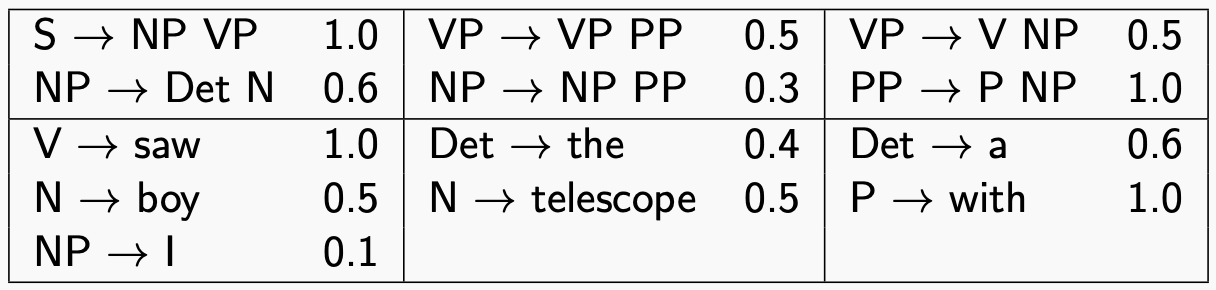
句子为 I saw the boy with a telescope. CYK 的过程为

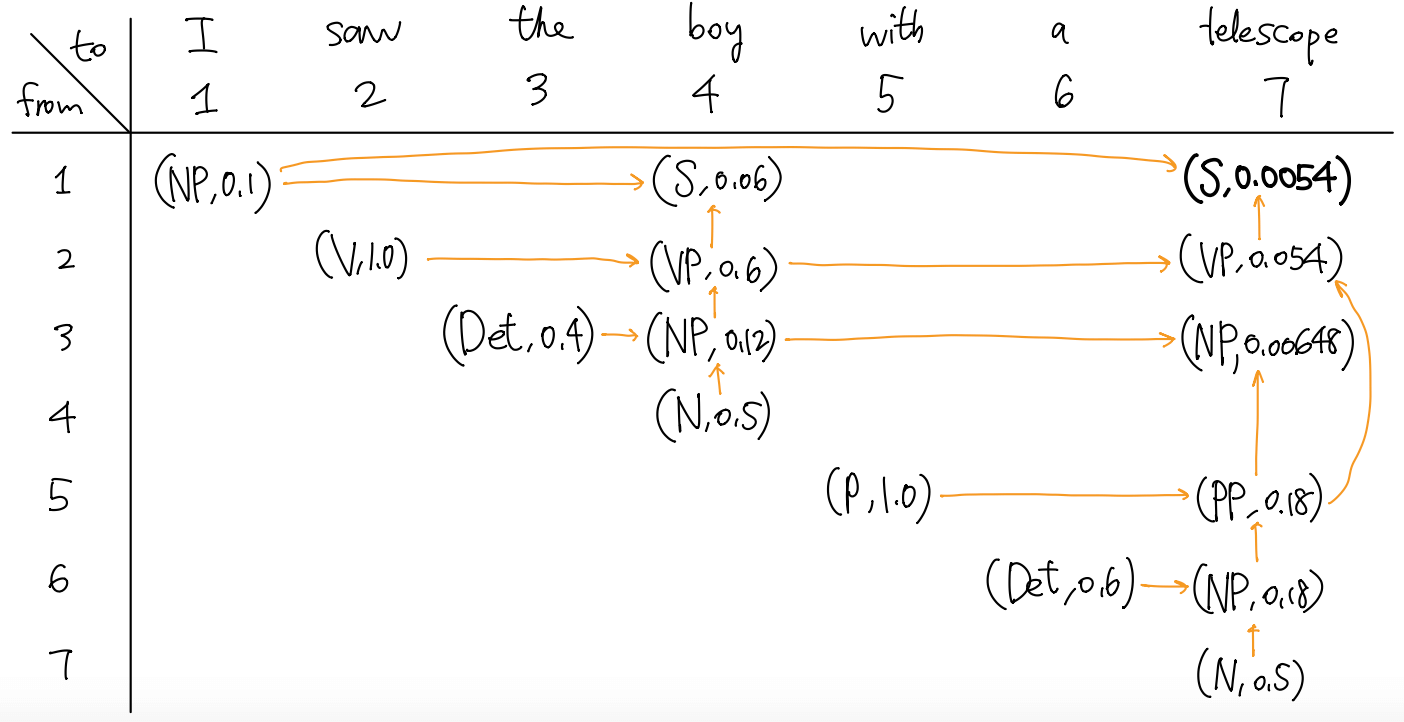
最终复原的语法分析树为

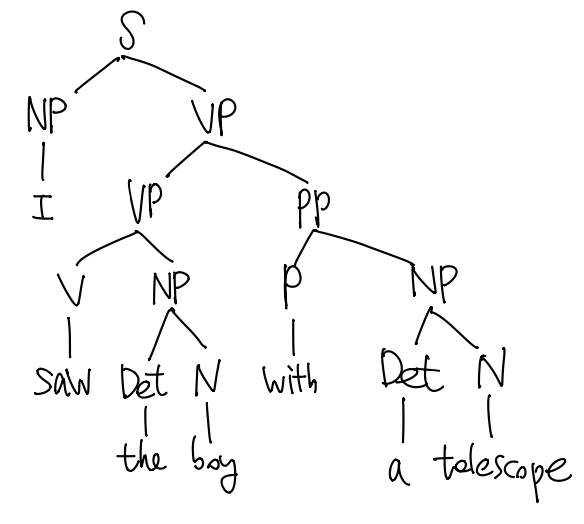
6.2.4 Evaluation

F1: compare the edge set produced by your parser and the gold ones.

这种语法分析方式有一些缺点:

• Lack of sensitivity to lexical information
• Lack of sensitivity to structural frequencies

6.3 Dependencies

6.3.1 Dependency structures

Relations to characterize the dependency structures:

• binary relations: head \(\to\) dependent
• head \(H\): the central organizing word
• dependent \(D\): often act as a modifier

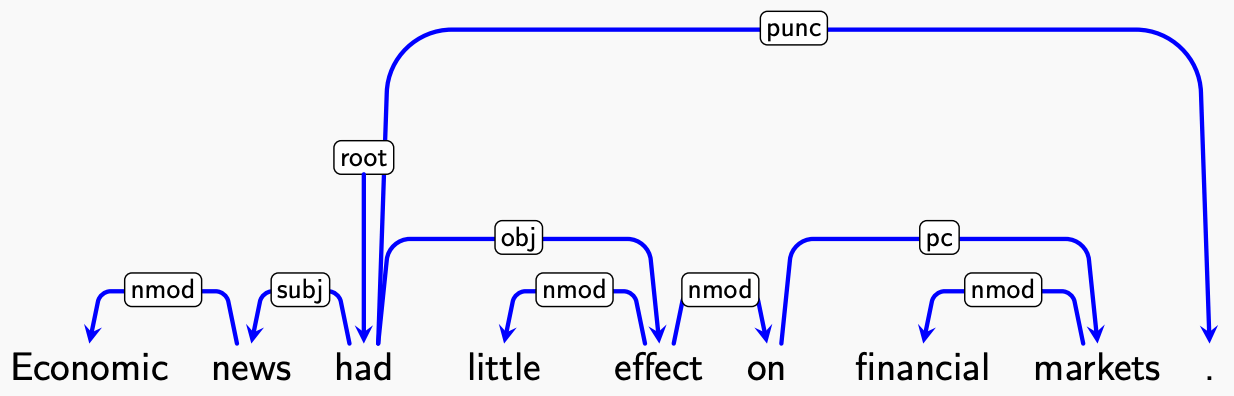
所有的依存关系可以构成一张有向图 \(G\), 其中的有向边形如 \((i,j,k)\) (\(i\to j\) with type \(k\)), 称为依存弧 (dependency arc). 我们希望 \(G\) 满足:

• 弱连通: \(G\) 对应的无向图连通.
• 无环: 若 \(i\to j\), 则不存在 \(j\) 到 \(i\) 的路径.
• 单头约束 (single-head): 若 \(i\to j\), 则不存在 \(k\neq i\) 使得 \(k\to j\).
  • 每个词只能依存一个 head.
• 投射性 (projective): 若 \(i\to j\), 则对任意 \(k\) 满足 \(i<k<j\) 或 \(j<k<i\), 有从 \(i\) 到 \(k\) 的路径.
  • 结合前面的性质, 投射性保证依存弧不会交叉. 投射性将单词在句子中的排序与 dep structure 联系起来. 一个非投射句子: A hearing is scheduled on the issue today, 其中 on the issue 修饰 hearing.
  • 有些时候不要求 projectivity:
    • 长距离依赖.
    • 自由词语顺序.

6.3.2 Dependency parsing

我们介绍基于转移的 (transition-based) 依存解析算法. 这是一种贪心思想的增量式算法 (不考虑历史; 不能保证得到全局最优).

一个转移系统 (transition system) 是一个四元组 \(S=(C,T,c_s,C_t)\), 其中:

• 配置集 \(C\), 即所有状态的集合.
• 转移集 \(T\).
• 初始状态映射 \(c_s\), 将一个句子映射到 \(C\) 中的某个状态.
• 终止状态集合 \(C_t\subset C\).

基于转移的依存解析的步骤如下: (输入一个句子 \(x=(w_i)_{i=0}^n\), 其中 \(w_0={\sf ROOT}\))

1. 初始状态 \(c\leftarrow c_s(x)\).
2. 重复执行直到 \(c\in C_t\):
   • 取得最佳转移 \(t\leftarrow o(c)\).
   • 状态转移 \(c\leftarrow t(c)\).

其中映射 \(o:C\to T\) 称为 oracle function, 它给出了每个状态下的最佳转移操作. Oracle 可以由一个分类器近似: \[ o(c) = \argmax_{t}[ \textsf{ScoreOfTransition}(c,t;\theta) ]. \]

6.3.3 The arc-standard transition algorithm

基于转移的依存解析可以用栈实现. 对于输入句子 \(x=(w_i)_{i=0}^n\), 状态 \(c\in C\) 是一个四元组 \(c=(x,\sigma,\beta,A)\), 其中

• \(\sigma\) 是一个包含 \(w_0,\dots,w_m\) 的栈 (\(m\leq n\)).
• \(\beta\) 是一个包含 \(w_{m+1},\dots,w_n\) 的队列.
• \(A\) 是一个包含了若干依存弧的集合.

此时转移系统的初始状态为 \(c_s(x):=([0],[1,\dots,n],\emptyset)\). 终止状态形如 \(c=(\sigma,[],A)\). 转移集 \(T\) 包含如下的元素:

• Shift: \((\sigma,i|\beta,A)\to(\sigma|i,\beta,A)\).
  • 从队列头移到栈顶.
• Left-arc of type \(k\): \((\sigma|i,j|\beta,A)\to(\sigma,j|\beta,A\cup\{(j,i,k)\})\).
  • \(i<j\), 所以该依存弧从较大的 \(j\) 指向较小的 \(i\), 是向左的.
  • 将 \(i\) 丢掉.
• Right-arc of type \(k\): \((\sigma|i,j|\beta,A)\to(\sigma|i,\beta,A\cup\{(i,j,k)\})\).

其中 \(\sigma|i\) 表示栈顶为 \(i\) 的栈; \(j|\beta\) 表示队列头为 \(j\) 的队列.

若句子长度为 \(n\) (不包含 ROOT), 则 action 的个数为 \(2n\). 该算法只能生成 projective 的依存图.

6.3.4 Evaluation

一些特点:

• Greedy algorithm can go wrong, but usually reasonable accuracy.
• No notion of grammaticality (so robust to typos).

如何评估一个解析结果?

• 精确匹配: 图完全一样.
• 边集匹配: 有多少条边正确.
  • Labeled Attachment Score (LAS): 边一样.
  • Unlabeled Attachment Score (UAS): 边和类型都一样.