自然语言处理基础 | 3 序列任务
4 Sequence Tagging
给句子中的每个词贴标签, 例如
- 词性标注
- 分词 (标记 B, I)
- NP Chunking: find basic noun phrases from text.
- B: beginning of a NP
- I: continuing NP
- O: other words
- Named Entity Recognition: find named entities from text, e.g., names of persons, locations, organizations, etc.
一大困难是歧义性 ambiguity.
4.1 Hidden Markov Models
4.1.1 Assumptions
设长度为 \(n\) 的句子 \((x_1,\dots,x_n)\), 每个单词的标签 (POS, part-of-speech) 为 \((y_1,\dots,y_n)\). 则我们关心的是在 \(x_i\) 条件下, \(y_i\) 概率的最大值: \[ \argmax_{(y_1,\dots,y_n)} p(y_1,\dots,y_n\mid x_1,\dots,x_n). \] 这等价于求解 \[ \argmax_{(y_1,\dots,y_n)}\; \underbrace{p(y_1,\dots,y_n)}_{\sf LM}\; p(x_1,\dots,x_n\mid y_1,\dots,y_n). \] 注意到第一项其实就是一个 language model, 可以用 bigram 或者 trigram 表示, 而对于第二项, 我们做出如下假设: (conditional independent assumption) \[ p(x_1,\dots,x_n\mid y_1,\dots,y_n)=\prod_{i=1}^np(x_i\mid y_i), \] 就得到了 hidden Markov model (HMM). 模型参数包括:
- (transition probabilities) 由标签得到下一个标签, 即 bigram 或者 trigram 的参数 \(p(y_n\mid y_{n-1})\) 或 \(p(y_n\mid y_{n-2},y_{n-1})\).
- (emmision probabilities) 由标签得到单词, \(p(x_n\mid y_n)\).
它的运作原理:
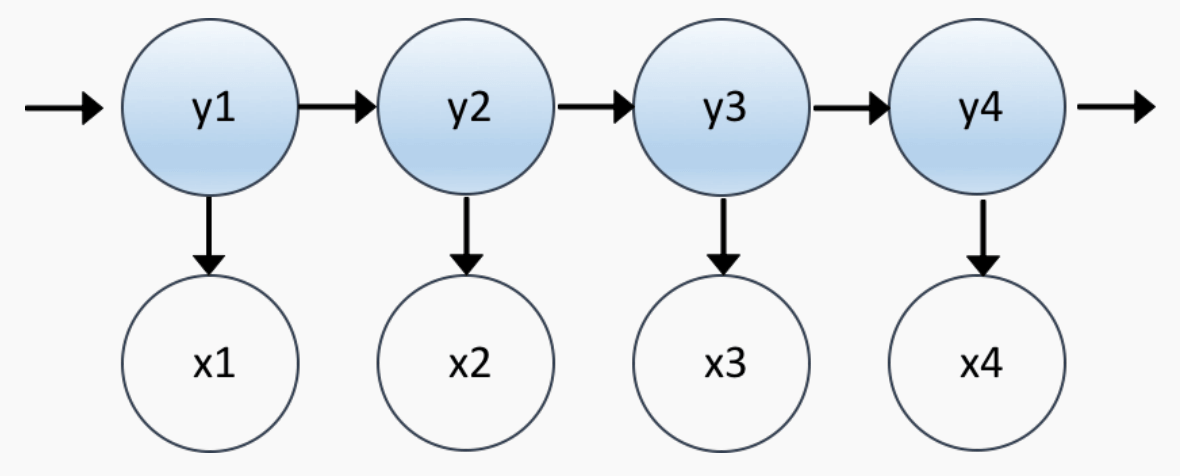
- 初始状态 \(y_1\sim P_{\sf start}(Y)\).
- 根据 \(y_1\) 得到 \(x_1\sim P_{\sf emmision}(X\mid y_1)\) (emmision).
- 根据 \(y_1\) 得到 \(y_2\sim P_{\sf transition}(Y\mid y_1)\) (transition).
以此类推, 直到结束.
4.1.2 Parameter estimation
类似于 n-gram, 通过 MLE 进行参数估计.
4.1.3 Decoding
给了一个训练好的 HMM 模型 (包括所有参数), 以及一个句子 \((x_1,\dots,x_n)\), 我们如何找到最优的 POS 序列 \((y_1,\dots,y_n)\) 使得其 transition probs (这里用 trigram) 和 emmision probs 的乘积最大?
暴力搜索肯定不行, 我们考虑动态规划, 即 Viterbi 算法. 该算法维护一个动态规划表 \(\pi(k,u,v)\), 表示 the maximum probability of any tag sequences ending with \(u,v\) at position \(k\), 即 \[ \pi(k,u,v) := \max_{\substack{y_{k-1}=u\\y_k=v}} \pqty{ \prod_{i=1}^k p(y_i\mid y_{i-2},y_{i-1}) \cdot \prod_{i=1}^k p(x_i\mid y_i) }. \] 记第 \(k\) 位置的所有可能的 POS 集合为 \(S_k\). 在第 \(0\) 位置为 \({\sf START}\), 第 \(n+1\) 位置为 \({\sf STOP}\).
初始化 \(\pi(0,{\sf START},{\sf START})=1\).
对所有 \(k\in\{1,2,\dots,n\}\) 以及 \(u\in S_{k-1}\) 和 \(v\in S_k\),
状态转移: \[ \pi(k,u,v) = \max_{w\in S_{k-2}} \pi(k-1,w,u) \cdot p(v\mid w,u) \cdot p(x_i\mid v). \]
记录路径: \[ {\sf path}(k,u,v) = \argmax_{w\in S_{k-2}} \pi(k-1,w,u) \cdot p(v\mid w,u) \cdot p(x_i\mid v). \]
复原路径 (POS):
- 枚举计算 \(y_n,y_{n-1}\).
- 迭代 \(y_{n-2}={\sf path}(n,y_{n-1},y_n)\) 等等.
计算复杂度: \(O(n|S|^3)\).
4.2 Perceptron models
A classifier for sequence tagging. 与 HMM 不同, classifier 为每个单词分别预测其 POS (individual decisions), 而 HMM 是 sequence of decisions.
4.2.1 Features
回顾 NLP 中的 feature, 这是一些关于 \((x,y)\) 的 0/1 函数. 如果我们要 tag 这句话 I love Beijing 中的 Beijing, 则我们可以构造一些关于该单词的 clues: \[ \Align{ &\verb|cur_Beijing|,& &\verb|pre1_love|,& &\verb|pref_Be|,& &\verb|cap_1|,&\dots } \] 把 clue 与 labels (NNP, VB...) 结合, 就得到了 feature: \[ \Align{ &\orange{\verb|cur_Beijing_NNP|},& &\orange{\verb|pre1_love_NNP|},& &\orange{\verb|pref_Be_NNP|},& &\orange{\verb|cap_1_NNP|},&\dots \\ &\blue{\verb|cur_Beijing_VB|},& &\blue{\verb|pre1_love_VB|},& &\blue{\verb|pref_Be_VB|},& &\blue{\verb|cap_1_VB|},&\dots \\ &\dots& &\dots& &\dots& &\dots&\dots } \] 每个 feature 的值为 0/1. 我们构建一个线性分类器, 为每个 feature 配一个权重 \(\lambda\), 有 \[ \Align{ &\orange{\lambda_\verb|cur_Beijing_NNP|},& &\orange{\lambda_\verb|pre1_love_NNP|},& &\orange{\lambda_\verb|pref_Be_NNP|},& &\orange{\lambda_\verb|cap_1_NNP|},&\dots \\ &\blue{\lambda_\verb|cur_Beijing_VB|},& &\blue{\lambda_\verb|pre1_love_VB|},& &\blue{\lambda_\verb|pref_Be_VB|},& &\blue{\lambda_\verb|cap_1_VB|},&\dots \\ &\dots& &\dots& &\dots& &\dots&\dots } \] 用优化算法求得 \(\lambda\)s 之后, 计算该句话中 Beijing 每个类别的得分: \[ \Align{ {\sf score}({\sf Beijing},\orange{\sf NNP}) &= \orange{\verb|cur_Beijing_NNP|}\cdot \orange{\lambda_\verb|cur_Beijing_NNP|} + \cdots \\ {\sf score}({\sf Beijing},\blue{\sf VB}) &= \blue{\verb|cur_Beijing_VB|}\cdot \blue{\lambda_\verb|cur_Beijing_VB|} + \cdots \\ \dots\hspace{3em} } \] 最终取得分最大的那一类作为预测值.
4.2.2 The perceptron alg.
感知机算法 (the perceptron algorithm) 是优化 \(\lambda\)s 的一种算法.
输入: 训练集 \(\{(x_k,y_k)\}\), 其中 \(x_k\) 是单词, \(y_k\) 为 POS label.
初始化 \(\lambda\)s 为零.
重复执行 \(T\) 次:
- 对每个训练数据 \((x_k,y_k)\):
- 计算预测值 \(z\leftarrow\argmax_{y\in{\sf GEN}(x_k)}\sum_i\lambda_{f_i(x_k,y)} f_i(x_k,y)\).
函数 \({\sf GEN}(x)\) 给出了单词 \(x\) 所有可能的标签的集合.
- 更新参数: 如果 \(z\neq y_k\)
(分类错误), 则:
- \(\lambda\leftarrow\lambda+f(x_k,y_k)-f(x_k,z)\).
惩罚导致分类错误的权重 (减一)、奖励使得分类正确的权重 (加一).
- 对每个训练数据 \((x_k,y_k)\):
输出 \(\lambda\)s.
4.2.3 The structured perceptron alg.
The perceptron algorithm 是纯粹局部的 (local), 将每个单词分开处理. 我们希望算法可以考虑一个句子中的历史 labels, 这需要我们将一个句子当成一个整体来预测 (global).
首先引入一些 global 的 features, 比如 \[ \Align{ &\pink{\verb|prev_N_cur_N|},& &\pink{\verb|prev2_DT_N_cur_N|},&\dots } \] 即 "前一个词标签为 N, 预测当前也为 N" 和 "前两个词标签为 DT, N, 预测当前为 N" 等等.
结构感知机算法 (the structured perceptron algorithm) 流程如下:
输入: 句子集 \(S\), 单词集 \(\{(x_k,y_k)\}\), 其中 \(x_k\) 是单词, \(y_k\) 为 POS label.
初始化 \(\lambda\)s 为零.
重复执行 \(T\) 次:
对每句话 \(s\in S\), 每个单词 \(x\in s\) 和可能的标签 \(y\in{\sf GEN}(x)\):
- 计算得分 \({\sf score}[x,y]\leftarrow\sum_i\lambda_{f_i(x,y)}f_i(x,y)\).
Score table 是一个 \(|s|\times|{\sf GEN}(x)|\) 大小的矩阵 / lattice.
- 用 Viterbi 算法解码出 \(s\) 的最佳 POS 序列 \(y\)s.
由于每个单词的 score 与前一个单词的 label 的预测值有关 (因为有 global features), 所以不能分别计算 score, 而是需要从头开始, 用动态规划算法计算出一个最优 score 序列.
- 比较 \(y\)s 和 gold-standard 序列 \(y^*\)s, 更新 \(\lambda\)s.
4.2.4 Beam search
Score table 大小可能非常大, 用 Viterbi 算法效率比较低. 束搜索 (beam search) 是一种近似算法. 比如说, \({\sf GEN}(x)\) 一共有 \(200\) 个元素, 我们觉得它太大了, 于是可以在 DP 时只保留 \(64\) 个得分最高的类别, 即在每次状态转移时只考虑 \(64\times200\) 种组合, 然后取得分最大的 \(64\) 个保存下来.
- Early stop.
- CRF.
5 Seq2seq NNs
序列 \(\to\) 序列的任务, 如序列翻译, 序列标注.
5.1 RNNs
Encoder-Decoder 架构. 将输入序列编码为一个固定长度向量, 再输入 decoder, 自回归生成翻译结果. RNN 采用 LSTM.
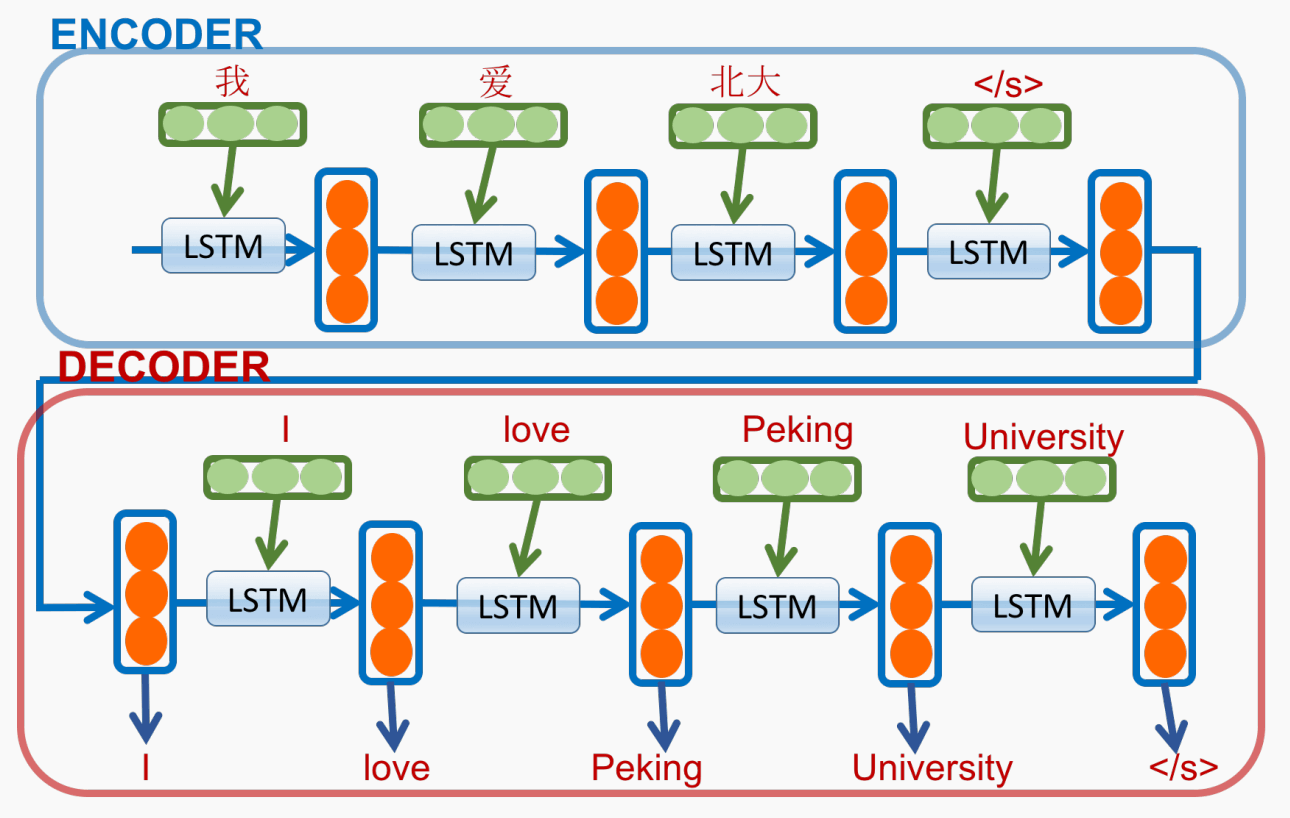
数学模型. 给定输入序列 \((x_1,\dots,x_T)\) (如中文句子), 目标是生成翻译后的句子 \((y_1,\dots,y_{T'})\) (如英语句子), 建模为 \[ p(y_1,\dots,y_{T'}) = \prod_{t=1}^{T'} p(y_t\mid v,y_1,\dots,y_{t-1}), \] 其中 \(v\) 是 LSTM 给出的 \((x_1,\dots,x_T)\) 的向量表示.
问题是不能明确捕获两个单词 (如 “爱” 和 ”love“) 间的明确对应.
5.2 Transformers
5.2.1 The attention mechanism
在 decoder 中, 显式地考虑每个输入单词对当前单词的影响.
- Query vector \(q\): decoder 的隐状态.
- Key vector \(k\): 所有 encoder 的隐状态.
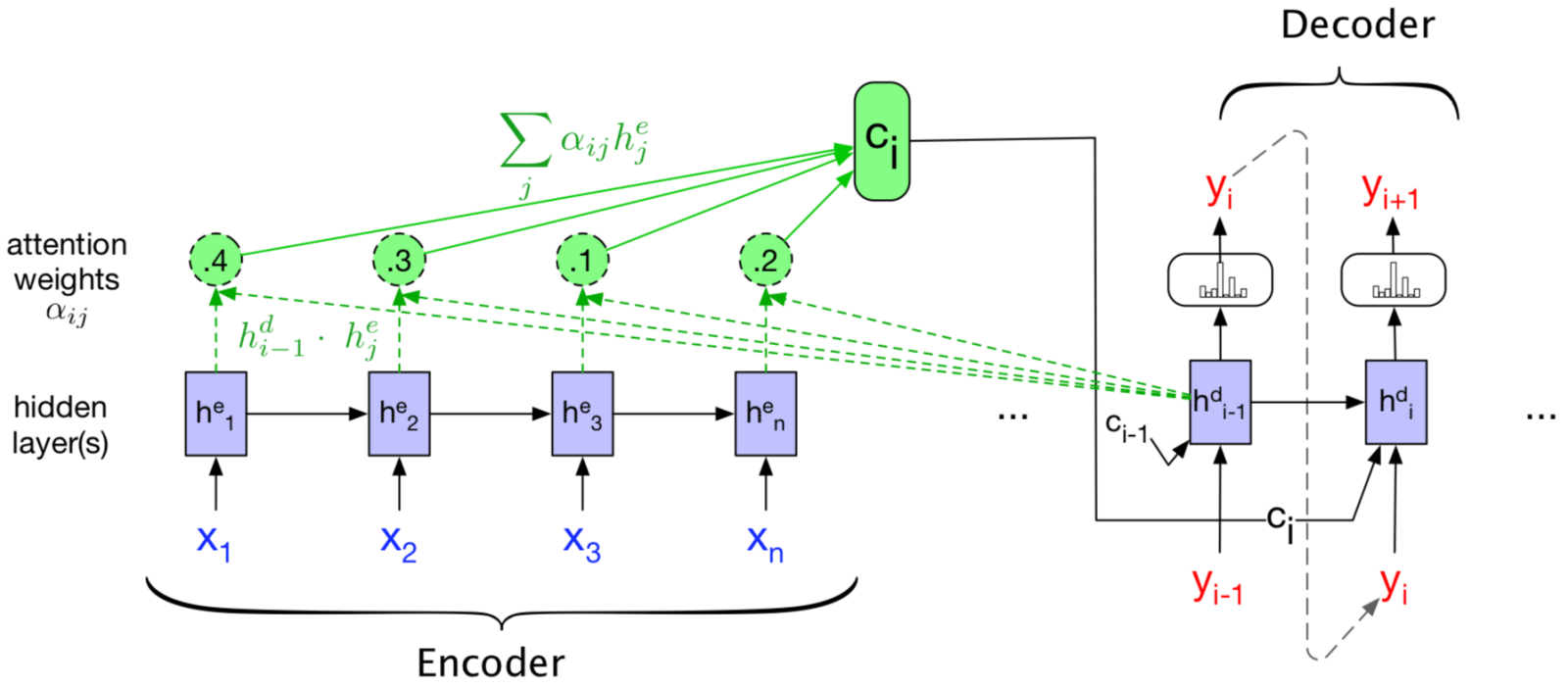
不同的计算方式:
MLP: \[ \operatorname{attn}(q,k) = w_2\T\tanh(W[q,k]). \] 当 \(q,k\) 长度较小时表现最佳.
Bilinear: \[ \operatorname{attn}(q,k) = q\T Wk. \]
Dot product: \[ \operatorname{attn}(q,k) = q\T k. \]
Scaled dot product: \[ \operatorname{attn}(q,k) = \frac{q\T k}{\sqrt{d}}, \] 其中 \(q,k\in\R^d\).
5.2.2 Self-attention
上面的 attention 是 encoder 与 decoder 间的联系, 我们也可以建立统一个序列中单词间的联系 (build contextual representation of a word by integrating information from surrounding words).
对于一个序列 \(X=(x_1\T,\dots,x_n\T)\T\) (原始 embedding), 通过三个线性层 \(W^Q,W^K,W^V\) 分别得到 query, key, value: \[ Q=XW^Q, \qquad K=XW^K, \qquad V=XW^V. \] 应用 scaled dot-product attention, \[ \operatorname{attn}(Q,K,V) = \operatorname{softmax}\!\left(\frac{1}{\sqrt{d}} Q\T K \right) V. \] Multi-head attention 是若干并行的 scaled dot product attention 的拼接, 再投影回原本的维度: \[ \operatorname{mha}(Q,K,V) = \left[ \bigoplus_{i=1}^h \operatorname{attn}(QU^Q_i,KU^K_i,VU^V_i) \right] U^O, \] 其中 \(U^Q_i,U^K_i,U^V_i\) 是每个 head 之前额外的线性层, \(U^O\) 是最后的投影层.
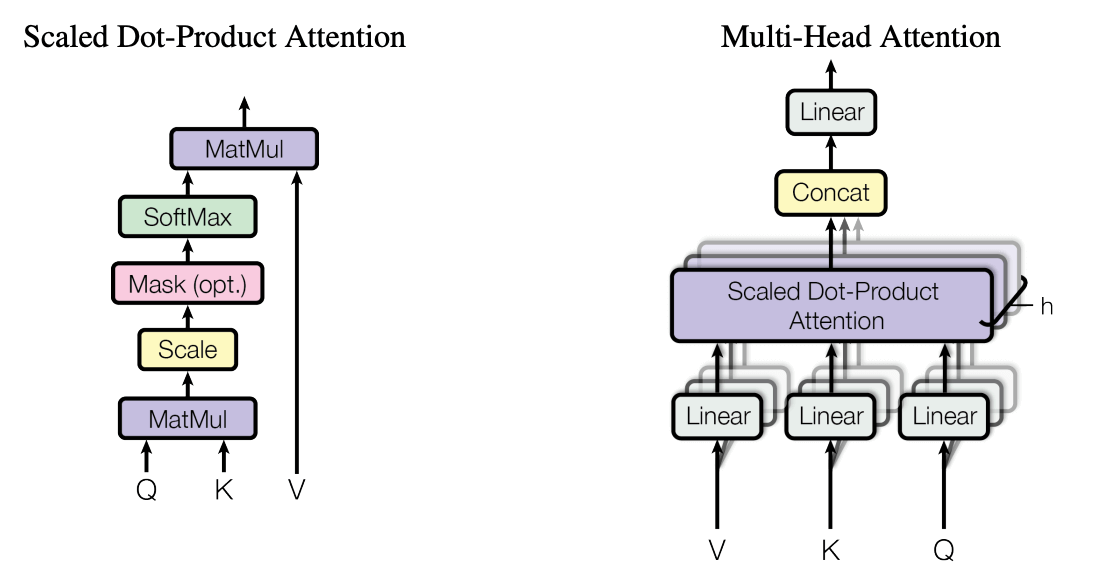
5.2.3 Additional tricks
Attention tricks:
- Self attention: Each layer combines words with others
- Multi-headed attention: 8 attention heads learned independently
- Scaled Dot-product attention: Remove bias in dot product when using large networks
- Positional Encodings: Attention 是排列不变的, 需要加入位置编码
- Make sure that even if we do not have RNN, can still distinguish positions
- 区分 “狗咬人” 和 “人咬狗”
Training Tricks
- Layer normalization: Help ensure that layers remain in reasonable
range
- Operate on each token level, \(\mu=0\), \(\sigma=1\).
- Specialized training schedule: Adjust default learning rate of the Adam optimizer
- Label smoothing: Insert some uncertainty in the training process
- Masking for efficient training
- We want to perform training in as few operations as possible using big matrix multiplies
- Causal mask