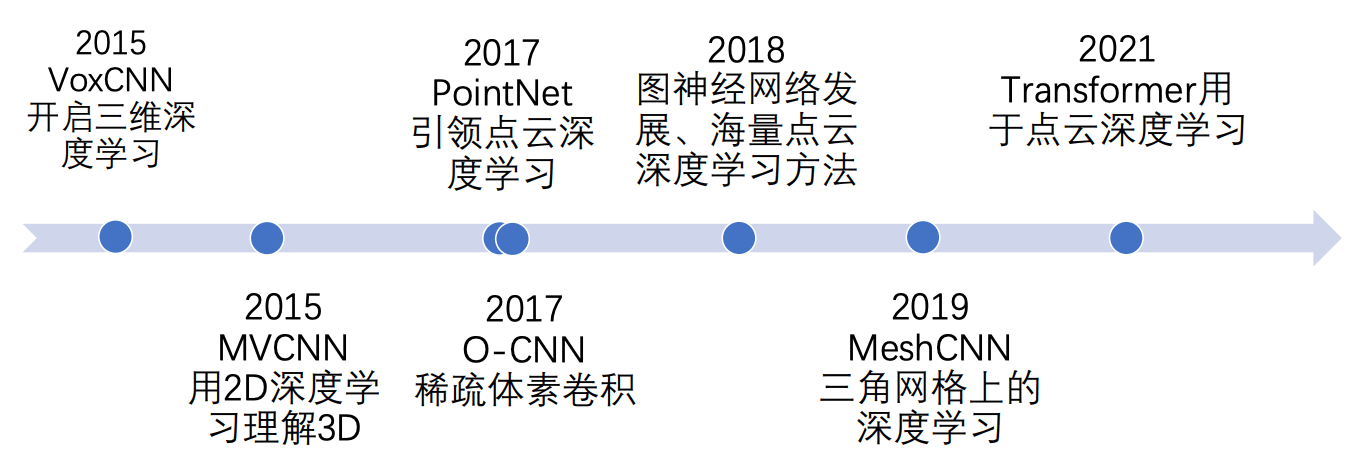
三维深度学习
与 CV 类似, 三维深度学习的基本任务包括:
- 三维理解: 分类、分割、检测...
- 三维生成: 从图像 / 文本等生成三维模型.
与二维深度学习相比, 三维深度学习有一些挑战:
- 计算代价高: 三维模型的数据量与 \(N^3\) (\(N\) 为分辨率) 成正比.
- 表达的多样性: 二维表达基本只有图像一种, 而三维表达方式多种多样 (体素、三角形网格、SDF、点云、样条...).
本文介绍几种 3D 深度学习中最主要的几种神经网络, 它们可以大致分为 CNN 和 Transformer.
3 3D CNNs
3.1 体素网络
3.1.1 VoxCNN
体素是图像的自然推广. 图像是 \(H\times W\) 个像素 (pixel) 组成的表格, 而体素是 \(H\times W\times D\) 个体素 (voxel) 组成的三维网格. 而体素卷积神经网络则是图像的卷积神经网络 (CNN) 的推广, 其卷积核是三维的.
体素 CNN 的优点是通用性强, 而缺点是三维卷积的计算量太大, 一般分辨率不超过 \(\sim60\). 体素 CNN 是最早的 3D 神经网络, 它证明了 3D 深度学习的可行性. 后续的工作集中在对体素 CNN 的改进上.
3.1.2 *Multiview CNN
原论文: Multi-view Convolutional Neural Networks for 3D Shape Recognition (ICCV 2015).
为了提升体素 CNN 的效率, 我们将三维物体表达为 \(n\) 个视角下的图像, 然后应用图像 CNN 对每个照片进行理解, 由此得到了得到 Multiview CNN (MVCNN). 为了将多个视角下图像 CNN 的输出 \(z_1,\dots,z_n\) 融合起来, 作者提出了 "view pooling" 层, 即取多视角输出的最大值 \(\max\{z_1,\dots,z_n\}\), 再将结果过一遍 CNN 得到分类结果. 下图展示了 MVCNN 的完整结构 (图自原论文).
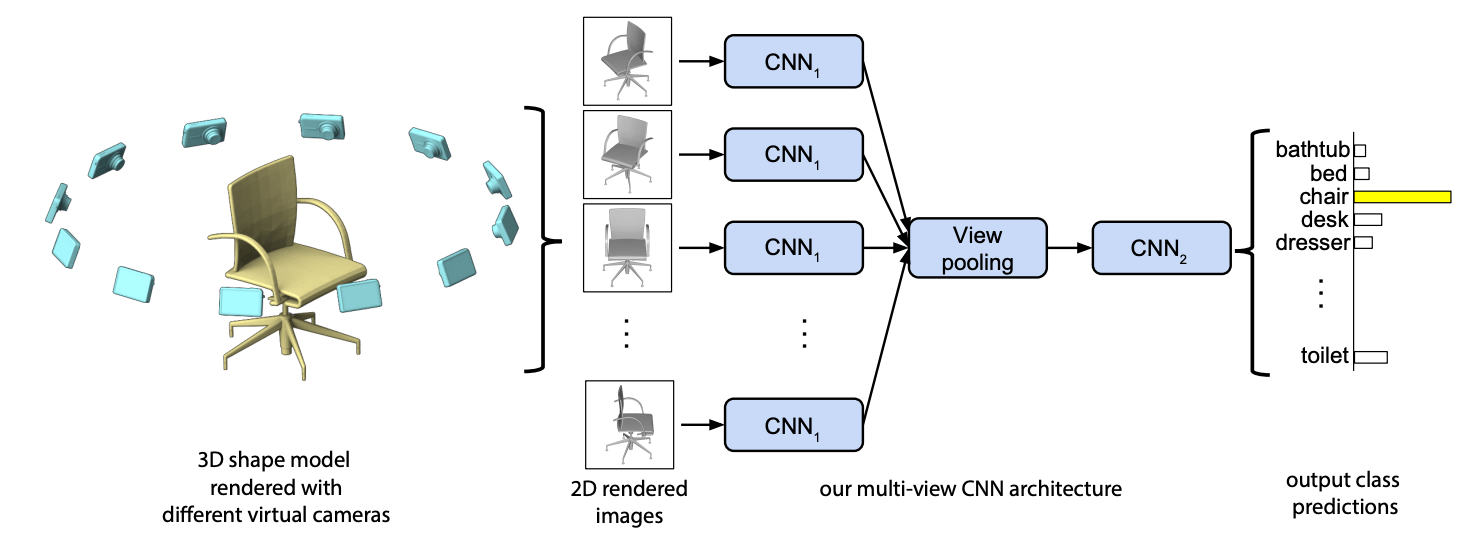
MVCNN 的优点是高效, 它有效利用了图像卷积神经网络. 它的缺点也很明显: 三维到二维的投影损失了许多信息, 可能存在自遮挡; 另外也很难确定最优视点.
Multiview Diffusion 在 MVCNN 的基础上做 3D 生成. 它首先利用扩散模型生成若干视角的图片, 然后利用 CV 中的三维重建算法构建一个三维模型 (比如利用二维草图进行三维建模).
3.2 点云网络
3.2.1 PointNet
原论文: PointNet: Deep Learning on Point Sets for 3D Classification and Segmentation (CVPR 2017).
点云 \({\cal P}=\{x_i\}_{i=1}^n\) 有三个特点: 散乱、无序、旋转与平移不变性. 无序性要求神经网络 \(F\) 关于点云满足:
- (对称性) \(F(x_1,\dots,x_n)=F(x_{\sigma(1)},\dots,x_{\sigma(n)})\), 对任意 \(\sigma\in S_n\).
这样的对称函数有很多, 比如求和, max, min 等. 如果我们能找到一个对称函数 \(g\), 那么就能设计出一个点云神经网络 \[ F := \gamma \circ g \circ (\underbrace{h \oplus\dots\oplus h}_n), \] (其中 \(h\), \(\gamma\) 为任意神经网络) 则 \(F\) 自动满足对称性. 具体来说, PointNet 的朴素版 (vanilla) 取 \(g=\operatorname{MAX}\) (element-wise maximum), 并将 \(h,\gamma\) 设为 MLP, 如下图.
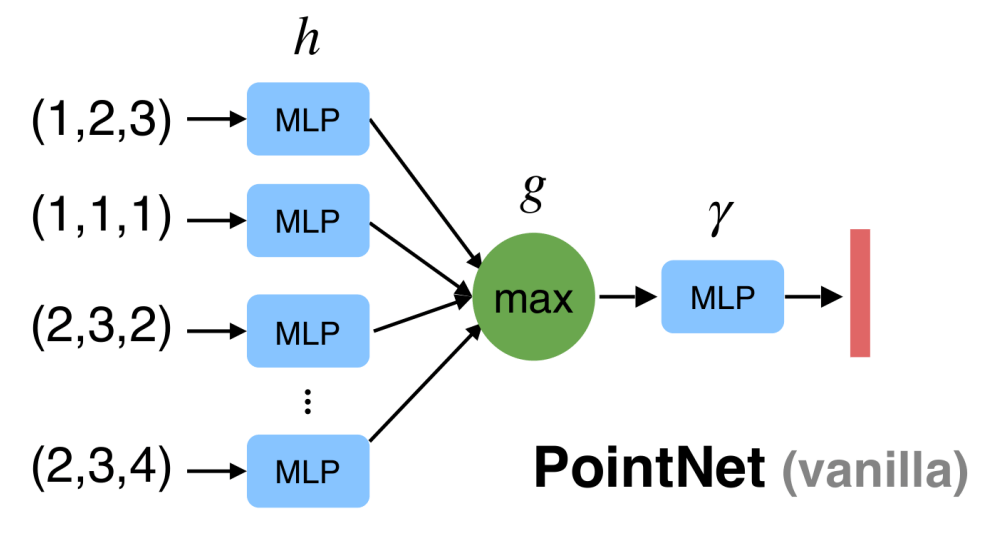
- 基于 MLP 的无穷逼近能力 (universal approximation thm.), 论文还证明了 PointNet vanilla 的无穷逼近能力.
点云还具有旋转和平移不变性, 一个点云 \({\cal P}\) 实际上代表了它被三维欧氏群作用所得的轨道 \({\cal O}\). 我们希望神经网络可以自动学习出 \({\cal O}\) 最佳的代表元 (点云的最佳姿态), 即欧氏变换 \((R,t)\). 由此我们引入 T-Net 用于学习最佳欧氏变换, 再将欧氏变换应用到点云 \({\cal P}\) 得到最佳姿态, 继而作为点云网络的输入.
将这些基本单元组合起来, 就可以得到用于分类 / 分割的 PointNet (图自原论文).
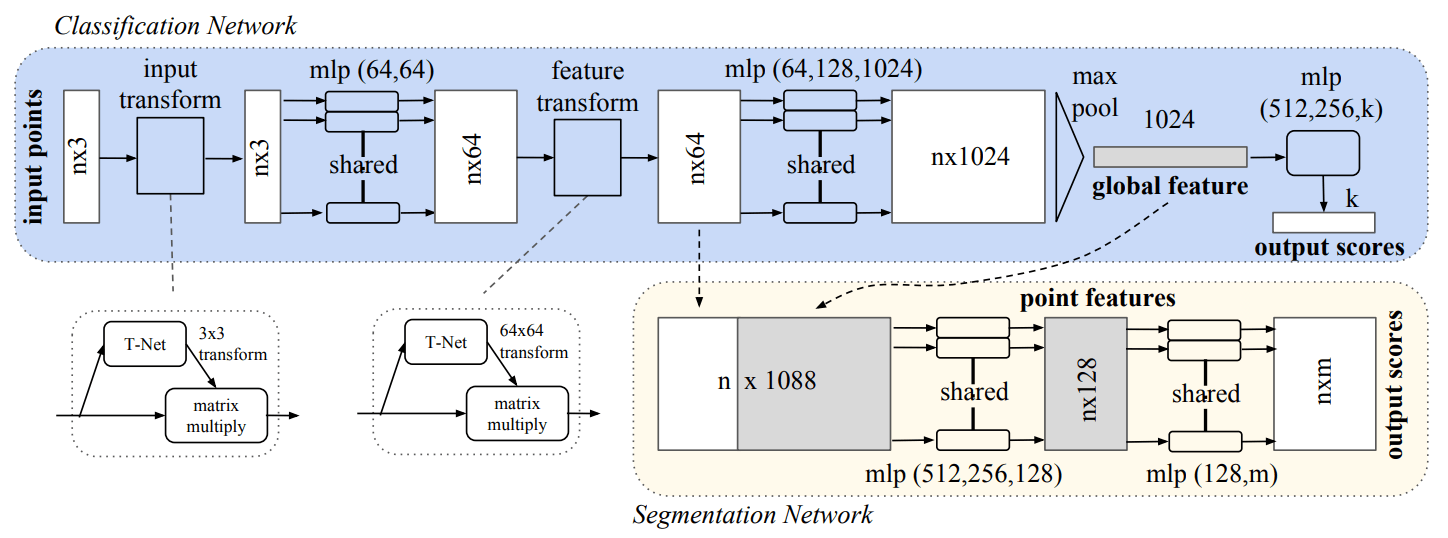
- 分类: 由若干 T-Net 和 vanilla 模块组合而成.
- 分割: 分割需要对每个点输出一个 feature, 因此 Segmentation Net 的输入既包含 global feature, 又包含每个点的 feature.
3.2.2 点云的卷积
PointNet 没有层次结构, 无法提取多尺度的特征. 注意到卷积是有层级结构的, 我们能否为点云引入卷积操作?
图像卷积可以写作 \(f'(x)=\sum_{y\in{\cal N}(x)}w(x,y)f(x)\), 我们将其抽象为如下的 "抽象卷积" 操作: \[ \phi(x) = \bigodot_{y\in{\cal N}(x)} w(x,y,f(x),f(y)), \] 其中:
- \(\odot\) 是一种运算 (比如求和 \(\sum\) 或者 element-wise maximum \(\operatorname{MAX}\)).
- \({\cal N}(x)\) 是 \(x\) 的邻域 (对于图像来说是 \(x\) 附近的 \(d\times d\) 像素, 对于图 (graph) 来说是邻居节点).
- \(w(x,y,f(x),f(y))\) 是权重函数, 它与 \(x,y\) 以及其上的 feature 都有关 (比如 bilateral filter 的权重与空间和特征都有关).
要把卷积引入点云, 重点在于选择合适的邻域 \({\cal N}(x)\) 与权重 \(w(x,y,f(x),f(y))\).
KPConv / SplineConv 使用样条基函数 \(\phi\) 作为权重函数: \[ w(x,y,f(x),f(y)) = \phi(y-x) \cdot f(y). \] 这是图卷积 / 图像卷积一个很自然的推广.
NNConv 用一个 MLP 来学习出一个权重函数: \[ w(x,y,f(x),f(y)) = {\sf MLP}(y-x) \cdot f(y). \]
PointNet++ 把 \(f(y)\) 也作为 MLP 的输入: \[ w(x,y,f(x),f(y)) = {\sf MLP}[(x-y)\oplus f(y)]. \] (直和 \(\oplus\) 表示将两个向量拼接起来, 即 concatenate.) 运算 \(\odot\) 为 \(\operatorname{MAX}\). PointNet++ 的具体结构在下一小节介绍, 该 MLP 与 \(\operatorname{MAX}\) 合起来其实是一个 PointNet.
DGCNN 考虑特征的差异而非点坐标的差异: \[ w(x,y,f(x),f(y)) = {\sf MLP}[f(x)\oplus (f(y)-f(x))]. \] 运算 \(\odot\) 为 \(\operatorname{MAX}\).
3.2.3 PointNet++
原论文: PointNet++: Deep Hierarchical Feature Learning on Point Sets in a Metric Space (NeurIPS 2017).
PointNet++ 是 PointNet 的升级版, 它的核心是上面提到的 "点云卷积". 卷积 + 降采样操作可以让网络学习到不同尺度的特征. PointNet++ 的具体流程如下图 (图自原论文).
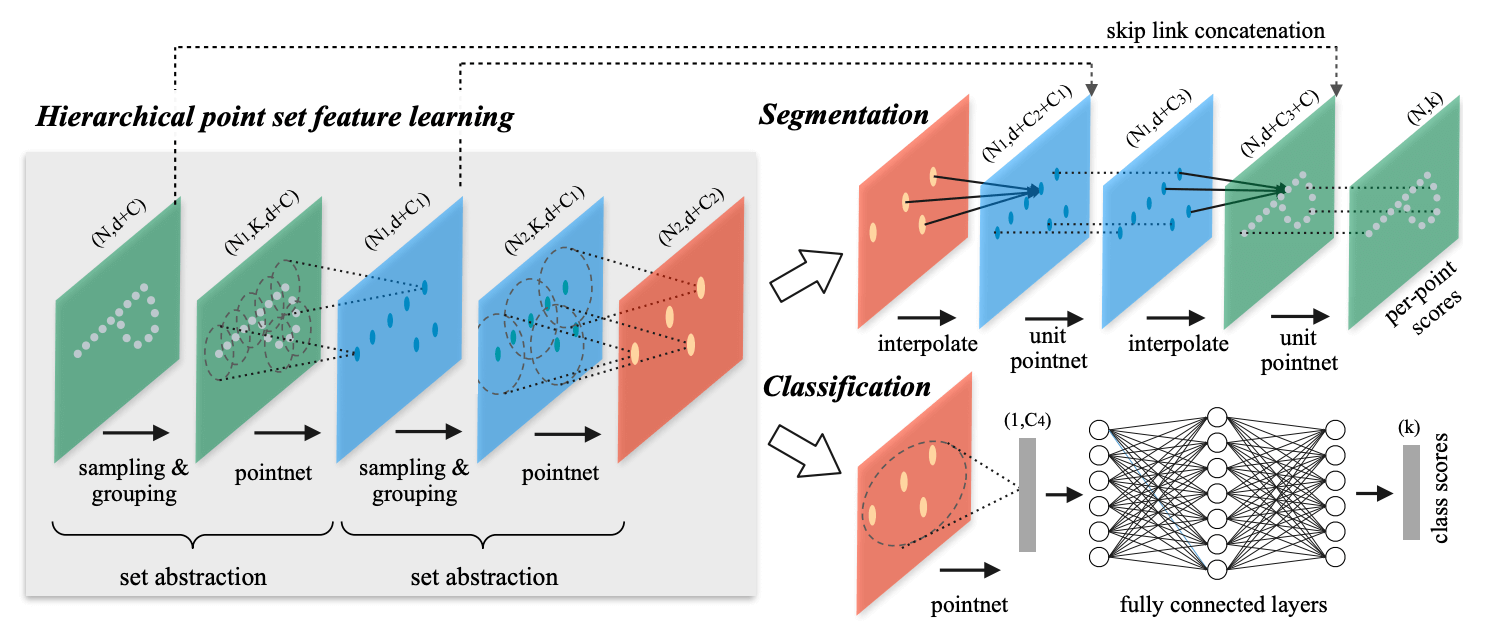
- Feature learning 由若干 set abstraction 模块组成,
每个模块都让点云更抽象化:
- Sampling: 利用最远点采样, 将点云降采样. (后续的研究表明, 效率更高的均匀格点采样也可以达到类似的效果.)
- Grouping: 以上面降采样得到的点作为中心点构造若干 local regions (所有到中心点的距离不超过某个半径的点) 为后面的 "卷积" 做准备.
- PointNet: 让每个 local region 分别过一遍 PointNet, 输出的特征作为中心点的特征. 将不是中心点的点删掉.
- Segmentation: 将稀疏的点云特征上采样, 最终得到原始点云中每个点的特征, 其中 unit PointNet 还接收来自 abstraction 模块的输入 (类似 ResNet).
- Classification: 一个 PointNet 加上一个全连接神经网络.
3.3 O-CNN
八叉树集稀疏性、层级性、序列性 (z-order curve) 于一体, 天然适合卷积、Transformer 等运算.
原论文: Wang et al, O-CNN: Octree-based Convolutional Neural Networks for 3D Shape Analysis (SIGGRAPH 2017).
基于八叉树的稀疏卷积 O-CNN 用八叉树存储稀疏的曲面信号, 并把神经网络的运算限制在非空信号上.
- 稀疏卷积: 八叉树的每个层级都有一些大小相同的正方体组成, 在上面可以进行三维卷积. 残缺不全的格子补零即可.
- 池化: 由于八叉树具有层级结构, 只需将八个子节点的特征取平均 / 最大值即可, 比图像的池化还方便.
稀疏卷积还可以基于别的数据结构——SparseConvNet 和 MinkowskiNet 在哈希表上进行稀疏卷积.
3.4 MeshCNN
最后我们介绍一个比较具有图形学特色的 mesh 上的神经网络.
原论文: MeshCNN: A Network with an Edge (SIGGRAPH 2019).
点云 CNN 和图 CNN 都围绕着顶点定义了卷积, MeshCNN 则在边上定义卷积.
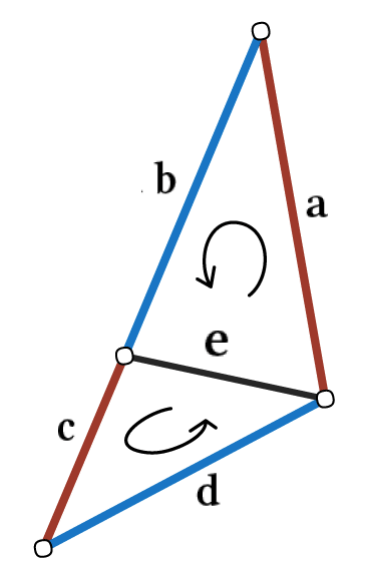
卷积: 如下图左 (图自原论文), 对于一个定向三角形网格, 一条边 \(e\) 的四个邻边有两种排列: \(abcd\) 或者 \(cdab\). 为了让特征与排列无关, 我们构造出 \[ (f_1,f_2,f_3,f_4) := (f_a+f_c,|f_a-f_c|,f_b+f_d,|f_b-f_d|). \] 有了如上的特征, 再配以可学习的权重 \((w_1,w_2,w_3,w_4)\), 就可以进行边卷积操作了: \[ \phi_i := \sum w_i f_i. \]
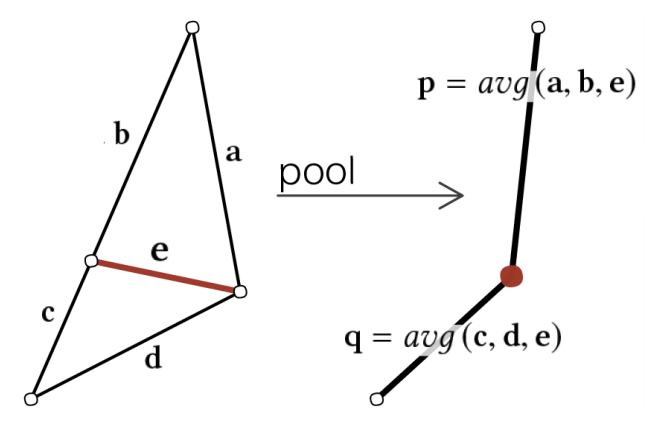
池化: 删除激活函数值最小的边, 下图右展示了 average pooling 操作 (图自原论文).
 |
 |
|---|
4 3D Transformers
Transformers 以其捕捉长距离依赖和多模态能力已经在语言、视觉、3D 多个领域广泛应用.
4.1 2D Transformers
Transformer 的核心是注意力 (attention) 模块, 它可以视作一种 "可微分的检索" (在上下文中检索信息). 输入 tokens 序列 \(X\), 该序列分别通过三个线性层 \(W_q,W_k,W_v\) 得到:
- \(Q=XW_q\) (query, 检索关键字),
- \(K=XW_k\) (key, 键),
- \(V=XW_v\) (value, 值),
注意力操作计算 query 和 key 的匹配程度, 并输出对应的 value: \[
\operatorname{attention}(X)
:= \operatorname{softmax}\pqty{
\frac1{\sqrt{D}}
QK\T
}V,
\] (其中 \(1/\sqrt{D}\)
是归一化项, \(D\) 为 key 的维数)
这也称作 scaled dot-product attention (下图左
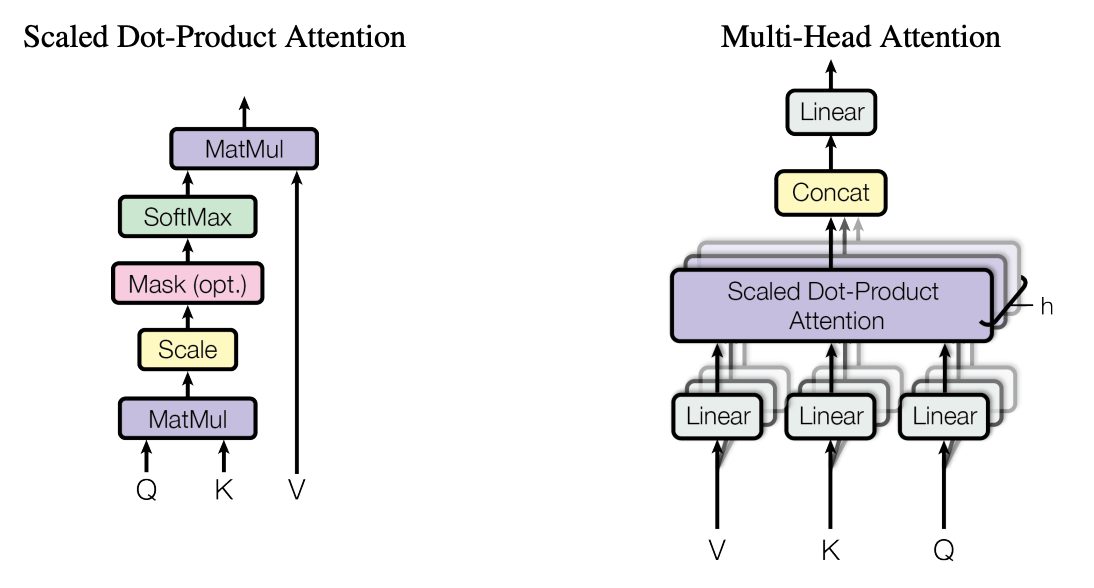 |
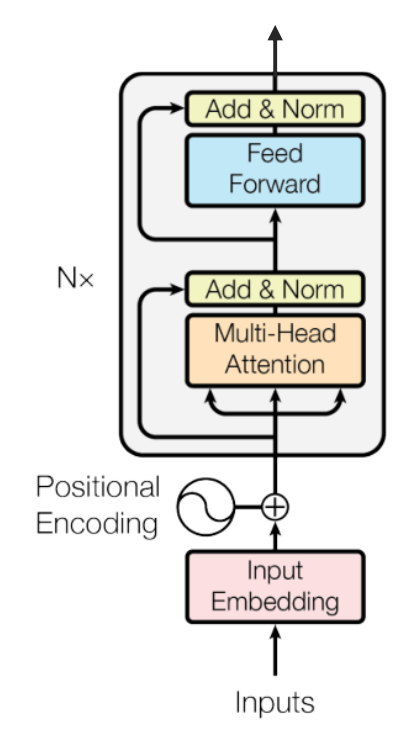 |
|---|
Vision Transformer (ViT)
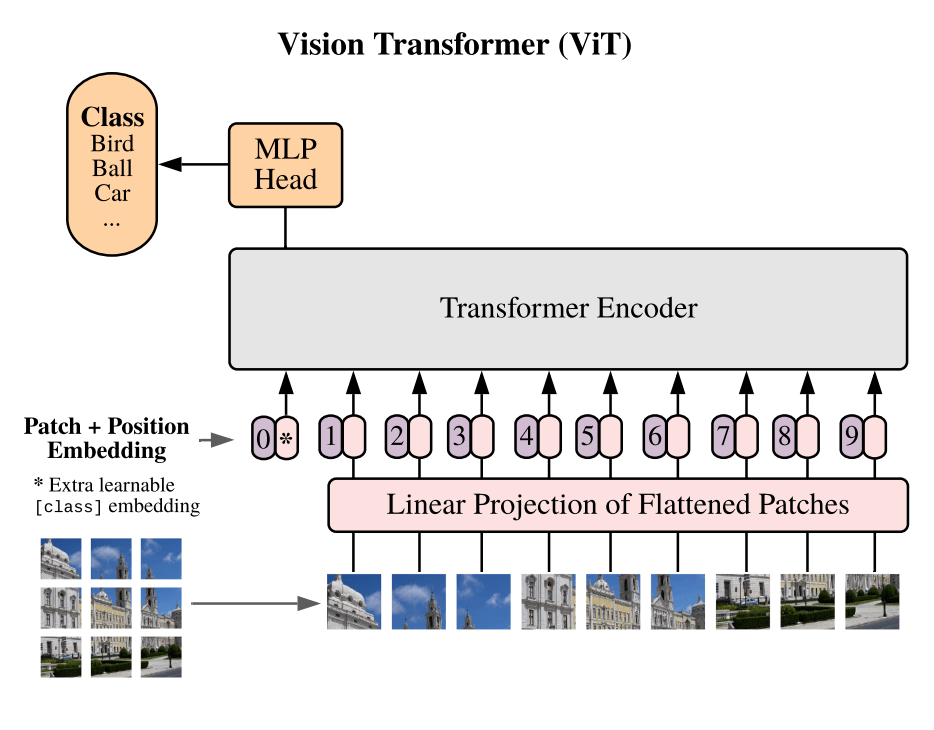
有趣的是, ViT 的作者认为该结构已完全抛弃了卷积, 只依赖 Transformer. 而 CNN 的发明者 Yann Le Cun 则指出, patch 上的线性层本质上还是一种卷积 (卷积核 \(P\times P\), 步长 \(P\)). 实际上, 卷积和线性层几乎是同一个东西:
- 全连接 \(\rightsquigarrow\) 核很大的卷积.
- 卷积 \(\rightsquigarrow\) patch-wise 共享权重的全连接.
设 token 序列长度为 \(N\), 则 attention 的矩阵乘法时间复杂度与 \(N^2\) 成正比, 导致 ViT 的序列长度 (即 patch 的数量 \(N=HW/P^2\)) 不能太长, 否则计算量和内存需求急剧增长.
Swin Transformer
- 第一层采用标准窗口划分.
- 下一层将窗口划分整体平移一个固定距离 (通常为窗口大小的一半), 让原来处于不同窗口的 token 现在被归入同一个窗口.
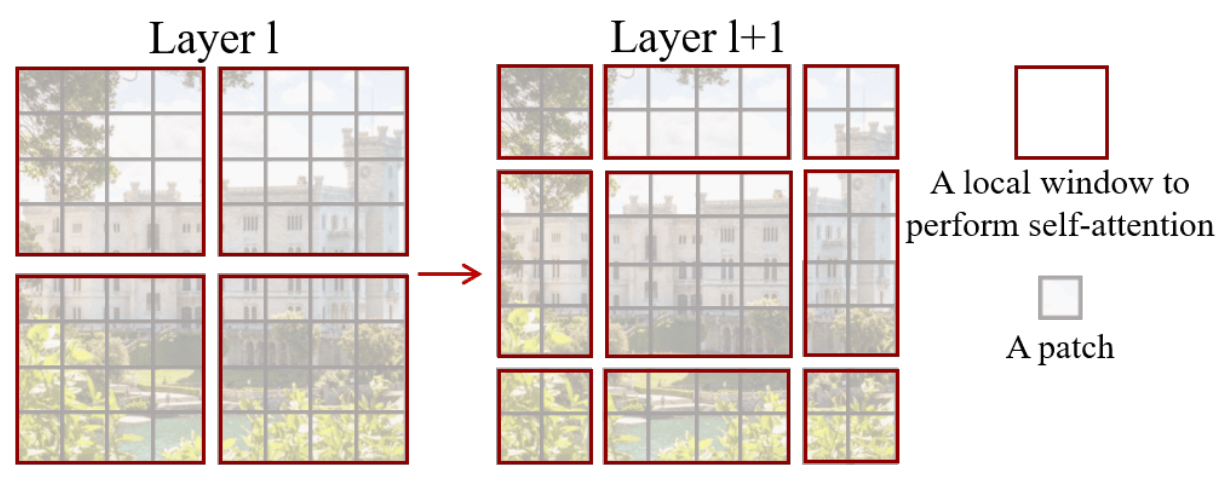
4.2 点云 Transformers
点云 transformer 需要解决两个任务:
- Scalable: overcome the \(\mathcal{O}(N^2)\) complexity in matrix multiplication.
- Unified: solve all 3D understanding tasks.
Global Transformers for Point Clouds:
- Related works: PCT [Guo et al. 2021]; Point-BERT [Yu et al. 2022];
Point-MAE [Pang et al. 2022]
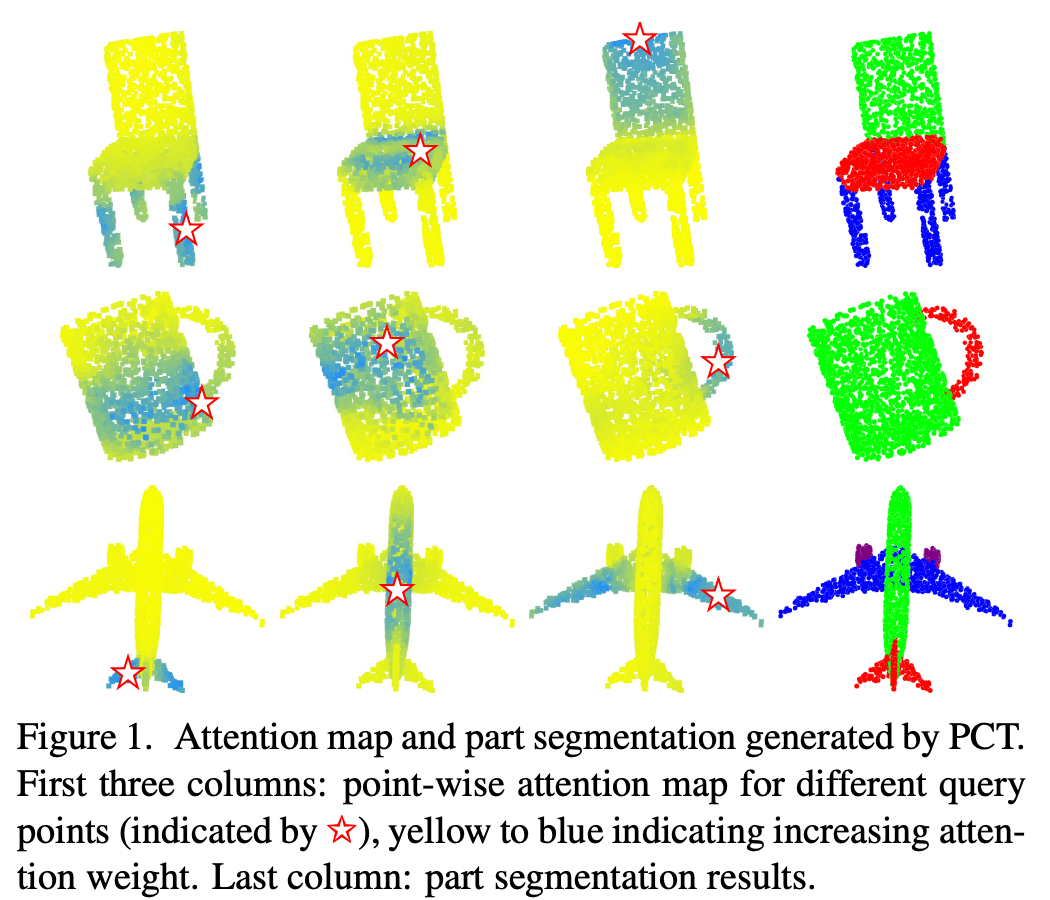
- 下图 (PCT): Each point attends to all the other points.
- Low efficiency: only process point clouds containing several thousands points.
Window Transformers for Point Clouds:
- Related works: Stratified Transformer [Lai et al. 2022]; SWFormer
[Sun et al. 2022]; SST [Fan et al. 2022]
- 下图 (Stratified Transformer): Each point attends to the points in the same window.
- 3D 点云和图像有本质区别: 后者稠密, 各个窗口内的 token 数量相同;
而前者是稀疏的, 不同窗口的点云数量差别很大. 这让该算法很难并行化.
- ScanNet, window size 7
- Average point number: 48
- Maximum point number: 343
- ScanNet, window size 7
Downsampled Transformers for Point Clouds:
- Related works: Fast Point Transformer [Park et al. 2022];
PatchFormer [Cheng et al. 2021]
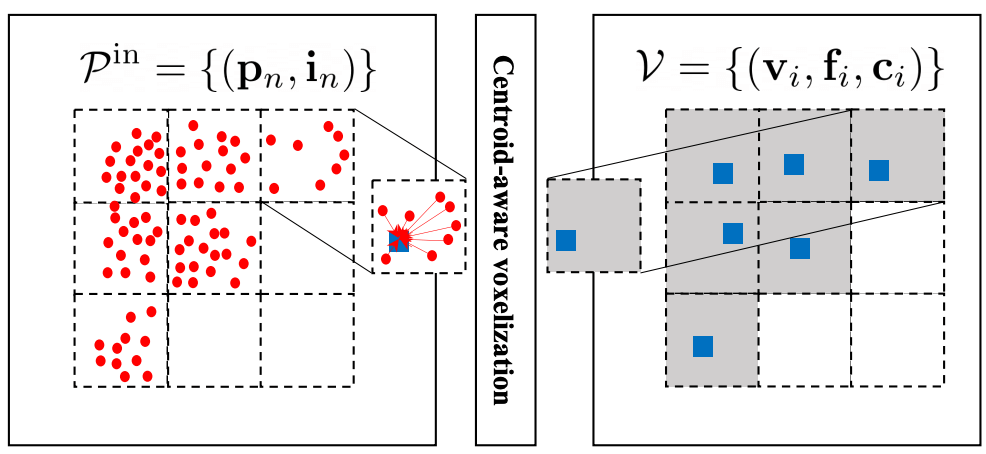
- 下图 (Fast Point Transformer): Apply attentions in downsampled feature maps.
- Weaken the network capability.
Neighborhood Transformers for Point Clouds:
- Point Transformer [Zhao et al. 2021]; Point Transformer V2 [Wu et
al. 2022]
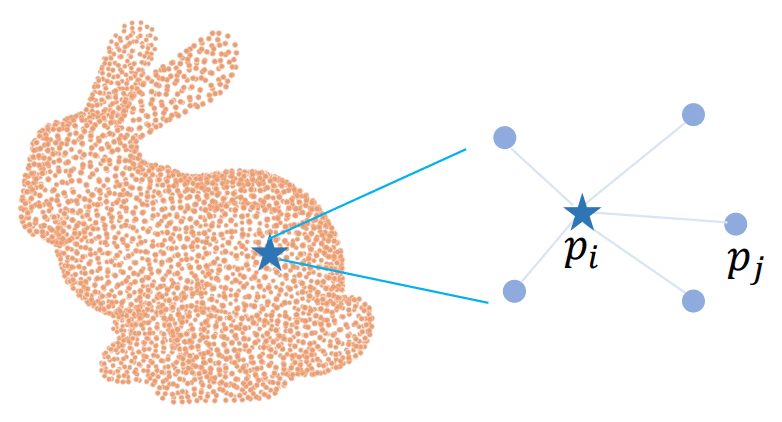
- 下图 (自 PPT): Apply attentions to k-nearest neighbors of each point.
- 丧失了一些 transformer 本质上的优势: 全局信息共享.
4.3 OctFormer
原论文: Peng-Shuai Wang, OctFormer: Octree-based Transformers for 3D Point Clouds (TOG 2023).
脱离思维定势, 不要画正方形 / 正方体的窗口, 而是用不规则窗口, 让每个窗口内的点数一样.
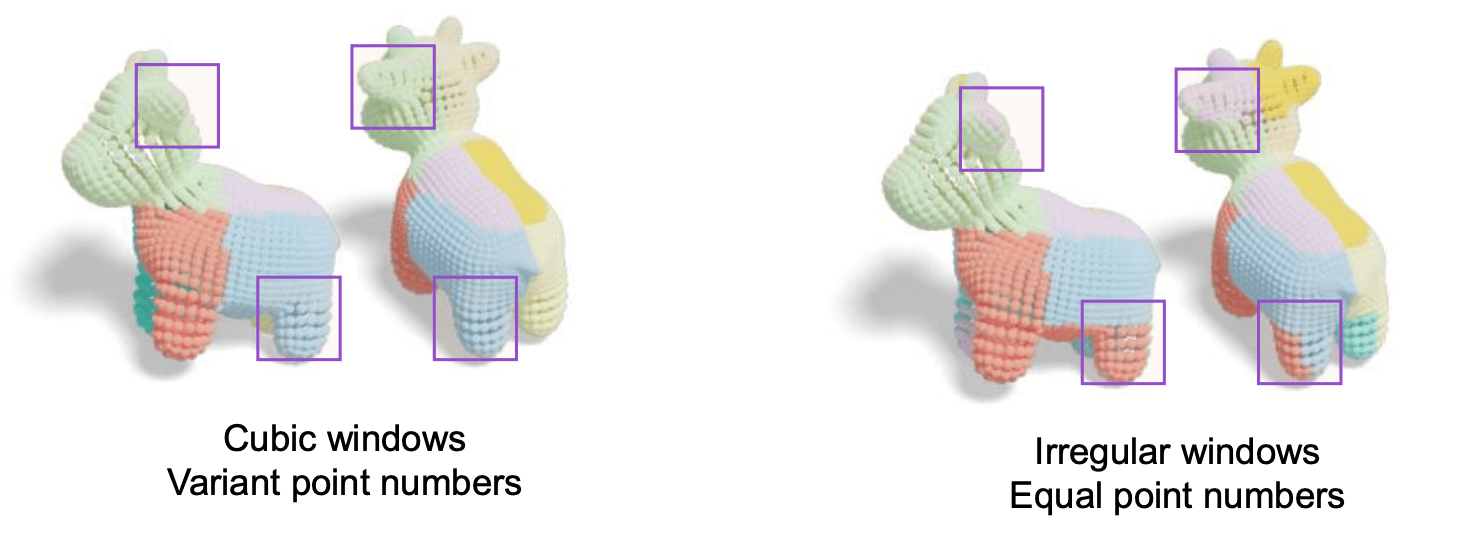
这带来两个问题:
- Transformer 能否在不规则窗口上运行?
- 如何快速画出不规则窗口?
问题一:
- 想法: 由于 attention 是基于对 token 特征做加权平均 (归一化后的 softmax 权重), 它对窗口中 token 的排列形状应该不太敏感.
- Swin 的长方形窗口提示我们不规则窗口是可能的.
- 实验: 使用一个在 \(16\times16\) 的正方形窗口上训练的 ViT, 对每个窗口随机 mask 掉 \(20\%\) 的 image patch (每个窗口内剩下的 patch 位置就不再构成规则的正方形, 形成 "高度不规则" 的局部窗口). ViT 在 ImageNet 验证集上的准确率仅从 \(85.1\%\) 降低到 \(84.2\%\), 表明 attention 仍然可以有效聚合信息.
问题二的答案还是八叉树.
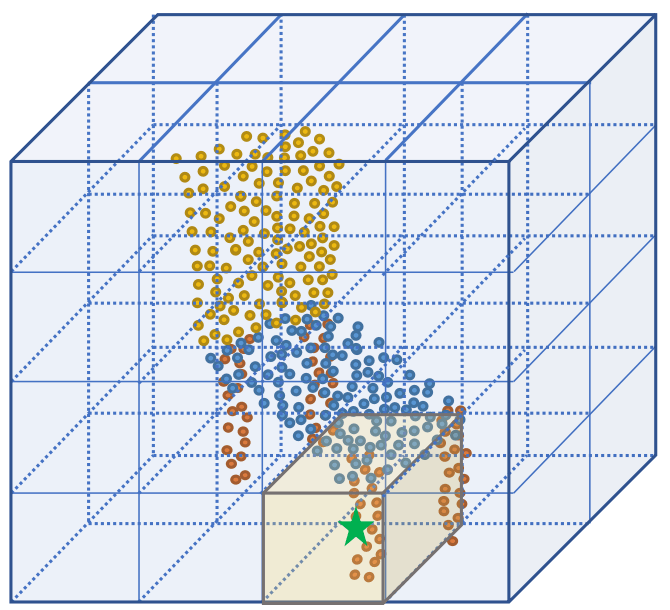
- 将所有点按照 z-order curve 排序, 然后让连续的 \(N\) 个点作为一个窗口.
- 得益于 z-order curve 良好的空间局部性, 一个窗口内的点在空间上排列紧密 (如下图, 图自 PPT).
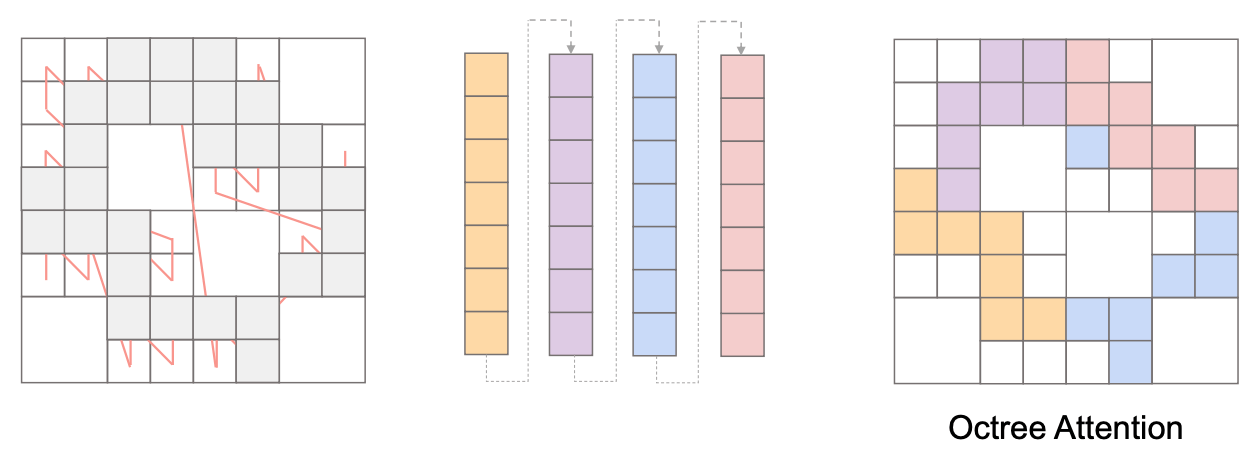
为了实现全局的信息交互, 可以应用 dilated attention ("膨胀注意力"), 即按照一定间隔选择 token.
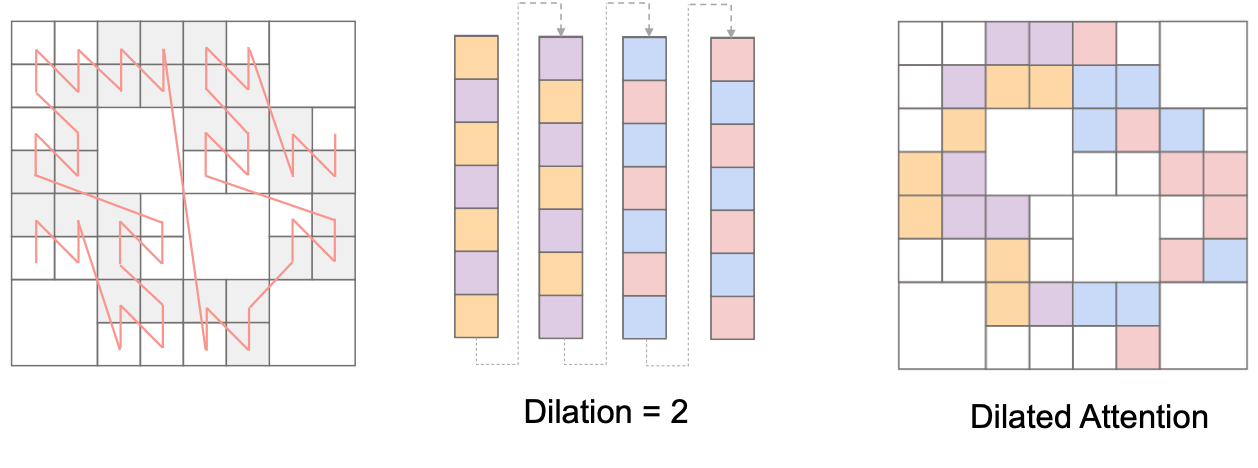
OctFormer 用稀疏卷积作为位置编码 (一种 conditional positional encoding), 与传统的位置编码相比在减少参数量的同时提升了表现.
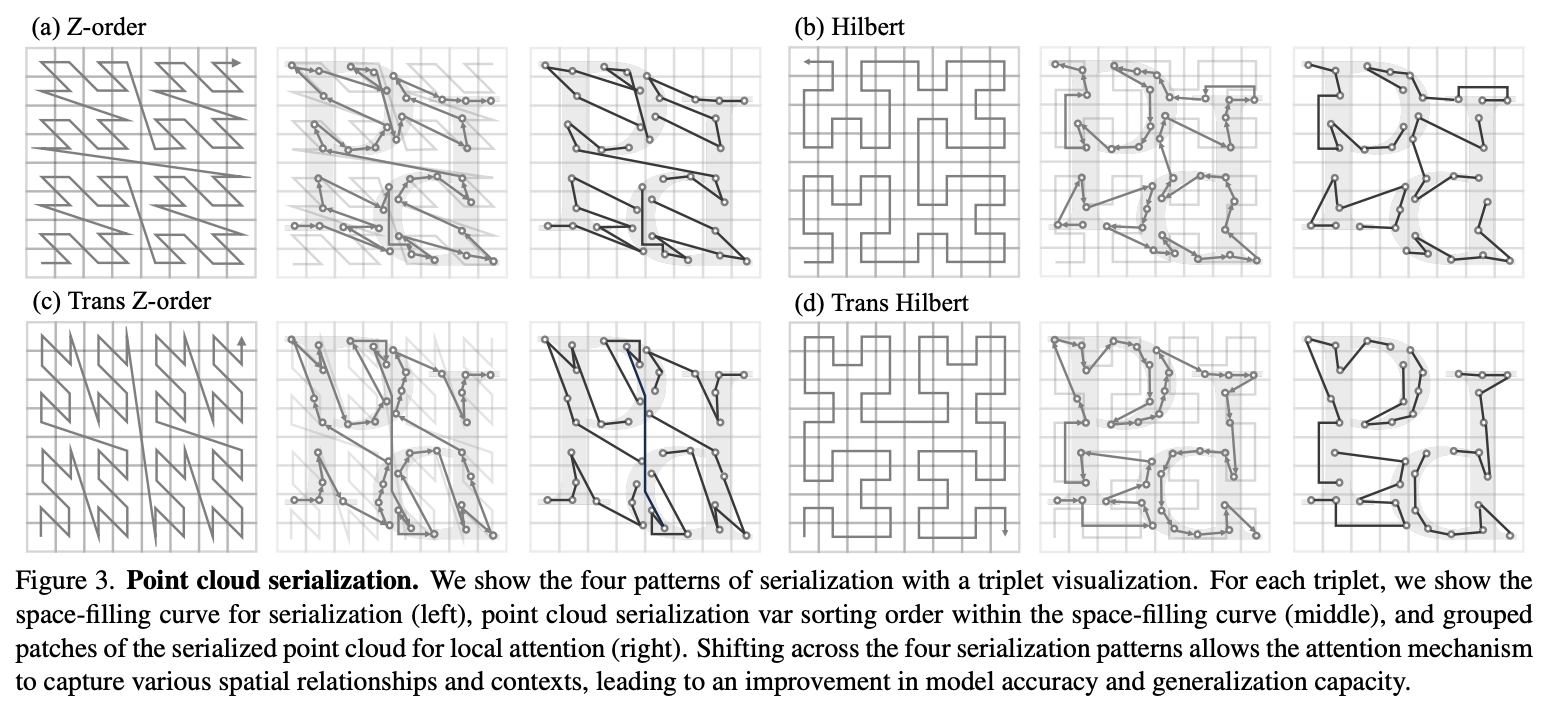
Point Transformer V3 [Wu et al. 2024] 在 OctFormer 的基础上进行改进, 其核心思想是使用不同的空间填充曲线来划分窗口.
- 使用两种空间填充曲线 (z-order 和 Hilbert) 和两种排列方向 (如下图),
使得 attention 可以捕捉各种上下文信息.
- 一个缺点是适合做理解, 不方便做生成.
- Scale up receptive fields with Flash Attentions!
- Achieved the best performance on over 20 3D benchmarks with one unified network!