几何表示前沿

为了实现更高效的几何处理, 并将深度学习技术应用到几何处理中, 研究人员开发出许多新的几何表示.

1 八叉树与哈希表

1.1 八叉树的构建

八叉树 (octree) 可以看作是对体素 (voxel) 的一种改进. 与体素的均匀网格不同, 八叉树只对非空的区域进行细分 (自适应分辨率), 得到一个层级结构.

在 CPU 上, 可以通过递归的方法构建八叉树, 即哪个子节点非空, 就对它进行劈分, 一分为八, 直到指定的最大深度为止. 该递归方法简单直接, 但缺点是不易并行化, 效率很低.

考虑一维的情形. 假设直线 \(\R\) 上有点列 \(\{x_1,\dots,x_n\}\) (\(x_i\leq x_{i+1}\)), 我们想为之构建一棵深度为 \(3\) 的二叉树, 则我们可以采取如下 "自底向上" 的策略.

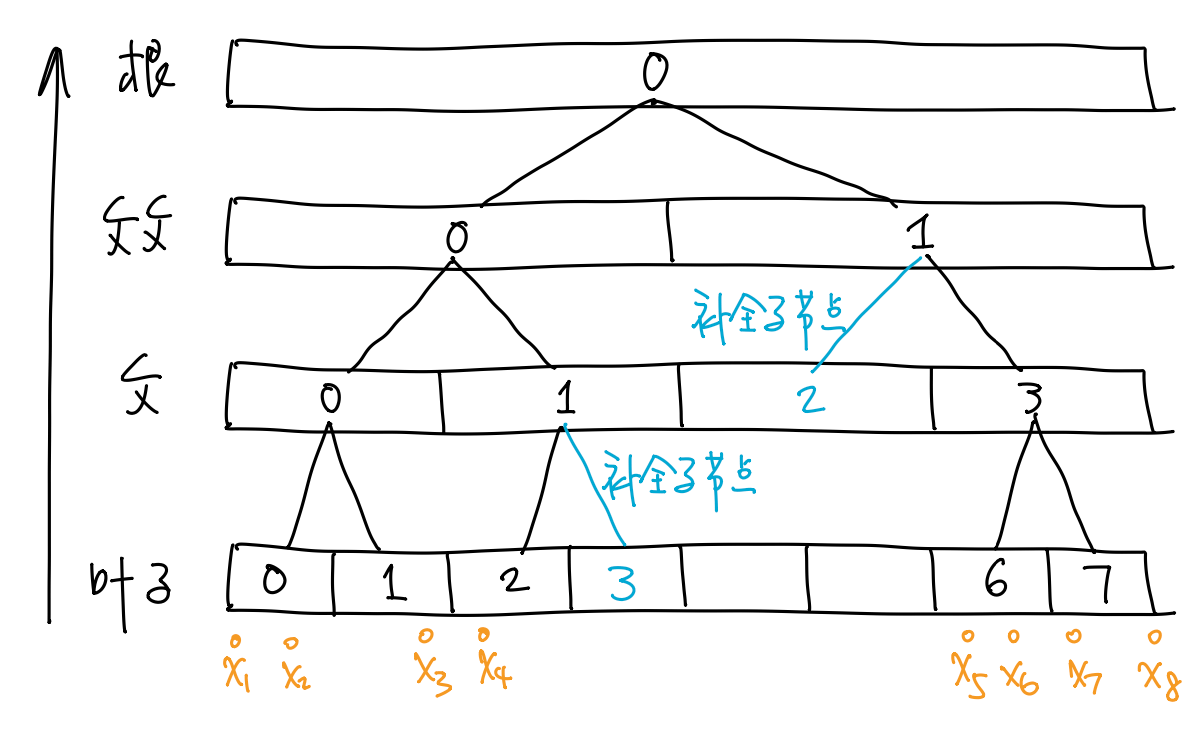
• 将区间 (即点列的包围盒) \([x_1,x_n]\) 平均分成 \(2^3=8\) 个子区间, 编号 \(0,\dots,7\).
• 所有包含着某个 \(x_i\) 的子区间就是叶子结点. 由此得到所有的叶子结点 \(0,1,2,6,7\).
• 对于每个叶子结点 \(j\), 注意到 \(\lfloor j/2\rfloor\) (即 \(j\) 右移一位) 就是其父节点的编号. 由此就得到了所有的父节点 \(0,1,3\).
  • 注意父节点 \(1\) 只有一个子节点 \(2\), 需要把另一个子节点 \(3\) 补上 (空节点).
• 以此类推, 得到父父节点 \(0,1\) 和根节点 \(0\).

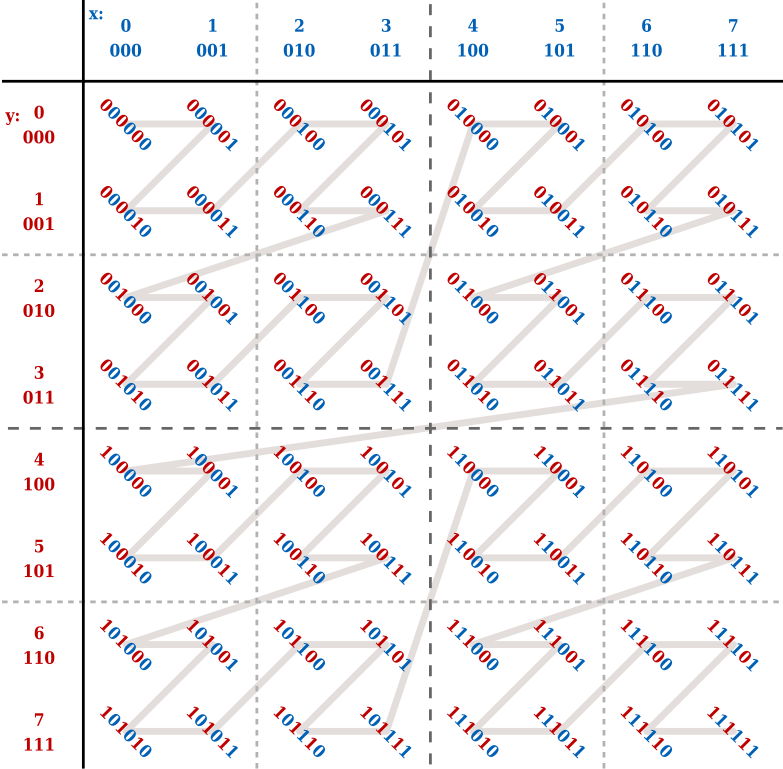
可以将该方法推广到二维和三维. 其中需要解决的关键问题是如何给节点排序. 这就要引入 shuffled key 与 z-order curve 了. 这里以二维的四叉树为例, 三维的八叉树是类似的.

参照下图图自 Wikimedia, 链接: 左图, 中图, 右图.^[1]. 将空间划分为 \(2^d\times 2^d\) 个格子, 组成一张表. 对于第 \(i\) 行第 \(j\) 列 (\(i,j\) 从 \(0\) 开始编号) 的格子, 其 shuffled key 定义为 \(i\) 的二进制表示与 \(j\) 的二进制表示通过一种交错的方式拼合起来组成的整数, 如下图左. 所有 shuffled key 如下图中间所示.

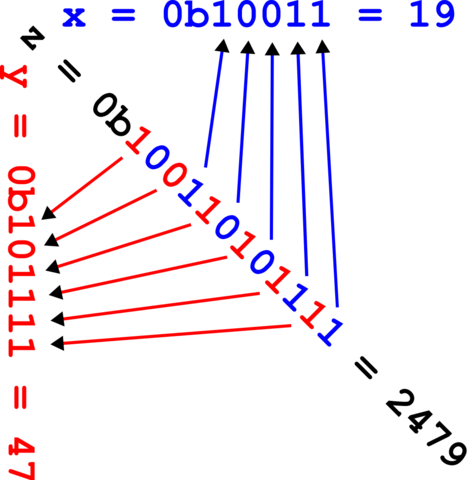
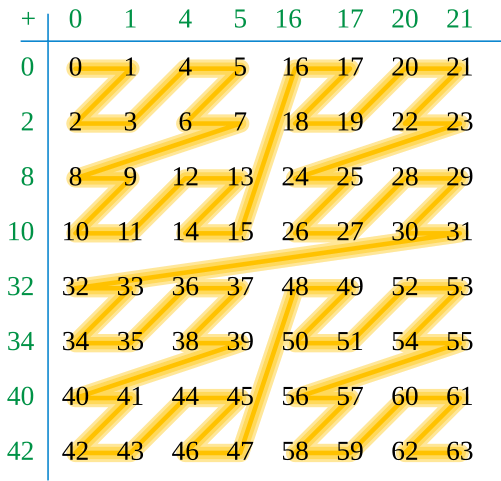
如下图右侧, 将 shuffled key 转化为十进制整数, 再将其从小到大连起来, 可以发现它们形成了一条有结构的曲线! 这称为 z-order curve.

Z-order curve 也叫 Monton curve 或者 Lebesgue curve, 是一种空间填充曲线, 它的极限可以填满整个正方形. 下图展示了其自相似结构图自 Wikimedia, 作者 David Eppstein, 原图链接 (CC-BY-SA 3.0).^[2].

Shuffled key 与 z-order curve 有如下特点:

• 叶子结点右移 \(3\) 位 (二维则是 \(2\) 位) 就得到了父节点的 shuffled key.
• 空间局部性: 父节点的所有叶子结点都是连续排列的.

八叉树的自底向上构建算法:

1. 计算点云的包围盒, 将每个方向离散化为 \(2^{d}\) 个格子.
2. 对点云中的每个点计算 shuffled key 并排序、去重, 就得到了该层节点的 z-order curve.
3. 将所有节点的 shuffled key 右移 \(3\) 位以得到父节点的 shuffled key. 排序后得到了 z-order curve. 注意需要补全缺失的子节点.
4. 以此类推, 直到根节点.

1.2 八叉树的节点信号

对于输入的点云, 八叉树的每个节点中都可以存储平均法向量 \(n\) 和平均偏移量 \(d\) (平均点离格子中心点的距离), 进而就得到了局部平面 \[ \lr{n,x-c} + d = 0. \] 对于输入的 SDF, 八叉树每个节点可以存储顶点处的 SDF 值, 进而任意一点的 SDF 可以通过三线性插值计算. 也可以通过局部基函数重建 SDF.

查找领域: 计算该点的 shuffled key, 右移不同位数可以得到不同尺度的邻域 (不同深度的八叉树节点).

1.3 哈希表

在一些图形学应用 (尤其是模拟与交互) 中, 需要更快的邻域查找. 在 2011 年, 图形学研究人员开发了 GPU 上的哈希表Efficient hash tables on the gpu (SIGGRAPH 2011).^[3], 实现了更快的邻域查找.

哈希表通过哈希函数 \(h:X\to\{0,1,\dots,N\}\) 将待插入元素映射到一个 index, 然后将元素插入到对应的 index 处. 哈希表的重点是找到一个哈希函数让哈希值尽可能均匀分布. 一般取 \[ h(k) = (ak+b) \mathbin{\rm mod} p \mathbin{\rm mod} N, \] 对于哈希值冲突的情况,

• 可以在将哈希表的元素变成子列表指针, 哈希值相同的元素放入同一个子列表中.
• 也可以不使用子列表, 直接把冲突的元素放入 index 之后的第一个空位置上.

在 CPU 上, 哈希表检索 / 插入的平均时间复杂度是 \(\mathcal{O}(1)\).

然而在 GPU 上, 如果多个线程同时对哈希表进行插入, 后面的线程必须等待前面的线程插入完毕后才能执行插入, 效率很低.

提升效率的答案是 2001 年提出的 Cuckoo 哈希算法Rasmus Pagh, Flemming Friche Rodler, Cuckoo Hashing.^[4]. 该算法使用 \(d\) 个哈希表, 每个哈希表有不同的哈希函数. 如果要插入一个元素 \(x\),

1. 计算第一个哈希表的哈希值 \(h_1(x)\), 直接将 \(x\) 插入该处. 如果该处已经有元素 \(y_1\), 则把 \(y_1\) 拿出来 (鸠占鹊巢Cuckoo 即杜鹃. 有些杜鹃会把自己的蛋放到其他鸟类的巢中, 替代原本的蛋. 论文用 Cuckoo 的这一行为来比喻该算法.^[5]).
2. 计算 \(y_1\) 在第二个哈希表的哈希值 \(h_2(y_1)\), 直接将 \(y_1\) 插入该处. 将该处已经存在的元素插入第三个哈希表, 以此类推...
3. 如果达到最大迭代深度, 但仍有元素没有插入表中, 则只能 "重启" (重新选择哈希函数).

可以证明, 该算法大概率能找到一个不冲突的配置. 对于元素查找, 只需计算 \(d\) 个哈希值, 然后在每个表中查找即可. 该操作是完全可并行的.

优点:

• 构建速度和基数排序相当
• 在查找元素数目大于 6M 时, 比二分查找快 \(2.5\) 倍以上
• 并行场景下，查找元素具有常数复杂度

缺点:

• 实现比较复杂, 基本无法使用 PyTorch 等深度学习框架实现.
• 构建时可能需要重启.
• 内存一致性不足, 查找排序好的元素时, 速度和二分查找相当.

实际上, 在对邻域查找效率要求不那么苛刻的情况下, 没有必要使用 GPU 哈希表.

2 基于 MLP 的几何表示

2.1 基于全连接神经网络的表示

使用一个全连接的 MLP 拟合 SDFDeepSDF: Learning Continuous Signed Distance Functions for Shape Representation (CVPR 2019).^[6]: \[ L(\theta) = \sum\|f_{\sf GT}(x) - f_\theta(x)\|^2, \] 也可以拟合 occupancy field (对于空间中的格点, 占据为 \(1\), 空为 \(0\)): \[ L(\theta) = \sum{\sf CrossEntropy}(f_{\sf GT}(x),f_\theta(x)). \]

可以直接用 MLP 做曲面重建IGR: Implicit Geometric Regularization for Learning Shapes (ICML 2020).^[7], 以点云 \({\cal P}\) 和点云法向量 \(n\) 作为监督: \[ L(\theta) = \frac1{|{\cal P}|} \sum_{p\in{\cal P}} \Big( \abs{f_\theta(p)} + \| \nabla f_\theta(p) - n(p) \| \Big) + \lambda \operatorname{E}_x\!\big[ \|\nabla f_\theta(x)\|-1\big ]^2. \]

损失函数的第一项令 \(f\) 的零点尽量接近点云, \(\nabla f\) 尽量接近法向量; 第二项 (Eikonal term) 令梯度为单位向量 (\(x\) 服从 \(\R^3\) 上的某个分布).

MLP 还可以拟合空间中的颜色场Texture Fields: Learning Texture Representations in Function Space (ICCV 2019).^[8] (输入坐标, 输出 occupancy 和颜色) 和辐射场NeRF: Representing Scenes as Neural Radiance Fields for View Synthesis (ECCV 2020).^[9] (输入坐标与视角方向, 输出颜色和体密度), 可以用于三维重建与渲染.

2.2 随机 Fourier 特征

原论文: Fourier Features Let Networks Learn High Frequency Functions in Low Dimensional Domains (NeurIPS 2020).

尽管 MLP 可以任意逼近任何连续函数 (universal approximation thm.), 在实际场景中, MLP 更倾向于学习信号的低频分量而非高频分量On the Spectral Bias of Neural Networks (ICML 2018).^[10] (spectral bias).

这一缺陷在三维重建 MLP 上的体现就是重建出的结果非常模糊 (如下图第一行, 图自原论文).

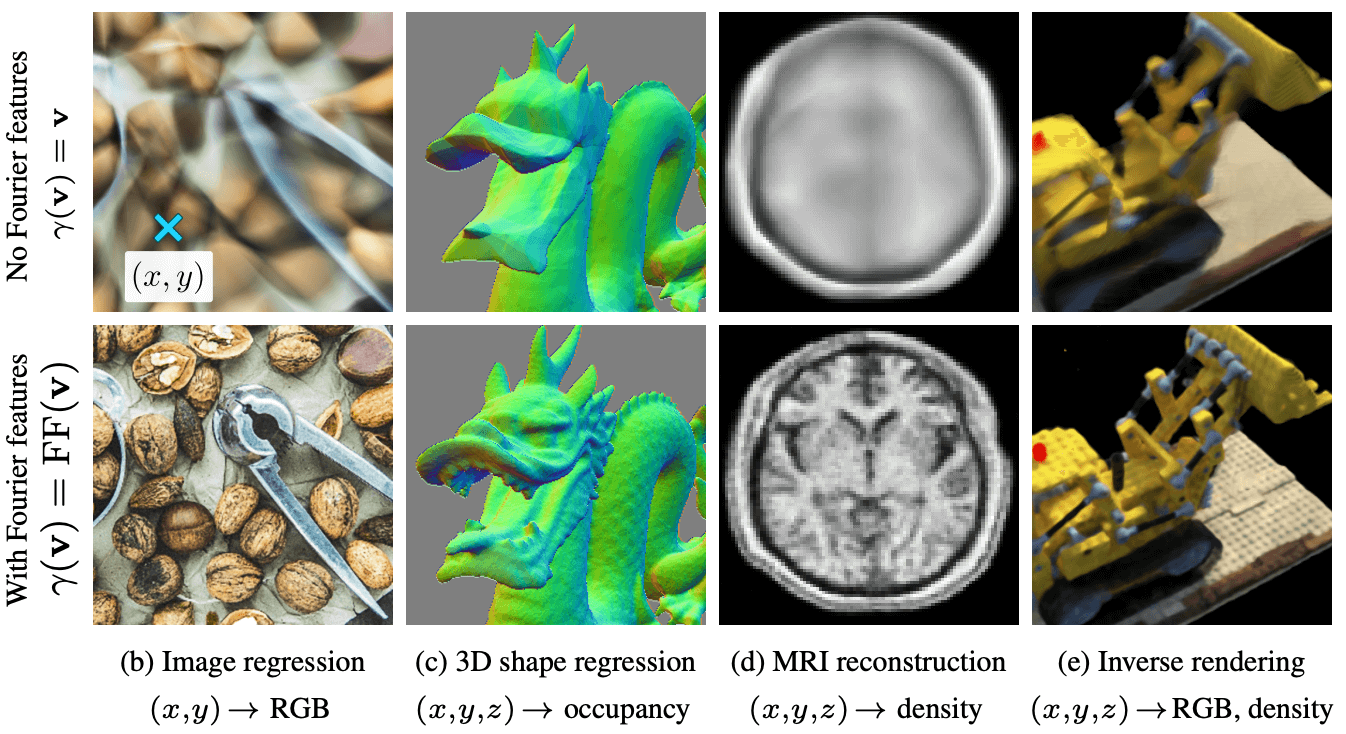
该论文提出, 让 MLP 的输入 \(x\in\R^d\) (比如空间坐标和角度等) 先经过一个 Fourier 特征映射 \[ \Align{ \gamma:\R^d&\to\R^{2L}, \\ x &\mapsto \bqty{ a_1\cos(\omega_1\T x+b_1),a_1\sin(\omega_1\T x+b_1),\dots, a_L\cos(\omega_L\T x+b_L),a_L\sin(\omega_L\T x+b_L) }\T. } \] 其中 \(a_i,\omega_i,b_i\) 都是可调的权重, 通常 \(2L\) 远大于 \(d\). 映射 \(\gamma\) 将输入映到了高维空间中的一个超球面上, 而且包含各个频率的信息, 让 MLP 容易学到高频成分. (原本靠得比较近的 \(\gamma\) 像彼此远离, 更容易让 MLP 区分两者.) 使用 Fourier 特征映射得到的结果如上图第二行所示.

实际上, 此前的 NeRF 就采用了类似的 Fourier 位置编码, 即让空间坐标 \((x,y,z)\) 和方向向量 \((n_x,n_y,n_z)\) 经过一个位置编码映射: \[ \gamma(x) := \bqty{ \sin(2^0\pi x),\cos(2^0\pi x),\dots \sin(2^{L-1}\pi x),\cos(2^{L-1}\pi x) }. \] 类似的 position encoding 在 Transformer 中也有.

2.3 SIREN

原论文: Implicit Neural Representations with Periodic Activation Functions (NeurIPS 2020).

随机 Fourier 特征的正弦函数内的频率都是写死的, 我们不妨将其当作神经网络的参数, 优化学习这些参数, 或许能达到更好的结果. 换言之, 可以使用正弦函数作为 MLP 的激活函数: \(y=\sin(Wx+b)\).

论文作者还推导出了正弦层参数初始化的策略.

---

1. 图自 Wikimedia, 链接: 左图, 中图, 右图.↩︎

2. 图自 Wikimedia, 作者 David Eppstein, 原图链接 (CC-BY-SA 3.0).↩︎

3. Efficient hash tables on the gpu (SIGGRAPH 2011).↩︎

4. Rasmus Pagh, Flemming Friche Rodler, Cuckoo Hashing.↩︎

5. Cuckoo 即杜鹃. 有些杜鹃会把自己的蛋放到其他鸟类的巢中, 替代原本的蛋. 论文用 Cuckoo 的这一行为来比喻该算法.↩︎

6. DeepSDF: Learning Continuous Signed Distance Functions for Shape Representation (CVPR 2019).↩︎

7. IGR: Implicit Geometric Regularization for Learning Shapes (ICML 2020).↩︎

8. Texture Fields: Learning Texture Representations in Function Space (ICCV 2019).↩︎

9. NeRF: Representing Scenes as Neural Radiance Fields for View Synthesis (ECCV 2020).↩︎

10. On the Spectral Bias of Neural Networks (ICML 2018).↩︎