一个简单的 SPH 流体模拟器
本文是《可视计算与交互》课程的大作业笔记, 主要参考一篇教程
本文侧重于介绍 SPH 算法的思想, 给出一些简单的公式和推导, 以及一些实现上的细节, 基本不会涉及 SPH 各种算法的理论细节.
🏗️ 施工中...
1 Foundations
计算机流体模拟有两种视角, Eulerian 和 Lagrangian. Eulerian 将空间离散化, 模拟空间网格上每一点的密度、速度和加速度场; 而 Lagrangian 将流体离散采样为粒子, 模拟每个采样点 (粒子) 处的密度、速度和加速度等. Lagrangian 方法在处理复杂或动态边界上比较有优势.
SPH (smoothed particles hydrodynamics, 光滑粒子流体动力学) 方法是一种基于 Lagrangian 视角的模拟算法. SPH 的基本思想是用 (空间中) 离散的采样点来代替连续的物理量, 如密度等. 这些离散的采样点也称为 "粒子", 每个粒子 \(p\in\R^d\) 都携带着物理量 \(A(p)\), 而任意一点处的物理量 \(A(x)\) (\(x\in\R^d\)) 可以通过 "核函数" 插值得到, 如下图.
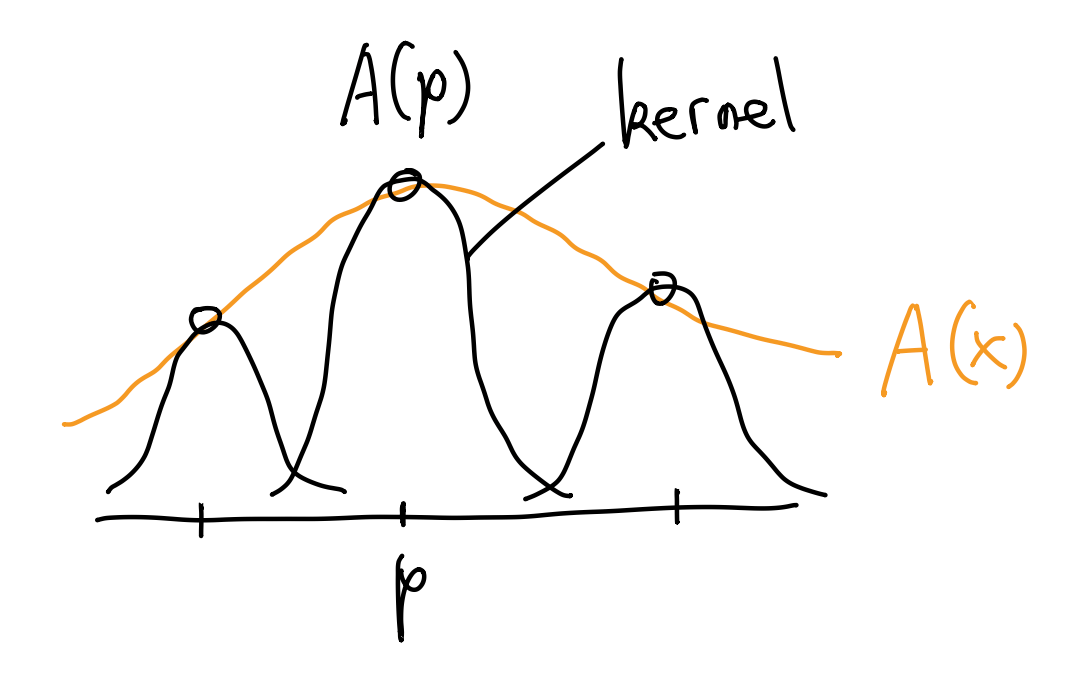
此外, 微分算子 (如梯度, 散度等) 也有其离散化版本. 将物理量和微分算子离散化之后, 我们就可以将流体力学方程写成离散的版本, 把连续流体动力学问题转化为粒子相互作用问题, 通过 Euler 积分法求解.
1.1 Kernel functions
取核函数为 Dirac delta 分布 \(\delta(x)\), 它可以粗略地理解为 \(\delta(x)=\Cases{\infty,&x=0,\\0,&x\neq0,}\) 并且满足归一化条件 \[ \int_{\R^d} \delta(x)\dd{x} = 1. \] 它的一个重要性质是对任意光滑紧支函数 \(A:\R^d\to\R\), 有 \[ A(x) = (A*\delta)(x) = \int_{\R^d} A(p)\delta(x-p)\dd{p}. \label{convDelta}\tag{a} \] 上式的含义是, 如果采样点 \(p\) 遍布整个空间 \(\R^d\), 那么就可以用这些采样点的值 \(A(p)\) 和 \(\delta(x)\) 的卷积来提取函数值 \(A(x)\). 但是 delta 分布是一个广义函数, 无法直接用于数值计算, 所以我们用一个核函数 \(W_h(x)\) 近似它 (\(h\) 是一个正实参数). 我们希望 \(W_h(x)\) 满足如下性质:
- (归一化) \(\int_{\R^d} W_h(x)\dd{x} = 1\).
- (逐点收敛到 delta 分布) \(\lim_{h\to0}W_h(x)=\delta(x)\).
- (对称性) \(W_h(x)=W_h(-x)\) 对任意 \(x\in\R^d\).
- (紧支性) \(W_h(x)\equiv0\) 对任意 \(\|x\|\geq h\), 其中 \(h>0\) 用于控制支集的半径. (有的文献中用另一个参数 \(\hbar\) 控制支半径, 本文中不做区分.)
- (\(C^2\) 可微性) \(W_h\) 是二阶连续可微的.
其中 \(C^2\) 可微性是因为我们需要离散化二阶微分算子. 为了物理模拟的合理性, 有时会加一个条件:
- (非负性) \(W_h(x)\geq0\) 对任意 \(x\in\R^d\).
有了核函数 \(W_h(x)\), 式 \(\eqref{convDelta}\) 就可以改写成
\[ A(x) \approx (A*W_h)(x) = \int_{\R^d} A(p)W_h(x-p)\dd{p}. \label{convApprox}\tag{b} \]
式 \(\eqref{convApprox}\) 的误差分析. 令 \(h\to0\). 根据 \(W_h\) 的紧支性, 被积函数只有 \(\|x-p\|<h\to0\) 时非零. 对 \(A\) 在 \(x\) 处 Taylor 展开, \[ \Align{ A(p) = A(x) &+{} \sum_i \partial_iA(x) (p^i-x^i) \\ &+{} \sum_{ij} \partial_{ij}A(x) (p^i-x^i)(p^j-x^j) \\ &+{} o(\|p-x\|^2), } \] 代入 \(\eqref{convApprox}\) 式得到 \[ \Align{ \int_{\R^d} A(p) W_h(x-p)\dd{p} &= A(x) \underbrace{\int_{\R^d} W_h(x-p) \dd{p}}_1 \\ &\hspace{1em}+{} \sum_i \partial_iA(x) \underbrace{\int_{\R^d} W_h(x-p) (p^i-x^i) \dd{p}}_0 \\ &\hspace{1em}+{} \sum_{ij} \underbrace{\partial_{ij}A(x)}_{\mathcal{O}(1)} \underbrace{ \int_{\R^d} W_h(x-p) (p^i-x^i)(p^j-x^j) \dd{p} }_{\mathcal{O}(h^2)} + o(h^2) \\ &= A(x) + \mathcal{O}(h^2), } \] (根据归一化性质, 第一个积分为 \(1\); 根据对称性, 第二个积分为零; 由光滑性和紧支性, \(A\) 的各阶偏导数有界) 因此式 \(\eqref{convApprox}\) 具有 \(h^2\) 级别的误差, 支半径 \(h\) 越小, 精度越高.
一个常用的核函数是三次样条核函数 (cubic spline
kernel) \[
W_h(x) = \sigma_d \Cases{
6(q^3-q^2) + 1, & 0\leq q\leq\frac12, \\
2(1-q^3), & \frac12<q\leq1, \\
0, & \textsf{otherwise},
}
\] 其中 \(q=\|x\|/h\);
归一化因子 \(\sigma_d\) 与维数有关,
对于 \(d=1,2,3\), 分别有 \(\sigma_d=\frac{4}{3h},\frac{40}{7\pi
h^2},\frac{8}{\pi h^3}\). 二维的 \(W_h\) 图像如下 (图源教程
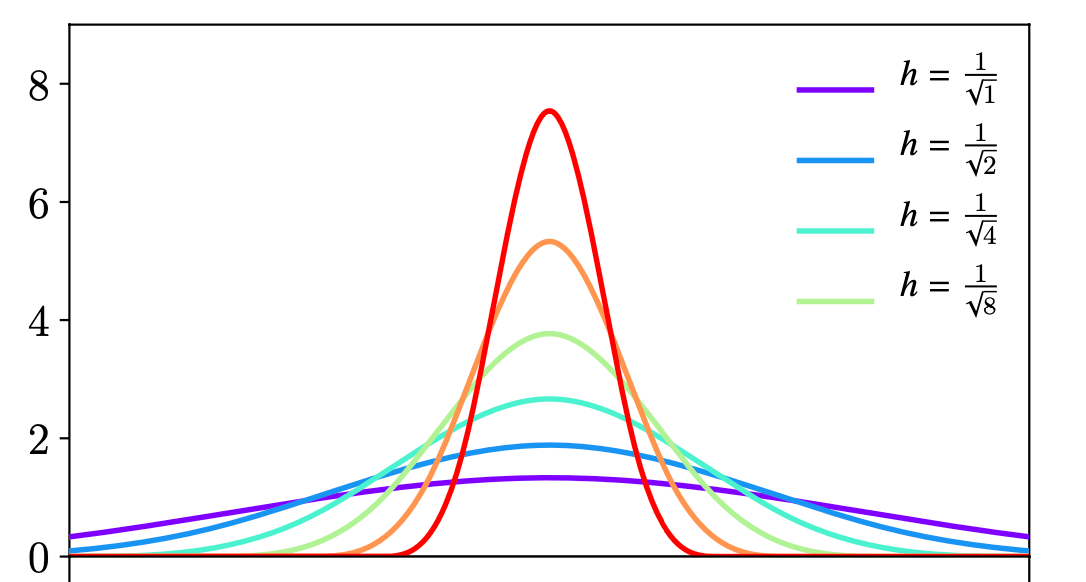
1.2 Discretizing field quantities
为了计算, 需要把积分离散为求和. 设流体的密度场为 \(\rho(x)\), 则质量 \(\dd{m}=\rho(x)\dd{V}=\rho(x)\dd{x}\). 取采样点 \(p_1,\dots,p_n\), 记 \(\rho_i:=\rho(p_i)\), \(A_i:=A(p_i)\), \(m_i\) 为粒子 \(p_i\) 的质量, 则 \[ \Align{ A_i = A(p_i) &\approx \int_{\R^n} \frac{A(p)}{\rho(p)} W_h(p_i-p) \cdot \underbrace{\rho(p)\dd{p}}_{\dd{m}} \\ &\approx \sum_{j=1}^n A_j\frac{m_j}{\rho_j} W_h(p_i-p_j) =: \lr{A_i} } \label{disField}\tag{c} \] 为了方便, 记 \(W_{ij}:=W_h(p_i-p_j)\). 注意核函数的紧支性条件, 这使得当 \(\|p_i-p_j\|\geq h\) 时 \(W_{ij}=0\), 大大减少了求和的项数, 提高了模拟的效率 (即只需考虑 \(h\)-邻域内的粒子).
特别地, 取 \(A(x)\) 为密度场 \(\rho(x)\), 即得到密度场的离散化公式 \[
\rho_i \approx \lr{\rho_i} = \sum_{j=1}^n m_j W_{ij},
\label{disRho}\tag{d}
\] 只需记录每个粒子的质量 \(m_i\), 就能还原出每个粒子处的密度.
需要注意的是, 由于靠近液体表面的粒子其邻域内粒子较少 (如下图, 图源教程
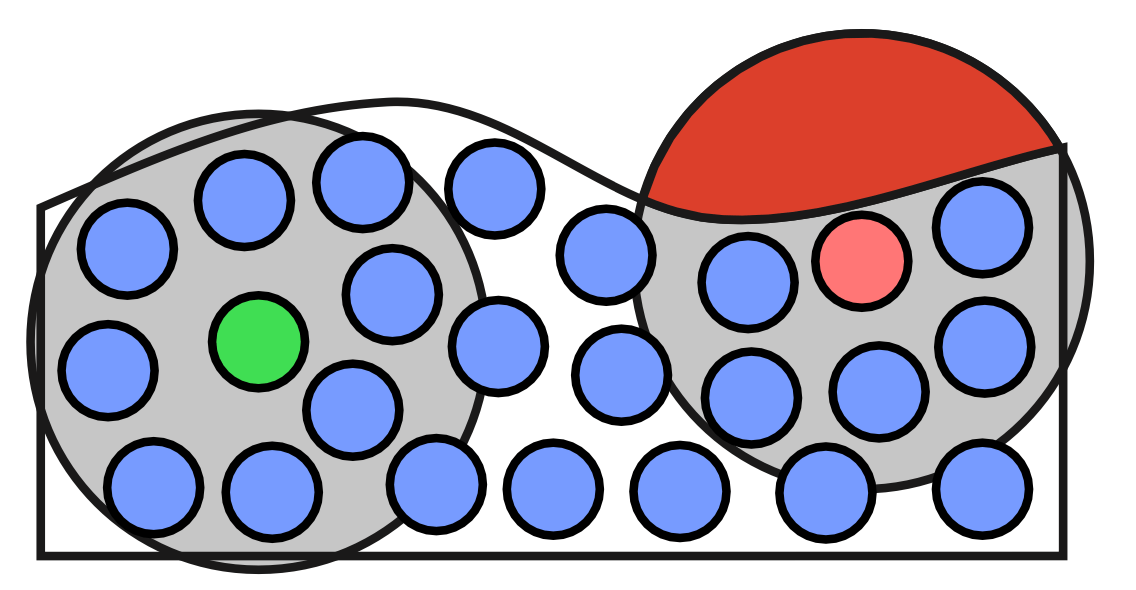
式 \(\eqref{disField}\) 的误差分析. 将 \(A\) 的 Taylor 展开代入 \(\eqref{disField}\) 式右边, 得到 \[ \Align{ \lr{A_i} &= \orange{A_i} \sum_j\frac{m_j}{\rho_j} W_h(p_i-p_j) \\ &\hspace{1em}{}+ \nabla A(p_i) \cdot\sum_j(p_j-p_i)\frac{m_j}{\rho_j} W_h(p_i-p_j) \\ &\hspace{1em}{}+ \mathcal{O}(\|p_j-p_i\|^2). } \] 可见, 为了达到零阶精度, 应有 \[ \sum_j\frac{m_j}{\rho_j}W_h(p_i-p_j)=1. \] 为了达到一阶精度, 应进一步有 \[ \sum_j(p_j-p_i)\frac{m_j}{\rho_j} W_h(p_i-p_j)=0. \]
1.3 Discretizing differential operators
直接对 \(\eqref{disField}\) 式求梯度, 可以得到梯度的直接近似, \[ \nabla A_i \approx \nabla \lr{A_i} = \sum_j A_j \frac{m_j}{\rho_j} \nabla W_{ij}. \]
该式的误差分析. 将 \(A\) 的 Taylor 展开代入上式, 得到 \[ \Align{ \nabla \lr{A_i} &= A_i \sum_j \frac{m_j}{\rho_j} \nabla W_{ij} \\ &\hspace{1em}{}+ \orange{\nabla A(p_i)} \cdot \sum_j (p_j-p_i) \frac{m_j}{\rho_j} \nabla W_{ij} \\ &\hspace{1em}{}+ \mathcal{O}(\|p_j-p_i\|^2). } \] 为了达到零阶 (一阶) 精度, 应成立下面左式 (两式) \[ \Align{ \lr{\nabla1}\equiv \sum_j \frac{m_j}{\rho_j} \nabla W_{ij} &= 0, & \sum_j \frac{m_j}{\rho_j} (p_j-p_i) \otimes \nabla W_{ij} &= {\rm id}_d. } \]
这种 "直接近似" 一般误差比较大, 且会导致模拟不稳定. 下面我们给出在实际中常用的两种梯度公式.
梯度的差分公式 (difference formula) 为 \[ \nabla A_i\approx \sum_j\frac{m_j}{\rho_j} (A_j-A_i)\nabla_iW_{ij}. \] 它可以保证 \(0\) 阶准确性 (即 \(\nabla A_i\) 的值准确).
梯度的对称公式 (symmetric formula) 为 \[ \nabla{A_i} \approx \rho_i \sum_j m_j \pqty{ \frac{A_i}{\rho_i^2}+\frac{A_j}{\rho_j^2} } \nabla_i W_{ij}. \label{symFormula}\tag{f} \] 它不能保证 \(0\) 阶准确性, 但其优点是能保证动量和角动量守恒 (对称性可以保证内力之和为零). 为保证真实性, 一般采用对称公式.
1.4 Fluid equations
为了模拟流体的运动, 我们需要引入一些物理方程. 在计算机图形学中, 我们主要关注流体的宏观行为, 忽略那些人类不可感知的微观行为. 下面我们介绍一些模拟流体时所需的定律.
连续性方程描述了流体密度的演化: \[ \frac{D\rho}{Dt} = -\rho(\nabla\cdot v). \label{contEq}\tag{g} \] 其中, \(D/Dt\) 称为随体导数 (material derivative), 指的是物理量随着流体微团运动而变化的时间变化率 (在我们的模拟中, 物质导数就是某个 "粒子" 携带的物理量的变化率). 随体导数可分解为两部分: \[ \frac{DA}{Dt} = \pdv{A}{t} + v\cdot\nabla A, \] 其中 \(\partial{A}/\partial{t}\) 是固定的一点处的物理量的变化率, \(v\cdot\nabla A\) 是物理量由于流体微团运动而产生的变化率.
一般的流体 (比如常温常压下低速流动的水, 油) 是不可压缩的, 即 \(D\rho/Dt=0\). 从连续性方程看出, 流体的不可压缩性等价于 \(\nabla\cdot v=0\). 我们的模拟需要在一定程度上保证不可压缩性.
动量守恒定律: \[ \rho\frac{Dv}{Dt} = \nabla\cdot T + f^{\sf ext}. \] 其中 \(T\) 为应力张量, \(f^{\sf ext}\) 为 (单位体积的) 外力. 应力张量描述了流体内部某一点的 (单位面积的) 受力状况.
Navier-Stokes 方程给出了应力张量, \[ T = -p1_{d} + \mu(\nabla v+\nabla v\T), \] 其中 \(p\) 为压强, \(\mu\) 为粘度系数. 粘滞阻力可以平滑速度场, 保证模拟的稳定性. 压强有两种计算方法:
(强不可压缩) 如果要严格保证不可压缩性, 则需要一些额外的功夫, 这里不做介绍.
(弱不可压缩) 如果无需严格保证不可压缩性, 则可以利用状态方程 \[ p = k\pqty{\pqty{\frac{\rho}{\rho_0}}^\gamma-1}, \label{stateEq}\tag{h} \] 通过密度 \(\rho\) 计算压强 \(p\). 其中, \(\rho_0\) 是密度的基准 (称为松弛密度, rest density), 如果密度 \(\rho>\rho_0\), 则给予一个较大的压强使得粒子间相互排斥, 减小密度. 常数 \(k,\gamma>0\) 控制流体不可压缩的级别, 值越大越不可压缩.
将 Navier-Stokes 方程代入动量守恒定律, 得到 \[ \rho\frac{Dv}{Dt} = -\nabla p + \mu\nabla^2v + f^{\sf ext}. \]
1.5 Operator splitting
求解上述偏微分方程的一个重要思想是化整为零. "算子分裂" (operator splitting) 即把一个大方程化为几个 (顺序的) 子问题, 并采用单独的技术来求解每个子问题.
在 SPH 问题中, 针对不同应用场景和流体性质可以有不同的分裂方法, 下面引入一种低粘度弱不可压缩流体的算子分裂方法.
对于每个 time step, 将模拟分为如下几个步骤:
计算每个粒子处的密度和压强: (式 \(\eqref{disRho}\) 和式 \(\eqref{stateEq}\)) \[ \Align{ \rho_i &\leftarrow \sum_j m_j W_{ij}, \\ p_i &\leftarrow k\pqty{\pqty{\frac{\rho_i}{\rho_0}}^\gamma-1}. } \]
计算每个粒子处的受力和加速度:
压力: (利用对称公式 \(\eqref{symFormula}\)) \[ \Align{ F_i^{\sf pressure} &\leftarrow -\frac1{\rho}\nabla p = -m_i\sum_j m_j\pqty{\frac{p_i}{\rho_i^2}+\frac{p_j}{\rho_j^2}} \nabla W_{ij}. } \]
粘滞阻力: \[ F_i^{\sf visc} \leftarrow \mu\sum_j \frac{m_j}{\rho_j}(v_j-v_i). \]
加速度: \[ a_i \leftarrow \frac1{m_i} (F_i^{\sf pressure}+F_i^{\sf visc}+F_i^{\sf ext}), \] 其中外力为重力.
根据加速度更新速度与位置 (半隐式 Euler 积分): \[ \Align{ v_i' &\leftarrow v_i + a_i\Delta t, \\ x_i' &\leftarrow x_i + v_i\Delta t. } \]
- 步长 \(\Delta t\) 即可以是固定值, 也可以根据模拟状况动态调整. 为了保证稳定性, 一般取 \[ \Delta t\leq \lambda\frac{\tilde h}{\|v\|_{\sf max}}, \] 其中 \(\tilde{h}\) 为粒子大小, \(\lambda\) 为参数 (可以取 \(0.4\)). 上式称为 Courant-Friedrichs-Lewy (CFL) 条件, 是保证模拟收敛的 \(\Delta t\) 的一个上界.
1.6 Neighbourhood search
计算密度和加速度的步骤都需要查找粒子的 \(h\)-邻域内的粒子, 朴素的算法复杂度为 \(O(n^2)\), 当粒子很多时显然不可行. 一种加速算法是将空间划分为间距为 \(h\) 的网格, 将粒子以网格索引 \((i,j,k)\) 为 key 存储在一张表里 (称为邻域表). 这样, 邻域搜索时只需查找该粒子周围 \(3×3×3\) 网格内的粒子即可.
为了达到 \(O(1)\) 的查找效率, 可以使用 hash 表. 处于第 \((i,j,k)\) 网格的粒子以 hash 值 \[ (pi\mathop{\rm XOR}qj\mathop{\rm XOR}rk)\mathop{\rm mod}{N} \] 为索引 (其中 \({\rm XOR}\) 为按位异或, \(p,q,r\) 是大质数, \(N\) 为表格长度).
1.7 Boundaries
SPH 处理边界有两种常用做法, 第一种是用固定不动的粒子模拟边界; 第二种是用符号距离场 (SDF) 记录边界, 当粒子靠近边界时令其反弹. 我们采用第一种, 因为它一方面实现起来较容易, 每一帧更新时无需额外的边界逻辑; 另一方面能够实现复杂的边界. 这种方法的一个不足是需要很多额外的粒子, 还可能出现粒子逸出的情况. 为了缓解粒子逸出, 程序采用双层边界.
初始化边界时需要为其赋予 "伪质量", 使得每个边界粒子处的密度值等于 \(\rho_0\).
2 An implementation
2.1 SPH solver
为了实时交互, 本程序采用计算负担较小的弱可压缩 SPH 算法 (WCSPH) 配合 symplectic Euler 积分. 具体步骤已经在上文给出.
WCSPH 算法. 更新步骤在上面已经给出, 只需在第一步之前再加入一步 "计算邻域表".
并行计算. 为了加速, 程序使用
std::thread 实现多线程. 在每一帧的更新过程中,
计算密度、压力、加速度、更新速度和位置这几个操作,
不同的粒子是完全不干扰的, 可以直接并行, 每个线程各负责一部分粒子.
但更新邻域表时, 不同粒子可能写到同一表项, 需要加锁. 实测发现并行计算对
2D 场景效果不明显, 对 3D 场景加速作用明显.
2.2 Visualization
Shader 2D. 二维的粒子渲染为小圆球. 为了更好观察小球的速度等信息, 小球按照其速度着色:
- 从速度慢到快, 分别为蓝色、黄色、红色. 颜色按照经过 sigmoid 函数变换后的速度 \(\|v\|\) 线性插值. 颜色可以调整.
在实现上, 只需给 particle 的 shader 传入 Velocities 向量, 在 vert shader 里面计算模长并传入 frag shader, 接着在 frag shader 里插值即可.
为了实现圆球的效果, 需要使用 gl_PointCoord 向量,
它记录了当前像素在当前 particle 中的归一化坐标. 将其缩放到 \([-1,1]^2\) 范围内后, 丢弃单位圆外的点.
Shader 3D. 三维的粒子渲染为 3D 立体小球. 颜色方案与 2D 一样. 此外还实现了 Phong-Blinn 光照.
不同的场景. 目前有 4 个 2D 场景 (Square, Circle, Rotating cirlce, Pool) 和 2 个 3D 场景 (Cube, Cylinder). 其中, 2D 场景 Rotating circle 是一个旋转的 "搅拌机", 通过在更新时旋转边界点来实现 (实现逻辑并不复杂, 可以看作 Lagrangian 方法的优势之一).
2.3 Interaction
受到已有模拟器的启发, 我在模拟程序中实现了添加粒子、施加外力这两个功能, 为模拟添加了不确定性和一些乐趣.
添加粒子. 按下按钮可以在场景上方固定位置生成固定大小的立方体. 需要注意的是, 添加粒子最好保证该区域内没有太多其他粒子, 否则可能导致粒子重叠而爆炸. 2D 和 3D 场景分别有最大粒子数的限制.
施加外力 (仅 2D). 鼠标左键按下并移动, 就会在半径 \(kh\) (\(h\) 是 kernel 半径) 之内施加与移动速度成正比的外力. 半径 \(k\) 可以调整. 需要注意的是, 移动速度过快可能导致能量过大而爆炸.
三维场景的施加外力功能没有实现. 由于相机投影的 ambiguity, 目前还没有想到一个好办法处理. 未来的工作还包括解决交互中 "爆炸" 的问题.
2.4 Results
2D.
渲染的帧率基本稳定在 120 fps, 模拟的速度与线上 demo 相比慢一点, 但也是可以接受的水平. 模拟速度和帧率受粒子数影响不大.
速度可视化让一些现象变得直观. 可以观察到流体中的多个漩涡: (为了直观, 将粒子大小调到最大)
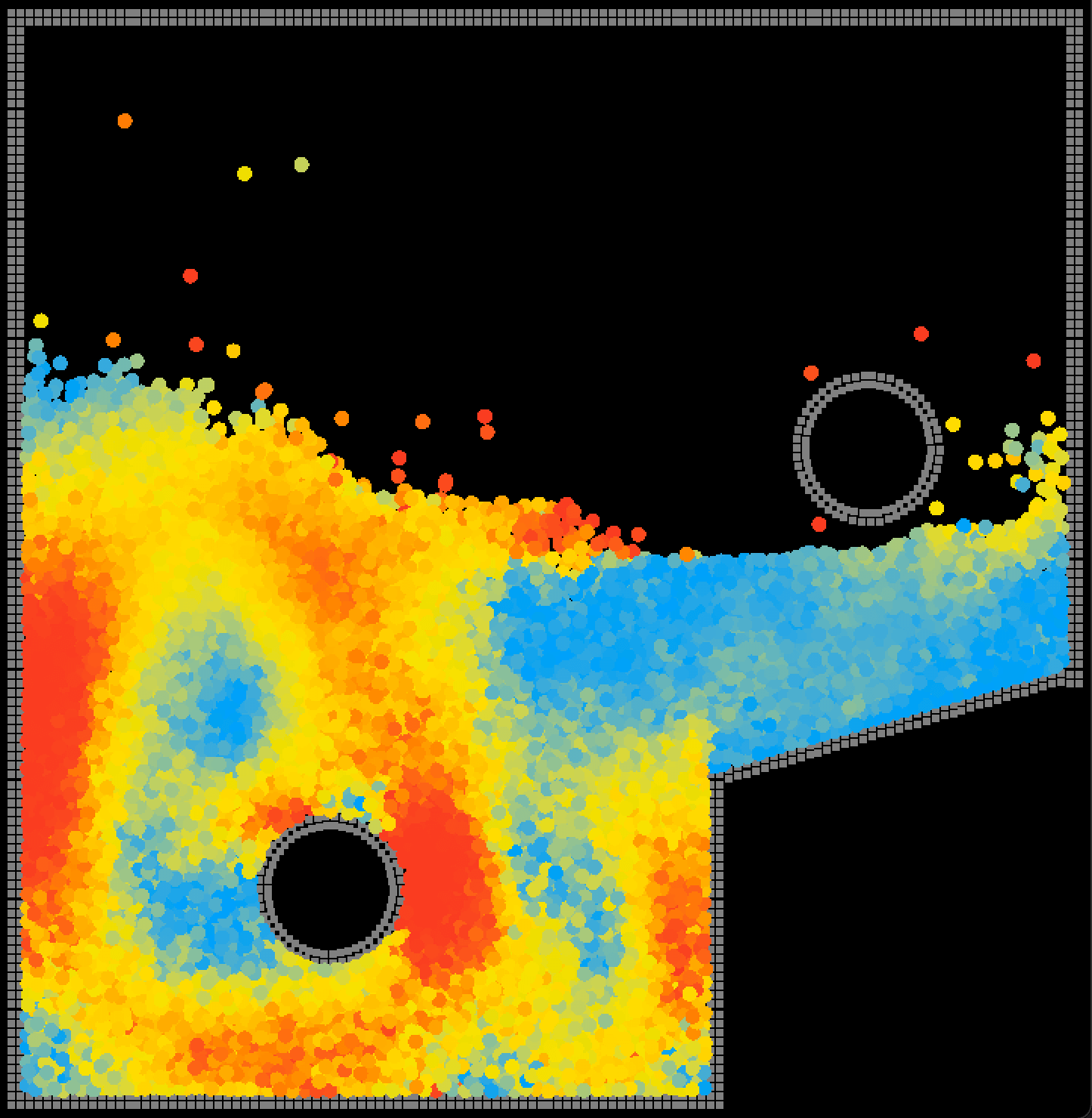 |
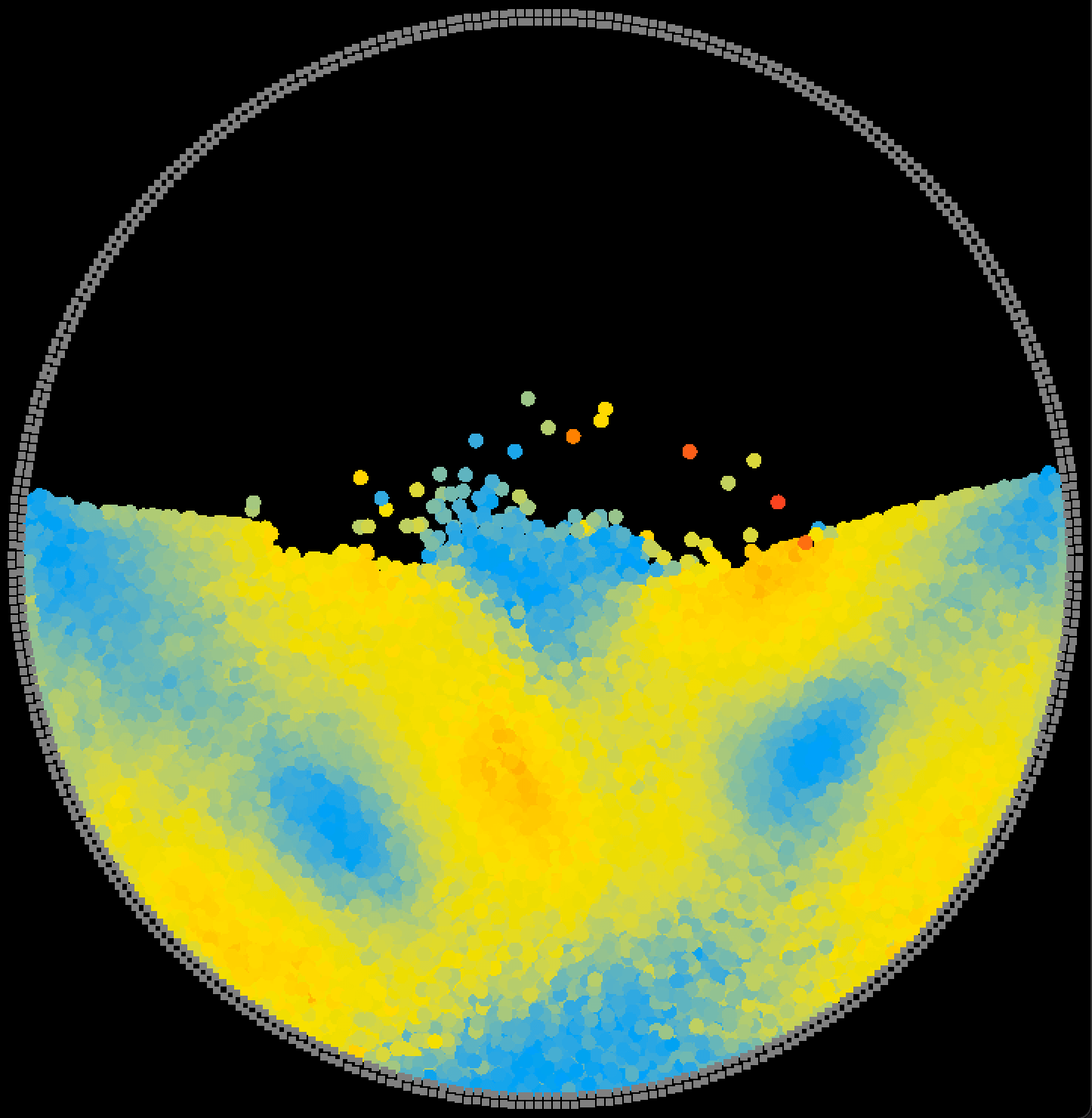 |
|---|
用鼠标添加外力, 可以明显观察到波的产生和反射:
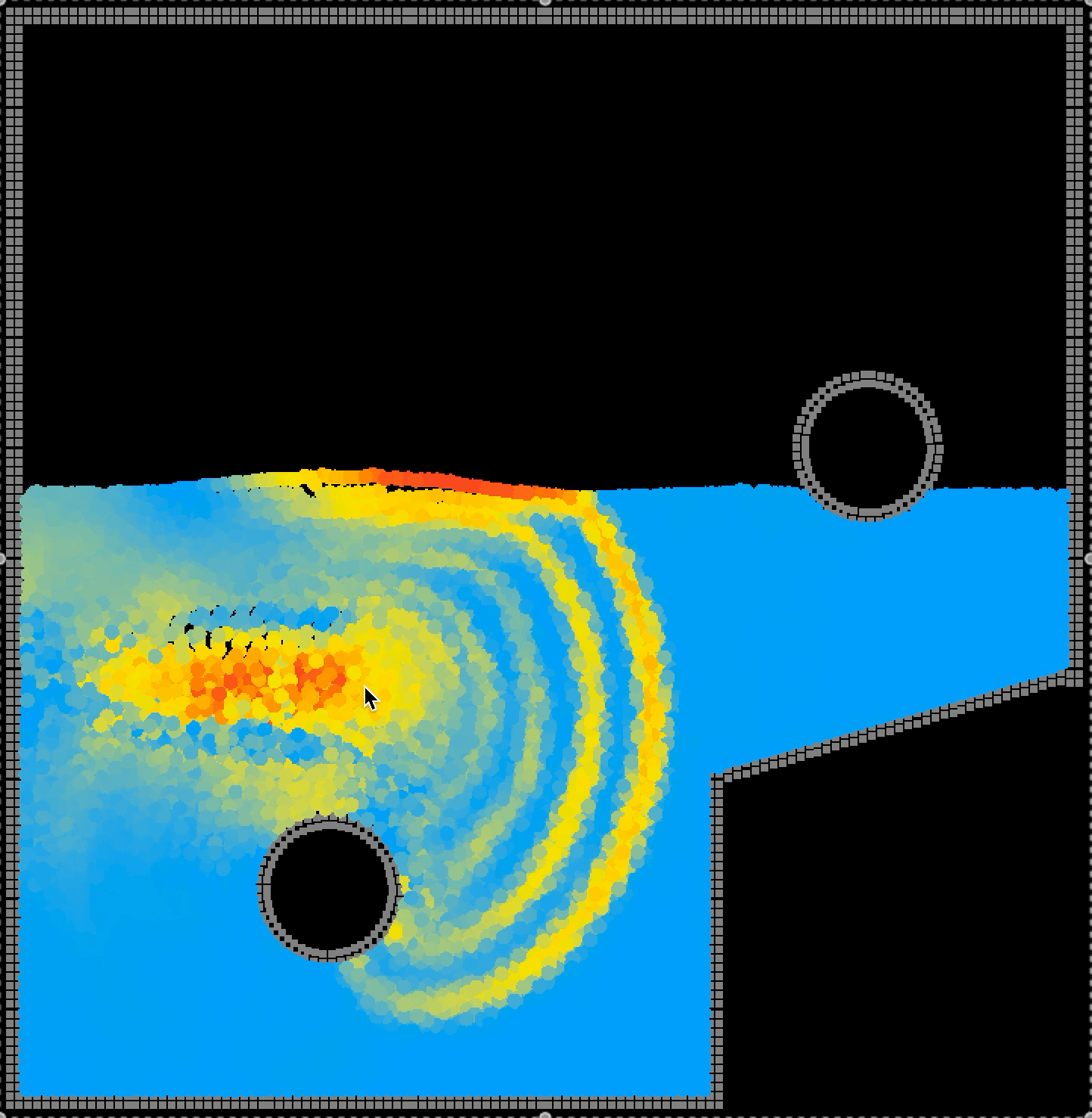 |
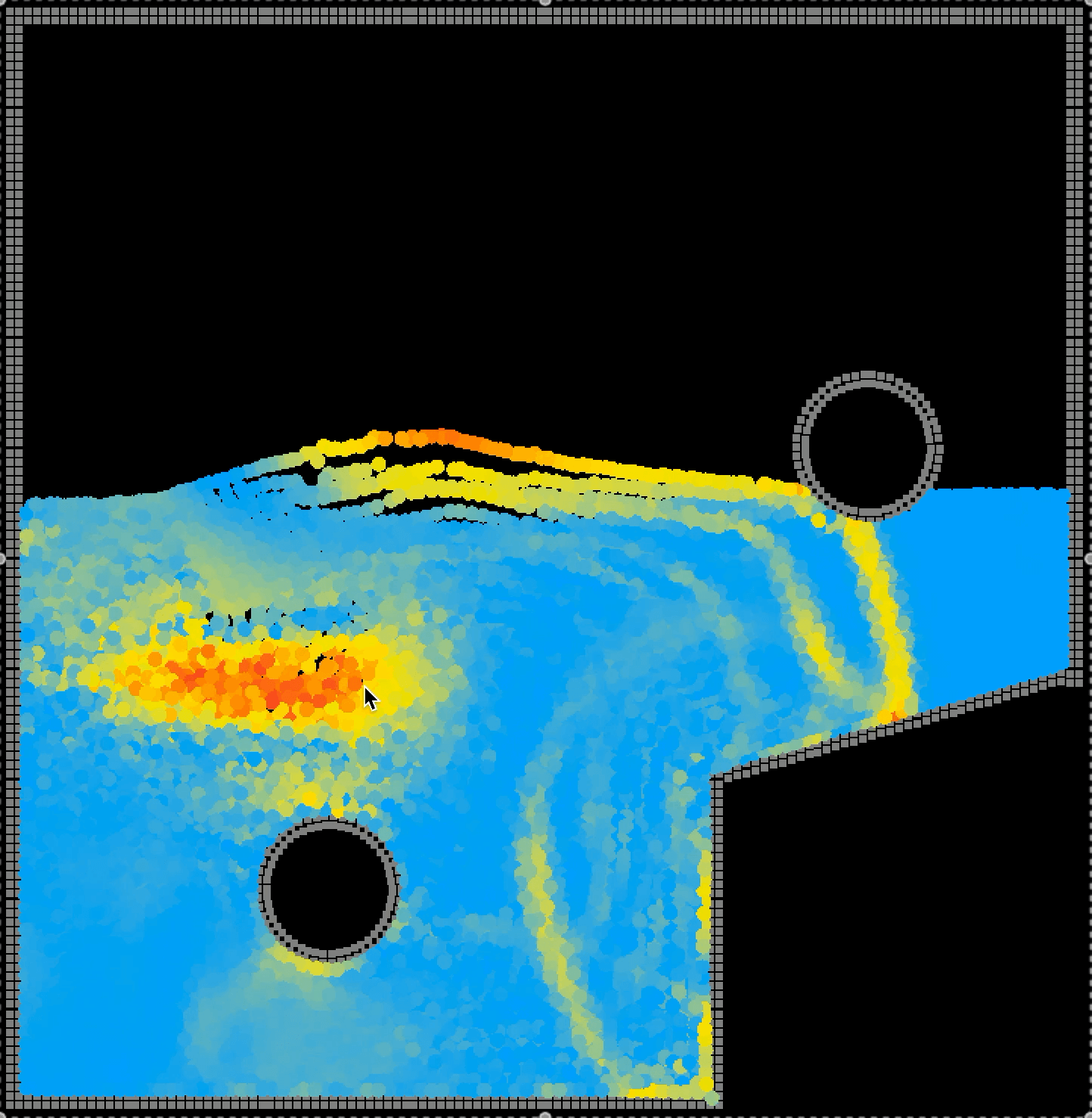 |
|---|
3D.
Cube 场景:
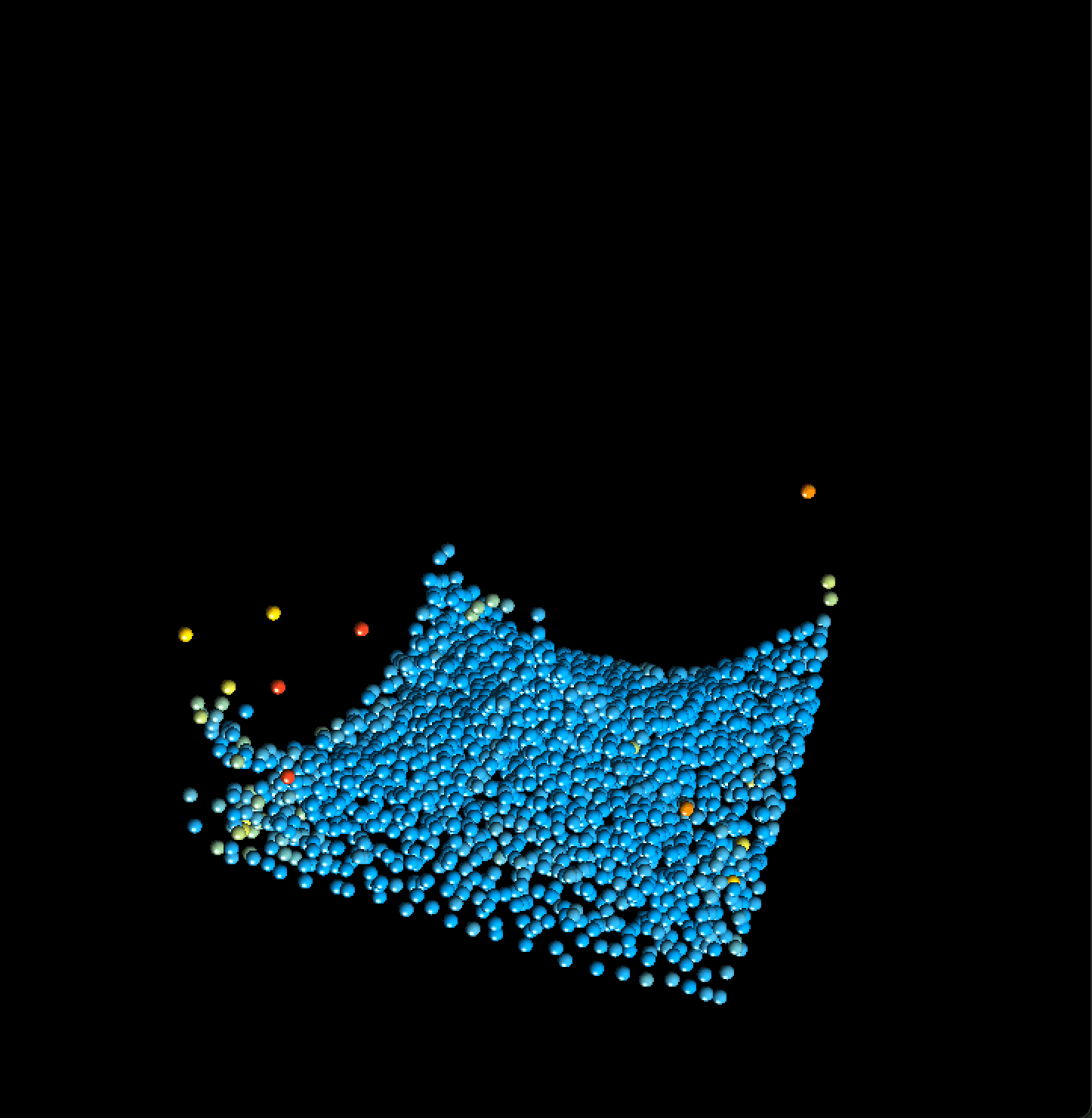 |
 |
 |
|---|
模拟和渲染的速度受粒子数量影响较大. 当粒子数较少时, 渲染的帧率稳定在 120 fps, 模拟速度略快于 2D. 当粒子数较大时, 模拟速度不太稳定 (特别是 add particles 后新旧流体接触时).