弹性体模拟

如无特殊说明, 本文图片均取自课程 PPT.

11 布料模拟

布料是一种特殊的二维弹性体, 可以考虑弹簧质点法或者 FEM. 线性 FEM 在上一篇文章已经详细讨论, 这里主要讲解弹簧质点法.

11.1 弹簧系统

弹簧质点系统的重点是根据布料的受力设计弹簧的连接方式. 分析受力:

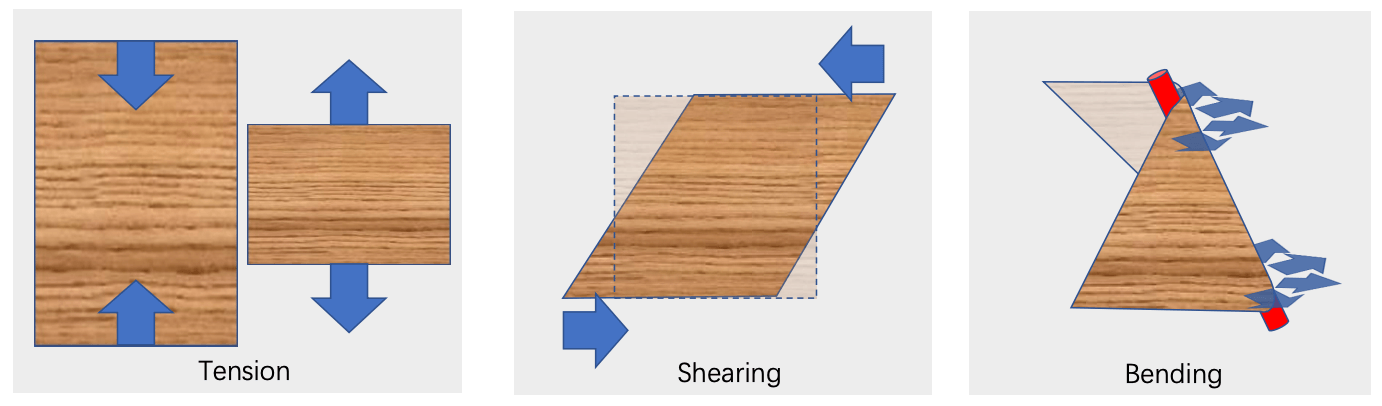
• 内力 (如下图):
  • Tension: 抵抗正拉伸
  • Shearing: 抵抗剪切 (斜着拉伸)
  • Bending: 抵抗弯曲
• 外力: Contact, Friction, Collision, Gravity, Environmental force (wind), Tearable Cloth…

使用特殊设计的弹簧网格模拟 tension, shearing 和 bending 力 (structured vs unstructured).

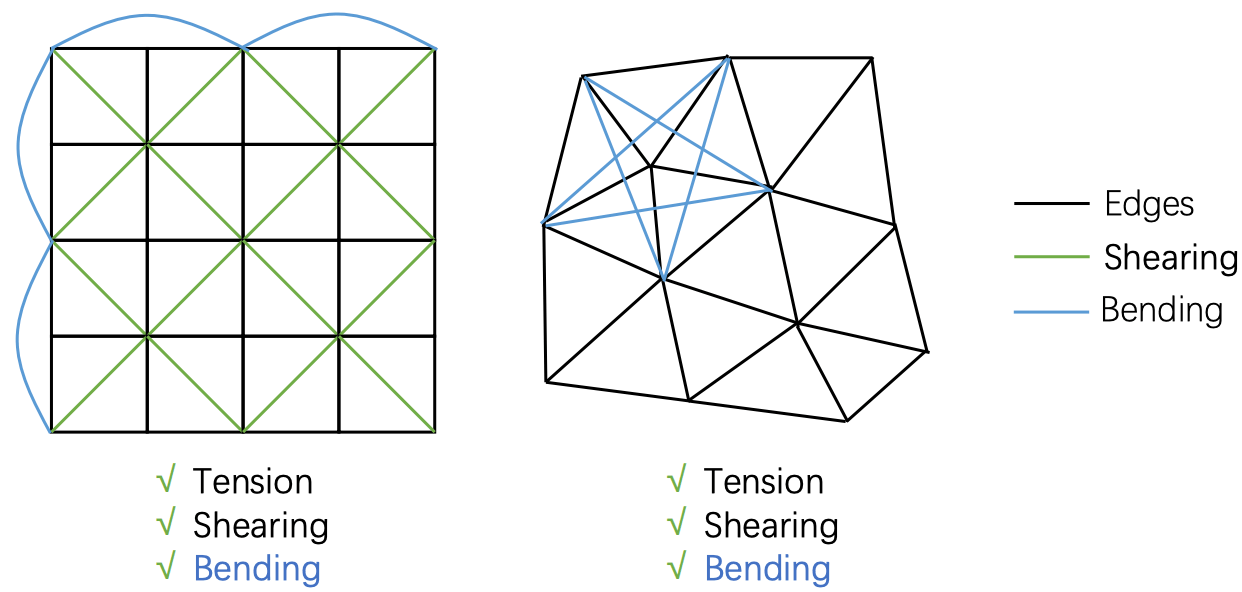
但这两种网格系统不能很好的模拟 bending. 当布料的弯曲很小的时候, 弹簧长度几乎不变, 几乎不产生回复力.

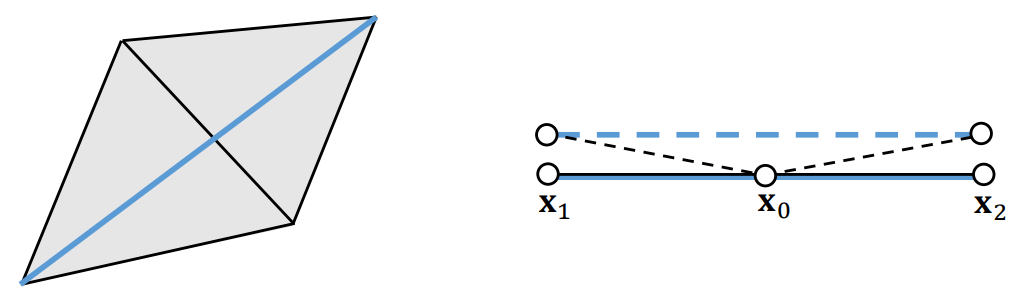
一种解决办法是使用二面角模型, 即 bending 与二面角的大小有关. 在下图所示的二面角中, 四个顶点的受力 \(f_i=f(\theta)u_i\), 其中实值函数 \(f(\theta)\) 控制力的大小, 向量 \(u_i\) 同时控制大小和方向, 应当满足:

• 向量 \(u_1,u_2\) 分别指向法向 \(n_1,n_2\).
• 因为弯曲不会改变边 \(\overline{x_3x_4}\) 的长度, 所以 \(u_4-u_3\) 应垂直于 \(\overline{x_3x_4}\), 即由 \(n_1,n_2\) 张成.
• 动量守恒 \(u_1+u_2+u_3+u_4=0\).

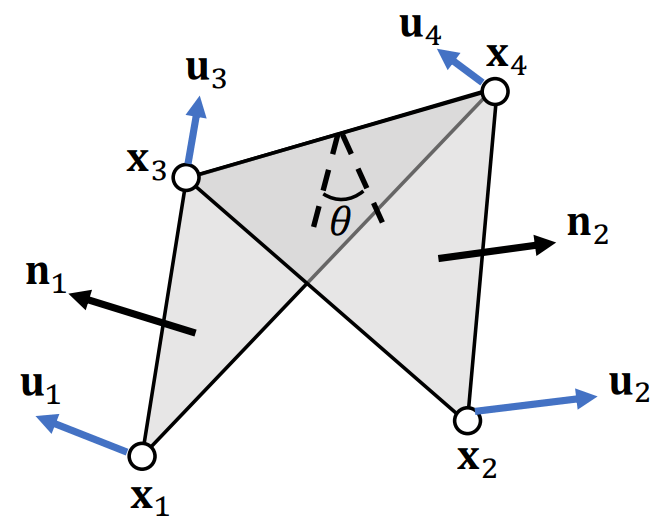
它们的具体公式如下: \[ \Align{ u_1 &= \frac{\|E\|}{\|N_1\|} n_1, & u_3 &= \hphantom- \frac{\lr{x_1-x_4,E}}{\|E\|\cdot\|N_1\|}n_1 + \frac{\lr{x_2-x_4,E}}{\|E\|\cdot\|N_2\|}n_2. \\ u_2 &= \frac{\|E\|}{\|N_2\|} n_2, & u_4 &= - \frac{\lr{x_1-x_3,E}}{\|E\|\cdot\|N_1\|}n_1 - \frac{\lr{x_2-x_3,E}}{\|E\|\cdot\|N_2\|}n_2. \\ } \] 其中 \(E=x_4-x_3\), \(N_1=(x_1-x_3)\times(x_1-x_4)\), \(N_2=(x_2-x_4)\times(x_2-x_3)\), 单位向量 \(n_1,n_2\). 下面给出了两种受力模型:

• Planar material: 稳定状态为 \(\theta=\pi\) (完全展平), \[ f(\theta) = \frac{k \|E\|^2}{\|N_1\|+\|N_2\|} \sin(\frac{\pi-\theta}{2}). \]

• Non-planar material: 稳定状态为 \(\theta=\theta_0\), \[ f(\theta) = \frac{k \|E\|^2}{\|N_1\|+\|N_2\|} \left[ \sin(\frac{\pi-\theta}{2}) - \sin(\frac{\pi-\theta_0}{2}) \right]. \]

11.2 The locking issue

真实布料的平面形变 (tension 和 shearing) 与弯曲 (bending) 是独立的. 然而弹簧系统的 stretch 和 bend 是耦合的.

• 下面矩形更倾向于沿着左边的虚线弯曲, 而不容易沿着右边的虚线弯曲, 破坏了布料的各向同性.
• 真实布料容易 bend, 难以 stretch. 然而如果我们增大 stretch 弹簧的劲度系数, 同时也会增加 bend 的难度.

核心原因是系统自由度太小了. 系统 (在稳定状态下) 的状态完全由网格边界点的位置确定.

12 Position-Based Methods

12.1 Position based dynamics

PBD 可以解决 locking issue. 之前刚体模拟就介绍过 PBD 方法, 其思想如下:

1. 让每个点按照自己的速度自由运动.
2. 强制施加约束条件, 恢复物体的形状.

12.1.1 两个质点的情形

先考虑两个质点的弹簧质点系统. 设质点 \(x_i,x_j\) 的质量分别为 \(m_i,m_j\), 弹簧原长 \(L\), 则约束条件为 \[ 0 = \phi(x) := \|x_i - x_j\| - L. \] 假设 \(x_i,x_j\) 按照其各自的速度移动了一段距离, 现在要它们满足约束 \(\phi(x)=0\). 这就相当于将点 \(x=(x_i,x_j)\) 投射到约束子流形 \(\phi(x)=0\) 上. 我们希望投影点 \(x^{\textsf{new}}=(x_i^{\textsf{new}},x_j^{\textsf{new}})\) 满足能量最小化: \[ \min_{x^{\textsf{new}}} \underbrace{\frac12 \Bigl[ m_i \| x_i^{\textsf{new}} - x_i \|^2 + m_j \| x_j^{\textsf{new}} - x_j \|^2 \Bigr]}_{\textsf{energy } J(x^{\textsf{new}})}, \qquad \textsf{s.t.}\; \phi(x^{\textsf{new }})=0. \] > 当 \(m_i=m_j\) 时, 能量函数 \(J(x^{\textsf{new}})=\frac12\|x^{\textsf{new}}-x\|^2\), 也就是将 \(x\) 投射到子流形上的最近点. 加权可以保证投射过程中动量和角动量守恒. 若投射过程中动量/角动量不守恒, 就会导致物体像是被某个看不见的力 (ghost force) 推了一下, 产生不真实的效果.

能量函数是凸的, 使用 Lagrange 乘子法可以解得 \[ \Align{ x_i^{\textsf{new}} &= x_i - \frac{m_j}{m_i+m_j} \phi(x) \cdot \hat{v}_{ij}, \\ x_j^{\textsf{new}} &= x_j + \frac{m_i}{m_i+m_j} \phi(x) \cdot \hat{v}_{ij}, } \] 其中单位向量 \(\hat{v}_{ij}=(x_i-x_j)/\|x_i-x_j\|\).

PBD 要强制保证约束条件, 似乎与之前相比更加限制了自由度? 非也. 在每个点自由移动的时候自由度是极大的. 如下图, 蓝色的为约束子流形, 红色的区域为 locking 区域, 黄色的向量为粒子各自的速度. PBD 先自由移动再投射, 使得粒子避开了 locking 区域.

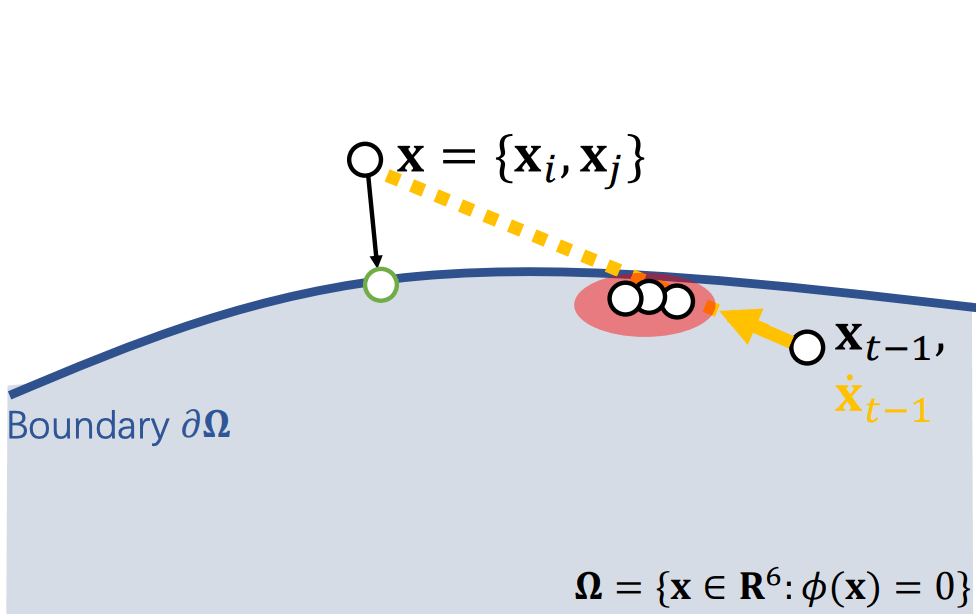
12.1.2 多个质点的情形

现在考虑一般的弹簧质点系统. 位置向量 \(x=(x_1,\dots,x_n)\), 方便起见, 所有质点的质量都为 \(m\). 无向边集 \(E=\{\textsf{all edges }\{i,j\}\}\) 记录了所有的弹簧, 边 \(\{i,j\}\) 的弹簧原长为 \(L_{ij}\). 现在, 每条边 \(\{i,j\}\in E\) 都对应一个约束条件 \[ 0 = \phi_{ij}(x) := \|x_i - x_j\| - L_{ij}. \] 我们采用一个类似 Jacobi 迭代的办法优化这些约束. 在每次迭代步中, 依次投射每个约束条件, 然后将这些投射点取平均:

1. 迭代 \(T\) 次:

   • 对所有顶点 \(i\), 初始化 \(\overline{x_i^{\textsf{new}}}\leftarrow0\), \(n_i\leftarrow0\).
   • 对所有边 \(\{i,j\}\in E\):
     • \(\overline{x_i^{\textsf{new}}}\leftarrow\overline{x_i^{\textsf{new}}}+x_i-\frac12\phi_{ij}(x)\hat{v}_{ij}\).
     • \(\overline{x_j^{\textsf{new}}}\leftarrow\overline{x_j^{\textsf{new}}}+x_i+\frac12\phi_{ij}(x)\hat{v}_{ij}\).
     • \(n_i\leftarrow n_i+1\).
     • \(n_j\leftarrow n_j+1\).
   • 对所有顶点 \(i\),
     • \(\overline{x_i^{\textsf{new}}}\leftarrow\overline{x_i^{\textsf{new}}}/n_i\).
     • \(x_i\leftarrow(\overline{x_i^{\textsf{new}}}+\alpha x_i)/(1+\alpha)\).

2. 输出 \(\overline{x_i^{\textsf{new}}}\).

PBD 完整的时间步为

1. (自由运动) 时间积分.
2. (约束投射)
   • \(x^{\textsf{new}}\leftarrow\mathsf{Projection}(x)\).
   • \(v\leftarrow v+(x^{\textsf{new}}-x)/h\).
   • \(x\leftarrow x^{\textsf{new}}\).

12.1.3 PBD 的优缺点

Pros

• Parallelable on GPUs (PhysX)
• Easy to implement
• Fast in low resolutions
• Generic, can handle other coupling and constraints, including fluids

Cons

• Not physically correct
• Low performance in high resolutions
  • Hierarchical approaches (can cause oscillation and other issues…)
  • Acceleration approaches, like Chebyshev

12.2 Strain limiting

应变约束类似于 PBD. 不同的是, SL 约束的是应变 \(\sigma\), 并且约束条件是不等式 \(\sigma_{\textsf{min}}\leq\sigma\leq\sigma_{\textsf{max}}\).

对于弹簧质点系统, 我们约束弹簧的应变 \[ \sigma = \frac1{L} \|x_i-x_j\| \] 到一个范围 \([\sigma_{\textsf{min}},\sigma_{\textsf{max}}]\) 内 (PBD 就是约束 \(\sigma=1\)). 过程和 PBD 几乎一样, 只是加了一步计算 target strain \(\sigma_0\): \[ \Align{ \sigma_0 &= \operatorname{clip}(\sigma,\sigma_{\textsf{min}},\sigma_{\textsf{max}}) \\ x_i^{\textsf{new}} &= x_i - \frac{m_j}{m_i+m_j} (\|x_i-x_j\|-\sigma_0 L) \cdot \hat{v}_{ij}, \\ x_j^{\textsf{new}} &= x_j - \frac{m_i}{m_i+m_j} (\|x_i-x_j\|-\sigma_0 L) \cdot \hat{v}_{ij}. } \] 我们也可以约束弹簧质点系统中三角形的面积. 考虑三角形 \((x_i,x_j,x_k)\), 面积约束为 \(A_{\textsf{min}}\leq A\leq A_{\textsf{max}}\). 记自由移动后的三角形面积为 \(A=\|(x_j-x_i)\times(x_k-x_i)\|/2\), 则首先计算 target ratio \[ s = \sqrt{ \frac{\operatorname{clip}(A,A_{\textsf{min}},A_{\textsf{max}})}{A} }, \] 然后将面积约束为 \(s^2A\), 即求解优化问题 \[ \min_{x^{\textsf{new}}} \frac12 \Bigl[ m_i \| x_i^{\textsf{new}} - x_i \|^2 + m_j \| x_j^{\textsf{new}} - x_j \|^2 + m_k \| x_k^{\textsf{new}} - x_k \|^2 \Bigr], \qquad \textsf{s.t. new area is }s^2A. \] 由于投射过程中动量守恒, 新旧三角形的质心重合, 为 \(c=(m_ix_i+m_jx_j+m_kx_k)/(m_i+m_j+m_k)\). 解得 \[ \Align{ x_i^{\textsf{new}} &= c + s(x_i - c), \\ x_j^{\textsf{new}} &= c + s(x_j - c), \\ x_k^{\textsf{new}} &= c + s(x_k - c). \\ } \] 应变约束在物理模拟中广泛应用:

• to avoid instability
• to avoid artifacts (due to large deformation)
• for nonlinear effects
• to address the locking issue

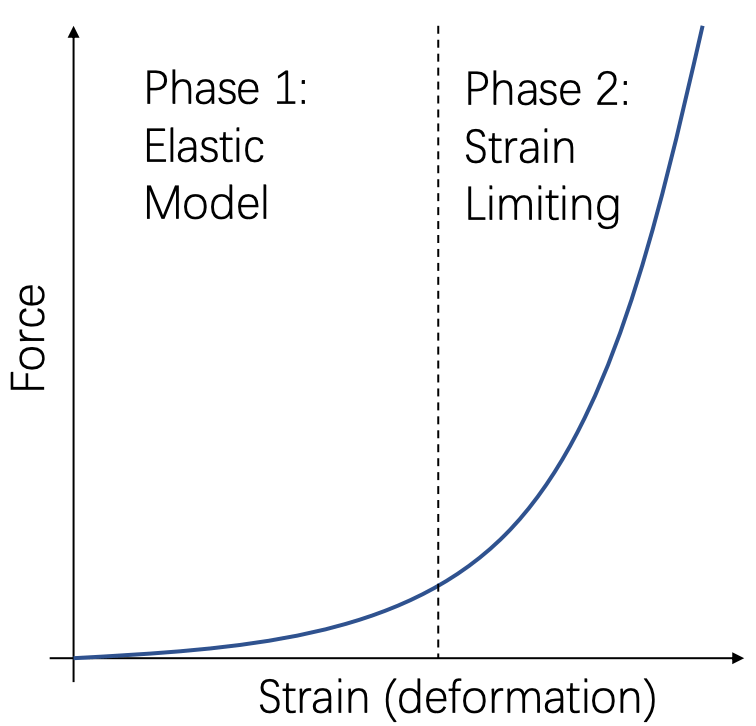
一般来说, 当应变比较小的时候可以使用弹性模型进行模拟; 当应变大于一个阈值, 就使用应变约束, 防止应变过大, 如下图.

13 Implicit Euler Methods

设一共有 \(n\) 个质点, 位置为 \(x_i\), 速度为 \(v_i\), 受力为 \(f_i\), 质量为 \(m_i\). 一些质点间连有弹簧, 质点 \(i\) 收到的来自质点 \(j\) 的力为 \[ f_{ij} = k(\|x_i-x_j\| - l_0) \cdot \frac{x_i-x_j}{\|x_i-x_j\|} = -f_{ji}. \] 质点 \(i\) 所受合力为 \[ f_i = f_{\sf ext} + \sum_{j\in{\cal N}(i)} f_{ij}. \] 组装矩阵 \[ \Align{ x &= \pmqty{x_1\\\vdots\\x_n}, & v &= \pmqty{v_1\\\vdots\\v_n}, & f &= \pmqty{f_1\\\vdots\\f_n}, & M &= \pmqty{m_1I_3\\&\ddots\\&&m_nI_3}. } \] 则有微分方程 \[ \left\{\Align{ x' &= v, \\ v' &= M^{-1} f = M^{-1} (f_{\sf int} + f_{\sf ext}). }\right. \]

13.1 时间积分

显式 Euler 法实现简单, 效率高, 但是数值不稳定, 容易导致能量爆炸. 一般考虑隐式方法. 隐式 Euler 方法的方程为: \[ \left\{\Align{ x^+ &= x + hv^+, \\ v^+ &= v + hM^{-1} (f_{\sf int}(x^+) + f_{\sf ext}). }\right. \] 消去 \(v^+\) 得到关于 \(x^+\) 的方程 \[ x^+ = \underbrace{[x + h(v + hM^{-1} f_{\sf ext})]} _{\textsf{$y$ (independent of $x^+$)}} + h^2M^{-1}f_{\sf int}(x^+). \] 该 \(x^+\) 实际上是如下能量函数的极值点: \[ g(x) = \frac1{2h^2} \|x - y\|_M^2 + E(x), \] 其中 \(\|z\|_M:=z\T Mz\), 内力是弹性势能的负梯度 \(f_{\sf int}(x^+)=-\partial E/\partial x|_{x^+}\).

13.2 Newton's method

可以使用 Newton 迭代法求出 \(g(x)\) 的极值点:

• Init \(x^{(1)}=x\).
• Update with \(x^{(k+1)}=x^{(k)} - H^{-1}|_{x^{(k)}}\nabla g|_{x^{(k)}}\).
  • Hessian \(H=\nabla^2g\).
  • 求 Hessian 的逆 (求解线性系统) 是性能瓶颈.

当能量函数为凸函数时, Newton 法可以收敛到极值点 (对于二次的能量函数, 一次迭代就可以达到). 对于非凸的能量函数, 往往需要一些手段避免 overshooting (错过极值点), 比如回溯线搜索 (backtracking line search).

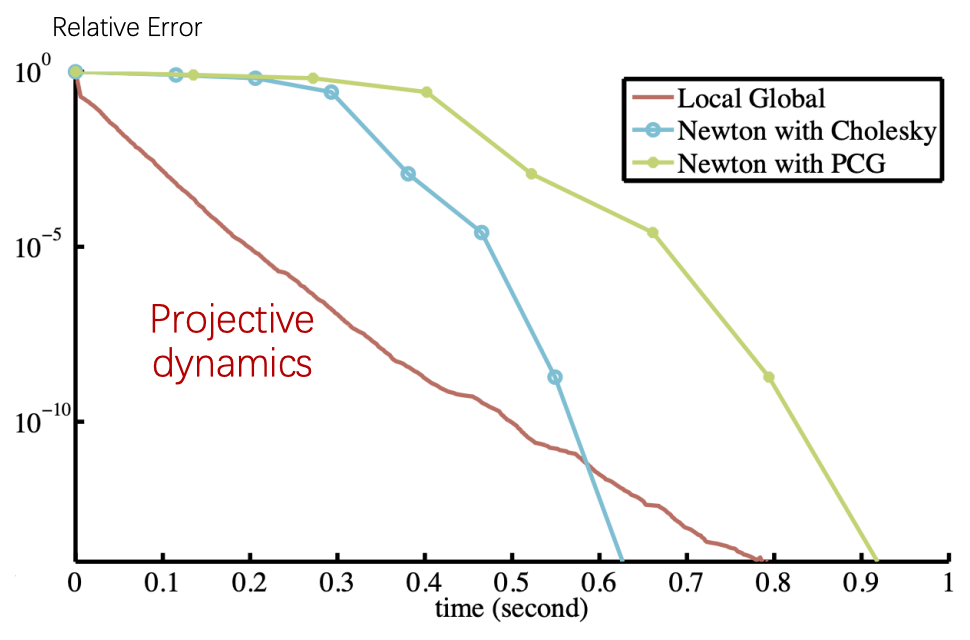
13.3 Projective dynamics

参考文献: Tiantian Liu et al, Fast Simulation of Mass-Spring Systems (SIGGRAPH Asia 2013).

弹簧系统 Newton 法的缺陷: Hessian 不一定可逆 / 不一定正定 (能量函数非凸), Newton 法只能找到局部极大/极小值, 而非全局最小值. Projective dynamics 方法可以保证找到全局最小值.

13.3.1 问题转化

将能量函数 \(g(x)\) 展开: \[ g(x) = \underbrace{\frac1{2h^2} \|x - y\|_M^2 \vphantom{\sum_{e\in E}}} _{\textsf{inertia}} + \underbrace{\sum_{e\in E} \frac12 k_e (\|x_{e_1}-x_{e_2}\| - L_e)^2} _{\textsf{potential}} , \] (其中弹簧 \(e\) 的两个顶点为 \(e_1,e_2\).) 注意到势能中的 \((\|x_{e_1}-x_{e_2}\|-L_e)^2\) 关于 \(x_{e_1},x_{e_2}\) 不是二次的, 导致势能非凸, 这是 Newton 法无法找到全局最小值的原因. Projective dynamics 的关键观察是将势能转化为一个 (二次) 优化问题的极值点:

\[ (\|x_{e_1}-x_{e_2}\| - L_e)^2 \equiv \min_{\|\orange{z}\|=L_e} \|(x_{e_1}-x_{e_2})-\orange{z}\|^2. \] 右式取最小值时, \(z\) 就是从 \(x_{e_2}\) 指向 \(x_{e_1}\) 的长度为 \(L_e\) 的向量. 将右式代入 \(g(x)\), 得到 \[ \min_{x}g(x) = \min_{ \substack{\|\orange{z_e}\|=L_e \\ \blue{x}\in\R^{3n}} } \biggl[ \frac1{2h^2} \|\blue{x} - y\|_M^2 + \sum_{e\in E} \frac12 k_e \|(\blue{x_{e_1}}-\blue{x_{e_2}}) - \orange{z_e}\|^2 \biggr]. \tag{$\spadesuit$} \]

13.3.2 Local and global steps

Projective dynamics 和 ARAP 优化类似. 它将 \((\spadesuit)\) 式分为 local 和 global 两步交替优化, 其中 local 步分开优化每个弹簧的能量, global 步优化系统整体的能量.

Local: 固定 \(x\) 不变, 优化 \(z_{ij}\). 由于各个 \(z_{ij}\) 是无关的 (没有交叉项), 所以可以分别优化每个 \(z_{ij}\), 该过程是纯粹 local 的.

Global: 固定 \(z_{ij}\) 不变, 优化 \(x\). 我们将 \((\spadesuit)\) 式转化为矩阵乘法形式 (略去常数项): \[ \min_{x} g(x) \rightsquigarrow \min_{x} \biggl[ \frac12 \blue{x} \T \Bigl( \frac1{h^2}M + L \Bigr) \blue{x} - \blue{x}\T \Bigl( \frac1{h^2} My + Jz \Bigr) \biggr], \tag{$\clubsuit$} \]

上式中 \(L\) 和 \(J\) 为: \[ \Align{ L &= \left( \sum_{e\in E} k_e A_e A_e\T \right) \otimes I_3, & J &= \left( \sum_{e\in E} k_e A_e S_e\T \right) \otimes I_3, } \] 其中,

• \(A_e\in\R^{n}\) 是弹簧的关联向量 (第 \(e_1\) 分量为 \(1\), 第 \(e_2\) 分量为 \(-1\), 其余为零); 矩阵 \(\sum_ek_eA_eA_e\T\) 其实就是图的 Laplace 矩阵 (以 \(k_e\) 为边权重).
• \(S_e\in\R^{|E|}\) 是弹簧的指示向量 (第 \(e\) 分量为 \(1\), 其余为零).

可以发现 \((\clubsuit)\) 式是一个关于 \(x\) 的二次函数! 可以直接求出最小值点的解析解: \[ x = \Bigl(\frac1{h^2}M + L\Bigr)^{-1} \Bigl(\frac1{h^2} My + Jz \Bigr). \] 二次项系数 \(\frac1{h^2}M+L\) 严格正定, 并且是常数 (若网格的拓扑不改变), 可以预计算其 Cholesky 分解.

综上所述, projective dynamics 时间步为:

• 初始化 \(x^{(1)}\leftarrow y\).

• 重复执行 \(K\) 次:

  • (Local) \(z_e \leftarrow L_e(x_{e_1}-x_{e_2})/\|x_{e_1}-x_{e_2}\|\) (对每个弹簧 \(e\)).

  • (Global) 求解线性系统 \[ \left(\frac1{h^2}M + L\right) x^{(k+1)} = \frac1{h^2}My + Jz. \]

  • 当 \(\|x^{(k+1)}-x^{(k)}\|\) 小于某阈值时停止.

• \(x^+\leftarrow x^{(K+1)}\).

• \(v^+\leftarrow(x^+-x)/h\).

13.3.3 PD 的优缺点

Pros:

• By building constraints into energy, the simulation now has a theoretical solution with physical meaning.
• Fast on CPUs with a direct solver. No more factorization!
• Fast convergence in the first few iterations.

Cons:

• Slow on GPUs (direct solver is not well supported).
• Slow convergence over time (fails to consider Hessian caused by projection).
  • Still suffering from high stiffness
• Cannot easily handle changes.
  • Remeshing due to fracture, etc

13.4 不同的迭代方法比较

隐式 Euler 积分法的核心是求解 \[ x^+ = \argmin_x g(x), \] 抽象地讲, 迭代优化方法 (如梯度下降, Newton, PD) 的更新策略为 \[ x^{(k+1)} \leftarrow x^{(k)} - \underbrace{a^{(k)} \mathstrut}_{\textsf{step size}} \underbrace{(A^{(k)})^{-1} \mathstrut}_{\textsf{matrix}} \, \underbrace{\nabla g|_{x^{(k)}} \mathstrut}_{\textsf{gradient}}. \]

• 梯度下降: 步长 \(a^{(k)}\) 是一个可调参数, 矩阵 \(A^{(k)}\) 为单位阵.
  • 线性收敛
  • 需要调节超参数
  • 可能陷入局部极小值
• Newton: 步长 \(a^{(k)}\equiv1\), 矩阵 \(A^{(k)}\) 为 \(g\) 的 Hessian.
  • 平方收敛
  • 可能陷入局部极小值
• PD: 步长 \(a^{(k)}\equiv1\), 矩阵 \(A^{(k)}\) 为近似的 Hessian \(\frac1{h^2}M+H\).
  • 线性收敛
  • 收敛到全局最小值