流体模拟

如无特殊说明, 本文图片均取自课程 PPT.

8 PIC & FLIP 方法

参考资料: Ten Minute Physics 的 FLIP 流体模拟.

8.1 PIC

由于 Euler 网格法 advection 步的 semi-Lagrange 方法会导致较大的数值误差, 这是因为我们并没有真正地采用 Lagrange 视角去模拟粒子, 而是用网格上的速度近似粒子速度. 但网格的精度肯定不如自由粒子. 我们不妨更进一步, 在网格系统中引入粒子来提高精度.

PIC (particle in cell) 方法结合了 Euler 和 Lagrange 视角. 它既包含了一个固定网格, 也包含了固定网格中的粒子. 网格通常比较稀疏, 因此性能比 Euler 网格法高 (因为需要在网格上求解线性系统). 粒子并行性比较好, 一个网格可以包含多个粒子.

PIC 方法同时维护一个粒子列表和一个 staggered grid.

1. 粒子时间积分: 用 Euler 积分法更新每个粒子的位置和速度.
   • Particles carry velocity \(\to\) can skip grid advection!
2. P2G: 将粒子的速度转移到网格上.
3. 不可压缩求解: 在网格上求解速度的不可压缩方程 (类似于网格法的 pressure projection).
4. G2P: 将网格的速度转移回粒子上.

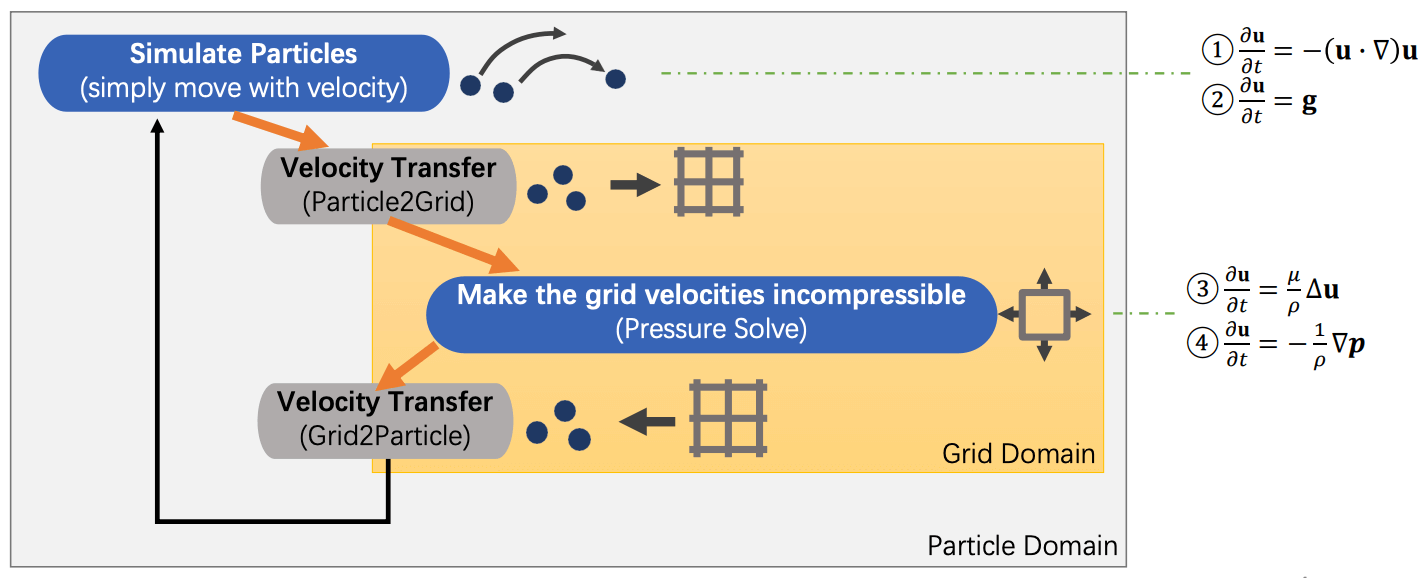
PIC 方法的关键步骤是网格与粒子间的速度转移 P2G 和 G2P. 它们都采用线性插值:

• P2G: 对于每个粒子的每个速度分量, 计算它在 staggered grid 上的八个相邻顶点, 将速度分量按照三线性插值分配到八个顶点上.
• G2P: 对于每个粒子的每个速度分量, 它的值为 staggered grid 八个相邻顶点三线性插值的结果.

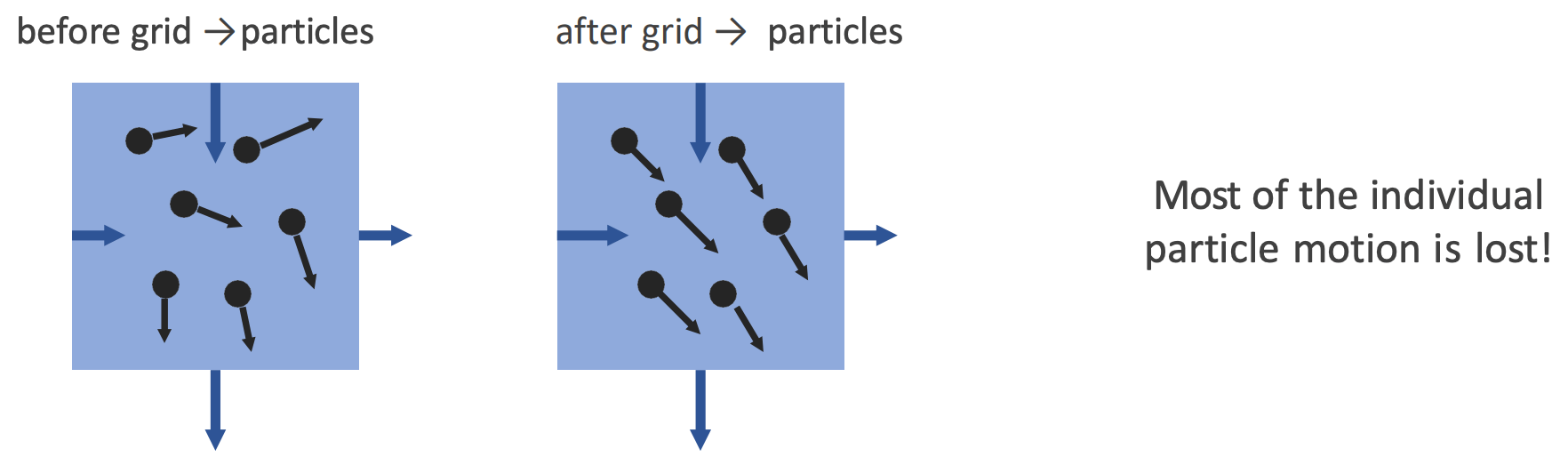
PIC 方法的速度转移是稳定的, 然而 G2P 插值会使得同一个 cell 内的粒子速度趋同, 粒子失去了原有的速度. 这会导致流体的能量耗散 (dissipation), 如下图.

8.2 FLIP

FLIP (fluid implicit particles) 可以解决 PIC 中的能量耗散问题. 与后者不同的是, FLIP 在进行 G2P 时只转移速度改变量. 其基本流程和 PIC 相似:

1. 粒子时间积分: 用 Euler 积分法更新每个粒子的位置和速度.
2. P2G: 将粒子的速度转移到网格上.
   • 将 grid 速度复制一份, 以便 G2P 使用.
3. 不可压缩求解: 在网格上求解速度的不可压缩方程.
4. G2P: 将网格的速度转移回粒子上.
   • 令当前的 grid 速度减去之前复制的 grid 速度, 得到速度改变量. 将速度改变量叠加到粒子速度上.

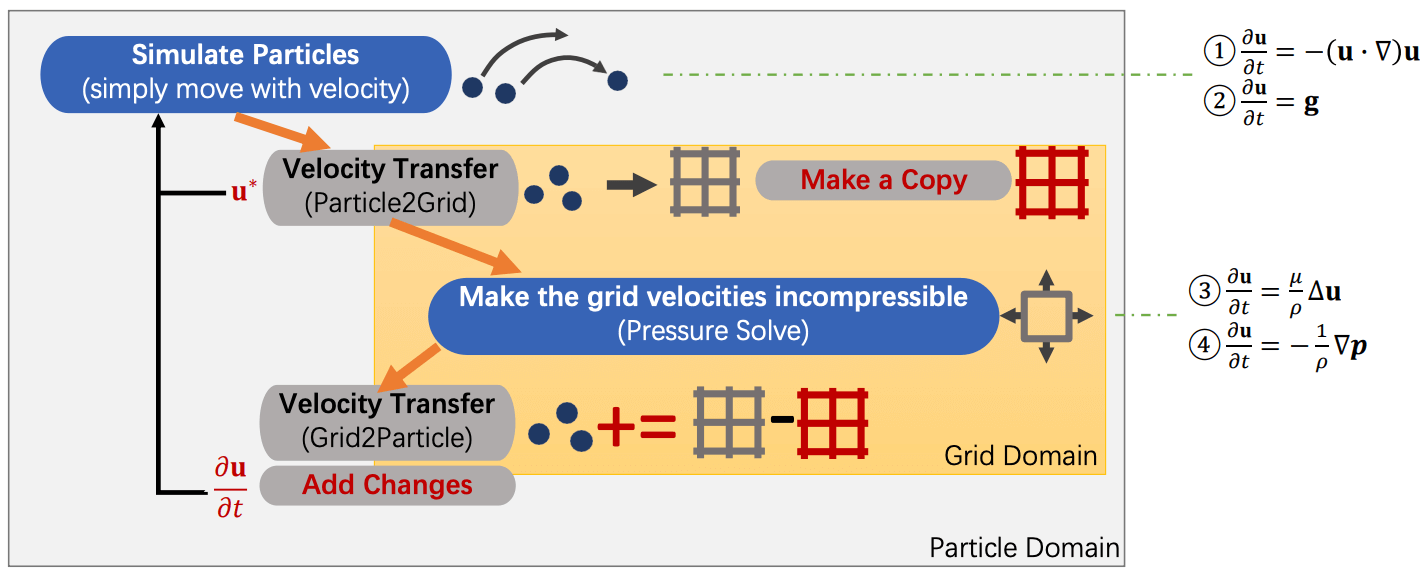
FLIP 方法没有能量耗散, 但是不是很稳定. 因此在实际应用中我们通常融合 PIC 和 FLIP 两种方法, 在 G2P 时按照如下公式计算粒子速度: \[ v^{\sf new} := (1-\lambda) \orange{v^{\sf PIC}} + \lambda(v^{\sf old} + \blue{\Delta v^{\sf FLIP}}), \] 其中 \(\orange{v^{\sf PIC}}\) 和 \(\blue{\Delta v^{\sf FLIP}}\) 分别是按照 PIC 方法和 FLIP 方法计算得到的速度和速度改变量, 系数 \(0\leq\lambda\leq1\), 通常取 \(\lambda=0.95\).

8.3 Making the velocity field incompressible

这一步的目的让网格上的速度场不可压缩, 即 \(\nabla\cdot v=0\), 离散化为 \[ U_{i+1,j}-U_{i,j}+V_{i,j+1}-V_{i,j} = 0. \]

可以采用 Gauss-Seidel 迭代法:

• 重复执行 \(T\) 次:

  • 对每个网格单元 \((i,j)\):

    • 计算散度和分母: \[ \left\{\Align{ d &\leftarrow U_{i+1,j}-U_{i,j}+V_{i,j+1}-V_{i,j}, \\ s &\leftarrow s_{i+1,j}+s_{i-1,j}+s_{i,j+1}+s_{i,j-1}. \\ }\right. \] 其中 \(s_{i,j}=0\) 代表固体单元; \(s_{i,j}=1\) 代表流体或者空气单元.

    • 更新速度:

    \[ \left\{\Align{ \rlap{U_{i,j}}\hphantom{U_{i+1,j}} &\leftarrow \hphantom{U_{i+1,j}}\llap{U_{i,j}} + d\,s_{i-1,j}/s, \\ \rlap{U_{i+1,j}}\hphantom{U_{i+1,j}} &\leftarrow \hphantom{U_{i+1,j}}\llap{U_{i+1,j}} + d\,s_{i+1,j}/s, \\ \rlap{V_{i,j}}\hphantom{U_{i+1,j}} &\leftarrow \hphantom{U_{i+1,j}}\llap{V_{i,j}} + d\,s_{i,j-1}/s, \\ \rlap{V_{i,j+1}}\hphantom{U_{i+1,j}} &\leftarrow \hphantom{U_{i+1,j}}\llap{V_{i,j+1}} + d\,s_{i,j+1}/s. }\right. \]

Overrelaxation 技巧可以加速 G-S 的收敛: \[ d \leftarrow \orange{o} \cdot (U_{i+1,j}-U_{i,j}+V_{i,j+1}-V_{i,j}), \] 其中系数 \(o\in(1,2)\), 可以取 \(o=1.9\).

8.4 Compensate drifts

基于速度的流体模拟方法 (velocity-based) 都存在一个问题——漂移 (drifting). 如果两个粒子有逐渐靠近的趋势 (速度), 那么 pressure solve 是可以正确地把粒子推开的 (下图左, 图自参考资料). 然而如果两个粒子已经贴上了, 相对速度为零, 那么 pressure solve 也无能为力 (下图右).

第一, 新增模拟步骤 "push particles apart": 遍历每一对粒子, 如果它们的距离 \(d\) 小于 \(2r\) (其中 \(r\) 为粒子半径), 则把它们格推离 \((d-2r)/2\). 有时需要多次迭代 (通常是性能瓶颈).

• 朴素的遍历方法很慢. 可以以略大于 \(2r\) 为边长构造一个网格 (hash 表), 将粒子放入网格中, 对一个粒子只需搜寻邻居网格内的粒子即可.

第二, 在 pressure solve 的散度中加入漂移修正项 (drift compensaiton): \[ d \leftarrow o(U_{i+1,j}-U_{i,j}+V_{i,j+1}-V_{i,j}) \orange{{}-k(\rho-\rho_0)}, \] 其中 \(\rho_0\) 是初始状态的所有格子的平均密度, \(\rho\) 是当前密度, \(k\) 是修正系数 (可取 \(k=1\)). 网格上的密度由粒子上的密度插值得到.

8.5 An implementation

参考 Ten Minute Physics 的思路, 我们采用如下的模拟框架:

• 对每个时间步 (可进一步分为若干 substeps):
  • Time integration (Symplectic Euler)
  • Collisions handling (处理粒子与边界和障碍物的碰撞)
  • Pushing particles apart
  • Collisions handling (处理粒子与边界和障碍物的碰撞)
  • P2G
  • Updating particle density (把网格上的密度插值到粒子上)
  • Solving incompressibility
  • G2P

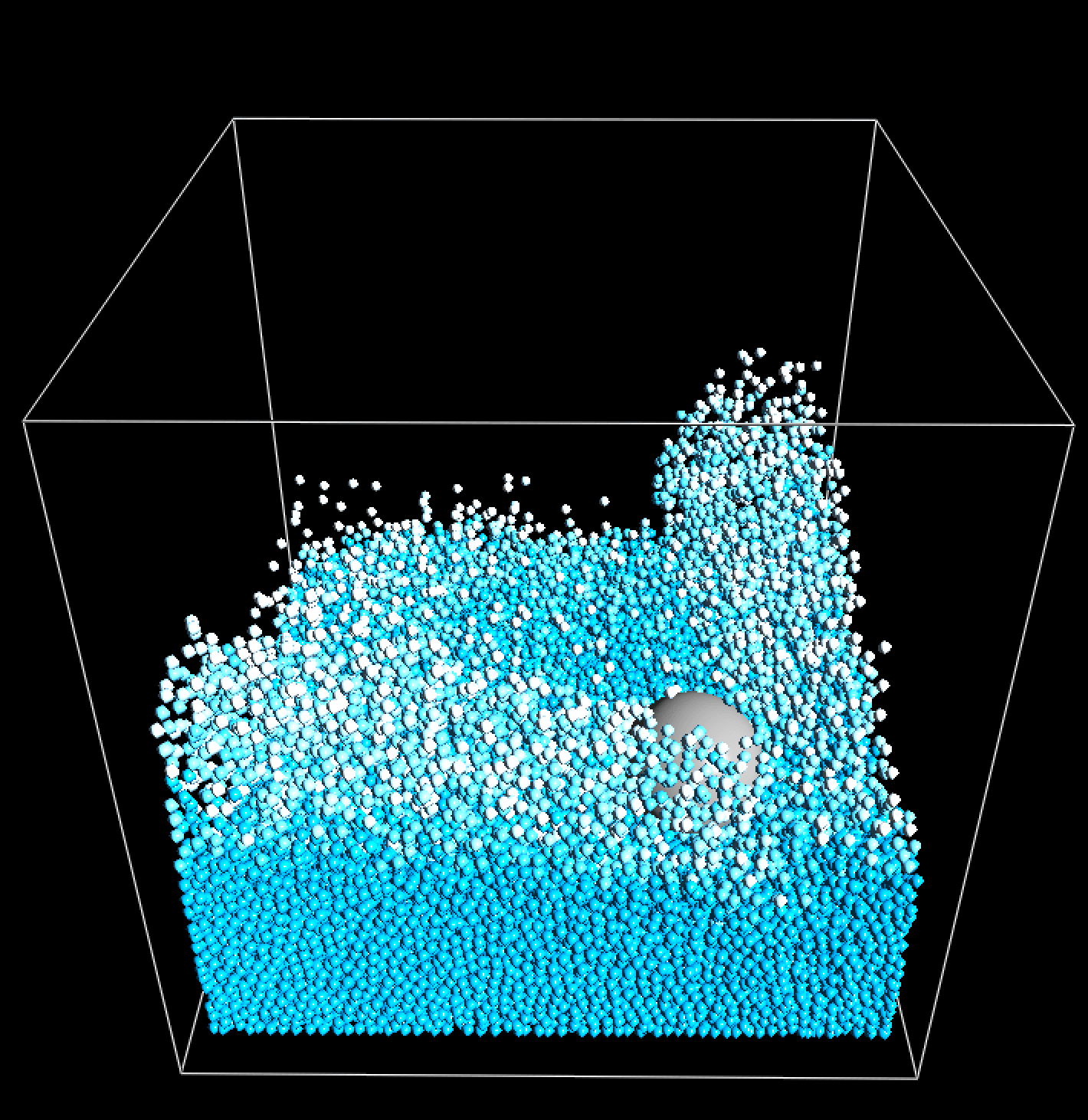
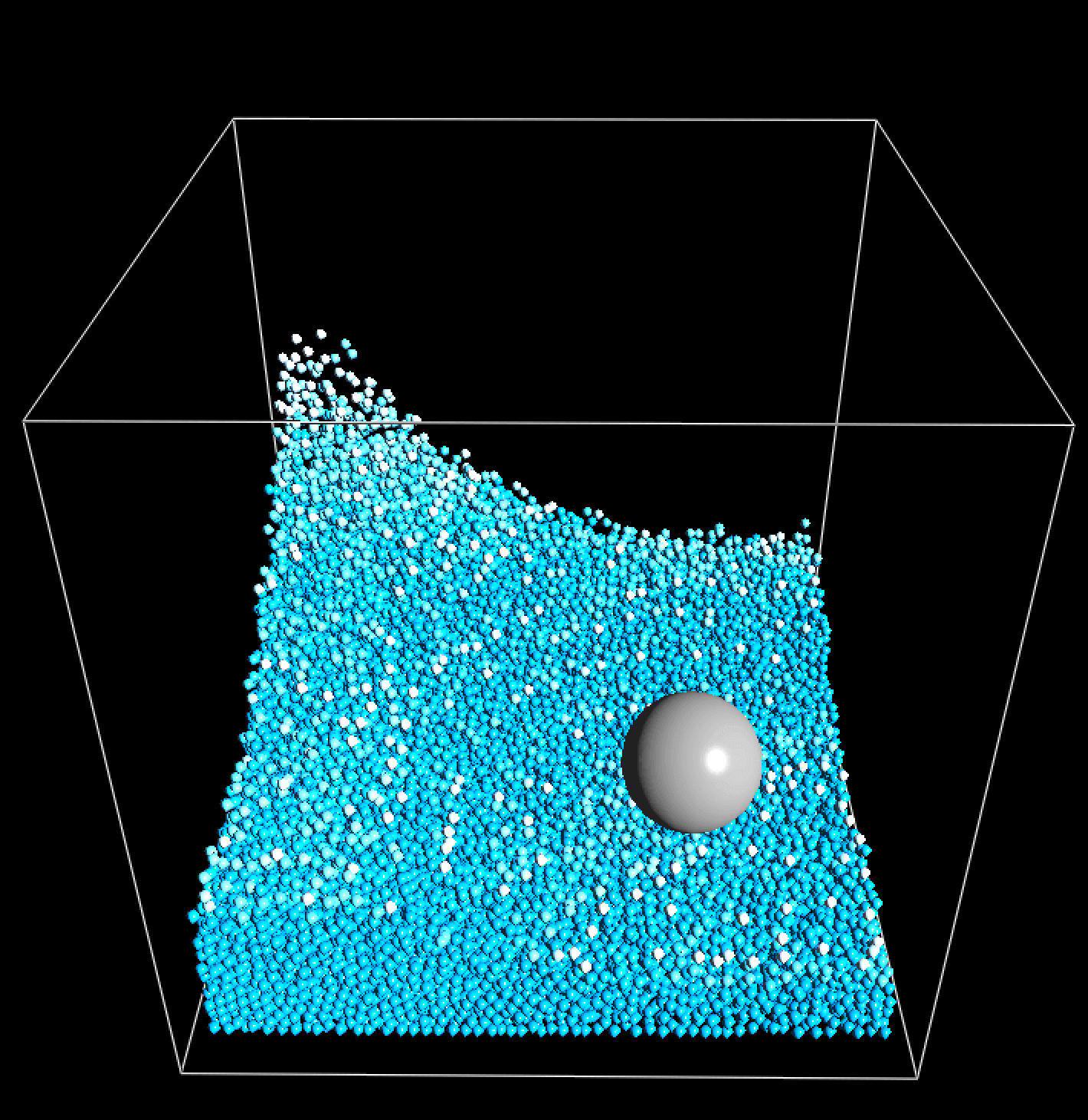
当网格分辨率比较小 (\(24^3\sim32^3\), 粒子数量 \(\sim10^4\)) 时, 在笔记本电脑下可以做到实时模拟 (帧率约为 \(25\sim70\) fps). 下面是模拟的截图.