刚体模拟
如无特殊说明, 本文图片均取自课程 PPT.
2 刚体模拟
刚体模拟的核心是接触与碰撞 (contact and collision) 问题.
2.1 运动方程
三维空间 \(\R^3\) 中一个刚体运动可分解为两部分: 质心的平动和绕质心的转动.
对于一个自由运动的刚体, 我们需要两个参数 (质心位置 \(x_c\), 空间朝向 \(Q\)) 来确定其状态, 故广义坐标 \(q=(x_c,Q)\), 自由度为 \(6\). 广义速度由质心速度 \(v_c\) 和角速度 \(\omega\) 组成: \(u=(v_c,\omega)\).
四元数 \(Q=(w,x,y,z)\) 可以描述空间朝向. 注意 \(Q\) 有 \(4\) 自由度, 但空间朝向只有 \(3\) 自由度, 故用 \(Q\) 描述空间朝向有一个自由度冗余 (即模长).
因为 \(Q\) 和 \(\omega\) 的维数不同, \(\dot{Q}\) 不等于 \(\omega\). 实际上有 \(\dot{Q}=\frac12(0,\omega)\times Q\), 其中 \(\times\) 是四元数乘法. 引入记号 \[ \tilde{H}(Q) := \frac12 \pmqty{ -x & -y & -z \\ w & z & -y \\ -z & w & x \\ y & -x & w }, \] 则 \(\dot{Q}=\tilde{H}(Q)\omega\) (矩阵乘法). 由此一来, 广义速度和广义坐标的关系为 \[ \pmqty{ \dot{x} \\ \dot{Q} } = \underbrace{\pmqty{ I_3 \\ & \tilde{H}\!\pqty{Q} }}_H \pmqty{ v \\ \omega }, \] 比 1.1 节中给出的 \(\dot{q}=u\) 多了一个修正项 \(H\).
我们在本节中用 \(\dot{Q}=\frac12(0,\omega)\times Q\) 推导 Euler 积分; 而在后面的 constraint dynamics 中用 \(\dot{q}=Hu\).
刚体的广义力由外力 \(f\) 和外力矩 \(\tau\) 组成, 分别负责改变刚体的速度和角速度. 由刚体运动的 Newton-Euler 方程, \[ \pmqty{mI_3 \\ & I} \pmqty{\dot{v_c} \\ \dot{\omega}} + \pmqty{0 \\ \omega\times I\omega} = \pmqty{f \\ \tau}, \] 其中 \(I\) 是质心参考系下的转动惯量. 如果刚体的姿态由旋转矩阵 \(R\) 描述, 则 \(I=RI_{\sf ref}R\T\), 其中 \(I_{\sf ref}\) 是刚体在标准姿态下的转动惯量.
总之, 我们得到了刚体运动的常微分方程: \[ \left\{\Align{ \dot{x_c} &= v_c, \\ \dot{v_c} &= M^{-1}f, \\ \dot{Q} &= \frac12(0,\omega)\times Q, \\ \dot\omega &= \tau - \omega\times I\omega. }\right. \] 在模拟时, 我们需要记录两组参数: \((x_c,v_c)\) 和 \((Q,\omega)\), 其更新规则 (Symplectic Euler) 如下: \[ \Cases{ f \leftarrow \sum f_i, \\ v_c^+ \leftarrow v_c + hM^{-1}f, \\ x_c^+ \leftarrow x_c + hv_c^+. }\qquad\Cases{ R \leftarrow \textsf{RotationMatrix}(Q), \\ \tau \leftarrow \sum_i (Rr_i)\times f_i, \\ I \leftarrow R I_{\sf ref}R\T, \\ \omega^+ \leftarrow \omega + h I^{-1}(\tau-\omega\times I\omega), \\ Q^+ \leftarrow Q + \frac{h}{2}\pmqty{0, \omega^+}\times Q, } \] 其中 \(f_i\) 是刚体中每个质点所受外力, \(r_i=R\T(x_i-x_c)\) 是质点相对于质心的位置. ### 几种碰撞模拟方法
刚体的碰撞模拟有三种方法:
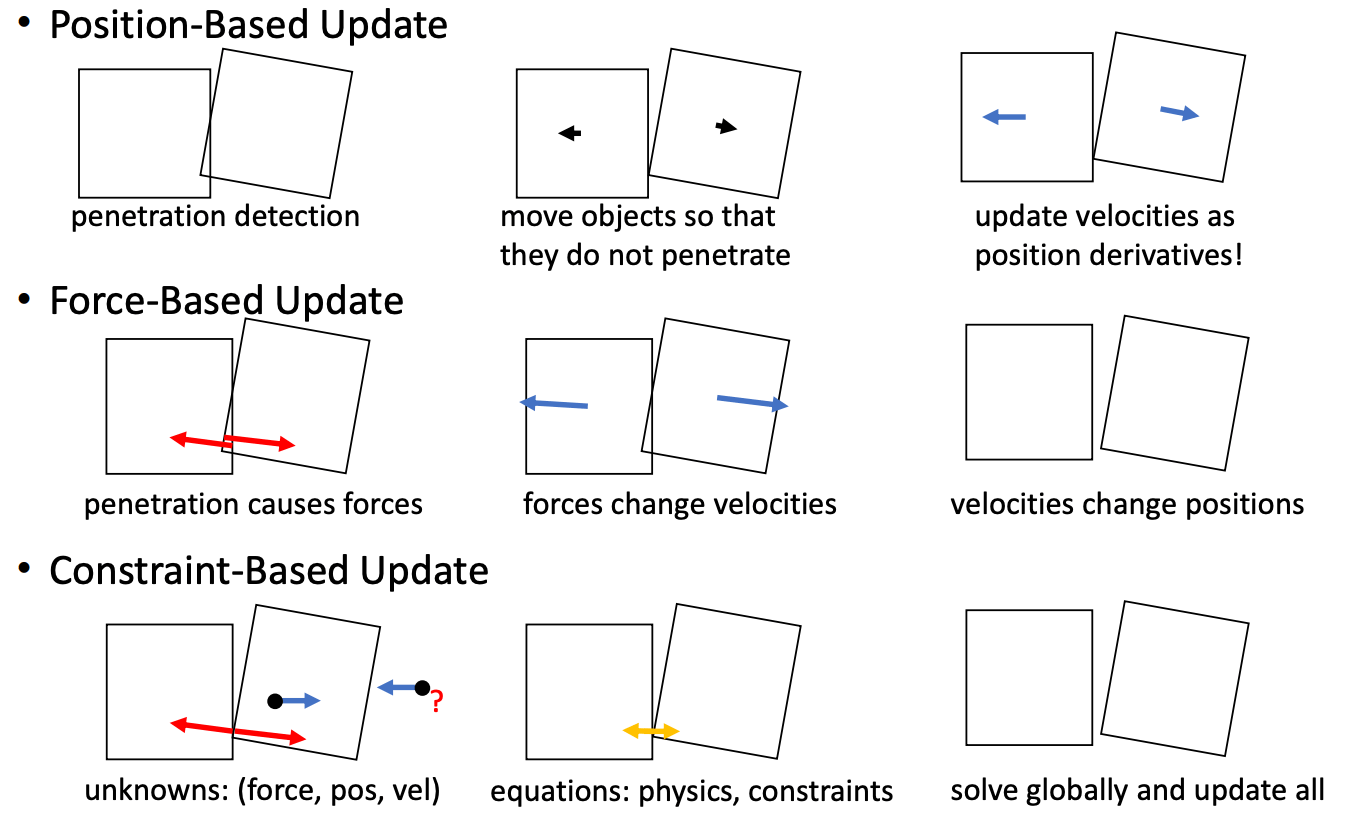
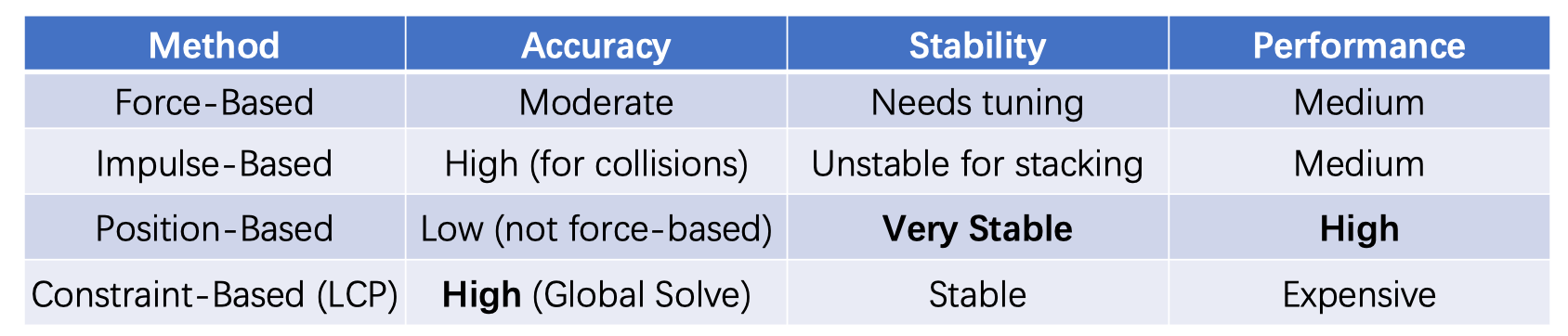
它们的表现与效率总结如下:
3 基于冲量的动力学
基于力的方法 (force-based dynamics) 有很强的物理直观, 并且能很好地融合进 Symplectic Euler 积分中. 它的不足是对于积分步长 \(h\) 十分敏感. 由此诞生出基于冲量的方法 (impluse-based dynamics), 将碰撞当成瞬时过程, 不考虑受力, 直接考虑动量的改变.
3.1 质点碰撞
如果一个质点 \(x\) 进入了另一个质点的 SDF 区域内, 即 \(\phi(x)<0\), 则基于力的方法为粒子施加朝外的力 (penalty). Quadratic penalty method 假设碰撞压缩时的势能为二次函数 \(E=-\frac12k\phi^2(x)\), 进而受力与重叠的长度成正比: \(F=-k\phi(x)n\), 其中 \(n\) 是 SDF 区域的外向单位法向量.
为了减少 "穿模", 我们在物体表面 \(\varepsilon\) 处即开始施力, \(F=-k(\phi(x)-\varepsilon)n\). 然而如果物体的速度很快的话, 线性增加的力还是不足以阻挡物体重叠. 因此我们可以引入 Log penalty \(E=\rho\ln\phi(x)\), 进而受力为 \(F=\rho\frac1{\phi(x)}n\). 它可以施加任意强度的力. 但是它的一个缺点是它对 \(\phi(x)\) 小于零情形是未定义的. 为了避免 \(\phi(x)<0\) 的情况, 该方法需要较小的 \(\Delta t\).
The use of step size adjustment is a must.
- To avoid overshooting.
- To avoid penetration in log-barrier methods.
由于基于力的方法依赖于时间步长的缺陷, 我们考虑基于冲量的方法. 该方法假设碰撞时瞬时的, 可以瞬间改变物体的速度和位置.
改变位置: 如果 \(\phi(x)<0\), 则令 \(x^+\leftarrow x+|\phi(x)|n\).
改变速度: 如果 \(\lr{v,n}<0\), 则将 \(v\) 分解为法向与切向, 分别更新为 \(v_N^+\leftarrow-cv_N\) 与 \(v_T^+\leftarrow av_T\) (考虑切向摩擦). 其中参数 \(a\) 应当尽可能小, 但要满足 Coulomb 摩擦定律. 有 \[ a \leftarrow \max\qty{0, 1-\mu(1+c)\frac{\|v_N\|}{\|v_T\|}}. \] 参数 \(c\in[0,1]\) 为恢复系数 (\(0\) 对应完全非弹性碰撞, \(1\) 对应完全弹性碰撞), \(\mu\in[0,1]\) 为摩擦系数.
3.2 两个刚体碰撞
我们的策略是先计算出碰撞点 \(x_i\) 处的速度改变 \(\Delta v_i\), 再计算出碰撞的冲量 \(j\), 最后根据冲量更新刚体状态.
设刚体 A 的质点 \(x_i\) 进入了刚体 B 的 SDF 区域内, 接触面的法向为 \(n\), 碰撞点的相对速度 \(v_r=v_i-v_j\) (A, B 碰撞点处的速度之差). 该碰撞分为三种情况:
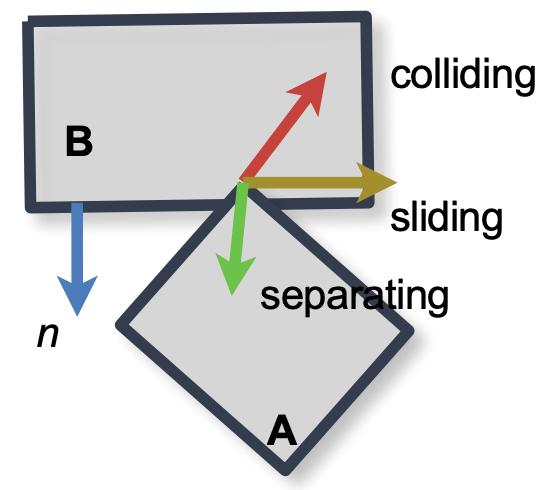
- \(\lr{v_r,n}<0\), 碰撞.
- \(\lr{v_r,n}=0\), 滑动.
- \(\lr{v_r,n}>0\), 碰撞后的分离, 无需处理.
我们只需要考虑 \(\lr{v_r,n}<0\) 的情况. 分为切向和法向两个方向考虑. 法向就是接触面法向量 \(n\), 而切向是相对速度 \(v_r\) 投影到 \(n\) 的法平面后单位化得到的单位向量 \(t\). (如果 \(v_r\parallel n\), 则 \(t=0\)).
- 法向速度 \(v_{i,N}^+\leftarrow-cv_{i,N}\), 其中恢复系数 \(c\in[0,1]\).
- 切向速度 \(v_{i,T}^+\leftarrow av_{i,T}\), 其中 \(a\) 的公式见上一小节.
如此就可以得到速度改变量 \(\Delta v_i\). 设 A 受到来自 B 的冲量为 \(j\), 则 A 的速度与角速度更新为 \[ \Cases{ v_c^+ \leftarrow v_c + M^{-1}j, \\ \omega^+ \leftarrow \omega + I^{-1}(Rr_i\times j), } \] 于是 \[ \Align{ \Delta v_i = v_i^+ - v_i &= [v_c^+ + \omega^+\times(Rr_i)] - [v_c+\omega\times(Rr_i)] \\ &= \underbrace{[M_a^{-1} - (Rr_i)^\times I^{-1} (Rr_i)^\times]}_{K_a}\; j, } \] 其中 \((X)^\times_{ij}:=\sum_k\varepsilon_{ijk}X_k\) 为叉乘矩阵. 因此, \[ j = K_a^{-1}\Delta v_i, \] 等式右边的都是已知量. 计算出 \(j\) 之后, 再更新 A 的速度和角速度 \(v_c,\omega_c\), 最后更新 A 的位置和朝向. 对于刚体 B, 它所受冲量为 \(-j\), 由此更新 B.
实际上我们可以解出 \(j\) 来. B 对 A 的法向冲量为 \[ j_n = \frac{-(1+c)\lr{v_r,n}} {\frac1{M_a}+\frac1{M_b} + \lr{n, (I_a^{-1}(r_a\times n))\times r_a + (I_b^{-1}(r_b\times n))\times r_b }}, \] (\(r_a,r_b\) 分别为碰撞点的质心坐标 \(x_i-x_c\)) 切向冲量为 \[ j_t = \operatorname{clamp}\pqty{ \frac{-\lr{v_r,t}} {\frac1{M_a}+\frac1{M_b} + \lr{n, (I_a^{-1}(r_a\times n))\times r_a + (I_b^{-1}(r_b\times n))\times r_b }}, -\mu j_n, \mu j_n }, \] (根据 Coulomb 摩擦定律, 我们需要保证 \(|j_t|\leq\mu|j_n|\).)
3.3 多个刚体的碰撞
对于多个刚体, 只需枚举它们所有的碰撞点, 对每个碰撞点计算速度改变, 最后解出每个碰撞的 \(j\). 考虑下面三个兔子与地面碰撞的场景:
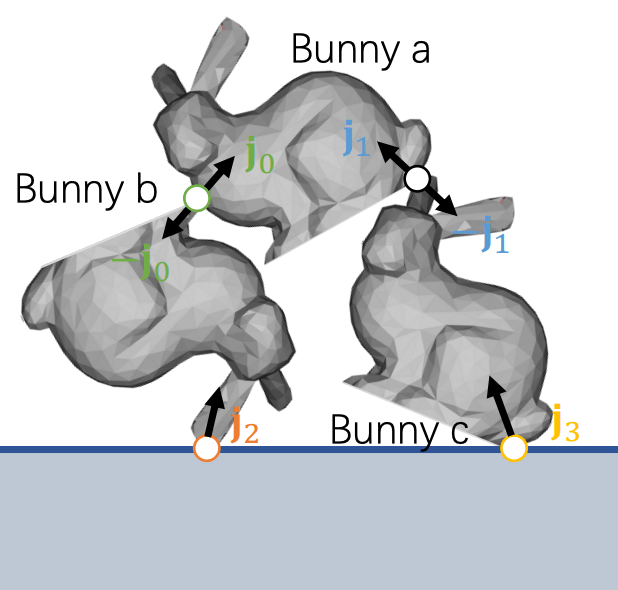
一共有四个碰撞点 \(0,1,2,3\), 记 \(j_i\) 是每个碰撞点处的冲量, 则 \(K_{a01}{\color[rgb]{.41,.60,.82} j_1}\) 代表冲量 \({\color[rgb]{.41,.60,.82} j_1}\) 对兔子 a 上的碰撞点 \(0\) 的速度改变量, 等等. 我们可以得到一个线性方程组: \[ \Cases{ {\color[rgb]{.49,.67,.33} \Delta v_0} = K_{a00}{\color[rgb]{.49,.67,.33} j_0} + K_{a01}{\color[rgb]{.41,.60,.82} j_1} - (-K_{b00}{\color[rgb]{.49,.67,.33} j_0} + K_{b02}{\color[rgb]{.87,.51,.27} j_2}), \\ {\color[rgb]{.41,.60,.82} \Delta v_1} = K_{a10}{\color[rgb]{.49,.67,.33} j_0} + K_{a11}{\color[rgb]{.41,.60,.82} j_1} - (-K_{c11}{\color[rgb]{.41,.60,.82} j_1} + K_{c13}{\color[rgb]{.96,.76,.26} j_3}), \\ {\color[rgb]{.87,.51,.27} \Delta v_2} = -K_{b20}{\color[rgb]{.49,.67,.33} j_0} + K_{b22}{\color[rgb]{.87,.51,.27} j_2}, \\ {\color[rgb]{.96,.76,.26} \Delta v_3} = -K_{c31}{\color[rgb]{.41,.60,.82} j_1} + K_{c33}{\color[rgb]{.96,.76,.26} j_3}. } \] 求解如下线性系统即可: \[ \pmqty{ K_{a00}+K_{b00} & K_{a01} & -K_{b02} \\ K_{a10} & K_{a11}+K_{c11} & & -K_{c13} \\ -K_{b20} & & K_{b22} \\ &-K_{c31} & & K_{c33} } \pmqty{ {\color[rgb]{.49,.67,.33} j_0} \\ {\color[rgb]{.41,.60,.82} j_1} \\ {\color[rgb]{.87,.51,.27} j_2} \\ {\color[rgb]{.96,.76,.26} j_3} \\ } = \pmqty{ {\color[rgb]{.49,.67,.33} \Delta v_0} \\ {\color[rgb]{.41,.60,.82} \Delta v_1} \\ {\color[rgb]{.87,.51,.27} \Delta v_2} \\ {\color[rgb]{.96,.76,.26} \Delta v_3} \\ } \] 基于冲量的方法的缺陷是不能模拟物体堆叠 (stacking). 桌子上的物体在重力作用下具有向下的动量 \(mv_0\), 然而桌子只能为其提供 \(cmv_0\) (恢复系数 \(c\in[0,1]\)) 的冲量, 导致物体穿模、下陷, 不能稳定在桌子上. 如果设定 \(c=1\), 尽管可以解决穿模问题, 但容易导致能量爆炸.
4 基于位置的动力学
基于位置的方法 (PBD, position-based dynamics) 尽管不能产生准确的物理模拟, 但具高效性与鲁棒性.
PBD 的想法是, 我们先让每个粒子自由地运动, 有自己的位置和速度, 然后再施加刚体约束, 把零散的点恢复成刚体, 如下图.
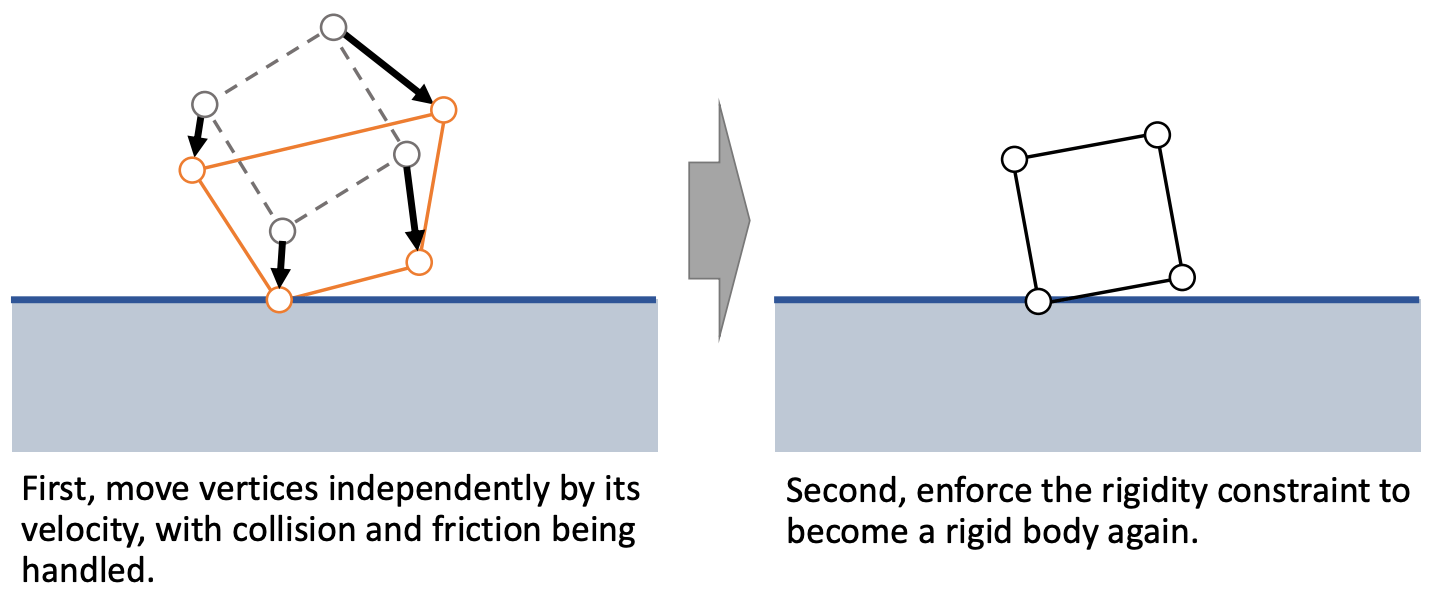
4.1 粒子碰撞
设粒子当前的位置和速度分别为 \(x_i,v_i\), 则下一步的位置预测值为 \(\tilde{y}_i=x_i+hv_i\). 如果 \(\tilde{y}_i\) 与在 SDF 外部, 则没有发生碰撞, 无需任何额外操作.
如果 \(\tilde{y}_i\) 在边界或内部, 则需要对其进行修正. 首先将位置沿着法向量投影到 SDF 表面, 得到 \(y_i\) 作为位置的更新值. 速度的更新则考虑恢复力 \(-k\phi(\tilde{y}_i)n\) 和摩擦力 \(-av_T\), 如下图.
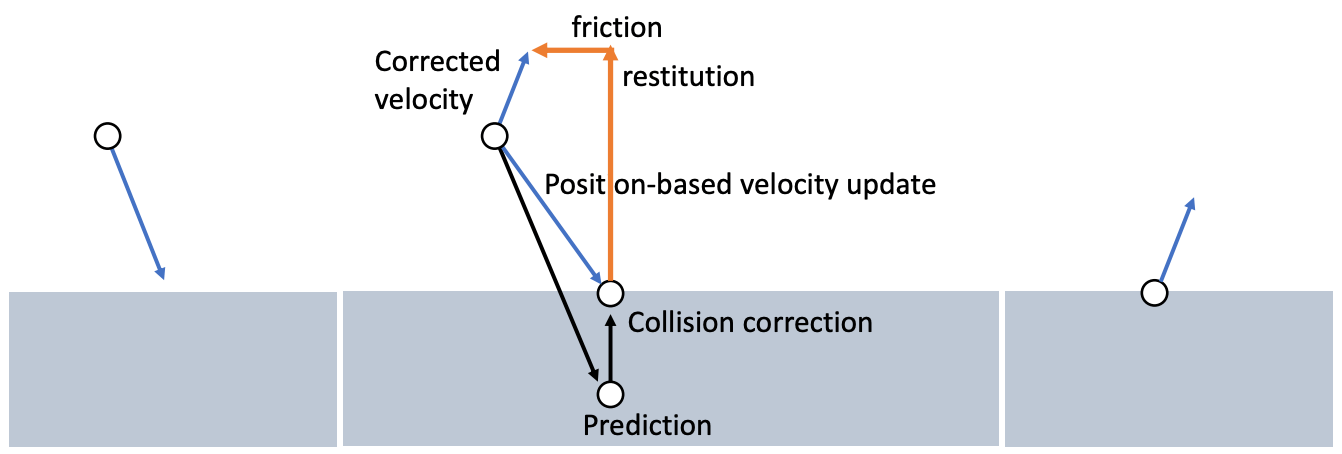
4.2 刚体碰撞
首先, 按照如上规则独立地更新每个粒子的速度 \(v_i\) 和位置 \(x_i\), 然后根据目前顶点的位置还原出刚体的质心 \(x_c\) 和旋转矩阵 \(A\). 记更新后的位置为 \(y_i\). 具体来说, 我们求解如下优化问题: \[ \min_{x_c,A} \sum_i \| x_c + Ar_i - y_i \|^2,\quad \textsf{s.t.}\quad AA\T=I. \]
注意到能量函数 \(J(x_c,A):=\sum_i\|x_c+Ar_i-y_i\|^2\) 关于 \(x_c\) 和 \(A\) 都是下凸函数 (Hessian 负定), 故能量函数的极小值点 (若存在) 就是最小值点.
令 \(J\) 对 \(x_c\) 的导数为零得到 \[
0 = \pdv{J}{x_c} = 2\sum_i (x_c+Ar_i-y_i),
\] 因为质心坐标满足 \(\sum
r_i=0\), 可解得 \[
x_c = \frac1N \sum_i y_i,
\] 即更新后粒子的质心. 下面我们解 \(A\). 为了方便, 记 \[
\Align{
Y &= \pmqty{y_1-x_c&\cdots&y_N-x_c} \in \R^{3\times N}, \\
R &= \pmqty{r_1&\cdots& r_N} \in \R^{3\times N}.
}
\] 则能量函数可以写作 \[
J(A) = \sum_i\|(y_i-x_c)-Ar_i\|^2 = \|Y-AR\|_F^2,\quad AA\T=I.
\] 这实际上是正交 Procrustes 问题, 其中 Frobenius 范数 \(\|X\|_F^2:=\tr(X\T X)\). 可以解得
- 实际上, 这个结果等价于在无约束条件下求解 \((x_c,A)\), 再将 \(A\) 投射到 \(O(n)\) (正交矩阵的集合) 中的最近点.
总之, 我们得到了 \[ \left\{\Align{ x_c &\leftarrow \frac1N \sum_i y_i, \\ R &\leftarrow UV\T, }\right. \] 其中 \(U,V\) 通过 SVD 分解 \(U\Sigma V\T=\sum_i(y_i-x_c)r_i\T\) 得到.
在解出刚体姿态后, 还需要反过来更新每个粒子的位置和速度: \[ \Cases{ v_i^+ \leftarrow (x_c+Rr_i-x_i)/h, \\ x_i^+ \leftarrow x_c+Rr_i. } \] 回顾 PBD 的求解过程, 它先求解碰撞约束 (将系统状态投射到碰撞约束子流形上), 再求解刚体约束 (将系统状态投射到刚体约束子流形上), 但这就不能保证碰撞约束了——重建出的刚体与其他物体可能重叠. 因此 PBD 不能保证产生物理准确的模拟.
PBD 的优点是计算过程简单, 稳定性高, 且高效、可并行化, 因此它 PBD 适用于刚体数量多、对效率要求高但对精度要求不高的场合. NVIDIA FLeX 模拟引擎采用的就是 PBD.
5 基于约束的动力学
Contact and Friction Simulation for Computer Graphics (SIGGRAPH 2022 Courses) 是介绍该方法的一篇详实的讲义.
基于约束的动力学 (constrained dynamics) 在每一步迭代过程中都严格保证约束条件. 回顾刚体的运动方程和 Symplectic Euler 积分公式: \[ \Cases{ \dot{q} = Hu , \\ M\dot{u} = f, } \quad\implies\quad \Cases{ q^+ \leftarrow q + hHu^+, \\ u^+ \leftarrow u + hM^{-1}f. } \] 基于约束的方法在 Symplectic Euler 的第二行引入一个 "约束力" 来保证约束条件满足. 与 impluse-based 方法不同的是, 后者事先计算好了刚体的速度改变量 \(\Delta u\), 然后再来求解冲量; 而基于约束的方法通过约束条件来求解 \(\Delta u\).
5.1 约束力
假设系统的状态量 \(q\in\R^n\), 则它在不受任何约束条件下可以在 \(\R^n\) 中自由运动. 对于 (连续可微) 约束函数 \(G:\R^n\to\R^m\), 施加约束 \(G(q)=0\) 等价于将 \(q\) 限制在子流形 \(M=G^{-1}(0)\) 上运动.
对约束条件 \(G(q(t))\equiv0\) 两边求导, 得到 \[ 0 = \pdv{G}{q}\pdv{q}{t} = \pdv{G}{q} Hu =: Ju, \] 其中 \(J=H(\partial G/\partial q)\in\R^{m\times n}\) 是约束函数的 Jacobi 矩阵. 如果初始条件 \(q(t_0)\) 满足约束, 并且系统演化过程中满足速度约束 \(Ju=0\) (即 \(u\) 与 \(M\) 相切), 则可以认为系统自始至终都是满足约束 \(G(q)=0\) 的. 因此我们的重点就是保证速度满足约束 \(Ju=0\). 为此我们引入约束力 (constraint force) \[ f_c := J\T\lambda \in \R^n, \] 其中参数向量 \(\lambda\in\R^m\) 称为 Lagrange 乘子. 约束力 \(f_c\) 永远垂直于速度: \[ \lr{f_c,u} = \lr{J\T\lambda,u} = \lr{\lambda,Ju} = 0, \] 因此约束力不做功. 约束流形 \(M\) 和约束力的示意图如下 (手绘):
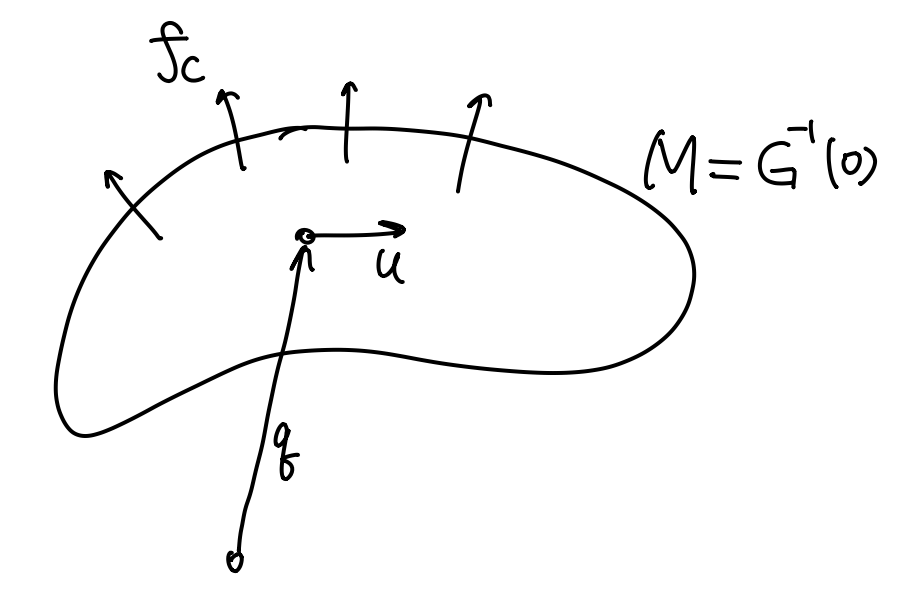
将约束力 (作为 implicit 项) 添加到 Euler 积分中: \[ Mu - \orange{J\T\lambda^+} = Mu + hf \] 其中 \(\lambda^+:=h\lambda(t+h)\). 上式等价于 \[ \pmqty{M & -J\T \\ J & 0} \pmqty{u^+ \\ \lambda^+} = \pmqty{Mu + hf \\ 0}. \] 从第一行解出 \(u^+\), 再代入第二行, 得到 \[ \underbrace{\bqty{JM^{-1}J\T}}_A \; \lambda^+ + \underbrace{JM^{-1} (Mu+hf)}_b = 0, \] 从中解出 \(\lambda^+\), 再代回第一行解出 \(u^+\) 就完成了一个时间步的求解.
5.2 碰撞约束
刚体碰撞约束指的是两个物体不能互相穿透, 称为 non-interpenetration contact constraint. 不同于上面提到的双边约束 \(G(q)=0\), 它是一个单边约束 \(\phi(q)\geq0\). 函数 \(\phi(q)\) 表示两个刚体之间的符号距离, \(\phi(q)<0\) 时两者相互穿透, \(\phi(q)=0\) 时刚好接触, \(\phi(q)>0\) 时分离.
当 \(\phi(q)<0\) 时, 施加一个法向力 \(J\T\lambda_n\). 下面我们来计算 \(J\).
两个刚体 A, B 的在碰撞点处的法向相对速度为 \[ v_{n} = \pdv{\phi}{t} = \pdv{\phi}{q}\pdv{q}{t} = \underbrace{\pdv{\phi}{q}H}_J\; u = Ju. \] 另一方面, \(v_n=\lr{v_r,n}\), 其中相对速度 \(v_r=(v_B+\omega_B\times r_A)-(v_A+\omega_A\times r_B)\). 于是 \[ v_n = \underbrace{ \pmqty{-n\T & n\T\pqty{r_A}^\times & n\T & -n\T\pqty{r_B}^\times} }_J \underbrace{ \pmqty{ v_A \\ \omega_A \\ v_B \\ \omega_B } }_u \] 这就得到了 \(J\) 的解析式.
5.3 Coulomb 摩擦
5.4 数值求解
证明可见 https://en.wikipedia.org/wiki/Orthogonal_Procrustes_problem↩︎