物理模拟简介
1 物理模拟简介
我们的目的是在计算机中模拟真实世界中物体的运动. 这涉及到两方面的离散化: 空间离散化和时间离散化. 空间离散化就是用离散的数据结构表达一个物体, 比如之前讲的点云 (point cloud) / 粒子集 (particles) 和三角形网格 (triangle mesh). 时间离散化指的是我们只计算物体在离散的时间序列 \(\{t_0,t_0+h,t_0+2h,\dots\}\) 上的状态.
1.1 运动方程
设物理系统的状态量 (广义坐标) \(q\in\R^n\), 则物理仿真做的就是根据外力 \(f\) 更新 \(q\), 即求解微分方程: \[ F_{\sf DE} (q,\dot{q},f,t) = 0. \] 其中 \(F_{\sf DE}\) 是系统的常微分方程或者偏微分方程, 由物理定律给出. 通常我们考虑 Newton 第二定律: \[ M(t)\dot{u}(t) = f(q(t),u(t),t), \] 其中 \(M(t)\in\R^{n\times n}\) 是质量矩阵, \(u(t)=\dot{q}(t)\in\R^n\) 是广义速度, \(f(\cdots)\in\R^n\) 是广义力, 与时间、广义坐标、广义速度有关.
- 所有可能的状态量 \(q\) 组成的空间的维数称为系统的自由度.
有时, 状态量还需要满足额外的约束条件 (比如在刚体系统中, 刚体不能穿模) \[ H(q) = 0,\quad\textsf{或者}\quad G(q)\geq0, \] 它们分别称为双边约束和单边约束.
Example 考虑两个通过弹簧连接的质点 \(m_1,m_2\) 在地面上方的空间中运动, 地面为平面 \(z=0\). 该系统的广义坐标为两个质点的位置, \(q=(x_1,x_2)\in\R^6\), 自由度为 \(6\). 广义速度 \(u=(v_1,v_2)\). Newton 第二定律给出 \[ \underbrace{\pmqty{m_1I_3\\&m_2I_3}}_M \cdot \underbrace{\pmqty{\dot{v}_1\\\dot{v}_2}}_{\dot u} = \underbrace{\pmqty{ -k\pqty{\|x_1-x_2\|-x_0}n + g \\ k\pqty{\|x_1-x_2\|-x_0}n + g }}_{f} \] 其中 \(k\) 为弹簧弹力系数, \(x_0\) 为弹簧原长, \(n\) 为 \(x_2\) 指向 \(x_1\) 的单位向量, \(g\) 为重力加速度向量. 此即系统满足的常微分方程.
该系统的约束条件是 "质点不能穿透到地面以下", 即 \[ x_{1,3}\geq0,\quad\textsf{且}\quad x_{2,3}\geq0. \] 另一个例子是平面摆. 它的自由度是 \(1\), 能用角度 \(\theta\) 完全描述. 其实我们也可以用 \(q=(x,y)\in\R^2\) 作为它的状态量, 然后施加约束条件 \(0=G(x,y):=x^2+y^2-l^2\). 因此, 状态量与约束条件的选择是有一定灵活性的.
1.2 时间积分
解析求解微分方程是非常困难的, 故在模拟中我们采用离散化的办法.
给定系统的初始状态 \(q(t_0)=q_0\), 我们要做的是根据微分方程和约束条件算出此后一系列状态的值: \[ q(t_0),q(t_0+h),q(t_0+2h),\dots \] 其中 \(h>0\) 称为时间步长 (time step), 它决定了模拟的精度.
1.2.1 Euler methods
在模拟时, 我们同时维护系统的 \(q\) 和 \(u\), 在每个时间步更新它们的值. 具体来说, 取一阶近似, \[ \left\{\Align{ q(t+h) &\leftarrow q(t) + hu(t), \\ u(t+h) &\leftarrow u(t) + hu'(t), \\ }\right. \] 再将 Newton 第二定律代入, 我们就得到了更新公式 \[ \left\{\Align{ q(t+h) &\leftarrow q(t) + h\orange{u(t)}, \\ u(t+h) &\leftarrow u(t) + hM^{-1}\orange{f(q(t),u(t),t)}, \\ }\right. \] 其中我们认为质量矩阵 \(M(t)\equiv M\) 不随时间变化. 上式称为显式 Euler 积分法. 显式 Euler 法计算简便, 容易实现, 但是精度低、稳定性差 (系统能量容易无限增大, 导致爆炸). 为此, 将上式的橙色部分改为在 \(t+h\) 步的值, 便得到隐式 Euler 积分法: \[ \left\{\Align{ q(t+h) &\leftarrow q(t) + h\blue{u(t+h)}, \\ u(t+h) &\leftarrow u(t) + hM^{-1}\blue{f(q(t+h),u(t+h),t+h)}, \\ }\right. \] 隐式 Euler 相当于给系统添加了一个内在的阻尼, 稳定性好, 但是需要求解方程组, 计算量比较大. 一个折中的方法是半隐式 Euler / Symplectic Euler 积分法: \[ \left\{\Align{ q(t+h) &\leftarrow q(t) + h\purple{u(t+h)}, \\ u(t+h) &\leftarrow u(t) + hM^{-1}\purple{f(q(t),u(t),t)}. \\ }\right. \]
对于 Euler 积分, 为了记号简便, 记 \(q^+:=q(t+h)\), \(u^+:=u(t+h)\), \(f^+:=f(q^+,u^+,t+h)\) (带 \(^+\) 的都是 implicit term) 以及 \(q:=q(t)\), \(u:=u(t)\), \(f:=f(q,u,t)\) (不带 \(^+\) 的都是 explicit term). 于是 Euler 法 (以 Symplectic 为例) 简化为 \[ \Cases{ q^+ \leftarrow q+hu^+, \\ u^+ \leftarrow u+hM^{-1}f. } \]
1.2.2 The midpoint method
通过 Taylor 展开可以证明, explicit Euler 和 implicit Euler 法都具有一阶精度: \[ \Align{ q^+ - \pqty{q + hu} &= \mathcal{O}(h^2), \\ q^+ - \pqty{q + hu^+} &= \mathcal{O}(h^2), }\qquad h\to0. \] 有没有精度更高的方法? 请看中点法 (midpoint method): \[ \Cases{ q(t+h) \leftarrow q(t) + hu(t + \orange{\frac{h}{2}}), \\ u(t+h) \leftarrow u(t) + h^{-1}Mf(t + \orange{\frac{h}{2}}), } \] 其中采用了中点时刻 \(t+\orange{\frac{h}{2}}\) 的 \(u\) 和 \(f\) 来更新. 中点时刻的 \(u,f\) 通过步长为 \(\frac{h}{2}\) 的 explicit Euler 计算. 因此, 中点法的完整迭代步骤为 \[ \Cases{ q_{\sf mid} \leftarrow q(t) + \frac{h}{2}u(t), \\ u_{\sf mid} \leftarrow u(t) + \frac{h}{2}M^{-1}f(t), \\ f_{\sf mid} \leftarrow f(q_{\sf mid},u_{\sf mid},t+\frac{h}{2}), \\ q(t+h) \leftarrow q(t) + hu_{\sf mid}, \\ u(t+h) \leftarrow u(t) + hM^{-1}f_{\sf mid}. } \] 下面的示意图对比了 Euler 法和中点法的迭代步:

中点法可以达到二阶精度: \[ \Align{ q^+ - (q + hu_{\sf mid}) &= q(t+h) - \bqty{q(t) + h\pqty{u(t) + \frac{h}{2}M^{-1}f(t)}} \\ &= hq'(t) + \frac{h^2}{2} q''(t) + \mathcal{O}(h^3) - h\pqty{u(t) + \frac{h}{2}M^{-1}f(t)} \\ &= \mathcal{O}(h^3). } \]
1.2.3 Runge-Kutta methods
实际上, Euler 法和中点法是 Runge-Kutta 法的特例. Runge-Kutta 法是一大类时间积分法, \(k\) 阶的 R-K 法可以达到 \(k\) 阶精度. Euler 法和中点法分别是 \(1\) 阶和 \(2\) 阶 R-K. 下面我们看看 \(4\) 阶 R-K 法的迭代步, 它将 \(\dot{q}\) 和 \(\dot{u}\) 估计为四个项的加权平均: \[ \Align{ &\Cases{ \dot{q}_1 \leftarrow u, & \dot{u}_1 \leftarrow M^{-1}f(q,u) \\ \dot{q}_2 \leftarrow u+\frac{h}{2}\dot{u}_1, & \dot{u}_2 \leftarrow M^{-1}f(q+\frac{h}{2}\dot{q}_1,v+\frac{h}{2}\dot{u}_1) \\ \dot{q}_3 \leftarrow u+\frac{h}{2}\dot{u}_2, & \dot{u}_3 \leftarrow M^{-1}f(q+\frac{h}{2}\dot{q}_2,v+\frac{h}{2}\dot{u}_2) \\ \dot{q}_4 \leftarrow u+\frac{h}{2}\dot{u}_3, & \dot{u}_4 \leftarrow M^{-1}f(q+\frac{h}{2}\dot{q}_3,v+\frac{h}{2}\dot{u}_3) \\ } \\ &{}\Cases{ q(t+h) \leftarrow q(t) + h\frac16(\dot{q}_1+2\dot{q}_2+2\dot{q}_3+\dot{q}_4), \\ u(t+h) \leftarrow u(t) + h\frac16(\dot{u}_1+2\dot{u}_2+2\dot{u}_3+\dot{u}_4). } } \] 具体见下图:
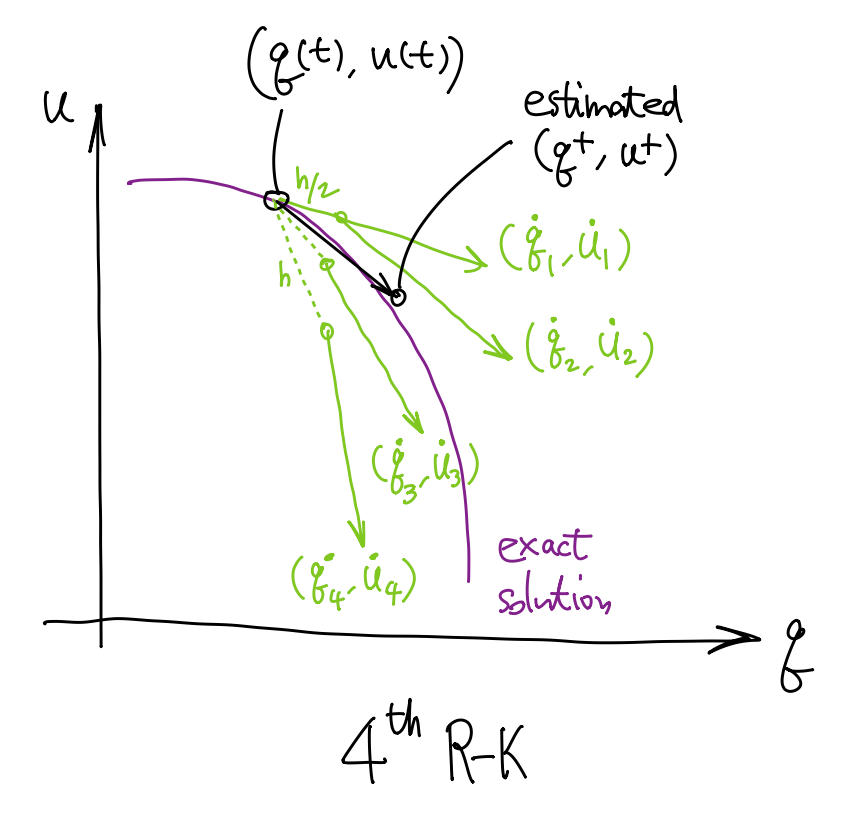
下面是在 Mathematica 中使用不同方法求解弹簧质点系统 (\(x'=v\), \(v'=-x\), \(x(0)=1\), \(v(0)=0\)) 所得的结果. 左边是显式与隐式
Euler 法, 右边是 \(2\) 阶与 \(8\) 阶 (显式) Runge-Kutta 法AccuracyGoal 分别设置为 \(2\) 和 \(1\).
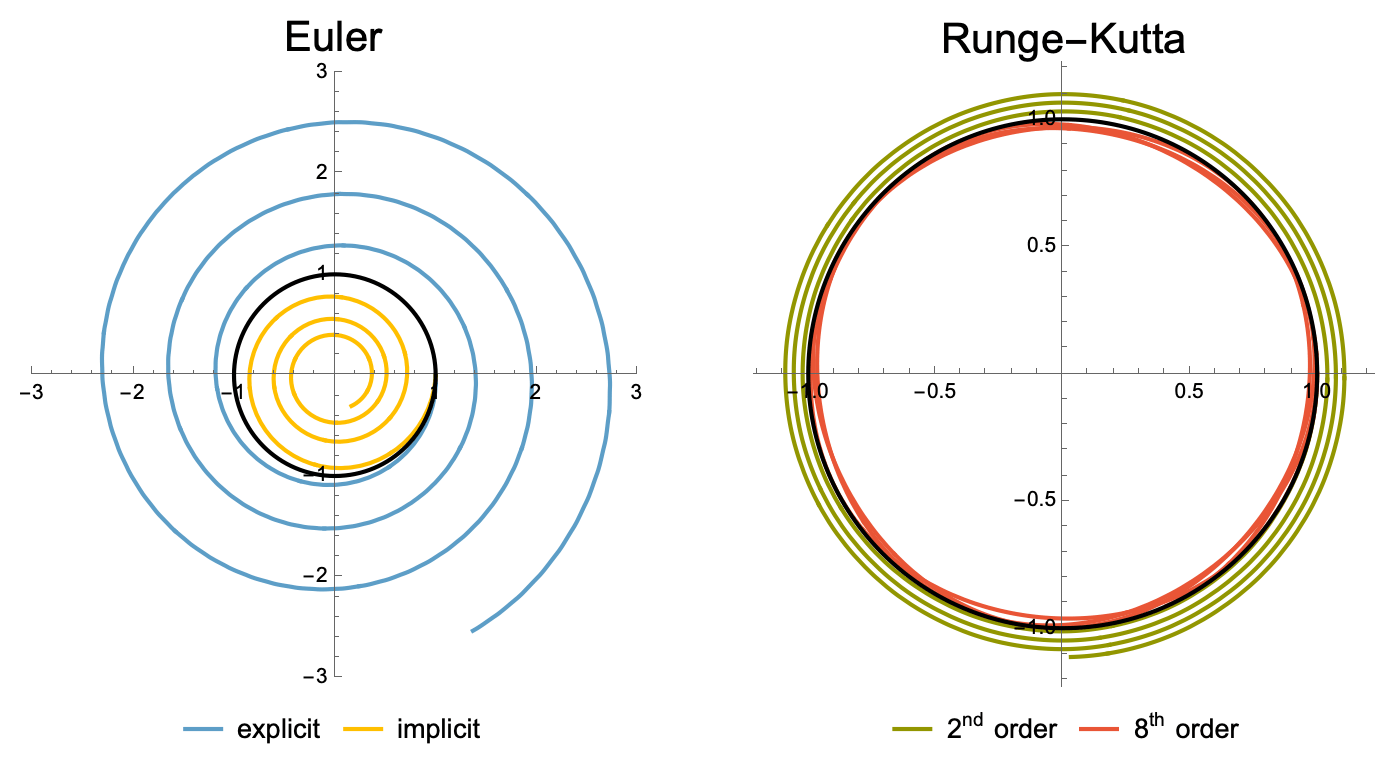
可以发现, Runge-Kutta 的确可以达到更高的精度. Explicit Euler 的系统能量会无节制增大; 而 implicit Euler 自带阻尼, 导致能量逐渐减小.
这篇文章给出了 explicit Euler 的一个详细可视化.
为了体现误差, 特意降低了求解精度. Euler 法和 Runge-Kutta 法的
AccuracyGoal分别设置为 \(2\) 和 \(1\).↩︎