网格变形
顾名思义, 网格变形就好比捏橡皮泥一样, 改变网格的形状.
我们介绍两类网格变形算法——曲面变形和空间变形. 曲面变形直接改变三角形顶点的位置; 空间变形改变空间中 grid 的形状, 通过空间的变形驱动其中曲面的变形.
12 基于曲面变形的网格变形
给定曲面 \(\Sigma\), 将其划分为两个区域: 可移动区域 \(R\) 和固定区域 \(F\). 假设用户在 \(H\subset R\) 施加了外力, 让区域 \(H\) 偏移了 \(d_0\). 我们需要求解 \(R\) 上的偏移量. 即求解映射 \(d:\Sigma\to\R^3\) 满足 \(d|_H=d_0\) 且 \(d|_F=0\).
12.1 变形传播
最简单的想法就是让偏移量平滑地从 \(H\) 扩散开来, 逐渐减小, 直到在 \(F\) 上变为零. 这种方法称为变形传播
(transformation propagation), 如下图所示 (绿色为 \(H\), 蓝色为 \(R\); 图自讲义

具体来说, 记插值系数 \[ s(p) := \frac{d(p,F)}{d(p,F)+d(p,H)}, \] 它满足 \(s|_H=1\), \(s|_F=0\). 则偏移函数 \(d(p) = d_0\cdot s(p)\).
- 距离函数 \(d(-,-)\) 可以取 \(\R^3\) 的欧氏距离. 一种更精确的办法是取 \(\Sigma\) 上的测地距离.
一种更平滑的方法是使用 Laplace 算子, 即从下面的 Laplace 方程中解出插值系数 \(s\): \[ \Align{ \Delta s&=0, & s|_{H}&=1, & s|_{F}=0. } \] 变形传播的好处是不光可以处理偏移, 还可以处理旋转等变换. 设 \(H\) 经过了仿射变换 \(x\mapsto M_0x+d_0\), 其中 \(M_0\) 可逆. 偏移量 \(d_0\) 的插值仍按照上面的方法. 将矩阵 \(M_0\) 进行极分解得到 \(M_0=P_0R_0\), 其中 \(P_0\) 和 \(R_0\) 分别为正定和正交矩阵, 它们的插值方法不同.
正定阵可以直接进行线性插值: \(P_t=(1-t)P_0+tI_3\).
正交阵需使用球面线性插值 (slerp). 将变换区域 \(H\) 上的变换 \(R_0\) 转化为四元数 \[ q_0 =\cos\frac{\theta_0}{2} +(u_x\i+u_y{\rm j}+u_z{\rm k})\sin\frac{\theta_0}{2}, \] 固定区域 \(F\) 上的变换为恒等变换, 即单位四元数 \(q_1=1\). 球面线性插值公式为 \[ q_t = \frac{\sin((1-t)\theta)}{\sin\theta} q_0 + \frac{\sin(t\theta)}{\sin\theta} q_1, \] 其中 \(\theta\) 是四维向量 \(q_0,q_1\) 间的夹角. Slerp 保证 \(q_t\) 在大圆弧上以恒定速率运动.
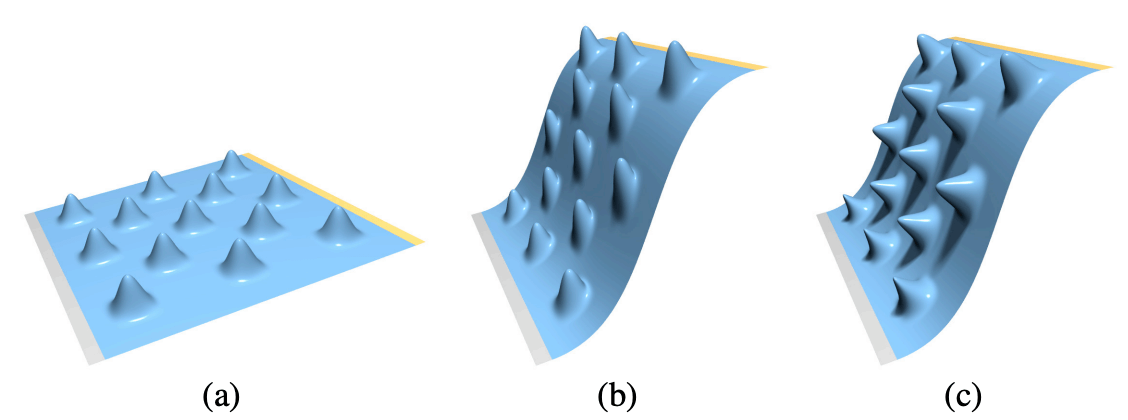
变形传播的不足是无法保持细节的形状, 如下图 (b), 而理想的结果应该是
(c) (图自论文
12.2 多尺度变形
为了保持细节, 只需要把几何细节和粗略形状分开, 对粗分辨率网格变形, 再将细节加回去就行了!
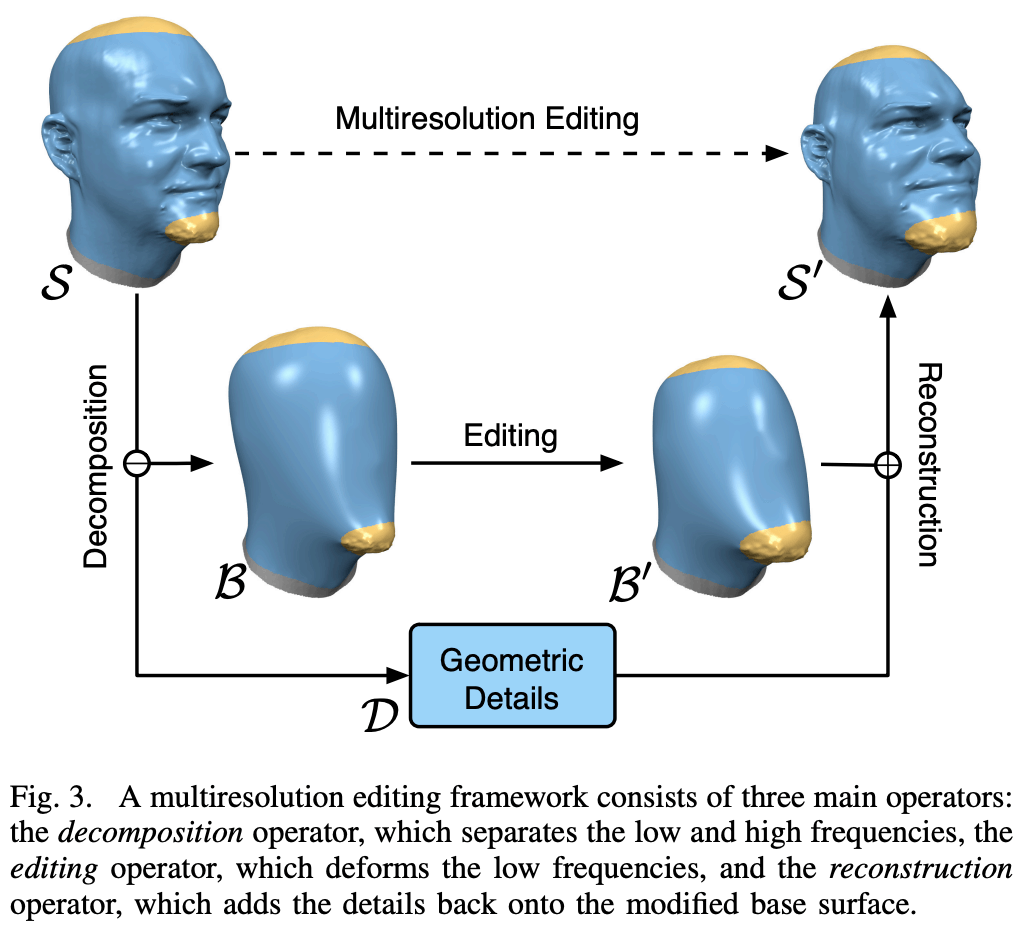
设曲面 \(\Sigma\) 分解为细节 \({\cal D}\) 和粗略 \({\cal B}\). 粗略网格可以对 \(\Sigma\) 做 Laplace 平滑来得到, \[ {\cal B} := {\sf LaplaceSmoothing}(\Sigma). \] 细节原网格减去粗略 \({\cal B}\). 需要注意的是, 顶点坐标不能直接相减, 而是需要在局部标架下表达. 在每个三角形 \(T_i\) 上选取标架 \(E_i\). 原网格 \(\Sigma\) 的顶点减去 \({\cal B}\) 的相应顶点所得差值在 \(E_i\) 下的坐标为 \(\{x_i\}\), 则这些坐标就是 \({\cal D}\).
对 \({\cal B}\) 进行变形传播之后得到了 \({\cal B}'\) (局部标架 \(E_i\) 也随之改变), 再将 \({\cal D}\) 加上就得到了变形后的网格.
多尺度变形的整体流程如下图 (图自论文
12.3 微分域变形
12.3.1 Poisson 网格变形
原论文: Yizhou Yu et al, Mesh editing with poisson-based gradient field manipulation (TOG 2004).
在梯度域进行编辑, 通过泊松方程重建网格.
通过变形传播改变三角形网格的法向量 (即 SDF 的梯度), 再通过求解 Poisson 方程得到变形后的三角形网格 \(\Sigma'\): \[ E(f) := \int_\Sigma \|\nabla f-g\|^2 \dd\sigma, \quad \textsf{极值点满足}\; \Delta f = \operatorname{div}g, \] 其中 \(f\) 为网格的 SDF, 初始值为原网格 \(\Sigma\). 能量函数优化目标是使得 \(f\) 的梯度尽量接近变形后的梯度场 \(g\). 求解时需要注意 \(F\) 的边界条件.
法向量的变换由 \(H\) 的变换 \(x\mapsto M_0x+d_0\) 中的正交变换 \(M_0\) 通过 slerp 得到. (三角形的平移 \(d_0\) 是无需考虑的, 因为 Poisson 方程会自动优化出最优的偏移量.) 下图展示了 Poisson 网格变形的步骤 (图自原论文).

12.3.2 Laplace 变形
原论文: Olga Sorkine et al, Laplacian surface editing (SGP 2004).
Laplacian editing 和 Poisson 网格变形很类似, 只不过对于后者我们调整的是每个三角形的法向量, 前者则是每个顶点的 Laplacian.
首先计算顶点 \(v_i\) 的 Laplace在坐标, \[ \delta_i := \Delta v_i, \] 通过变形传播改变 Laplace 坐标 \(\delta\), 再求解优化问题 \[ E(v) := \int_\Sigma \|\Delta v-\delta'\|^2 \dd\sigma, \quad \textsf{极值点满足}\; \Delta^2 v = \Delta\delta'. \]
12.3.3 ARAP 变形
原论文: Olga Sorkine, Marc Alexa, As-rigid-as-possible surface modeling (SGP 2007).
ARAP 网格变形可以在大幅度变形的同时尽量保持网格局部的度量结构, 其核心思想是让每个三角形的变形尽量接近欧氏变换.
定义 ARAP 能量为 \[ \Align{ E(f,R) :=&\, \int_\Sigma \|\nabla f - R \nabla f^{\sf old}\|^2 \dd\sigma \\ \approx&\, \sum_i\sum_{j\in{\cal N}(i)} w_{ij} \| (v_i'-v_j') - R_i(v_i-v_j) \|^2, } \]
该能量希望变形后边向量 \(v'_i - v'_j\) 能够近似于原始边向量 \(v_i - v_j\) 经局部旋转 \(R_i\) 后的结果. ARAP 采用交替 local-global 迭代:
- Local: 固定顶点位置, 利用 SVD / 极分解计算最优旋转矩阵 \(R_i\).
- Global: 固定旋转矩阵, 此时能量函数为 \(v_i'\) 的二次型, 通过最小二乘法求解最优的 \(v_i'\).
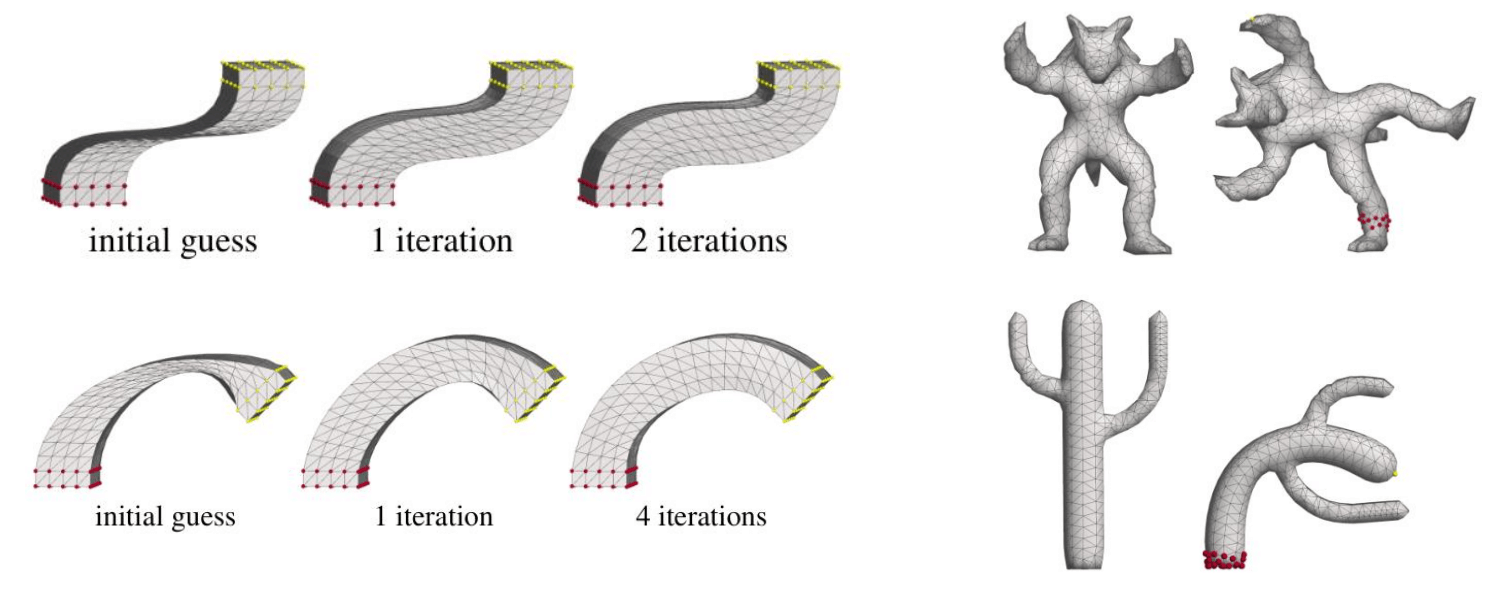
ARAP 变形只需很少的迭代步数就可以达到令人满意的效果, 如下图 (图自原论文).
13 基于空间变形的网格变形
基于曲面变形的网格变形算法, 其主要缺点是依赖于底层的网格. 如果网格质量不好, 变形质量就不高.
13.1 Freeform deformation
原论文: T. Sederberg, S. Parry, Free-form deformation of solid geometric models (SIGGRAPH 1986).
在空间取均匀的控制顶点 \(p_{ijk}\),
记 \(\delta c_{ijk}\)
为控制顶点上的偏移量. 则空间任意位置的偏移量可以定义为 \[
d(u,v,w) := \sum_{i,j,k} \delta c_{ijk} N_{ijk}(u,v,w),
\] 其中 \(N_{ijk}(u,v,w):=N_i(u)N_j(v)N_k(w)\)
是以顶点 \(p_{ijk}\)
为中心的三个插值基函数的乘积. 用户通过改变控制点来驱动曲面形变 (下图左,
图自讲义

优点:
- 除了网格变形, 还可以用于点云等变形
- 算法复杂度只与控制顶点有关
缺点:
- 变形的自由度被控制顶点决定
- 线性方程欠定/超定的时候, 结果不令人满意
- 控制顶点的位置不考虑 \(\Sigma\) 的几何, 会产生瑕疵 (上图右)
13.2 蒙皮动画
蒙皮动画 (skinning) 通过骨骼 (skeleton) 的运动来带动三角形网格的形变. 设骨骼点为 \(\{p_j\}\), 每个骨骼点处的变换为 \(\{(R_j,t_j)\}\), 则三角形网格顶点 \(v_i\) 的变换是骨骼变换的加权平均: \[ v_i' := \sum_j w_{ij}(R_jv_i + t_j), \] 其中系数 \(w_{ij}\) 表示骨骼点 \(j\) 对顶点 \(i\) 的权重, 如下图所示 (图自课程 PPT).

具体来说, 蒙皮动画算法包含以下几个步骤:
- 确定骨架 \(p_j\).
- 可以通过不断进行 Laplace 平滑得到, 也可以由艺术家手动放置骨架点.
- 确定权重 \(w_j\).
- 执行变换.
dual quaternion skinning
13.3 Deformation graphs
原论文: Embedded Deformation for Shape Manipulation (TOG 2007).
蒙皮动画的骨架点通常来说比较少, 因此变换的自由度比较低. 变形图 (defomation graph) 可以实现较高的自由度.
在 \(\R^3\) 中构造一个包含 \(K\) 个节点的图 \(G\) (均匀采样构建 k-近邻图即可), 节点记作 \(\{g_j\}\), 每个节点处的变换为 \(\{(R_j,t_j)\}\). 因此, 对于空间中一点 \(x\), 它按照 \(g_j\) 的变换所得的结果为 \[ T_j(x') = R_j(x-g_j) + g_j + t_j. \] 类似于蒙皮动画, 我们为每个节点定义权重函数 \[ w_j(x) := \pqty{ 1 - \min\qty{ \frac{\|x-g_j\|}{d_{\sf max}},1 } }^2, \] 其中 \(d_{\sf max}\) 是节点的 "最大作用范围". 我们于是得到了三角形网格顶点 \(v_i\) 变换后的位置 \[ v_i' = \sum_j w_j(v_i)T_j(v_i) = \sum_j w_j(v_i)\bqty{ R_j(v_i-g_j) + g_j + t_j }. \] 用户可以拖拽一部分顶点 \(v_i\), 也可以指定某些节点 \(g_j\) 不动. 在这些边界条件下, 我们可以优化得到所有节点处的 \((R_j,t_j)\). 能量函数分为三部分:
旋转能量, 让 \(R_j\) 尽量接近旋转矩阵: \[ \Align{ E_{\sf rot}(R,t) &:= \sum_j {\sf Rot}(R_i), \\ {\sf Rot}(r_1,r_2,r_3) &:= \lr{r_1,r_2}^2 + \lr{r_1,r_3}^2 + \lr{r_2,r_3}^2 + \\ &\hspace{1.7em} (\lr{r_1,r_1}-1)^2 + (\lr{r_1,r_3}-1)^2 + (\lr{r_2,r_3}-1)^2. } \]
平滑化能量, 让相邻顶点的变换尽可能平滑: \[ \Align{ E_{\sf reg}(R,t) &= \sum_j \sum_{k\in{\cal N}(j)} \alpha_{jk} \|T_j(g_k) - T_k(g_k)\|^2 \\ &= \sum_j \sum_{k\in{\cal N}(j)} \alpha_{jk} \|R_k(g_k-g_j) + g_j + t_j - (g_k+t_k)\|^2 } \] 权重 \(\alpha_{jk}\) 可以取为 \(1\).
约束能量, 即用户的拖动: \[ E_{\sf con}(R,t) = \sum_l \| v_{i_l}' - q_{l} \|^2, \] 其中用户拖动三角形网格顶点 \(v_{i_l}\) 到 \(q_l\).
最终的优化问题是 \[ \min_{R,t} E(R,t) = \min_{R,t}( w_{\sf rot}E_{\sf rot} + w_{\sf reg}E_{\sf reg} + w_{\sf con}E_{\sf con} ), \] 其中, 用户可以指定一些图节点为固定节点, 我们只需将其 \((R_i,t_j)\) 置为 \((I_3,0)\), 再把它们当作常量即可.
将 \(R,t\) 压缩成一个列向量, 则该能量函数可以写作 \(E(x)=f(x)\T f(x)\). 我们的目标是求解 \(f(x)=0\). 考虑 Gauss-Newton 算法, 将 \(f\) 线性化, \[ f(x + \delta) = f(x) + J\delta, \] 每次迭代时求解如下优化问题 (是一个二次型): \[ \Align{ \delta_k = \argmin_\delta \|f(x^{(k)}) + J\delta\|^2, } \] 更新参数值为 \(x^{(k+1)}=x^{(k)}+\delta_k\).
Deformation graph 算法的优点有实现简单, 且效果与一些非线性方法相当; 此外它还适用于非连通网格、多边形集 (polygon soup) 和点云等. Deformation graph 一方面让算法复杂度不受三角形网格复杂度影响, 另一方面也保持了一些细节. 算法效果图如下 (图自原论文).
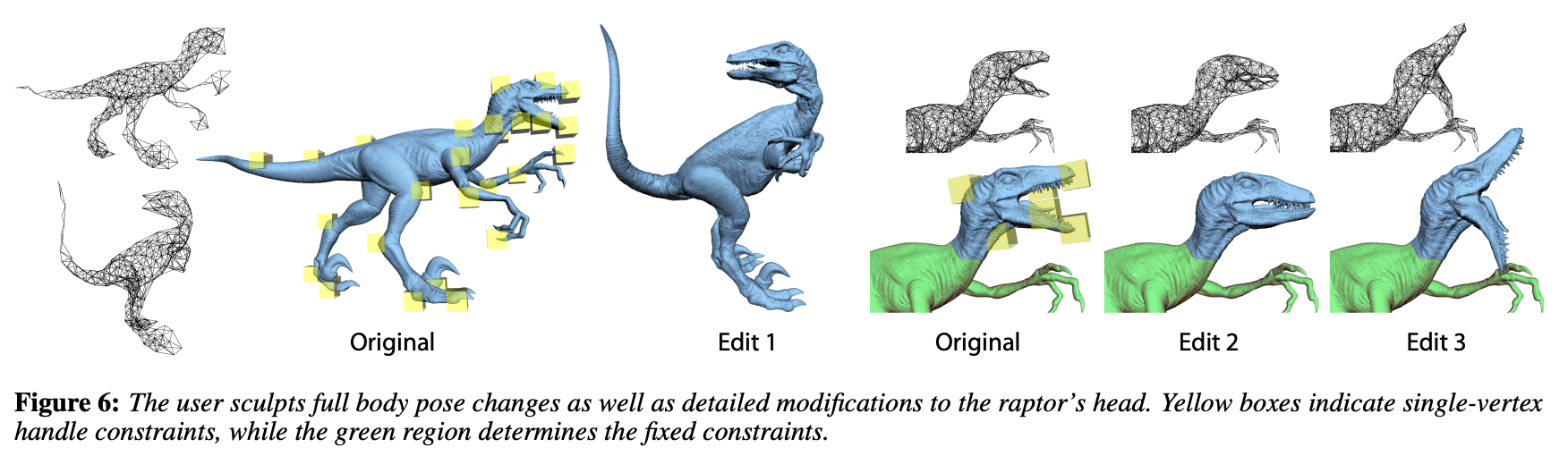
Mario Botsch et al, Geometric modeling based on triangle meshes (SIGGRAPH 2006 Courses).↩︎
Mario Botsch, Olga Sorkine, On Linear Variational Surface Deformation Methods (TVCG 2008).↩︎
Mario Botsch, Olga Sorkine, On Linear Variational Surface Deformation Methods (TVCG 2008).↩︎
Mario Botsch et al, Geometric modeling based on triangle meshes (SIGGRAPH 2006 Courses).↩︎
Lijuan Liu et al, NeuroSkinning: automatic skin binding for production characters with deep graph networks (TOG 2019).↩︎
Alec Jacobson et al, Bounded biharmonic weights for real-time deformation (SIGGRAPH 2011).↩︎