参数化与纹理
纹理映射 (texture map) 可以为三角形网格上的每个点添加颜色和法向量等信息, 进而实现更细致、真实的渲染. 纹理映射最经典也最常用的方法是参数化, 即建立起曲面与平面区域的一一对应.
9 参数化
设三角形网格 \({\cal K}\), 欧氏平面
\(\R^2\) 称为 uv-平面.
参数化指的是分片线性映射 \(\varphi:|{\cal
K}|\to\R^2\)
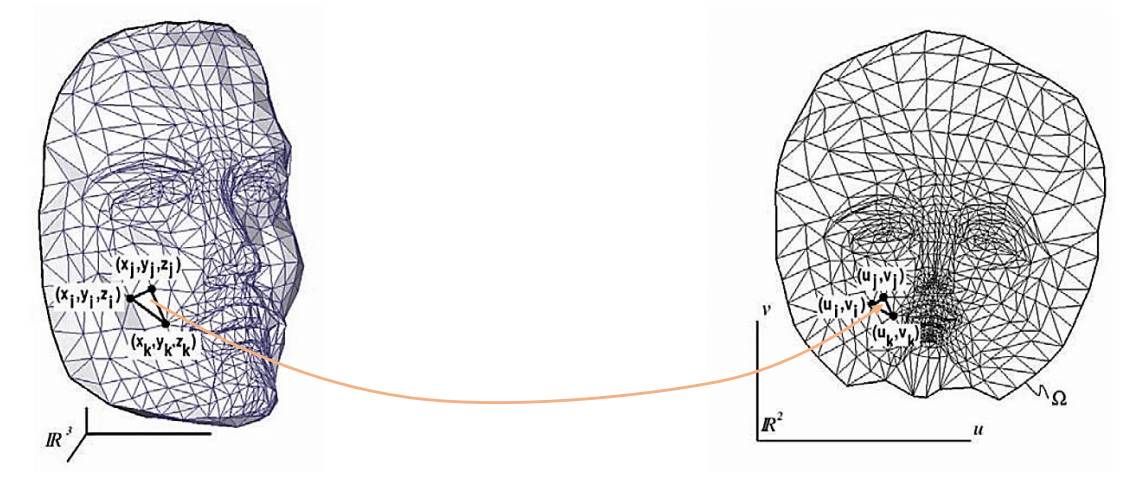
- \(\varphi\) 也叫 uv-map.
- \(\varphi\) 在每个三角形上都是非退化线性映射.
- 作为单纯复形间的映射, \(\varphi\) 完全由所有顶点的像确定.
一般而言, \(|{\cal K}|\)
的拓扑是非平凡的, 它不同胚于某个平面区域 \(U\subset\R^2\). 这时我们就不能强求 \(\varphi\) 是连续的,
即认为它在某些三角形的边界上非连续. 换言之, 我们将 \(|{\cal K}|\) 沿着其中的某些边 "剪开",
令其作为 \({\cal K}\) 的流形边界.
在某些情况下, 我们甚至需要把 \({\cal
K}\) 完全剪断, 切成若干连通分量 (如下图, 图自论文

我们的目标就是找到一个尽量好的参数化, 它满足:
- 减小边界 \(\partial|{\cal K}|\) 的长度和个数, 减少 \(|{\cal K}|\) 连通分量的个数 (减少碎片).
- 不重叠 (即 \(\varphi\) 单).
- 三角形不翻转 (即 \(\varphi\) 保持定向. 在这里我们认为 \({\cal K}\) 可定向).
- 变形小 (low distortion), 可以保持面积、角度甚至度量.
- 这是很强的条件.
下面介绍的几种优化办法都是定义一个形变能量 \(E(\varphi)\) (形变越大, 能量越大), 然后通过优化能量的办法来优化 \(\varphi\).
9.1 Tutte 嵌入
Tutte 映射首先把 \(|{\cal K}|\) 沿着一条线段剪开, 于是 \(\partial|{\cal K}|\) 的边界同胚于 \(\mathbb{S}^1\), 然后把 \(\partial|{\cal K}|\) 均匀的放到凸域 \(A\) 的边界上 (比如圆或者正方形), 而 \(|{\cal K}|\) 的内部一一映射到凸域的内部, 如下图所示 (将牛沿着肚子切开, 然后展平到单位圆上. 图自课程 PPT).
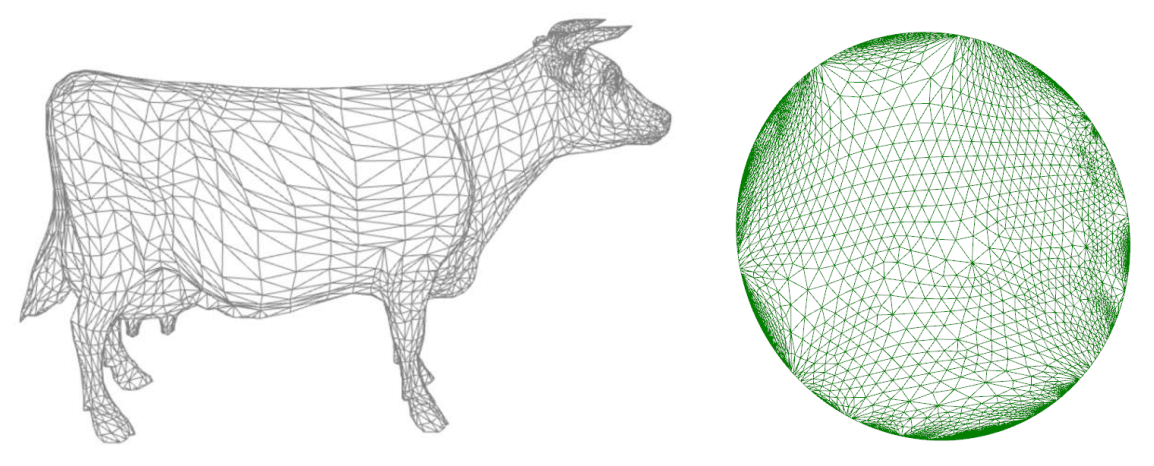
内部顶点 \(v\) 的像 \(u=\varphi(v)\) 如何求解? 我们把 \(\varphi({\cal K})\) 想像成一个弹簧系统, 每条边 \((u_i,u_j)\) 都是一根弹簧, 劲度系数为 \(D_{ij}\). 我们把弹簧系统的稳态作为 \(u\) 的位置. 该系统的能量为 \[ E = \frac12 \sum_{i=1}^n\sum_{j\in{\cal N}(i)} \frac12 D_{ij}\|u_i-u_j\|^2. \] 该能量函数是凸函数, 考虑求导. 为了简便, 记 \(\lambda_{ij}=D_{ij}/\sum_k D_{ik}\), 则 \[ \Align{ 0 = \pdv{E}{u_i} &= \sum_{j\in{\cal N}(i)} D_{ij} (u_i-u_j) \\ \iff u_i &= \sum_{j\in{\cal N}(i)} \lambda_{ij} u_j. } \] 为了方便, 不妨设前 \(m\) 个点为内部点 (未知量), 后面的点为边界点 (已知量). 将已知与未知分离, 得到 \[ u_i - \sum_{\substack{j\in{\cal N}(i)\\j\leq m}} \lambda_{ij}u_j = \sum_{\substack{j\in{\cal N}(i)\\j>m}} \lambda_{ij}u_j. \] 也就是求解下面的线性系统 (带边界条件的 Laplace 方程): \[ LX = B, \] 其中:
- \(X=\pmqty{u_1&\cdots&u_m}\T\),
- \(B_i=\sum_{j\in{\cal N}(i),j>m}\lambda_{ij}u_j\T\),
- 稀疏的 \(m\times m\) 对称矩阵 \(L_{ij}=\Cases{1,&i=j,\\-\lambda_{ij},&j\in{\cal
N}(i),\\0,&\textsf{otherwise}.}\)
- 若取 uniform \(D_{ij}=1\), \(L\) 就是图的 Laplace 矩阵. 此时的优化只考虑网格的拓扑连接, 不考虑几何.
- 若取 cotangent \(D_{ij}=\frac12(\cot\alpha_{ij}+\cot\beta_{ij})\), \(L\) 就是三角形网格的离散 Laplace-Beltrami 算子.
上面的方程 \(LX=B\) 的解使得 uv 坐标的 Laplace-Beltrami 为零, 即 \(\varphi\) 为调和映射. 这类似于网格去噪的 Laplace 平滑, 即给定初始温度 (边界点的 uv 坐标) 之后让温度梯度 \(\int_{|{\cal K}|}\|\nabla u\|^2\dd{V}\) (即 Dirichlet 能量) 尽可能小.
Tutte 映射可以保证 uv-map 没有翻转 (直观来看, 翻转的三角形必然导致弹簧能量增大). 但是它的优化结果通常有很大的变形 (如下图, 图自课程 PPT), 适合作为后续进一步优化的初始状态.
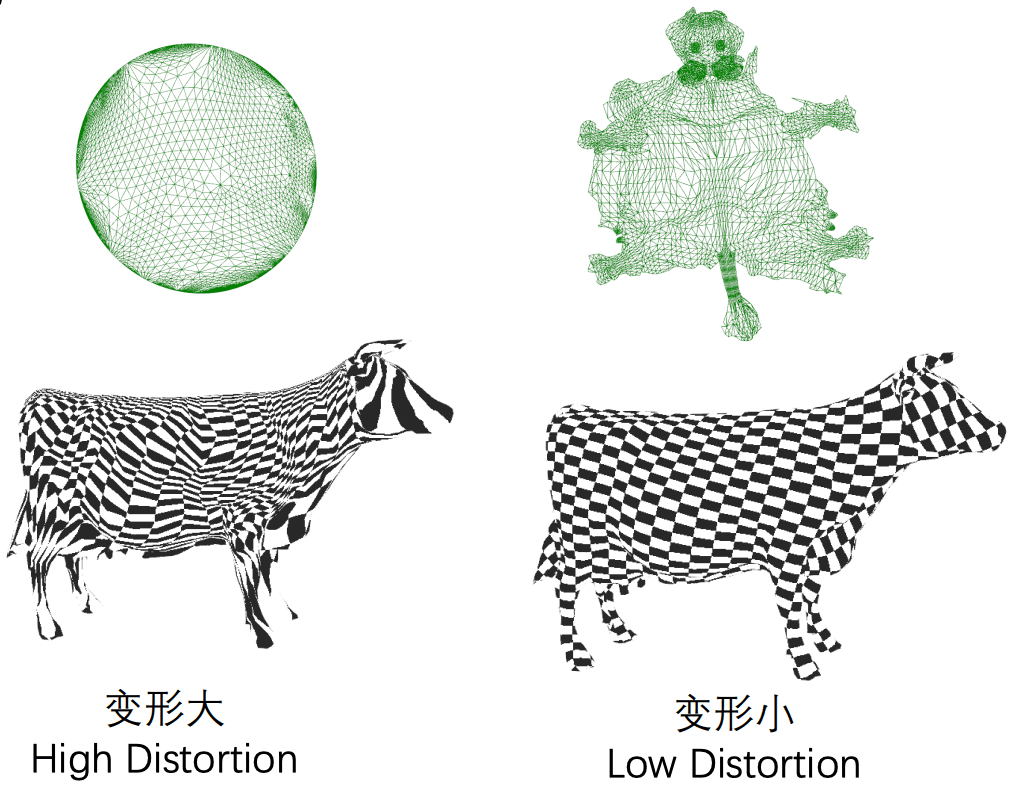
9.2 Orbifold Tutte 嵌入
原论文: Noam Aigerman, Yaron Lipman Orbifold Tutte Embeddings (SIGGRAPH Asia 2015).
Tutte 嵌入变形比较大的一个原因是它对边界 \(\varphi(\partial|{\cal K}|)\) 做了过强的约束, 把它固定在了给定 \(\partial{A}\) 上. Orbifold-Tutte 映射放松这个条件, 它只要求边界上的四个点 \(v_i\) 固定在单位正方形的四个顶点处, 如下图的四个彩色点 (图自原论文).

除此之外, 它还要求 uv-平面内的四条折边两两旋转认同, 如上图, 两条红色的边通过旋转 \(\pi/2\) 可以重合; 两条蓝色的边也是. 如此一来, 其实我们只需选择 \({\cal K}\) 上的 \(3\) 个顶点 (如左侧的模型上的三个点), 然后用两条路径连接它们, 将网格沿着路径切开即可.
- 接下来的步骤就和 Tutte 一样了, 求解线性系统得到调和映射 \(\varphi\).
- 可以证明, 路径的选择不影响 \(\varphi\) (在旋转对称性意义下). 算法的结果只取决于 \(3\) 个顶点的选择.
Orbitfold Tutte 的好处是它一方面有更高的灵活度, 可以尽量减少扭曲; 另一方面, 旋转认同的条件保证了 \(\varphi(|{\cal K}|)\) 可以在 uv-平面上密铺 (如下图, 图自原论文).
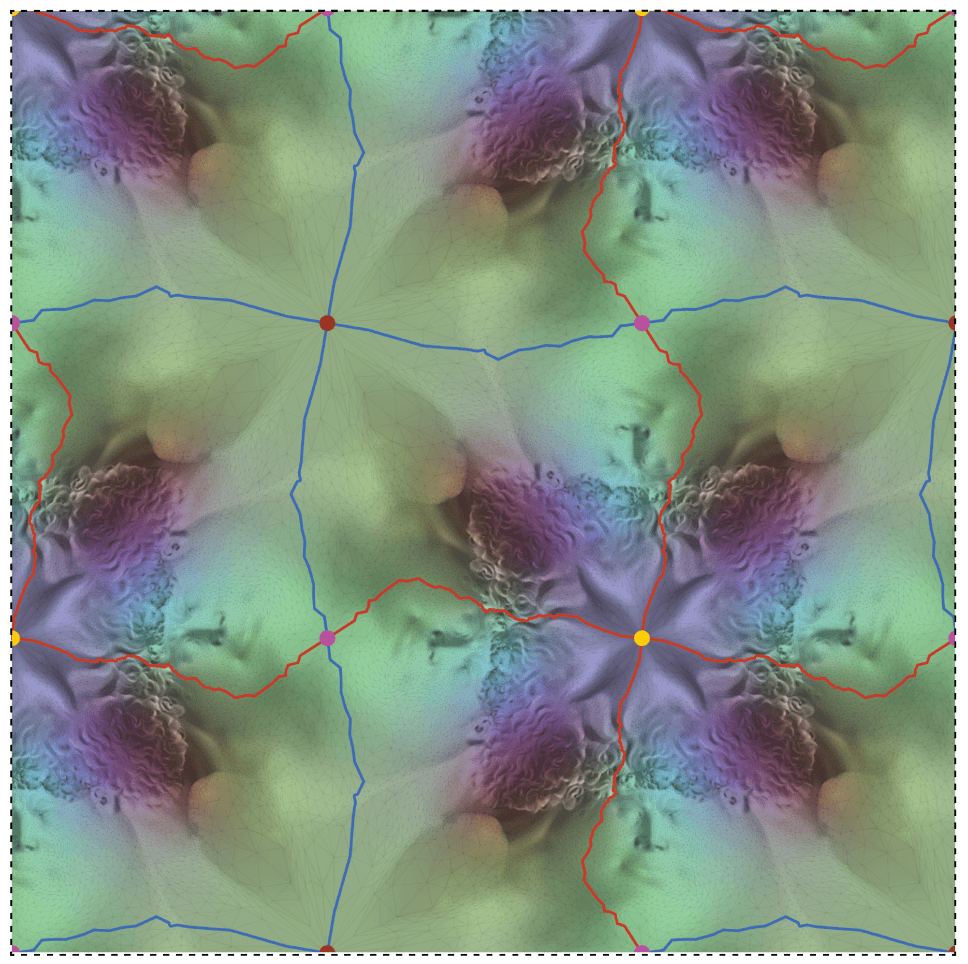
原论文基于轨形 (orbifold) 的概念, 还探讨了其他的切割与密铺方式, 这里不细展开. 感兴趣的可以阅读原论文.
9.3 参数化的微分
让我们从一种更几何的角度考察映射 \(\varphi:|{\cal K}|\to\R^2\). 设三角形 \(T\subset|{\cal K}|\) 上有局部正交归一坐标系, 在此之下三个顶点的坐标为 \((x_i,y_i)\). 在每个 \(T\) 上, \(\varphi\) 都是线性映射, 它将 \((x_i,y_i)\) 映到平面上不共线的三个点 \((u_i,v_i)\).该线性映射的矩阵表示为 \[ \pmqty{u_i\\v_i} = \underbrace{ \pmqty{\displaystyle\pdv{u}{x} & \displaystyle\pdv{u}{y} \\ \displaystyle\pdv{v}{x} & \displaystyle\pdv{v}{y}} }_{J} \pmqty{x_i\\y_i}, \] (\(i=1,2,3\)) 其中 \(J\) 是 \(\varphi\) 的 Jacobi 矩阵 (由于 \(\varphi\) 分片线性, \(J\) 在 \(|{\cal K}|\) 上分片常值). 对 \(J\) 进行奇异值分解: \[ J = U \pmqty{\sigma_1\\&\sigma_2} V\T, \] 其中 \(U,V\) 是 \(2\) 阶正交阵, 奇异值 \(\sigma_1>\sigma_2>0\). 奇异值决定了 \(\varphi\) 的几何性质:
- \(\varphi\) 保持面积当且仅当 \(\sigma_1\sigma_2=1\).
- \(\varphi\) 保持角度当且仅当 \(\sigma_1=\sigma_2\), 此时 \(J\) 称为相似变换, \(\varphi\) 是一个共形映射 (conformal map).
- \(\varphi\) 保持度量当且仅当 \(\sigma_1=\sigma_2=1\), 此时 \(J\) 为正交阵, \(\varphi\) 是一个等距同构 (isometry).
下面介绍的两种方法分别将 \(\varphi\) 优化为共形映射与等距同构.
9.4 最小二乘共形映射
原论文: Bruno Lévy et al, Least Squares Conformal Maps for Automatic Texture Atlas Generation (TOG, 2002).
9.4.1 共形能量
我们希望最终的 \(\varphi\) 是共形映射. 此时 uv 坐标的等值线互相正交; uv 平面上的三角形与 \({\cal K}\) 上的三角形相差一个相似变换, 可以尽量保证图形的 "形状" 不变 (虽然面积可能发生较大的缩放).
我们将 uv-平面认同于复平面 \(\C\), 标准坐标为 \(u+\i v\); 同时将三角形 \(T\) 的局部坐标也认同于 \(\C\), 标准坐标为 \(x+\i y\), 则 \(\varphi\) 是复变函数. 此时共形条件等价于 Cauchy-Riemann 方程 \[ \pdv{\varphi}{x} + \i\pdv{\varphi}{y} = 0. \] 由此定义共形能量 \[ \Align{ E(\varphi) :={}& \int_{|{\cal K}|} \abs{\pdv{\varphi}{x} + \i\pdv{\varphi}{y}}^2 \dd{A} \\ ={}& \sum_{T} A_T \abs{\pdv{\varphi}{x} + \i\pdv{\varphi}{y}}^2, } \] 其中\(A_T\) 为三角形面积.
9.4.2 LSCM
在局部坐标下, \(\varphi\) 的 Jacobian 为 \[ \Align{ \pmqty{\displaystyle\pdv{u}{x} & \displaystyle\pdv{u}{y} \\ \displaystyle\pdv{v}{x} & \displaystyle\pdv{v}{y}} = \frac1{2A_T} \pmqty{u_1&u_2&u_3\\v_1&v_2&v_3} \pmqty{ y_2-y_3 & x_3-x_2 \\ y_3-y_1 & x_1-x_3 \\ y_1-y_2 & x_2-x_1 \\ }, } \] 引入记号 \[ \Align{ \omega_1 &:= (x_3-x_2) + \i(y_3-y_2), \\ \omega_2 &:= (x_1-x_3) + \i(y_1-y_3), \\ \omega_3 &:= (x_2-x_1) + \i(y_2-y_1), \\ } \] 以及 \(\zeta_i=u_i+\i v_i\), 则 C-R 方程的左边为 \[ \pdv{\varphi}{x} + \i\pdv{\varphi}{y} = \frac{\i}{2A_T} \pmqty{\omega_1&\omega_2&\omega_3} \pmqty{\zeta_1\\\zeta_2\\\zeta_3}, \] 故能量函数为 \[ E(\varphi) = \frac12\sum_T\abs{ \pmqty{\omega_{j_1,T}&\omega_{j_2,T}&\omega_{j_3,T}} \pmqty{\zeta_{j_1}&\zeta_{j_2}&\zeta_{j_3}}\T }^2. \] 其中 \((j_1,j_2,j_3)\) 是三角形 \(T\) 的三个顶点. 能量 \(E(\varphi)\) 是关于未知量 \(Z=(\zeta_1,\dots,\zeta_n)\) 的二次型. 它的一个极小值点是平凡解 \(0\). 为了防止它陷入平凡解, 我们需要事先给定一些点的 uv 坐标 (称为固定点). 论文使用最小二乘法求解该二次型的极小值点, 得到的 \(\varphi\) 称为 LSCM (least squares conformal map).
可以证明 (见原论文), 该最小二乘解具有如下性质:
- 当固定点个数大于等于 \(2\) 时有唯一解.
- 最小二乘解在 uv-平面的相似变换下不变.
- 最小二乘解与网格 \({\cal K}\) 的分辨率无关.
- 若固定点都在 \(|{\cal K}|\) 的边界上, 则参数化 \(\varphi\) 保持定向 / 三角形不翻转.
9.5 As-rigid-as-possible
原论文: Olga Sorkine, Marc Alexa, As-rigid-as-possible surface modeling.
LSCM 可以尽量保证 uv 等值线正交, 但不能保证 uv 网格面积均匀 (下图左,
注意牛的头在 uv 平面被压缩得很小; 图自课程 PPT
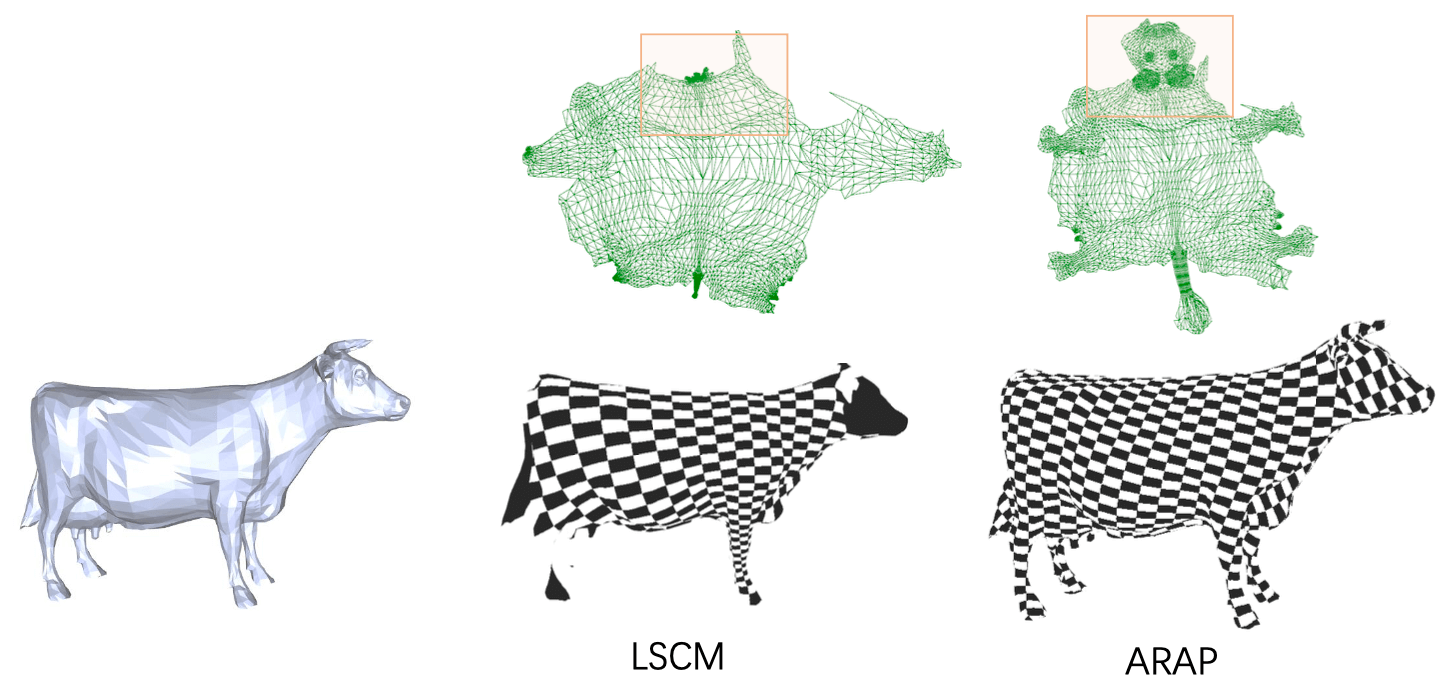
等距同构的条件是 \(J\) 的奇异值 \(\sigma_1=\sigma_2=1\), 即 \(J\) 是正交阵. 该论文引入了辅助矩阵 \(L_T\) (对每个三角形 \(T\)), 并使用 local-global 交替优化 (类似之前在网格去噪提到的 \(L_0\)-稀疏优化), 最终把 \(J\) 和 \(L_T\) 都优化为正交阵. 能量函数为 \[ \Align{ E(\varphi) &= \sum_T A_T \|J_T-L_T\|_F^2 \\ &= \sum_T \sum_{\textsf{边 }(x_i,x_j)} \cot(\theta_{ij}) \Big\|(\varphi(x_i)-\varphi(x_j)) - L_T(x_i-x_j)\Big\|^2 } \] 其中 \(J_T\) 是三角形 \(T\) 处的 Jacobian, \(\theta_{ij}\) 是边 \((x_i,x_j)\) 在三角形 \(T\) 中的对角, \(\|X\|_F:=\sqrt{\tr(X\T X)}\) 为矩阵的 Frobenius 范数.
ARAP 可以使用 Tutte 映射或者 LSCM 作为初始化, 其迭代步骤如下:
Local 步优化 \(L_T\) 为正交阵. 注意每个三角形的 \(L_T\) 互不相干, 因此对每个三角形优化出一个 \(L_T\) 即可. 记矩阵 \[ S_T := \sum_{\textsf{边 }(x_i,x_j)} \cot(\theta_{ij}) (\varphi(x_i)-\varphi(x_j))(x_i-x_j)\T, \] 它的 SVD 分解为 \(S_T=U\Sigma V\T\), 则 \(L_T\leftarrow UV\T\). 可能要对 \(UV\T\) 的某一列取负号, 保证 \(L_T\) 的行列是为正, 保持定向.
Global 步优化顶点位置 \(\varphi(x_i)\). 即求解线性系统 (最小二乘法): \[ \Align{ &\sum_{j\in{\cal N}(i)} (\cot\theta_{ij}+\cot\theta_{ji}) (\varphi(x_i)-\varphi(x_j)) \\ &= \sum_{j\in{\cal N}(i)} \bqty{\cot\theta_{ij}L_T + \cot\theta_{ji}L_{T'}} (x_i-x_j), } \] 其中 \(T,T'\) 是边 \((x_i,x_j)\) 的两个相邻三角形.
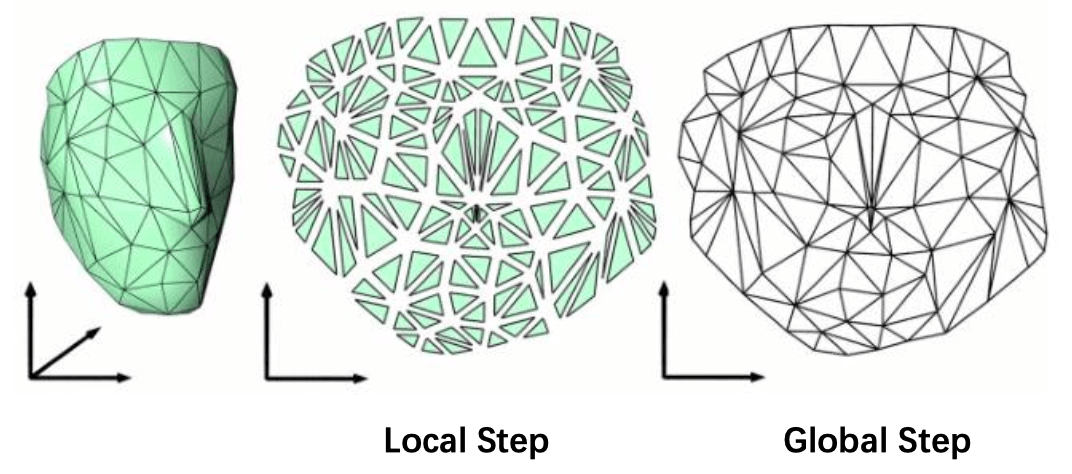
下图是 local-global 的可视化 (图自课程 PPT), local 步让 uv-平面内的三角形尽量和原三角形相同; global 步将 uv-平面中的三角形拼合起来.
10 参数化的应用
10.1 纹理映射
参数化最大的应用就是纹理映射. 将三角形网格 \({\cal K}\) 映到 uv-平面上的 \([0,1]\times[0,1]\) 区域之后, 我们在该区域的每个点都存储几何体的颜色、法向量等信息, 就得到了纹理映射 (texture mapping).
本文开头的 bunny 图片就展示了一个纹理映射.
下面展示了在球面上映上不同纹理 (左
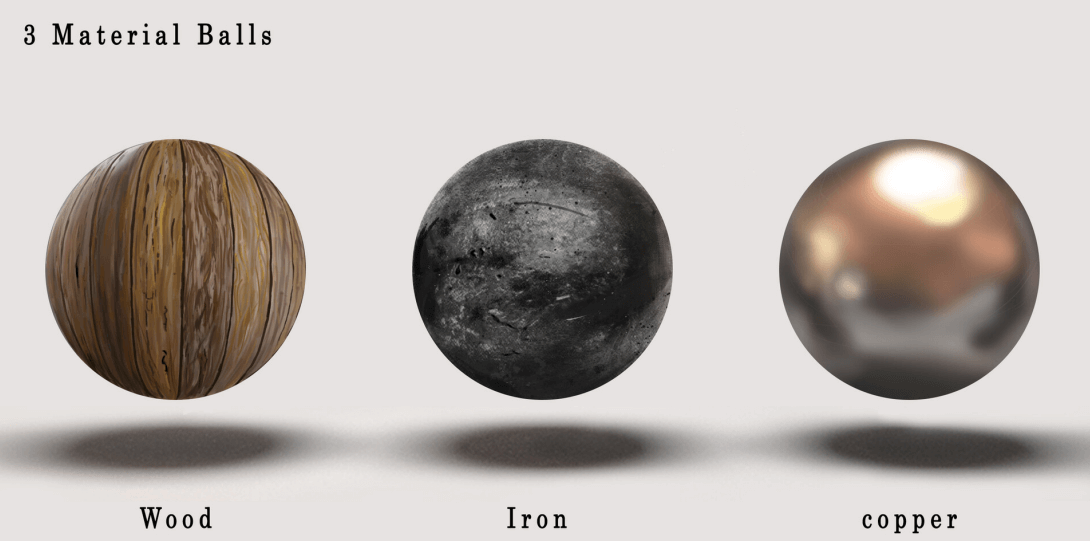 |
 |
|---|
纹理 (texture) 一般用图片的形式存储 (法向量的三个分量可以分别作为 RGB
来存储). 三角形网格的 uv 坐标可以和顶点坐标一起存储在文件里 (例如
.obj):
1 | |
但是这样有一个小缺陷. 由于顶点在文件中并不是连续存储的 (即在文件中连续的顶点, 在空间中不一定连续), 这就导致文件中相邻顶点的 uv 坐标可能差距很大, 渲染器根据 uv 读取 texture 的时候空间局部性不是很好, 其性能还有提升空间.
10.2 几何图像
原论文: Xianfeng Gu, Steven J. Gortler, Hugues Hoppe, Geometry Images (SIGGRAPH 2002).
一作是 Yau 的学生顾险峰, 在图形学颇有造诣, 将微分几何的诸多理论应用到图形学中; 而 Hugues Hoppe 就是提出 Progressive Mesh 的大佬.
10.2.1 几何图像渲染法
参数化另一个很厉害的应用就是几何图像, 它在纹理映射上更进一步: 纹理映射既然可以存储几何体的表面材质, 那能不能直接存储几何体的顶点位置? 答案是肯定的.
将网格参数化之后, 我们在 uv-平面上的每个点用 RGB
的三个分量存储顶点位置, 即 \((R,G,B)=(x,y,z)\) (位置归一化后),
这样就将一个 3D 几何体转化为了一个彩色图片. 并且, 这个过程是无损压缩
(一一对应), 可以从彩色图片还原出 3D 形体! (如下图, 图自论文的 PPT
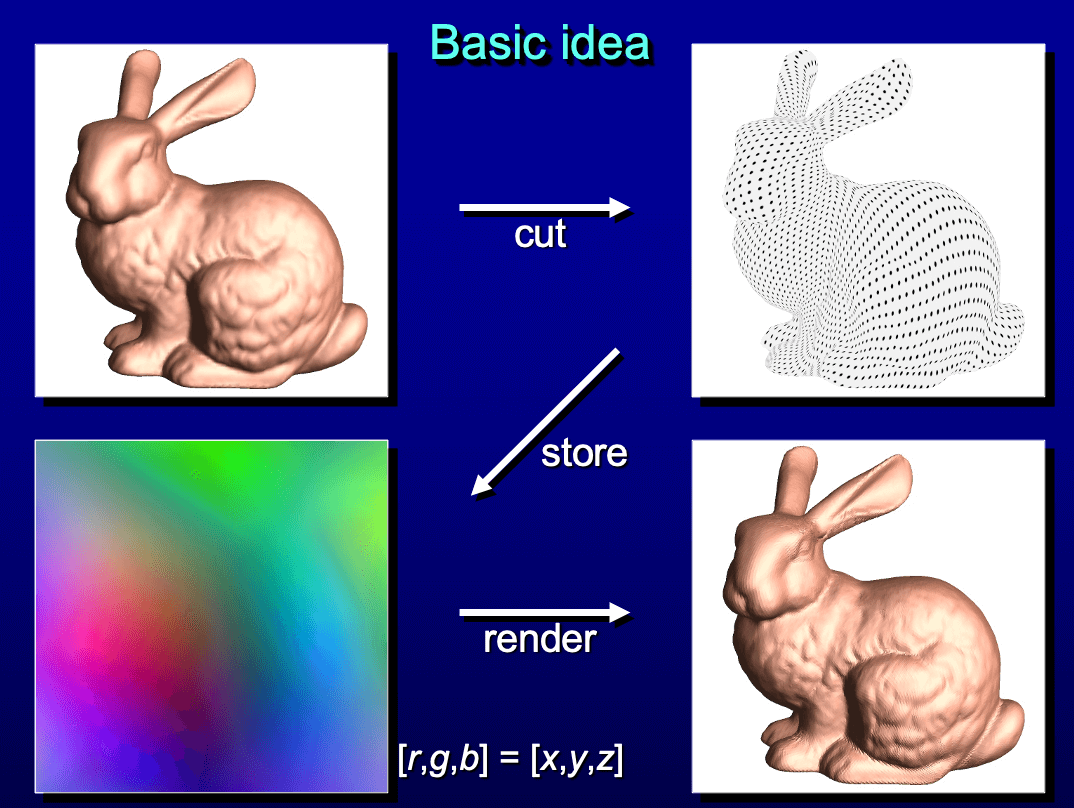
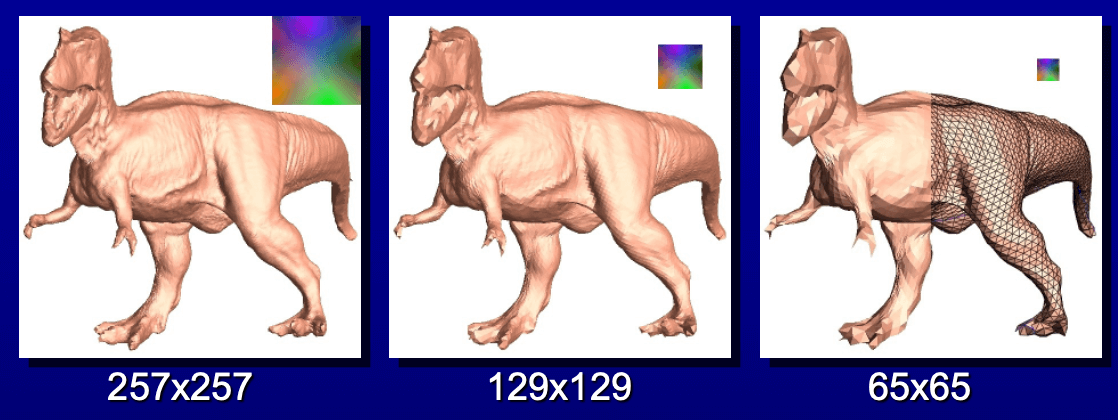
在渲染时, 把图像上相邻的像素点连接成三角形网格, 再塞进渲染管线里. 另外还可以实现带属性的渲染, 比如用一张粗分辨率的几何图像表示粗糙的几何形体, 再用一张高分辨率的 normal map 表示法向量信息, 如下图.

几何图像还可以用于压缩和多分辨率表示 (LOD), 存储不同分辨率的几何图像来实现动态的分辨率和 level-of-details.
几何图像渲染法的好处多多, 论文 PPT 中总结如下:
- Simple rendering: compact, no indirection, raster-scan stream.
- 所有信息都存储在几张图片里面, 无需
.obj文件和 uv 坐标. 渲染时逐行扫描图像, 局部性良好.
- 所有信息都存储在几张图片里面, 无需
- Mipmapped geometry
- Hierarchical culling
- Compressible
10.2.2 与深度学习结合
把几何体变成图像之后, 就可以使用图像处理技巧处理 3D 问题了, 比如用神经网络进行几何理解、几何生成.
11 表示纹理的其他方法
参数化与纹理映射存在一些问题, 比如:
- 怎样切缝?
- 良好的参数化依赖切缝 / 切点的选取.
- 怎样将不同的片拼到一个正方形区域内?
- \(\varphi(|{\cal K}|)\) 的几个每个分量形状都不规则.
- 创建纹理后, 怎么修改?
- 2D 的纹理图像缺乏 3D 直观性.
- 纹理通常是为某个网格设计的, 换个模型怎么复用?
- 不同的网格有不同的参数化.
一些更 "3D" 的方法可以解决这些问题.
11.1 八叉树纹理
论文: David Benson, Joel Davis, Octree textures (SIGGRAPH 2002).
用八叉树将空间细分, 在每个叶子结点上存储颜色和材质.
八叉树纹理的一个缺点是获取一个点需要寻址多次——从根节点走到叶子结点. 可以用下面的方法改进:
- \(N^3\)-tree, 即每次将空间一分为 \(N^3\) (八叉树是一分为 \(2^3\)), 这样可以减少树的深度.
- 将叶子结点存储到 hash 表里, 只需进行常数次次寻址.
11.2 Mesh colors
原论文: Cem Yuksel, John Keyser, Donald H. House, Mesh colors (TOG, 2010).
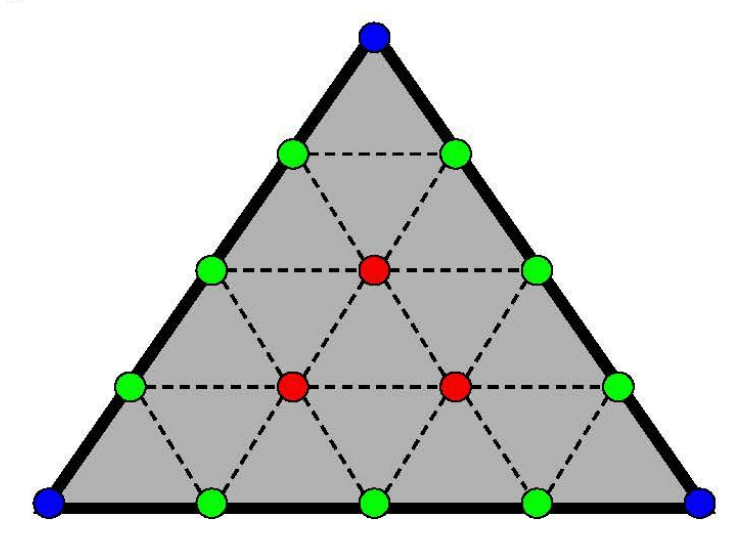
Mesh colors 直接把颜色存储在三角形网格上. 不光顶点处可以存储颜色, 边上和面内都可以存储颜色. 在确定某点 \(p\) 的颜色时, 只需在 \(p\) 所在的小三角形内 (虚线组成) 进行线性插值. 下图展示了分辨率 \(R=4\) 的一个三角形, 顶点、边和面内一共有 \(15\) 个颜色点 (图自论文 PPT, 下同).
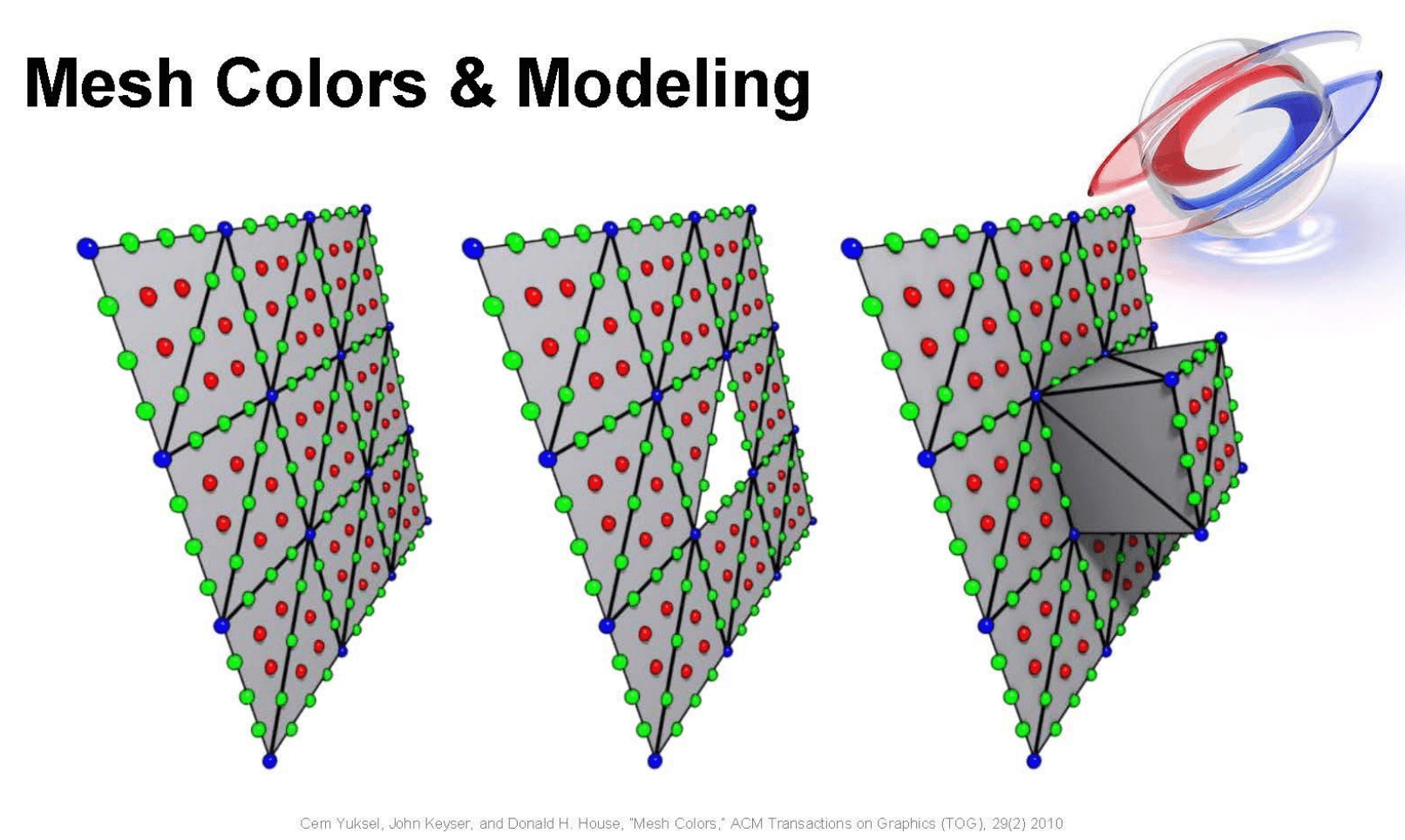
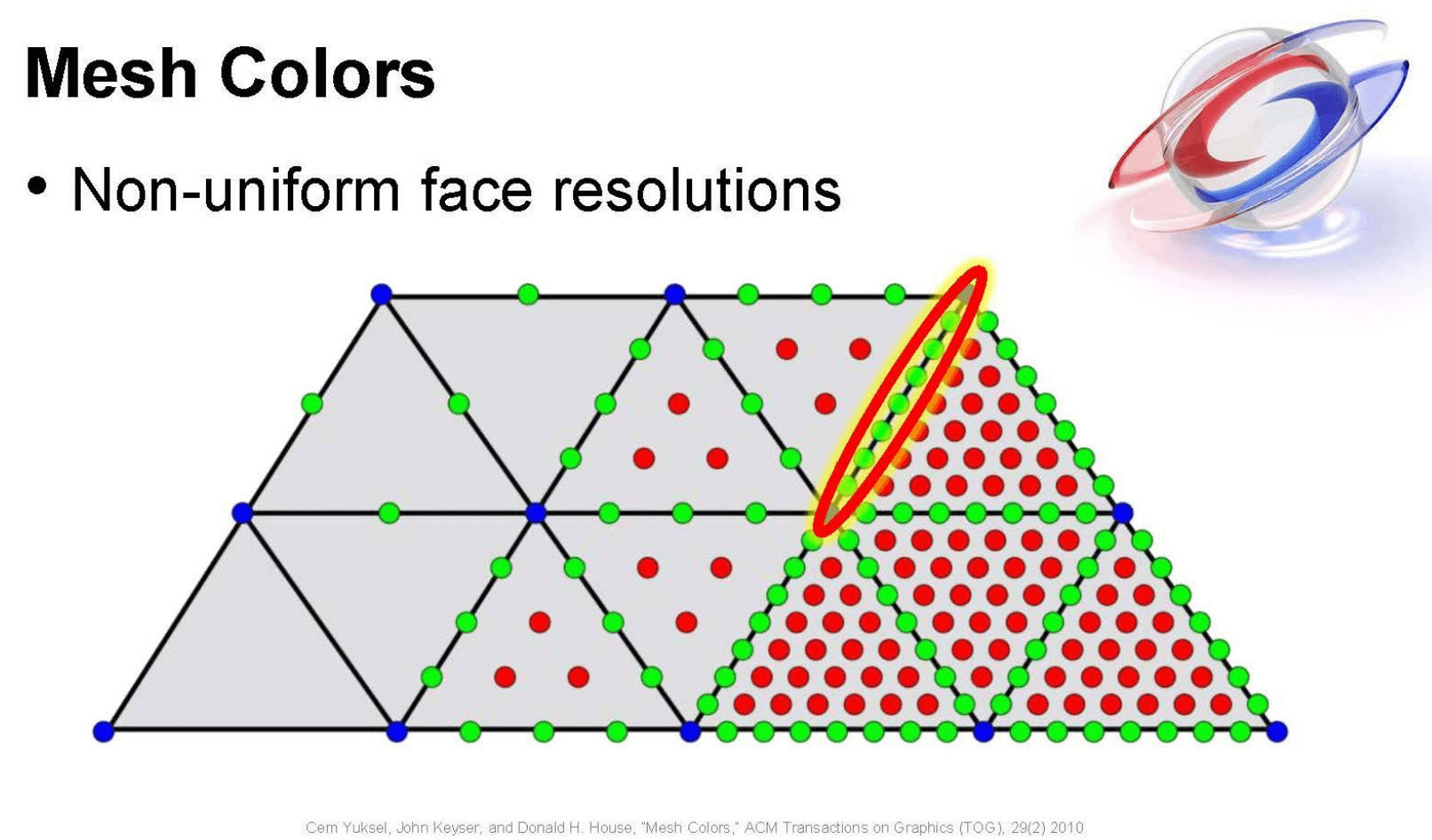
Mesh colors 的一大优点是易于编辑. 当改动网格时, 不必重新进行参数化, 只需将涉及到的三角形上的颜色点进行改动即可 (下图左). 此外, mesh colors 还可以实现非均匀分辨率, 即在不同的三角形上可以有不同数量的颜色点 (下图右).
 |
 |
|---|
Mesh colors 是一个很好的渲染办法, 然而却没有得到广泛的应用, 这大概是因为在论文发表的时候 (2010 年), 基于参数化渲染管线已经发展成熟, 在游戏、电影等各个领域根深蒂固, 难以改变了.