重网格化
重网格化 (remeshing) 指的是在保证几何误差的前提下, 改变网格连接关系.
- 上次讲的网格去噪不改变连接关系, 指改变顶点位置, 故不属于重网格化.
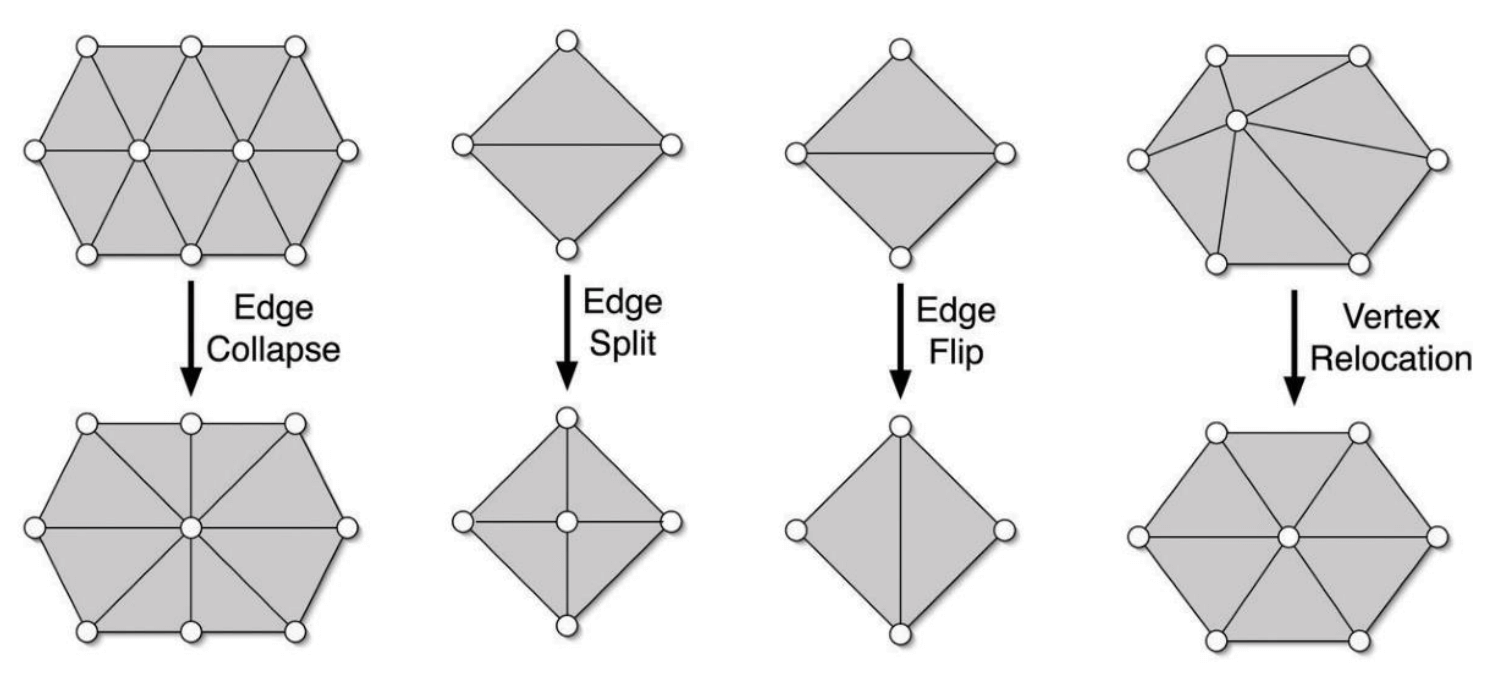
三角形网格的重网格化主要基于下面几个基本操作:
5 网格简化
Marching cubes 算法重建出的三角形网格是均匀的, 在平滑的地方和细节之处都有相同的分辨率. 这就带来一个问题, 如果在 marching cubes 时想要保留 SDF 的细节, 就需要很大的分辨率, 进而重建出的网格占用空间很大 (几十上百兆). 但在几十年前, 网络带宽较低, 传输如此大的网格是很慢的. "网格简化" 算法便应运而生. 发送方对复杂的网格进行简化, 发送粗糙的网格; 接收方接收后再进行网格细分, 还原精细的网格.
网格简化有很多方法, 这里介绍基于 "边坍缩" (edge collapsing) 的网格简化. 顾名思义, 边坍缩指的是将一条边坍缩为一个点, 如上图最左边. 边坍缩要解决两个问题:
- 选择哪一对边坍缩?
- 坍缩后的新顶点应该在哪?
5.1 基于顶点聚类
顶点聚类 (vertex clustering) 方法很简单, 用一个包围盒包住三角形网格, 将包围盒切分成若干个小立方体, 然后让处于同一个立方体内的顶点坍缩为一个 (如下图, 图自课程 PPT).
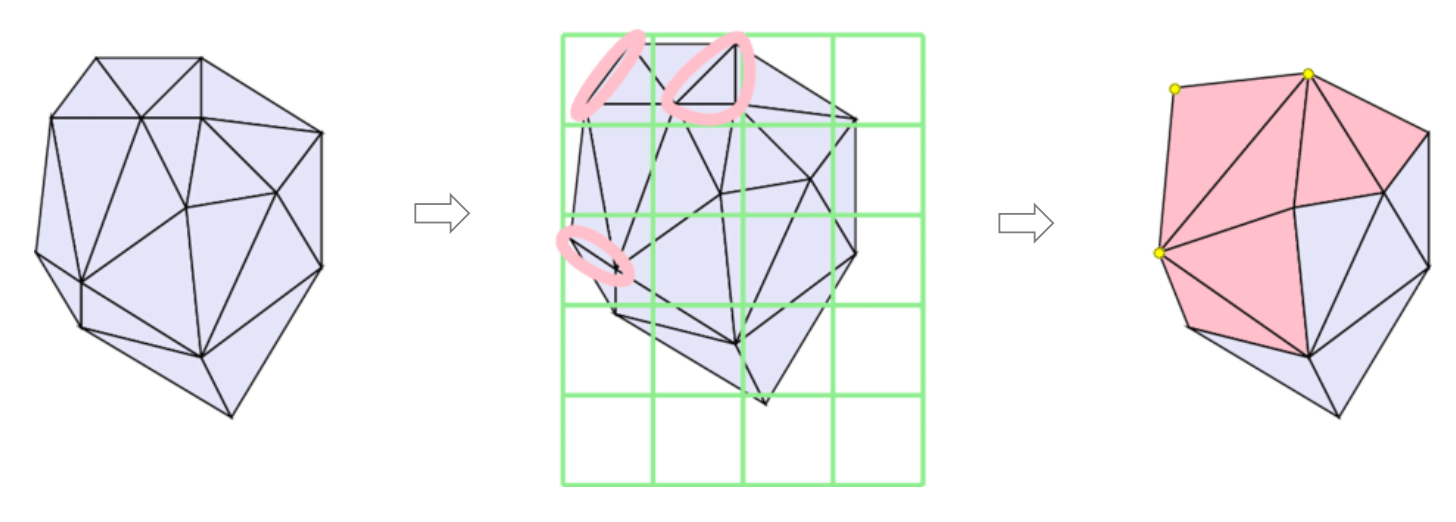
在坍缩位置的选择上, 最简单的方法是取坍缩点的平均值, 但这样会导致几何体的边界变得扭曲. 有没有更好的办法?
5.2 QEM
原论文: Michael Garland, Paul S. Heckbert, Surface Simplification Using Quadric Error Metrics (SIGGRAPH, 1997).
假设我们要把边 \(e=(v_1,v_2)\) 坍缩为一个点 \(v\). 所谓 QEM (quadratic error metric), 就是衡量该坍缩操作的几何误差. 点 \(v\) 的 QEM 定义为它到 \(v_1,v_2\) 所有相邻平面的距离的平方和 (如下图, 红色点是 \(v_1,v_2\), 绿色点是 \(v\), 黄色的是所有相邻平面; 图自课程 PPT).
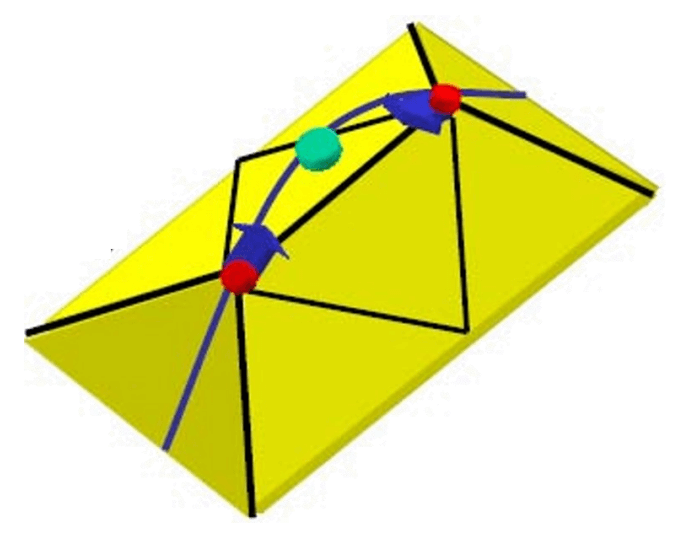
如果三角形 \(T\) 所在平面的方程是 \(ax+by+cz+d=0\), 则它的法向量是 \(n=(a,b,c)\T\), 偏移量 \(d=\lr{n,v_0}\), 其中 \(v_0\) 是平面上一点. 空间中一点 \(v\) 到该平面的距离的平方就是 \[ h^2_T(v) := \frac{(\lr{n,v}+d)^2}{\lr{n,n}}. \] 我们引入齐次坐标来以化简上式. 记 \(\tilde{n}=(a,b,c,d)\T\), \(\tilde{v}=(v\T,1)\T\), 并假设 \(a^2+b^2+c^2=1\) (即 \(n\) 是单位向量), 则 \[ h^2_T(v) = \lr{\tilde{n},\tilde{v}}^2 = \tilde{v}\T(\tilde{n}\tilde{n}\T)\tilde{v}. \] 如果记 \(Q_T:=\tilde{n}\tilde{n}\T\) (这是一个实对称矩阵), 则 \(h^2_T(v)\) 就是 \(Q_T\) 的二次型 (所以叫做 quadratic error). 顶点 \(v_i\) 的 QEM 定义为它相邻边的 QEM 之和, 换言之, \(v_i\) 对应了对称阵 \(Q_i:=\sum_{T\ni v_i}Q_T\).
最后, 坍缩操作 \((v_1,v_2)\to v\) 的 QEM 就是两个顶点的误差之和: \[ {\sf Error}(v) := \tilde{v}\T Q_1\tilde{v} + \tilde{v}\T Q_2\tilde{v} = \tilde{v}\T Q \tilde{v}, \] 其中 \(Q=Q_1+Q_2\).
因此, 最优坍缩位置 \(v\) 应当是使得二次型 \({\sf Error}(v)\) 取最小值的点. 由于 \(Q\) 半正定, 我们只需解方程 \(Q\tilde{v}=0\). 将它还原成非齐次坐标, 得到 \[ \underbrace{\pqty{\sum_{T} {n}_T{n}_T\T}}_A \; v + \underbrace{\pqty{\sum_{T} {n}_Td_T}}_b = 0. \]
如果 \(A\) 可逆, 则 \(v=-A^{-1}b\).
如果 \(A\) 不可逆 (这意味着 \(e\) 周围的三角形至多有两个线性无关的法向量), 我们加入正则化约束: \[ (\lambda I+A)v + b = 0. \] 此时 \(\lambda I+A\) (\(\lambda>0\)) 一定是可逆的. 该正则化的含义是使得 \(v\) 尽量靠近 \(e\) 的中点.
为了实现上的方便, 一般我们不论 \(A\) 是否可逆, 都考虑正则化, 即 \(v=-(\lambda I+A)^{-1}b\).
顶点聚类配合 QEM 可以保持几何体的边界, 如下图中间 (左为原网格; 图自课程 PPT):
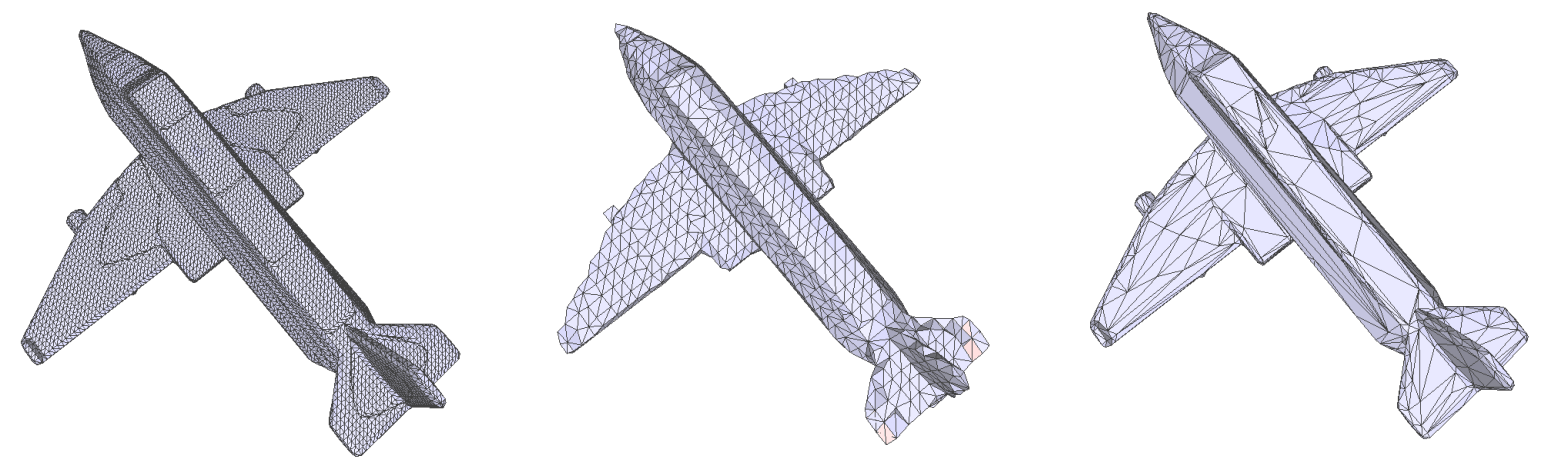
然而顶点聚类算法对底层几何无感知地均匀简化. 理想的效果 (上图最右) 应当是在几何体较平缓的区域进行简化 (比如飞机顶部), 在几何体棱角和细节的地方尽量不简化 (比如机翼和尾翼前缘). 这就要请出增量式算法了.
5.3 Progressive mesh
原论文: Hugues Hoppe, Progressive Meshes (SIGGRAPH 1996).
对于坍缩操作 \((v_1,v_2)\to v\), 它的坍缩误差定义为 \({\sf Error}(v)\) 的最小值.
增量式算法一次次地遍历每一对可以坍缩的顶点, 每次都选择坍缩误差最小的那一对进行坍缩... 具体来说, 算法分为下面几个步骤:
- 对于每一条边 \(e=(v_i,v_j)\), 计算坍缩代价, 并插入到一个优先队列中.
- (迭代) 重复执行, 直到达成简化目标 (比如剩余点的比例低于某一值):
- 从队列中取出坍缩代价最小的边 \(e=(v_i,v_j)\).
- 进行坍缩操作, 对附近的网格进行重连.
- 标记队列中失效的边; 向队列中插入新的边.
顶点的 QEM 二次型 \(\tilde{v}\T Q_i\tilde{v}\) 的等值面是一个椭球面 (若非退化). 取 \(\varepsilon>0\), 我们将所有顶点的 \(\varepsilon\)-等值面都画出来, 就得到了下图 (图源 QEM 论文).

较大的椭球面对应了较小的误差. 每次坍缩的时候, 我们都要选择顶点处椭球面较大的边.
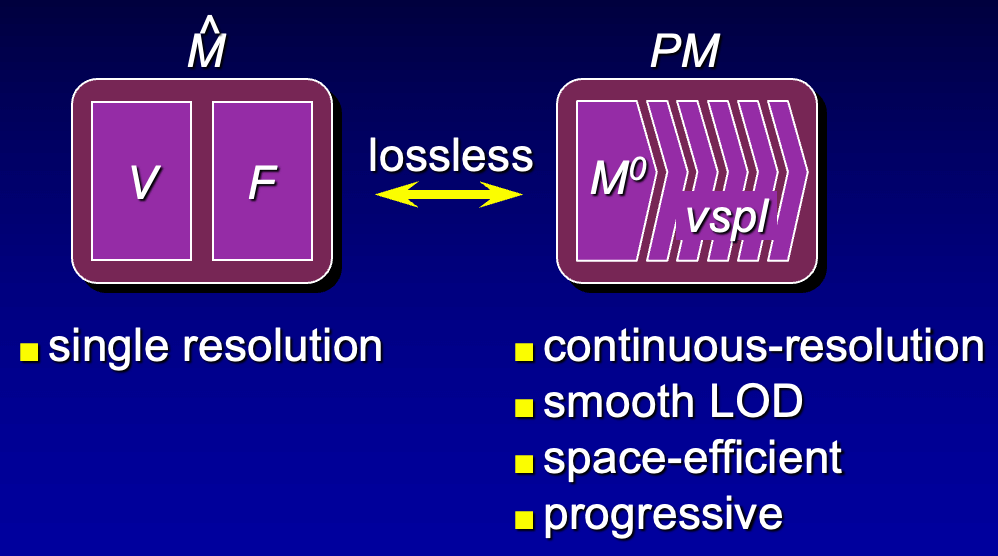
随着迭代次数的增加, 增量式网格简化算法可以产生一系列不同分辨率的网格 (从原始网格, 到最简化的网格). 如果考虑该过程的逆过程, 即在最简化网格上进行 "顶点分裂" (与 "边坍缩" 互逆), 就能逐渐得到细分辨率网格, 直到最高质量的原始网格.
因此, 我们只需要存储一个最低分辨率的网格, 再额外记录所有 "顶点分裂"
的操作, 即可还原出各个分辨率的网格. 这种网格表示方法称为 Progressive
Mesh. 下面的视频是原论文作者给出的一个 demo
5.4 应用
图神经网络的 pooling 层实际上就是基于顶点聚类的边坍缩, 它的效率很高, 但是效果不如增量式算法. 为什么图神经网络不使用后者? 一方面, 增量式算法无法并行, 效率很低. 另一方面, 尽管基于聚类的算法的效果不够好, 但是神经网络有一定 robustness, 可以补偿之.
关于 Progressive Mesh, 它的实际应用非常广泛.
- 在 3D 游戏中, 它可以帮助节省大量资源: 在物体距离玩家较远的时候用粗分辨率网格; 当玩家靠近时逐渐应用细分辨率网格 (自适应细节度, LOD, level-of-details). 更进一步地, 对于同一个物体, 它朝向玩家的一面可以用高分辨率表示, 背离玩家的一面则用低分辨率表示 (view-dependent LOD).
- 在网格传输时, 可以先传输最粗分辨率的网格, 接着传输顶点分裂操作的序列
(如下图, 图自原作者的 PPT
https://hhoppe.com/pm.ppt [2]). 这样, 只要接收方收到了最粗分辨率的网格, 就可以在屏幕上显示, 然后再往上填补细节. 这样, 就算网速比较慢, 也不需要等到接受完所有数据才能在屏幕上显示了.
6 提升网格的质量
增量式算法还可以用于提升网格的质量, 使得网格边长更均一、顶点分布更均匀. 该算法输入一个目标边长, 通过迭代的方法让网格边长逐渐靠近目标边长.
- 计算边长下界为 \(4/5\) 倍目标边长, 上界为 \(4/3\) 倍目标边长 (参数可调).
- 重复执行 \(N\) 次:
(其实就是基本操作的组合, 见文初图)
- 对过长的边执行 "边分裂" (edge split).
- 对过短的边执行 "边坍缩" (edge collapse).
- (均一化顶点的度数) 执行 "边翻转" (edge flip), 使得顶点的度数为 \(6\) (边界点为 \(4\)).
- 考虑四个顶点距离其目标度数 (\(4\) 或 \(6\)) 的偏差的绝对值之和 \(\delta\), 若翻转后 \(\delta\) 变小, 则执行翻转.
- (切向重定位) 将顶点 \(p\) 的坐标设为附近顶点的平均值 \(p'\), 这能让顶点分布尽量均匀.
- (法相重定位) 将顶点 \(p'\) 沿着法相投影回曲面表面 (\(p\) 处的切平面).
该算法可以产生质量很高的均匀网格. 在该算法的基础上还可以做一些微调:
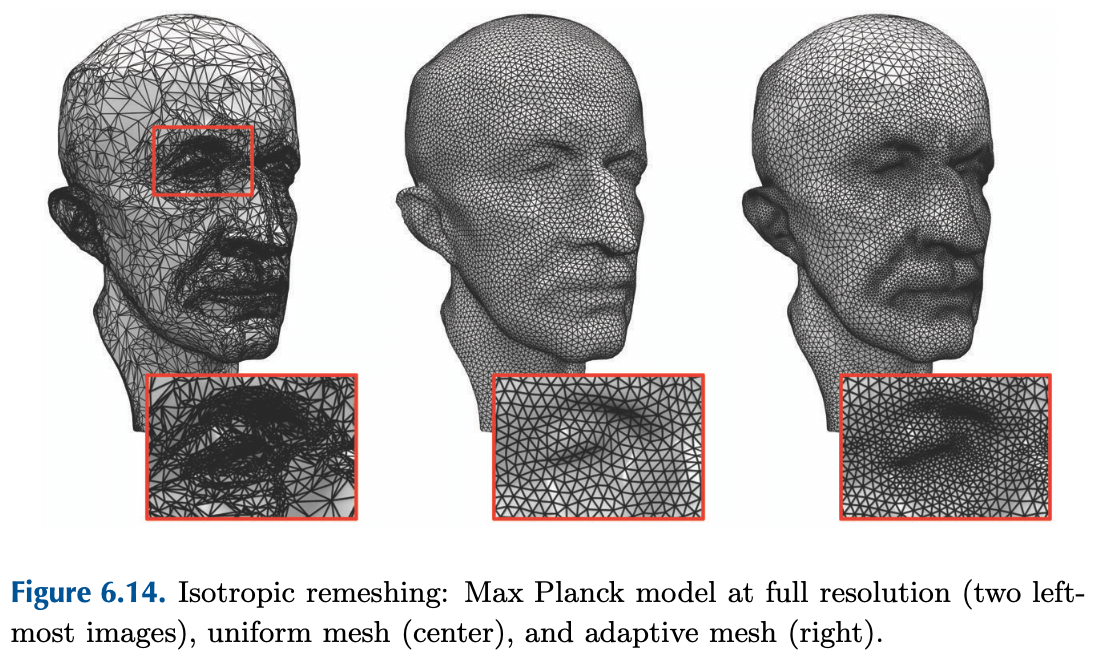
- 人为标记一些顶点或者边为 "特征点/边", 并强制改算法保持特征点/边不变, 进而保证原模型的边缘、细节特征得到保留.
- 调整切向重定位阶段的求和权重, 实现自适应重网格化, 在细节区域加密网格 (如下图, 图自 Polygon mesh processing).
7 网格细分
Loop 细分和 \(\sqrt3\) 细分的本质都是向网格中加入新的顶点.
7.1 Loop 细分
原论文: Charles Teorell Loop 的硕士论文 Smooth Subdivision Surfaces Based on Triangles (1987).
这是一种迭代算法. 每次迭代的时候, 更新策略分为新旧顶点两类:
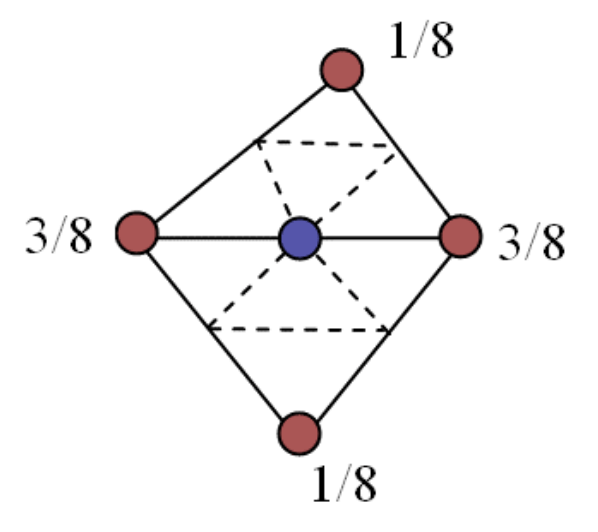
加入新顶点: (如上图蓝色点, 图自课程 PPT) 遍历网格的每条边,
若为边界边 (只有一条 halfedge), 则这条边上的新顶点是中点.
若为内部边 (有两条 halfedge), 则这条边上的新顶点为 \[ v_{\sf new} = \frac38(v_0+v_1) + \frac18(v_2+v_3), \] 其中 \(v_0,v_1\) 是这条边的两个端点, \(v_2,v_3\) 是这条边的 (在相邻三角形中的) 两个对点.
加入新顶点之后, 构建对应的边和三角形.
平滑化: 每个旧顶点向其相邻顶点的均值靠拢. 具体来说, 设旧顶点 \(v\) 的相邻顶点为 \(\{w_i\}_{i=1}^n\), 则 \(v\) 更新为 \[ v' = (1-nu)v + \sum_{i=1}^n u w_i, \] 其中权重 \(u=3/(8n)\), 特别地, 当 \(n=3\), \(u=3/16\).
下图展示了对一个正二十面体和一只三角龙进行 Loop 细分的过程, 分别进行
\(5\) 次和 \(2\) 次迭代. (由 Mathematica 制作, 代码自
Mathematica Stack Exchange

可以看出, Loop 算法可以把正二十面体逐渐变成一个球, 其平滑效果还是很好的; 同时它也能保持三角龙角部的细节信息 (Loop 的平滑参数和顶点权重都是经过理论计算的).
在 Loop 算法提出之前, 还有四边形网格上类似的细分算法——Catmull–Clark 细分算法 (1978).
7.2 \(\sqrt{3}\) 细分
原论文: Leif Kobbel, \(\sqrt3\)-Subdivision (SIGGRAPH 2000).
Loop 细分在边上插入顶点, 把一个三角形分成四个; 而 \(\sqrt{3}\) 细分在面上插入顶点, 把一个三角形分成三个.
加入新顶点: 遍历网格的每个三角形 \(T=(v_1,v_2,v_3)\), 加入新顶点 \(v'=(v_1+v_2+v_3)/3\) (重心). 并将旧三角形划分成三个新三角形 (分别把三个顶点与重心相连).
平滑化: 每个旧顶点向其相邻顶点的均值靠拢: \[ v' = (1-n\alpha)v + \sum_{i=1}^n \alpha w_i, \] 其中权重 \(\alpha=\dfrac{4-2\cos(2\pi/n)}{9}\).
每次更新后, 网格的边长缩小为原来的 \(1/\sqrt3\), 故得名 \(\sqrt{3}\) 细分. 该算法每次细分仅生成 \(3\) 倍个三角形, 比 Loop 细分 (生成 \(4\) 倍) 更高效.
8 四边形化
四边形网格在实际中用得比较多, 比如孟买的 Cybertecture Egg 和电影 Big
Buck Bunny 的兔子模型 (左图自网络

四边形网格方便设计师设计, 在建筑上也节省建材.
网格四边形化是一个高度非平凡的问题, 目前仍是研究前沿之一. 这里主要介绍一种基于方向场和位置场的局部优化算法, 并简略地提及一些整体优化算法.
8.1 局部优化算法
原论文: Wenzel Jakob et al, Instant Field-Aligned Meshes (SIGGRAPH Asia 2011).
这篇论文的想法是很直观的: 首先在曲面上优化出一个方向场 (在每个顶点处给出两个正交的方向), 在此基础上优化出一个位置场, 再抽取四面体网格, 如下图 (图自课程 PPT, 原图自原论文).

本节的图片均取自原论文.
8.1.1 方向场
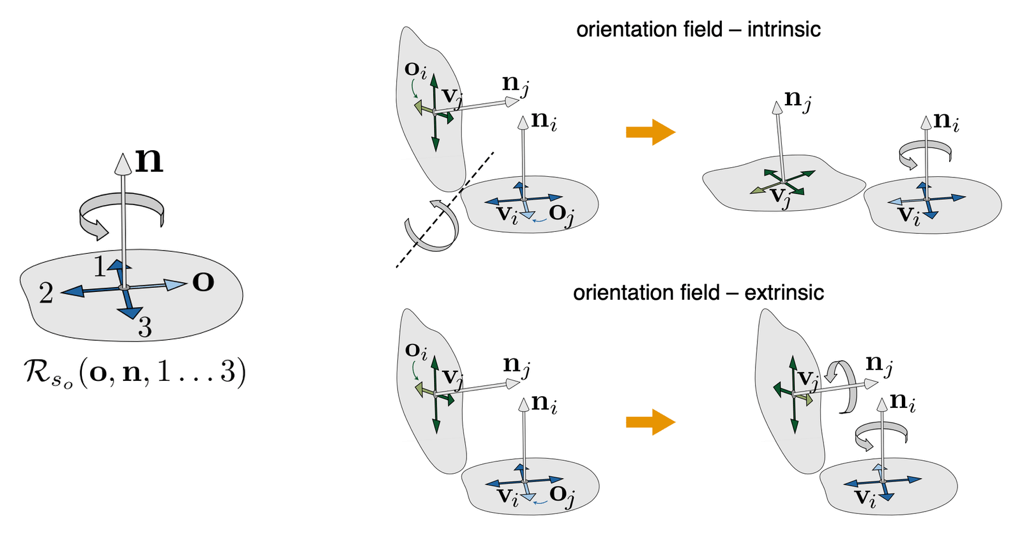
方向场就是在三角形网格 \({\cal K}\) 的每个顶点都放一个 "十字", 指向两个正交的方向. 设顶点 \(v\) 处的单位法向量为 \(n\), 则 \(v\) 处的 "十字" 指的是四个单位向量组成的集合 \[ {\cal R}_4(o,n) := \{ {\cal R}_4(o,n,0),{\cal R}_4(o,n,1),{\cal R}_4(o,n,2),{\cal R}_4(o,n,3) \}, \] (如下图左) 其中 \({\cal R}_4(o,n,k)\) 是单位切向量 \(o\) 旋转 \(k\pi/2\) 得到的单位向量.
- 实际上, \({\cal R}_4(o,n)\) 是商群 \(\mathbb{S}^1/\{1,\i,-1,-\i\}\) 中的元素. 该商群称为 \(v\) 处的 \(4\)-旋转对称群 (\(4\)-RoSy group); \(4\)-旋转对称场是从顶点到旋转对称群的映射. 所谓方向场, 其实就是 \(4\)-旋转对称场.
- 原论文考虑了 \(N\)-旋转对称场, 这里只讨论 \(N=4\) 的特殊情况, 一般的情形是类似的.
为了平滑这个方向场, 我们构造一个能量函数来衡量这个方向场的
"非平滑性". 对于两个相邻的 "十字" \({\cal
R}_4(o_i,n_i)\) 和 \({\cal
R}_4(o_j,n_j)\), 有两种办法衡量它们的差距 (如上图右
(intrinsic smoothness) 将 \({\cal R}_4(o_j,n_j)\) 旋转到与 \({\cal R}_4(o_i,n_i)\) 共面后, 计算两者夹角的最小值: \[ E(O,k) := \sum_{(i,j)\in E({\cal K})} \angle\bqty{o_i,{\sf Rotate}({\cal R}_4(o_{j},n_j,k_{ji}))}^2, \] 其中 \({\sf Rotate}\) 的旋转轴为 \(n_j\times n_i\), 旋转角为 \(\angle(n_j,n_i)\). 引入参数 \(k_{ji}\in\Z\) 的目的是记录 \({\cal R}_4(o_j,n_j)\) 的哪个代表元在旋转后与 \(o_i\) 夹角最小.
(extrinsic smoothness) 不旋转到同一平面, 直接考虑 \({\cal R}_4(o_j,n_j)\) 和 \({\cal R}_4(o_i,n_i)\) 两者夹角的最小值: \[ E_{\sf e}(O,k) := \sum_{(i,j)\in E({\cal K})} \angle\bqty{ {\cal R}_4(o_i,n_i,k_{ij}),{\cal R}_4(o_j,n_j,k_{ji}) }^2, \] 其中 \((k_{ij},k_{ji})\in\Z^2\), 记录夹角最小的代表元. 要确定 \((k_{ij},k_{ji})\), 只需枚举 \(4\times4\) 种情况.
优化方法采用 Gauss-Seidel 迭代. 类似于 Laplace 平滑, 它让每个点的场趋向于附近点的平均值. 因为 intrinsic smoothness 总是将网格局部展平, 所以它并不能捕捉 \({\cal K}\) 在空间中的嵌入信息, 只能捕捉 \({\cal K}\) 的整体拓扑. Extrinsic 的提出解决了这一问题. 下图展示了 intrinsic 和 extrinsic 优化的结果, 可以看到 extrinsic 优化的结果能够较好对齐几何体的边界.

实际上, 之前的论文尝试过用其他先验方法捕捉几何体的嵌入信息, 例如让
"十字" 对齐主曲率方向
8.1.2 位置场
有了位置场, 正方形网格便在相差一个平移的意义下确定 (边长 \(\rho\) 预先给定). 每个顶点 \(v\) 附近都有一个正方形网格, 我们需要让这些网格对齐. 设 \(v\) 处网格的原点是 \(p\), 则格点的集合为 \[ {\cal T}_4(p,n,o) := \{ {\cal T}_4(p,n,o,t) \mid t\in\Z^2 \}, \] 其中 \({\cal T}_4(p,n,o,t):=p+\rho\sum_{k=0}^1 t_k{\cal R}_4(o,n,k)\).
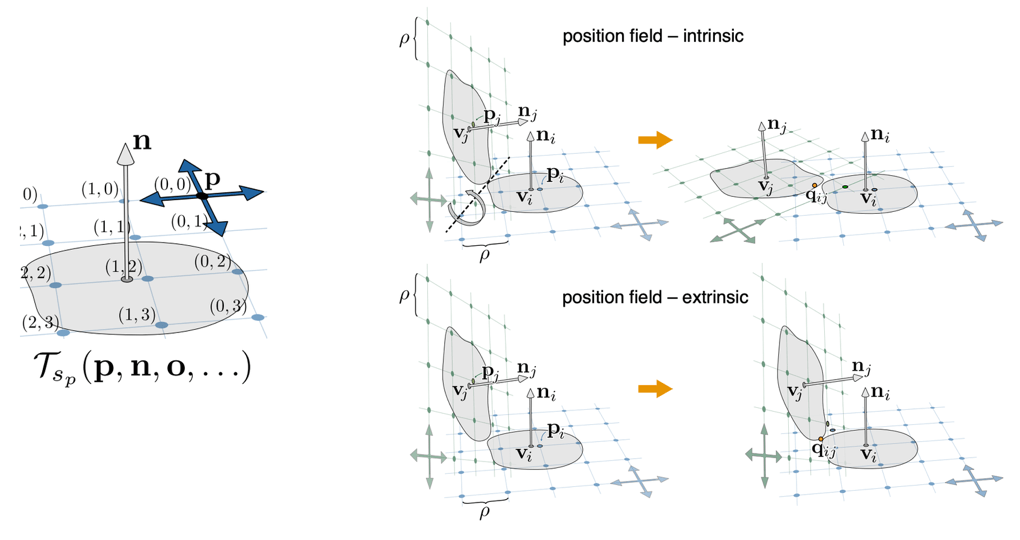
- \({\cal T}_4(p,n,o)\) 是商群 \(\R^2/\Z^2\) 的元素, 该商群称为 \(v\) 处的 \(4\)-位置对称群 (\(4\)-PoSy group).
衡量相邻两个顶点的位置平滑性同样有两种办法:
(intrinsic) 将两个网格旋转到同一个平面后, 计算最近两个格点的距离平方: \[ E(P,t) := \sum_{(i,j)\in E({\cal K})} \| p_i - {\sf Rotate}({\cal T}_4(p_j,n_j,o_j,t_{ji})) \|^2, \] 其中 \(t_{ji}\in\Z^2\) 用于记录 \({\cal T}_4(p_j,n_j,o_j)\) 旋转后的哪个格点距离 \(p_i\) 最近. 要确定 \(t_{ji}\), 只需遍历 \(p_i\) 所在格子的四个格点即可.
(extrinsic) 不旋转, 直接计算最近的两个个点的距离平方: \[ E_{\sf e}(P,t) := \sum_{(i,j)\in E({\cal K})} \| {\cal T}_4(p_i,n_i,o_i,t_{ij}) - {\cal T}_4(p_j,n_j,o_j,t_{ji}) \|^2, \] 其中 \((t_{ij},t_{ji})\in\Z^2\). 要确定 \((t_{ij},t_{ji})\), 并不需要枚举无穷多种组合, 只需考虑 \(v_i,v_j\) 处的切平面以及 \(n_i,n_j\) 所确定的平面, 这三者的交点 \(q_{ij}\) 所在的格子即可, 共 \(4\times4\) 种情况.
Intrinsic 和 extrinsic 的优化结果如下:
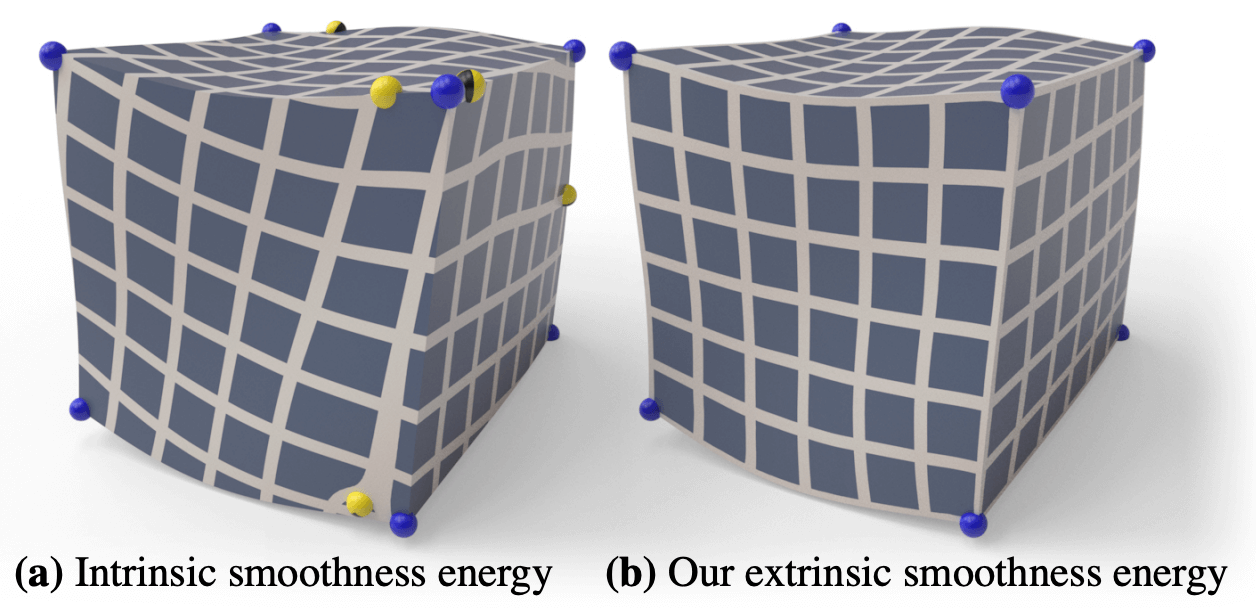
8.1.3 迭代与网格抽取
为了避免 GS 迭代陷入局部最小值, 论文采用由粗到细的优化策略. 算法首先把输入的三角形网格按照逐渐简化, 得到不同分辨率的网格. 接着, 算法首先在最低分辨率的网格上进行 GS 迭代, 将结果作为更高一级分辨率迭代的初始值, 以此类推, 最终可以达到较好的结果.
得到了位置场之后, 可以按照如下规则抽取四面体网格. 四面体网格 \({\cal Q}\) 的顶点是所有 \(v_i\) 所对应的 \(p_i\) 的集合. 作为初始化, \(p_i,p_j\) 在 \({\cal Q}\) 中有边相连当且仅当 \(t_{ij}\) 是单位整数向量 (\((0,\pm1)\) 或 \((\pm1,0)\)).
由于三角形网格 \({\cal K}\) 中的很多边 \((v_i,v_j)\) 都很短 (假设 \({\cal K}\) 足够细分), 有 \(t_{ij}=-t_{ji}\) 或者 \(t_{ij}=0\) (即它们对应同一个整数格点), 这意味着 \(p_i,p_j\) 应当在 \({\cal Q}\) 中视作同一个顶点. 我们按照如下策略将其合并:
- 我们记下所有这些顶点对 \((v_i,v_j)\), 并按照距离 \(\|p_i-p_j\|\) 升序排序.
- 遍历这些顶点对 \((v_i,v_j)\),
- 若 \(p_i,p_j\) 已经有边相连, 则暂时不做操作.
- 若 \(p_i,p_j\) 不相连, 则将 \(p_i,p_j\) 合并.
8.2 整体优化算法
上面提到的局部优化算法的原理和实现都不困难, 运行效率也很高. 但局部优化的一个缺点是会产生较多的奇点 (singularity, 即度数不为 \(4\) 的顶底). 为了得到质量更高的四边形网格, 可以采用整体优化算法.